Simple, Fast, and Accurate Broadband Complex Permittivity Characterization Algorithm: Methodology and Experimental Validation from 140 GHz up to 220 GHz
Abstract
:1. Introduction
2. Theories and Algorithms
2.1. Circuit Theory of the Sensing Device
2.2. Characterization Algorithm
3. Device Fabrication and Measurements
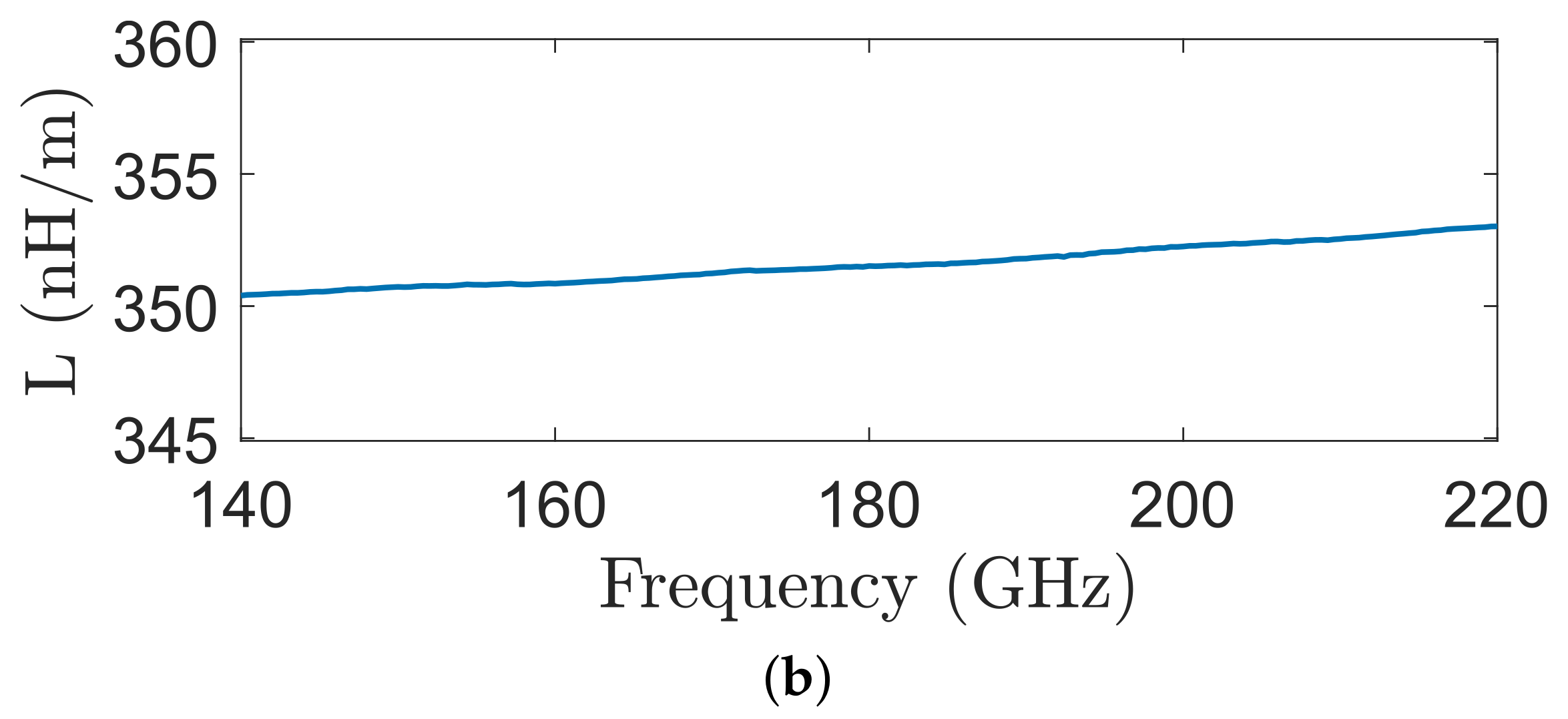
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MUT | material under test |
| TL | transmission line |
| CPW | coplanar waveguide |
| VNA | vector network analyzer |
| p.u.l | per unit length |
| GSG | signal-ground-signal |
| TRL | thru-reflect-line |
| DI | de-ionized |
| FEM | finite element method |
References
- Yeo, J.; Lee, J.I. Slot-loaded microstrip patch sensor antenna for high-sensitivity permittivity characterization. Electronics 2019, 8, 502. [Google Scholar] [CrossRef] [Green Version]
- Sethi, W.; Ibrahim, A.; Issa, K.; Albishi, A.; Alshebeili, S. A new approach to determining liquid concentration using multiband annular ring microwave sensor and polarity correlator. Electronics 2020, 9, 1616. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, G.H.; Mohyuddin, W.; Choi, H.C.; Kim, K.W. Design of an ultra-wideband microstrip-to-slotline transition on low-permittivity substrate. Electronics 2020, 9, 1329. [Google Scholar] [CrossRef]
- Kawarasaki, M.; Tanabe, K.; Terasaki, I.; Fujii, Y.; Taniguchi, H. Intrinsic enhancement of dielectric permittivity in (Nb + In) co-doped TiO2 single crystals. Sci. Rep. 2017, 7, 5351. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.; Zhang, X.; Zhang, X.; Cui, H.L. Accurate determination of dielectric permittivity of polymers from 75 GHz to 1.6 THz using both S-parameters and transmission spectroscopy. Appl. Opt. 2017, 56, 3287–3292. [Google Scholar] [CrossRef]
- Bao, X.; Ocket, I.; Bao, J.; Liu, Z.; Puers, B.; Schreurs, D.M.P.; Nauwelaers, B. Modeling of coplanar interdigital capacitor for microwave microfluidic application. IEEE Trans. Microw. Theory Tech. 2019, 67, 2674–2683. [Google Scholar] [CrossRef]
- Ivanov, A.; Agliullin, T.; Laneve, D.; Portosi, V.; Vorobev, A.; Nigmatullin, R.R.; Nasybullin, A.; Morozov, O.; Prudenzano, F.; D’Orazio, A.; et al. Design and characterization of a microwave planar sensor for dielectric assessment of vegetable oils. Electronics 2019, 8, 1030. [Google Scholar] [CrossRef] [Green Version]
- Itami, G.; Sakai, O.; Harada, Y. Two-dimensional imaging of permittivity distribution by an activated meta-structure with a functional scanning defect. Electronics 2019, 8, 239. [Google Scholar] [CrossRef] [Green Version]
- Chao, H.W.; Chen, H.H.; Chang, T.H. Measuring the complex permittivities of plastics in irregular shapes. Polymers 2021, 13, 2658. [Google Scholar] [CrossRef]
- Ermilova, E.; Bier, F.F.; Hölzel, R. Dielectric measurements of aqueous DNA solutions up to 110 GHz. Phys. Chem. Chem. Phys. 2014, 16, 11256–11264. [Google Scholar] [CrossRef]
- Bao, X.; Zhang, M.; Ocket, I.; Liu, Z.; Nauwelaers, B.; Schreurs, D. Impact of measurement uncertainty on modeling of dielectric relaxation in aqueous solutions. IEEE Trans. Microw. Theory Tech. 2021, 69, 4082–4092. [Google Scholar] [CrossRef]
- Wang, H.C.; Zyuzin, A.; Mamishev, A.V. Measurement of coating thickness and loading using concentric fringing electric field sensors. IEEE Sens. J. 2013, 14, 68–78. [Google Scholar] [CrossRef]
- Ma, J.; Wu, Z.; Xia, Q.; Wang, S.; Tang, J.; Wang, K.; Guo, L.; Jiang, H.; Zeng, B.; Gong, Y. Complex permittivity measurement of high-Loss biological material with improved cavity perturbation method in the range of 26.5–40 GHz. Electronics 2020, 9, 1200. [Google Scholar] [CrossRef]
- Rocco, G.M.; Barmuta, P.; Bao, X.; Schreurs, D.; Bozzi, M. Efficient approach for dielectric permittivity measurements of liquids adopting a 3D-printed cavity resonator. Microw. Opt. Technol. Lett. 2021, 63, 2797–2802. [Google Scholar] [CrossRef]
- Tiwari, N.; Jha, A.; Singh, S.; Akhter, Z.; Varshney, P.; Akhtar, M.J. Generalized multimode SIW cavity-based sensor for retrieval of complex permittivity of materials. IEEE Trans. Microw. Theory Tech. 2018, 66, 3063–3072. [Google Scholar] [CrossRef]
- Bao, X.; Zhang, M.; Ocket, I.; Bao, J.; Kil, D.; Liu, Z.; Puers, R.; Schreurs, D.; Nauwelaers, B. Integration of interdigitated electrodes in split-ring resonator for detecting liquid mixtures. IEEE Trans. Microw. Theory Tech. 2020, 68, 2080–2089. [Google Scholar] [CrossRef]
- Raveendran, A.; Raman, S. Complex permittivity extraction of planar dielectrics using a noninvasive microwave transmission line resonant technique. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Jiang, Q.; Yu, Y.; Zhao, Y.; Zhang, Y.; Liu, L.; Li, Z. Ultra-compact effective localized surface plasmonic sensor for permittivity measurement of aqueous ethanol solution with high sensitivity. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Crupi, G.; Bao, X.; Babarinde, O.J.; Schreurs, D.M.P.; Nauwelaers, B. Biosensor using a one-port interdigital capacitor: A resonance-based investigation of the permittivity sensitivity for microfluidic broadband bioelectronics applications. Electronics 2020, 9, 340. [Google Scholar] [CrossRef] [Green Version]
- Shim, J.Y.; Chung, J.Y. Complex permittivity measurement of artificial tissue emulating material using open-ended coaxial probe. IEEE Sens. J. 2020, 20, 4688–4693. [Google Scholar] [CrossRef]
- Casacuberta, P.; Muñoz-Enano, J.; Vélez, P.; Su, L.; Gil, M.; Martín, F. Highly sensitive reflective-mode defect detectors and dielectric constant sensors based on open-ended stepped-impedance transmission lines. Sensors 2020, 20, 6236. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, F.J.F.; Pinto, A.G.; Mesquita, R.C.; Silva, E.J.; Brancaccio, A. Free-space materials characterization by reflection and transmission measurements using frequency-by-frequency and multi-frequency algorithms. Electronics 2018, 7, 260. [Google Scholar] [CrossRef] [Green Version]
- Ghodgaonkar, D.; Varadan, V.; Varadan, V.K. Free-space measurement of complex permittivity and complex permeability of magnetic materials at microwave frequencies. IEEE Trans. Instrum. Meas. 1990, 39, 387–394. [Google Scholar] [CrossRef]
- Janezic, M.D.; Williams, D.F. Permittivity characterization from transmission-line measurement. In Proceedings of the 1997 IEEE MTT-S International Microwave Symposium Digest, Denver, CO, USA, 8–13 June 1997; Volume 3, pp. 1343–1346. [Google Scholar]
- Janezic, M.D.; Williams, D.F.; Blaschke, V.; Karamcheti, A.; Chang, C.S. Permittivity characterization of low-k thin films from transmission-line measurements. IEEE Trans. Microw. Theory Tech. 2003, 51, 132–136. [Google Scholar] [CrossRef]
- Grenier, K.; Dubuc, D.; Poleni, P.E.; Kumemura, M.; Toshiyoshi, H.; Fujii, T.; Fujita, H. Integrated broadband microwave and microfluidic sensor dedicated to bioengineering. IEEE Trans. Microw. Theory Tech. 2009, 57, 3246–3253. [Google Scholar] [CrossRef]
- Bao, X.; Ocket, I.; Bao, J.; Doijen, J.; Zheng, J.; Kil, D.; Liu, Z.; Puers, B.; Schreurs, D.; Nauwelaers, B. Broadband dielectric spectroscopy of cell cultures. IEEE Trans. Microw. Theory Tech. 2018, 66, 5750–5759. [Google Scholar] [CrossRef]
- Booth, J.C.; Orloff, N.D.; Mateu, J.; Janezic, M.; Rinehart, M.; Beall, J.A. Quantitative permittivity measurements of nanoliter liquid volumes in microfluidic channels to 40 GHz. IEEE Trans. Instrum. Meas. 2010, 59, 3279–3288. [Google Scholar] [CrossRef]
- Costa, F.; Borgese, M.; Degiorgi, M.; Monorchio, A. Electromagnetic characterisation of materials by using transmission/reflection (T/R) devices. Electronics 2017, 6, 95. [Google Scholar] [CrossRef] [Green Version]
- Hasar, U.C.; Westgate, C.R. A broadband and stable method for unique complex permittivity determination of low-loss materials. IEEE Trans. Microw. Theory Tech. 2009, 57, 471–477. [Google Scholar] [CrossRef]
- Minteer, S.D. Microfluidic Techniques: Reviews and Protocols; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 321. [Google Scholar]
- Stojanović, G.; Paroški, M.; Samardžić, N.; Radovanović, M.; Krstić, D. Microfluidics-based four fundamental electronic circuit elements resistor, inductor, capacitor and memristor. Electronics 2019, 8, 960. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Orloff, N.D.; Little, C.A.; Zhao, W.; Booth, J.C.; Williams, D.F.; Ocket, I.; Schreurs, D.M.P.; Nauwelaers, B. Hybrid characterization of nanolitre dielectric fluids in a single microfluidic channel up to 110 GHz. IEEE Trans. Microw. Theory Tech. 2017, 65, 5063–5073. [Google Scholar] [CrossRef]
- Lee, M.Q.; Nam, S. An accurate broadband measurement of substrate dielectric constant. IEEE Microw. Guid. Wave Lett. 1996, 6, 168–170. [Google Scholar]
- Bao, X.; Liu, S.; Ocket, I.; Bao, J.; Schreurs, D.; Zhang, S.; Cheng, C.; Feng, K.; Nauwelaers, B. A general line–line method for dielectric material characterization using conductors with the same cross-sectional geometry. IEEE Microw. Wirel. Components Lett. 2018, 28, 356–358. [Google Scholar] [CrossRef]
- Farcich, N.J.; Salonen, J.; Asbeck, P.M. Single-length method used to determine the dielectric constant of polydimethylsiloxane. IEEE Trans. Microw. Theory Tech. 2008, 56, 2963–2971. [Google Scholar] [CrossRef]
- Lorenz, H.; Despont, M.; Fahrni, N.; LaBianca, N.; Renaud, P.; Vettiger, P. SU-8: A low-cost negative resist for MEMS. J. Micromech. Microeng. 1997, 7, 121. [Google Scholar] [CrossRef]
- Marks, R.B.; Williams, D.F. A general waveguide circuit theory. J. Res. Natl. Inst. Stand. Technol. 1992, 97, 533–562. [Google Scholar] [CrossRef]
- Williams, D.F.; Marks, R.B. Accurate transmission line characterization. IEEE Microw. Guid. Wave Lett. 1993, 3, 247–249. [Google Scholar] [CrossRef]
- Bao, X.; Bao, J.; Ocket, I.; Liu, S.; Schreurs, D.; Kil, D.; Liu, Z.; Zhang, M.; Puers, R.; Nauwelaers, B. A simplified dielectric material characterization algorithm for both liquids and solids. IEEE Trans. Electromagn. Compat. 2018, 61, 1639–1646. [Google Scholar] [CrossRef]
- Marks, R.B. A multiline method of network analyzer calibration. IEEE Trans. Microw. Theory Tech. 1991, 39, 1205–1215. [Google Scholar] [CrossRef] [Green Version]
- Williams, D. StatistiCAL Software Package; National Institute of Standards and Technology: Gaithersburg, MA, USA.
- Ellison, W. Permittivity of pure water, at standard atmospheric pressure, over the frequency range 0–25 THz and the temperature range 0–100 °C. J. Phys. Chem. Ref. Data 2007, 36, 1–18. [Google Scholar] [CrossRef]
- Bao, X.; Liu, S.; Ocket, I.; Bao, J.; Kil, D.; Zhang, M.; Puers, B.; Schreurs, D.; Nauwelaers, B. A multiline multimaterial calibration method for liquid characterization. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 732–734. [Google Scholar] [CrossRef]





| Coefficient | Value | Coefficient | Value | Coefficient | Value |
|---|---|---|---|---|---|
| 79.42385 | 3.611638 | 132.6248 | |||
| 0.004319728 | 0.01231281 | ||||
| 1.352835 × | 1.005472 × | ||||
| 653.3092 | 743.0733 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, X.; Wang, L.; Wang, Z.; Zhang, J.; Zhang, M.; Crupi, G.; Zhang, A. Simple, Fast, and Accurate Broadband Complex Permittivity Characterization Algorithm: Methodology and Experimental Validation from 140 GHz up to 220 GHz. Electronics 2022, 11, 366. https://doi.org/10.3390/electronics11030366
Bao X, Wang L, Wang Z, Zhang J, Zhang M, Crupi G, Zhang A. Simple, Fast, and Accurate Broadband Complex Permittivity Characterization Algorithm: Methodology and Experimental Validation from 140 GHz up to 220 GHz. Electronics. 2022; 11(3):366. https://doi.org/10.3390/electronics11030366
Chicago/Turabian StyleBao, Xiue, Li Wang, Zeyu Wang, Jiabei Zhang, Meng Zhang, Giovanni Crupi, and Anxue Zhang. 2022. "Simple, Fast, and Accurate Broadband Complex Permittivity Characterization Algorithm: Methodology and Experimental Validation from 140 GHz up to 220 GHz" Electronics 11, no. 3: 366. https://doi.org/10.3390/electronics11030366
APA StyleBao, X., Wang, L., Wang, Z., Zhang, J., Zhang, M., Crupi, G., & Zhang, A. (2022). Simple, Fast, and Accurate Broadband Complex Permittivity Characterization Algorithm: Methodology and Experimental Validation from 140 GHz up to 220 GHz. Electronics, 11(3), 366. https://doi.org/10.3390/electronics11030366








