Next Article in Journal
Simulated Hough Transform Model Optimized for Straight-Line Recognition Using Frontier FPGA Devices
Previous Article in Journal
Performance Evaluation of Deep Learning Based Network Intrusion Detection System across Multiple Balanced and Imbalanced Datasets
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Electronics
Volume 11
Issue 4
10.3390/electronics11040516
electronics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Voltage Pulse Driven VO2 Volatile Resistive Transition Devices as Leaky Integrate-and-Fire Artificial Neurons

by
Zhen Xu
1,
Ayrton A. Bernussi
1,* and
Zhaoyang Fan
2,*
1
Department of Electrical and Computer Engineering, Nano Tech Center, Texas Tech University, Lubbock, TX 79409, USA
2
School of Electrical, Computer and Energy Engineering, Arizona State University, Tempe, AZ 85281, USA
*
Authors to whom correspondence should be addressed.
Electronics 2022, 11(4), 516; https://doi.org/10.3390/electronics11040516
Submission received: 28 December 2021 / Revised: 3 February 2022 / Accepted: 6 February 2022 / Published: 9 February 2022
(This article belongs to the Special Issue Synaptic Devices and Artificial Neurons for Neuromorphic Computation)
Browse Figures
Versions Notes

Abstract

:
In a hardware-based neuromorphic computation system, using emerging nonvolatile memory devices as artificial synapses, which have an inelastic memory characteristic, has attracted considerable interest. In contrast, the elastic artificial neurons have received much less attention. An ideal material system that is suitable for mimicking biological neurons is the one with volatile (or mono-stable) resistive change property. Vanadium dioxide (VO2) is a well-known material that exhibits an abrupt and volatile insulator-to-metal transition property. In this work, we experimentally demonstrate that pulse-driven two-terminal VO2 devices behave in a leaky integrate-and-fire (LIF) manner, and they elastically relax back to their initial value after firing, thus, mimicking the behavior of biological neurons. The VO2 device with a channel length of 20 µm can be driven to fire by a single long-duration pulse (>83 µs) or multiple short-duration pulses. We further model the VO2 devices as resistive networks based on their granular domain structure, with resistivities corresponding to the insulator or metallic states. Simulation results confirm that the volatile resistive transition under voltage pulse driving is caused by the formation of a metallic filament in an avalanche-like process, while this volatile metallic filament will relax back to the insulating state at the end of driving pulses. The simulation offers a microscopic view of the dynamic and abrupt filament formation process to explain the experimentally observed LIF behavior. These results suggest that VO2 insulator–metal transition could be exploited for artificial neurons.

1. Introduction

Artificial neural networks (ANNs) are the backbone of machine learning and have been attracting considerable interest [1,2]. In an ANN, a large number of artificial neurons are interconnected by an even larger number of artificial synapses. They are commonly implemented through machine learning software, running on silicon-based hardware, and such an approach has been proved to be successful, evidenced by the rapid development of deep learning applications [3,4]. However, this approach also faces the challenge of limited computation capability, and its low energy efficiency will ultimately constrain the maximum number of neurons that could be simulated to a level less than the human brain, by several orders of magnitudes [5].
In this regard, biological neurons mimic neuromorphic systems, in which artificial neurons and artificial synapses are directly implemented by dedicated devices and have intrinsic superiority [6,7]. Such a hardware-based ANN commonly uses a crossbar architecture to simulate dendrites and axons for interconnections between neurons and conducting wires to simulate the transmission of processed signals from the neuron body down to the axons. Different devices have been proposed to mimic the distributed processing function of individual neurons, and for the distributed memory function of synapses between the pre-synaptic neurons and the post-synaptic neurons. It is true that Si-based devices, including transistors, resistors and capacitors, could be used to build artificial neurons and synapses, but multiple components are needed for one neuron or synapse, giving rise to a complex implementation [8]. Therefore, intense efforts have been devoted to exploring non-Si materials with unique properties that could be exploited to construct artificial neurons and synapses, with a simple configuration for easy large-scale integration [6,9,10,11].
It turns out that nonvolatile memory (NVM) devices, such as those based on nonvolatile resistive switching, are superior candidates for synapses that require learning and memory function, while the artificial neurons might be constructed from certain materials that have mono-state volatile resistive transiting property. The fundamental reason for the difference in artificial neuron and synapse implementation comes from the “elastic” property of neurons vs. “inelastic” synapses [12,13]. It is noted that in an M × N crossbar matrix configuration, the number of synapses is M   ×   N , which is much more than the ( M + N ) number of neurons. Much work has been reported on synapses, with much less attention on artificial neurons [14].
The information processing or signaling function of biologic neurons comes from their dynamic process and spiking behavior that have been described by different models. In particular, the leaky integrate-and-fire (LIF) model has been widely adapted for neuromorphic computation. LIF describes the relationship between the neuronal membrane current as the input, and the membrane voltage as the output. In this model, the input spiking current train is accumulated, accompanied by current leakage through the membrane, to change the membrane potential from the resting value; when this potential reaches a threshold, the neuron fires with a spiking output and the potential of the neuron membrane then “elastically” restores to its resting state after a refractory period. In addition, stochastics is another property of neuron dynamics. Long-term chaotic fluctuations in human brain waves exhibit significant functions in memory recall, inferences, and other high-level brain functions, which are desirable to be mimicked in advanced ANNs. Probabilistic computing, by using truly stochastic artificial neurons but not quasi-random noise generated by extra circuits or algorithms, might be essential for ANNs to achieve high-level brain functions, such as imagination and inference.
Artificial neurons have been created using silicon devices [15,16], which have multiple components, nonideal for dense integration and energy efficiency. Si neurons also lack intrinsic stochastic dynamics and are applied for deterministic computation. Various non-Si materials, investigated for NVM devices, are also in study for developing resistive switching neurons [17], phase change neurons [18], ferroelectric neurons [19], spintronic neurons [20], and others, some of which may also have intrinsic stochastic properties. Each of these approaches have their pros and cons, in terms of complexity (number of devices), energy efficiency, firing rate, on/off ratio, etc. All of them are under investigation, and none have shown performance dominance over others.
It turns out that those materials with abrupt insulator–metal transition (IMT) properties could be good candidates for artificial neurons, including stochastic neurons, as demonstrated by Mott insulators, such as GaTa4Se8 [21] and NbO2 [22]. The volatile and abrupt IMT process in these materials produces “S”-shape negative differential resistance, ensuring the artificial neuron “elastically” restores to its resting state after firing a spike, without using any feedback resetting circuit. With proper designs using a few components, many functions of biological neurons can be emulated. The random conductive filament formation makes them truly stochastic. Taken together, Mott insulators could be an ideal candidate for biologically plausible and stochastic artificial neurons.
In this work, we investigate vanadium dioxide (VO2) based two-terminal devices that show an LIF behavior. VO2 has attracted much attention due to its IMT at ~67 °C, which results in an abrupt electrical resistivity change, by 3–5 orders of magnitude, along with significant changes in the index of refraction [23]. Besides thermally triggering IMT, optical, electrical, mechanical and doping have all been reported as successfully inducing the transition [24,25]. This unusual phenomenon has been exploited in various applications, such as smart window, optical storage, switch devices, and THz modulators [26,27,28,29,30]. Exploiting VO2 for neuromorphic and quantum computations are also in progress [31,32,33,34,35]. The volatile and abrupt features of its IMT may suggest its LIF signature. Here, we apply electrical pulses to induce the IMT in two-terminal VO2 devices, demonstrating its LIF function for artificial neuron applications [36]. We further conduct numerical simulation to explain the observed phenomena.

2. Materials and Methods

VO2 thin films (~120 nm thick) were prepared by reactive dc magnetron sputtering of a vanadium metal target (99.9% purity) in an Ar/O2 gas on c-cut sapphire substrates, as previously reported [37]. Briefly, the substrate temperature was heated to 600 °C. The pressure of the gas mixture was maintained at 3 mTorr with 6% O2/Ar flow ratio, which translates to O2 and Ar flow rates of ~1.05 and ~17.43 sccm, respectively. The sputtering power was controlled at ~130 watt for the 2-inch target to maintain a deposition rate of 2 nm/min. After growth, the temperature was ramped down at a rate of 5 °C/min in the same gas environment. No post-growth annealing was conducted for the VO2 films. The material quality was characterized using scanning electron microscopy (SEM) and X-ray diffraction (XRD) analysis, and its temperature-dependent electrical resistivity was measured using the Van der Pauw method. Two-terminal VO2 devices were fabricated via photolithography patterning, with Ti/Au deposited by e-beam evaporation as the metal contact. Driven by voltage pulses, these devices were characterized to confirm their LIF behavior. Using a resistive network model and considering the field effect on the IMT, the metallic filament formation process and the leak, integration, and fire behavior of VO2 devices driven by voltage pulses were simulated in MATLAB.

3. Results

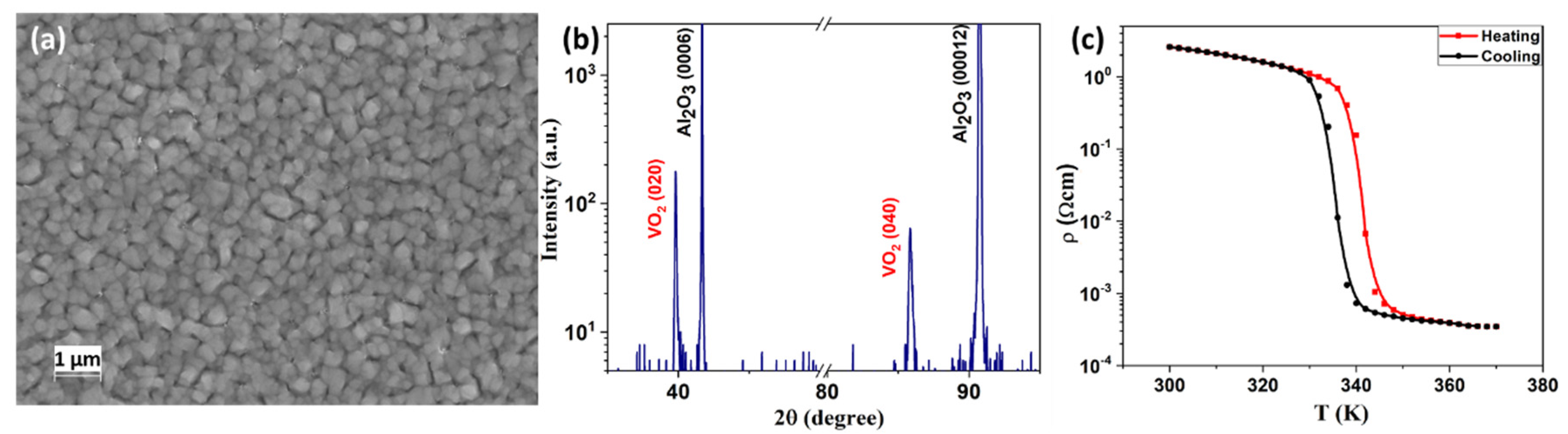
3.1. VO2 Material Properties

As shown in the SEM image in Figure 1a, the deposited VO2 film has a granular morphology with a grain size ~100 nm, and several small grains aggregate into a large cluster with a dimension up to around half a micrometer. XRD measurement (Figure 1b) confirms the monocrystalline structure of the VO2 film, with monoclinic (020) as the growth plane on the c-cut sapphire substrate. The temperature-dependent resistivity of the VO2 thin film is shown in Figure 1c. The resistivity has more than three orders of magnitude change across its IMT, which occurs around 342 K (or 69 °C). This transition is relatively abrupt, with a small hysteresis window of 3–4 K.

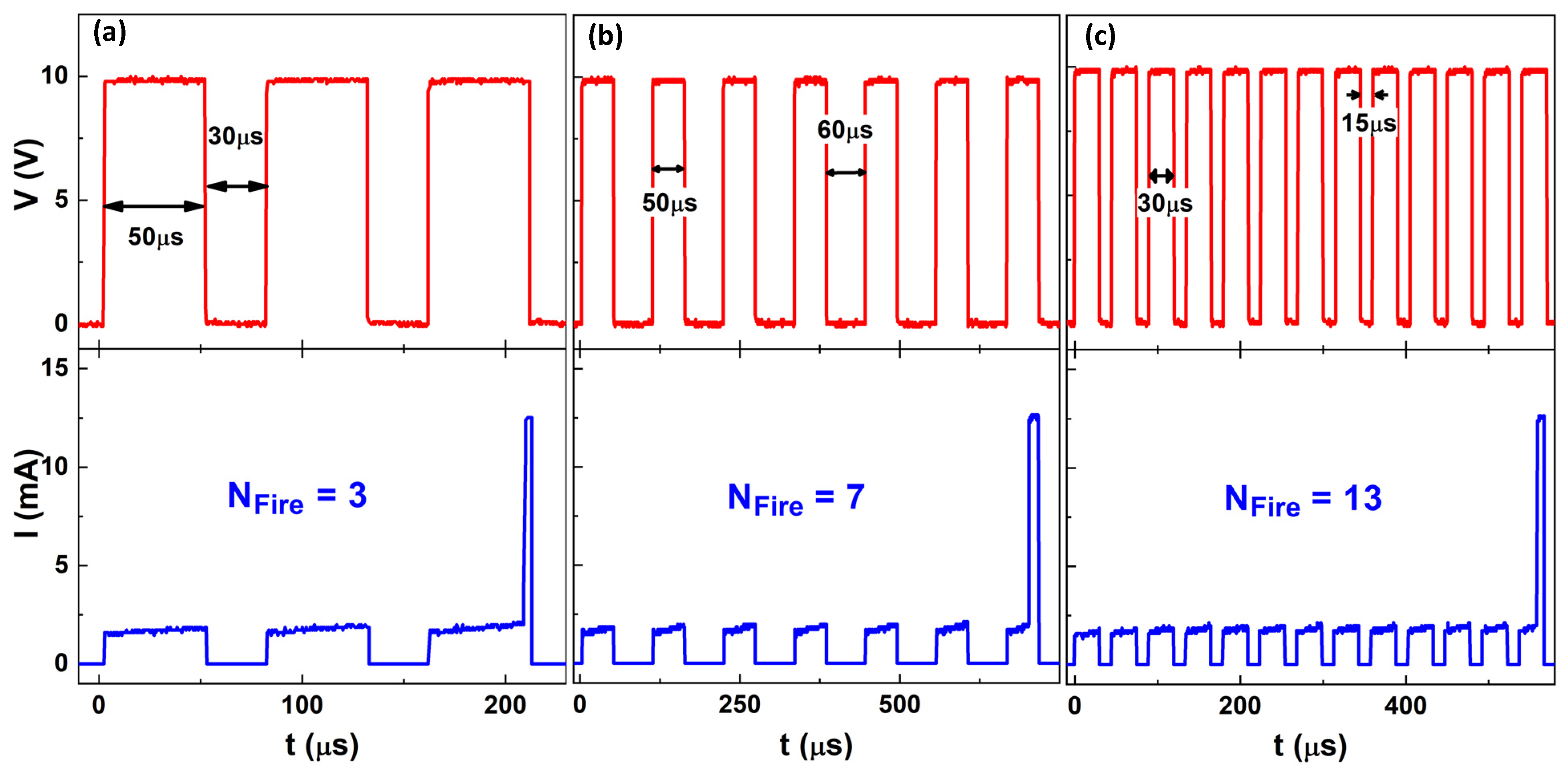
3.2. VO2 Behavior under Voltage Pulses

In two-terminal VO2 devices, the abrupt IMT can also be triggered by electric pulses above a threshold electric field. The experimental circuit is shown schematically in Figure 2a, where a two-terminal VO2 device under test (DUT) is protected by a current-limiting resistor (RL) of 5 kΩ and the voltage drop on the DUT is monitored by a digital oscilloscope. A representative example of voltage pulse-driven resistive transition behavior of VO2 devices at room temperature is presented in Figure 2b, where the VO2 DUT has a channel length of 20 µm and a single 10 V and 100 µs driving pulse (VD) is applied to the DUT and RL. After a delay time of 83 µs, the voltage across the DUT decreases by only 0.4 V, but then it abruptly decreases from 8.5 V to 0.6 V. Correspondingly, the current in the circuit increases abruptly during the 83–100 µs time range, in analogy to the firing of a biological neuron (Figure 2c). This current firing is a direct consequence of the resistive transition of the DUT from a high to a low resistance state, as verified in Figure 2d. When a bias is applied, VO2 resistance initially only shows a slight reduction due to sparse individual metallic domain formation; then, a filamentary metallic conductive path is abruptly formed, shortening the two electrodes, resulting in dramatic diminishing in the resistance and increase in the current. This firing delay time depends on the amplitude of the driving pulse and the separation between the two electrodes. The observed current spiking, firing delay time (tFire), and only a small change in resistance during this delay time (Figure 2b–d) suggest that the VO2 device behaves similarly to the integrating function of a biological neuron.
With the abrupt formation of a filamentary conductive path bridging the two electrodes, the VO2 device abruptly jumps to its low resistance state, firing a large current in the circuit. On the other hand, this metastable filamentary path can also be easily disrupted at the end of the driving pulse; the device will then recede back to its high resistive state after a short delay. Unlike the resistive random-access memory (ReRAM) devices that have high and low two stable resistance states and the resistive switching is nonvolatile, the resistive transition in VO2 under pulse driven is volatile, with the high resistance as the stable mono-state. However, the VO2 device does need time to transit from its low resistance to the stable high resistance state. This is caused by the thermally activated relaxation of the metallic domains in the conductive filament [38]. We speculate that immediately after the driving pulse is null, the device resistance will abruptly soar up as the consequence of the conductive filament breaking up, following which it will slowly relax back to its high resistance value, as all metallic domains transit to the insulating state by thermally surmounting an energy barrier. It is this relaxation time (tr) that is corelated to the leaky performance of the VO2 device. A fast relaxation time corresponds to a large leak, or a rapid transition of VO2 domains from the metallic to the insulating phase, clearly indicating that this parameter is dependent on the material properties and device design. The device temperature is also a key parameter, since it is a thermally activated process.
Depending on the amplitude of the voltage pulse, a given VO2 device needs different tFire, during which individual metallic domains grow, until a continuous metallic filament is formed to fire. This observation indicates that the growth of metallic domains is an accumulative process, which brings out another feature of the LIF neuromorphic functionality—integration. To better understand this behavior and to provide a direct analogy to the LIF characteristic of biological neurons, we injected a train of electric pulses into the DUT. For a defined pulse amplitude (10 V in this work), as long as the pulse duration (ton) is shorter than tFire (~83 µs), multiple pulses will be required for the DUT firing. Meanwhile, the pulse off time duration (toff) must also be shorter than the metallic domain relaxation time (tr), to ensure a net growth in the quantity of individual metallic domains before a threshold is reached for the abrupt formation of a conductive filament. Figure 3 shows the voltage waveforms applied to a VO2 device using a fixed 10 V amplitude but different duty cycles and the corresponding device current response. In Figure 3a, with the on/off 50/30 µs pulse train, the VO2 device fires in the 3rd pulse, while for the on/off 50/60 µs pulse train, it does not fire until the 7th pulse (Figure 3b). When the pulse train is changed to 30/15 µs, the number of pulses required for firing further extends to 13 (Figure 3c). These three examples show that the total pulse duration necessary to trigger the firing depends on the pulse train on/off setting. The fact that the firing can be triggered by pulses with time duration shorter than tFire suggests an integration effect of short pulses in the VO2 device. Moreover, the sheer fact that the total pulse duration before firing is much longer than tFire reveals the leaky behavior of the device, which is further corroborated by noting that, for pulses with the same ton = 50 µs, when toff is extended from 30 µs to 60 µs, the needed pulses to fire (NFire) increases from three to seven.

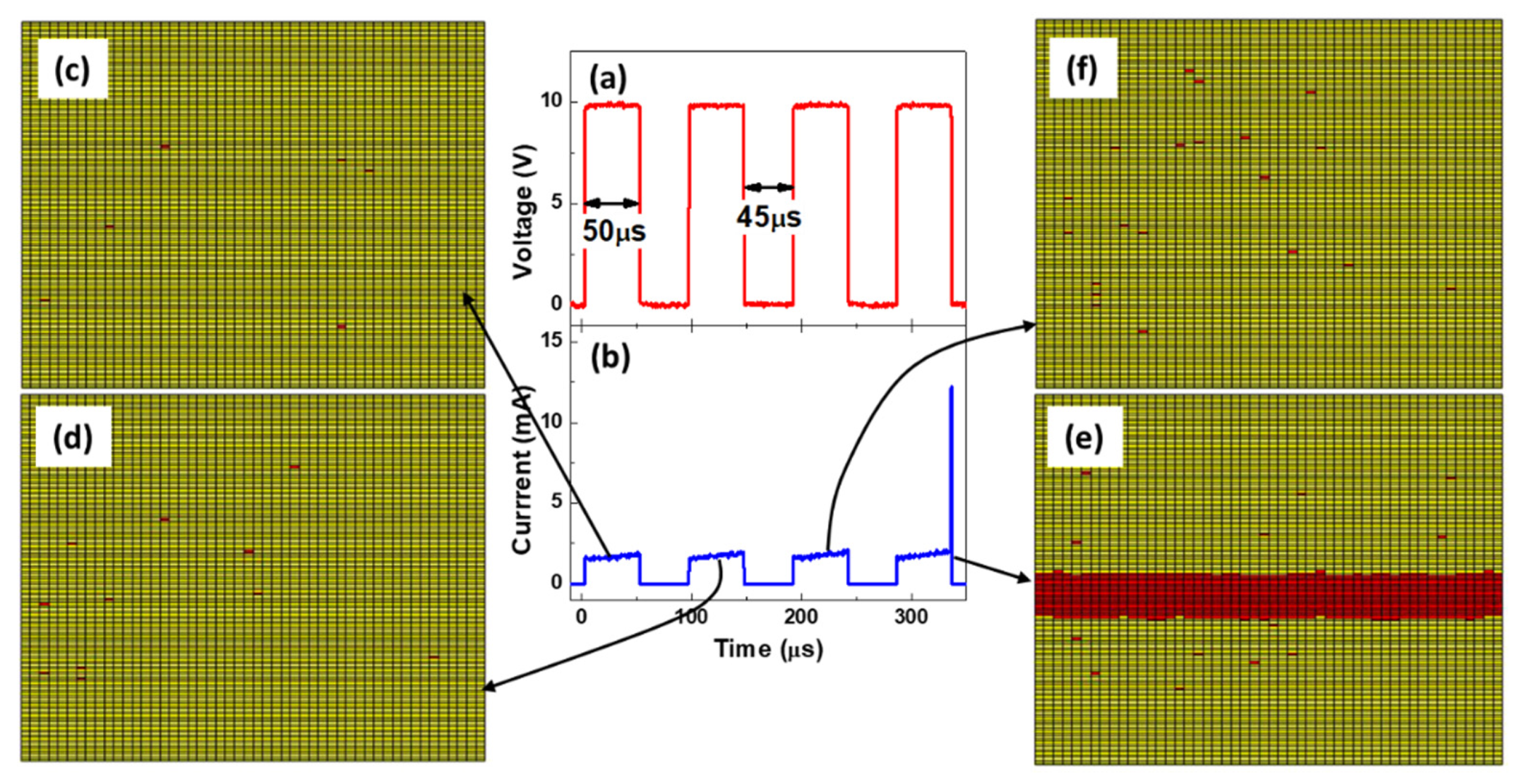
3.3. Simulating VO2 LIF Behavior

To visualize the voltage-driven phase transition process in the VO2 devices and understand the mechanism of leaky-integral and fire function, a 2D resistor network model [39] was developed to simulate its resistance transition behavior and particularly, the avalanche process of the conductive filament formation. Considering the granular structure of the VO2 film, the device can be modeled as a multi-domain-based resistive network, as shown in Figure 4a, where each domain is represented by a pixel. Following Refs. [40,41], each domain contains four identical resistors, which connect to the neighboring domains. The average voltage across a domain (ΔV) is formulated as follows:
Δ V = ( ( V 1 − V 3 ) 2 + ( V 2 − V 4 ) 2 ) 1 / 2
As illustrated in Figure 4b, at room temperature, without voltage biasing, VO2 is more stable in the insulating phase than the metallic phase. As the voltage bias is applied, the electric field energy will raise the energy level of the insulting phase, thus reducing the corresponding energy barrier and enhancing the probability of insulator–metal transition (PIMT), while that for metal–insulator transition PMIT does not change, shown below (Figure 4c):
P I M T = e − ( E B − q Δ V ) / k T
P M I T = e − ( E B − E M ) / k T
where E B is the energy barrier for the IMT and EM is the energy difference between the two phases, while q, k and T are the electronic charge, Boltzmann constant, and temperature, respectively.
The simulation was conducted in MATLAB. In the time sweeping used in the simulation, the voltage across each domain and its phase state are calculated. Once a domain switches from the insulating phase to the metallic phase, its reduced ΔV will result in slightly higher voltage drop on its surrounding insulating domains. According to Equation (2), a higher voltage drop on a domain will enhance its probability to switch into the metallic phase. Therefore, although initially very few random pixels are in the metallic phase, as their density increases to a certain threshold, the positive feedback will suddenly cause an avalanching process, leading to the metallic conducting filament formation along the electric field direction (Figure 4d), as revealed by the simulation results in Figure 5.
In these simulations, we used a resistance network comprising of 150 × 50 pixels. All the parameters, including the external voltage bias and load resistance, were set to the same as those to test the device in Figure 2. We considered 10,000 simulation steps. After the bias is applied on the device (Figure 5a), the VO2 device enters the “integration” stage. Only a few random domains become metallic (Figure 5c), and its number grows very slowly, which only has trivial influence on the total resistance of the device. However, after the bias is applied for enough time, a small number of metallic domains are formed on the same rows (see Figure 5d) and this number will dramatically increase, resulting in the formation of a narrow metallic filament (see Figure 5d). Once this filament is created, both the resistance of the VO2 device and the applied voltage across it are dramatically reduced, accompanied by a current flow (“firing”). The newly established dynamic equilibrium will maintain the metallic filament with this current flow; in other words, the ratio of the metallic domains stays at a relatively stable number, as shown in Figure 5b. The phenomena observed in these simulations are in good agreement with the experimental data shown in Figure 2.
This resistor network modeling was also applied to simulate the VO2 LIF behavior, when applying a train of voltage pulses into the device. Figure 6a,b show the applied driving pulses and the corresponding current, experimentally measured. The metallic domain distribution is shown in Figure 6c–f. Initially, the number of metallic domains starts to slowly grow (the integration stage), and some of them switch back to the insulating state particularly when the pulse is off (the leaky stage). When the metallic domains have accumulated enough, an abrupt avalanching process sets in, with a metallic filament created in a short period of time, and a burst current pulse erupts (the firing stage). The simulation clearly reveals that the formation of the metallic filament is a nearly instantaneous event, although a process is needed for a particular series of driven pulses, during which the integrating and leaking processes take place.

4. Discussion

In this work, the experimental results, further verified by numerical modelling, suggest that the electric pulse-driven resistive transition in VO2 is a volatile process with elastic properties. Its elastic properties come from the fact that at the end of the individual driving pulse, in which VO2 fires, it will restore to its original high-resistance state after a short relaxation time. This non-memory property prevents VO2 from being used for synaptic devices that must provide memory function. However, this same volatile resistive transition, combined with the firing delay and the relaxation time, can be prospectively used to implement the leaky integrate-and-fire function, which mimics the basic biological neuron behavior.
In the LIF model of biological neurons, the input spiking current train is accumulated across the membrane capacitor, with the membrane current as the leak channel to change the membrane potential. In our VO2 neuron, which has a simple design, consisting of one single VO2 resistor and a current limiting resistor, the input is the voltage pulse train, which increases the ratio of metallic domains over the total domains in the VO2 device, with the thermal relaxation of metallic domains to insulating domains as the leak channel. When the metallic domain ratio reaches a certain threshold for percolative conducting filament formation, a strong nonlinear avalanche process sets in, causing the device firing with a current pulse generation. The width of this current pulse is determined by the ending edge of the input voltage pulse. Since in the LIF model, and the more general spiking neural network, information is encoded in the timing of spike sequences but not each spike shape, the width of the output current pulse is not critical. However, for energy-efficient computation, this pulse width should be minimized. To improve this simple design, so that the output pulse is more like that of LIF neuron model, an integration capacitor can be included to form a Pearson–Anson relaxation oscillator [43], by exploiting the negative resistive behavior in VO2 when a conductive filament is formed [44].
The LIF neuron model, however, has fewer neuron-computation functions than more accurate biological neuron models [45], such as the Hodgkin–Huxley model, in which, specific voltage-dependent ion channels, one for sodium and another one for potassium, control the flow of those ions through the cell membrane. Similarly, a two-stage VO2 neuron can be designed to implement biologically more plausible neurons [22,35].
The mature digital and analog silicon-based metal oxide semiconductor (MOS) technologies have been used for fabricating Si neurons. However, dozens of MOS transistors and other components are needed for a single neuron, which limits the integration density and energy efficiency. Another critical issue for Si neurons is the lack of intrinsic stochasticity, which hinders them in implementing some complex computational tasks that require stochastic neuronal populations, such as Bayesian inference [18]. In contrast, leveraging the IMT in Mott insulators, including VO2, multifunctional neurons with rich neuronal dynamic behaviors could be designed with very few components to achieve high integration density and energy efficiency. Furthermore, the intrinsic stochastic phenomenon in the VO2 IMT process [46] can also be exploited to emulate the stochastic processes in biological neurons.

5. Conclusions

We performed a study, by combing experimental measurements and simulation, on VO2-based resistive transition devices, aiming for leaky integrate-and-fire model based artificial neurons. The experimental data shows that two-terminal VO2 devices, thanks to their abrupt and volatile insulator-to-metal transition, exhibit the basic LIF spiking neuron characteristic with elasticity. A resistor network model was used to simulate the behavior of the voltage pulse-driven VO2 resistive transition by incorporating the effect of the electric field across each VO2 domain, on their insulator-to-metal transition, under single long pulse or multiple short pulse conditions. The simulations confirm that the volatile and elastic resistive transition under voltage pulse is caused by an avalanche-like creation and relaxation of volatile metallic filament. The simulation offers a microscopic view on the dynamic and abrupt filament formation process to explain its LIF behavior. This study suggests that two-terminal VO2 volatile resistive transition devices could be prospectively used for artificial neurons.

Author Contributions

Conceptualization, Z.X. and Z.F.; methodology, Z.X.; software, Z.X.; resources, A.A.B.; data curation, Z.X.; writing—original draft preparation, Z.X.; writing—review and editing, Z.X., A.A.B. and Z.F.; supervision, A.A.B. and Z.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef] [Green Version]
  2. Kang, M.; Lee, Y.; Park, M. Energy efficiency of machine learning in embedded systems using neuromorphic hardware. Electronics 2020, 9, 1069. [Google Scholar] [CrossRef]
  3. Bouvier, M.; Valentian, A.; Mesquida, T.; Rummens, F.; Reyboz, M.; Vianello, E.; Beigne, E. Spiking neural networks hardware implementations and challenges: A survey. ACM J. Emerg. Technol. Comput. Syst. 2019, 15, 1–35. [Google Scholar] [CrossRef]
  4. Schuman, C.D.; Potok, T.E.; Patton, R.M.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A survey of neuromorphic computing and neural networks in hardware. arXiv 2017, arXiv:1705.06963. [Google Scholar]
  5. Kim, M.-K.; Park, Y.; Kim, I.-J.; Lee, J.-S. Emerging Materials for Neuromorphic Devices and Systems. Iscience 2020, 23, 101846. [Google Scholar] [CrossRef] [PubMed]
  6. Burr, G.W.; Shelby, R.M.; Sebastian, A.; Kim, S.; Kim, S.; Sidler, S.; Virwani, K.; Ishii, M.; Narayanan, P.; Fumarola, A. Neuromorphic computing using non-volatile memory. Adv. Phys. X 2017, 2, 89–124. [Google Scholar] [CrossRef]
  7. Sangwan, V.K.; Hersam, M.C. Neuromorphic nanoelectronic materials. Nat. Nanotechnol. 2020, 15, 517–528. [Google Scholar] [CrossRef]
  8. Poon, C.-S.; Zhou, K. Neuromorphic silicon neurons and large-scale neural networks: Challenges and opportunities. Front. Neurosci. 2011, 5, 108. [Google Scholar] [CrossRef] [Green Version]
  9. Yu, S. Neuro-inspired computing with emerging nonvolatile memorys. Proc. IEEE 2018, 106, 260–285. [Google Scholar] [CrossRef]
  10. Zidan, M.A.; Strachan, J.P.; Lu, W.D. The future of electronics based on memristive systems. Nat. Electron. 2018, 1, 22–29. [Google Scholar] [CrossRef]
  11. Park, J. Neuromorphic Computing Using Emerging Synaptic Devices: A Retrospective Summary and an Outlook. Electronics 2020, 9, 1414. [Google Scholar] [CrossRef]
  12. Kim, K.-H.; Gaba, S.; Wheeler, D.; Cruz-Albrecht, J.M.; Hussain, T.; Srinivasa, N.; Lu, W. A functional hybrid memristor crossbar-array/CMOS system for data storage and neuromorphic applications. Nano Lett. 2011, 12, 389–395. [Google Scholar] [CrossRef] [PubMed]
  13. Jeong, D.S.; Kim, I.; Ziegler, M.; Kohlstedt, H. Towards artificial neurons and synapses: A materials point of view. RSC Adv. 2013, 3, 3169–3183. [Google Scholar] [CrossRef]
  14. Del Valle, J.; Ramírez, J.G.; Rozenberg, M.J.; Schuller, I.K. Challenges in materials and devices for resistive-switching-based neuromorphic computing. J. Appl. Phys. 2018, 124, 211101. [Google Scholar] [CrossRef]
  15. Indiveri, G.; Linares-Barranco, B.; Hamilton, T.J.; Van Schaik, A.; Etienne-Cummings, R.; Delbruck, T.; Liu, S.-C.; Dudek, P.; Häfliger, P.; Renaud, S. Neuromorphic silicon neuron circuits. Front. Neurosci. 2011, 5, 73. [Google Scholar] [CrossRef] [Green Version]
  16. Stoliar, P.; Akita, I.; Schneegans, O.; Hioki, M.; Rozenberg, M. A spiking neuron implemented in VLSI. J. Phys. Commun. 2022, 6, 021001. [Google Scholar] [CrossRef]
  17. Lu, Y.-F.; Li, Y.; Li, H.; Wan, T.-Q.; Huang, X.; He, Y.-H.; Miao, X. Low-power artificial neurons based on Ag/TiN/HfAlOx/Pt threshold switching memristor for neuromorphic computing. IEEE Electron. Device Lett. 2020, 41, 1245–1248. [Google Scholar] [CrossRef]
  18. Tuma, T.; Pantazi, A.; Le Gallo, M.; Sebastian, A.; Eleftheriou, E. Stochastic phase-change neurons. Nat. Nanotechnol. 2016, 11, 693–699. [Google Scholar] [CrossRef]
  19. Dutta, S.; Schafer, C.; Gomez, J.; Ni, K.; Joshi, S.; Datta, S. Supervised learning in all fefet-based spiking neural network: Opportunities and challenges. Front. Neurosci. 2020, 14, 634. [Google Scholar] [CrossRef]
  20. Kurenkov, A.; DuttaGupta, S.; Zhang, C.; Fukami, S.; Horio, Y.; Ohno, H. Artificial neuron and synapse realized in an antiferromagnet/ferromagnet heterostructure using dynamics of spin–orbit torque switching. Adv. Mater. 2019, 31, 1900636. [Google Scholar] [CrossRef]
  21. Stoliar, P.; Tranchant, J.; Corraze, B.; Janod, E.; Besland, M.-P.; Tesler, F.; Rozenberg, M.; Cario, L. A Leaky-Integrate-and-Fire Neuron Analog Realized with a Mott Insulator. Adv. Funct. Mater. 2017, 27, 1604740. [Google Scholar] [CrossRef]
  22. Pickett, M.D.; Medeiros-Ribeiro, G.; Williams, R.S. A scalable neuristor built with Mott memristors. Nature Mater. 2013, 12, 114–117. [Google Scholar] [CrossRef] [PubMed]
  23. Shao, Z.; Cao, X.; Luo, H.; Jin, P. Recent progress in the phase-transition mechanism and modulation of vanadium dioxide materials. NPG Asia Mate. 2018, 10, 581–605. [Google Scholar] [CrossRef] [Green Version]
  24. Shi, R.; Shen, N.; Wang, J.; Wang, W.; Amini, A.; Wang, N.; Cheng, C. Recent advances in fabrication strategies, phase transition modulation, and advanced applications of vanadium dioxide. Appl. Phys. Rev. 2019, 6, 011312. [Google Scholar] [CrossRef]
  25. Karaoglan-Bebek, G.; Hoque, M.; Holtz, M.; Fan, Z.; Bernussi, A. Continuous tuning of W-doped VO2 optical properties for terahertz analog applications. Appl. Phys. Lett. 2014, 105, 201902. [Google Scholar] [CrossRef] [Green Version]
  26. Chen, Z.; Gao, Y.; Kang, L.; Du, J.; Zhang, Z.; Luo, H.; Miao, H.; Tan, G. VO2-based double-layered films for smart windows: Optical design, all-solution preparation and improved properties. Sol. Energy Mater. Sol. Cells 2011, 95, 2677–2684. [Google Scholar] [CrossRef]
  27. Balberg, I.; Trokman, S. High-contrast optical storage in VO2 films. J. Appl. Phys. 1975, 46, 2111–2119. [Google Scholar] [CrossRef]
  28. Stefanovich, G.; Pergament, A.; Stefanovich, D. Electrical switching and Mott transition in VO2. J. Phys. Condens. Matter 2000, 12, 8837. [Google Scholar] [CrossRef]
  29. Xu, Z.; Qin, G.; Bernussi, A.A.; Fan, Z. Electrothermally control of dynamic infrared switching of VO2 thin film on FTO glass. J. Alloys Compd. 2021, 858, 157640. [Google Scholar]
  30. Hoque, M.N.F.; Karaoglan-Bebek, G.; Holtz, M.; Bernussi, A.A.; Fan, Z. High performance spatial light modulators for terahertz applications. Opt. Commun. 2015, 350, 309–314. [Google Scholar] [CrossRef]
  31. Dutta, S.; Khanna, A.; Assoa, A.; Paik, H.; Schlom, D.; Toroczkai, Z.; Raychowdhury, A.; Datta, S. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators. Nat. Electron. 2021, 4, 502–512. [Google Scholar] [CrossRef]
  32. Shi, Y.; Duwel, A.E.; Callahan, D.M.; Sun, Y.; Hong, F.A.; Padmanabhan, H.; Gopalan, V.; Engel-Herbert, R.; Ramanathan, S.; Chen, L.-Q. Dynamics of voltage-driven oscillating insulator-metal transitions. Phys. Rev. B 2021, 104, 064308. [Google Scholar] [CrossRef]
  33. Bohaichuk, S.M.; Kumar, S.; Pitner, G.; McClellan, C.J.; Jeong, J.; Samant, M.G.; Wong, H.-S.P.; Parkin, S.S.; Williams, R.S.; Pop, E. Fast spiking of a Mott VO2–carbon nanotube composite device. Nano Lett. 2019, 19, 6751–6755. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Pattanayak, M.; Hoque, M.N.F.; Zhao, Y.; Fan, Z.; Bernussi, A.A. Tunable VO2 relaxation oscillators for analog applications. Semicond. Sci. Technol. 2019, 34, 105028. [Google Scholar] [CrossRef]
  35. Yi, W.; Tsang, K.K.; Lam, S.K.; Bai, X.; Crowell, J.A.; Flores, E.A. Biological plausibility and stochasticity in scalable VO2 active memristor neurons. Nat. Commun. 2018, 9, 1–10. [Google Scholar] [CrossRef]
  36. Belyaev, M.; Velichko, A. A Spiking Neural Network Based on the Model of VO2–Neuron. Electronics 2019, 8, 1065. [Google Scholar] [CrossRef] [Green Version]
  37. Zhao, Y.; Hwan Lee, J.; Zhu, Y.; Nazari, M.; Chen, C.; Wang, H.; Bernussi, A.; Holtz, M.; Fan, Z. Structural, electrical, and terahertz transmission properties of VO2 thin films grown on c-, r-, and m-plane sapphire substrates. J. Appl. Phys. 2012, 111, 053533. [Google Scholar] [CrossRef]
  38. Zhao, Y.; Hao, J.; Chen, C.; Fan, Z. Electrically controlled metal–insulator transition process in VO2 thin films. Phys. Condens. Matter 2011, 24, 035601. [Google Scholar] [CrossRef]
  39. Poklonski, N.; Kocherzhenko, A.; Benediktovitch, A.; Mitsianok, V.; Zaitsev, A. Simulation of dc conductance of two-dimensional heterogeneous system: Application to carbon wires made by ion irradiation on polycrystalline diamond. Phys. Status Solidi 2006, 243, 1212–1218. [Google Scholar] [CrossRef] [Green Version]
  40. Stoliar, P.; Cario, L.; Janod, E.; Corraze, B.; Guillot-Deudon, C.; Salmon-Bourmand, S.; Guiot, V.; Tranchant, J.; Rozenberg, M. Universal Electric-Field-Driven Resistive Transition in Narrow-Gap Mott Insulators. Adv. Mater. 2013, 25, 3222–3226. [Google Scholar] [CrossRef] [Green Version]
  41. Madan, H.; Jerry, M.; Pogrebnyakov, A.; Mayer, T.; Datta, S. Quantitative mapping of phase coexistence in Mott-Peierls insulator during electronic and thermally driven phase transition. ACS Nano 2015, 9, 2009–2017. [Google Scholar] [CrossRef] [PubMed]
  42. Stoliar, P.; Rozenberg, M.; Janod, E.; Corraze, B.; Tranchant, J.; Cario, L. Nonthermal and purely electronic resistive switching in a Mott memory. Phys. Rev. B 2014, 90, 045146. [Google Scholar] [CrossRef]
  43. Pickett, M.D.; Williams, R.S. Sub-100 fJ and sub-nanosecond thermally driven threshold switching in niobium oxide crosspoint nanodevices. Nanotechnology 2012, 23, 215202. [Google Scholar] [CrossRef] [PubMed]
  44. Pattanayak, M.; Hoque, M.N.F.; Fan, Z.; Bernussi, A.A. Electrical oscillation generation with current-induced resistivity switching in VO2 micro-channel devices. Sci. Technol. Adv. Mater. 2018, 19, 693–701. [Google Scholar] [CrossRef] [Green Version]
  45. Izhikevich, E.M. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070. [Google Scholar] [CrossRef]
  46. Jerry, M.; Ni, K.; Parihar, A.; Raychowdhury, A.; Datta, S. Stochastic insulator-to-metal phase transition-based true random number generator. IEEE Electron. Device Lett. 2017, 39, 139–142. [Google Scholar] [CrossRef]
Electronics 11 00516 g001 550
Figure 1. (a) SEM image and (b) XRD θ-2θ measurement of VO2 thin films grown on c-cut sapphire substrate. (c) Temperature-dependent resistivity showing the IMT of VO2.
Figure 1. (a) SEM image and (b) XRD θ-2θ measurement of VO2 thin films grown on c-cut sapphire substrate. (c) Temperature-dependent resistivity showing the IMT of VO2.
Electronics 11 00516 g001
Electronics 11 00516 g002 550
Figure 2. (a) Schematic of the circuit used to test VO2 devices. An example of VO2 IMT stimulated by a 10 V pulse of 100 µs time duration: (b) applied voltage (red curve) and measured device voltage (blue curve), measured device current (c) and resistance (d), during a 100 µs pulse.
Figure 2. (a) Schematic of the circuit used to test VO2 devices. An example of VO2 IMT stimulated by a 10 V pulse of 100 µs time duration: (b) applied voltage (red curve) and measured device voltage (blue curve), measured device current (c) and resistance (d), during a 100 µs pulse.
Electronics 11 00516 g002
Electronics 11 00516 g003 550
Figure 3. Applied voltage pulse waveforms (top) and measured device current (bottom) for different pulse duty cycles and fixed 10 V amplitude. (a) ton = 50 µs and toff = 30 µs, (b) ton = 50 µs and toff = 60 µs, and (c) ton = 15 µs and toff = 30 µs.
Figure 3. Applied voltage pulse waveforms (top) and measured device current (bottom) for different pulse duty cycles and fixed 10 V amplitude. (a) ton = 50 µs and toff = 30 µs, (b) ton = 50 µs and toff = 60 µs, and (c) ton = 15 µs and toff = 30 µs.
Electronics 11 00516 g003
Electronics 11 00516 g004 550
Figure 4. (a) Resistive network model of the VO2 device under voltage bias used in the simulation. A few random pixels (light red) are shown in the metallic phase. Energy barriers for IMT and MIT without bias (b) and with bias (c). (d) A conducting filament formed between two electrodes, leading to an abrupt decrease in VO2 device resistance. (after [41,42]).
Figure 4. (a) Resistive network model of the VO2 device under voltage bias used in the simulation. A few random pixels (light red) are shown in the metallic phase. Energy barriers for IMT and MIT without bias (b) and with bias (c). (d) A conducting filament formed between two electrodes, leading to an abrupt decrease in VO2 device resistance. (after [41,42]).
Electronics 11 00516 g004
Electronics 11 00516 g005 550
Figure 5. (a) The applied single voltage used in the simulation. (b) The percentage of metallic domain changes with the simulation steps (time elapsed after the bias is applied). (c–e) The distribution of the metallic domains at the different stage after voltage bias is applied (yellow: insulating domains; red: metallic domains).
Figure 5. (a) The applied single voltage used in the simulation. (b) The percentage of metallic domain changes with the simulation steps (time elapsed after the bias is applied). (c–e) The distribution of the metallic domains at the different stage after voltage bias is applied (yellow: insulating domains; red: metallic domains).
Electronics 11 00516 g005
Electronics 11 00516 g006 550
Figure 6. (a) Applied voltage pulse train and (b) measured device current for ton = 50 µs and toff = 45; (b–f) Simulated metallic domain distribution during each of the pulses (yellow: insulating domains; red: metallic domains).
Figure 6. (a) Applied voltage pulse train and (b) measured device current for ton = 50 µs and toff = 45; (b–f) Simulated metallic domain distribution during each of the pulses (yellow: insulating domains; red: metallic domains).
Electronics 11 00516 g006
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Xu, Z.; Bernussi, A.A.; Fan, Z. Voltage Pulse Driven VO2 Volatile Resistive Transition Devices as Leaky Integrate-and-Fire Artificial Neurons. Electronics 2022, 11, 516. https://doi.org/10.3390/electronics11040516

AMA Style

Xu Z, Bernussi AA, Fan Z. Voltage Pulse Driven VO2 Volatile Resistive Transition Devices as Leaky Integrate-and-Fire Artificial Neurons. Electronics. 2022; 11(4):516. https://doi.org/10.3390/electronics11040516

Chicago/Turabian Style

Xu, Zhen, Ayrton A. Bernussi, and Zhaoyang Fan. 2022. "Voltage Pulse Driven VO2 Volatile Resistive Transition Devices as Leaky Integrate-and-Fire Artificial Neurons" Electronics 11, no. 4: 516. https://doi.org/10.3390/electronics11040516

APA Style

Xu, Z., Bernussi, A. A., & Fan, Z. (2022). Voltage Pulse Driven VO2 Volatile Resistive Transition Devices as Leaky Integrate-and-Fire Artificial Neurons. Electronics, 11(4), 516. https://doi.org/10.3390/electronics11040516

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop