Next Article in Journal
Convincing 3D Face Reconstruction from a Single Color Image under Occluded Scenes
Previous Article in Journal
Satellite to Ground Station, Attenuation Prediction for 2.4–72 GHz Using LTSM, an Artificial Recurrent Neural Network Technology
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Electronics
Volume 11
Issue 4
10.3390/electronics11040542
electronics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Survey on Fatigue Life Prediction of BGA Solder Joints

by
Baojun Qiu
1,†,
Jingang Xiong
2,†,
Han Wang
2,
Shuai Zhou
1,*,
Xiuding Yang
2,
Zhengpei Lin
2,
Maolin Liu
2 and
Nian Cai
3,*
1
China Electronic Product Reliability and Environmental Testing Research Institute, Guangzhou 510006, China
2
School of Mechanical and Electrical Engineering, Guangdong University of Technology, Guangzhou 510006, China
3
School of Information Engineering, Guangdong University of Technology, Guangzhou 510006, China
*
Authors to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Electronics 2022, 11(4), 542; https://doi.org/10.3390/electronics11040542
Submission received: 4 January 2022 / Revised: 31 January 2022 / Accepted: 4 February 2022 / Published: 11 February 2022
(This article belongs to the Section Microelectronics)
Browse Figures
Versions Notes

Abstract

:
With the development of science and technology, consumers’ requirements for various electronic devices present a trend of more diverse functions and thinner bodies. This makes integrated circuits mounted in electronic products and their packaging more vital to satisfying the above requirements. Ball grid array (BGA) packaging is widely used in the field of microelectronic manufacturing industries due to its multiple I/O volumes and excellent electric characteristics. However, due to environmental loads such as vibration and impact during its production and application, defects inevitably emerge in BGA solder joint defects, which will lead to the failure of electronic products. This article summarizes the state-of-the-art research on the factors, analysis methods, and models for the fatigue failure of BGA chips. After rigorous discussions concerning this research, some theoretical suggestions are provided for BGA packaging in reliability analysis and the establishment of evaluation standards.

1. Introduction

In recent years, with the development of consumers’ demand for electronic products, electronic products have displayed the trends of miniaturization, high performance, and high integration [1,2,3,4,5]. BGA packaging, a new type of surface mount multi-terminal packaging technology, overcomes the limitation of the number of I/O ports in the peripheral for wire bonding [6,7]. The BGA chip is mounted on the carrier board through solder joints in the form of an array [8,9,10]. This packaging technology not only expands the space of electronic devices but also greatly expands the number of I/O ports [11]. Since it has the advantages of a high packaging density, high-speed signal processing, and low cost, BGA packaging has been widely applied in electronic industries [12].
The BGA chip works in the environment and is inevitably by external loads, which are possibly caused by crashes or falls of the electronic product from a height [13]. This results in the BGA chip malfunctioning and even failing, although its package plays the role of cushion protection and mechanical support. This is because the BGA solder joints are deformed and even damaged due to external loads [14,15,16,17,18]. Therefore, analysis of mechanical properties and fatigue life prediction of BGA solder joints are hotspot studies in the field of electronic products’ reliability [19,20].
The rest of this paper is organized as follows. Section 2 analyzes fatigue failure factors of BGA solder joints. Section 3 summarizes the research methods and results of solder joints under vibration loads, temperature loads, and shear stress loads. Section 4 introduces several common models for fatigue life prediction of solder joints, involving the Coffin–Manson life model, Darveaux life model, Paris life model, and two creep life models. The analysis and discussions are presented in Section 5, and the conclusion is drawn in Section 6.

2. Fatigue Failure Factors of BGA Solder Joints

Electronic products in real life work in a complex, changing environment, in which some environmental factors such as temperature, humidity, vibration, crashes, and dust affect their reliabilities [21,22]. BGA solder joints, which have the functions of mounting [23], electric connection [24], protection [25], heat dissipation [21], and mechanical support [26]. When BGA solder joints crash, this influences the reliability of BGA chips, and, further, the reliability of the electronic device [21,27]. The U.S. Air Force Electronics Industry Department has reported that the failure of electronic components is mostly contributed by temperature changes, vibration and shock, moisture, and dust [28,29], as illustrated in Figure 1.
A large amount of heat is consequentially produced when the electronic components are working [30]. If this heat cannot be effectively dissipated to the external environment, most of the heat will be concentrated in the electronic components to make the temperature inside the packaged chip rapidly rise, resulting in a burnout risk of the chip. If the temperature distribution inside the chip package is not uniform, the signal transmission characteristics of the chip will be influenced, thereby affecting the life and reliability of the electronic device. Additionally, because of the differences in the thermal expansion coefficient between chip packaging materials [31,32,33,34,35,36,37,38,39,40,41,42,43,44], different materials have different degrees of thermal expansion and contraction under the influence of temperature. This results in additional stress and strain inside the electronic components, especially inside solder joints. This endless procedure will make the deformation large enough to result in the fatigue failure of the electronic device. Figure 2a illustrates two SEM images of BGA solder joints with cracks due to the influence of the temperature [21].
When electronic components are influenced by random vibration, relative movement occurs between the solder joint and the substrate, which results in stress or strain inside the solder joint. When the stress or strain is large enough, fatigue failure of the BGA solder joint will occur [45]. Figure 2b shows that some cracks emerge inside BGA lead-free solder joints under the vibration load of the power spectral density, 60 (m/s2)2/Hz [22].
The polymer materials commonly used in BGA packaging also absorb moisture in the environment [46], which influences the soldering performance. First, the moisture will generate a large amount of water vapor due to the solder reflow temperature, which will further form a high vapor pressure. This pressure will cause the internal expansion and cracking of the solder joint or the cracking of the metal compound between the solder joint and the pad. Second, the moisture inside the solder joints will reduce the bonding strength between the polymers, which leads to the failure of the bonding of the solder joints in the components [47]. Figure 2c shows the SEM cross-sectional view of the microcracks inside the solder joints after a high-accelerated temperature and humidity test [48].
A broad understanding of the key failure factors of BGA solder joints is beneficial to accurately predict the fatigue life of the components and to provide preventive maintenance recommendations for microelectronic components [49]. Table 1 illustrates the failure factors and failure reasons for electronic components.
Among the four major factors that mainly affect the reliability of solder joints, the influence of temperature and vibration shock is as high as 75% [50,51,52]. Nowadays, a large number of experiments and theoretical studies have been conducted on the reliability of microelectronic packaging influenced by temperature and vibration [53]. Thus, we focus on the fatigue failure of BGA solder joints caused by temperature and vibration.

3. Research Methods for Fatigue Failure of BGA Solder Joints

The reliability of microelectronic packaging usually depends on the fatigue life of the solder joints [54], which can be predicted by experimental observation and empirical mathematical models [55].
Commonly, experimental studies require special experimental equipment and test samples to observe the process of cracking inside the BGA solder joint, which can be used to judge its failure [56]. Figure 3 shows the main failure modes for BGA solder joints due to cracks [57]. They are the fracture failures of the IMC layer on one side of the component, the solder joint neck, the IMC on the PCB side, and the junction of the PCB board and the pad. The test methods commonly used in experimental studies are summarized in Table 2.
Another method is to use finite element simulation software to predict the fatigue life of solder joints [58,59]. Finite element software is employed to model and simulate the fatigue failure for specific components or solder joints under specific environmental parameters. Thus, significant information can be achieved, involving the stress and strain of key solder joints. Combined with the real working conditions of the packaging device, a suitable prediction model is selected to predict the fatigue life of the solder joint [55]. Due to the powerful simulation and analysis functions, some commonly used finite element software packages, such as ANSYS, ABAQUS, MARC, and WELSIM, are used to study the reliability of solder joints during packaging [60,61].
Finite element simulation analysis provides theoretical guidance for experiments. In turn, the simulation model is improved through experimental verification to obtain more accurate results. To avoid the limitations that only experimental studies or finite element analysis are employed, their combination is an alternative, which is shown in Figure 4.

3.1. Research Methods for Fatigue Failure of BGA Solder Joints under Vibration Load

In commercial, industrial, and military applications, microelectronic devices often need to work under different vibration load conditions. Therefore, it is necessary to study the fatigue failure mechanism of BGA solder joints under vibration load [62,63].
Fang Liu and Ye Lu [64] et al. used a combination of finite element analysis and an experimental study to predict the fatigue life of BGA solder joints under random vibration loads. They used ABAQUS software to establish a three-dimensional finite element model of PCB components for random vibration simulation analysis. Then, the power density of the PCB components was obtained. Comparison experiments showed that the simulation results have a good correlation with the experimental results, which can validate the simulation model. Finally, the Miner rule and random vibration theory were used to determine the fatigue life of BGA solder joints under random vibration loads [64].
Yang et al. [65] used sinusoidal vibration tests to study the fatigue failure of PBGA solder joints. Their study indicated that the resonant frequency of the PCB board is excited under the load of sinusoidal vibration. This causes the PCB board to bend back and forth, which makes the solder joints produce higher stress, resulting in fatigue failure of the solder joints. Zhou et al. [66] used equal amplitude incentives to study the fatigue failure of solder joints. A narrow bandwidth harmonic vibration test was performed to study the vibration durability of solder joints, which was performed on SAC305 and Sn37Pb solder joints at the first natural frequency of the test. Their study indicated that SAC305 interconnection solder joints have lower fatigue durability than similar Sn37Pb ones under the narrow bandwidth harmonic excitation. Chen et al. [67] changed the constant acceleration amplitude to perform sinusoidal vibration experiments under different excitation levels. The failure time was correlated with the stresses obtained by the finite element analysis to obtain the fatigue curve of the solder joints. In order to estimate the life of solder joints under sinusoidal vibration loads, Chen et al. [67] used Miner’s rule to predict the life of PBGA components under sinusoidal vibration loads. The cumulative damage index (CDI) was approximately equal to 1. To overcome the limitations of Steinberg theory in the mechanical reliability of solder joints in aerospace devices in a random vibration emission environment, a failure analysis method was proposed based on critical strain [68]. It installs PCB components with BGA packages on different positions of the circuit board. Then, the components are exposed to a random vibration test environment to evaluate the fatigue life of solder joints. Jinwoo Jang [69] implemented overall local finite element simulation on solder joints in a solid-state disk to achieve the position of the weakest solder joint. The solid-state disk was fixed on the fixture to verify the simulation results. The stress–failure cycle curve was derived based on the vibration experiment analysis. The above studies are summarized in Table 3.

3.2. Research Method for Fatigue Failure of Solder Joints under Thermal Stress

BGA solder joints are usually influenced by thermal shock loads when BGA-packaged devices are working, which reduces the mechanical strength of solder joints. If the mechanical strength decreases to a critical level, fatigue failure of the solder joint will occur [21]. Driven by the thermal cycling, the difference in the thermal expansion coefficient between the BGA package and the PCB [70,71,72], the alloy composition, and temperature changes in the solder joint matrix significantly affect the reliability of the solder joint [25,32]. Thus, many studies have been performed on the fatigue failure of solder joints under thermal stress.
Vasu Vasudevan [73] et al. experimentally studied the failure of 1295 solder joints in a BGA package. The thermal fatigue reliabilities of solder joints with different lead contents were analyzed under thermal stress by an accelerated temperature cycle test. They found that the reliability of the solder joints with a low lead content was low, and metallographic analysis showed that the solder joint failure occurred on the PCB side.
In addition, some researchers have used theoretical simulations to predict the fatigue life of solder joints. Jiahao Liu et al. [74] adopted finite element analysis to simulate the stress and strain distribution of a lead BGA solder joint array under a temperature cycle load, and to determine the position of the dangerous solder joint. Additionally, they predicted the life of the solder joint by the Coffin–Manson model. Joshua A. Depivera et al. [21] used Solidworks to establish BGA package component models with different alloy solders, which were imported into ANSYS software. The plastic strain, shear strain, plastic shear strain, and cumulative creep energy density response of the solder joint were obtained under the temperature cycle following the IEC 60749-25 standard, which were input into the established life prediction model to determine the thermal fatigue life of the model.
Some researchers have combined theoretical simulation with experiment analysis to explore the fatigue life of solder joints under thermal stress. Leilei Zhang et al. [75] combined a temperature cycle test and finite element analysis to study the thermal fatigue life of solder joints of large BGA package components. Their study showed that the three-dimensional finite element model based on the volume-weighted average viscoplastic strain energy accumulated by the interface element in each temperature cycle was successfully applied to the FG680 chip.
The above studies conducted under thermal stress are summarized in Table 4.

3.3. Research Method for Fatigue Failure of Solder Joints under Shear Stress

Electronic products will be subjected to high temperature and mechanical loads during normal operation. Since the thermal expansion coefficients of electronic components, intermetallic compounds, solders, and substrates are different, solder joints will be repeatedly subjected to periodic shear stress. Due to external forces, stress concentration will occur in the solder joints. If the load is large enough, solder joints are prone to shear fracture. Therefore, studying the failure mechanism of solder joints under shear force is important to improve the mechanical properties of solder joints [76].
Shear tests of solder joints are widely used to evaluate the bonding quality of solder joints in BGA package components [77,78,79,80]. Julian Yan Hon Chiaa et al. [81] designed a servo-hydraulic test machine to perform a solder point shear test. The experimental results showed that the maximal load at a low shear rate is closely related to the toughness of the solder. Although the failure mechanism of solder joints under shear force cannot be determined solely from the relationship between the shear force and the solder, it is essential for us to understand the quality of solder joints.
Jong-Woong Kim et al. [82] used an experimental study and nonlinear finite element analysis of an elasto-viscoplastic constitutive model to study the effect of the shear speed on the shear force of BGA solder joints. The shear test of two different solder compositions (Sn-3.5Ag and Sn-3.5Ag-0.75Cu) indicated that the shear force increases with the increase in the shear speed when the shearing tool is above the welding plate at the height of 50 μm and the shear speed is in the range of 10~700 μm/s. The shear force reaches the maximum when the shear speed reaches the maximum. At this time, all the samples have ductile fractures. Finally, the failure mechanism was discussed from the distribution of the stress and plastic strain energy density.
Ogunsemi et al. [20] analyzed the influence of the overall solder ball height on the shear strength of BGA solder joints. Failure treatment had been performed on the samples at 150 °C for 8 days to establish the relationship between the height of the gap between the pads under different pad sizes and the shear strength of solder joints. The experimental results showed that, with the increase in the pad size and the decrease in the spacing between the pads, the shear strength of the solder joints increased.
The above studies conducted under shear stress are summarized in Table 5.

4. Several Common Models for Fatigue Life Prediction of Solder Joints

As the fatigue performance requirements of solder joints are becoming higher and higher, it is important to understand the differences in fatigue behavior under different mathematical models [83,84]. Many researchers have proposed a number of fatigue failure models to study the reliabilities of solder joints [85,86]. Several commonly used failure models are summarized as follows.

4.1. Coffin–Manson Life Model

The Coffin–Manson model is the earliest low-cycle fatigue model, proposed by L.F. Coffin and S. S. Manson in 1954 [87]. They pointed out that fatigue fracture was primarily caused by cyclic plastic strain of materials and solder joints [88]. This model is a fatigue life prediction model based on plastic deformation. However, it ignores the influence of time and temperature on the life of solder joints [89]. Later, Engelmaier considered the influence of the temperature and temperature cycle on the fatigue life to modify the Coffin–Manson model [23]. Since it has a better prediction performance than the traditional model in [87], it is widely used at present [90]. However, this modified model is only effective for packages in which the thermal expansion coefficient of the material of each layer is different and suitable for shear stress, which is the principal stress of solder joints. The traditional fatigue life of solder joints is formulated as [91]
N f = A Δ γ m × f n × e − β / k T m a x
where Nf is the number of failure cycles; A, ∆γ, f, and β are the material constant, cyclic plastic shear strain, thermal cycle frequency, and activation energy [11], respectively; Tmax is the highest temperature in the cycle; k and n are Boltzmann’s constant and an empirical constant, respectively; m is a constant with the range of 1.89~2.5 [92].
The Coffin–Manson model is widely used to predict the low-cycle fatigue failure of solder alloy joints due to cyclic plastic deformation, in which the involved stress and strain are generally plastic. However, when predicting the life of solder joints, it is easily influenced by the cycle frequency, the thermal expansion coefficient of the chip packaging material, and the type of stress and strain.

4.2. Darveaux Life Model

The Darveaux model utilizes the stress, strain, or energy between solder joints to characterize the relationship between their physical constants and their actual life under thermal or mechanical stress [93]. The model divides the fatigue process into two stages, which are steady-state and nonlinear acceleration. In the first stage, the fatigue crack growth proceeds at a constant speed [94]. In the second stage, the mechanical characteristics of the solder joint deteriorate sharply. The model can be formulated as [95]
N O = K 1 Δ W a v e K 2
d a d N = K 3 Δ W a v e K 4
N s = N O + a d a / d N
where Ns and NO are the characteristic life of interconnected solder joints and the number of cycles for crack initiation, respectively; a, d a d N , and ∆Wave are the characteristic length of the fracture, the crack growth rate, and the average inelastic strain energy density accumulated in each cycle, respectively; K1, K2, K3, and K4 are the coefficients obtained from experiments and related to crack growth, which is related to the finite element model structure and the thickness of the material connecting the solder joints and the substrate.
The Darveaux model is mainly applied for SnPb solder joints due to crack initiation and propagation. However, due to a number of theoretical correlation coefficients, it is not easy to evaluate the fatigue life of solder joints of micro-packaged devices. At the same time, for most solder joint failures, the device cannot be used normally not because the solder joints are completely broken, but because the electrical properties fail after the cracks expand to a certain extent [96,97]. Therefore, the widespread use of this model is limited.

4.3. Paris Life Model

Paris proposed the famous Paris formula to demonstrate the principle of crack growth [98], which is based on fracture mechanics. This formula combines fracture mechanics with fatigue life and provides a new direction for studying crack growth life [99]. It uses the stress intensity factor to characterize the stress field intensity at the crack tip. Only the stress intensity factor is the main reason for crack growth. The model is formulated as [100]
d a d N = C ″ Δ k n ′
Δ k = k m a x − k m i n
where d a d N , N, and a are the crack growth rate, the number of failure cycles, and the crack length, respectively; ∆k is the amplitude of the stress intensity factor in a load cycle; kmax and kmin are the maximal and minimal stress intensity factors in a load cycle, respectively; C ″ and n ′ are material constants, which are related to environmental factors, such as temperature, humidity, medium, and loading frequency.
The Paris life model is used to describe the crack growth caused by fatigue in engineering materials, in which a close relationship is established between the crack growth rate and the stress intensity. It is typically used under linear elastic fracture conditions and only for stable crack growth in fatigue testing, which are its limitations.

4.4. Creep Life Model

Creep is a phenomenon in which the strain of a solid material increases with the increase in the loading time under a constant external force. Early creep modeling was carried out by separating the elastic and plastic deformation mechanisms. The creep, plastic, elastic, and other deformations were overlapped to form the creep [61,101], which is the main deformation failure mechanism of materials at high temperature. In particular, in microelectronic packaging, for example, for Sn-based lead-free solders, creep will occur when the operating temperature for the solder joint is 0.5 times more than the melting point of the solder [102]. Two commonly used creep life models are briefly introduced as follows [103].

4.4.1. Knecht–Fox Model

The Knecht–Fox model is a simple matrix creep fatigue model proposed by Knecht and Fox, which correlates the solder microstructure with the creep shear strain range of the substrate. It is mainly used for power-level creep and based on matrix dislocation theory, which is formulated as
N f = C Δ γ m c
where C is the material constant related to the microstructure of the solder, and Δ γ m c is the creep stress amplitude of the matrix.

4.4.2. Syed Model

The Syed model considers steady-state creep as the main reason for the thermal fatigue failure of solder joints [104]. Two expressions of cyclic creep fatigue life due to changes and repeated stresses under a single creep mechanism are provided below.
For a single creep mechanism, it is formulated as
N f = C ′ × ε a c c − 1
where εacc is the accumulated creep strain of each cycle, and C ′ is the constant reciprocal of creep ductility. Combined with (7), it is transformed into a model based on the energy density, as follows:
N f = W ′ × w a c c − 1
where wacc is the creep strain energy density accumulated in each cycle, and W ′ is the creep strain energy density at failure.
The Knecht–Fox model is a matrix creep model that can be applied to all package types. The Syed model is a cumulative creep strain energy model, mainly applied for PBGA, SMD, and NSMD package types [61]. However, the Knecht–Fox model and the Syed model ignore the effect of the plastic strain of solder joints during temperature loading. In practice, the influence of plastic strain on the fatigue life of solder joints is significant, which gives the two models evident limitations in the analysis of the fatigue life of solder joints. Additionally, the creep mechanism is complicated and affected by many factors. Therefore, it is difficult for this model to accurately describe the creep process [105]. Moreover, it ignores the influence of plastic strain [106].
Table 6 summarizes several commonly used fatigue life prediction models.

5. Analysis and Discussions

Many factors influence the reliability of BGA solder joints, including internal factors and external environmental factors. The former mainly involve the size, morphology, and characteristics of the material of the solder joint, the structural size of the pad, and the array structure of the solder joint. Environmental factors such as temperature, vibration, and impact will affect the fatigue life of the solder joint. Most of the present studies focus on finite element simulation and experimental studies to study the reliability of solder joints. Additionally, appropriate life prediction models and failure analysis methods are employed in the case of specific microelectronic packaging devices. The dangerous locations of the main failures of solder joints and the failure mechanisms under different factors have been primarily clarified, which can provide a theoretical basis for the early chip structure design and the selection of soldering materials.
Existing fatigue failure studies mainly focus on failure principle analysis, failure mechanism coupling, and finite element simulation. Failure principle analysis mainly studies the principle and mechanism of solder joint cracking, and the influences of solder joint appearances, welding materials, and welding methods on the reliability of solder joints. However, few studies have been reported on the real influences of different welding processes and the differences caused by the specific process in different environments (such as temperature and humidity). In practice, the failure of a solder joint results from many factors rather than only a single factor. Furthermore, these factors are coupled together rather than separated independently to influence the fatigue life of the solder joint. However, many existing fatigue failure studies focus on failure mechanism research under a single factor. Some studies analyze the failure of the solder joint by linearly superimposing each failure caused by each factor. However, failures caused by a single factor cannot be simply superimposed due to their coupling characteristics. Although finite element simulation has been successfully applied to the fatigue life prediction of solder joints, few researchers have studied the endogenous mechanism between the fatigue life of solder joints and microscopic electron migration, grain orientation and structure, and the boundary size and number of grains. Additionally, the reliability models for thermal cycles are mostly established based on component-level simulation. However, they are not suitable for devices mounted on PCB boards. For this situation, board-level reliability simulation is preferred.
In summary, reliability analysis of solder joints mainly depends on an effective analysis method and fatigue life prediction model. Board-level or component-level simulation is selected according to specific work requirements. Thermo-electric-mechanical coupling simulation analysis can be applied in the specific working environment of specific microelectronic components. Thus, the temperature distribution stress and strain of solder joints can be macroscopically analyzed to locate the dangerous solder joints. The geometric parameters of the solder joint grains and the heat generated by electron migration are microscopically analyzed to determine the life prediction model of solder joints, as well as the endogenous relationship between the solder joint life and different influencing factors.

6. Conclusions

We first analyzed the causes of fatigue failure based on BGA package solder joints and summarized the research methods and research results of fatigue failure of BGA solder joints under different loads, such as vibration loads, temperature loads, and shear stress loads. Additionally, some non-destructive testing and destructive testing technologies were enumerated, which are widely used in chip solder joint inspection. Then, according to several common failure conditions of BGA solder joints, four categories of commonly used prediction models for fatigue life prediction were introduced. They are the Coffin–Manson life model based on low-cycle fatigue, the Darveaux life model based on energy, the Paris life model based on fracture mechanics, and the Knecht–Fox model and Syed model based on the creep phenomenon. A suitable life prediction model can be adopted for failure analysis according to the specific microelectronic packaging device and the specific working environment.
In summary, reliability analysis of solder joints mainly depends on the establishment of an effective analysis method and a fatigue life prediction model. For BGA solder joints, the following aspects should be dealt with when performing fatigue life analysis.
Research method: The research method should be established by combining finite element simulation technology and experimental verification. Board-level finite element simulation can be used for finite element simulation according to the actual situation. Different mesh densities can be divided for different key parts to improve the simulation efficiency and to obtain more accurate simulation results. Then, the dangerous solder joints of the chip can be located according to two simulation results, when the chip component is simulated. For the determination of the simulation load, the load coupling simulation method should be adopted according to the actual working environment of the components, which can closely simulate the actual working environment of the components. At the same time, the failure model should be purposively established for life prediction according to the chip failure mode and load conditions. Finally, the simulation analysis results should be compared with the experimental results achieved by the experimental verification, so as to modify the simulation model to improve its simulation accuracy. Thus, the fatigue life of solder joints can be obtained.
Characterization method: Traditional characterization methods observe surface appearances of solder joints, such as cracks and deformation, to determine the failure of solder joints, which will inevitably result in some errors. Thus, electrical performance tests, such as resistance measurements, combined with functional verification can be employed to determine whether the chip fails. This can improve the performance of the characterization method for solder joint failure.
The above research methods are beneficial to determine an effective prediction process for predicting the fatigue life of BGA solder joints. Additionally, they can further enrich the research path of the fatigue life prediction of BGA solder joints and improve the prediction accuracy of BGA solder joints.

Author Contributions

Conceptualization, B.Q.; methodology, J.X., H.W. and N.C.; formal analysis, B.Q.; investigation, H.W.; resources, S.Z.; data curation, X.Y., Z.L. and M.L.; writing—original draft preparation, B.Q. and J.X.; writing—review and editing, X.Y., Z.L., M.L. and N.C.; visualization, X.Y.; supervision, S.Z. and N.C.; project administration, B.Q., S.Z. and N.C.; funding acquisition, H.W., S.Z. and N.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work was in part supported by the National Natural Science Foundation of China (Nos. 62171142 and 61901123), the Key Laboratory Construction Projects in Guangdong (No. 2017B030314178), the Research Fund for Colleges and Universities in Huizhou (No. 2019HZKY003), the Project of Jihua Laboratory (No.X190071UZ190) and the National Natural Science Foundation of Guangdong Province, China (No. 2021A1515011908).

Acknowledgments

This work was in part supported by the National Natural Science Foundation of China (Nos. 62171142 and 61901123), the Key Laboratory Construction Projects in Guangdong (No. 2017B030314178), the Research Fund for Colleges and Universities in Huizhou (No. 2019HZKY003), the Project of Jihua Laboratory (No.X190071UZ190) and the National Natural Science Foundation of Guangdong Province, China (No. 2021A1515011908).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chung, S.; Kwak, J.B.J.E. Comparative study on reliability and advanced numerical analysis of BGA subjected to product-level drop impact test for portable electronics. Electronics 2020, 9, 1515. [Google Scholar] [CrossRef]
  2. Ren, J.; Huang, M.L. Board-level drop reliability and fracture behavior of low-temperature soldering Sn–Ag–Cu/Sn–Bi–X hybrid BGA solder joints for consumer electronics. J. Mater. Sci. Mater. Electron. 2021, 32, 15453–15465. [Google Scholar] [CrossRef]
  3. Lin, Y.; Kang, C.; Chua, L.; Choi, W.K.; Yoon, S.W. Advanced 3D eWLB-PoP (embedded wafer level ball grid array-package on package) technology. In Proceedings of the 2016 IEEE 66th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 31 May–3 June 2016; pp. 1772–1777. [Google Scholar]
  4. Huang, J.; Zhou, M.; Zhang, X.P. The melting characteristics and interfacial reactions of Sn-ball/Sn-3.0 Ag-0.5 Cu-paste/Cu joints during reflow soldering. J. Electron. Mater. 2017, 46, 1504–1515. [Google Scholar] [CrossRef]
  5. Ye, H.; Xue, S.; Zhang, L.; Ji, F.; Dai, W. Reliability evaluation of CSP soldered joints based on FEM and Taguchi method. Comput. Mater. Sci. 2010, 48, 509–512. [Google Scholar] [CrossRef]
  6. Jin, Y.; Baraton, X.; Yoon, S.; Lin, Y.; Marimuthu, P.C.; Ganesh, V.; Meyer, T.; Bahr, A. Next generation eWLB (embedded wafer level BGA) packaging. In Proceedings of the 2010 12th Electronics Packaging Technology Conference, Singapore, 8–10 December 2010; pp. 520–526. [Google Scholar]
  7. Huang, J.; Zhou, M.; Liang, S.; Zhang, X. Size effects on the interfacial reaction and microstructural evolution of Sn-ball/Sn3.0Ag0.5Cu-paste/Cu joints in board-level hybrid BGA interconnection at critical reflowing temperature. J. Mater. Sci. Mater. Electron. 2018, 29, 7651–7660. [Google Scholar] [CrossRef]
  8. Gagnon, P.; Fortin, C.; Weiss, T. Package-on-Package Micro-BGA Microstructure Interaction with Bond and Assembly Parameter. In Proceedings of the 2019 IEEE 69th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2019; pp. 306–313. [Google Scholar]
  9. Petrosyants, K.O.; Ryabov, N.I. Quasi-3D Thermal Model of Stacked IC-TSV-BGA Package. In Proceedings of the 2019 25th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Lecco, Italy, 25–27 September 2019; pp. 1–4. [Google Scholar]
  10. Kamoji, R.; Oberai, A. Fault Isolation of 2.5 D and 3D Packages through Analysis Across Entire System. In Proceedings of the 2018 IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits (IPFA), Singapore, 16–19 July 2018; pp. 1–5. [Google Scholar]
  11. Shohji, I.; Mori, H.; Orii, Y. Solder joint reliability evaluation of chip scale package using a modified Coffin–Manson equation. Microelectron. Reliab. 2004, 44, 269–274. [Google Scholar] [CrossRef]
  12. Du, J.H.; Raz, Z.E. A Reliability Qualification Process for BGA Rework Limit. In Proceedings of the 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 776–781. [Google Scholar]
  13. Tee, T.Y.; Ng, H.S.; Lim, C.T.; Pek, E.; Zhong, Z. Impact life prediction modeling of TFBGA packages under board level drop test. Microelectron. Reliab. 2004, 44, 1131–1142. [Google Scholar] [CrossRef]
  14. Li, B.; Zhang, X.; Yang, Y.; Yin, L.; Pecht, M. Size and constraint effects on interfacial fracture behavior of microscale solder interconnects. Microelectron. Reliab. 2013, 53, 154–163. [Google Scholar] [CrossRef]
  15. Loukia, M.; Deshpande, A.; Dasgupta, A. Vulnerability of Copper Pad in BGA Solder Interconnects Under Temperature Cycling. In Proceedings of the 2021 20th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (iTherm), Marina, San Diego, CA, USA, 31 May–3 June 2021; pp. 679–683. [Google Scholar]
  16. Ho, C.; Yang, S.; Kao, C.R. Interfacial reaction issues for lead-free electronic solders. Lead-Free Electron. Solder. 2006, 18, 155–174. [Google Scholar] [CrossRef]
  17. Park, Y.-S.; Kwon, Y.-M.; Moon, J.-T.; Lee, Y.-W.; Lee, J.-H.; Paik, K.-W. Effects of fine size lead-free solder ball on the interfacial reactions and joint reliability. In Proceedings of the 60th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 1–4 June 2010; pp. 1436–1441. [Google Scholar]
  18. Huang, M.; Yang, F. Size effect on interfacial reactions of Sn–3.0 Ag–0.5 Cu solder balls on Cu and Ni–P pads. J. Mater. Sci. Mater. Electron. 2015, 26, 933–942. [Google Scholar] [CrossRef]
  19. Gan, G.; Yang, D.; Wu, Y.-p.; Liu, X.; Sun, P.; Xia, D.; Cao, H.; Jiang, L.; Tian, M.J.S.; Technology, S.M. Property of Sn-37Pb solder bumps with different diameter during thermal shock. Solder. Surf. Mt. Technol. 2021, 33, 94–104. [Google Scholar] [CrossRef]
  20. Ogunsemi, B.T.; Ikubanni, P.P.; Adediran, A.A.; Agboola, O.O. Effect of stand-off height on the shear strength of ball grid array solder joints under varying pad sizes. SN Appl. Sci. 2018, 1, 36. [Google Scholar] [CrossRef] [Green Version]
  21. Depiver, J.A.; Mallik, S.; Amalu, E.H. Thermal fatigue life of ball grid array (BGA) solder joints made from different alloy compositions. Eng. Fail. Anal. 2021, 125, 105447. [Google Scholar] [CrossRef]
  22. Liu, F.; Meng, G. Random vibration reliability of BGA lead-free solder joint. Microelectron. Reliab. 2014, 54, 226–232. [Google Scholar] [CrossRef]
  23. Men, W.; Chen, Y.; Kang, R. Thermal fatigue lifetime prediction of BGA solder joint via a novel fatigue crack propagation model. In Safety and Reliability–Safe Societies in a Changing World; CRC Press: Boca Raton, FL, USA, 2018; pp. 2269–2275. [Google Scholar]
  24. Tu, K.-N.; Gusak, A.; Li, M. Physics and materials challenges for lead-free solders. J. Appl. Phys. 2003, 93, 1335–1353. [Google Scholar] [CrossRef]
  25. Dalton, E.; Ren, G.; Punch, J.; Collins, M.N.J.M. Accelerated temperature cycling induced strain and failure behaviour for BGA assemblies of third generation high Ag content Pb-free solder alloys. Mater. Des. 2018, 154, 184–191. [Google Scholar] [CrossRef]
  26. Shen, L.; Chen, C.; Niu, X. Random vibration analysis of BGA with different size of the SAC0307 solder joint. In Proceedings of the 2018 19th International Conference on Electronic Packaging Technology (ICEPT), Shanghai, China, 8–11 August 2018; pp. 1019–1021. [Google Scholar]
  27. Thanu, D.P.; Antoniswamy, A.; Danaei, R.; Keswani, M. Adhesion Phenomena Pertaining to Thermal Interface Materials and Solder Interconnects in Microelectronic Packaging: A Critical Review. Rev. Adhes. Adhes. 2018, 6, 1–25. [Google Scholar] [CrossRef]
  28. Tee, T.Y.; Luan, J.-e.; Pek, E.; Lim, C.T.; Zhong, Z. Advanced experimental and simulation techniques for analysis of dynamic responses during drop impact. In Proceedings of the 54th Electronic Components and Technology Conference (IEEE Cat. No. 04CH37546), Las Vegas, NV, USA, 4 June 2004; pp. 1088–1094. [Google Scholar]
  29. Yang, Z. An energy-based crack growth criterion for modelling elastic–plastic ductile fracture. Mech. Res. Commun. 2005, 32, 514–524. [Google Scholar] [CrossRef] [Green Version]
  30. Suhir, E.; Ghaffarian, R.; Nicolics, J. Could thermal stresses in a BGA/CGA-system be evaluated from a model intended for a homogeneously bonded assembly? J. Mater. Sci. Mater. Electron. 2016, 27, 570–579. [Google Scholar] [CrossRef]
  31. Hwang, J.; Vargas, R.J.S.; Technology, S.M. Solder Joint Reliability—Can Solder Creep? Solder. Surf. Mount Technol. 1990, 2, 38–45. [Google Scholar] [CrossRef]
  32. Lau, J.H.; Pao, Y.-H. Solder Joint Reliability of BGA, CSP, Flip Chip, and Fine Pitch SMT Assemblies; McGraw-Hill Professional Publishing: New York, NY, USA, 1997. [Google Scholar]
  33. Lau, J.H.; Wong, C.; Lee, N.-C.; Lee, S.-W.R. Electronics Manufacturing: With Lead-Free, Halogen-Free, and Conductive-Adhesive Materials; McGraw-Hill Education: New York, NY, USA, 2003. [Google Scholar]
  34. Wang, J.; Niu, Y.; Park, S.; Yatskov, A. Modeling and design of 2.5 D package with mitigated warpage and enhanced thermo-mechanical reliability. In Proceedings of the 2018 IEEE 68th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 29 May–1 June 2018; pp. 2477–2483. [Google Scholar]
  35. Shao, S.; Niu, Y.; Wang, J.; Liu, R.; Park, S.; Lee, H.; Refai-Ahmed, G.; Yip, L. Comprehensive study on 2.5 D package design for board-level reliability in thermal cycling and power cycling. In Proceedings of the 2018 IEEE 68th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 29 May–1 June 2018; pp. 1668–1675. [Google Scholar]
  36. Depiver, J.A.; Mallik, S.; Amalu, E.H. Comparing and Benchmarking Fatigue Behaviours of Various SAC Solders under Thermo-Mechanical Loading. In Proceedings of the 2020 IEEE 8th Electronics System-Integration Technology Conference (ESTC), Tønsberg, Norway, 15–18 September 2020; pp. 1–11. [Google Scholar]
  37. Hamasha, S.; Qasaimeh, A.; Jaradat, Y.; Borgesen, P. Correlation between solder joint fatigue life and accumulated work in isothermal cycling. IEEE Trans. Compon. Packag. Manuf. Technol. 2015, 5, 1292–1299. [Google Scholar] [CrossRef]
  38. Qasaimeh, A.; Hamasha, S.d.; Jaradat, Y.; Borgesen, P. Damage evolution in lead free solder joints in isothermal fatigue. J. Electron. Packag. Trans. ASME 2015, 137, 021012. [Google Scholar] [CrossRef]
  39. Obaidat, M.; Hamasha, S.; Jaradat, Y.; Qasaimeh, A.; Arfaei, B.; Anselm, M.; Borgesen, P. Effects of varying amplitudes on the fatigue life of lead free solder joints. In Proceedings of the 2013 IEEE 63rd Electronic Components and Technology Conference, Las Vegas, NV, USA, 28–31 May 2013; pp. 1308–1314. [Google Scholar]
  40. Batieha, F.; Hamasha, S.; Jaradat, Y.; Wentlent, L.; Qasaimeh, A.; Borgesen, P. Challenges for the prediction of solder joint life in long term vibration. In Proceedings of the 2015 IEEE 65th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 26–29 May 2015; pp. 1553–1559. [Google Scholar]
  41. Borgesen, P.; Wentlent, L.; Khasawneh, S.; Shirazi, S.; Schmitz, D.; Alghoul, T.; Greene, C.; Yin, L. A mechanistic thermal fatigue model for SnAgCu solder joints. J. Electron. Mater. 2018, 47, 2526–2544. [Google Scholar] [CrossRef] [Green Version]
  42. Hamasha, S.d.; Borgesen, P. Effects of strain rate and amplitude variations on solder joint fatigue life in isothermal cycling. J. Electron. Packag. 2016, 138, 021002. [Google Scholar] [CrossRef]
  43. Su, S.; Akkara, F.; Dawahdeh, A.; Borgesen, P.; Qasaimeh, A. Solder joint reliability in isothermal varying load cycling. In Proceedings of the 2017 16th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 30 May–2 June 2017; pp. 1331–1336. [Google Scholar]
  44. Su, S.; Jian, M.; Akkara, F.J.; Hamasha, S.d.; Suhling, J.; Lall, P. Fatigue and shear properties of high reliable solder joints for harsh applications. In Proceedings of the SMTA International, Rosemont, IL, USA, 14–18 October 2018. [Google Scholar]
  45. Wong, T.; Reed, B.; Cohen, H.; Chu, D. Development of BGA solder joint vibration fatigue life prediction model. In Proceedings of the 49th Electronic Components and Technology Conference (Cat. No. 99CH36299), San Diego, CA, USA, 1–4 June 1999; pp. 149–154. [Google Scholar]
  46. Van Gils, M.; Van Driel, W.; Zhang, G.; Bressers, H.; van Silfhout, R.B.; Fan, X.; Janssen, J. Virtual qualification of moisture induced failures of advanced packages. Microelectron. Reliab. 2007, 47, 273–279. [Google Scholar] [CrossRef]
  47. Chen, X.; Zhao, S.; Zhai, L. Moisture absorption and diffusion characterization of molding compound. J. Electron. Packag. 2005, 127, 460–465. [Google Scholar] [CrossRef]
  48. Gan, C.; Hashim, U. Reliability assessment and mechanical characterization of Cu and Au ball bonds in BGA package. J. Mater. Sci. Mater. Electron. 2013, 24, 2803–2811. [Google Scholar] [CrossRef]
  49. Amalu, E.H. Modelling of the Reliability of Flip Chip Lead-Free Solder Joints at High-TEMperature Excursions. Ph.D. Thesis, University of Greenwich, London, UK, March 2012. [Google Scholar]
  50. Guo, Q.; Zhao, M.; Wang, H. SMT solder joint’s semi-experimental fatigue model. Microelectron. Reliab. 2005, 32, 351–358. [Google Scholar] [CrossRef]
  51. Bart, V.; Gonzalez, M.; Limaye, P.; Ratchev, P.; Beyne, E. Thermal cycling reliability of SnAgCu and SnPb solder joints: A comparison for several IC-packages. Microelectron. Reliab. 2007, 47, 259–265. [Google Scholar]
  52. Gonzalez, M.; Vandevelde, B.; Vanfleteren, J.; Manessis, D. Thermo-mechanical FEM analysis of lead free and lead containing solder for flip chip applications. In Proceedings of the 15th European Microelectronics and Packaging Conference & Exhibition, Brugge, Belgium, 12–15 June 2005; pp. 440–445. [Google Scholar]
  53. Wu, M.-L.; Barker, D. Rapid assessment of BGA fatigue life under vibration loading. IEEE Trans. Adv. Packag. 2009, 33, 88–96. [Google Scholar]
  54. Hamasha, S.; Akkara, F.; Su, S.; Ali, H.; Borgesen, P. Effect of cycling amplitude variations on SnAgCu solder joint fatigue life. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 1896–1904. [Google Scholar] [CrossRef]
  55. Qi, H.; Osterman, M.; Pecht, M. A rapid life-prediction approach for PBGA solder joints under combined thermal cycling and vibration loading conditions. IEEE Trans. Compon. Packag. Manuf. Technol. 2009, 32, 283–292. [Google Scholar] [CrossRef]
  56. Pustan, D.; Wilde, J. Modern test methods for a comprehensive thermo-mechanical deformation analysis in area-array-assemblies. In Proceedings of the 2008 58th Electronic Components and Technology Conference, Lake Buena Vista, FL, USA, 27–30 May 2008; pp. 599–605. [Google Scholar]
  57. Syed, A. Overview of Reliability Models and Data Needs. In Proceedings of the Workshop on modeling and Data Needs for Lead-Free Solders, New Orleans, LA, USA, 15 February 2001. [Google Scholar]
  58. Muhammad Nubli, Z. Temperature Cycling Test for a Ball Grid Array (BGA) Package Using Finite Element Analysis (FEA). Master’s Thesis, University Malaysia Perlis, Perlis, Malaysia, January 2008. [Google Scholar]
  59. Ying, C.; Zebing, H.; Rui, K. Lifetime prediction and impact factors analysis of ball grid array solder joint based on FEA. In Proceedings of the 2010 11th International Conference on Electronic Packaging Technology & High Density Packaging, Xi’an, China, 16–19 August 2010; pp. 1142–1146. [Google Scholar]
  60. Ramachandran, V.; Wu, K.; Chiang, K.N. Overview study of solder joint reliablity due to creep deformation. J. Mech. 2018, 34, 637–643. [Google Scholar] [CrossRef]
  61. Lee, W.; Nguyen, L.; Selvaduray, G. Solder joint fatigue models: Review and applicability to chip scale packages. Microelectron. Reliab. 2000, 40, 231–244. [Google Scholar] [CrossRef]
  62. Steinberg, D.S. Vibration Analysis for Electronic Equipment; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
  63. Kinyanjui, R.; Chu, Q.; Snugovsky, P.; Coyle, R. Solder Joint Reliability of Pb-free SnAgCu Ball Grid Array (BGA) Components in SnPb Assembly Process. Proc. APEX 2008, 2008, S02–S15. [Google Scholar]
  64. Liu, F.; Lu, Y.; Wang, Z.; Zhang, Z. Numerical simulation and fatigue life estimation of BGA packages under random vibration loading. Microelectron. Reliab. 2015, 55, 2777–2785. [Google Scholar] [CrossRef]
  65. Yang, Q.; Wang, Z.; Lim, G.; Pang, J.; Yap, F.F.; Lin, R. Reliability of PBGA assemblies under out-of-plane vibration excitations. IEEE Trans. Compon. Packag. Technol. 2002, 25, 293–300. [Google Scholar] [CrossRef]
  66. Zhou, Y.; Al-Bassyiouni, M.; Dasgupta, A. Vibration durability assessment of Sn3. 0Ag0. 5Cu and Sn37Pb solders under harmonic excitation. J. Electron. Packag. 2009, 131, 011016. [Google Scholar] [CrossRef]
  67. Chen, Y.; Wang, C.; Yang, Y. Combining vibration test with finite element analysis for the fatigue life estimation of PBGA components. Microelectron. Reliab. 2008, 48, 638–644. [Google Scholar] [CrossRef]
  68. Park, T.-Y.; Oh, H.-U. Validation of the Critical Strain-Based Methodology for Evaluating the Mechanical Safety of Ball Grid Array Solder Joints in a Launch Random Vibration Environment. J. Electron. Packag. 2022, 144, 011006. [Google Scholar] [CrossRef]
  69. Jang, J.; Jang, G.; Lee, J.; Cho, Y.; Cinar, Y. Fatigue life estimations of solid-state drives with dummy solder balls under vibration. Int. J. Fatigue 2016, 88, 42–48. [Google Scholar] [CrossRef]
  70. Shen, Y.-L. Thermo-mechanical stresses in copper interconnects—A modeling analysis. Microelectron. Eng. 2006, 83, 446–459. [Google Scholar] [CrossRef]
  71. Lau, J. Thermal Stress and Strain in Microelectronics Packaging; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
  72. Noda, N.; Hetnarski, R.B.; Tanigawa, Y. Thermal Stresses; Routledge: London, UK, 2018. [Google Scholar]
  73. Vasudevan, V.; Coyle, R.; Aspandiar, R.; Tisdale, S.; Kinyanjui, R.; Long, G. Thermal cycling reliability, microstructural characterization, and assembly challenges with backward compatible soldering of a large, high density ball grid array. In Proceedings of the 2011 IEEE 61st Electronic Components and Technology Conference (ECTC), Lake Buena Vista, FL, USA, 31 May–3 June 2011; pp. 954–964. [Google Scholar]
  74. Liu, J.; He, L.; Chen, H.; Zhao, P.; Su, Y.; Chao, L.; Pan, Q. Reliability Simulation and Life Prediction of Sn63Pb37 BGA Solder Joint Under Thermal Cycling Load. In Proceedings of the 2020 China Semiconductor Technology International Conference (CSTIC), Shanghai, China, 26 June–17 July 2020; pp. 1–4. [Google Scholar]
  75. Zhang, L.; Chee, S.-S.; Maheshwari, A.; Funcell, A. Experimental and finite element analysis of cavity down BGA package solder joint reliability. In Proceedings of the 3rd Electronics Packaging Technology Conference (EPTC 2000) (Cat. No. 00EX456), Singapore, 7 December 2000; pp. 391–397. [Google Scholar]
  76. Koo, J.-M.; Jung, S.-B. Effect of displacement rate on ball shear properties for Sn–37Pb and Sn–3.5 Ag BGA solder joints during isothermal aging. Microelectron. Reliab. 2007, 47, 2169–2178. [Google Scholar] [CrossRef]
  77. Huang, X.; Lee, S.-W.; Yan, C.C.; Hui, S. Characterization and analysis on the solder ball shear testing conditions. In Proceedings of the 51st Electronic Components and Technology Conference (Cat. No. 01CH37220), Orlando, FL, USA, 29 May–1 June 2001; pp. 1065–1071. [Google Scholar]
  78. Erich, R.; Coyle, R.J.; Wenger, G.M.; Primavera, A. Shear testing and failure mode analysis for evaluation of BGA ball attachment. In Proceedings of the Twenty Fourth IEEE/CPMT International Electronics Manufacturing Technology Symposium (Cat. No. 99CH36330), Austin, TX, USA, 19 October 1999; pp. 16–22. [Google Scholar]
  79. Coyle, R.J.; Solan, P.P. The influence of test parameters and package design features on ball shear test requirements. In Proceedings of the Twenty Sixth IEEE/CPMT International Electronics Manufacturing Technology Symposium (Cat. No. 00CH37146), Santa Clara, CA, USA, 3 October 2000; pp. 168–177. [Google Scholar]
  80. Coyle, R.J.; Solan, P.P.; Serafino, A.J.; Gahr, S.A. The influence of room temperature aging on ball shear strength and microstructure of area array solder balls. In Proceedings of the 50th Electronic Components and Technology Conference (Cat. No. 00CH37070), Las Vegas, NV, USA, 21–24 May 2000; pp. 160–169. [Google Scholar]
  81. Chia, J.Y.H.; Cotterell, B.; Chai, T.C. The mechanics of the solder ball shear test and the effect of shear rate. Mater. Sci. Eng. A 2006, 417, 259–274. [Google Scholar] [CrossRef]
  82. Kim, J.-W.; Jung, S.-B. Experimental and finite element analysis of the shear speed effects on the Sn–Ag and Sn–Ag–Cu BGA solder joints. Mater. Sci. Eng. A 2004, 371, 267–276. [Google Scholar] [CrossRef]
  83. Chapetti, M.D.; Jaureguizahar, L. Fatigue behavior prediction of welded joints by using an integrated fracture mechanics approach. Int. J. Fatigue 2012, 43, 43–53. [Google Scholar] [CrossRef]
  84. Yang, Q.; Shim, D.; Spearing, S. A cohesive zone model for low cycle fatigue life prediction of solder joints. Microelectron. Eng. 2004, 75, 85–95. [Google Scholar] [CrossRef]
  85. Knecht, S.; Fox, L. Integrated matrix creep: Application to accelerated testing and lifetime prediction. In Solder Joint Reliability; Springer: Berlin/Heidelberg, Germany, 1991; pp. 508–544. [Google Scholar]
  86. Solomon, H. Fatigue of 60/40 solder. IEEE Trans. Compon. Hybrid Manuf. Technol. 1986, 9, 423–432. [Google Scholar] [CrossRef]
  87. Sornette, D.; Magnin, T.; Brechet, Y.J.E. The physical origin of the Coffin-Manson law in low-cycle fatigue. Europhys. Lett. 1992, 20, 433. [Google Scholar] [CrossRef]
  88. Feltner, C.E.; Morrow, J.D. Microplastic strain hysteresis energy as a criterion for fatigue fracture. J. Basic Eng. 1961, 83, 15–22. [Google Scholar] [CrossRef]
  89. Bhate, D.; Subbarayan, G. A nonlinear fracture mechanics prespective on solder joint failure: Going beyond the coffin-manson equation. In Proceedings of the Thermal and Thermomechanical Proceedings 10th Intersociety Conference on Phenomena in Electronics Systems, San Diego, CA, USA, 30 May–2 June 2006; pp. 1220–1225. [Google Scholar]
  90. Clatterbaugh, G. Thermomechanical Behavior of Solid Interconnects for Surface Mounting: A Comparison of Theory and Experiment. In Proceedings of the 35th Electronic Components Conference, Washington, DC, USA, 20–22 May 1985; pp. 60–72. [Google Scholar]
  91. Gektin, V.; Bar-Cohen, A.; Ames, J. Coffin-Manson fatigue model of underfilled flip-chips. IEEE Trans. Compon. Packag. Manuf. Technol. Part A 1997, 20, 317–326. [Google Scholar] [CrossRef]
  92. Ju, T.-H.; Lin, W.; Lee, Y.; Liu, J.J. Effects of ceramic ball-grid-array package’s manufacturing variations on solder joint reliability. J. Electron. Packag. 1994, 116, 242–248. [Google Scholar] [CrossRef]
  93. Qu, X.; Chen, Z.; Qi, B.; Lee, T.; Wang, J.J. Board level drop test and simulation of leaded and lead-free BGA-PCB assembly. Microelectron. Reliab. 2007, 47, 2197–2204. [Google Scholar] [CrossRef]
  94. Xiao, H.; Li, X.; Hu, Y.; Guo, F.; Shi, Y. Damage behavior of SnAgCu/Cu solder joints subjected to thermomechanical cycling. J. Alloys Compd. 2013, 578, 110–117. [Google Scholar] [CrossRef]
  95. Li, J.; Xu, H.; Hokka, J.; Mattila, T.T.; Chen, H.; Paulasto-Kröckel, M.J.S. Finite element analyses and lifetime predictions for SnAgCu solder interconnections in thermal shock tests. Solder. Surf. Mount Technol. 2011, 23, 161–167. [Google Scholar] [CrossRef]
  96. Su, S.; Akkara, F.J.; Thaper, R.; Alkhazali, A.; Hamasha, M.; Hamasha, S. A state-of-the-art review of fatigue life prediction models for solder joint. J. Electron. Packag. 2019, 141, 040802. [Google Scholar] [CrossRef]
  97. Ghavifekr, H.; Michel, B.J.S.; Physical, A.A. Generalized fracture mechanical integral concept JG and its application in microelectronic packaging technology. Sens. Actuators A 2002, 99, 183–187. [Google Scholar] [CrossRef]
  98. Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
  99. Pugno, N.; Ciavarella, M.; Cornetti, P.; Carpinteri, A. A generalized Paris’ law for fatigue crack growth. J. Mech. Phys. Solids 2006, 54, 1333–1349. [Google Scholar] [CrossRef]
  100. McEvily, A. A modified constitutive relation for fatigue crack growth. In Proceedings of the 7th International Fatigue Congress (Fatigue’99), Beijing, China, 1 May 1999; pp. 329–336. [Google Scholar]
  101. Depiver, J.a.; Mallik, S.; Harmanto, D. Solder joint failures under thermo-mechanical loading conditions—A review. Adv. Mater. Process. Technol. 2021, 7, 1–26. [Google Scholar] [CrossRef]
  102. Shrestha, T.; Gollapudi, S.; Charit, I.; Murty, K.L. Creep deformation behavior of Sn–Zn solder alloys. J. Mater. Sci. 2014, 49, 2127–2135. [Google Scholar] [CrossRef]
  103. Knecht, S.; Fox, L. Constitutive relation and creep-fatigue life model for eutectic tin-lead solder. IEEE Trans. Compon. Hybrid Manuf. Technol. 1990, 13, 424–433. [Google Scholar] [CrossRef]
  104. Syed, A. Updated life prediction models for solder joints with removal of modeling assumptions and effect of constitutive equations. In Proceedings of the EuroSime 2006—7th International Conference on Thermal, Mechanical and Multiphysics Simulation and Experiments in Micro-Electronics and Micro-Systems, Como, Italy, 24–26 April 2006; pp. 1–9. [Google Scholar]
  105. Li, C.-G.; Lin, D.-H.; Zhou, J.-M. Thermal reliability analysis of package in PBGA. Electron. Compon. Mater. 2008, 27, 65. [Google Scholar]
  106. Basit, M.M.; Motalab, M.; Suhling, J.C.; Hai, Z.; Evans, J.; Bozack, M.J.; Lall, P. Thermal cycling reliability of aged PBGA assemblies-comparison of Weibull failure data and finite element model predictions. In Proceedings of the 2015 IEEE 65th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 26–29 May 2015; pp. 106–117. [Google Scholar]
Electronics 11 00542 g001 550
Figure 1. Factors affecting the failure of electronic components.
Figure 1. Factors affecting the failure of electronic components.
Electronics 11 00542 g001
Electronics 11 00542 g002 550
Figure 2. Failure of the solder joints of the BGA chips under the influences of (a) temperature, (b) vibration, and (c) humidity.
Figure 2. Failure of the solder joints of the BGA chips under the influences of (a) temperature, (b) vibration, and (c) humidity.
Electronics 11 00542 g002
Electronics 11 00542 g003 550
Figure 3. Main failure modes of BGA solder joints.
Figure 3. Main failure modes of BGA solder joints.
Electronics 11 00542 g003
Electronics 11 00542 g004 550
Figure 4. Combination of experimental studies and finite element analysis.
Figure 4. Combination of experimental studies and finite element analysis.
Electronics 11 00542 g004
Table
Table 1. Summary of failure factors and failure reasons for electronic components.
Table 1. Summary of failure factors and failure reasons for electronic components.
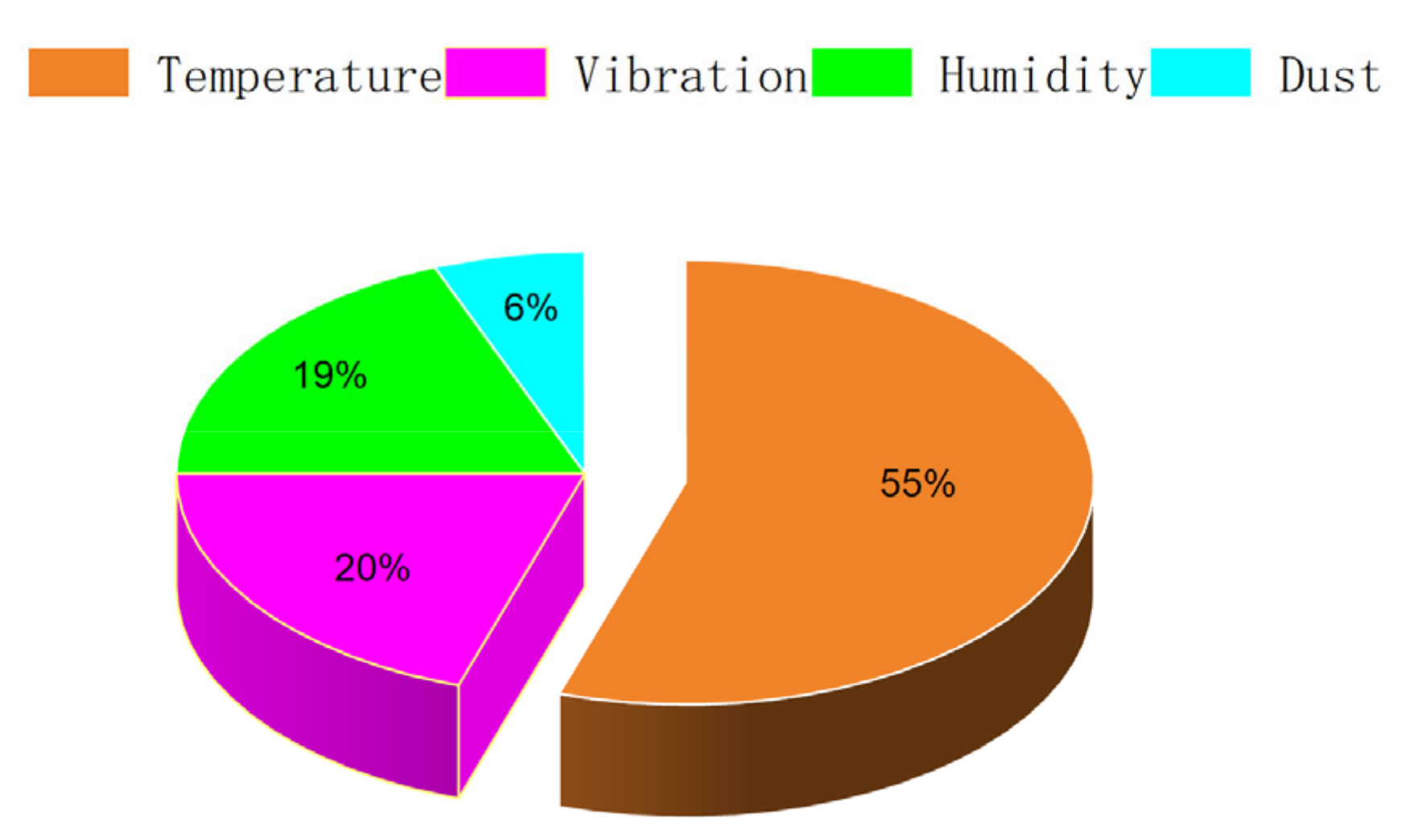
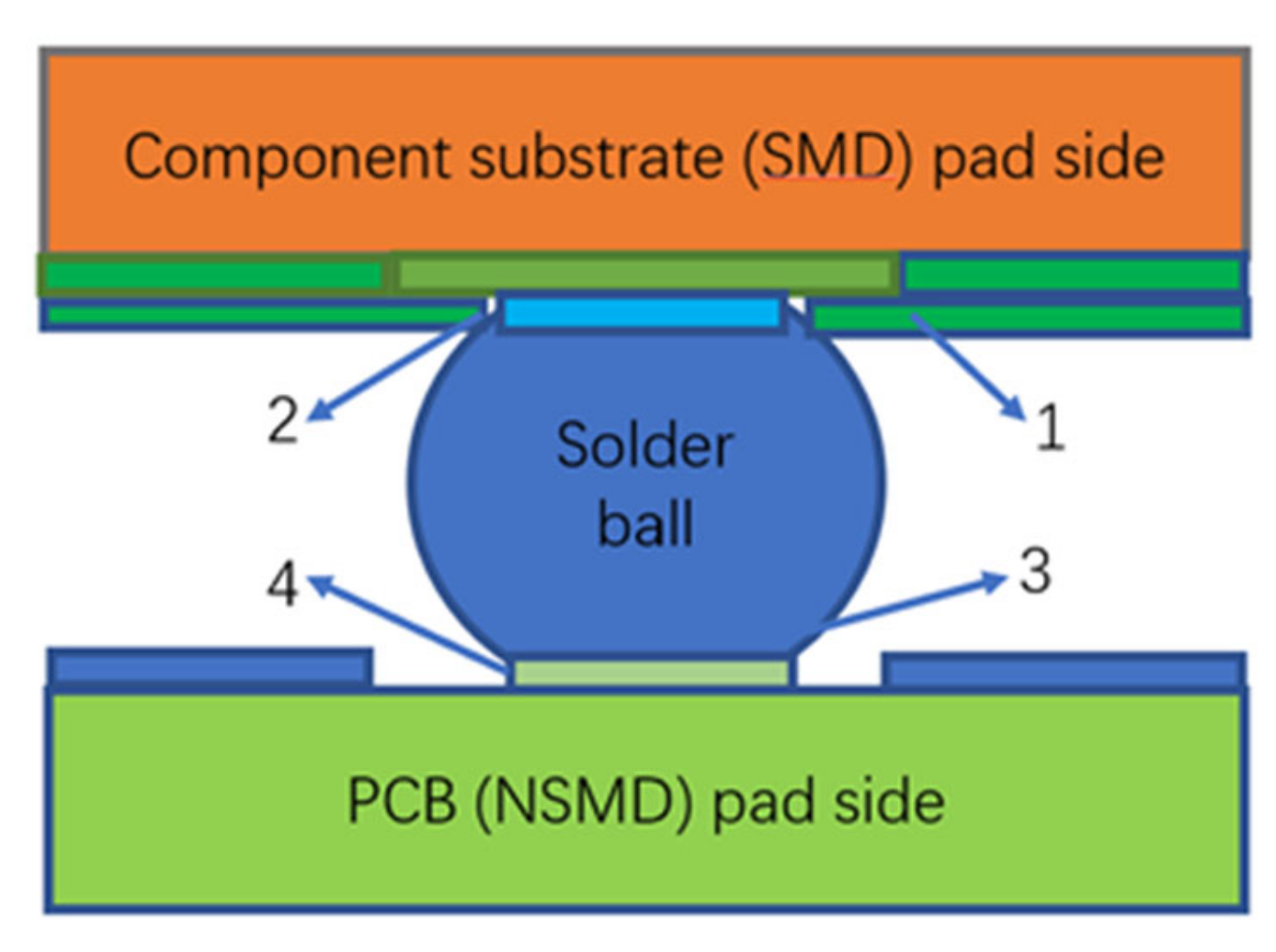
FactorReason for Failure
temperature(1) The difference in thermal expansion coefficients between materials causes different degrees of deformation of the materials, which generates stress and strain inside the solder joints; (2) high temperature results in the burnout of the chip.
vibration and shockRelative movement between the solder joint and the substrate causes cracks, which are contributed by vibration and shock.
moisture(1) The moisture inside the solder joint generates a high vapor pressure at high temperature, which will result in cracks; (2) the moisture reduces the adhesion between materials and causes the bonding failure of solder joints.
dust(1) The dust influences the heat dissipation of components, which accelerates the insulation aging; (2) the dust influences the short-circuit conduction of some solder joints, which burns out electronic components.
Table
Table 2. Common test methods [56].
Table 2. Common test methods [56].
Test MethodsTest ResultsScopes of Application
White light interferometerGeometric size, displacement along the Z direction. Resolution: nanometer.Used at normal temperature. The sample surface is relatively flat.
Electronic speckle interferometer
(ESPI)		Three-direction displacement and deformation. Resolution: 20 nanometers.Temperature range for the experimental environment: −40~150, component level (including solder joints).
Moire interferometerIn-plane displacement and deformation. Resolution: sub-pixel.Experimental test environment is the same as that for the ESPI. The iso-displacement line can be directly compared with the results obtained by the finite element simulation method.
Digital image correlation
(DIC)		In-plane displacement and deformation. Resolution: sub-pixel.Experimental test environment is the same as that for the ESPI. Large observation range (>cm to 1/10 pixel). It can be combined with a microscope and an SEM.
Silicon chip testingStress and strain of the chip with the displacement. Resolution: MPa.Device-level test. Connected in the circuit. It can be applied to the field environment.
X-ray reflectionBending radius of crystal material (such as silicon material).Experimental environment temperature: −40~120. In principle, internal packaging and testing can be carried out.
X-ray diffractionMechanical stress and strain of crystalline materials (such as silicon materials).Experimental environment temperature: −40~120. In principle, internal packaging and testing can be carried out.
Scanning electron microscope
(SEM)		In-plane displacement. Resolution: nanometer.While observing the morphology, the composition of the micro-area is analyzed.
Table
Table 3. Summary of the failure studies under vibration loads.
Table 3. Summary of the failure studies under vibration loads.
Load ConditionMethodsConclusionsReferences
Random vibrationPCB components were used for testing under random vibration loads to record the center displacement response and failure time of the components. ABAQUS software was used for simulation verification.The solder joints at the four corners of the outermost layer of the BGA package had high peel stresses. The critical stress response of the solder joint increased with the increase in the vibration load.Fang Liu, Ye Lu [64]
Sinusoidal vibrationPCB components were installed on the front and back sides of the vibrator in the test vehicle for testing.The failed solder joints were located at the corners of the BGA module, and most of the failures were caused by cracks near the copper pad on the PCB side.Yang [65]
Harmonic vibrationThe combination of a harmonic vibration test and finite element simulation was used to study the vibration durability of Sn37Pb and SAC305 solders.The study found that SAC305 interconnects have lower fatigue durability than Sn37Pb interconnects under the level of narrow-band harmonic excitation.Zhou [66]
Sinusoidal vibrationA vibration failure test, finite element analysis, and a theoretical formula were used to calculate the fatigue life of electronic components under the vibration load.The stress–failure cycle curve of the solder joint component was established. The stress analysis of the solder joint indicated that the maximum stress occurs at the corner of the component, and the local maximum stress of the solder joint is located at the joint between the solder joint and the PCB board.Chen [67]
Random vibrationPCB component samples were created at different board positions and exposed to random vibration. Then, a critical strain-based method was proposed to evaluate the fatigue life of solder joints.The effectiveness of the method was verified by comparing the fatigue life of each component and the safety margin estimated by various analysis methods.Yong Park, Hyun-Ung Oh [68]
Sinusoidal vibrationFinite element analysis and a vibration experiment were used to calculate the stress in the solder joints. The first resonance frequency was used to excite the solder joints until the component entirely failed.The stress–failure cycle number curve was achieved by simulations and experiments. The solder joints at the corners of the SSD package were the most vulnerable.Jinwoo Jang [69]
Table
Table 4. Summary of studies conducted under thermal stress.
Table 4. Summary of studies conducted under thermal stress.
Research ApproachMethodsConclusionsReferences
ExperimentAccelerated temperature cycling was used to evaluate the thermal fatigue reliability of lead-free and lead solder joints.The failure analysis showed that low-level lead mixing reduced the reliability of solder joints. Lead solder joints had better reliabilities than lead-free ones.Vasu Vasudevan [73]
Finite element simulation, model predictionThe finite element simulation and Coffin–Mason model were used to predict the fatigue life of solder joints under a temperature cycle load.Simulation analysis indicated that cracks emerge in the solder joints near the connection between the IMC layer and the solder joints, and the thickness of the PCB board and the height of the solder joints can affect the fatigue life of the solder joints.Jiahao Liu, Liang He [74]
Finite element simulation, model predictionSolder joints with different alloy compositions were characterized by their thermal fatigue responses to predict their failure time.Finite element analysis indicated that the materials of SAC405 and SAC387 have the highest and lowest thermal fatigue life, respectively. A new life prediction model was proposed by combining several damage parameters.Joshua A. Depivera [21]
Experiment, finite element simulationA temperature cycle experiment and finite element analysis were used to analyze the thermal fatigue life of solder joints.Three-board-level reliability experiments showed that the method meets the requirements of industrial applications, and the three-dimensional finite element model was successfully applied to FG680.Leilei Zhang [75]
Table
Table 5. Summary of studies conducted under shear stress.
Table 5. Summary of studies conducted under shear stress.
Research ApproachMethodsConclusionsReferences
ExperimentA high-speed shear test was used to shear lead solder balls and lead-free ones at different speeds.The high-speed shear test can cause unstable fractures at the interface between the solder ball and the pad. Since lead-free solder balls are prone to brittle interface fracture, their interface toughness should be improved. The shear strength and maximal shear for lead solder balls increased with the increase in the shear speed within the maximal load.Julian Yan Hon Chiaa [81]
Test, finite element simulation, elasto-viscoplastic constitutive modelAn elasto-viscoplastic constitutive model, experiment, and nonlinear finite element analysis were used to study the influence of the shear speed on the shear force of solder joints.The nonlinear finite element analysis and the elastic-viscoplastic constitutive model analysis indicated that the shear force of Sn-3.5Ag solder joints and Sn-3.5Ag-0.75Cu solder joints increased with the increase in the shear speed at a fixed shear height.Jong-Woong Kim [82]
TestDifferent pad sizes and different overall solder ball heights were used to study the reliability of the shear strength of the solder ball.The shear strength was the highest when the overall solder ball height was the lowest and the pad size was the largest, and vice versa.Ogunsemi, B.T. [20]
Table
Table 6. Summary of fatigue life prediction models.
Table 6. Summary of fatigue life prediction models.
Fatigue ModelEquationsModel ClassApplicable PackagesCoverageRequired Parameters
1Coffin–Manson1Plastic strainAllLow-cycle fatigueNf = Number of failure cycle, A = Material constant,
∆γ = Cyclic plastic shear strain, f = Thermal cycle frequency,
β = Activation energy, Tmax = The highest temperature in the cycle,
k = Boltzmann constant, n = Empirical constant,
m = Constant value
2Darveaux2, 3, 4Damage leads to crack initiation and propagationAssemblies with SnPb
solder joints		Thermal cycling with
different thermal
profiles		Ns = Characteristic life of interconnected solder joints, NO = Number of cycles of crack initiation, a = Characteristic length of fracture,
da⁄dN = Crack growth rate, ∆Wave = Average inelastic strain energy density accumulated in each cycle, K1, K2, K3, K4 = the coefficients obtained from experiments and related to crack growth,
3Paris5, 6Elastoplastic fracture and fatigueAllSubcritical propagation of cracksda⁄dN = Crack growth rate, N = Number of failure cycles, a = Crack length, ∆k = Amplitude of stress intensity factor in each stress cycle, kmax = Maximum stress intensity factor in a load cycle, kmin = Minimum stress intensity factor in a load cycle, C" = Material constant, n′ = Material constant
4Knecht–Fox7Matrix creepAllMatrix creep onlyC = Material constants related to the microstructure of solder, ∆γmc = the creep stress amplitude of the matrix
5Syed8, 9Accumulation of creep strain energyPBGA, SMD, NSMDImplies full coverageεacc = accumulated creep strain of each cycle, C′ = Constant reciprocal of creep ductility
wacc = the creep strain energy density accumulated in each cycle, W′ = Creep strain energy density at failure
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Qiu, B.; Xiong, J.; Wang, H.; Zhou, S.; Yang, X.; Lin, Z.; Liu, M.; Cai, N. Survey on Fatigue Life Prediction of BGA Solder Joints. Electronics 2022, 11, 542. https://doi.org/10.3390/electronics11040542

AMA Style

Qiu B, Xiong J, Wang H, Zhou S, Yang X, Lin Z, Liu M, Cai N. Survey on Fatigue Life Prediction of BGA Solder Joints. Electronics. 2022; 11(4):542. https://doi.org/10.3390/electronics11040542

Chicago/Turabian Style

Qiu, Baojun, Jingang Xiong, Han Wang, Shuai Zhou, Xiuding Yang, Zhengpei Lin, Maolin Liu, and Nian Cai. 2022. "Survey on Fatigue Life Prediction of BGA Solder Joints" Electronics 11, no. 4: 542. https://doi.org/10.3390/electronics11040542

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop