TAWSEEM: A Deep-Learning-Based Tool for Estimating the Number of Unknown Contributors in DNA Profiling
Abstract
:1. Introduction
2. Background
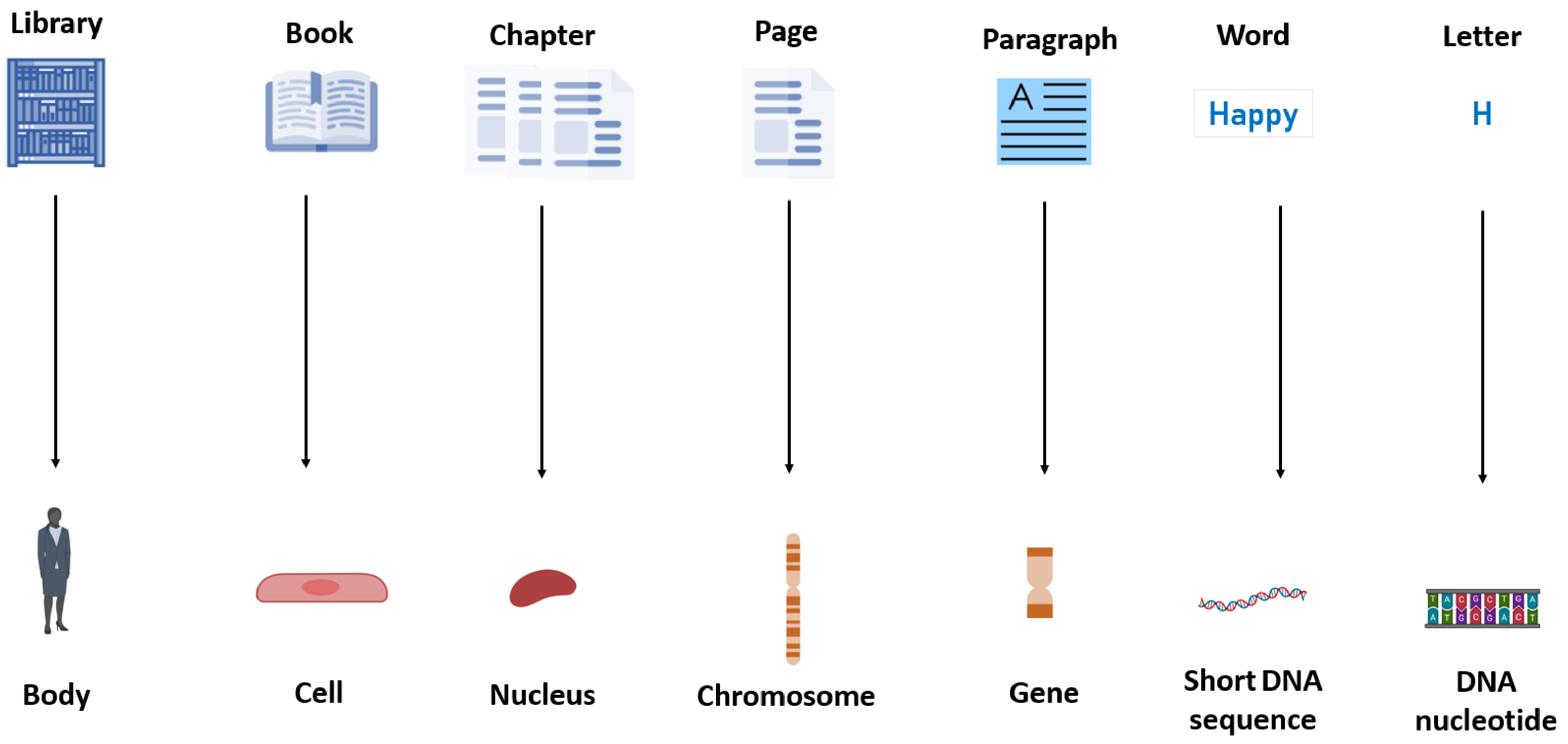
2.1. DNA Biology and Genetics
2.2. DNA Mixtures
2.3. Genetic Markers
2.4. Challenges in Analysing DNA Profiles
2.5. Forensic Science and DNA Profiling
2.6. Likelihood Estimation
2.7. DNA Databases
3. Related Works
3.1. Basic Methods and Tools
3.2. HPC Methods and Tools
3.3. Machine Learning in DNA Profiling
3.4. Machine Learning in Bioinformatics
4. Methodology and Design
4.1. PROVEDIt Dataset
4.1.1. Single Multiplex Profiles
4.1.2. Four Multiplex Profiles (14 Loci)
4.1.3. Three Multiplexes Profiles (16 Loci)
4.2. Pre-Processing
4.2.1. Data Imputation
4.2.2. Missing Values
4.2.3. Out of Ladder (OL) Values
4.2.4. Amel, Yindel Loci, and Profile Name
4.2.5. Dye Symbols and Marker Names
4.2.6. Profile Loci
4.2.7. Feature Importance
4.3. The Deep Learning Model
4.4. Evaluation Metrics
- Accuracy shows how good the predictions are, on average.
- Precision shows how accurate our model is out of those predicted positive, and how many of them are actual positive.
- Recall shows how many of the actual positives our model captures through labeling it as positive.
- F1-score is the weighted average of precision and recall.
5. Results and Analysis
5.1. The Single Multiplex Profiles
5.2. The Four Multiplexes Profiles (14 Loci)
5.3. The Three Multiplex Profiles (16 Loci)
5.4. TAWSEEM: Comparison with Other Works
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DNA | Deoxyribonucleic acid |
| HPC | High-performance computing |
| OL | Three-letter acronym |
| RMP | Random match probability |
| MAC | Maximum allele count |
| TAC | Total allele count |
| MLP | Multilayer perceptron |
| TP | True positive |
| TN | True negative |
| FN | False negative |
| FP | False positive |
| GPU | Graphical processing unit |
| STR | Short tandem repeats |
| PCR | Polymerase chain reaction |
References
- Butler, J.M. Fundamentals of Forensic DNA Typing; Elsevier Inc.: Amsterdam, The Netherlands, 2010. [Google Scholar] [CrossRef]
- Alamoudi, E.; Mehmood, R.; Albeshri, A.; Gojobori, T. A Survey of Methods and Tools for Large-Scale DNA Mixture Profiling. In Smart Infrastructure and Applications; Springer: Cham, Switzerland, 2020; pp. 217–248. [Google Scholar] [CrossRef]
- Clayton, T.M.; Whitaker, J.P.; Sparkes, R.; Gill, P. Analysis and interpretation of mixed forensic stains using DNA STR profiling. Forensic Sci. Int. 1998, 91, 55–70. [Google Scholar] [CrossRef]
- Egeland, T.; Dalen, I.; Mostad, P.F. Estimating the number of contributors to a DNA profile. Int. J. Leg. Med. 2003, 117, 271–275. [Google Scholar] [CrossRef] [PubMed]
- Taylor, D.; Bright, J.A.; Buckleton, J. Interpreting forensic DNA profiling evidence without specifying the number of contributors. Forensic Sci. Int. Genet. 2014, 13, 269–280. [Google Scholar] [CrossRef] [PubMed]
- Alotaibi1, H.; Alsolami, F.; Mehmood, R. DNA Profiling: An Investigation of Six Machine Learning Algorithms for Estimating the Number of Contributors in DNA Mixtures. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2021, 12. [Google Scholar] [CrossRef]
- Swaminathan, H.; Grgicak, C.M.; Medard, M.; Lun, D.S. NOCIt: A computational method to infer the number of contributors to DNA samples analyzed by STR genotyping. Forensic Sci. Int. Genet. 2015, 16, 172–180. [Google Scholar] [CrossRef]
- Alamoudi, E.; Mehmood, R.; Albeshri, A.; Gojobori, T. DNA Profiling Methods and Tools: A Review. In International Conference on Smart Cities, Infrastructure, Technologies and Applications; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Bleka, Ø.; Storvik, G.; Gill, P. EuroForMix: An open source software based on a continuous model to evaluate STR DNA profiles from a mixture of contributors with artefacts. Forensic Sci. Int. Genet. 2016, 21, 35–44. [Google Scholar] [CrossRef] [Green Version]
- Balding, D.J.; Steele, C.D.; Building, D.; Street, G. likeLTD v6.3: An Illustrative Analysis, Explanation of the Model, Results of Validation Tests and Version History. Available online: https://blogs.unimelb.edu.au/statisticalgenomics/publications-software/likeltd-software/ (accessed on 5 February 2022).
- Alamoudi, E.M. Parallel Analysis of DNA Profile Mixtures with a Large Number of Contributors. Master’s Thesis, King Abdulaziz University, Jeddah, Saudi Arabia, 2019. [Google Scholar]
- Marciano, M.A.; Adelman, J.D. PACE: Probabilistic Assessment for Contributor Estimation—A machine learning-based assessment of the number of contributors in DNA mixtures. Forensic Sci. Int. Genet. 2017, 27, 82–91. [Google Scholar] [CrossRef]
- Benschop, C.C.G.; Linden, J.V.; Hoogenboom, J.; Ypma, R.; Haned, H. Automated estimation of the number of contributors in autosomal short tandem repeat profiles using a machine learning approach. Forensic Sci. Int. Genet. 2019, 1–33. [Google Scholar] [CrossRef]
- Alfonse, L.E.; Garrett, A.D.; Lun, D.S.; Duffy, K.R.; Grgicak, C.M. A large-scale dataset of single and mixed-source short tandem repeat profiles to inform human identification strategies: PROVEDIt. Forensic Sci. Int. Genet. 2018, 32, 62–70. [Google Scholar] [CrossRef]
- Kruijver, M.; Kelly, H.; Cheng, K.; Lin, M.H.; Morawitz, J.; Russell, L.; Buckleton, J.; Bright, J.A. Estimating the number of contributors to a DNA profile using decision trees. Forensic Sci. Int. Genet. 2021, 50, 102407. [Google Scholar] [CrossRef]
- Coquoz, R. FORENSIC SCIENCES|DNA Profiling. Encycl. Anal. Sci. 2005, 384–391. [Google Scholar] [CrossRef]
- Graversen, T. Statistical and Computational Methodology for the Analysis of Forensic DNA Mixtures with Artefacts. Ph.D. Thesis, Oxford University, Oxford, UK, 2014; p. 229. [Google Scholar]
- Garofano, P.; Caneparo, D.; D’Amico, G.; Vincenti, M.; Alladio, E. An alternative application of the consensus method to DNA typing interpretation for Low Template-DNA mixtures. Forensic Sci. Int. Genet. Suppl. Ser. 2015, 5, e422–e424. [Google Scholar] [CrossRef]
- Fedushko, S.; Ustyianovych, T.; Gregus, M. Real-Time High-Load Infrastructure Transaction Status Output Prediction Using Operational Intelligence and Big Data Technologies. Electronics 2020, 9, 668. [Google Scholar] [CrossRef] [Green Version]
- Alam, F.; Almaghthawi, A.; Katib, I.; Albeshri, A.; Mehmood, R. iResponse: An AI and IoT-Enabled Framework for Autonomous COVID-19 Pandemic Management. Sustainability 2021, 13, 3797. [Google Scholar] [CrossRef]
- Muhammed, T.; Mehmood, R.; Albeshri, A.; Katib, I. UbeHealth: A personalized ubiquitous cloud and edge-enabled networked healthcare system for smart cities. IEEE Access 2018, 6, 32258–32285. [Google Scholar] [CrossRef]
- Alomari, E.; Katib, I.; Albeshri, A.; Yigitcanlar, T.; Mehmood, R. Iktishaf+: A Big Data Tool with Automatic Labeling for Road Traffic Social Sensing and Event Detection Using Distributed Machine Learning. Sensors 2021, 21, 2993. [Google Scholar] [CrossRef]
- Omar Alkhamisi, A.; Mehmood, R. An Ensemble Machine and Deep Learning Model for Risk Prediction in Aviation Systems. In 2020 6th Conference on Data Science and Machine Learning Applications (CDMA); Institute of Electrical and Electronics Engineers (IEEE): Riyadh, Saudi Arabia, 2020; pp. 54–59. [Google Scholar] [CrossRef]
- Aqib, M.; Mehmood, R.; Alzahrani, A.; Katib, I.; Albeshri, A.; Altowaijri, S.M. Rapid Transit Systems: Smarter Urban Planning Using Big Data, In-Memory Computing, Deep Learning, and GPUs. Sustainability 2019, 11, 2736. [Google Scholar] [CrossRef] [Green Version]
- Mehmood, R.; Alam, F.; Albogami, N.N.; Katib, I.; Albeshri, A.; Altowaijri, S.M. UTiLearn: A Personalised Ubiquitous Teaching and Learning System for Smart Societies. IEEE Access 2017, 5, 2615–2635. [Google Scholar] [CrossRef]
- Mehmood, R.; See, S.; Katib, I.; Chlamtac, I. Smart Infrastructure and Applications: Foundations for Smarter Cities and Societies; Springer International Publishing; Springer Nature: Cham, Switzerland, 2020; p. 692. [Google Scholar] [CrossRef]
- Yigitcanlar, T.; Kankanamge, N.; Regona, M.; Maldonado, A.R.; Rowan, B.; Ryu, A.; Desouza, K.C.; Corchado, J.M.; Mehmood, R.; Li, R.Y.M. Artificial Intelligence Technologies and Related Urban Planning and Development Concepts: How Are They Perceived and Utilized in Australia? J. Open Innov. Technol. Mark. Complex. 2020, 6, 187. [Google Scholar] [CrossRef]
- Yigitcanlar, T.; Regona, M.; Kankanamge, N.; Mehmood, R.; D’Costa, J.; Lindsay, S.; Nelson, S.; Brhane, A. Detecting Natural Hazard-Related Disaster Impacts with Social Media Analytics: The Case of Australian States and Territories. Sustainability 2022, 14, 810. [Google Scholar] [CrossRef]
- Alam, F.; Mehmood, R.; Katib, I.; Albogami, N.N.; Albeshri, A. Data Fusion and IoT for Smart Ubiquitous Environments: A Survey. IEEE Access 2017, 5, 9533–9554. [Google Scholar] [CrossRef]
- Mohammed, T.; Albeshri, A.; Katib, I.; Mehmood, R. DIESEL: A Novel Deep Learning based Tool for SpMV Computations and Solving Sparse Linear Equation Systems. J. Supercomput. 2020, 77, 6313–6355. [Google Scholar] [CrossRef]
- Muhammed, T.; Mehmood, R.; Albeshri, A.; Katib, I. SURAA: A novel method and tool for loadbalanced and coalesced SpMV computations on GPUs. Appl. Sci. 2019, 9, 947. [Google Scholar] [CrossRef] [Green Version]
- Bosaeed, S.; Katib, I.; Mehmood, R. A Fog-Augmented Machine Learning based SMS Spam Detection and Classification System. In Proceedings of the 2020 Fifth International Conference on Fog and Mobile Edge Computing (FMEC), Paris, France, 20–23 April 2020; pp. 325–330. [Google Scholar] [CrossRef]
- Gustisyaf, A.I.; Sinaga, A. Implementation of Convolutional Neural Network to Classification Gender based on Fingerprint. Int. J. Mod. Educ. Comput. Sci. (IJMECS) 2021, 13, 55–67. [Google Scholar] [CrossRef]
- Hung, C.L.; Tang, C.Y. Bioinformatics tools with deep learning based on GPU. In Proceedings of the 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Kansas City, MO, USA, 13–16 November 2017; pp. 1906–1908. [Google Scholar] [CrossRef]
- Larranaga, P.; Calvo, B.; Santana, R.; Bielza, C.; Galdiano, J.; aki Inza, I.; Lozano, A.; Anzas, A.; Pe, A.; Robles, V.; et al. Machine learning in bioinformatics Downloaded from. Briefings Bioinform. 1991, 7, 112. [Google Scholar] [CrossRef] [Green Version]
- Olson, R.S.; La Cava, W.; Mustahsan, Z.; Varik, A.; Moore, J.H. Data-driven advice for applying machine learning to bioinformatics problems. Pac. Symp. Biocomput. 2018, 0, 192–203. [Google Scholar] [CrossRef] [Green Version]
- Schmauch, B.; Romagnoni, A.; Pronier, E.; Saillard, C.; Maillé, P.; Calderaro, J.; Kamoun, A.; Sefta, M.; Toldo, S.; Zaslavskiy, M.; et al. A deep learning model to predict RNA-Seq expression of tumours from whole slide images. Nat. Commun. 2020, 11, 3877. [Google Scholar] [CrossRef] [PubMed]
- AlAhmadi, S.; Mohammed, T.; Albeshri, A.; Katib, I.; Mehmood, R. Performance Analysis of Sparse Matrix-Vector Multiplication (SpMV) on Graphics Processing Units (GPUs). Electronics 2020, 9, 1675. [Google Scholar] [CrossRef]
- Alyahya, H.; Mehmood, R.; Katib, I. Parallel Iterative Solution of Large Sparse Linear Equation Systems on the Intel MIC Architecture. In Smart Infrastructure and Applications; Springer: Cham, Switzerland, 2020; pp. 377–407. [Google Scholar] [CrossRef]
- Usman, S.; Mehmood, R.; Katib, I. Big Data and HPC Convergence for Smart Infrastructures: A Review and Proposed Architecture. EAI/Springer Innov. Commun. Comput. 2020, 561–586. [Google Scholar] [CrossRef]
- Alotaibi, S.; Mehmood, R.; Katib, I. Sentiment analysis of Arabic tweets in smart cities: A review of Saudi dialect. In Proceedings of the 2019 4th International Conference on Fog and Mobile Edge Computing, Rome, Italy, 10–13 June 2019. [Google Scholar] [CrossRef]
- Mohammed, T.; Albeshri, A.; Katib, I.; Mehmood, R. UbiPriSEQ—Deep Reinforcement Learning to Manage Privacy, Security, Energy, and QoS in 5G IoT HetNets. Appl. Sci. 2020, 10, 7120. [Google Scholar] [CrossRef]
- Yigitcanlar, T.; Mehmood, R.; Corchado, J.M. Green Artificial Intelligence: Towards an Efficient, Sustainable and Equitable Technology for Smart Cities and Futures. Sustainability 2021, 13, 8952. [Google Scholar] [CrossRef]
- Yigitcanlar, T.; Corchado, J.M.; Mehmood, R.; Li, R.Y.M.; Mossberger, K.; Desouza, K. Responsible Urban Innovation with Local Government Artificial Intelligence (AI): A Conceptual Framework and Research Agenda. J. Open Innov. Technol. Mark. Complex. 2021, 7, 71. [Google Scholar] [CrossRef]
- Yan, X.; Cui, B.; Xu, Y.; Shi, P.; Wang, Z. A Method of Information Protection for Collaborative Deep Learning under GAN Model Attack. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 871–881. [Google Scholar] [CrossRef]
- Li, X.; Du, Z.; Huang, Y.; Tan, Z. A deep translation (GAN) based change detection network for optical and SAR remote sensing images. ISPRS J. Photogramm. Remote. Sens. 2021, 179, 14–34. [Google Scholar] [CrossRef]
- Leka, H.L.; Fengli, Z.; Kenea, A.T.; Tegene, A.T.; Atandoh, P.; Hundera, N.W. A Hybrid CNN-LSTM Model for Virtual Machine Workload Forecasting in Cloud Data Center. In Proceedings of the 2021 18th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 17–19 December 2021; pp. 474–478. [Google Scholar]
- De Oliveira, L.T.; Colaço, M.; Prado, K.H.; de Oliveira, F.R. A Big Data Experiment to Evaluate the Effectiveness of Traditional Machine Learning Techniques Against LSTM Neural Networks in the Hotels Clients Opinion Mining. In Proceedings of the 2021 IEEE International Conference on Big Data (Big Data), Orlando, FL, USA, 15–18 December 2021; pp. 5199–5208. [Google Scholar]





























| Locus | Gene | Allele | |
|---|---|---|---|
| Definition | A unique physical position on the chromosome where a gene exists. | A sequence of DNA that shapes a specific trait. | An alternate version of a specific gene. |
| Purpose or task | Each gene resides at one locus. | Determines traits | Responsible for transmitting the possible variations for each trait. |
| Number of copies | One locus in each location. | One gene in each locus. | Two (one from the mother and one from the father). |
| Examples | D3S1358, TH01 | Weight, Height | Fat, Short |
| Wife | Son | Potential (Father) | Actual Profile | |
|---|---|---|---|---|
| D5S818 | 11, 13 | 11, 13 | 11, ? or ?, 13 | 12, 13 |
| D13S317 | 8, 12 | 8, 14 | ?, 14 | 11, 14 |
| D7S820 | 8, 12 | 8, 9 | 9, ? | 9, 9 |
| D16S539 | 8, 9 | 9, 13 | ?, 13 | 11, 13 |
| CSF1PO | 10, 12 | 10, 10 | ?, 10 | 10, 10 |
| Penta D | 8, 10 | 9, 10 | 9, ? | 9, 12 |
| Identifiler Plus (28 Cycles) | Identifiler Plus (29 Cycles) | GlobalFiler (29 Cycles) | PowerPlex (32 Cycles) |
|---|---|---|---|
| D8S1179 | D8S1179 | D8S1179 | D8S1179 |
| D21S11 | D21S11 | D21S11 | D21S11 |
| D7S820 | D7S820 | D7S820 | D7S820 |
| CSF1PO | CSF1PO | CSF1PO | CSF1PO |
| D3S1358 | D3S1358 | D3S1358 | D3S1358 |
| TH01 | TH01 | TH01 | TH01 |
| D13S317 | D13S317 | D13S317 | D13S317 |
| D16S539 | D16S539 | D16S539 | D16S539 |
| D5S818 | D5S818 | D5S818 | D5S818 |
| D18S51 | D18S51 | D18S51 | D18S51 |
| vWA | vWA | vWA | vWA |
| TPOX | TPOX | TPOX | TPOX |
| FGA | FGA | FGA | FGA |
| AMEL | AMEL | AMEL | AMEL |
| D19S433 | D19S433 | D19S433 | Penta D |
| D2S1338 | D2S1338 | D2S1338 | Penta E |
| SE33 | |||
| Yindel | |||
| D22S1045 | |||
| D2S441 | |||
| D10S1248 | |||
| DAS1656 | |||
| D12S391 | |||
| DYS391 |
| Four Multiplex Profiles (14 Loci) | Three Multiplex Profiles (16 Loci) | Single Multiplex Profiles (24 Loci) |
|---|---|---|
| D8S1179 | D8S1179 | D8S1179 |
| D21S11 | D21S11 | D21S11 |
| D7S820 | D7S820 | D7S820 |
| CSF1PO | CSF1PO | CSF1PO |
| D3S1358 | D3S1358 | D3S1358 |
| TH01 | TH01 | TH01 |
| D13S317 | D13S317 | D13S317 |
| D16S539 | D16S539 | D16S539 |
| D5S818 | D5S818 | D5S818 |
| D18S51 | D18S51 | D18S51 |
| vWA | vWA | vWA |
| TPOX | TPOX | TPOX |
| FGA | FGA | FGA |
| AMEL | AMEL | AMEL |
| D19S433 | D19S433 | |
| D2S1338 | D2S1338 | |
| SE33 | ||
| Yindel | ||
| D22S1045 | ||
| D2S441 | ||
| D10S1248 | ||
| DAS1656 | ||
| D12S391 | ||
| DYS391 |
| Specifications | Value |
|---|---|
| Number of hidden layers | 15 |
| Number of neurons in each hidden layer | 64 |
| Number of dropout layers | 7 |
| Rate of dropout | 20% |
| The activation function for hidden layers | Relu |
| The activation function for the output layer | Softmax |
| The loss function | Categorical cross-entropy |
| Optimizer | adam |
| Epochs | 100 |
| Batch size | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alotaibi, H.; Alsolami, F.; Abozinadah, E.; Mehmood, R. TAWSEEM: A Deep-Learning-Based Tool for Estimating the Number of Unknown Contributors in DNA Profiling. Electronics 2022, 11, 548. https://doi.org/10.3390/electronics11040548
Alotaibi H, Alsolami F, Abozinadah E, Mehmood R. TAWSEEM: A Deep-Learning-Based Tool for Estimating the Number of Unknown Contributors in DNA Profiling. Electronics. 2022; 11(4):548. https://doi.org/10.3390/electronics11040548
Chicago/Turabian StyleAlotaibi, Hamdah, Fawaz Alsolami, Ehab Abozinadah, and Rashid Mehmood. 2022. "TAWSEEM: A Deep-Learning-Based Tool for Estimating the Number of Unknown Contributors in DNA Profiling" Electronics 11, no. 4: 548. https://doi.org/10.3390/electronics11040548
APA StyleAlotaibi, H., Alsolami, F., Abozinadah, E., & Mehmood, R. (2022). TAWSEEM: A Deep-Learning-Based Tool for Estimating the Number of Unknown Contributors in DNA Profiling. Electronics, 11(4), 548. https://doi.org/10.3390/electronics11040548







