Design and Analysis of Anti-Noise Parameter-Variable Zeroing Neural Network for Dynamic Complex Matrix Inversion and Manipulator Trajectory Tracking

Abstract

Dynamic complex matrix inversion (DCMI) problems frequently arise in the territories of mathematics and engineering, and various recurrent neural network (RNN) models have been reported to effectively find the solutions of the DCMI problems. However, most of the reported works concentrated on solving DCMI problems in ideal no noise environment, and the inevitable noises in reality are not considered. To enhance the robustness of the existing models, an anti-noise parameter-variable zeroing neural network (ANPVZNN) is proposed by introducing a novel activation function (NAF). Both of mathematical analysis and numerical simulation results demonstrate that the proposed ANPVZNN model possesses fixed-time convergence and robustness for solving DCMI problems. Besides, a successful ANPVZNN-based manipulator trajectory tracking example further verifies its robustness and effectiveness in practical applications.

1. Introduction

Complex-valued matrix inversion (CMI) has been frequently encountered in signal processing [1], hyperparameters estimation [2] and MIMO systems [3,4]. Many numerical iterative algorithms have been reported to handle CMI problems. As an effective CMI problem solver, the Newton iterative method is deeply studied [5]. However, with the increase of matrix dimension, the Newton iterative method cannot deal with the sharply increasing computational workload. Generally, the computational complexity of numerical iterative method is O(n³) in each iteration [6]. For example, the Newton iterative method and the neural network method are both used to solve matrix inversion problem in reference [7], although the iterative method is effective in some situations, it may have high computational complexity when handling large-scale data.

As the parallel computing and distributed storage for large scale computation, the neural network method has been paid more in recent years. For example, the Gradient neural network (GNN) is applied to solve static matrix inversion (SMI) [8,9], and they can find the solutions of the SMI problems effectively. However, the GNN method is only suitable for static problems solving, and they cannot effectively deal with dynamic problems [10].

In order to solve large-scale dynamic problems properly, the zeroing neural network (ZNN) model was proposed [11]. With the development of ZNN model in last two decades, it has been widely applied in various practical dynamic problems, such as dynamic algebraic matrix equations solving [12,13,14,15], linear and quadratic programming problems solving [16] and robotic manipulator path tracking [17,18,19]. It is worth mentioning that some intelligent control systems and NARX neural networks have been applied in unmanned aerial vehicle control and path tracking [20,21,22,23]. There are two methods to improve its convergence and robustness, one is the improvement of ZNN model, and the other is to find new activation functions (AF). Many novel modified ZNN models are reported in reference [24,25,26], and the modified models improved its performance greatly. Besides, many novel new AFs have been proposed in reference [27,28,29,30], and these new AFs further improve its convergence performance. However, most of the reported works focus on the improvement of its convergence, and the robustness to noises is rarely considered. It is worth to mention that the inevitable noises, in reality, greatly reduce the performance of dynamic systems. Although, several anti-noise ZNN models have been reported in reference [31,32], they only achieve exponential convergence. Based on the above-mentioned issues, it can be known that the further improvement of the effectiveness and robustness to noise of the ZNN model is still open.

Dynamic complex matrix problems exist in many fields, such as input signals contain both amplitude and phase information [33,34,35]. How to find the solutions of dynamic complex matrix equations efficiently becomes more and more important. Till now, there are two methods to solve dynamic CMI problems. The first method is transforming the complex value problem into two real value problems, which means the real and imaginary parts of a complex matrix are separately considered, and a complex matrix should be transformed into two real matrices [36,37,38]. For example, in reference [36], Xiao et al. proposed a NTZNN to solve the CMI problem with noises. In reference [37], Jin proposed an IFTCRNN to solve the CMI problem with fast convergent speed. However, the calculation workload of this method is relatively heavy, as its real and imaginary parts are calculated separately. The other method is adopting complex modulus conversion technique (CMCT), which has less calculation workload than the former method [39].

Moreover, considering the noises, in reality, the robustness of the dynamic model should also be taken into account. In reference [40], an HZNN model is designed to solve time-varying matrix inversion, and it has fast convergent speed than the GNN and ZNN model. In reference [41], a varying parameter recurrent neural network is proposed for solving time-varying matrix inversion, and it has accelerated convergence time. In reference [42], a TVDZNN is designed to realize matrix inversion. In reference [43], a CVZNN is used for dynamic Moore–Penrose inverse solving, and it relaxes convex constraint of the AF. However, all the above mentioned works only consider the ideal no noise condition, and their robustness is unpredictable in noisy environment.

Motivated by the above issues, an NAF-based ANPVZNN model with fixed-time convergence and robustness to noises for solving DCMI problems is proposed. The proposed ANPVZNN model not only improves the effectiveness and robustness of the original ZNN (OZNN) model, but also adopts the CMCT to reduce the calculation workload for solving DCMI problems. Thus, the contributions of this paper are summarized below.

(1)

On the basis of the OZNN model and existing AFs, an ANPVZNN model is proposed;

(2)

Compared with the OZNN model activated by existing AFs, the proposed ANPVZNN model has better effectiveness and robustness for dynamic time-varying problems solving, which guarantees its fast online solving dynamic time-varying problems in real noisy environment;

(3)

Both of strict mathematical theoretical proof and experimental simulation results are provided to validate its fixed-time convergence and robustness to noises.

2. Problem and Mathematical Preparation

2.1. Problem Formulation

The DCMI problem is introduced below.

$$A(t)B(t)=I\in {ℂ}^{n\times n}$$

(1)

where $A(t)\in {ℂ}^{n\times n}$ is a known complex matrix, B(t) is the unknown complex matrix to be solved, $I\in {ℂ}^{n\times n}$ is the unit matrix. In other words, B(t) is the inverse of A(t) which need to be solved. Our purpose is to find the complex matrix B(t) quickly and efficiently by using the proposed ANPVZNN model under various external noises.

2.2. OZNN Model

The construction of the OZNN consists of three steps.

Firstly, a dynamic complex error matrix is defined.

$$E(t)=A(t)B(t)-I\in {ℂ}^{n\times n}$$

(2)

Obviously, if E(t) converges to 0, B(t) is obtained. Therefore, we adopt the following formula for the convergence of E(t).

$$\frac{dE(t)}{dt}=-\gamma \Phi (E(t))$$

(3)

where the adjustable parameter γ > 0. Φ(●) is a monotonically increasing AF array, φ(●) is the element of Φ(●). Both of γ and AF φ(●) are related to the convergent speed of E(t).

Finally, substituting Equation (2) into (3) yields

$$\stackrel{•}{A(t)}B(t)=-A(t)\stackrel{•}{B(t)}-\gamma \Phi (A(t)B(t)-I)$$

(4)

The recently reported AFs are listed below.

• Linear activation function (LAF)

$$\varphi (y)=y$$

(5)

• Power activation function (PAF)

$$\varphi (y)=y^r$$

(6)

where r is an odd number and r > 3.

• Bi-power activation function (BPAF)

$$\varphi (y)=\frac{1-{\mathrm{e}}^{(-\theta y)}}{1+{\mathrm{e}}^{(-\theta y)}},y>1$$

(7)

• Power-sigmoid activation function (PSAF)

$$\varphi (y)=\{\begin{array}{cc}{y}^k,& \left|y\right|\ge 1\\ \frac{1+e^{-\theta }-e^{-\theta y}}{1-e^{-\theta }+e^{-\theta y}},& \left|y\right|\le 1\end{array}$$

(8)

• Sign-bi-power activation function (SBPAF)

$$\varphi (y)=\begin{array}{cc}\frac{({\left|y\right|}^{\epsilon }+{\left|y\right|}^{\frac{1}{\epsilon }})\mathrm{sgn}(y)}{2},& 0<\epsilon <1\end{array}$$

(9)

• Versatile activation function (VAF)

$$\begin{array}{cc}\varphi (y)={\left|y\right|}^{p}sign(y)+y,& 0<p<1\end{array}$$

(10)

ZNN model (4) with AFs (5)–(8) realizes exponential or super-exponential convergence; it realizes finite-time convergence activated by AF (9), and fixed-time convergence activated by AF (10). To further enhance its convergence and robustness, a NAF is proposed in this work, and its analysis will be discussed in the following section.

Remark 1.

The convergence and robustness of the OZNN model is related to the parameter γ and AF φ(●) in Equation (3). Generally, the parameter γ is a constant, and most of the recently reported works focus on the improvement of the AF φ(●) to enhance the performance of the ZNN model. This work focus on the improvements both on the parameter γ and AF φ(●), and the variable parameter γ and new AF φ(●) will be presented in the following Section 3.

3. PVCZNN Model and Its Theoretical Analysis

3.1. Design of PVCZNN Model

As mentioned in Equation (3), the parameter γ is related to the convergent speed of E(t), and the following new formula with variable parameter $\gamma =\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)$ is proposed.

$$\stackrel{•}{E}(t)=-\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)\phi (E(t))$$

(11)

where δ₁, δ₂, α > 0.

Besides, on the basis of the existing SBPAF (9) and VAF (10), the following new AF φ(●) is proposed for its further improvement.

$$\phi (x)=(k_1|x{|}^p+k_2|x{|}^q)sgn(x)+k_{3}x$$

(12)

where $k_1,k_2,k_3>0,0<p<1,q>1$, sgn(●) denotes the sign function.

On the basis of Equations (11) and (12), the ANPVZNN for solving DCMI problems is obtained below.

$$\stackrel{•}{A(t)}B(t)=-A(t)\stackrel{•}{B(t)}-\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)\phi (A(t)B(t)-I)$$

(13)

The ANPVZNN model with additive noise is

$$\stackrel{•}{A(t)}B(t)=-A(t)\stackrel{•}{B(t)}-\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)\phi (A(t)B(t)-I)+\Delta N(t)$$

(14)

where ∆N(t) represents the external noise.

3.2. Convergence Analysis of the ANPVZNN Model

Theorem 1 guarantees fixed-time convergence of the ANPVZNN (13).

Theorem 1.

The error matrix E(t) of ANPVZNN model (13) converges to 0 in fixed-time with arbitrary initial states, and the convergent time t_c is

$$t_c\le \frac{1}{{\delta }_2}\ln \left[1+\frac{{\delta }_2}{\alpha k_1(1-p)}\right]$$

(15)

where$\alpha$,$k_1$,$k_2$are the same as defined before.

Proof. 

First, a Lyapunov function is defined.

$$w_{ij}(t)=\left|e_{ij}(t)\right|$$

(16)

Its time derivative is

$$\stackrel{•}{w_{ij}}(t)={\stackrel{•}{e}}_{ij}(t)sign(e_{ij}(t))=-\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_2\mathrm{t})\phi (e_{ij}(t))sign(e_{ij}(t))$$

(17)

As ${\delta }_1\mathrm{arccot}(t)$ > 0, Formula (17) can be written in the following form as

$$\stackrel{•}{w_{ij}}(t)\le -\alpha \exp ({\delta }_{2}t)\phi (e_{ij}(t))sign(e_{ij}(t))$$

(18)

Then, substitute NAF (12) into the above equation, inequation (19) is obtained.

$$\stackrel{•}{w_{ij}}(t)=-\alpha \exp ({\delta }_{2}t)\phi (e_{ij}(t))=-\alpha \exp ({\delta }_{2}t)\left[k_1{\left|e_{ij}(t)\right|}^p+k_2{\left|e_{ij}(t)\right|}^q+k_3\left|e_{ij}(t)\right|\right]\le -\alpha k_1{\left|e_{ij}(t)\right|}^p$$

(19)

The following inequation can be obtained by transforming inequality (19).

$$w_{ij}{(t)}^{-p}d{w}_{ij}(t)\le -\alpha k_1\exp ({\delta }_{2}t)dt$$

(20)

Integrating Equation (20) from 0 to t_c yields

$${\displaystyle {\int }_{w_{ij}(0)}^{w_{ij}(t)}{w}_{ij}{(t)}^{-p}d{w}_{ij}(t)\le {\displaystyle {\int }_0^{t_c}-\alpha k_1\exp ({\delta }_{2}t)dt}}{\frac{1}{1-p}{w}_{ij}{}^{1-p}|}_{w_{ij}(0)}^{w_{ij}(t)}\le {-\frac{\alpha k_1}{{\delta }_2}\exp ({\delta }_2{t}_c)|}_0^{t_c}-\frac{1}{1-p}{w}_{ij}{}^{1-p}\le -\frac{\alpha k_1}{{\delta }_2}\left[\exp ({\delta }_2{t}_c)-1\right]$$

(21)

Then, solving Equation (21) yields

$$t_c\le \frac{1}{{\delta }_2}\ln \left[1+\frac{{\delta }_2}{\alpha k_1(1-p)}\right]$$

(22)

□

3.3. Robustness Analysis of the ANPVZNN

The robustness to noises of the ANPVZNN (14) will be guaranteed by the following Theorem 2.

Theorem 2.

If ∆N(t) in Equation (14) is an unknown dynamic bounded or unbounded noise, and the error matrix E(t) of ANPVZNN model (14) will converge to 0 even under noises.

Proof. 

Error matrix E(t) of the ANPVZNN (14) is

$$\stackrel{•}{E(t)}=-\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)\phi (E(t))+\Delta N(t)$$

(23)

The n² subsystems of E(t) are

$$\stackrel{•}{e_{ij}(t)}=-\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)\phi (e_{ij}(t))+\Delta n_{ij}(t)$$

(24)

where e_ij(t) is the ijth element of E(t).

Define the Lyapunov function h_ij(t).

$$h_{ij}(t)=\frac{1}{2}{\left|e_{ij}(t)\right|}^2$$

(25)

Deriving Equation (25) yields

$$\stackrel{•}{h_{ij}}(t)=\stackrel{•}{e_{ij}}(t)e_{ij}(t)=e_{ij}(t)(-\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)\phi (e_{ij}(t))+\Delta n_{ij}(t))$$

(26)

Equation (26) should be divided into two cases to be discussed.

The first case: if $\stackrel{•}{h_{ij}}(t)$ < 0, $\left|e_{ij}(t)\right|$ will decrease to 0.

The second case: if $\stackrel{•}{h_{ij}}(t)$ > 0, $\left|e_{ij}(t)\right|$ will increase.

Obviously, $e_{ij}(t)\Delta n_{ij}(t)>0$ and $\stackrel{•}{h_{ij}}(t)$ > 0, inequality (27) is obtained.

$$\left|\Delta n_{ij}(t)\right|>\left|\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)\phi (e_{ij}(t))\right|$$

(27)

It is clear that $\left|e_{ij}(t)\right|$ will stop increasing when $\Delta n_{ij}(t)-\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)\phi (e_{ij}(t))=0$.

Therefore, we can obtain the inequality of $\left|e_{ij}(t)\right|$ when $t\to \infty$.

$$0\le \left|e_{ij}(t)\right|\le \left|{\phi }^{-1}(\frac{\Delta n_{ij}(t)}{\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)})\right|$$

(28)

where φ⁻¹(●) is the inverse function of φ(●).

On the basis of NAF (12), $\left|\phi (x)\right|\ge \left|k_{3}x\right|$, hence $\left|{\phi }^{-1}(x)\right|\le \left|x/k_3\right|$. The inequality (28) can be written as

$$0\le \left|e_{ij}(t)\right|\le \left|\frac{\Delta n_{ij}(t)}{\alpha k_3\exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)}\right|$$

(29)

The convergent analysis is given in the following subsection.

Case one: In this case, we consider ∆N(t) in Equation (14) is an unknown dynamic bounded noise. Define a constant parameter μ with $\left|\Delta n_{ij}(t)\right|\le \mu$, and then inequality (29) can be written as

$$\left|e_{ij}(t)\right|\le \left|\frac{\mu }{\alpha k_3\exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)}\right|$$

(30)

The limit of $\left|e_{ij}(t)\right|$ can be obtained when $t\to \infty$.

$$\underset{t\to \infty }{\lim }\left|e_{ij}(t)\right|\le \underset{t\to \infty }{\lim }\left|\frac{\mu }{\alpha k_3\exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)}\right|\le 0$$

(31)

Therefore,

$$\underset{t\to \infty }{\lim }\left|E(t)\right|=\sqrt{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\underset{t\to \infty }{\lim }{\left|e_{ij}(t)\right|}^2}}}=0$$

(32)

Case two: In this case, we consider ∆N(t) in Equation (14) is an unknown dynamic unbounded noise. Its derivation is $\Delta n_{ij}^{(\mu )}(t)\in (0,\tau ]$, where μ is a non-zero nature number and τ is a non-zero constant number. The limit of $\left|e_{ij}(t)\right|$ can be obtained when $t\to \infty$.

$$\underset{t\to \infty }{\lim }\left|e_{ij}(t)\right|\le \underset{t\to \infty }{\lim }\left|\frac{\Delta n_{ij}(t)}{\alpha k_3\exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)}\right|=\underset{t\to \infty }{\lim }\left|\frac{\Delta n_{ij}(t)}{\alpha k_3\exp ({\delta }_{2}t)}\right|=\underset{t\to \infty }{\lim }\left|\frac{\Delta n_{ij}^{(\mu )}(t)}{\alpha k_3{\delta }_2^{\mu }\exp ({\delta }_{2}t)}\right|$$

(33)

Because $\Delta n_{ij}^{(\mu )}(t)\in (0,\tau ]$, Equation (33) can be written as

$$\underset{t\to \infty }{\lim }\left|e_{ij}(t)\right|\le \underset{t\to \infty }{\lim }\left|\frac{\tau }{\alpha k_3{\delta }_2^{\mu }\exp ({\delta }_{2}t)}\right|=0$$

(34)

Therefore,

$$\underset{t\to \infty }{\lim }\left|E(t)\right|=\sqrt{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\underset{t\to \infty }{\lim }{\left|e_{ij}(t)\right|}^2}}}=0$$

(35)

In conclusion, the proposed ANPVZNN model is stable under the noise ∆N(t). □

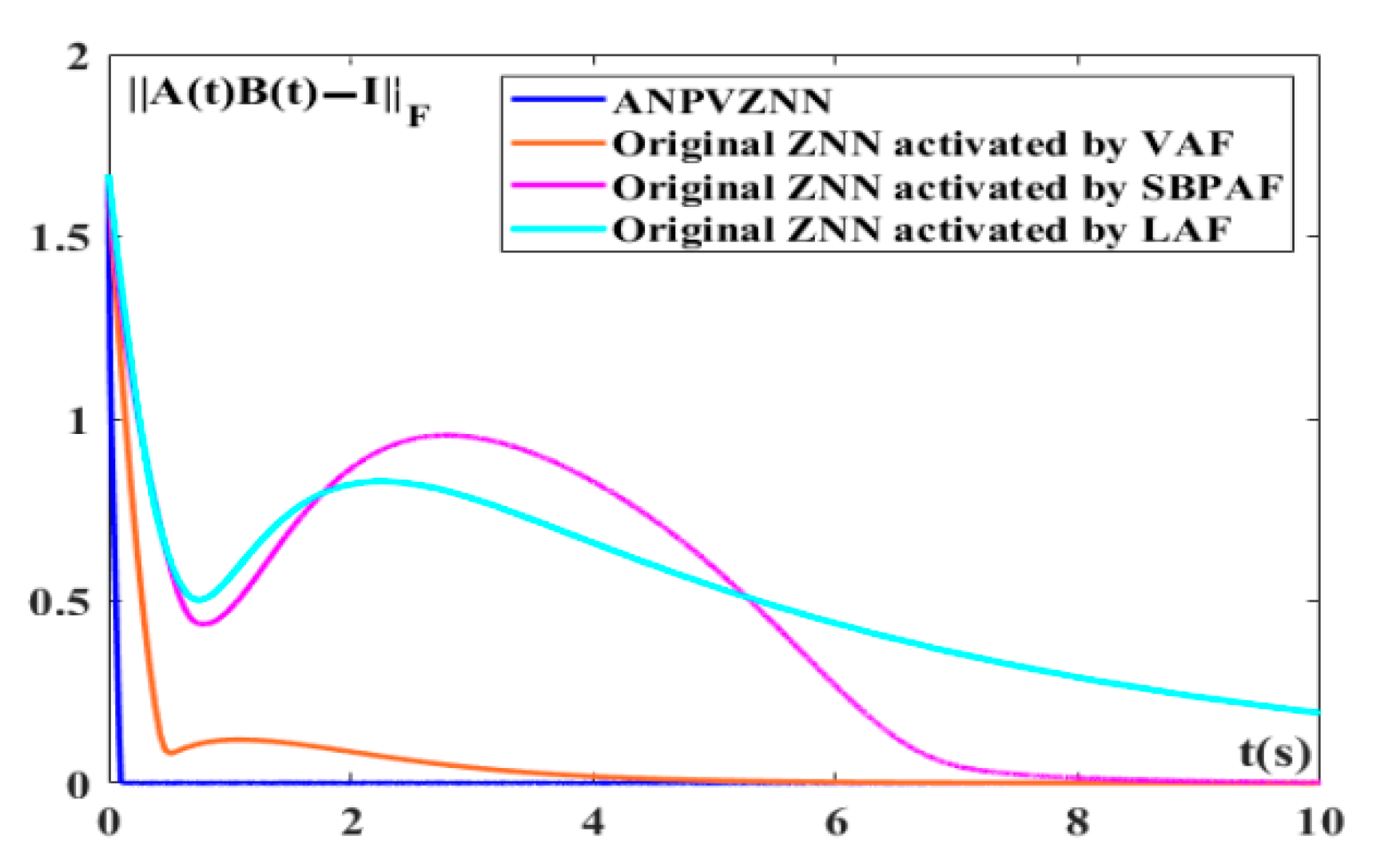
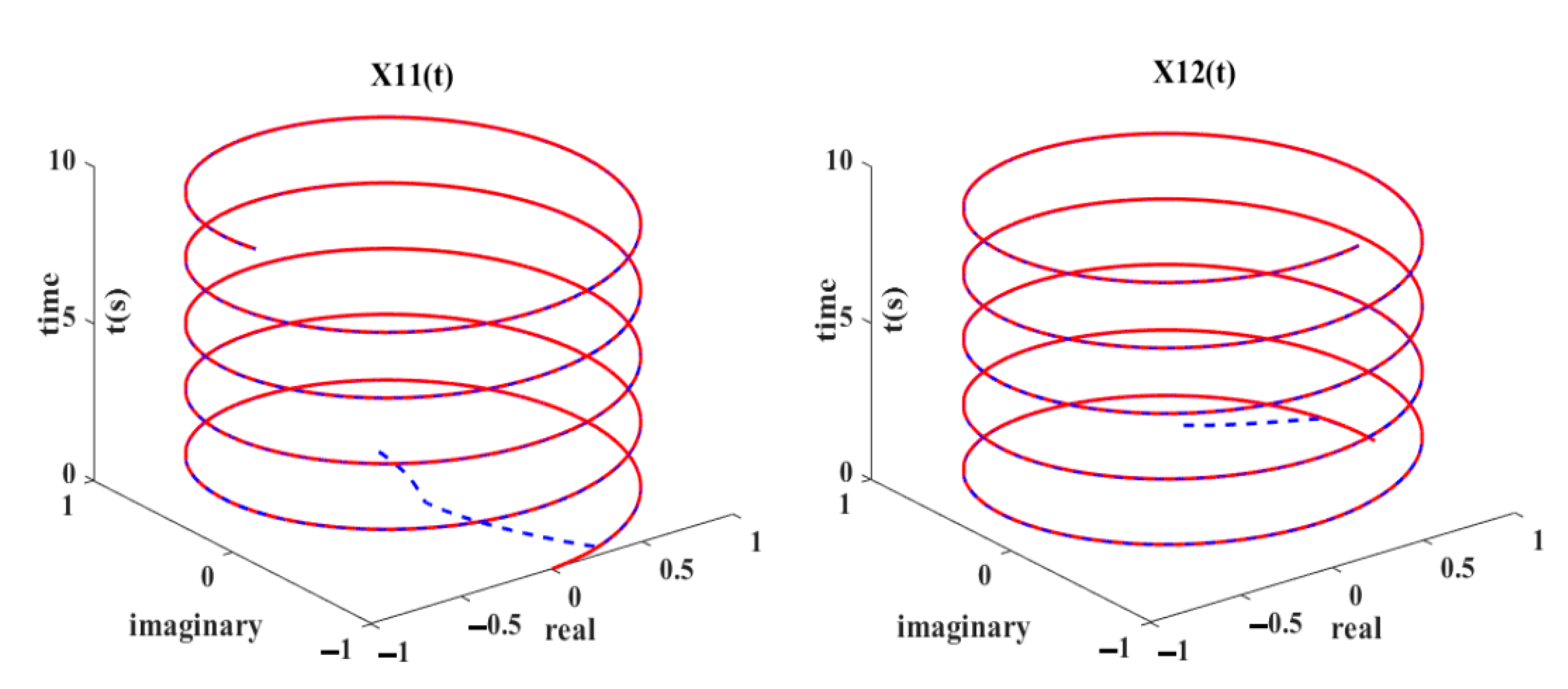
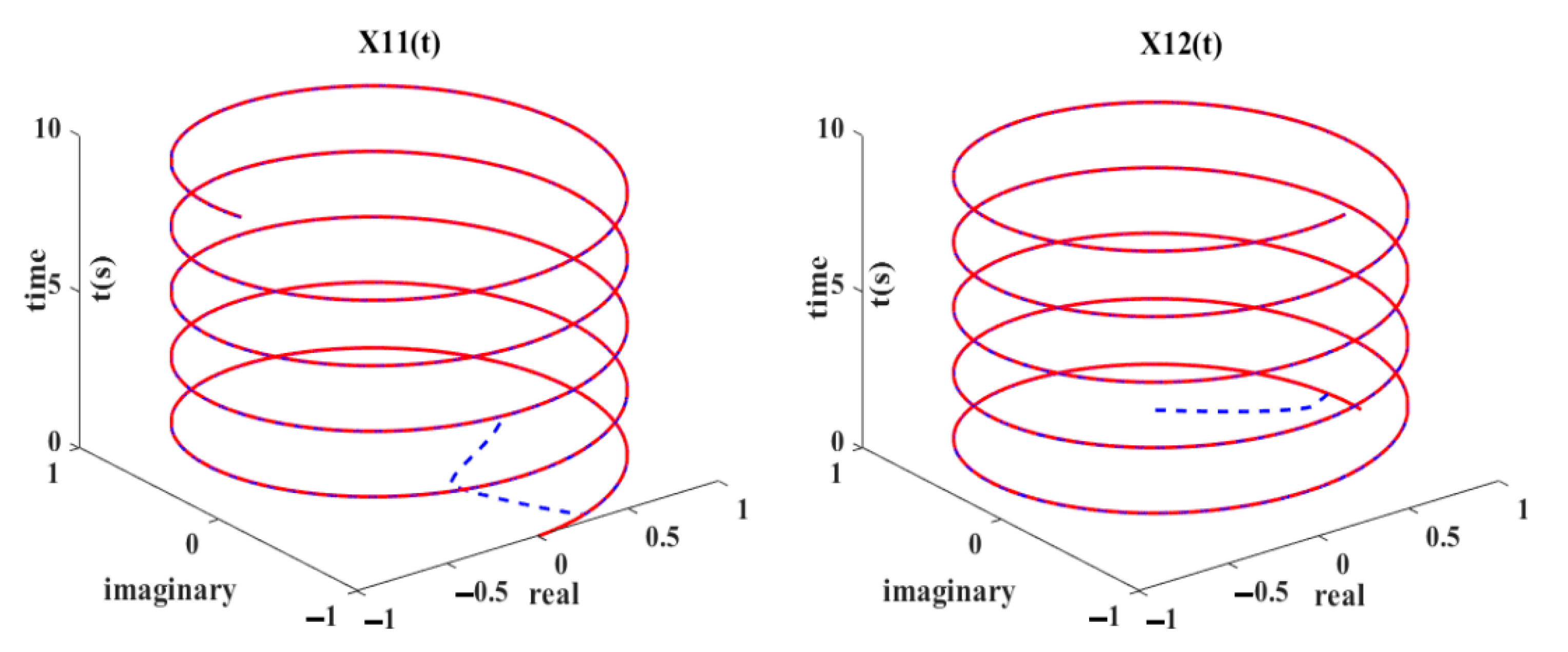
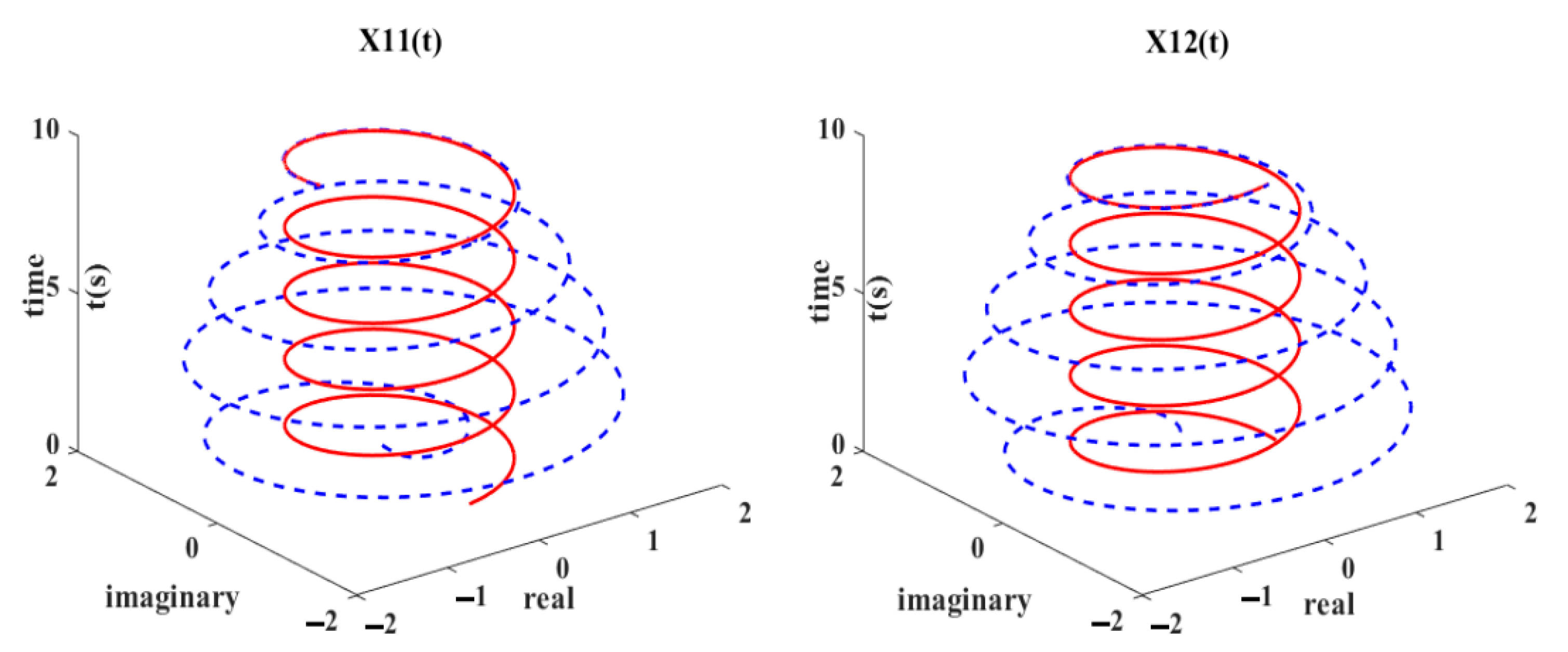
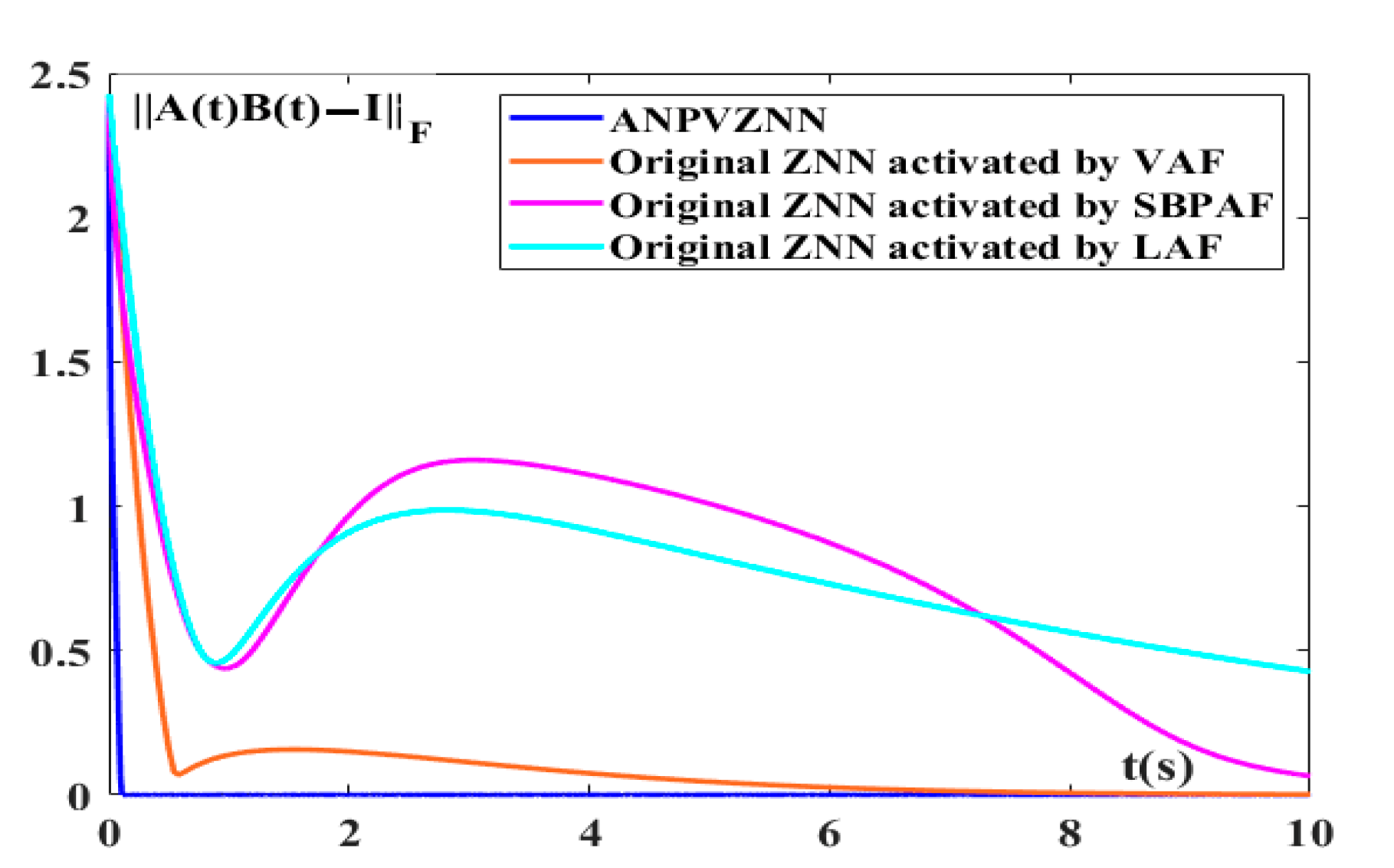
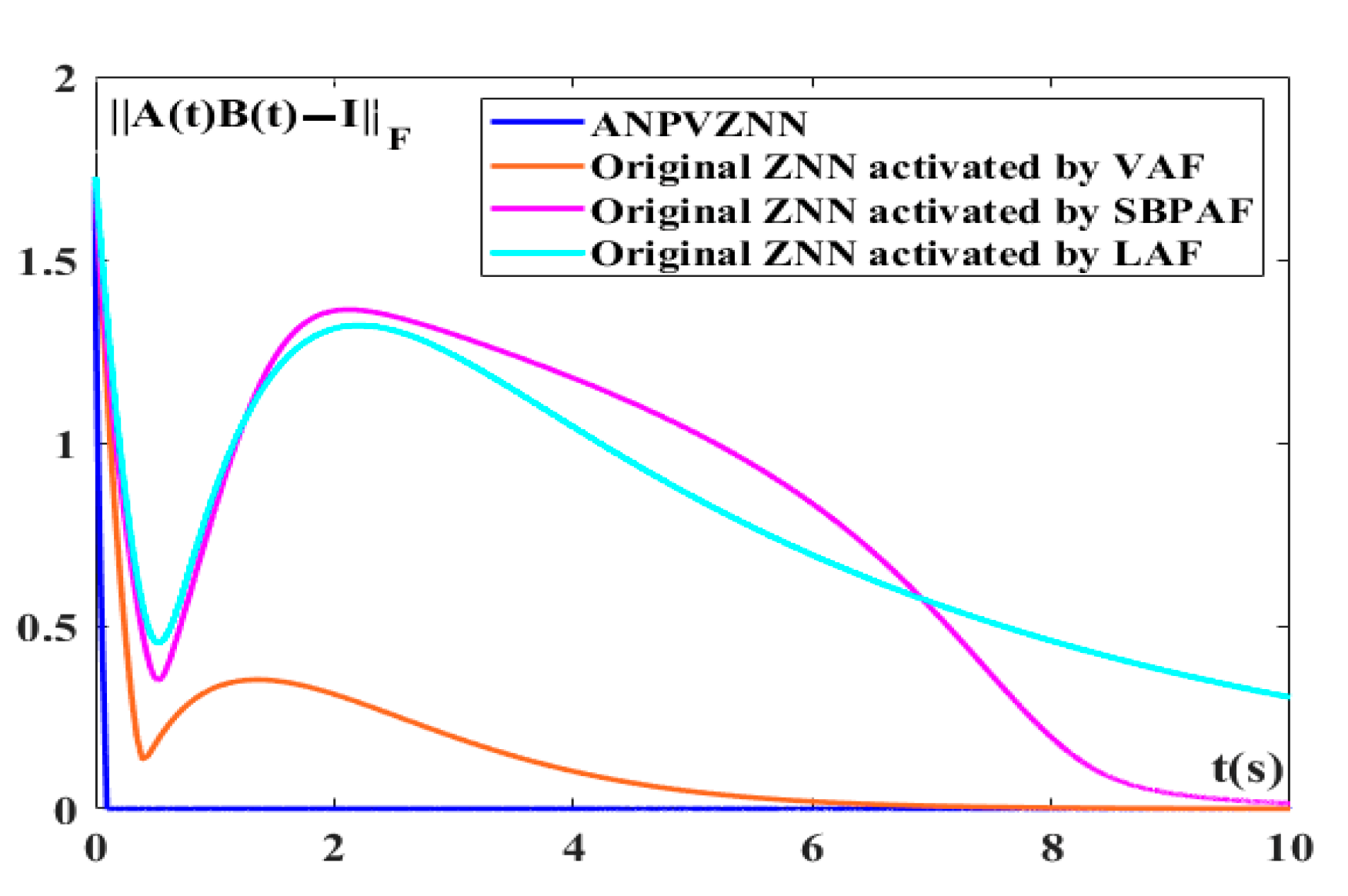
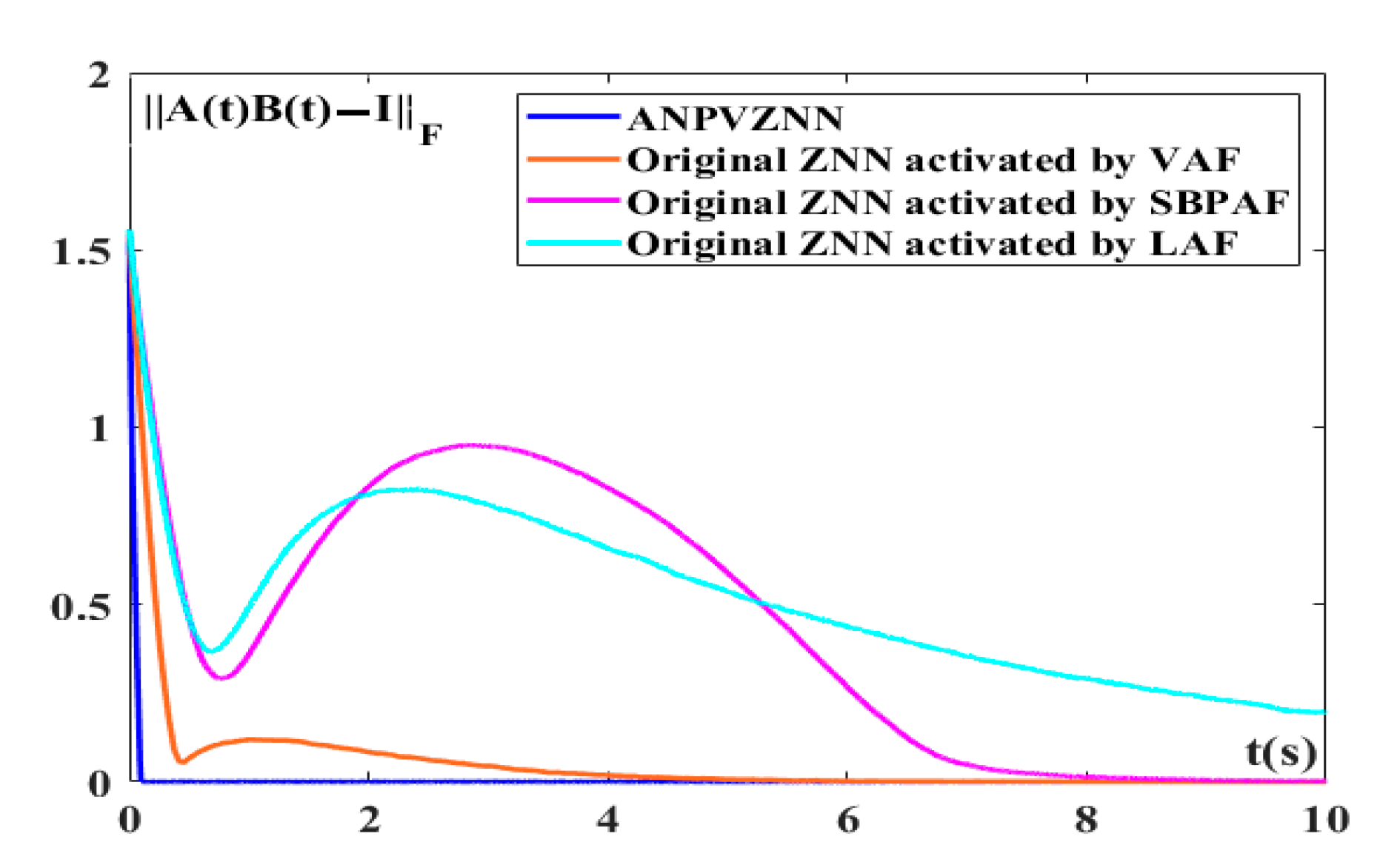
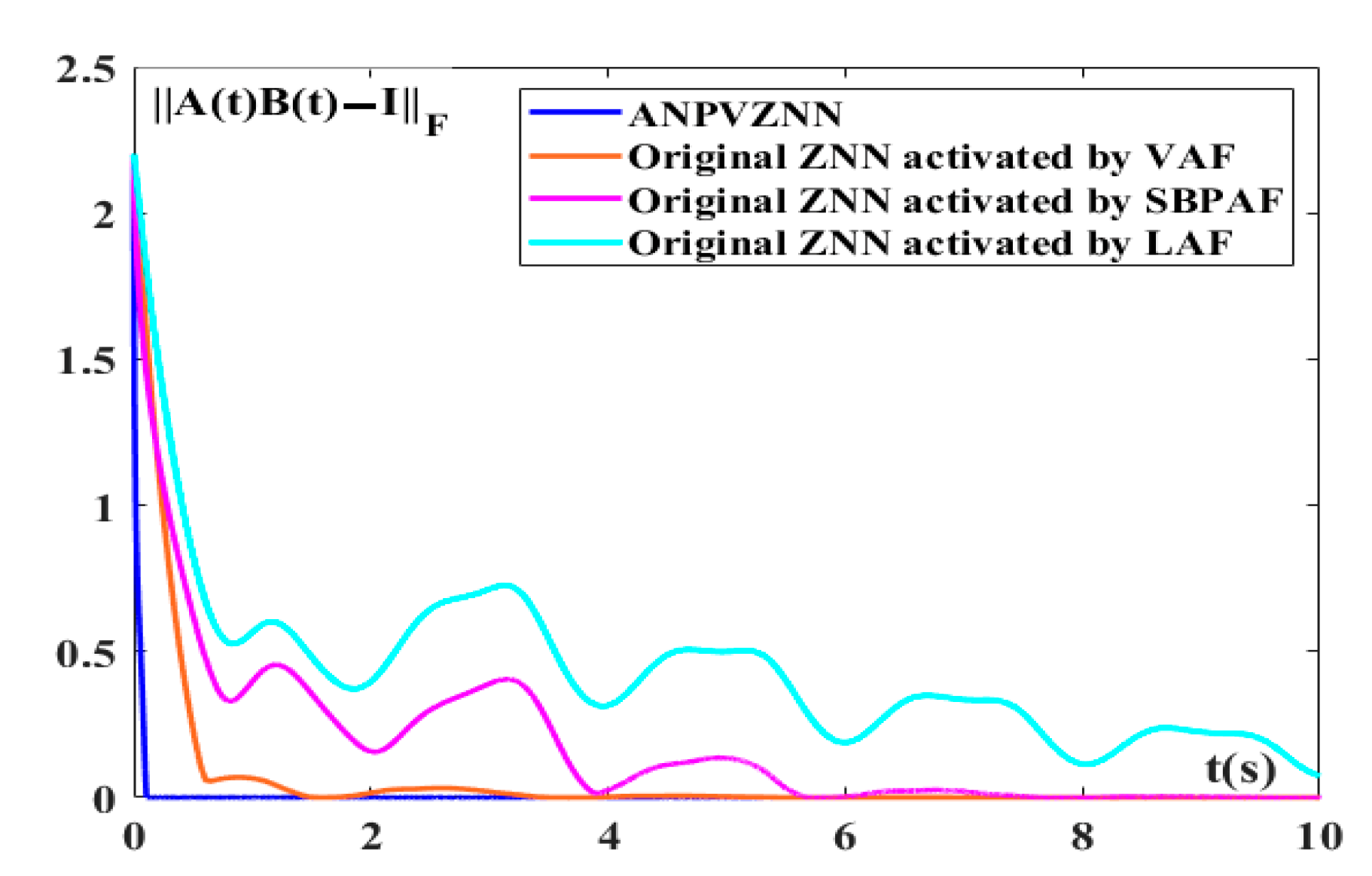
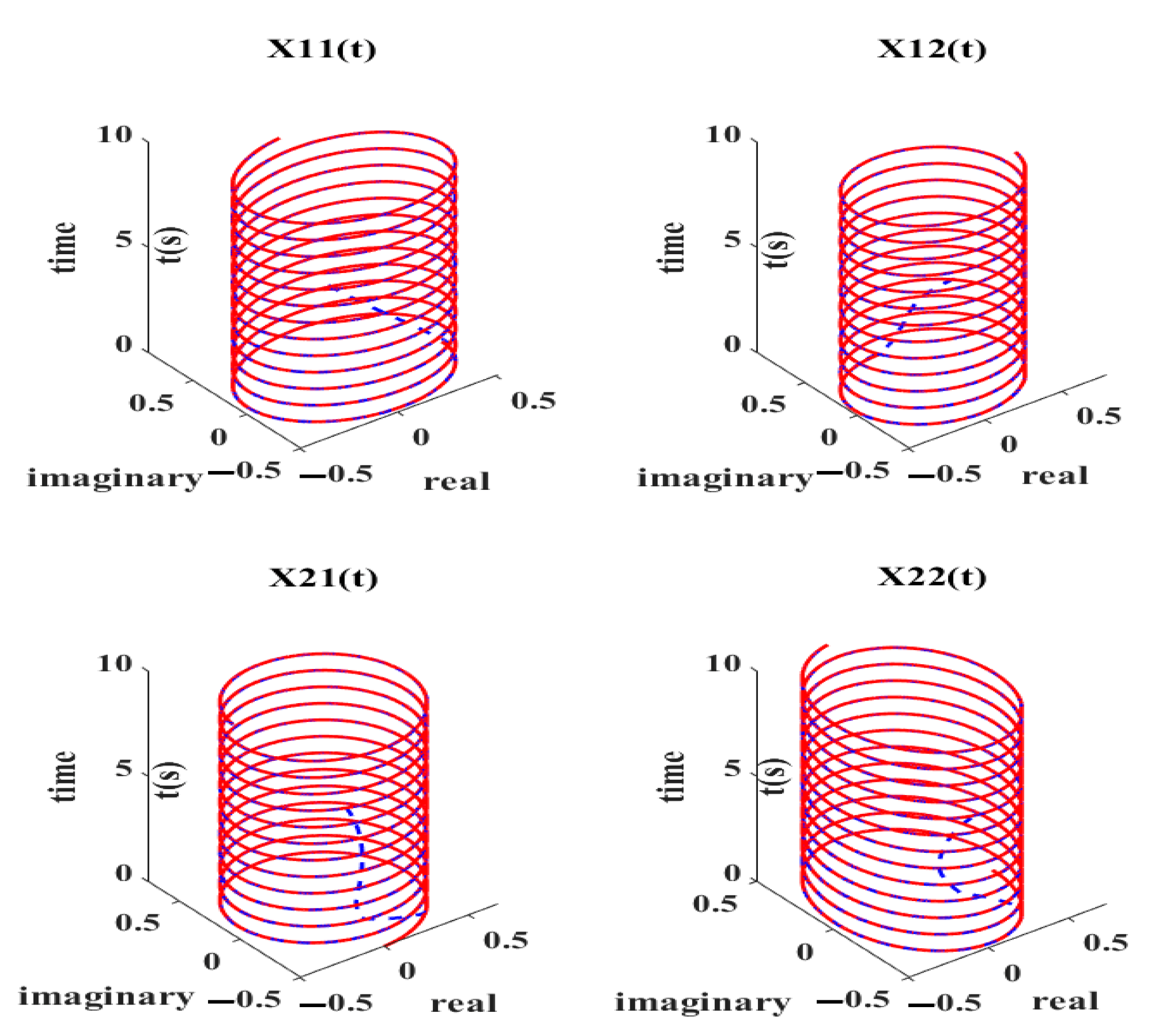
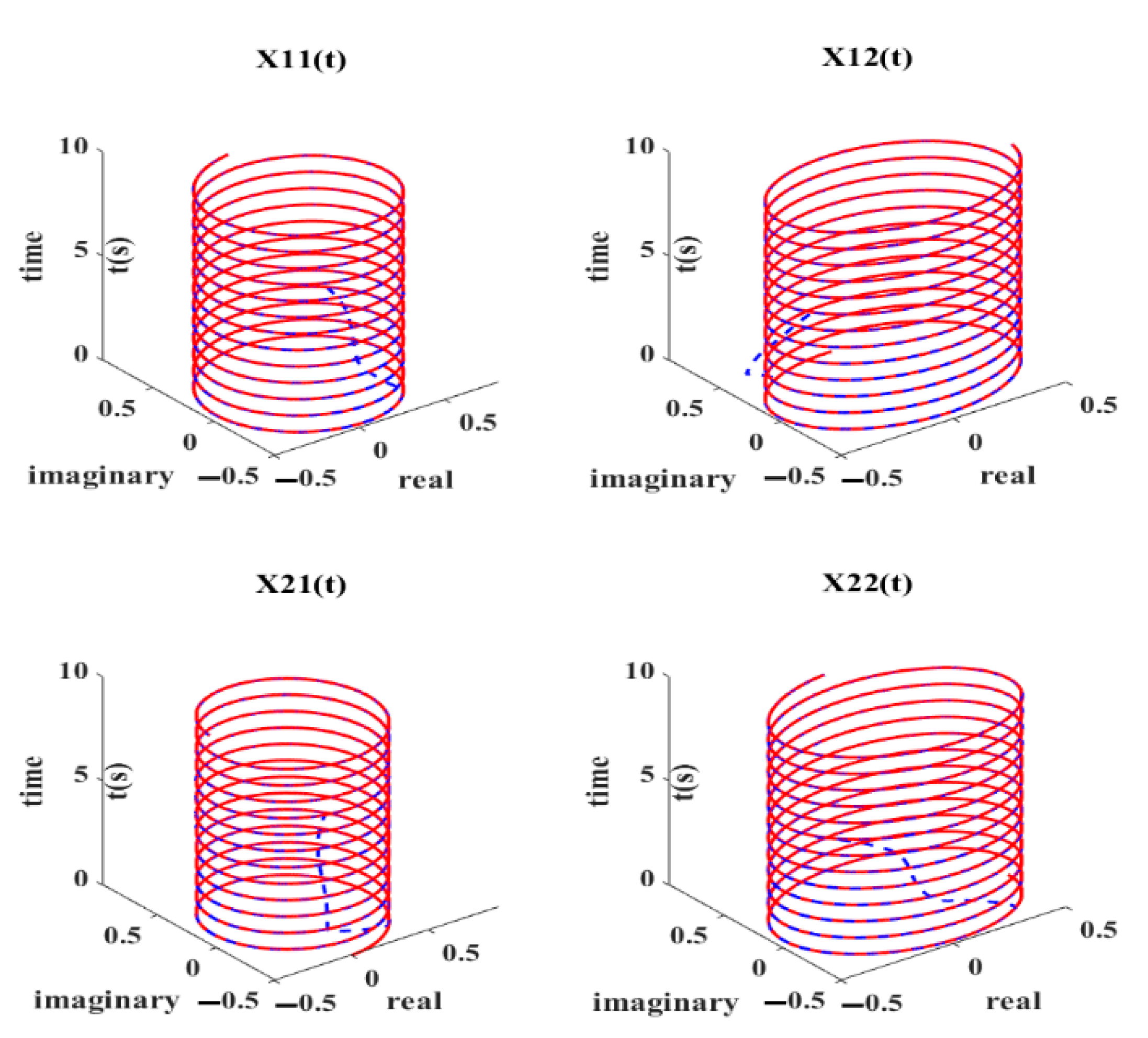
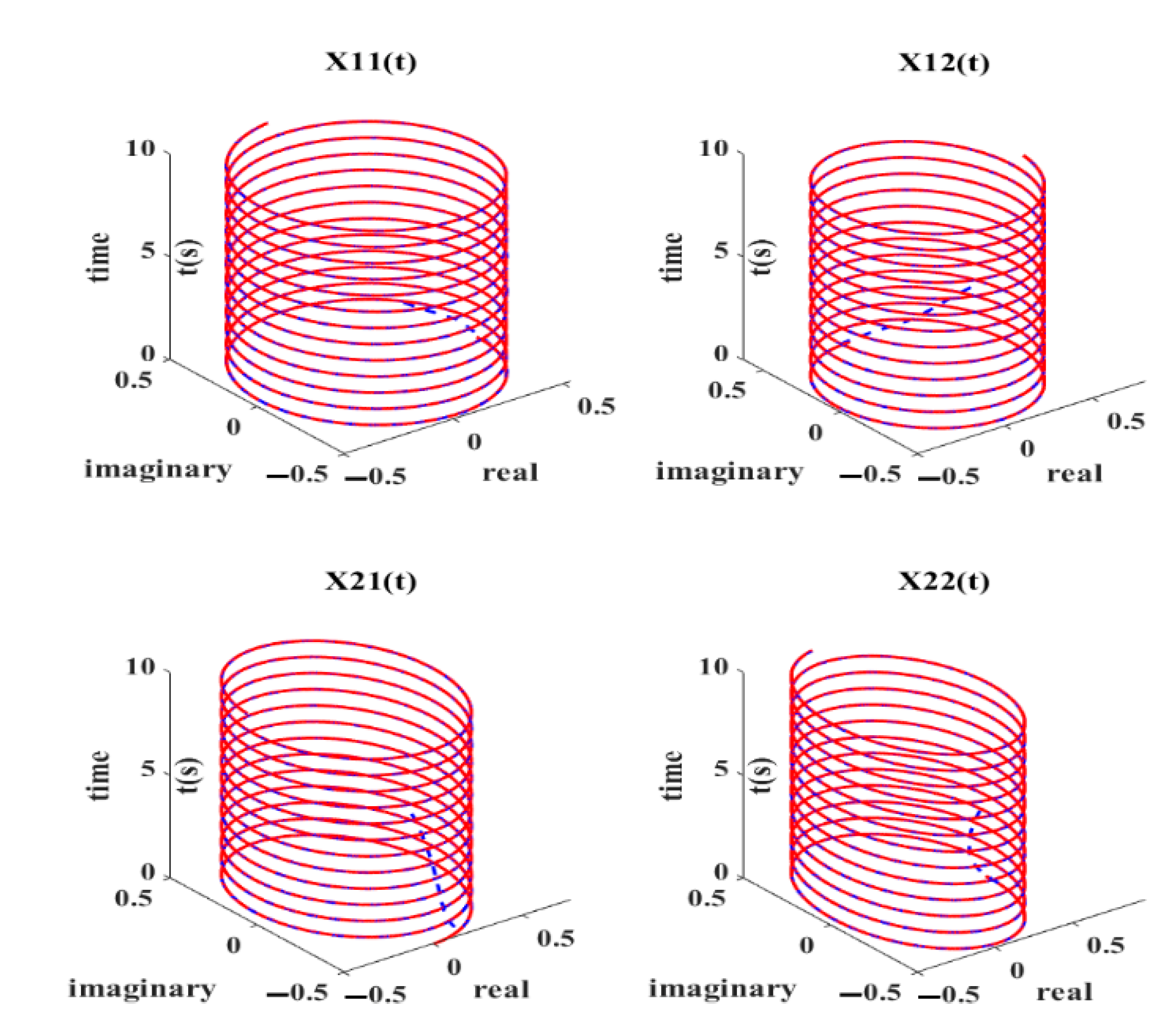
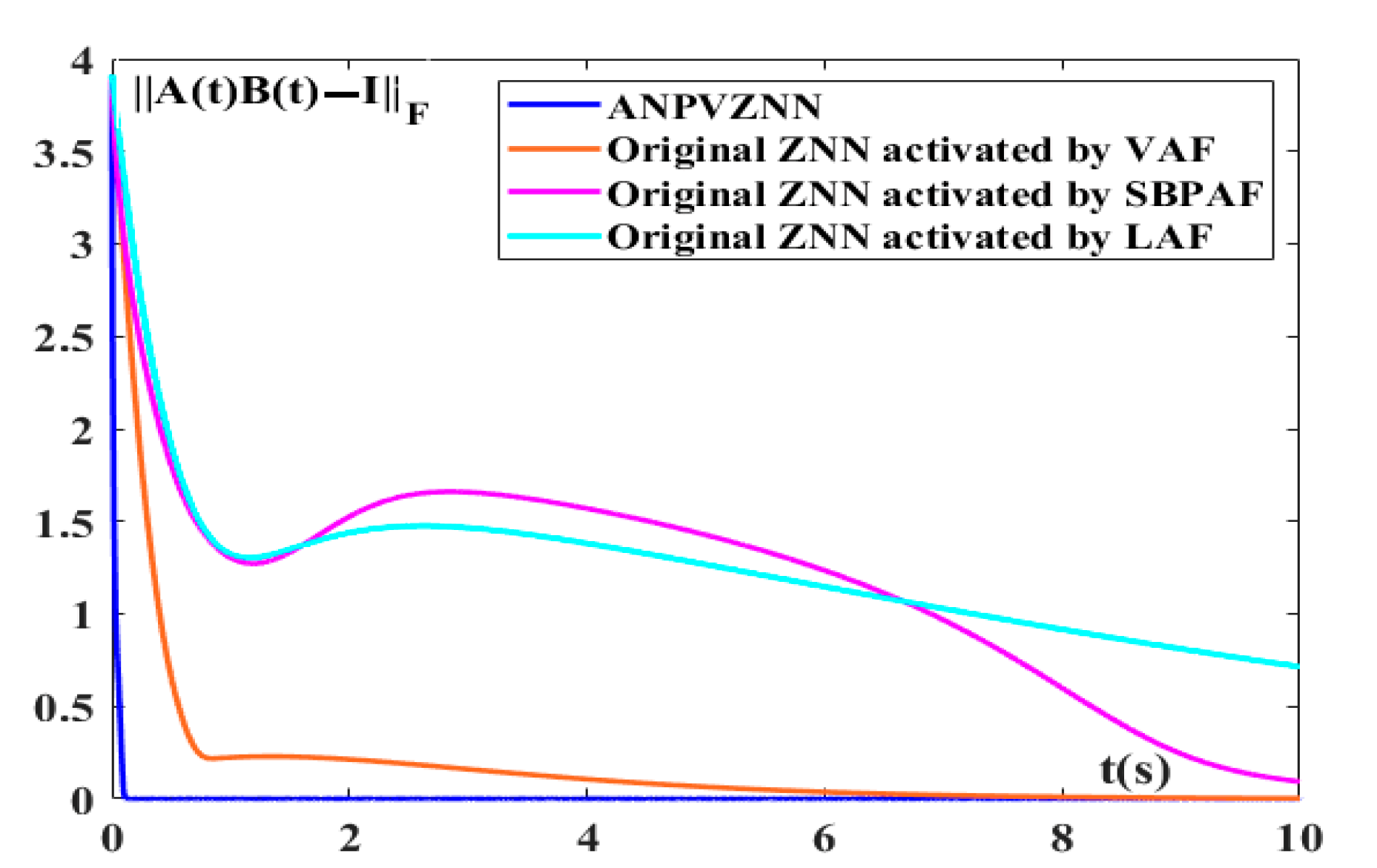
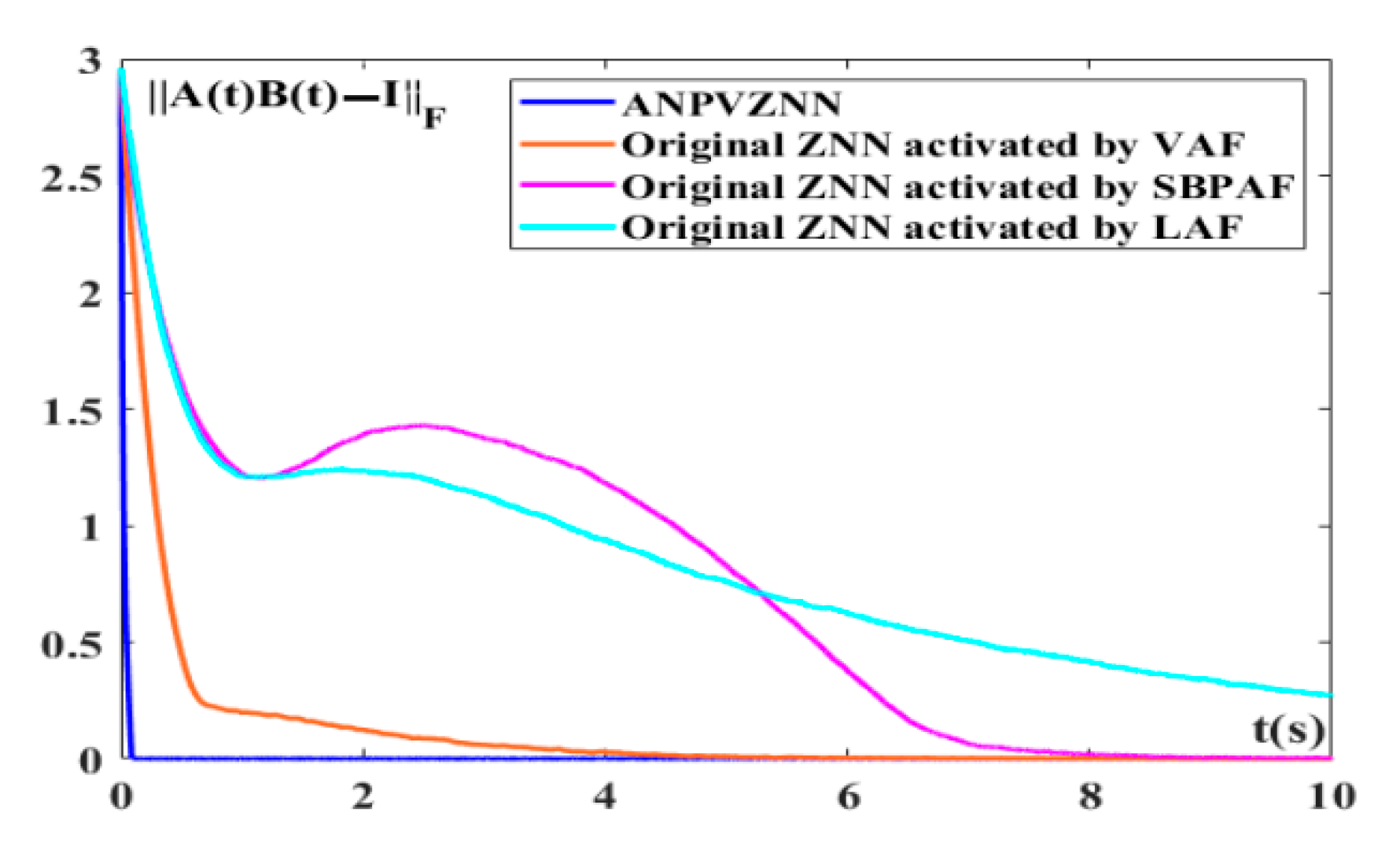
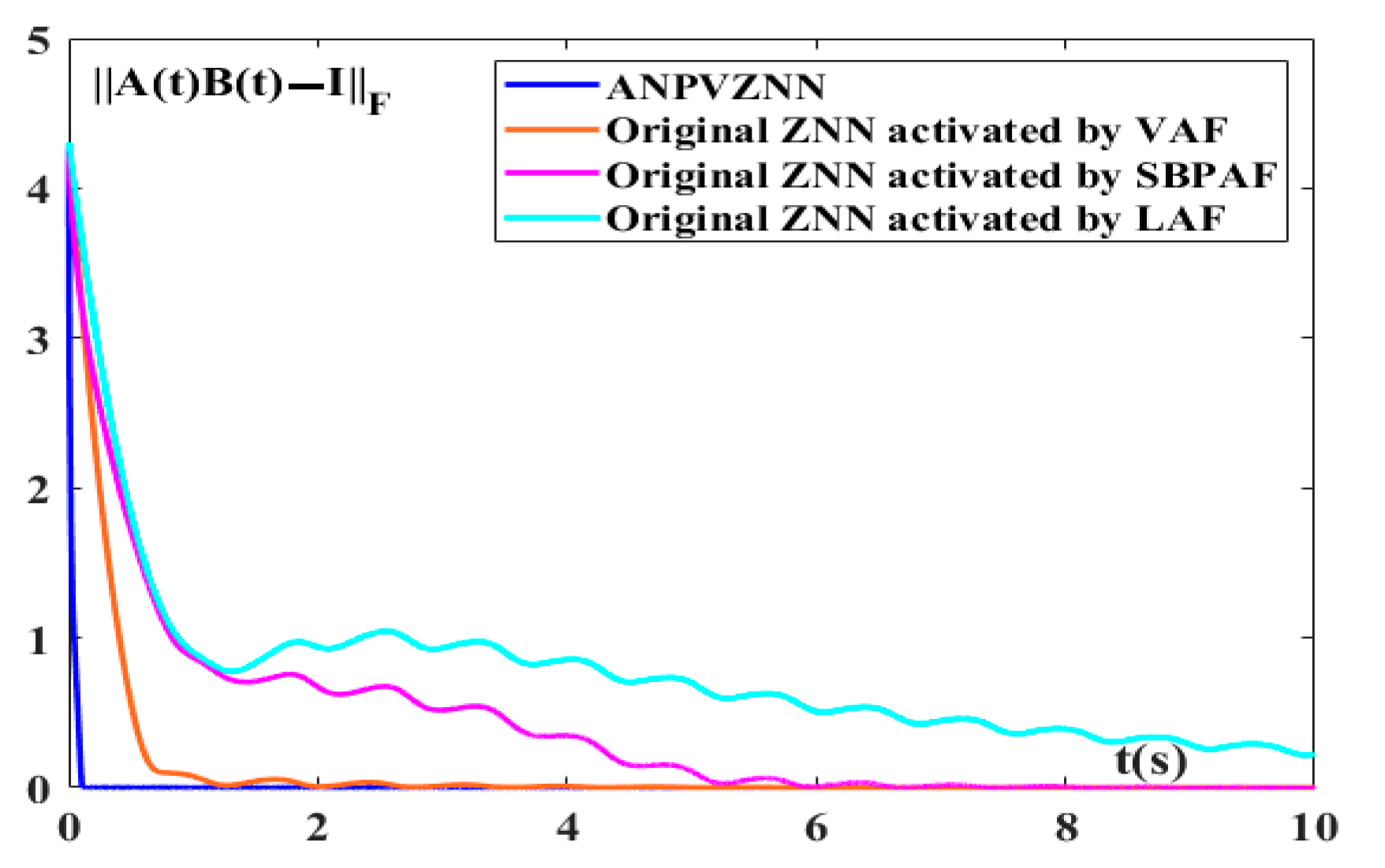
4. ANPVZNN Model Applications

The ANPVZNN model will be used to solve two DCMI problems in this section.

Example 1.

First-order DCMI problem solving

Consider the following first-order DCMI (FODCMI).

$$\begin{array}{l}A(t)B(t)=I\in {ℂ}^{1\times 1}\\ A(t)=\left[\sin 3t+i\cos 3t\right]\end{array}$$

(36)

Here, for the comparison purpose, the proposed ANPVZNN and the OZNN (4) activated by LAF, SBPAF and VAF will be applied to solve the above FODCMI problem, and the following two cases are considered, respectively.

Case one: Noiseless

Figure 1 and Figure 2 are the simulated results of ANPVZNN (13) and the SBPAF-based OZNN model (4) for solving the above FODCMI (36), respectively.

As shown in Figure 1 and Figure 2, the state solutions (blue solid curves) generated by ANPVZNN (13) and the SBPAF-based OZNN model (4) all accurately converge to theoretical solution (red dotted curves) of the above FODCMI (36) in noiseless environment. Besides, the residual errors ${\Vert A(t)B(t)-I\Vert }_F$ of ANPVZNN model (13) and the OZNN model (4) activated by the AFs (LAF, SBPAF and VAF) are presented in Figure 3. As seen in Figure 3, although the ANPVZNN model (13) and the OZNN model (4) all solve FODCMI (36) properly, the ANPVZNN model (13) is the most effective model among them for solving DCMI problems in noiseless environment. Specifically, the ANPVZNN model (13) takes about 0.1 s to find the solution of FODCMI (36), and the OZNN models (4) activated by the AFs (LAF, SBPAF and VAF) spend more than 4 s to find the solution of FODCMI (36).

Case two: With various noises

In this subsection, the proposed ANPVZNN model (14) and the OZNN (4) activated by the LAF and SBPAF for solving FODCMI (36) are discussed, and the following Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 are the state solutions of ANPVZNN (14) and OZNN (4) in various noise environments.

Figure 4 and Figure 5 are the state solutions of ANPVZNN model (14) for solving FODCMI (36) with constant noise and random noise, respectively. As observed in Figure 4 and Figure 5, the proposed ANPVZNN model (14) successfully finds the solution of FODCMI (36) in noisy polluted environment, which indicates its strong robustness to noises. Figure 6 and Figure 7 are the state solutions of the OZNN model (4) activated by the SBPAF for solving FODCMI (36) in noisy environment and it fails to solve FODCMI (36) due to noises.

Besides, the residual errors ${\Vert A(t)B(t)-I\Vert }_F$ of the ANPVZNN model (14) and the OZNN model (4) activated by other AFs with various noises are presented in Figure 8, Figure 9, Figure 10 and Figure 11. As observed in Figure 8, Figure 9, Figure 10 and Figure 11, the OZNN model (4) activated by other AFs fails to find theoretical solution of FODCMI (36) due to the noises, and their residual errors cannot effectively converge to 0. The proposed ANPVZNN model (14) and the OZNN model (4) activated by VAF still accurately converge to the theoretical solution of FODCMI (36) in noisy environment, but the proposed ANPVZNN model (14) possess better robustness and effectiveness than OZNN model (4) activated by VAF.

Example 2.

Second-order DCMI problem solving

Consider the following second-order DCMI (SODCMI).

$$\begin{array}{l}A(t)B(t)=I\in {ℂ}^{2\times 2}\\ A(t)=\left[\begin{array}{cc}\exp (8it)& -i\exp (-8it)\\ -i\exp (8it)& \exp (-8it)\end{array}\right]\end{array}$$

(37)

Similar as Example 1, the proposed ANPVZNN model and the OZNN model (4) activated by other AFs (LAF, SBPAF and VAF) are all applied to solve the above SODCMI (37), and the simulation results are presented in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22.

Case one: Noiseless

Figure 12 is the simulated results of the ANPVZNN model (13) for solving SODCMI (37), and Figure 13 is the residual errors of the ANPVZNN (13) and the OZNN (4) activated by other AFs.

As observed in Figure 12 and Figure 13, both of the ANPVZNN model (13) and the OZNN model (4) activated by the VAF still solve SODCMI (37) in noiseless environment. However, the OZNN model (4) activated by the LAF and VAF cannot deal with high-dimensional DCMI problems effectively, and their residual errors ${\Vert A(t)B(t)-I\Vert }_F$ take a long time to converge to 0. Based on the above analysis, we can draw the conclusion that the proposed ANPVZNN model (13) is the most effective model among them for the FODCMI problem solving in noiseless environment. Specifically, the ANPVZNN model (13) takes about 0.1 s to find the solution of SODCMI (37), and the OZNN models (4) activated by the AFs (LAF, SBPAF and VAF) spend more than 4 s.

Case two: With various noises

Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 are the state solutions of ANPVZNN (14) and the SBPAF-based OZNN (4) for solving SODCMI (37) with various noises.

It can also be observed from Figure 14, Figure 15 and Figure 16 that the proposed ANPVZNN (14) still effectively solves SODCMI (37) in various noises polluted environment, and its performance is not affected by noises. As seen in Figure 17 and Figure 18, the state solutions (blue solid curves) generated by the SBPAF-based OZNN model (4) cannot converge to the theoretical solution (red dotted curves) of SODCMI (37), which indicates the SBPAF-based OZNN model (4) fails to effectively find the solution of SODCMI (37) due to noises.

Figure 19, Figure 20 and Figure 21 are the residual errors of the ANPVZNN model (14) and the OZNN model (4) activated by other AFs with various noises. As observed in Figure 19, Figure 20 and Figure 21, the proposed ANPVZNN model (14) successfully solved SODCMI (37) within 0.1 s; the residual errors of the OZNN model (4) activated by other AFs cannot converge to 0, and they fail to find the theoretical solution of SODCMI (37) due to noises.

Remark 2.

Based on the above two examples of the ANPVZNN model and the OZNN model for solving FODCMI (36) and SODCMI (37), we can know that the proposed ANPVZNN model works properly in both of noiseless and noisy environment, it solves FODCMI (36) and SODCMI (37) within 0.1 s with strong robustness to noises. Besides, the VAF-activated OZNN model (4) also possesses anti-noise ability, and it can successfully solve FODCMI (36) and SODCMI (37) in noisy environment, but its convergence time is more than 4 s. The OZNN model (4) activated by the AFs (LAF, SBPAF and VAF) can work in noiseless environment, but it is sensitive to noises. The proposed ANPVZNN model (14) is the best DCMI problem solver in noiseless and noisy environments.

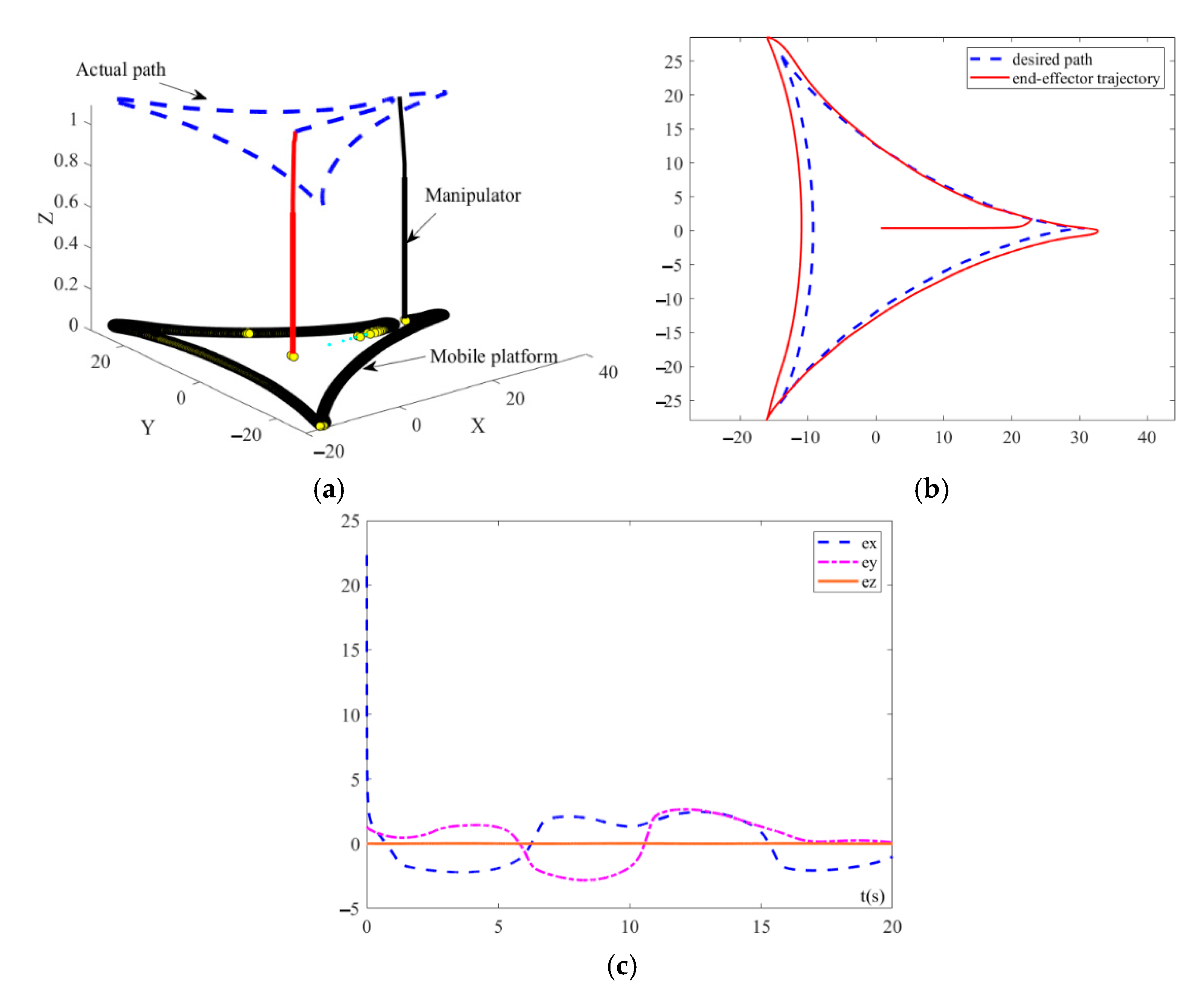
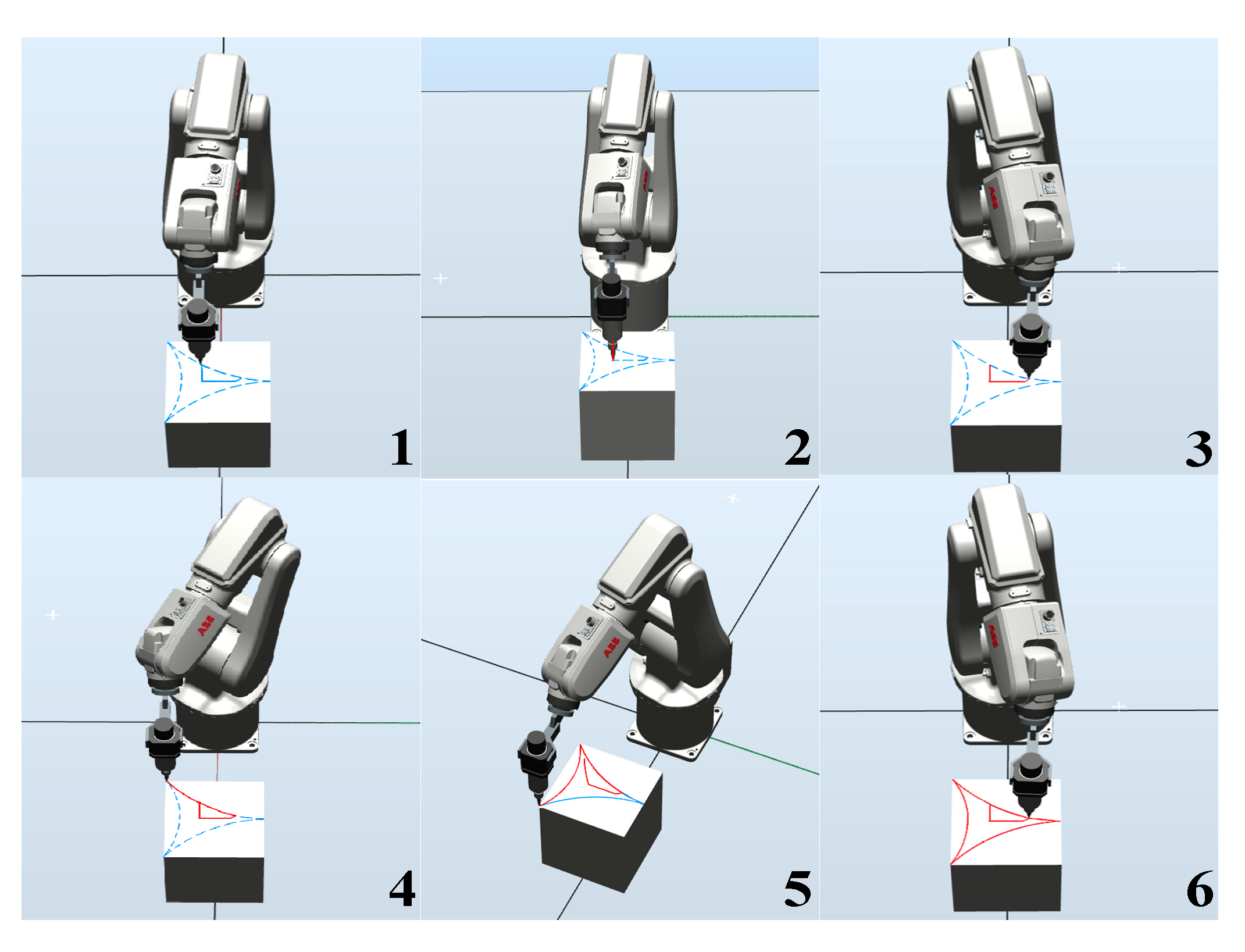
5. Application to Robotic Manipulator

With the development of AI technology, the robots have become a hot research spot in recent years [44,45,46,47,48]. To further validate the effectiveness and robustness of the ANPVZNN on real-time applications, comparative simulation results of the ANPVZNN and SBPAF-activated OZNN for robotic manipulator trajectory tracking with periodic noise is applied this section.

According to reference [49,50], the kinematics model of wheeled mobile manipulator is established below.

$$R(t)=W(\Theta (t))$$

(38)

where R(t) represents the position of the end effector in spatial coordinates. W(●) stands for a nonlinear mapping function. $\Theta ={\left[\begin{array}{cc}{\xi }^T(t),& {\omega }^T(t)\end{array}\right]}^T$ represents the angle vector and it consists of the platform angle vector $\xi (t)={[{\xi }_L(t),{\xi }_R(t)]}^T$ and the manipulator angle vector $\omega (t)={[w_1(t),\cdots ,w_n(t)]}^T$.

The ANPVZNN-based and OZNN-based mobile manipulator tracking models are presented the following dynamic equations.

$$V(\Theta (t))\stackrel{•}{\Theta }(t)=\stackrel{•}{R}(t)+\alpha \exp ({\delta }_1\mathrm{arccot}(t)+{\delta }_{2}t)\phi (R(t)-W(\Theta (t)))$$

(39)

$$V(\Theta (t))\stackrel{•}{\Theta }(t)=\stackrel{•}{R}(t)+\phi (R(t)-W(\Theta (t)))$$

(40)

where $\alpha ,{\delta }_1,{\delta }_2$ are same as previously defined, and $V(\Theta (t))$ is the derivative of $W(\Theta (t))$. φ(●) in Equations (39) and (40) is the proposed AF in Equation (12) and SBPAF in Equation (9), respectively.

The desired path is a tricuspid valve, and the ANPVZNN-based model (39) and OZNN-based model (40) are applied to control the mobile manipulator to track the desired tricuspid valve path in periodic noise cos(t) polluted environment, and the simulated results are presented in Figure 23 and Figure 24.

Figure 23a and Figure 24a present the entire trajectories of ANPVZNN-based and OZNN-based mobile manipulator; Figure 23b and Figure 24b are the desired path and the actual manipulator trajectories. It can be seen directly from Figure 23b and Figure 24b, the ANPVZNN-based mobile manipulator completes the trajectory tracking task accurately in noisy environment, while the OZNN-based mobile manipulator fails due to the periodic noise.

Figure 23c and Figure 24c are the tracking errors of the ANPVZNN-based and OZNN-based mobile manipulator. From Figure 23c and Figure 24c, it can be seen that the tracking errors of ANPVZNN-based model (39) are much smaller than the OZNN-based model (40) in noisy environment, which further demonstrates its accuracy and robustness.

To further validate the accurateness and practicability of the ANPVZNN in manipulator trajectory tracking application, the physical experiments are conducted with IRB120 robot manipulator, and the experiment results are presented in Figure 25. The dotted blue tricuspid valve is the desired path, and the red curve is the tracking trajectory of the manipulator.

It can be observed in Figure 25, the IRB120 robot manipulator controlled by NTPVZNN-based model (39) successfully finishes the tracking task, which further validates its accurateness and practicability.

6. Conclusions

By designing a NAF, an ANPVZNN model is proposed. On the basis of the OZNN model and existing AFs, the mathematical model of the ANPVZNN model has been derived. The stability and robustness of the ANPVZNN model has been verified by strict mathematical analysis, and the performance of the proposed ANPVZNN model has been validated comparing with the OZNN model in various scenarios. This work successfully demonstrates the applications of the ANPVZNN model for DCMI problems solving and manipulator path tracking under external noises. Taking into account its performance, the applications of the ANPVZNN model for natural language processing and dynamic electronic circuit currents computing will be considered in our future work.