Quasi-Distributed Magnetic Field Fiber Sensors Integrated with Magnetostrictive Rod in OFDR System
Abstract
:1. Introduction
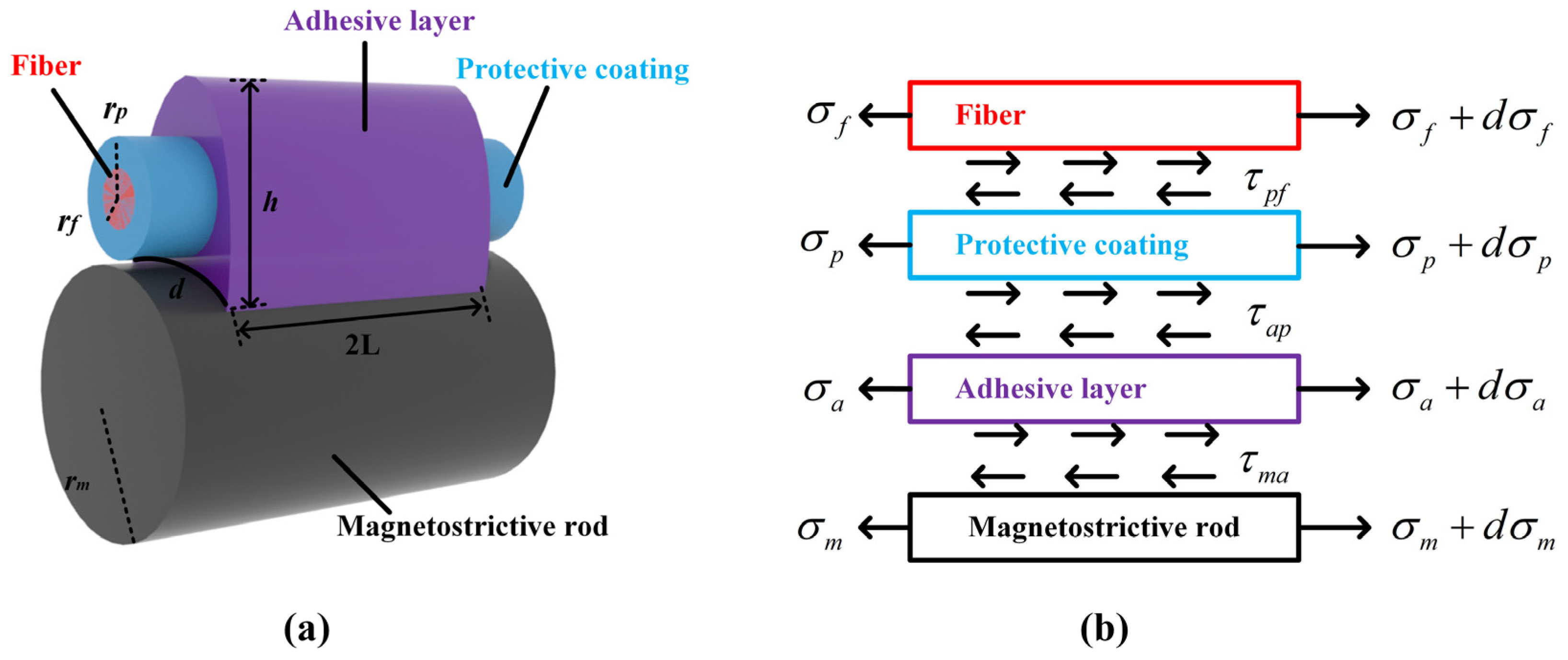
2. Operation Principle of the Sensor
3. Experiments and Results
3.1. Fabrication of the Sensors
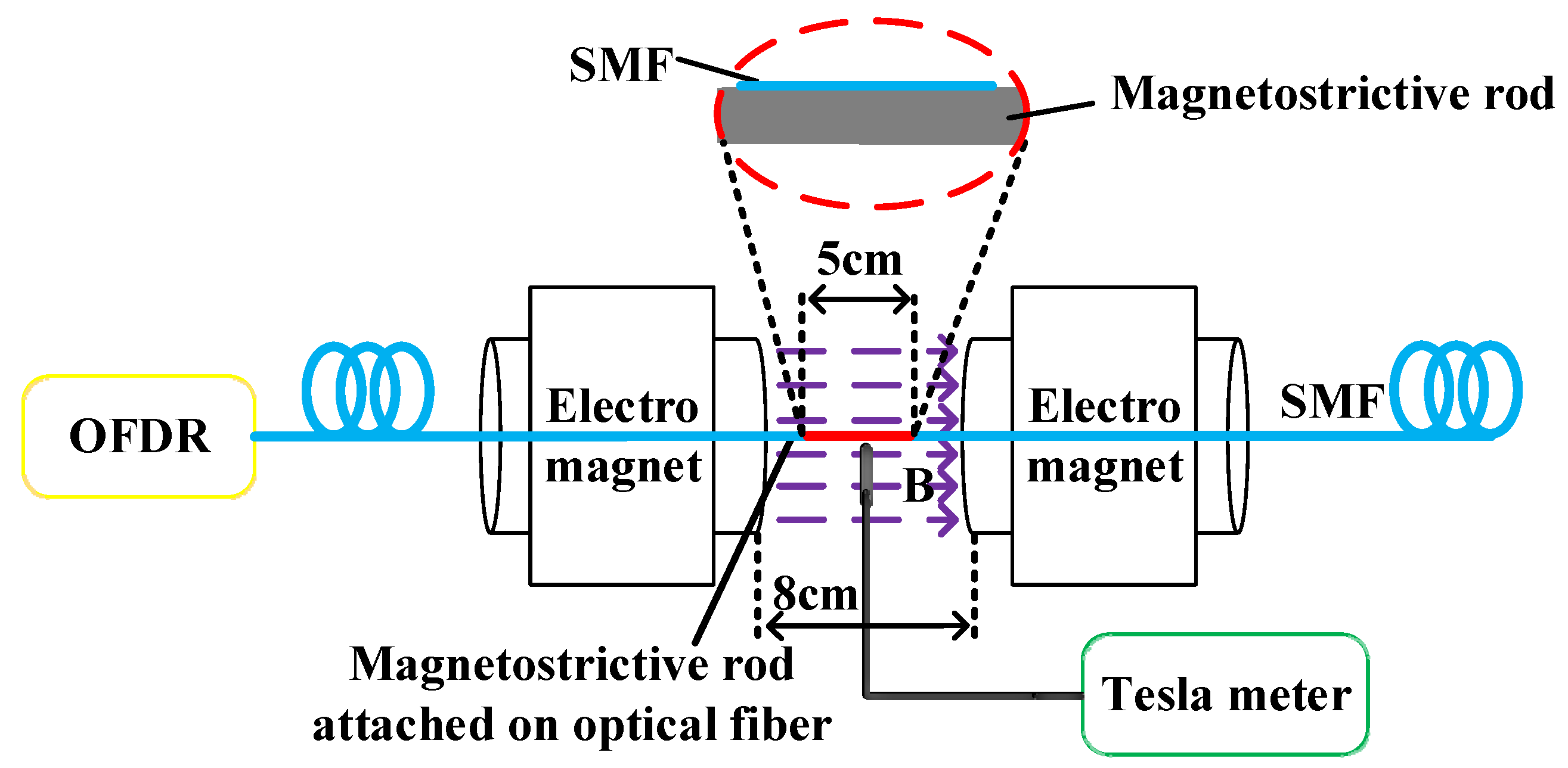
3.2. Experimental Setup
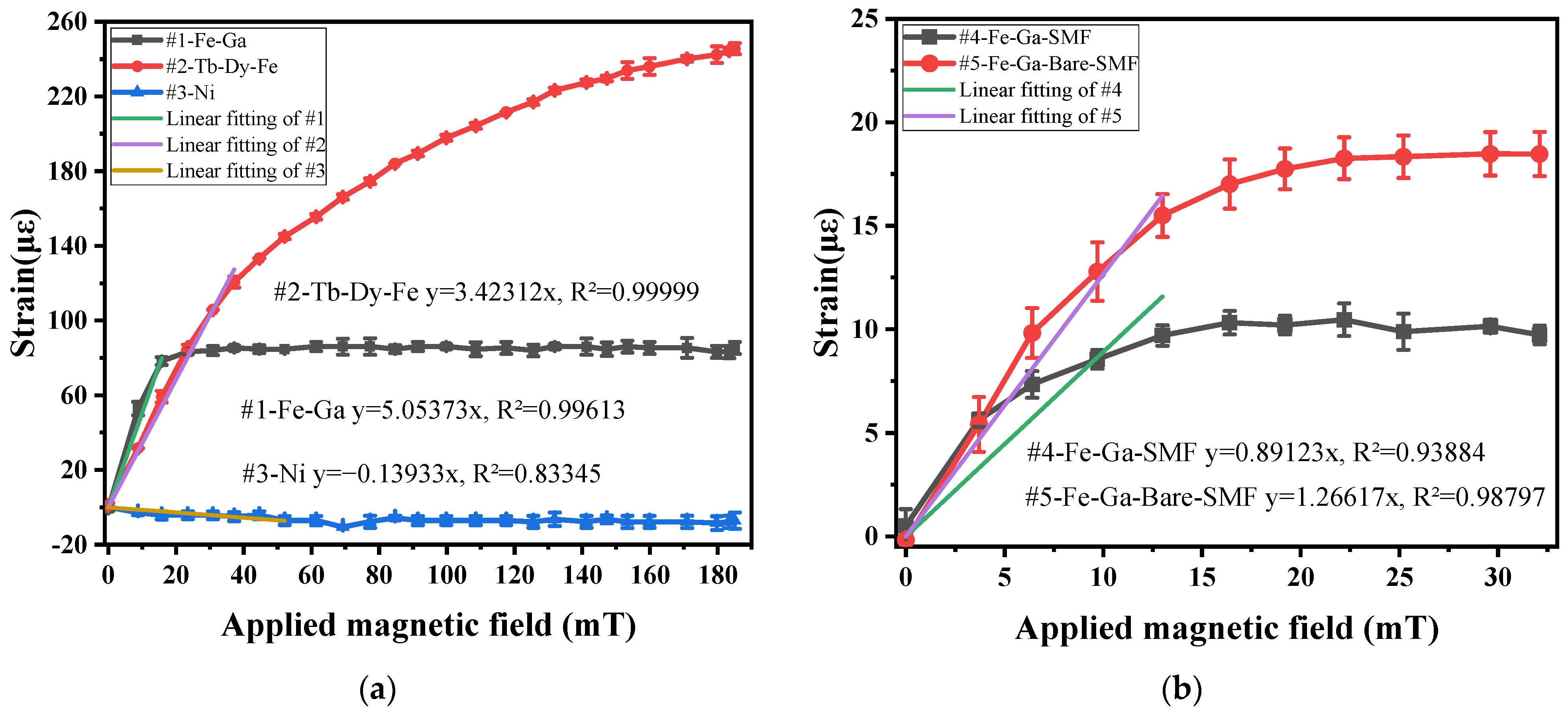
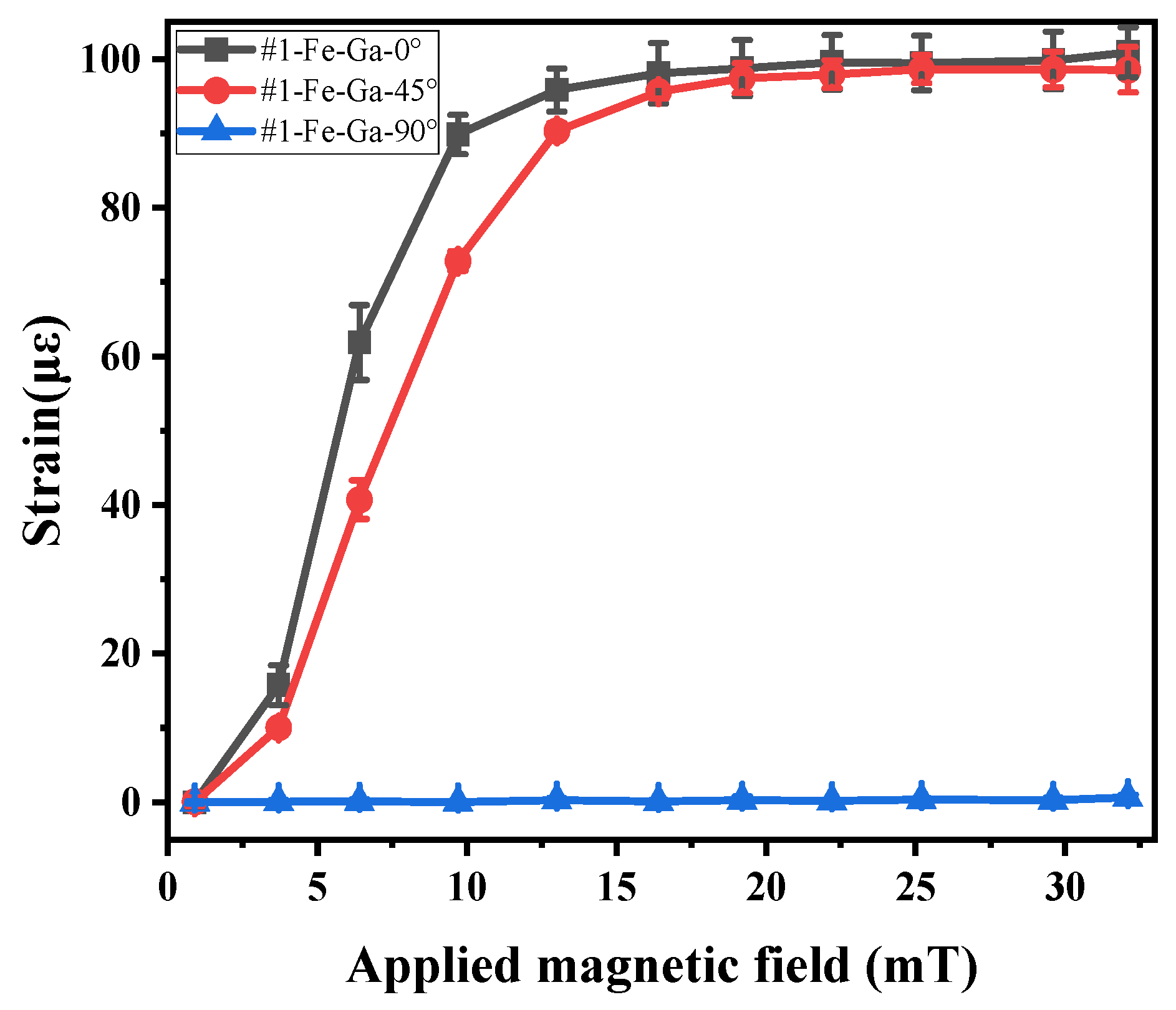
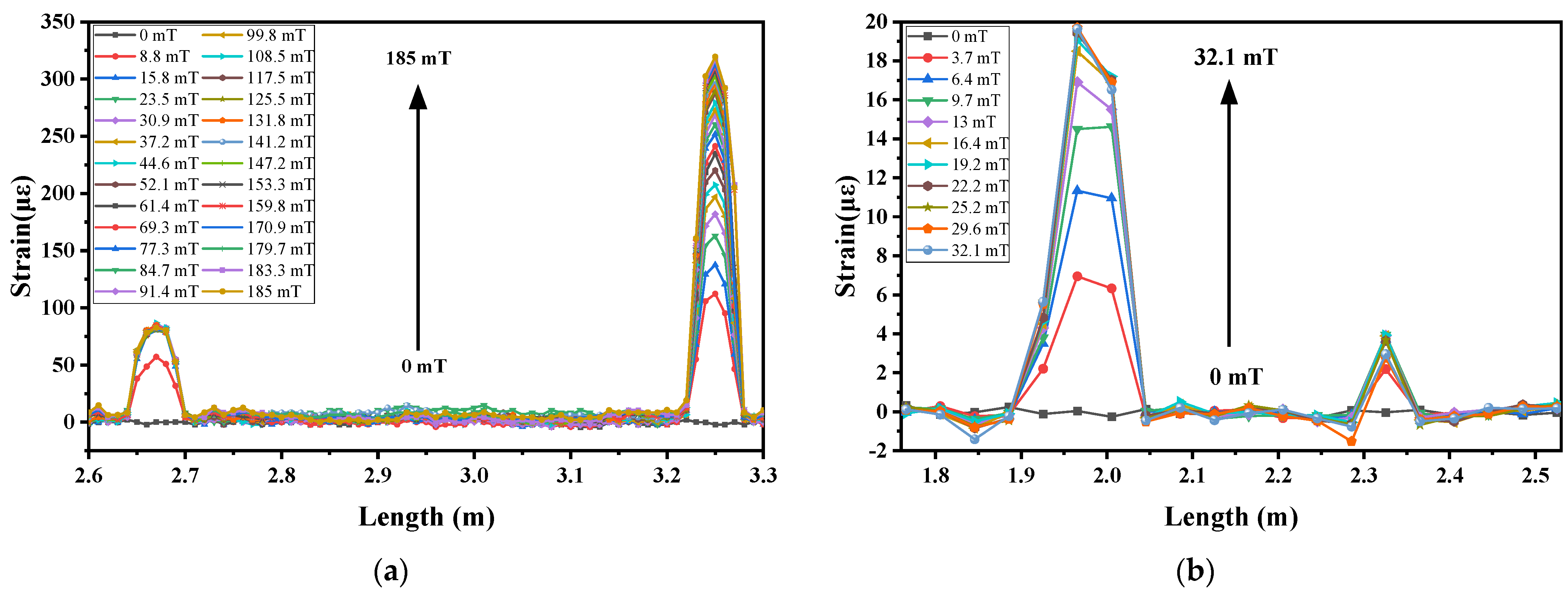
3.3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lenz, J.; Edelstein, S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Satpathi, D.; Moore, J.A.; Ennis, M.G. Design of a terfenol-D based fiber-optic current transducer. IEEE Sens. J. 2005, 5, 1057–1065. [Google Scholar] [CrossRef]
- Liu, C.; Shen, T.; Wu, H.-B.; Feng, Y.; Chen, J.-J. Applications of magneto-strictive, magneto-optical, magnetic fluid materials in optical fiber current sensors and optical fiber magnetic field sensors: A review. Opt. Fiber Technol. 2021, 65, 102634. [Google Scholar] [CrossRef]
- Faraday, M. I. Experimental researches in electricity.—Nineteenth series. Philos. Trans. R. Soc. Lond. 1846, 136, 1–20. [Google Scholar]
- Landau, L.; Lifshitz, E.; Pitaevskii, L. Course of Theoretical Physics: Electrodynamics of Continuous Media; Butterworth-Heinemann: Oxford, UK, 1984. [Google Scholar]
- Rashleigh, S.C. Magnetic-field sensing with a single-mode fiber. Opt. Lett. 1981, 6, 19–21. [Google Scholar] [CrossRef] [PubMed]
- Mora, J.; Diez, A.; Cruz, J.L.; Andres, M.V. A magnetostrictive sensor interrogated by fiber gratings for DC-current and temperature discrimination. IEEE Photonics Technol. Lett. 2000, 12, 1680–1682. [Google Scholar] [CrossRef]
- Li, M.; Zhou, J.; Xiang, Z.; Lv, F. Giant magnetostrictive magnetic fields sensor based on dual fiber Bragg gratings. In Proceedings of the 2005 IEEE Networking, Sensing and Control, Tucson, AZ, USA, 19–22 March 2005; pp. 490–495. [Google Scholar]
- Masoudi, A.; Newson, T.P. Distributed optical fiber dynamic magnetic field sensor based on magnetostriction. Appl. Opt. 2014, 53, 2833. [Google Scholar] [CrossRef] [PubMed]
- Ou, Y.; Chen, J.; Chen, W.; Cheng, C.; Zhu, Y.; Xiao, W.; Lv, H. A quasi-distributed fiber magnetic field sensor based on frequency-shifted interferometry fiber cavity ringdown technique. Opt. Laser Technol. 2022, 146, 107607. [Google Scholar] [CrossRef]
- Du, Y.; Liu, T.; Ding, Z.; Liu, K.; Feng, B.; Jiang, J. Distributed magnetic field sensor based on magnetostriction using Rayleigh backscattering spectra shift in optical frequency-domain reflectometry. Appl. Phys. Express 2015, 8, 012401. [Google Scholar] [CrossRef]
- Ding, Z.; Du, Y.; Liu, T.; Liu, K.; Feng, B.; Jiang, J. Distributed Optical Fiber Current Sensor Based on Magnetostriction in OFDR. IEEE Photonics Technol. Lett. 2015, 27, 2055–2058. [Google Scholar] [CrossRef]
- Ansari, F.; Libo, Y. Mechanics of Bond and Interface Shear Transfer in Optical Fiber Sensors. J. Eng. Mech. 1998, 124, 385–394. [Google Scholar] [CrossRef]
- Froggatt, M.; Moore, J. High-spatial-resolution distributed strain measurement in optical fiber with Rayleigh scatter. Appl. Opt. 1998, 37, 1735–1740. [Google Scholar] [CrossRef] [PubMed]
- Optical Backscatter Reflectometer Model 4600. User Guide 6. Luna Technologies. 2013, pp. 187–193. Available online: https://lunainc.com/sites/default/files/assets/files/resource-library/OBR-4600-UG6_SW3.10.1.pdf (accessed on 10 February 2022).
- Luo, M.; Liu, J.; Tang, C.; Wang, X.; Lan, T.; Kan, B. 0.5 mm spatial resolution distributed fiber temperature and strain sensor with position-deviation compensation based on OFDR. Opt. Express 2019, 27, 35823–35829. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Chen, L.; Bao, X. Compensation of temperature and strain coefficients due to local birefringence using optical frequency domain reflectometry. Opt. Commun. 2013, 311, 26–32. [Google Scholar] [CrossRef]
- Zhou, H.-M.; Zhou, Y.-H.; Zheng, X.-J.; Ye, Q.; Wei, J. A general 3-D nonlinear magnetostrictive constitutive model for soft ferromagnetic materials. J. Magn. Magn. Mater. 2009, 321, 281–290. [Google Scholar] [CrossRef]
- Olabi, A.G.; Grunwald, A. Design and application of magnetostrictive materials. Mater. Des. 2008, 29, 469–483. [Google Scholar] [CrossRef] [Green Version]
- Snodgrass, J.D.; McMasters, O.D. Optimized TERFENOL-D manufacturing processes. J. Alloy. Compd. 1997, 258, 24–29. [Google Scholar] [CrossRef]
| Case | Materials | Fiber | |
|---|---|---|---|
| #1 | Fe-Ga | 1.2 | SMF |
| #2 | Tb-Dy-Fe | 1.2 | SMF |
| #3 | Ni | 1.2 | SMF |
| #4 | Fe-Ga | 0.4 | SMF |
| #5 | Fe-Ga | 0.4 | Bare SMF |
| Case | Materials | Sensitivity (με/mT) | R2 (Linear of Fit) |
|---|---|---|---|
| #1 | Fe-Ga | 5.05 | 0.996 |
| #2 | Tb-Dy-Fe | 3.42 | 0.999 |
| #3 | Ni | −0.14 | 0.833 |
| #4 | Fe-Ga | 0.89 | 0.939 |
| #5 | Fe-Ga | 1.27 | 0.988 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, R.; Zhang, L.; Wei, H.; Gu, Y.; Pang, F.; Liu, H.; Wang, T. Quasi-Distributed Magnetic Field Fiber Sensors Integrated with Magnetostrictive Rod in OFDR System. Electronics 2022, 11, 1013. https://doi.org/10.3390/electronics11071013
Sun R, Zhang L, Wei H, Gu Y, Pang F, Liu H, Wang T. Quasi-Distributed Magnetic Field Fiber Sensors Integrated with Magnetostrictive Rod in OFDR System. Electronics. 2022; 11(7):1013. https://doi.org/10.3390/electronics11071013
Chicago/Turabian StyleSun, Ruoqi, Liang Zhang, Heming Wei, Yunzhe Gu, Fufei Pang, Huanhuan Liu, and Tingyun Wang. 2022. "Quasi-Distributed Magnetic Field Fiber Sensors Integrated with Magnetostrictive Rod in OFDR System" Electronics 11, no. 7: 1013. https://doi.org/10.3390/electronics11071013
APA StyleSun, R., Zhang, L., Wei, H., Gu, Y., Pang, F., Liu, H., & Wang, T. (2022). Quasi-Distributed Magnetic Field Fiber Sensors Integrated with Magnetostrictive Rod in OFDR System. Electronics, 11(7), 1013. https://doi.org/10.3390/electronics11071013









