P-Ride: A Shareability Prediction Based Framework in Ridesharing
Abstract
:1. Introduction
- We study the dynamic ridesharing problem and optimize the efficiency of batch-based methods.
- We propose a request group enumeration strategy based on k-clique listing on the shareability graph to optimize request group enumeration for batch-based methods.
- We devise the P-Ride ridesharing framework with a shareability prediction model that supports the batch prediction of shareable relationships among a arbitrary number of requests in a fixed time.
- Through extensive experiments, we demonstrate that the proposed method in this paper can significantly reduce the computational cost of batch-based methods. The P-Ride framework proposed in this paper can significantly improve efficiency with little impact on service quality.
2. Literature Review
3. Preliminary
3.1. Definitions
- Sequential constraint. The pickup location of request should be located before the drop-off location in the feasible route.
- Capacity constraint. At any location , the total number of requests on the vehicle should not exceed the capacity of the vehicle.
- Deadline constraint. For any location , , where satisfied following Equation (1) for different location type (source or destination).
3.2. Hardness of Dynamic Ridesharing Problem
3.3. Brute-Force Solution
| Algorithm 1 Brute-Force Solution |
|
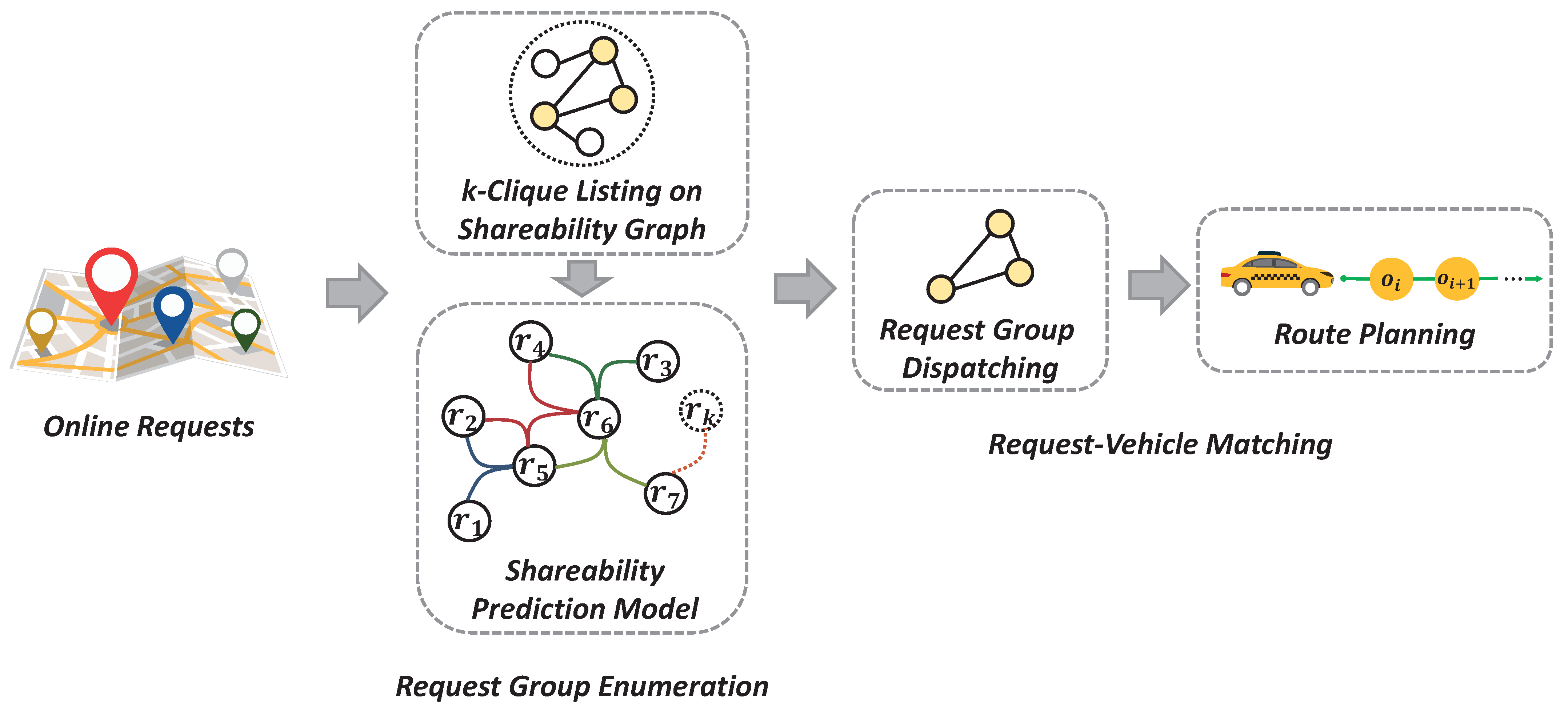
4. Shareability-Prediction-Based Ridesharing Framework
4.1. Shareability Graph
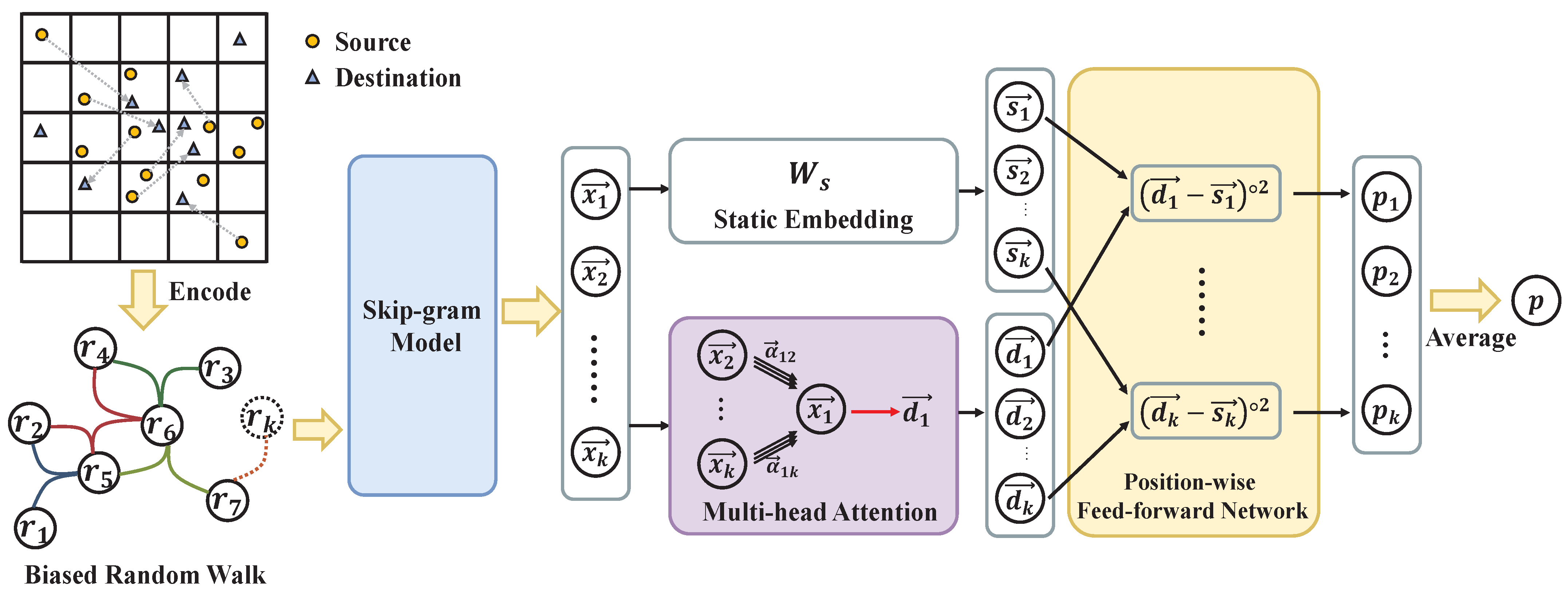
4.2. Shareability Prediction with Hyper Graph
4.3. P-Ride: Shareability Prediction Based Ridesharing Framework
| Algorithm 2 P-Ride |
|
5. Experimental Study
5.1. Data Set
5.2. Environment Settings
5.3. Approaches and Measurements
- pruneGDP [16]. It inserts the request into the vehicle’s current schedule sequentially and selects the vehicle with the least increased distance for service.
- BF. The Brute-Force method shown in Algorithm 1. It is in batch mode and enumerates all request groups among each vehicle’s candidate requests.
- P-Ride. The proposed prediction-based ridesharing framework in this paper. It achieves the prediction of shareability of request groups in a batch mode based on historical shareable requests by the shareability prediction model proposed in Section 4.1, which significantly reduces the unnecessary request group enumeration.
5.4. Experimental Results
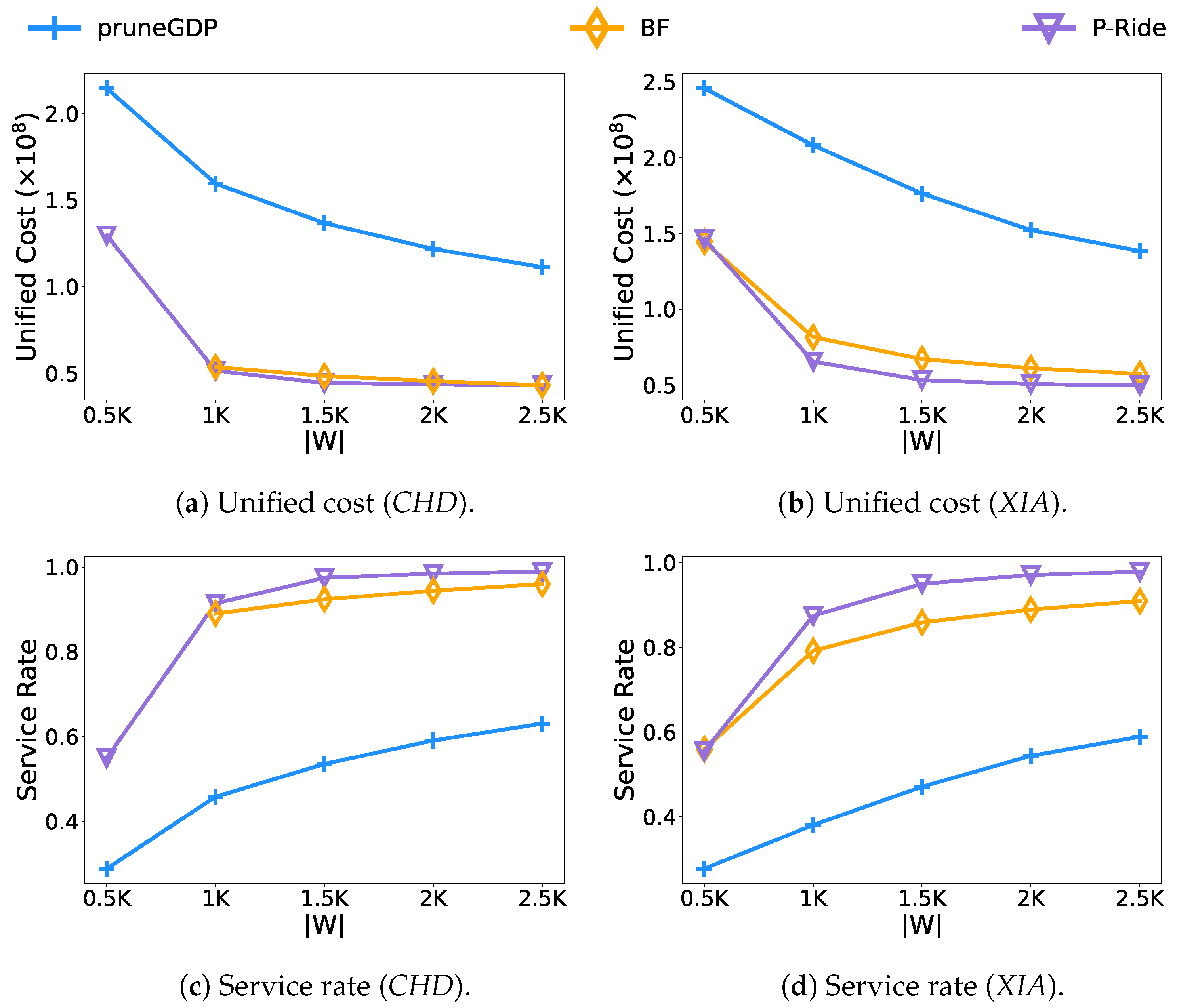
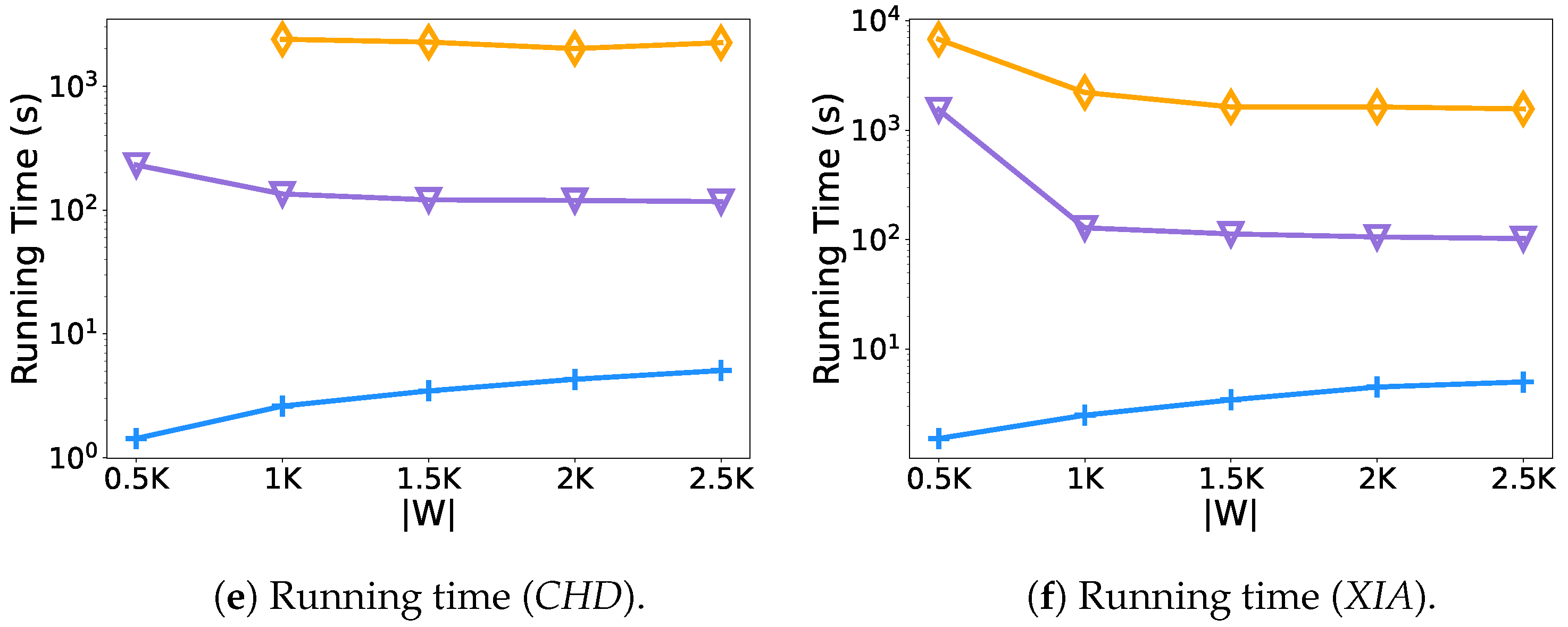
- Effect of the number of vehicles.Figure 6 shows the results of varying the number of vehicles from 0.5 K to 2.5 K. As the number of vehicles increases, so does the service quality of the evaluated methods. The BF algorithm leads other methods for the uniform cost, which mainly benefit from its brute force enumeration strategy. The P-Ride performs very similarly to the BF algorithm. However, in terms of the overall running time, because of the high time complexity of the brute force computation in the BF algorithm, it takes nearly up to 40 min and h to run on the two test datasets, respectively. In contrast, the performance of the P-Ride method proposed in this paper is times and times faster compared with the BF algorithm on the CHD and XIA datasets (as shown in Figure 6e,f), which mainly results from the fact that the clique enumeration strategy proposed in Section 4.1 avoids unnecessary enumeration of request groups. In addition, we further filter the candidate request groups using the shareability prediction model proposed in Section 4.2. Benefiting from the linear time complexity of the online algorithm pruneGDP, it leads in terms of overall running time. However, it performs poorly in terms of service quality (service rate and unified cost) because it lacks the analysis of the shareable relationships among requests. It should be noted that on the CHD dataset, the results of the BF algorithm at K are not presented because there are too few vehicles and most requests cannot be served, resulting in a backlog in the platform, and the BF algorithm repeatedly processes these unexpired requests in each round of calculation. Moreover, it is also the main reason for the significant increase in the running time of P-Ride in Figure 6f.
- Effect of the number of requests.Figure 7 presents the results of varying the number of requests from 10 K to 90 K. Because the number of accepted and rejected requests increased significantly, the unified costs of all experiment algorithms grew. For the service rate shown in Figure 7c,d, the BF and pruneGDP gradually appear to be inadequate as the number of requests continues to increase. P-Ride performs the best, achieving a service rate improvement ranging from 2.91∼35.85% and 6.93∼38.99% over other methods at K on the two datasets CHD and XIA, respectively. For the running time, the insertion-based method pruneGDP is still the fastest. In Figure 7e, P-Ride is up to and faster than BF on two datasets, respectively. When the number of requests K, there are enough vehicles in the platform to serve all the requests, so the requests can be allocated quickly. Therefore, the running time gap between BF and P-Ride is greatly reduced in Figure 7e,f.
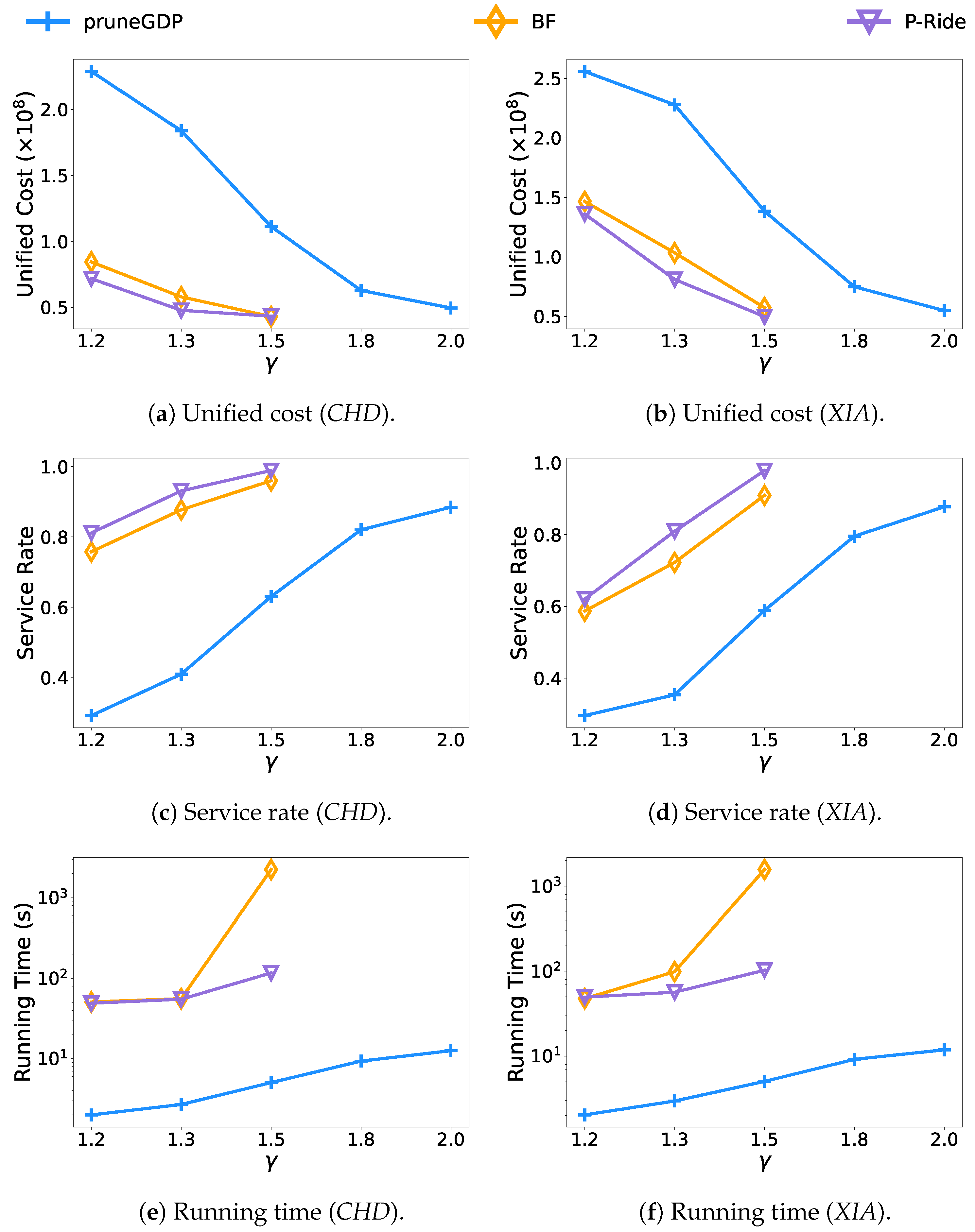
- Effect of the deadline.Figure 8 presents the results of the varying deadline of requests by changing the deadline parameter from to . With the gradual relaxation of deadlines, the quality of service achieved by all testing methods has increased. The performances of P-Ride and BF are similar when we strictly set the deadline of requests, i.e., or . The reason for this is that the number of candidate request groups for each request greatly reduced with a minor deadline, making it challenging to achieve noticeable performance improvements by applying request group enumeration strategies. We note that when the request deadline parameter , the BF causes a significant increase in runtime due to a sharp increase in the request groups. In this case, P-Ride achieves a similar service rate and unified cost with only about of the running time used by BF. However, when the parameter , both BF and P-Ride are incapable of processing all requests within the specified time limit on two datasets due to the dramatic increase in the number of candidate request groups. That is primarily because the number of feasible request groups cannot be reduced no matter how much of the pruning strategy is performed during the request group enumeration. Additionally, Figure 9e,f presents similar results for a similar reason.
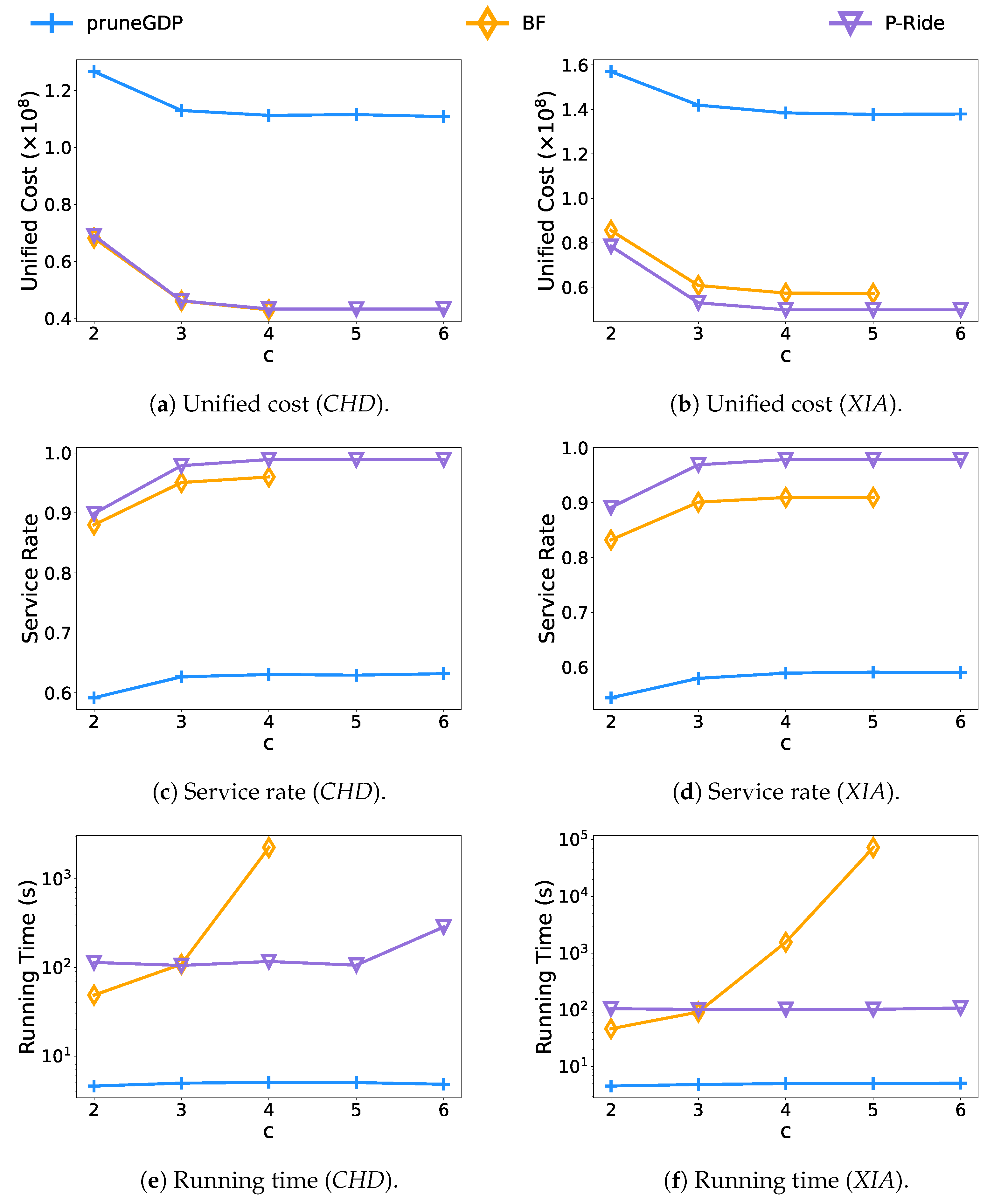
- Effect of the vehicle’s capacity constraint.Figure 9 illustrates the results of varying the vehicle’s capacity from 2 to 6. In terms of unified cost, BF and P-Ride have similar performance in terms of service quality. However, since the number of request groups increases significantly with vehicle capacity for the BF method (e.g., when , the BF algorithm needs to enumerate different request groups), the BF algorithm cannot finish within the given time limit when and on two datasets, respectively. When the capacity constraint of the vehicle , we observe that the BF algorithm can run in a shorter time than P-Ride. That is because the capacity constraint means that the maximum number of request groups is 2, and the cost of constructing the shareability graph is already higher than the direct enumeration of BF at this time. However, the superiority of P-Ride gradually realizes with the increase of vehicle capacity constraint. We notice that when the vehicle capacity constraint , the running time of P-Ride is up to faster than that of BF on the CHD dataset. Additionally, on the XIA dataset, the P-Ride performs faster than the BF algorithm as shown in Figure 9f. Therefore, P-Ride works better in request groups with diverse sizes.
- The group-based methods (i.e., BF, P-Ride) have superior performance in terms of service quality (i.e., higher service rates and lower unified costs) compared to the online-based methods (i.e., pruneGDP). For example, the P-Ride achieves a service rate improvement of up to compared to the other tested algorithm (servicing approximately more requests for the platform).
- The P-Ride shows excellent performance in most cases. For example, P-Ride runs up to times faster than BF in Figure 9f. In other words, P-Ride can process the requests of XIA in min, but BF takes up to h.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Didi Chuxing. Available online: https://www.didiglobal.com/ (accessed on 2 March 2022).
- uberPOOL. Available online: https://www.uber.com/ (accessed on 2 March 2022).
- Cici, B.; Markopoulou, A.; Laoutaris, N. Designing an on-line ride-sharing system. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, Bellevue, WA, USA, 3–6 November 2015; pp. 60:1–60:4. [Google Scholar]
- Yeung, S.; Miller, E.; Madria, S. A Flexible Real-Time Ridesharing System Considering Current Road Conditions. In Proceedings of the IEEE 17th International Conference on Mobile Data Management, MDM 2016, Porto, Portugal, 13–16 June 2016; pp. 186–191. [Google Scholar]
- Asghari, M.; Deng, D.; Shahabi, C.; Demiryurek, U.; Li, Y. Price-aware real-time ride-sharing at scale: An auction-based approach. In Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, GIS 2016, Burlingame, CA, USA, 31 October–3 November 2016; pp. 3:1–3:10. [Google Scholar]
- Asghari, M.; Shahabi, C. An On-line Truthful and Individually Rational Pricing Mechanism for Ride-sharing. In Proceedings of the 25th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, GIS, Redondo Beach, CA, USA, 7–10 November 2017; pp. 7:1–7:10. [Google Scholar]
- Ma, S.; Zheng, Y.; Wolfson, O. T-share: A large-scale dynamic taxi ridesharing service. In Proceedings of the 29th IEEE International Conference on Data Engineering, ICDE 2013, Brisbane, Australia, 8–12 April 2013; pp. 410–421. [Google Scholar]
- Huang, Y.; Bastani, F.; Jin, R.; Wang, X.S. Large Scale Real-time Ridesharing with Service Guarantee on Road Networks. PVLDB 2014, 7, 2017–2028. [Google Scholar] [CrossRef]
- Cheng, P.; Xin, H.; Chen, L. Utility-aware ridesharing on road networks. In Proceedings of the 2017 ACM International Conference on Management of Data, SIGMOD Conference 2017, Chicago, IL, USA, 14–19 May 2017; pp. 1197–1210. [Google Scholar]
- Cordeau, J.F.; Laporte, G. A tabu search heuristic for the static multi-vehicle dial-a-ride problem. Transp. Res. Part Methodol. 2003, 37, 579–594. [Google Scholar] [CrossRef] [Green Version]
- Alonso-Mora, J.; Samaranayake, S.; Wallar, A.; Frazzoli, E.; Rus, D. On-demand high-capacity ride-sharing via dynamic trip-vehicle assignment. Proc. Natl. Acad. Sci. USA 2017, 114, 462–467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeng, Y.; Tong, Y.; Song, Y.; Chen, L. The Simpler The Better: An Indexing Approach for Shared-Route Planning Queries. Proc. VLDB Endow. 2020, 13, 3517–3530. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, L.; Ye, J. Order dispatch in price-aware ridesharing. Proc. VLDB Endow. 2018, 11, 853–865. [Google Scholar] [CrossRef] [Green Version]
- Bei, X.; Zhang, S. Algorithms for Trip-Vehicle Assignment in Ride-Sharing. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, AAAI 18, New Orleans, LA, USA, 2–7 February 2018; pp. 3–9. [Google Scholar]
- Xu, Y.; Tong, Y.; Shi, Y.; Tao, Q.; Xu, K.; Li, W. An Efficient Insertion Operator in Dynamic Ridesharing Services. In Proceedings of the 35th IEEE International Conference on Data Engineering, ICDE 2019, Macao, China, 8–11 April 2019; pp. 1022–1033. [Google Scholar]
- Tong, Y.; Zeng, Y.; Zhou, Z.; Chen, L.; Ye, J.; Xu, K. A Unified Approach to Route Planning for Shared Mobility. PVLDB 2018, 11, 1633–1646. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Zhang, Y.; Zhang, W.; Qin, L.; Yang, J. Efficient Maximal Spatial Clique Enumeration. In Proceedings of the 35th IEEE International Conference on Data Engineering, ICDE 2019, Macao, China, 8–11 April 2019; pp. 878–889. [Google Scholar]
- Danisch, M.; Balalau, O.; Sozio, M. Listing k-cliques in Sparse Real-World Graphs. In Proceedings of the 2018 World Wide Web Conference on World Wide Web, WWW 2018, Lyon, France, 23–27 April 2018; pp. 589–598. [Google Scholar]
- Cheng, J.; Ke, Y.; Fu, A.W.; Yu, J.X.; Zhu, L. Finding maximal cliques in massive networks by H*-graph. In Proceedings of the ACM SIGMOD International Conference on Management of Data, SIGMOD 2010, Indianapolis, IN, USA, 6–10 June 2010; pp. 447–458. [Google Scholar]
- Wilson, N.H.; Weissberg, R.; Higonnet, B.; Hauser, J. Advanced Dial-a-Ride Algorithms; Technical Report; In Tech Report R76-20; Department of Civil Engineering, MIT: Cambridge, MA, USA, 1975. [Google Scholar]
- Cordeau, J.F.; Laporte, G. The dial-a-ride problem (DARP): Variants, modeling issues and algorithms. Q. J. Belg. Fr. Ital. Oper. Res. Soc. 2003, 1, 89–101. [Google Scholar] [CrossRef]
- Wong, K.I.; Bell, M.G. Solution of the Dial-a-Ride Problem with multi-dimensional capacity constraints. Int. Trans. Oper. Res. 2006, 13, 195–208. [Google Scholar] [CrossRef]
- Cordeau, J.F. A branch-and-cut algorithm for the dial-a-ride problem. Oper. Res. 2006, 54, 573–586. [Google Scholar] [CrossRef] [Green Version]
- Zheng, L.; Cheng, P.; Chen, L. Auction-based order dispatch and pricing in ridesharing. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 8–11 April 2019; pp. 1034–1045. [Google Scholar]
- Jaw, J.J.; Odoni, A.R.; Psaraftis, H.N.; Wilson, N.H. A heuristic algorithm for the multi-vehicle advance request dial-a-ride problem with time windows. Transp. Res. Part Methodol. 1986, 20, 243–257. [Google Scholar] [CrossRef]
- Ioachim, I.; Desrosiers, J.; Dumas, Y.; Solomon, M.M.; Villeneuve, D. A request clustering algorithm for door-to-door handicapped transportation. Transp. Sci. 1995, 29, 63–78. [Google Scholar] [CrossRef]
- Häme, L. An adaptive insertion algorithm for the single-vehicle dial-a-ride problem with narrow time windows. Eur. J. Oper. Res. 2011, 209, 11–22. [Google Scholar] [CrossRef]
- Wang, C.; Song, Y.; Wei, Y.; Fan, G.; Jin, H.; Zhang, F. Towards Minimum Fleet for Ridesharing-Aware Mobility-on-Demand Systems. In Proceedings of the 40th IEEE Conference on Computer Communications, INFOCOM, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, J. Mobility Sharing as a Preference Matching Problem. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2584–2592. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Zou, Y.; Ma, J. Hyper-SAGNN: A self-attention based graph neural network for hypergraphs. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Ma, S.; Zheng, Y.; Wolfson, O. Real-Time City-Scale Taxi Ridesharing. IEEE Trans. Knowl. Data Eng. 2015, 27, 1782–1795. [Google Scholar] [CrossRef]
- Cheng, P.; Jian, X.; Chen, L. An experimental evaluation of task assignment in spatial crowdsourcing. Proc. VLDB Endow. 2018, 11, 1428–1440. [Google Scholar] [CrossRef]
- Data Source: Didi Chuxing GAIA Initiative. Available online: https://outreach.didichuxing.com/research/opendata/ (accessed on 18 November 2020).
- Wang, J.; Cheng, P.; Zheng, L.; Feng, C.; Chen, L.; Lin, X.; Wang, Z. Demand-Aware Route Planning for Shared Mobility Services. Proc. VLDB Endow. 2020, 13, 979–991. [Google Scholar] [CrossRef] [Green Version]
- Geofabrik. Available online: https://download.geofabrik.de/ (accessed on 10 March 2022).
- Osmconverter. Available online: https://wiki.openstreetmap.org/wiki/Osmconvert (accessed on 10 March 2022).
- OpenStreetMap. Available online: https://www.openstreetmap.org/ (accessed on 10 March 2022).
- Relation: Chengdu. Available online: https://www.openstreetmap.org/relation/2110264 (accessed on 10 March 2022).
- Relation: Xi’an. Available online: https://www.openstreetmap.org/relation/3226004 (accessed on 10 March 2022).
- Yianilos, P.N. Data Structures and Algorithms for Nearest Neighbor Search in General Metric Spaces. In Proceedings of the Fifth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), Austin, TX, USA, 25–27 January 1993; pp. 311–321. [Google Scholar]


| Request | Source | Destination | Release Time | Deadline |
|---|---|---|---|---|
| a | d | 0 | 14 | |
| c | f | 0 | 11 | |
| b | e | 2 | 10 | |
| c | g | 3 | 9 |
| Symbol | Description |
|---|---|
| R | a set of m time-constrained request requests |
| request request of request i | |
| the planned route for vehicle | |
| Q | a candidate request group with size |
| Name | # Nodes | # Edges | # Trainning Requests | # Testing Requests |
|---|---|---|---|---|
| CHD | 6066 | 13,242 | 3,090,337 | 110,190 |
| XIA | 5148 | 11,042 | 2,888,979 | 97,533 |
| Parameters | Values |
|---|---|
| the number, n, of requests | 10 K, 30 K, 50 K, 70 K, 90 K |
| the number, m, of vehicles | 0.5 K, 1 K, 1.5 K, 2 K, 2.5 K |
| the capacity of vehicles c | 2, 3, 4, 5, 6 |
| the deadline parameter | 1.2, 1.3, 1.5, 1.8, 2.0 |
| the penalty coefficient () | 10 |
| the batching time (s) | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, L. P-Ride: A Shareability Prediction Based Framework in Ridesharing. Electronics 2022, 11, 1164. https://doi.org/10.3390/electronics11071164
Chen Y, Wang L. P-Ride: A Shareability Prediction Based Framework in Ridesharing. Electronics. 2022; 11(7):1164. https://doi.org/10.3390/electronics11071164
Chicago/Turabian StyleChen, Yu, and Liping Wang. 2022. "P-Ride: A Shareability Prediction Based Framework in Ridesharing" Electronics 11, no. 7: 1164. https://doi.org/10.3390/electronics11071164
APA StyleChen, Y., & Wang, L. (2022). P-Ride: A Shareability Prediction Based Framework in Ridesharing. Electronics, 11(7), 1164. https://doi.org/10.3390/electronics11071164







