A Realistic, Flexible and Extendible Network Emulation Platform for Space Networks

Abstract

Wide attention has been drawn to the application of space networks (SN) in recent years. Compared with terrestrial networks, SN have a set of unique characteristics, e.g., a long propagation delay, time-varying channel quality, and dynamic link connection, which causes the inapplicability of mature terrestrial networking technologies. Therefore, the focus of SN application is to innovate and break through a series of key networking technologies and protocols. Network emulation is critical for evaluation and verification in the research of networking technologies and protocols. This paper concentrates on designing an emulation platform which provides a realistic, flexible, and extensible experimental environment for the SN. The architecture of platform includes four components, namely the logical plane, control plane, data plane and measurement plane. Container technology is adopted to flexibly symbolize network nodes. The emulation method of dynamic connection relationships and time-varying link characteristics between pairwise nodes are considered so as to realize the real space environment and arbitrary topology. Furthermore, an extensible structure is described to emulate large-scale scenarios and access external emulation resources. Finally, experiment results show that the proposed platform is capable of emulating diverse, dynamic, and complex SN scenarios with high precision.

1. Introduction

With the proliferation of low cost spatial information systems, powerful on-board processing capacity, and mature inter-satellite link techniques, space networks (SN) are emerging as an important part of the national infrastructure and research frontier. However, due to some unique characteristics of SN, e.g., long propagation delay, frequent link disruption, etc., mature terrestrial networking technologies cannot be applied to SN directly. To tackle this problem, network researchers propose various new network protocols and technologies. Meanwhile, the process of designing and developing network protocols and technologies is complex, in which the experiment phase plays an important role to decipher the performance and make helpful suggestions for improvement. So it is urgent to set up a testbed to carry out the research on basic theory and key technologies for SN.

Network emulation provides manageable and reproducible environments for deploying real applications and communicating practical data flow. However, owing to the particularity of the SN communication environment, existing emulation methods find it difficult to balance the authenticity, flexibility and extendibility of the emulation, some lack enough authenticity, such as NPVT [1], some lack flexibility and are only designed for a specific protocol system, such as EmuStack [2], VITT [3], or only support some specific network topologies, such as DEN [4], and some do not have extendibility and can only emulate small-scale scenes, such as SCNT [5]. Therefore, the challenge in the research on SN emulation methods is to realize the reliable emulation of dynamic network topology, time-varying link characteristics, multiple protocol architectures and large-scale network scenarios with the goal of authenticity, flexibility and extendibility.

This paper aims to present an SN emulation platform. When we design this platform, following goals are taken in mind:

• Authenticity. (a) Network nodes in the platform have the same functionality as real hardware and execute exactly the same code. (b) The network of the platform can change automatically as does the real space communication environment.
• Extendibility. (a) The platform should have an extensible structure used to support computing resource expansion. (b) The platform should provide access interfaces for external physical devices to fulfil the special needs of researchers.
• Flexibility. (a) The platform should be agile enough to create any target networks, and deploy various network protocols and upper application software conveniently. (b) Experiments conducted on the platform could follow a workflow. For the same experiment, any researcher can obtain identical results in the same manner.

To meet our goals, an SN emulation architecture, which consists of a logical plane, control plane, data plane, and a measurement plane, is proposed. On the basis of the emulation architecture, the SN emulation platform is constructed in a hierarchical star structure to support hardware resource expansion and access external physical devices. Integrating with software-defined networking (SDN) and a traffic control mechanism, the platform supports the emulation of dynamic SN. Combining with container technology, various SN protocols and communication technologies could be implemented on the platform flexibly as real deployments. Considering changeable simulation scenarios and different network concerns, the flexible configuration of network measurement on demand is realized. Furthermore, the verification and analysis workflow of SN technologies based on the platform are given.

The structure of the paper is presented as follows. Section 2 provides an overview of related work. Section 3 describes the architecture of the emulation platform and the physical implementation model. According to different emulation elements, the design of this architecture is presented in Section 4. Section 5 includes the proposed experiments, experimental results and discussion. In the last section, we conclude this paper and identify future research directions.

2. Related Work

2.1. Research Works on Space Network

To promote the development of SN, and ensure the efficient interconnection of various SN nodes as well as full sharing of information and resources, various research works have been conducted in fields of the network architecture, the constellation and the network protocol.

Aiming at the problem of lacking a stable end-to-end path for data transmission, which is caused by long transmission delay and frequent link interruption in SNs, researchers propose a Delay/Disruption-Tolerant Network (DTN) and CCSDS (Consultative Committee for Space Data Systems).

Constellation system deployment plans have been carried out in recent years, such as OneWeb [6] and Starlink [7] according to different constellation systems, application requirements and optimization objectives, [8] and some other researches present multiple inter satellite topology design algorithms.

Aiming at the problem that traditional global optimal routing strategies is only suitable for static network topologies, the topologically predictable routing protocol, namely OSPF+ [9], is presented. Pointing at the problem of low data transmission efficiency, which is caused by long transmission delay and high bit error rate in space networks, an erasure code-based LTP (Licklider transmission protocol) protocol [10] is designed. Considering the transmission of the video stream under the harsh communication conditions in the deep space a BSS (Bundle Streaming Service) protocol [11] is proposed. In addition, there are many related works in the fields of Ad-Hoc Networks [12] and 5G [13,14].

2.2. Space Network Experimental Validation Approaches

Typical network experimental validation approaches include simulation, a live testbed, and emulation. Discrete-event network simulation has enough flexibility, e.g., ns-2 [15] and OPNET [16]. However, the network simulation has no real network traffic and is hard to realize the real description of complex SN equipment and its environment through the abstraction of various environmental parameters. An actual hardware-based testbed has the highest emulation authenticity, e.g., ORBIT [17], UMass DieselNet [18]. However, for the high cost and poor extendibility of SN nodes, it is difficult for the testbed to support the requirements of changeable SN emulation scenarios.

Compared with network simulation and the live testbed, network emulation is a hybrid approach which balances authenticity and flexibility. Typical emulators are Mininet [19], vEmulab [20], and NEaaS [21]. However, these emulation options only support the emulation of static terrestrial networks rather than dynamic SN. Ref. [22] proposes TUNIE which is capable of simulating reliable DTN environments and obtaining an accurate system performance evaluation. Ref. [23] presents a state-of-the-art DTN testbed for satellite and space communications. The core of the testbed relies on the Bundle Protocol and its architecture have been designed to support multiple DTN implementations and a variety of underlying and overlying protocols. Based on OpenStack, Ref. [2] proposes a large-scale, real-time and distributed emulation platform for DTN, namely EmuStack. These platforms are designed for some types of network architecture, such as DTN, and lack support for others. Ref. [1] designs a network protocol validation testbed for integrated space–terrestrial network. However, large-scale scenarios emulated on the testbed is realized by the expansion of routing table, which lacks enough authenticity. As shown in

Table 1. Comparisons among existing space network emulation systems.

Literature	Dynamic Topology Connection	Dynamic Link Characteristics	Protocol Architecture	Supported Various Scenarios	Supported Scalability	Construction Cost
NPVT	yes	yes	TCP/IP, CCSDS	yes	yes	low
EmuStack	yes	no	DTN	yes	yes	low
VITT	-	-	different TCP variants	-	yes	low
SCNT	no	no	BP, TCP/IP	no	Limited scalability	low
TUNIE [22]	yes	yes	DTN, other new routing protocols and applications	yes	yes	low
SPICE [23]	no	-	CCSDS, DTN	yes	yes	high
SCT [24]	yes	yes	CCSDS, TCP/IP	yes	-	high
TATPA [25]	-	-	different TCP variants	-	yes	low
MACHETE [26]	-	-	CCSDS, DTN, TCP/IP	yes	-	low
DEN	-	yes	BSP, BP, LTP	no	yes	low

, comparisons among different SN emulation systems are listed. Overall, in consideration of authenticity, flexibility and extendibility, all the emulators above focus on limited aspects.

3. Architecture of the Network Emulation Platform

3.1. Architecture

As shown in Figure 1, the proposed platform can be divided into four planes, namely the logical plane, control plane, data plane, and measurement plane. A particular network scenario is set at the logical plane. Corresponding settings are stored in the database. The control plane reads these setting and procedure commands to drive emulation in the data plane. The measurement plane serves to monitor network performances of simulation scenarios.

3.1.1. Logical Plane

According to the specific network scenario, a network model could be built by the logical plane which includes a space-based backbone transmission network, satellite links, space-based access network, ground stations, terrestrial network, and end-users. The network model contains not only parameters of network nodes, but also a specific connection plan, channel parameters, software deployments, and network protocols.

3.1.2. Control Plane

The control plane consists of two parts: the front-end service and the back-end service. The front-end service offers a Web UI to interact with researchers. Researchers can configure various parameters of the network model and visualize the network scenario through the Web UI. The back-end service is backed by the main controller which is responsible for implementing commands and parameters from the logical plane into the data plane. The main controller is a software and operates all elements in the data plane. Researchers can configure and control the environment parameters with different emulation scenarios, as well as monitoring the traffic for each testing through the control plane. The emulation architecture is thus configurable and controllable.

3.1.3. Data Plane

The data plane serves to emulate network scenarios directly, and contains SDN switches, servers, emulation nodes, etc. These underlying network resources are connected with each other in a hierarchical star network structure. Emulation nodes are connected to the virtual switch on the server and represent SN nodes at the logical plane. Diverse software and applications are installed in the emulation node. Servers and external devices or networks are linked to each other by the SDN hardware switch.

3.1.4. Measurement Plane

The measurement plane mainly has two functions, namely real-time network information collection and full packet capture. The capture container is the basic unit of the measurement plane. Each capture container covers a Python-based Daemon which realizes network information collection and supports full packet capture according to the configuration of researchers. Measurements are stored in the database and real-time network information is displayed by the Web UI.

3.2. Physical Implementation Model

Corresponding to the platform architecture, a typically physical implementation model is presented, which has four principal parts: the Web UI, main controller, emulation node and SDN switch, as shown in Figure 2.

3.2.1. Web UI

Researchers interact with the proposed platform through the Web UI. The Web UI stores network model parameters configured by researchers in the database, and shows network models in real time to allow researchers to observe the emulation process intuitively.

3.2.2. Main Controller

The main controller interacts with the Web UI and is used for parameter calculation, SDN switch control and node management. The calculation results are written in the database for subsequent emulation operations.

The parameter calculation refers to the process that the main controller reads the network model parameters, obtains the relationships of visibility and link characteristics between nodes, filters the connection relationships, and assigns the network configuration of emulation nodes. The SDN switch control [27] refers to the process that the main controller sends topology control flow tables to SDN switches in real time according to the target network topology. The node management refers to the process in which the main controller creates emulation nodes, binds nodes with SDN switches, and allocates emulation resources. Moreover, the main controller is also responsible for generating the experimental start time and transmitting the operation state of the experiment to the Web UI.

3.2.3. Emulation Node

All emulation nodes run real network protocol stacks and applications to complete network traffic exchange. Due to the advantages of flexible configuration, easy extension and convenient management, virtual nodes are generally used to simulate the nodes in the target network. For some special needs or cases where emulation can not be supported by pure virtual nodes, physical nodes are used, including embedded devices, satellite links, and etc.

3.2.4. Sdn Switch

According to assigned network parameters, each emulation node is linked to the corresponding SDN switch by the main controller. The SDN software switch is responsible for the connection of virtual nodes. Meanwhile the SDN hardware switch is in charge of the connection of physical nodes, and provides access to external networks or links for the emulation platform. SDN software switch and SDN hardware switch are connected with each other to form an interconnected emulation network. Once the emulation experiment starts, the main controller sends real-time flow tables to each SDN switch to simulate the dynamic topology of the target network model. SDN switches can also collect and send their own states back to the Web UI for display, or save these states for subsequent analysis.

3.3. Platform Characteristics Analysis

Through the above designs, the proposed emulation platform effectively provides a realistic, flexible, and extensible experimental environment for SN.

Virtual emulation nodes have the same functionality as physical hardware and can execute exactly the same code in a real deployment. Meanwhile, the proposed emulation platform supports the joint emulation method among virtual nodes, physical nodes, real networks and real links, bringing credible emulation results.

Integrating with SDN and traffic control mechanism, the networking of platform can change automatically like that of a real space communication environment (especially, time-varying link quality and dynamic link connection). In addition, various network protocol architectures are reconstructed by container images. These realize the reliable and flexible emulation of different SN scenarios

The platform architecture has extendibility including the horizontal extension of hardware resources and the access of external physical emulation devices. The main controller offers a novel unified control for the connection relationships between emulation nodes under different switches through flow tables. These features allow multiple nodes with huge individual differences to become a part of the proposed platform and to be managed.

4. Designs

In this section, the specific implementation manners of the platform are described from three basic aspects, that is, the node, link, and network topology.

4.1. Node

The emulation node is the basic emulation element of the proposed platform which is the actual carrier of network protocols and communication technologies.

4.1.1. Node Virtualization

Virtualization is a resource management technology, which realizes the goal of virtualizing a physical computer system into multiple virtual computer systems. The virtual computer system has a strong consistency with the real computer system. Typical virtualization methods include virtual machines and containers. Compared with the virtual machine, the container which relied on the Linux kernel features is more flexible and lightweight. Due to these advantages, the container-based virtualization is applied to realize the emulation node in the proposed platform. Moreover, container orchestration, such as Kubernetes [28], is employed to achieves functions that cannot be supported by native container-based virtualization. If needed, we can develop container orchestration ourselves. The Pod is the basic building block of Kubernetes. A Pod contains a group of one or more containers, such as Docker [29]. Containers in a Pod share some resources with each other, e.g., storage and network resources.

As shown in Figure 3, an emulation node is a Pod which comprises an emulation container and a capture container. Network protocols or technologies which need to be validated are deployed at the emulation container. The capture container is responsible for real-time network measurement and full packets capture in simulation scenarios. Considering changeable simulation scenarios and different networks, researchers need to set network measurement points as needed. Via binding to each other in the form of Pods and sharing network resources, the capture container can measure and monitor all network information of the emulation container. Thus, the flexible configuration of network measurement on demand is realized.

4.1.2. Node Parameters

Each emulation node has corresponding physical parameters which are used to describe real network nodes in simulation scenarios. Physical parameters contain communication settings, location parameters, and service configurations. The web front-end in the control plane provides interactive interfaces for researchers to set these parameters. Corresponding settings are stored in a database.

The communication settings reflect the communication characteristics of the network node, e.g., effective isotropic radiated power (EIRP), G/T, modulation, communication frequency, and etc. According to the different placements of the network node in SN, the location parameters should be discussed separately. For space-based nodes, the location parameters contain eccentricity, period, inclination, right ascension of the ascending node, argument of perigee, and true anomaly. For terrestrial-based nodes, the location parameters refer to longitude and latitude. Through communication settings and location parameters, the calculation of connection relationships and link characteristics between nodes could be gained. The details of calculation principles would be demonstrated in Section 4.2. Service configurations are applied to initialize the function of the emulation node, involving protocol selection, data transmission models, node type selection, etc.

4.1.3. Multiple Network Protocols

An emulation container is created based on container images. The network protocol implementation software and other applications would be deployed among the container image in advance. According to different types of network protocol architecture, the emulation container can be divided into three types, namely the DTN node, TCP/IP node and custom node, as shown in Figure 4. The DTN node and TCP/IP node correspond to DTN and the TCP/IP network protocol architecture, respectively. Furthermore, custom node provides an extension method for new or modified protocol architectures in the proposed platform.

• DTN node. The DTN node is built by the ION-DTN container image. ION-DTN is a software which includes the implementations of LTP, BP, CGR routing protocol and some other DTN protocols.
• TCP/IP node. The TCP/IP node is generated by the Quagga container image. Quagga is a software which supports various routing protocols, such as BGP, OSPF, RIP and etc.
• Custom node. Various dependencies were installed in the custom container image previously to provide runtime environment for the software implementation of new or modified protocols and technologies. The virtual switch is also deployed in the custom container image. Based on virtual switch and flow tables, the custom node can support custom forwarding rules.

4.2. Link

The dynamic behaviors, especially the time-varying connection relationship and the dynamic link characteristic, are the main features of SN and also pose challenges to emulate the SN environment.

4.2.1. Time Slot

In order to analyze the dynamic behaviors, a specific SN scenario is divided into multiple time slots. The network status is regarded as static and represented by the initial state in each slot. The more time slots are divided, the more accurate an SN environment is emulated.

4.2.2. Implementation of a Time-Varying Connection Relationship

(1) Computation Principle

The link types in SN can be classified into three categories, namely the space-based link, ground-based link, and space–terrestrial link. Due to the mobility of space platforms, the time-varying connection relationship is mainly reflected in the space-based link and space–terrestrial link. The mutual visibility between two space platforms or between a space platform and a ground-based node determines whether there exists a corresponding link. Relying on the location parameters of emulation nodes, the main controller calculates the actual position of nodes, and then achieves the mutual visibility between nodes at each time slot. The calculation principle is described as follows.

a. Space-based Link

In a space-based link, the mutual visibility is defined as the direct line of sight between two space platforms at a certain time. Considering the geometry defined in Figure 5a, in which Sat. 1 and Sat. 2 are visible to each other.

$\overrightarrow{r_1}$ and $\overrightarrow{r_2}$ are the position vectors of Sat. 1 and Sat. 2, respectively. $\overrightarrow{S}$ emanates from the Earth’s dynamical center perpendicular to $\overrightarrow{C}=\left(\overrightarrow{x_1}+\overrightarrow{x_2}\right)$ at h and intersect the Earth’s surface at q, where $\overrightarrow{x_1}$ and $\overrightarrow{x_2}$ are unknown vectors, $\overrightarrow{x_1}$ is the distance vector from Sat. 1 to h to Sat. 2. The magnitude of $\overrightarrow{S}$ is divided into $\left|\overrightarrow{oq}\right|=R_E$ which is the Earth’s radius and $\left|\overrightarrow{qh}\right|=R_V$ which is the thickness of the atmosphere from the Earth’s surface to the vector $\overrightarrow{C}$. From Figure 5, two fundamental vector closure equations are:

$$\overrightarrow{r_1}=\overrightarrow{S}-\overrightarrow{x_1}$$

(1)

$$\overrightarrow{r_2}=\overrightarrow{S}+\overrightarrow{x_2}$$

(2)

According to variables, mentioned above, the magnitude of $\overrightarrow{C}$ can be described by the following equations:

$$C=\sqrt{{r_1}^2+{r_2}^2-2\left(\overrightarrow{r_1},\overrightarrow{r_2}\right)}$$

(3)

$$C=x_1+x_2=\sqrt{{r_1}^2-S^2}+\sqrt{{r_2}^2-S^2}$$

(4)

Equating Equations (3) and (4) and then squaring twice, we obtain an analytical expression for the visibility function as:

$$R_V=\left(\sqrt{\frac{{r_1}^2{r_2}^2-{\left(\overrightarrow{r_1},\overrightarrow{r_2}\right)}^2}{{r_1}^2+{r_2}^2-2\left(\overrightarrow{r_1},\overrightarrow{r_2}\right)}}\right)-R_E$$

(5)

The visibility function defined by Equation (5) can be used to predict explicitly whether satellites are visible to one another or not. The sign of $R_V$ associated with visibility can be obtained by constructing a case in which direct line-of-sight visibility is impossible, as shown in Figure 5b. For this case we have:

$$\left(\overrightarrow{r_1},\overrightarrow{r_2}\right)=r_1{r}_{2}cos\left(180\right)=-r_1{r}_2$$

(6)

Then Equation (3) can be written as:

$$R_V=-R_E$$

(7)

Hence, we can put this rule:

$$R_V=\left\{\begin{array}{cc}\mathrm{Positive}\mathrm{value},\hfill & \mathrm{Derect}\mathrm{line}-\mathrm{of}-\mathrm{sight}\hfill \\ \mathrm{Zero}\mathrm{or}\mathrm{negative}\mathrm{value},\hfill & \mathrm{Nonvisibility}\mathrm{case}\hfill \end{array}\right.$$

(8)

b. Space–terrestrial Link

In the space–terrestrial link, the mutual visibility is defined as the direct line of sight between a space platform and a ground-based node at a certain time. Considering the geometry defined in Figure 6, in which a satellite and ground station are visible to each other. The two points represent the satellite (Sat) and ground station (GS), and then the third is the Earth’s center. The subsatellite point is indicated by T, which is the point where the joining line of the satellite and Earth’s center intersect the Earth’s surface. Distance d represents slant range between a satellite and ground station. This range changes over time since the satellite flies too fast above the ground station. In Figure 6a, the radius r is:

$$r=R_E+H$$

(9)

$R_E$ is Earth’s radius and H is satellite’s altitude. The line crossing point GS means the tangent plane to Earth’s surface at point GS, which by definition is in fact the ideal horizon plane. The angle formed between the ideal horizon plane and the slant range is elevation angle ${\epsilon }_0$. Figure 6b is the plane form of the triangle from Figure 6a.

Two sides of this triangle are usually known as the distance from the ground station to the Earth’s center $R_E$, and the distance from the satellite to the Earth’s center-orbital radius. The angle under which the satellite sees the ground station is called the nadir angle. There are four variables in this triangle: ${\epsilon }_0$ is the elevation angle, ${\alpha }_0$ is the nadir angle, ${\beta }_0$ is the central angle and d is the slant range. As soon as two quantities are known, the others can be found with the following equations:

$${\epsilon }_0+{\alpha }_0+{\beta }_0=90$$

(10)

$$dcos\left({\epsilon }_0\right)=rsin\left({\beta }_0\right)$$

(11)

$$dsin\left({\alpha }_0\right)=R_{E}sin\left({\beta }_0\right)$$

(12)

The most important parameter is the slant range d which represents the distance from the ground station to the satellite. It is expressed through the elevation angle ${\epsilon }_0$. Applying the cosines law for the triangle at Figure 6 yields:

$$r^2=R_E^2+d^2-2R_{E}dcos(90+{\epsilon }_0)$$

(13)

Solving Equation (5) by d yields:

$$d=R_E\left[\sqrt{{\left(\frac{r}{R_E}\right)}^2-{cos}^2{\epsilon }_0}-sin{\epsilon }_0\right]$$

(14)

Substituting, $r=H+R_E$ at Equation (14), finally we will obtain the slant range as function of elevation angle ${\epsilon }_0$:

$$d=R_E\left[\sqrt{{\left(\frac{H+R_E}{R_E}\right)}^2-{cos}^2{\epsilon }_0}-sin{\epsilon }_0\right]$$

(15)

or elevation ${\epsilon }_0$ expressed for a known slant range d as:

$$sin{\epsilon }_0=\frac{H(H+2R_E)-d^2}{2d{R}_E}$$

(16)

When $sin{\epsilon }_0=0$⇒${\epsilon }_0=0$, the maximum slant range d is found:

$$d^2=H(H+2R_E)$$

(17)

If the distance between the Sat and the GS is outside of the maximum value of d, the two nodes are considered invisible.

Finally, on the basis of link establishment strategies set by researchers, these mutual visibilities are filtered to obtain connection relationships in a specific scenario.

(2) Implementation Method

Connection relationships are stored in databases, which are formulated as follows. Link_id is the link name. Srcnode_port and dstnode_port represent the connection port of

link_id

srcnode_port

dstnode_port

start_time

end_time

the source node and destination node on virtual switches separately. The srcnode field in srcnode_port means the host name of the emulation node. It is the same for dstnode_port. Start_time and end_time represent the beginning and ending times of a link connection, respectively.

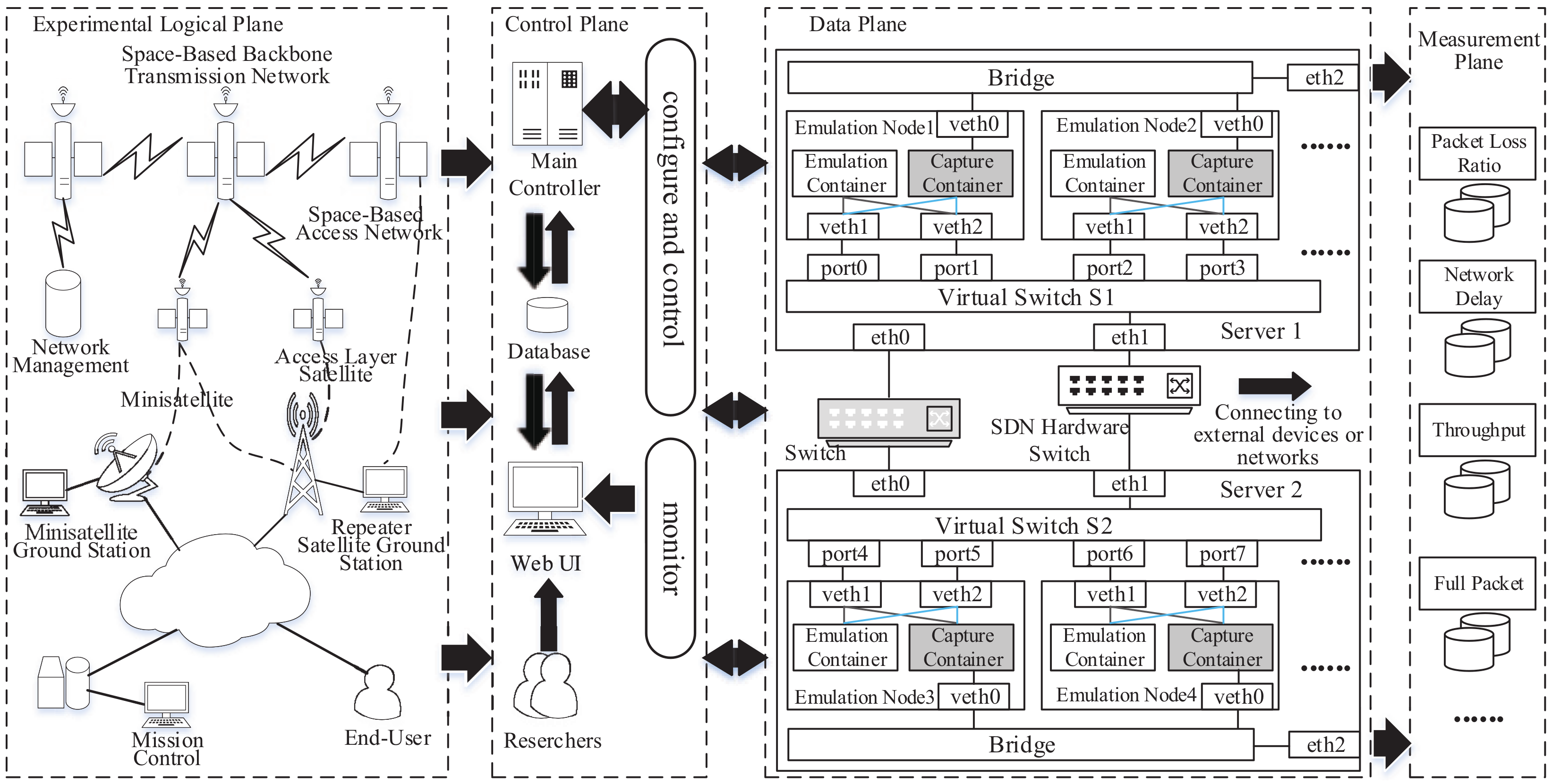
Emulation nodes use virtual ethernet (veth) devices [30] to access the virtual switch on the server where it is located. Each veth represents an antenna or a communication channel in the network scenario. Veth devices are created in pairs. One device in the pair is assigned to the emulation node as a network interface and the other is assigned to the virtual programmable switch as a port. When either device is down, the link state of the pair is down. So, the variation of connection relationships between pair-wise nodes equates to deleting/adding corresponding flow entries on virtual switches to control the port up and down. However, a port-based flow entry can only control the one-way link. Thus, two flow entries are needed to control a link connection, which is two-way, on or off.

The main controller later allocates corresponding network parameters for network interfaces at the emulation node, including IP addresses, MAC addresses, interface names, etc. The neighboring veths which are connected with each other in one hop have the same subnetwork segment. Whenever corresponding forwarding rules between these veths are deployed, the links between neighboring emulation nodes are working.

Upon the emulation starts, flow entities are issued by the main controller. As shown in Figure 7, each dynamic link corresponds to a timer and two flow entities. At the start time of emulation, several timers are activated and the on/off time points of each dynamic link are set within them. When the timers expire, the link connection or disconnection functions are executed to deploy corresponding connection or delete corresponding flow entities on virtual switches.

A problem which must be taken into consideration is to emulate the dynamic link connection at the distributed virtual server cluster. When deploying two emulation nodes in a connection link, there are two relative position situations: two nodes located at the same server, and two nodes located at different servers. For the former, the main controller can directly deploy two flow entries at the same virtual switches. Meanwhile, this deployment method is no longer applicable when two emulation nodes are linked to different virtual switches. To solve this issue, the placement of the emulation node in the server cluster and the corresponding host name is recorded when creating the emulation node. Integrated with the fields of srcnode_port and dstnode_port, the corresponding relationship between flow entries and virtual switches can be cleared.

Figure 8 and Figure 9 show the change of link connection in timeslots TS1 and TS2. When Node3 disconnects with Node2 and connects with Node1 directly, the main controller first deletes the bidirectional flow entries between S1-4 and S2-6 ports, and then adds the bidirectional forwarding rules between S1-2 and S2-5 ports in S1 and S2 separately. Because the forwarding rule is a map between two physical ports in the programmable switch, we can emulate the connectivity of link connections in the physical layer easily.

4.2.3. Implementation of Dynamic Link Characteristic

(1) Computation Principle

On the basis of the signal modulation method and $\frac{E_b}{N_0}$, the bit error rate (BER) can be gained. The modulation method is a parameter of the emulation node, including FSK, PSK, DPSK, and etc. For example, BER of 2PSK can be expressed by (18).

$$BER=\frac{1}{2}\times erfc\left(\sqrt{\frac{E_b}{N_0}}\right)$$

(18)

$\frac{E_b}{N_0}$ is described in Formula (19), representing the received energy per bit over noise power density.

$$\frac{E_b}{N_0}=EIRP-L_p+\frac{G}{T}-k-R$$

(19)

$$L_p=20lg\left(d\right)+20lg\left(f\right)+92.45$$

(20)

$$R=10lg\left(R_b\right)$$

(21)

In Formula (19), $EIRP$ is the transmitter effective isotropic radiated power, in dBW. $\frac{G}{T}$ is the receiver antenna gain divided by the receiver system noise temperature, in dB/K. $L_p$ is the sum of all path losses, described by Formula (20), in dB. k is a constant and equal to −228.6 dB. R is the transmission code rate loss which can be expressed by Formula (21), and $R_b$ is bandwidth, in bps. As parameters of the satellite node, $EIRP$, $\frac{G}{T}$, f, and $R_b$ are known values. When calculating the mutual visibility between nodes, mentioned in Section 4.2.2, d can also be obtained. Thus, $\frac{E_b}{N_0}$ is a computable value.

(2) Implementation Method

In our emulation architecture, the SDN switch only offers the topology management and do not support the simulation of link characteristics. So, another supplementary method is needed to fulfill this function.

All emulation nodes installed the Linux-based operation system in advance. The link characteristic configuration is performed via the Linux traffic control (TC) mechanism [31]. NetEm is part of TC and supports the emulation of network delay, packet loss ratio, etc. This mechanism also includes a Token Bucket Filter (TBF) for bandwidth limitation. TC has been evaluated in [32] and has been found to emulate most parameters accurately.

TC can classify different parts of the data packet according to its characteristics and provide different traffic control mechanisms for these packets. The queuing rule is one of the most important parts in TC which can be used to realize the classification function. Before packets are sent by network interfaces, they are added to different send queues according to the characteristics of packets. Then the kernel takes packets from these queues and delivers packets to network interfaces to complete the process of data transmission.

The FIFO algorithm forms the basis for the default queuing disciplines (qdisc) on all Linux network interfaces. It transmits packets as soon as it can receive and queue them, as shown in Figure 10. A real FIFO qdisc must have a size parameter to prevent it from overflowing in case it is unable to dequeue packets as quickly as it receives them, i.e., when we have a requirement to emulate a high bandwidth with a certain delay, we need to calculate the queue size to avoid discarding packets. The size of the queue is defined by the parameter $limit$, and the unit of $limit$ is the packet in TC. We consider the value of $limit$ in the worst case. The $limit$ would be greater than the average delay t multiplied by the maximum packet rate. The maximum packet rate equals to the maximum bandwidth B divided by the maximum transmission unit (MTU). MTU is the largest length of the frame. Its default value is 1500 bytes and this value can be changed according to the needs of experiments.

$$limit⩾\frac{B\times t}{8\times MTU}$$

(22)

Via the Formula (3), the setting value of $limit$ in a specific network scenario can be obtained.

4.3. Network Topology

The network topology of the proposed platform can be divided into the lower physical network topology and the upper logical network topology.

4.3.1. Lower Physical Network Topology

The lower physical network topology is the basis of the emulation system, which is constructed by the main controller, switches, and servers. For each server in the data plane, a virtual switch is implemented. Some network interfaces of the server are attached to the virtual switch. To communicate with other servers, other ends of attached network interfaces are connected to a high performance SDN hardware switch in the form of Virtual Extensible LAN. In this way, a distributed server cluster is constructed in a star structure. The main controller is linked to virtual switches and SDN hardware switches, and it controls them directly. When researchers create a specific network scenario in the logical plane, the main controller, integrated with container orchestration, allocates resources and places emulation nodes at the server cluster. Emulation nodes are linked to a virtual switch at each server in a star network topology. Physical nodes and external emulation devices can also be linked to the SDN hardware switch and managed by the main controller. From top to bottom, all the switches, servers, and emulation nodes are constructed in a hierarchical star network structure. This network topology makes the platform have high scalability. If computing resources need to be expanded, more virtual node servers can be simply accessed through the SDN hardware switch.

4.3.2. Upper Logical Network Topology

The upper logical network topology remains consistent with the SN emulation scenario. With the scene information, including time-varying connection relationships, dynamic link characteristics, emulation node parameters, etc., the main controller generates corresponding commands, such as flow entities. Then the data plane is driven by these commands. In this way, the proposed platform emulates a network scenario with the arbitrary logical topology described in logical plane.

5. Experiments and Discussion

In this section, we present the deployment manner of the emulation platform and conduct corresponding experiments.

5.1. Deployment

The workflow of the experiment approach is presented in Figure 11. When setting up an experiment, researchers could follow the steps outlined below.

5.1.1. Preparatory Phase

In the preparatory phase, a particular network scenario is created and corresponding configurations are inputted through Web UI. Researchers need to decide the network architecture, the number and the type of nodes, node parameters, as well as link establishment strategies. According to user demands and settings, the main controller calculates connection relationships and link characteristics between nodes, as well as network parameters of emulation nodes. Calculations are stored in the database for subsequent use. In service modeling, a specific network service is determined. Researchers decide which network protocol to be used, thus defining the size of packets and the scheme of data communications. Data collection configurations should also be set at this phase, covering measurement modes and data capture modes.

5.1.2. Implementation Phase

After researchers click the Start Button at Web UI, the start signal is sent to the main controller. Based on connection relationships and assigned network parameters recorded in the database, the main controller creates emulation nodes, binds them to SDN switches, and informs the start time of emulation. Then an initialization daemon is activated in each emulation node and reads the database to fulfill automatic configurations, including the implementation of the dynamic link characteristic, routing setting, protocol stacks establishment, and etc. Subsequently, emulation nodes are suspended until the beginning of emulation.

During the process of emulation, the main controller issues flow entries to SDN switches to realize the dynamic network. Designated source nodes transfer data packets through the emulation network and finally arrive at the destination. If researchers want to change the network scenario, they can go back to the step of creating the network model. If they need to change protocols and services, they can go back to the service modeling step. It is flexible and easy to change the scenario by reconfiguring emulation parameters.

5.1.3. Data Collection Phase

In the experiment process, selected measurement nodes served for real time network monitoring and full packet capture, respectively. The metrics of network monitoring include throughput, end-to-end delay, and packet loss ratio. In the meantime, all the received and forwarded data packets are captured at the designated nodes. On the basis of these metrics and captured packets, researchers can evaluate network performances among different simulation scenarios.

5.2. Link Characteristics Validation

To check our experimental validity partly, the performance of one single link on the platform is tested. The required levels of the link characteristics are listed in the first columns of

Table 2. Results of measurement of delay.

Required Level (ms)	Measured Level (ms)	Absolute Deviation (ms)	Relative Deviation (%)
5.000	5.130	−0.130	2.600
50.000	50.135	−0.135	0.270
100.000	100.136	−0.136	0.136
500.000	500.150	−0.150	0.030
1000.000	1000.147	−0.147	0.015

,

Table 3. Results of measurement of packet loss.

Required Level (%)	Measured Level (%)	Absolute Deviation (%)	Relative Deviation (%)
1.00	0.93	−0.07	7.00
5.00	5.17	−0.17	3.40
10.00	9.80	0.20	2.00

and

Table 4. Results of measurement of bandwidth.

Required Level (Mbps)	Measured Level (Mbps)	Absolute Deviation (Mbps)	Relative Deviation (%)
50.00	55.28	−5.28	10.56
100	108.20	−8.20	8.20
500	530.00	−30.00	6.00
1000	1085.44	−85.44	8.54
1200	1300.48	−100.48	8.37

. In each measurements, we repeated data transmission ten times and averaged the results. As can be seen in the tables, no matter which required level we adopted, it achieved approximate performance.

5.3. Moon to Earth Communication Scenario

5.3.1. Experimental Scenario

In order to evaluate the reliability of the proposed platform, a DTN experiment, described in [33], was reproduced. The aim of this experiment is to assess the ability of BP, and test the joint use of many advanced features in ION, e.g., Contact Graph Routing (CGR), scheduled links, etc., in a case of real practical interest.

The topology of the experimental scenario is summarized in Figure 12. It consists of four DTN nodes: a Moon lander (Lander), a satellite orbiting the Moon (Sat), a Mission Control Center (MCC), and an auxiliary terrestrial Gateway Station (GW). Scheduled space links between nodes are represented by dotted lines, while continuous lines denote continuous wired links. The contact plan excerpt is shown in

Table 5. Contact plan excerpt.

Link	Contact	Start-Stop Time (s)	Speed (Downlink)	Latency (s)
Lander-Sat	1	20–40	128 kbit/s	0
	2	100–120	128 kbit/s	0
Sat-GW	1	70–80	1 Mbit/s	1.3
	2	160–170	1 Mbit/s	1.3
Sat-MCC		150–180	1 Mbit/s	1.3
GW-MCC		0–180	10 Mbit/s	0

. It should be noted that the links from the satellite to Earth have a propagation delay of 1.3 s, while other links are negligible. Moreover, losses were assumed to be negligible in all links.

5.3.2. Experimental Results

In the above scenario, ten bundles of 50 kB were transferred from the Moon Lander to the MCC. As illustrated in Figure 13, ten bundles were first generated and taken into custody on the Lander. Upon the first Lander-Sat contact started at 20 s, therefore six bundles were transferred and taken into custody at the Moon Sat. Then these six bundles were delivered to GW when the Sat-GW contact was on at 70 s. As the GW-MCC link was continuous, these data were immediately transferred to the MCC. The remaining four bundles were transferred to Sat during the second Lander-Sat contact, working at 100 s, and taken into custody as before.Finally, when the Sat-MCC contact first opened at 150 s, they were directly delivered to MCC according to CGR. The comparison of obtained experimental results between [33] and our study indicates the reliability of the proposed platform.

5.4. Ip Satellite Network Scenario

5.4.1. Experimental Scenario

An IP satellite network scenario was designed and experiments were conducted to evaluate the performance of different network protocols. The experimental scenario, described in Figure 14, included a Ground Station (GS), 12 LEOs, and 6 GEOs. Satellite orbit parameters are listed in

Table 6. LEO satellite orbit parameters and corresponding values.

Orbit Parameter	Value
Period (s)	5400
Eccentricity	0.0
Orbital Inclination (deg)	28.5
Argument of Perigee (deg)	0.0
Right Ascension of the Ascending Node	107.419/137.419/167.419/192.419/287.419/17.419
True Anomaly (deg)	0/60

and

Table 7. GEO satellite orbit parameters and corresponding values.

Orbit Parameter	Value
Period (s)	86,400
Eccentricity	0.0
Orbital Inclination (deg)	0.113287
Argument of Perigee (deg)	0.0
Right Ascension of the Ascending Node (deg)	90
True Anomaly (deg)	0/60/120/180/240/300

separately. Different right ascension of ascending nodes represented different satellite orbits, while distinct true anomalies refer to different initial positions of satellites in the same orbit. GEOs were evenly distributed in the geosynchronous orbit above the equator which constructed a backbone link for data transmission. LEOs served as remote sensing satellites [34] and were directly linked to GEOs. The GS located at 116.40 deg longitude and 39.90 deg latitude only communicated with GEO3.

Link parameters and corresponding values between nodes are presented in

Table 8. Link parameters and corresponding values.

Link Parameter	Value
Frame Length (byte)	1500
$G/T$ (db/k)	23
$R_b$ (Mbps)	1000
$EIRP$ (dbm)	70
f (Ghz)	30
Modulation Type	BPSK

.

5.4.2. Experimental Results

(1) Mobile IP

Considering the location-independent routing of IP datagrams in SN, Mobile IP (MIP) is deployed and compared with the performance of pure IP in this scenario. Each GEO serves as the home agent for LEOs linked directly at the beginning time. The IP address of LEO which is assigned by the home agent is a permanent IP address. Regardless of the change of connection relationships, LEOs could communicate with other nodes via respective permanent IP addresses [35]. We focus on the end-to-end delay between LEO1 and LEO2 or GS, the concrete topology is shown in Figure 15. LEO1 and LEO2 are initially connected to GEO1 and GEO2 separately, and access to each GEO is in a clockwise direction. Corresponding measurement results from 0 to 30 min are show in Figure 16.

Figure 16a presents the bidirectional end-to-end delay between LEO1 and GS with or without deploying MIP. Because LEO1 moves from GEO1 to GEO3 during this period, the routing hops between LEO1 and GS are reduced. So the delay from LEO1 to GS is also reduced. However, owing to the home agent mechanism in MIP where all packets sent to LEO1 need to be forwarded by GEO1, the delay from GS to LEO1 is not changed. Referring to the scheme without deploying MIP, the communication between nodes is interrupted immediately when the access point is changed. Figure 16b describes the bidirectional end-to-end delay between LEO1 and LEO2 with or without deploying MIP. Even though LEO1 and LEO2 move in the same direction simultaneously, the delay between them is increased for the home agent mechanism.

(2) Backup Routing and OSPF

The routing convergence process, caused by links variation, makes OSPF routing unstable. In SN, the node mobility and the instability of channel quality cause the uncertain communication connections between nodes which further aggravate OSPF’s shortcoming. Our lab proposes a OSPF-based backup routing. Compared with OSPF, except for the optimal path, backup routing saves a sub-optimal path. When links change and the optimal path cannot work, the sub-optimal path takes effect immediately. After the links are restored, backup routing switches to the optimal path again. This process omits the convergence process in OSPF and improves the stability of routing. To verify the performance of this routing strategy, OSPF and backup routing are deployed on GEOs respectively. The experimental scenario is presented in Figure 17. We choose the time period from 0 to 500 s. LEO1 is connected to GEO1, and GS is connected to GEO3 at the start. A 60 s interrupt is inserted between GEO2 and GEO3 every 60s, and repeats four times.

First, LEO1 continuously sends UDP packets to GS at a rate of 100 Mbps during this period. Figure 17, Figure 18a and Figure 19, respectively, give the receive throughput at GS, end-to-end link delay, and connection variation between LEO1 and GS in different routing strategies which show backup routing has a better link connectivity. When the transmission path has no burst interruption, the performance of OSPF and backup routing has no significant difference. When the link is interrupted, OSPF triggers the process of discovering the interruption and routing reconvergence as presented in Figure 18a. While the backup routing directly switches to the sub-optimal path, it switches back to the original optimal path when the interrupted link is restored.

Then, the effect of bandwidth on the routing convergence time, which could be reflected by packet loss ratio, is taken into consideration. We configure the maximum bandwidth to 10 Mbps, 100 Mbps, and 1000 Mbps, respectively, while other link relationships and parameters remain unchanged. The end-to-end packet loss ratio in different maximum bandwidth is shown in Figure 20. The bandwidth variation has little effect on backup routing. However, it has a great impact on OSPF, and the impact increases with the decrease in bandwidth. Because OSPF monitors the link status through the Hello packet, less bandwidth increases the transmission time of the Hello packet. Backup routing selects the sub-optimal path directly, thus avoiding this problem.

6. Conclusions

In this study, we propose a laboratory testing platform, which consists of logical plane, control plane, data plane, and measurement plane, for the fundamental problems with SN and its applications. Based on the SDN and traffic control mechanism, the networking of the platform can change automatically like that of a real space communication environment. In addition, integrating with container technology, various emulation scenarios are reconstructed flexibly with the same deployment as real target networks. Furthermore, the platform has an extensible structure which supports the horizontal extension of hardware resources and the access of external physical emulation devices. Lastly, we reproduce the Earth–Mars communication scene. The experimental results and the comparison results are nearly the same, which verifies the reliability of the proposed platform. Furthermore, more emulation experiments are carried out for different network protocol architectures, network scenarios, and improved protocol technologies to prove the flexible emulation ability of the platform. Compared with existing SN emulation methods, the proposed platform effectively balances the authenticity, flexibility and extendibility of the emulation. Hopefully, the proposed platform can provide a reliable basis for accurately grasping the future development direction of the key technologies in SN.