Global Formulation of the Synthetic Storm Technique Oriented to Satellite Link–Budget Design
Abstract
:1. Introduction
2. The Full SST and the Global SST
2.1. The Full SST
2.2. The Global SST
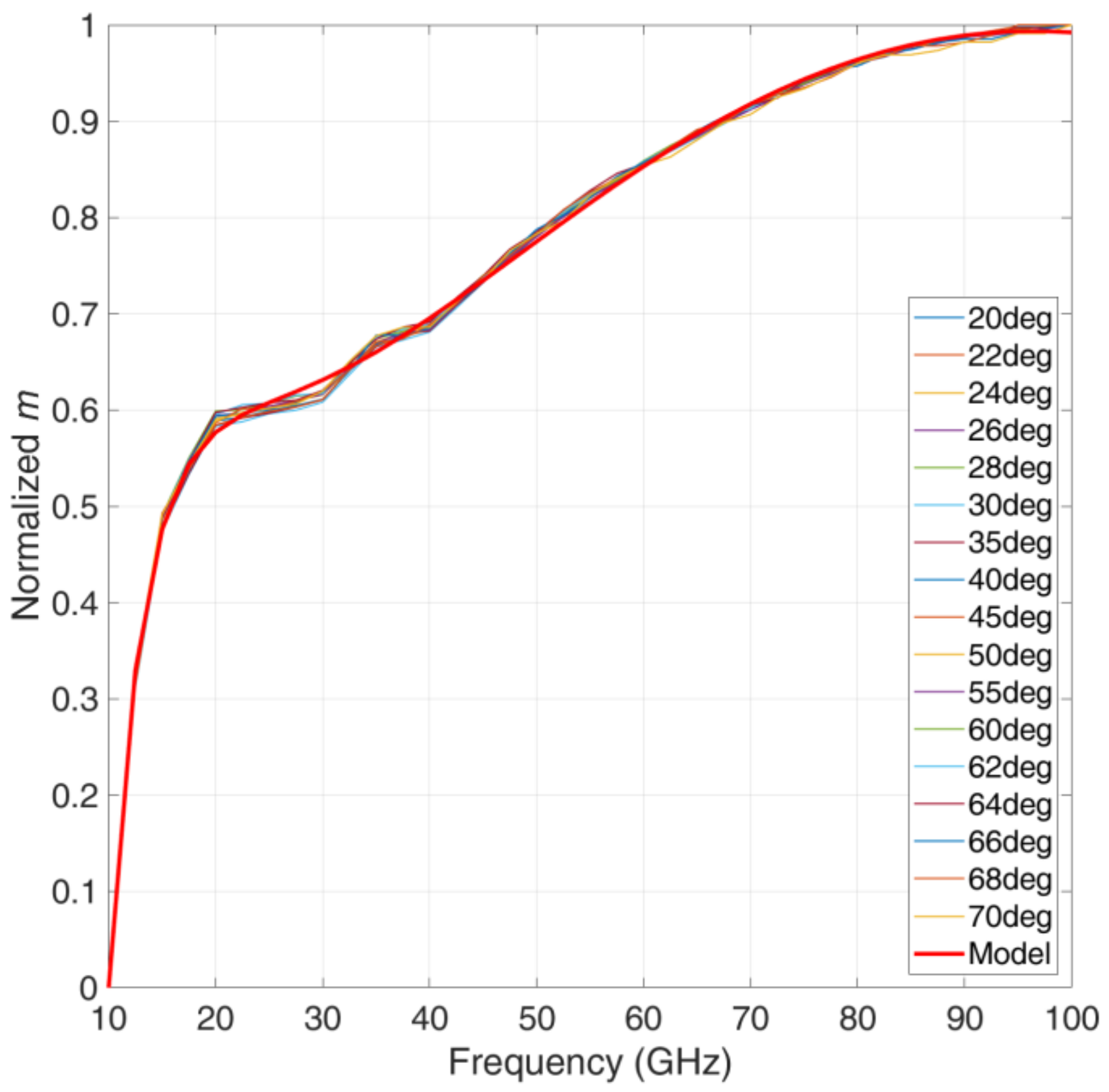
3. Model of the Average Exponent of the Global SST
- Calculate the value at 10 GHz,
- Calculate the value at 100 GHz
- Calculate the normalized average value see Figure 1
- Calculate, finally, the denormalized value to use in Equation (2)
- Calculate the probability (%)This probability ranges between at GHz, and at GHz.
- For , calculatewith
- For , no correction is required.
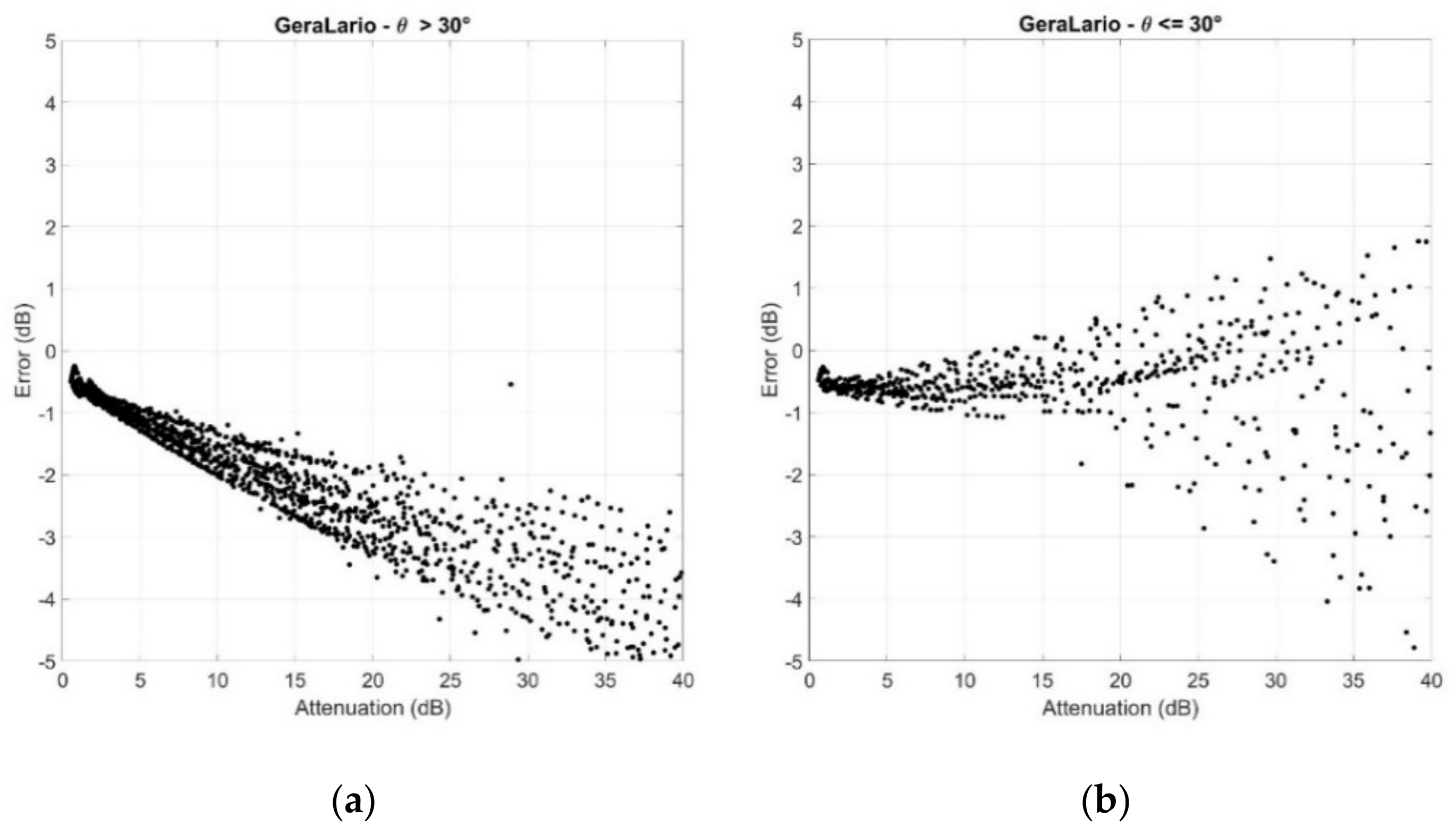
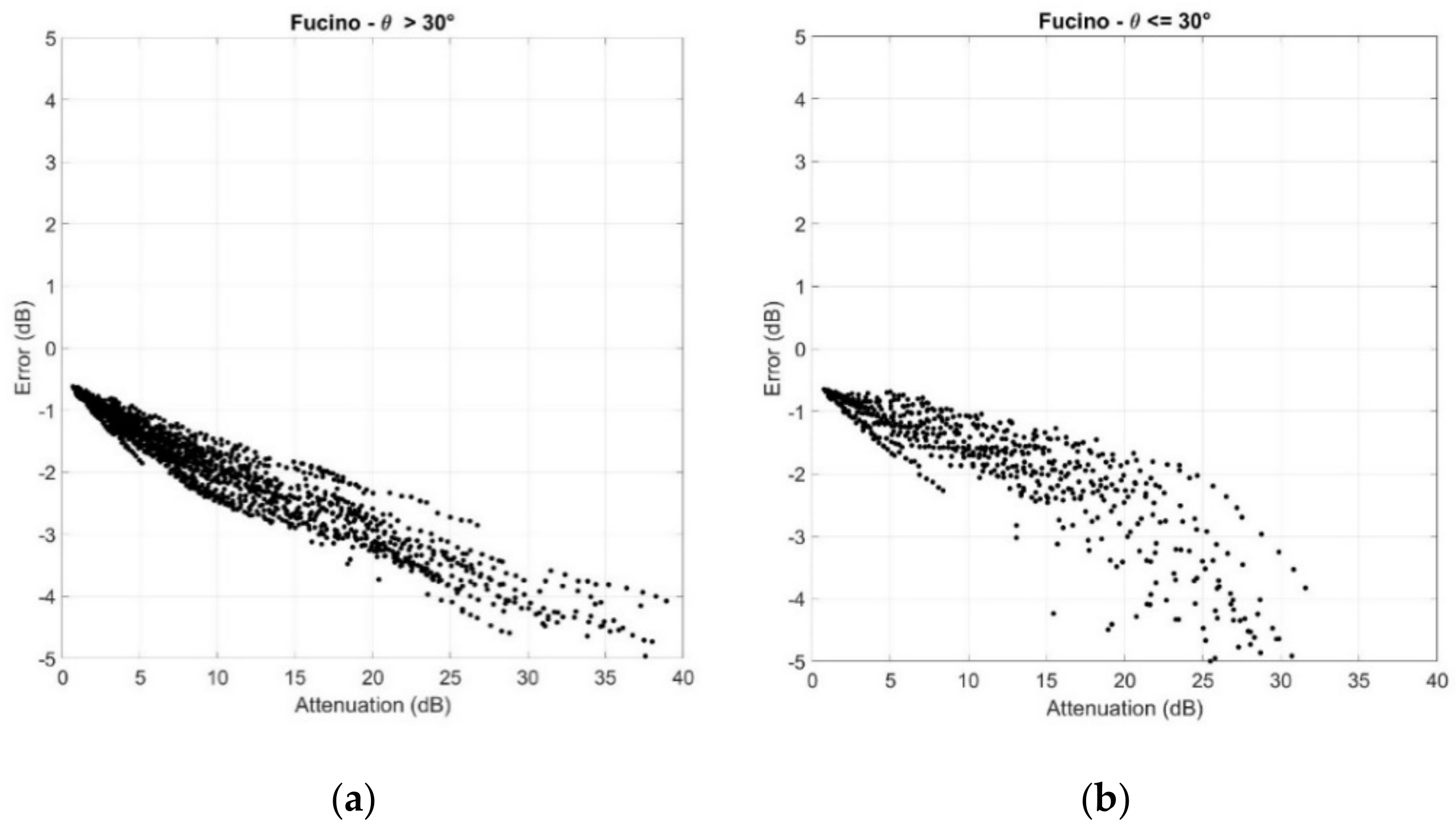
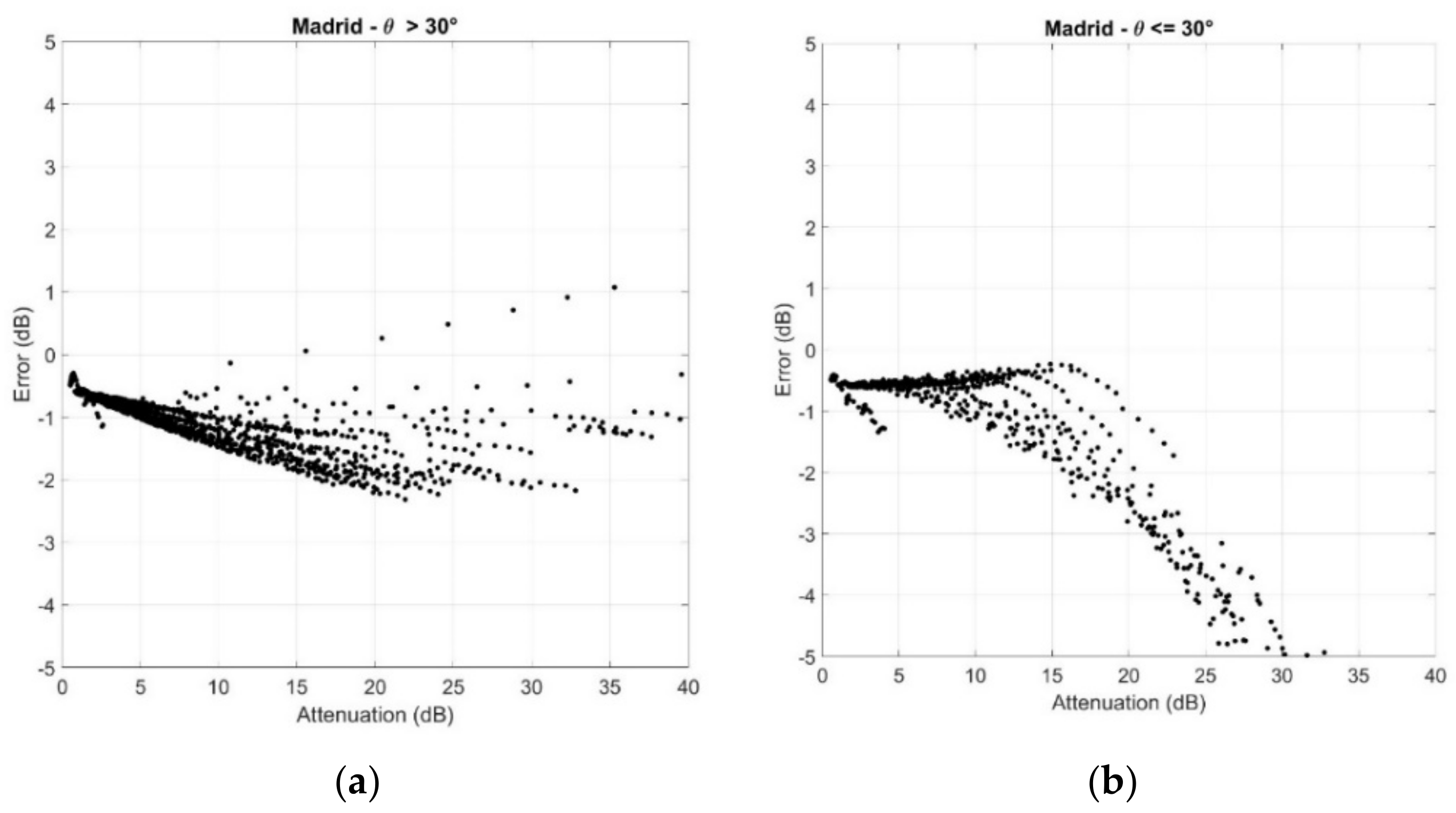
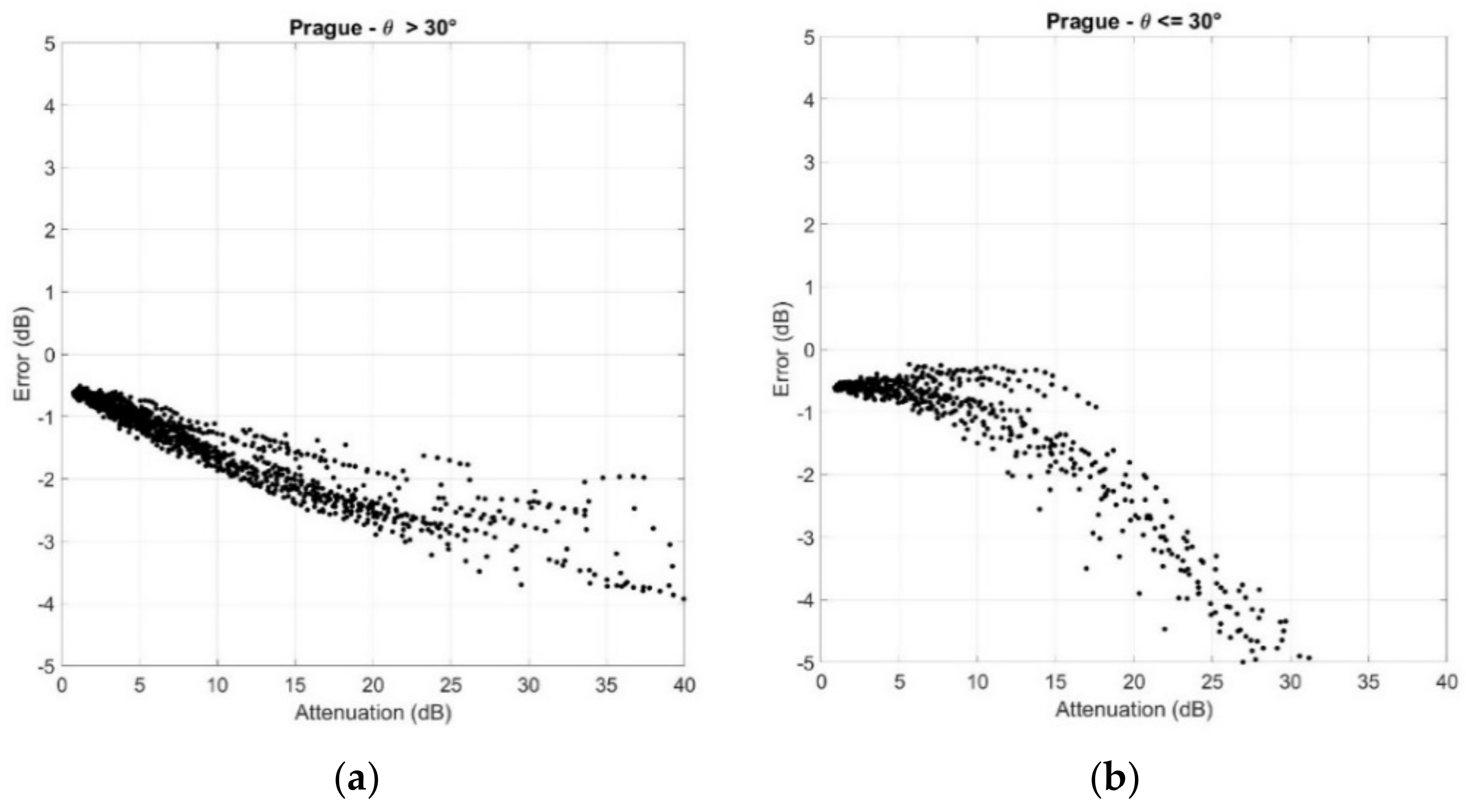
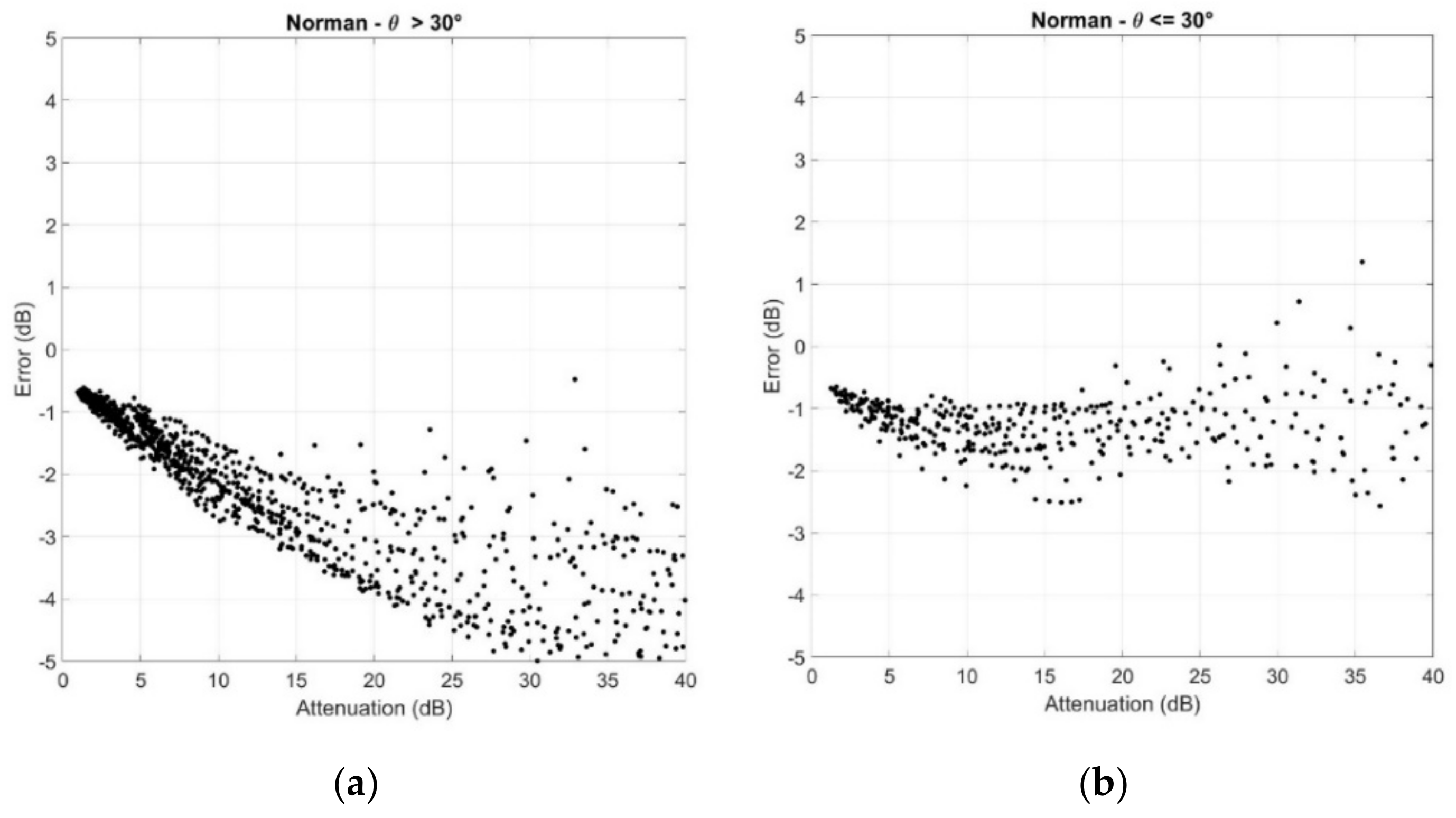
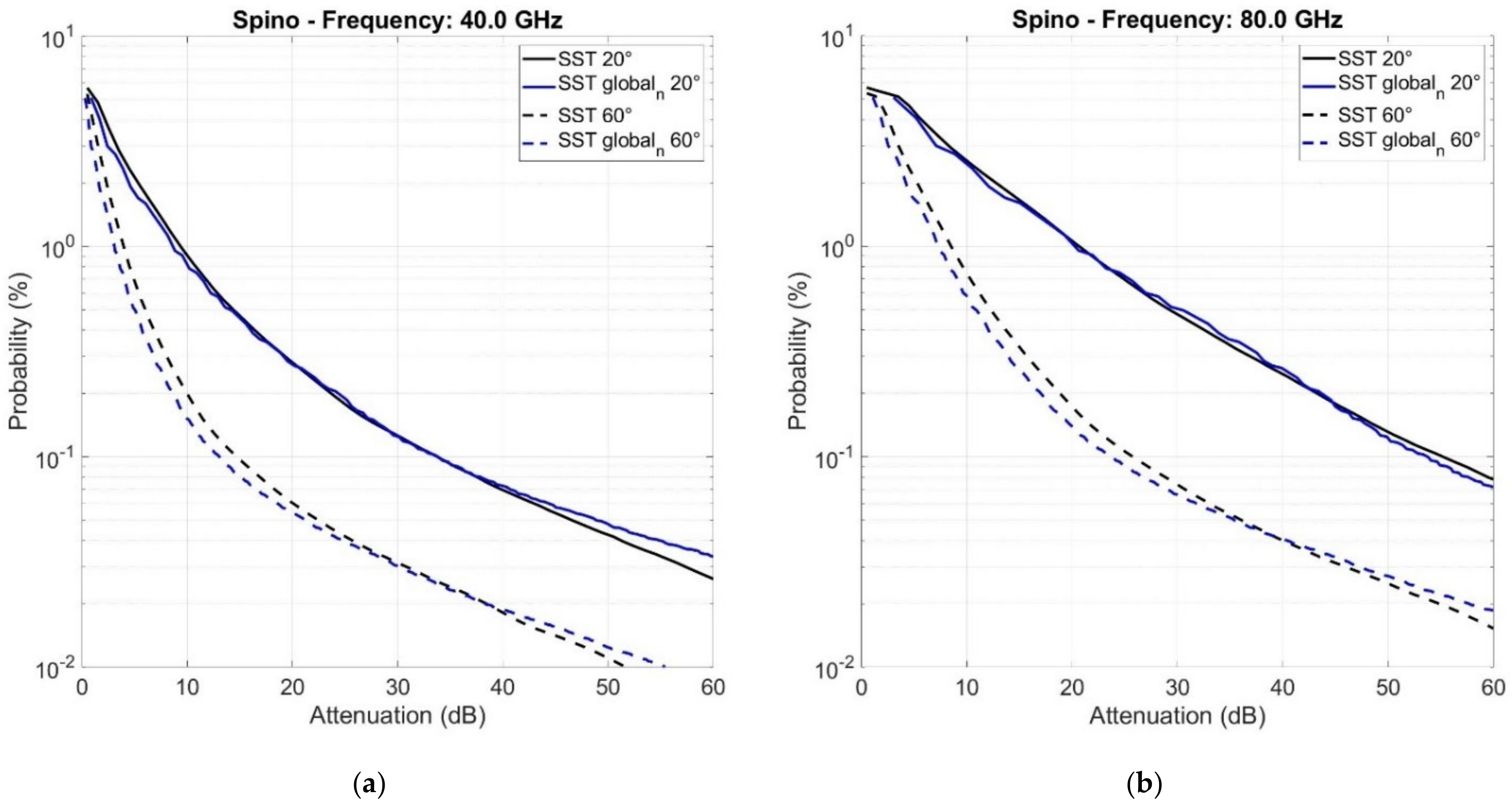
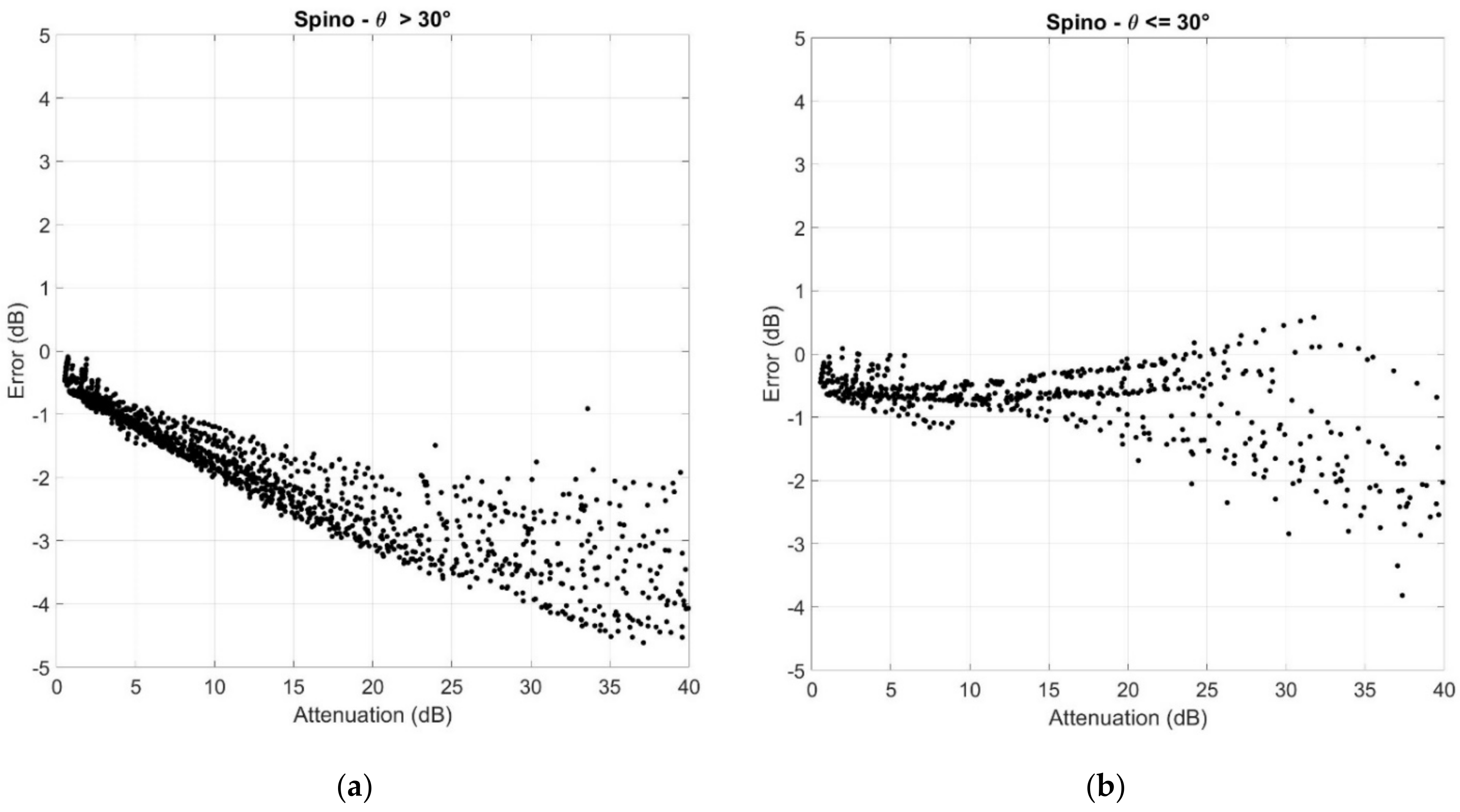
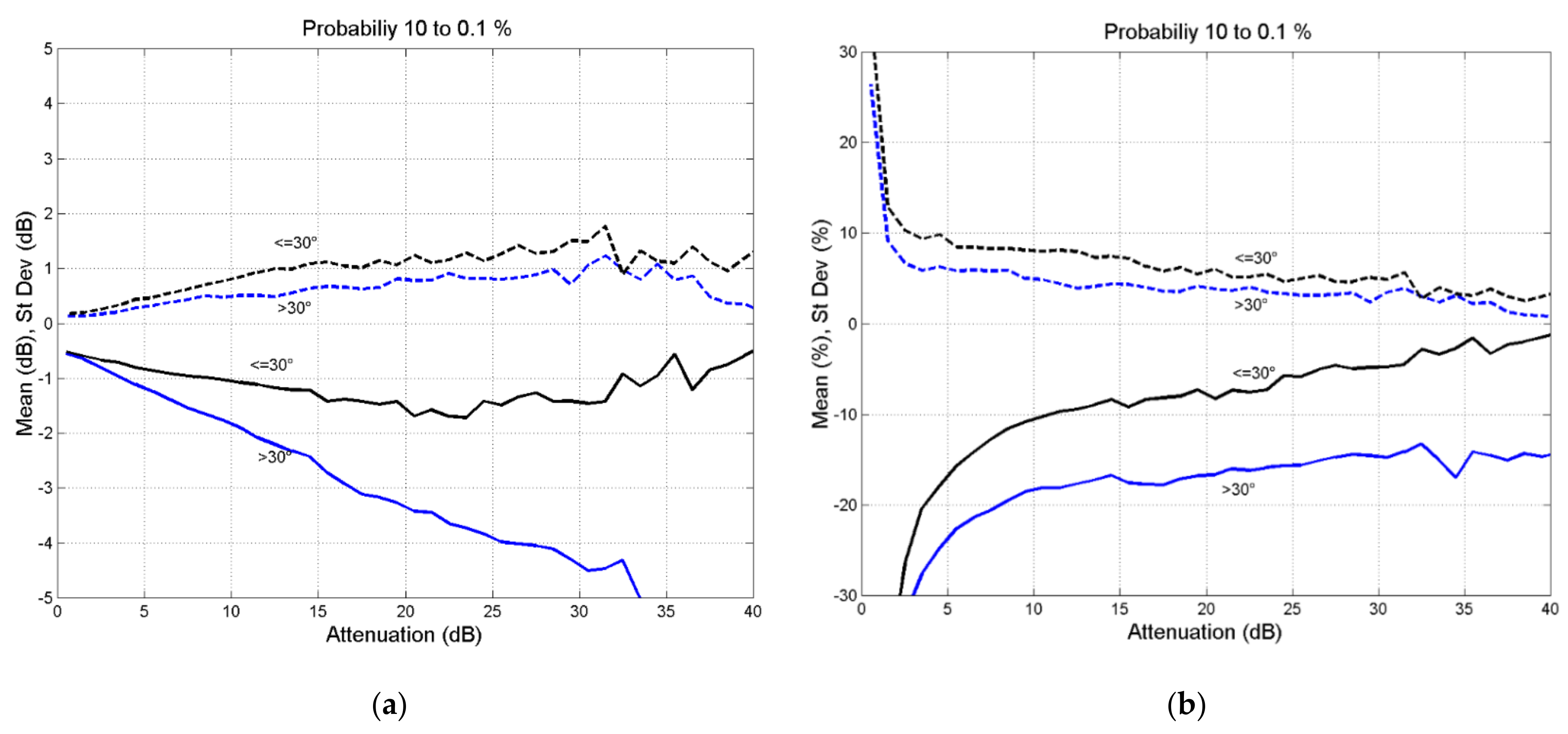
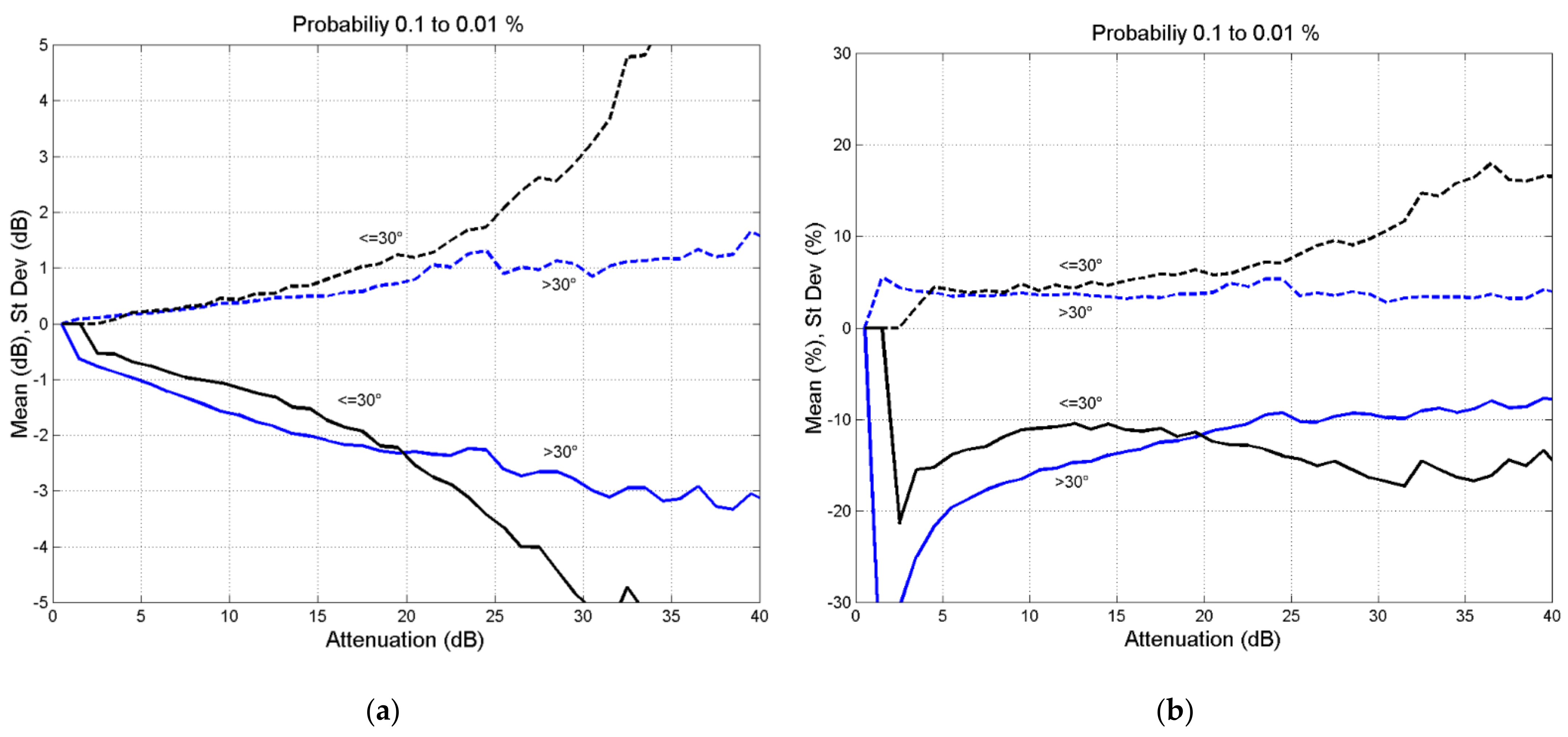
4. Results
5. Overall Error and Discussion
- The error is always negative; in other words, the global SST tends to underestimate the attenuation.
- There is a significant difference between the elevation angle ranges, with the lower elevation angle range more accurate.
- The relative error is approximately for and about for .
- The standard deviation is about 5% for both elevation angle ranges.
- The error is always negative; the global SST tends to underestimate the attenuation.
- There is not a significant difference between the two elevation angle ranges.
- The relative error is approximately .
- The standard deviation is about 5% for and reaches 15% for .
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A




References
- Matricciani, E. Physical–mathematical model of the dynamics of rain attenuation based on rain rate time series and a two–layer vertical structure of precipitation. Radio Sci. 1996, 31, 281–295. [Google Scholar] [CrossRef]
- Matricciani, E.; Riva, C. The search for the most reliable long–term rain attenuation cdf of a slant path and the impact on pre-diction models. IEEE Trans. Antennas Propag. 2005, 53, 3075–3079. [Google Scholar] [CrossRef]
- Matricciani, E. Physical–mathematical model of dynamics of rain attenuation with application to power spectrum. Electron. Lett. 1994, 30, 522–524. [Google Scholar] [CrossRef]
- Matricciani, E. Prediction of fade durations due to rain in satellite communication systems. Radio Sci. 1997, 32, 935–941. [Google Scholar] [CrossRef]
- Matricciani, E.; Moretti, S. Rain attenuation statistics useful for the design of mobile satellite communication systems. IEEE Trans. Veh. Technol. 1998, 47, 637–648. [Google Scholar] [CrossRef]
- Matricciani, E. Diurnal distribution of rain attenuation in communication and broadcasting satellite systems at 11.6 GHz in Italy. IEEE Trans. Broadcast. 1998, 44, 250–258. [Google Scholar] [CrossRef]
- Matricciani, E. Wide area joint probability of rain attenuation useful to design satellite systems with a common onboard resource: Experimental results obtained with the synthetic storm technique in Italy. In Proceedings of the Fourth Ka Band Utilization Conference, Venice, Italy, 2–4 November 1998; pp. 271–277. [Google Scholar]
- Matricciani, E. Worst–month statistics of rain attenuation in a satellite link at 19.77 GHz: Experimental results derived with the synthetic storm technique for the station of Gera Lario. In Proceedings of the Fourth Ka Band Utilization Conference, Venice, Italy, 2–4 November 1998; pp. 287–292. [Google Scholar]
- Matricciani, E.; Ordano, L.; Iorio, L. Large Distance Site Diversity in Satellite Communication Systems: Long Term Experimental Results obtained in Italy with the Synthetic Storm Technique. In Proceedings of the Fifth International Mobile Satellite Conference, Ottawa, ON, Canada, 16–18 June 1999; pp. 150–156. [Google Scholar]
- Matricciani, E. An assessment of rain attenuation impact on satellite communication: Matching service quality and system design to the time of the day. Space Commun. 2000, 16, 195–205. [Google Scholar]
- Matricciani, E. Micro Scale Site Diversity In satellite and Troposphere Communication Systems Affected By Rain Attenuation. Space Commun. 2003, 19, 83–90. [Google Scholar]
- Matricciani, E.; Riva, C. Statistics of Interruption Time Due to Rainfall in Satellite Communication Systems. In Proceedings of the 9th Ka Band Communications Conference, Ischia, Italy, 5–7 November 2003; pp. 207–214. [Google Scholar]
- Matricciani, E. Service Oriented Statistics of Interruption Time Due to Rainfall in Earth–Space Communication Systems. IEEE Trans. Antennas Propag. 2004, 52, 2083–2090. [Google Scholar] [CrossRef]
- Kanellopoulos, S.; Panagopoulos, A.; Matricciani, E.; Kanellopoulos, J. Annual and Diurnal Slant Path Rain Attenuation Statistics in Athens Obtained With the Synthetic Storm Technique. IEEE Trans. Antennas Propag. 2006, 54, 2357–2364. [Google Scholar] [CrossRef]
- Matricciani, E.; Riva, C.; Castanet, L. Performance of the Synthetic Storm Technique in a Low Elevation 5° Slant Path at 44.5 GHz in the French Pyrénées. In Proceedings of the EuCAP 2006, Nice, France, 6–10 November 2006. [Google Scholar]
- Matricciani, E. Time diversity as a rain attenuation countermeasure in satellite links in the 10–100 GHz frequency bands. In Proceedings of the EuCAP 2006, Nice, France, 6–10 November 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Matricciani, E. Correlation between speed of rain storms and temporal properties of precipitation: Applications to the synthetic storm technique. In Proceedings of the EuCAP 2007, Edinburgh, UK, 11–16 November 2007. [Google Scholar] [CrossRef]
- Matricciani, E. Time diversity in satellite links affected by rain: Prediction of the gain at different localities. In Proceedings of the EuCAP 2007, Edinburgh, UK, 11–16 November 2007. [Google Scholar] [CrossRef]
- Sánchez-Lago, I.; Fontán, F.P.; Mariño, P.; Fiebig, U.C. Validation of the Synthetic Storm Technique as Part of a Time–Series Generator for Satellite Links. IEEE Antennas Wirel. Propag. Lett. 2007, 6, 372–375. [Google Scholar] [CrossRef]
- Mahmudah, H.; Wijayanti, A.; Mauludiyanto, A.; Hendrantoro, G.; Matsushima, A. Analysis of Tropical Attenuation Statistics using Synthetic Storm for Millimeter–Wave Wireless Network Design. In Proceedings of the 5th IFIP International Conference on Wireless and Optical Communications Networks (WOCN ’08), Surabaya, East Java, Indonesia, 5–7 May 2008. [Google Scholar]
- Matricciani, E. A Relationship between Phase Delay and Attenuation Due to Rain and Its Applications to Satellite and Deep-Space Tracking. IEEE Trans. Antennas Propag. 2009, 57, 3602–3611. [Google Scholar] [CrossRef]
- Matricciani, E. Phase delay and differential attenuation due to rain in large phased array antennas for deep-space communications at 32 GHz. In Proceedings of the EuCAP 2011, Rome, Italy, 11–15 April 2011; pp. 1–4. [Google Scholar]
- Acosta, R.; Matricciani, E.; Riva, C. Slant Path Attenuation and Microscale Site Diversity Gain Measured and Predicted in Guam with the Synthetic Storm Technique at 20.7 GHz. In Proceedings of the EuCAP 2013, Gothenburg, Sweden, 8–12 April 2013; pp. 1–4. [Google Scholar]
- Matricciani, E. Efficiency of Satellite Channels affected by Rain attenuation and Ideal Fade-Countermeasure Method. In Proceedings of the 20th Ka and Broadband Communications, Navigation and Earth Observation Conference, Florence, Italy, 14–17 October 2013. [Google Scholar]
- Matricciani, E. Space communications with variable elevation angle faded by rain: Radio links to the Sun–Earth first Lagrangian point L1. Int. J. Satell. Commun. Netw. 2016, 34, 809–831. [Google Scholar] [CrossRef] [Green Version]
- Matricciani, E.; Riera, J.M. Variable elevation–angle radio links faded by rain at Ka Band from Madrid to the Sun–Earth La-grangian point L1. In Proceedings of the 22th Ka and Broadband Communications Conference, Cleveland, OH, USA, 17–20 October 2016. [Google Scholar]
- Matricciani, E. A method to achieve clear-sky data-volume download in satellite links affected by tropospheric attenuation. Int. J. Satell. Commun. Netw. 2016, 34, 713–723. [Google Scholar] [CrossRef] [Green Version]
- Lyras, N.K.; Kourogiorgas, C.I.; Panagopoulos, A.D.; Ventouras, S. Rain Attenuation Statistics at Ka and Q band in Athens using SST and Short Scale Dynamic Diversity Gain Evaluation. In Proceedings of the 2016 Loughborough Antennas & Propagation Conference (LAPC), Loughborough, UK, 14–15 November 2016. [Google Scholar]
- Matricciani, E. Probability distributions of rain attenuation obtainable with linear combining techniques in space-to-Earth links using time diversity. Int. J. Satell. Commun. Netw. 2017, 36, 220–237. [Google Scholar] [CrossRef]
- Nandi, A. Prediction of Rain Attenuation Statistics from Measured Rain Rate Statistics using Synthetic Storm Technique for Micro and Millimeter Wave Communication Systems. In Proceedings of the 2018 IEEE MTT–S International Microwave and RF Conference (IMaRC), Kolkata, India, 28–30 November 2018. [Google Scholar]
- Jong, S.L.; Riva, C.; D’Amico, M.; Lam, H.Y.; Yunus, M.M.; Din, J. Performance of synthetic storm technique in estimating fade dynamics in equatorial Malaysia. Int. J. Satell. Commun. Netw. 2018, 36, 416–426. [Google Scholar] [CrossRef]
- Papafragkakis, A.Z.; Kourogiorgas, C.I.; Panagopoulos, A.D. Performance Evaluation of Ka- and Q-band Earth–Space Diversity Systems in Attica, Greece using the Synthetic Storm Technique. In Proceedings of the 13th European Conference on Antennas and Propagation (EuCAP 2019), Krakow, Poland, 31 March–5 April 2019. [Google Scholar]
- Das, D.; Animesh Maitra, A. Application of Synthetic Storm Technique to Predict Time Series of Rain Attenuation from Rain Rate Measurement for a Tropical Location. In Proceedings of the 5th International Conference on Computers and Devices for Communication (CODEC), Kolkata, India, 17–19 December 2021. [Google Scholar]
- Recommendation ITU-R P.837-7. Characteristics of Precipitation for Propagation Modelling; ITU: Geneva, Switzerland, 2017. [Google Scholar]
- Matricciani, E. A mathematical theory of de-integrating long-time integrated rainfall and its application for predicting 1-min rain rate statistics. Int. J. Satell. Commun. Netw. 2011, 29, 501–530. [Google Scholar] [CrossRef]
- Matricciani, E. A mathematical theory of de–integrating long–time integrated rainfall statistics. Part II: From 1 day to 1 minute. Int. J. Satell. Commun. Netw. 2013, 31, 77–102. [Google Scholar] [CrossRef]
- Matricciani, E. Global formulation of the Synthetic Storm Technique to calculate rain attenuation only from rain rate probability distributions. In Proceedings of the 2008 IEEE International Symposium on Antennas and Propagation, San Diego, CA, USA, 5–11 July 2008. [Google Scholar] [CrossRef]
- Matricciani, E. A fundamental differential equation that links rain attenuation to the rain rate measured at one point, and its applications in slant paths. In Proceedings of the EuCAP 2006, Nice, France, 6–10 November 2006. [Google Scholar] [CrossRef]
- Matricciani, E.; Mauri, M.; Riva, C. A Rain Rate Data Base Useful to Simulate Reliable Rain Attenuation Time Series for Ap-plications to Satellite and Tropospheric Communication Systems. In Proceedings of the 2002 European Conference on Wireless Technology (ECWT 2002), Milan, Italy, 26–27 September 2002; pp. 265–268. [Google Scholar]
- ECMWF. Available online: https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5 (accessed on 28 March 2022).
- Matricciani, E. Rain attenuation predicted with a two-layer rain model. Eur. Trans. Telecommun. 1991, 2, 715–727. [Google Scholar] [CrossRef]
- Recommendation ITU-R P.839-4. Rain Height Model for Prediction Methods; ITU: Geneva, Switzerland, 2013. [Google Scholar]
- Maggiori, D. Computed transmission through rain in the 1–400 GHz frequency range for spherical and elliptical drops and any polarization. Alta Freq. 1981, 50, 262–273. [Google Scholar]

| Reference, Year | SST Application |
|---|---|
| 1996 [1] | Mathematical theory of the Synthetic Storm Technique (SST), with two vertical layers of precipitation: 0 °C (melting layer), 20 °C (rainfall) |
| 2005 [2] | SST-derived can substitute missing experimental data (Italsat). |
| 1994 [3] | The power spectrum of experimental falls off as (anticipation of the SST theory). |
| 1997 [4] | Fade durations. |
| 1998 [5] | Satellite communications with mobile transmitters/receivers. |
| 1998 [6] | Diurnal distribution of rain attenuation in communication and broadcasting satellite systems. |
| 1998 [7] | Wide area joint probability of rain attenuation in satellite systems with a common on-board resource. |
| 1998 [8] | Worst-month statistics of rain attenuation. |
| 1999 [9] | Large distance site diversity. |
| 2000 [10] | Matching service quality and system design to the time of the day. |
| 2003 [11] | Small scale (“micro”) site diversity. |
| 2003 [12] | Statistics of interruption time due to rain attenuation. |
| 2004 [13] | Service oriented statistics of interruption time. |
| 2006 [14] | Annual and diurnal satellite rain attenuation statistics in Athens. |
| 2006 [15] | Low elevation angle (5°) terrestrial paths. |
| 2006 [16] | Time diversity as a rain attenuation countermeasure. |
| 2007 [17] | Rain storms speed and temporal properties of precipitation. |
| 2007 [18] | Time diversity gain in satellite links. |
| 2007 [19] | SST as part of a time series generator. |
| 2008 [20] | Tropical attenuation statistics. |
| 2009 [21] | Phase delay and attenuation in deep-space tracking. |
| 2011 [22] | Phase delay and differential attenuation in phased array antennas for deep-space communications. |
| 2013 [23] | Small scale site diversity in Guam. |
| 2013 [24] | Efficiency of satellite channels and ideal fade-countermeasure. |
| 2016 [25] | Space communications to the Sun–Earth Lagrangian point L1 from Spino d’Adda. |
| 2016 [26] | Space communications to the Sun–Earth Lagrangian point L1 from Madrid. |
| 2016 [27] | A method to achieve clear-sky data-volume download in satellite links affected by tropospheric attenuation. |
| 2016 [28] | Rain Attenuation Statistics at Ka and Q band in Athens. |
| 2017 [29] | Linear combining techniques using time diversity. |
| 2018 [30] | Rain attenuation statistics for micro and millimeter wavelengths. |
| 2018 [31] | Fade dynamics in equatorial Malaysia. |
| 2019 [32] | Space diversity in Attica, Greece. |
| 2021 [33] | Time series of rain attenuation in a tropical location. |
| Site | Lat. N (°) | Long. E (°) | Altitude (m) | Precipitation Height (km) | Years of Rain Rate Measurements | Wind Speed at 700 Mbar (m/s) |
|---|---|---|---|---|---|---|
| Spino d’Adda (Italy) | 45.4 | 9.5 | 84 | 3.341 | 8 | 10.6 |
| Gera Lario (Italy) | 46.2 | 9.4 | 210 | 3.483 | 5 | 8.2 |
| Fucino (Italy) | 42.0 | 13.6 | 680 | 2.905 | 5 | 10.4 |
| Madrid (Spain) | 40.4 | 356.3 | 630 | 3.001 | 8 | 10.9 |
| Prague (Czech Republic) | 50.0 | 14.5 | 250 | 3.051 | 5 | 12.6 |
| Tampa (Florida) | 28.1 | 277.6 | 50 | 4.528 | 4 | 9.6 |
| Norman (Oklahoma) | 35.2 | 262.6 | 420 | 4.145 | 4 | 12.4 |
| White Sands (New Mexico) | 32.5 | 253.4 | 1463 | 4.744 | 5 | 9.1 |
| Vancouver (British Columbia) | 49.3 | 236.8 | 80 | 2.612 | 1 | 8.9 |
| Fairbanks (Alaska) | 64.9 | 212.2 | 184 | 2.688 | 3 | 12.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matricciani, E.; Riva, C. Global Formulation of the Synthetic Storm Technique Oriented to Satellite Link–Budget Design. Electronics 2022, 11, 1325. https://doi.org/10.3390/electronics11091325
Matricciani E, Riva C. Global Formulation of the Synthetic Storm Technique Oriented to Satellite Link–Budget Design. Electronics. 2022; 11(9):1325. https://doi.org/10.3390/electronics11091325
Chicago/Turabian StyleMatricciani, Emilio, and Carlo Riva. 2022. "Global Formulation of the Synthetic Storm Technique Oriented to Satellite Link–Budget Design" Electronics 11, no. 9: 1325. https://doi.org/10.3390/electronics11091325







