Abstract
The 5th generation mobile communication technology (5G) authentication and key management (AKA) protocol specified by the 3rd generation partnership project (3GPP) includes three cases because it introduces synchronization failure and message authentication code (MAC) failure procedures. Thus, there may be interactions between these cases, forming vulnerabilities that do not exist in any single case. However, this is not fully considered in the existing formal analysis and improvement of the 5G AKA protocol. To solve this problem, this paper formally analyzes the security of the latest version of the 5G AKA protocol based on the mixed strand space model for mixed protocols and finds many new attacks, including cross attacks for mixed cases. Then, a secure and efficient primary authentication and key agreement protocol for 5G networks is proposed, which is named the 5G-AKA’. In the 5G-AKA’ protocol, the pre-shared key between the user equipment (UE) and the home network (HN) is replaced with a derivation key of the pre-shared key, the challenge–response mechanism between the serving network (SN) and the HN is added, the subscription permanent identifier (SUPI) of the UE is added to the second message between the SN and the HN, and the MAC failure is replaced with a timeout mechanism on the HN. Finally, the 5G-AKA’ protocol is proved secure in the mixed strand space model and can overcome these attacks of the latest version of the 5G AKA protocol. Additionally, the comparative analysis shows that the 5G-AKA’ protocol is better than the recently improved 5G AKA protocols in security, and the 5G-AKA’ protocol is efficient and is backward compatible with the 5G AKA protocol.
1. Introduction
With the continuous popularization of the 5th generation mobile communication technology (5G), in the near future, the 5G network, as an important communication infrastructure, will penetrate into diversified vertical industries and fields such as transportation, medical treatment and industry, and support various information interactions between people, people and things, and things and things [1]. In the 5G network, three different primary authentication and key agreement protocols are defined in the related 3rd generation partnership project (3GPP) specifications [2,3,4], including the 5G authentication and key agreement (AKA) protocol, the improved extensible authentication protocol method for 3rd generation authentication and key agreement (EAP-AKA’) protocol and the 5G extensible authentication protocol method for transport layer security (EAP-TLS) protocol. The first two protocols are based on the shared key cryptography, while the last one is based on the public key cryptography. These protocols all aim to provide mutual authentication of subscribers and networks. Currently, they are in the process of standardization.
The 5G AKA protocol [2,3,4] is developed directly from the evolution packet system (EPS)-AKA protocol of the long-term evolution (LTE)/4th generation mobile communication technology (4G) network [3], so it inherits certain security vulnerabilities from the EPS-AKA protocol such as impersonation attacks, man-in-the-middle attacks (MitM) and denial of service (DoS) attacks [5,6,7,8,9,10,11]. Dehnel-Wild et al. [12] analyzed the 5G AKA protocol of technical specification (TS) 33.501 v0.7.0. They discovered a protocol vulnerability that would enable the attacker to impersonate another user to a serving network (SN). Based on the Tamarin model checker [13], Basin et al. [14] investigated the security properties of the 5G AKA protocol of TS 33.501 v15.1.0, and several major issues were revealed, which are related to user localization, leakage of activity, the impact of active attackers and the presence of malicious SN while roaming. In [15], Liu et al. pointed out that the 5G AKA protocol suffers from link-ability attacks, and then proposed a new authentication scheme by making use of the Diffie–Hellman key exchange algorithm for generating the session key. This scheme was successful in preventing link-ability attacks along with a MitM attack.
For the more recent 5G AKA protocol, Borgaonkar et al. [16] found a new attack. They claimed that the protection mechanism of the sequence number (SQN) can be defeated under specific replay attacks due to its use of exclusive-or (XOR) and a lack of randomness. In [17], Cremers et al. modeled all the key components of the 5G AKA protocol (i.e., the user equipment, the serving network and the home network) according to the definition in the 3GPP specification document. They discovered an attack that exploits a potential race condition and additionally showed that solving the race condition for the honest case does not necessarily prevent the attack. In [18], Koutsos et al. investigated the privacy properties of the 5G AKA protocol using the Bana–Comon logic [19,20]. They discovered a novel de-synchronization attack and proved that their proposed protocol guarantees the privacy properties. In [21], Braeken et al. proposed a novel version of the 5G AKA protocol to prevent active attacks and gain resistance against malignant serving networks. Unfortunately, there is a possibility of having SN impersonation, so this scheme does not eliminate the vulnerability towards the MitM attack. Further, Gharsallah et al. [22] also attempted to launch a revised version of the 5G AKA protocol. However, their proposed protocol suffers from privacy preservation as the device identities are clearly transmitted in the air which leads to numerous security attacks.
As time goes on, more and more attacks of the 5G AKA protocol were found due to the insecure channel between different network domains in the legacy mobile network. In [23], Hu et al. discovered an attack exploiting the subscription concealed identifier (SUCI) to track a subscriber in the 5G network, which is directly caused by the insecure air channel. To cover this issue, they proposed a secure authentication scheme by utilizing the existing public key infrastructure (PKI) mechanism. Further, they found a location sniffing attack, which can be implemented by an attacker through inexpensive devices [24]. Similarly, they proposed a fix scheme based on the existing PKI mechanism. In [25], Edris et al. modeled the 5G AKA protocol with symbolic modeling using ProVerif based on three and four entities models, and then proposed their security consideration. Further, Mariya et al. [26] proposed an enhanced version of the authentication and key agreement protocol for the 5G system that surmounts the limitations existing in the 5G AKA protocol. Parne et al. [27] introduced a protocol that preserves the privacy of the user identity and overcomes the identified problems of the 5G AKA protocol. Similarly, 3GPP has also been enhancing the security of the 5G AKA protocol [2,3,4].
Because the 5G AKA protocol [2,3,4] introduces synchronization failure and message authentication code (MAC) failure procedures, it has three cases, so there may be interactions between these cases, forming vulnerabilities that do not exist in any single case. However, this is not fully considered in the above security analysis and improvement of the 5G AKA protocol. Therefore, we formally analyze the security of the latest version of the 5G AKA protocol considering three cases at the same time. Then, we propose a secure and efficient primary authentication and key agreement protocol for 5G networks, named the 5G-AKA’. Finally, we prove that the 5G-AKA’ protocol is secure, and it is efficient and backward compatible.
The main contributions of this paper are as follows:
- We formally analyze the security of the latest version of the 5G AKA protocol in the mixed strand space model for mixed protocols [28] and give twenty-one attack scenarios of the 5G AKA protocol. Based on these attack scenarios, we find many new attacks of the 5G AKA protocol, including cross attacks for mixed cases.
- We propose the 5G-AKA’ protocol, and then formally analyze its security in the mixed strand space model for mixed protocols [28]. As a result, no attack scenario is obtained. By discussion and analysis, the 5G-AKA’ protocol can overcome these attacks of the 5G AKA protocol, thus it is secure.
- Based on comparative analysis, the 5G-AKA’ protocol is better than the 5G AKA protocol and the recently improved 5G AKA protocols in security, and is efficient and backward compatible.
The rest of this paper is organized as follows. Section 2 provides an overview of the latest version of the 5G AKA protocol. In Section 3, we formally analyze the security of the latest version of the 5G AKA protocol in the mixed strand space model. Section 4 describes our proposed 5G-AKA’ protocol and gives the security analysis of the 5G-AKA’ protocol in the mixed strand space model. In Section 5, we present some discussions and we conclude the paper in Section 6.
2. Overview of the 5G AKA Protocol
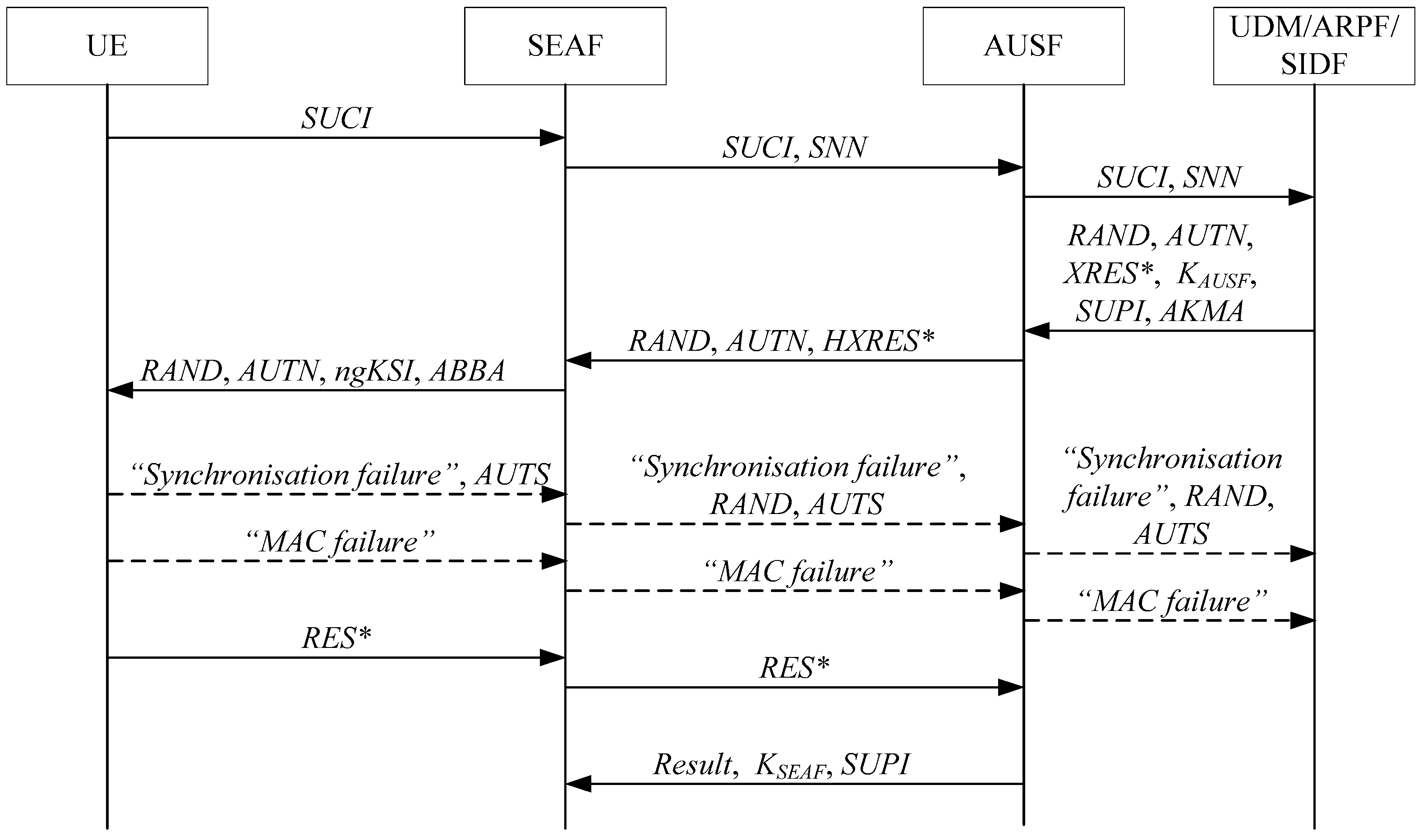
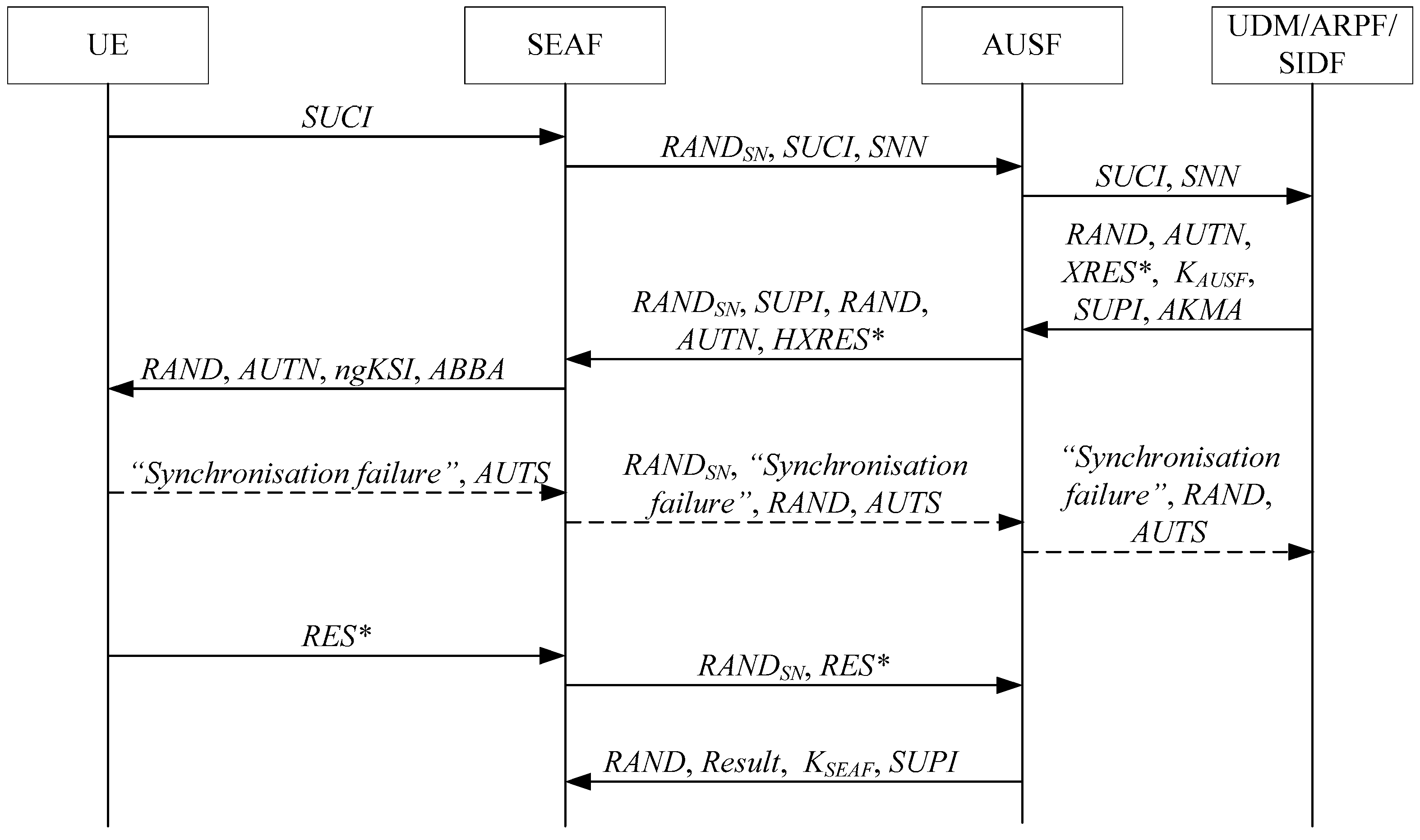
According to [2,3,4], the steps of the latest version of the 5G AKA protocol in the 3GPP standard version v17.4.0 of TS 33.501 are illustrated in Figure 1.
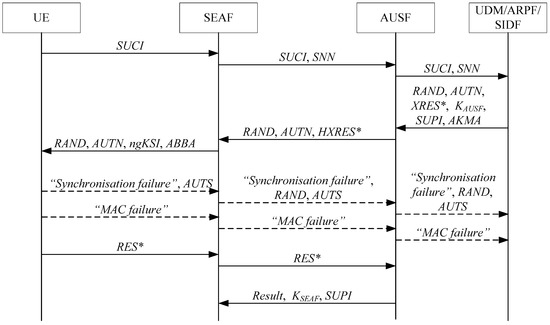
Figure 1.
The steps of the latest version of the 5G AKA protocol. In the following notations, various fields in the figures have been described, including these fields marked with *. In detail, is an expected response, while is an expected response from , then is a hashing expected response from . is response, while is a response from .
In Figure 1, the detailed steps of the latest version of the 5G AKA protocol are as follows:
- When the security anchor function (SEAF) initiates authentication with the user equipment (UE), the UE sends to the SEAF, where the UE includes mobile equipment (ME) and a universal subscriber identity module (USIM).where denotes a SUCI of the UE, denotes the subscription permanent identifier (SUPI) of the UE, and are an ephemeral public/private key pair of the UE for the Diffie–Hellman exchange, and are an ephemeral public/private key pair of the home network (HN) for the Diffie–Hellman exchange, is an encryption key, is an initial counter block (ICB), is a MAC key, is a MAC of the UE, is a key derivation function and is a hash function for computing MAC, denotes a cascade of fields.
- Upon receiving , the SEAF sends and to the authentication server function (AUSF). denotes the serving network name (SNN) of the SN.
- If the SEAF is entitled to use , then the AUSF stores the receiving and sends and to the unified data management (UDM).
- The UDM invokes the subscriber identity de-concealing function (SIDF) whether is received. Then, the SIDF de-conceals to gain before the UDM can process the request. Based on , the UDM/ARPF (authentication credential repository and processing function) chooses the authentication method.
- When 5G AKA is selected, the UDM/ARPF generates , calculates and , and derives , and then creates a 5G home environment authentication vector from , , and . is an unpredictable challenge of the HN.where is an authentication token of the HN, is a fresh sequence number generated by the HN, is an anonymity key, is the authentication management field (AMF) and the separation bit of the AMF is set 1, is a MAC of the HN, is a long-term key between the UE and the HN, and are two message authentication functions, , and is three key generating functions, is a cipher key, is an integrity key, is a key derived from and , is an expected response and is an expected response derived from and .
- The UDM sends the 5G home environment authentication vector to the AUSF together with . When an authentication and key management for applications (AKMA) subscription is used, the UDM also sends to the AUSF. denotes the AKMA indication and routing indicator.
- The AUSF stores the temporarily together with the received .
- The AUSF generates a 5G authentication vector from the 5G home environment authentication vector received from the UDM/ARPF by computing from , computing from , replacing with , and replacing with in the 5G home environment authentication vector.where is a hashing , is a hash function.
- The ASUF creates a 5G serving environment authentication vector by removing from the 5G authentication vector, and then sends the 5G serving environment authentication vector (i.e., , and ) to the SEAF.
- The SEAF stores , and then sends , , and to the UE. is used by the UE and the access and mobility management function to identify the and the partial native security context that is created if the authentication is successful. denotes the anti-bidding down between architectures (ABBA) parameter.
- In the UE, the ME forwards and to the USIM. Upon receipt of and , the USIM first computes the anonymity key and retrieves the sequence number . Next, the USIM computes and compares this with which is included in . Then, the USIM verifies that the received is in the correct range. If is the same as and is in the correct range (i.e., , where denotes the highest sequence number the USIM has accepted), then the USIM computes a response , and , and then returns , and to the ME. The ME then computes , and .where is a response and is a response derived from and .
- The UE sends to the SEAF.
- The SEAF computes and compares this with . If they coincide, then the SEAF considers the authentication as successful from the serving network’s point of view. If not, then the SEAF considers the authentication as unsuccessful.where is a hashing .
- The SEAF sends the received to the AUSF.
- The AUSF compares the received with the stored . If and are equal, then the AUSF considers the authentication as successful from the home network point of view. Then, the AUSF informs the UDM about the authentication result.
- The AUSF indicates to the SEAF whether the authentication was successful or not from the home network point of view (i.e., ). If the authentication was successful, then the ASUF also sends and to the SEAF.
In step 11, if and are different, then the USIM indicates to the ME a MAC failure of . Then, the UE sends the “MAC failure” indication to the SEAF. Further, the SEAF sends the “MAC failure” indication to the AUSF. Finally, the ASUF sends the “MAC failure” indication to the UDM/ARPF.
In step 11, if is not in the correct range (i.e., ), then the USIM computes , and then sends with a “Synchronization failure” indication to the ME. Then, the UE sends with the “Synchronization failure” indication to the SEAF. Further, the SEAF sends and with the “Synchronization failure” indication to the AUSF. Finally, the ASUF sends and with the “Synchronization failure” indication to the UDM/ARPF.
where is an anonymity key, is a MAC of the UE, is a dummy value of all zeros, is a message authentication function and is a key generating function.
Upon receiving the “MAC failure” indication or the “Synchronization failure” indication, the UDM/ARPF creates a new 5G home environment authentication vector and runs a new authentication procedure with the UE, i.e., go to step 5 to continue the 5G AKA protocol. Under normal communication conditions, these failures do not often occur [2,3,4]. However, they can often be used by the penetrator to perform many attacks on the 5G AKA protocol (see Section 3). In [14,15,18,24], the authors also exploited the usage of the different types of failures, MAC-based or synchronization-based, to track a specific subscriber, and then given the corresponding revised schemes.
3. Formal Verification and Analysis of the 5G AKA Protocol
To simplify the formal verification and analysis, we assume that:
- The parties of the 5G AKA protocol shown in Figure 1 are simplified as the UE, the SN and the HN. The USIM and the ME are located in the UE, and the SEAF is located in the SN. The AUSF, the UDM, the ARPE and the SIDF are located in the HN.
- There is a session key between the SN and the HN, and it is secure.
- and do not affect the security of the 5G AKA protocol, so they are ignored here.
According to these assumptions, the 5G AKA protocol shown in Figure 1 can be summarized into three cases as follows:
Case (I): the verification of succeeds and the authentication is successful. The steps of this case are as follows:
- : ;
- : ;
- : ;
- : ;
- : ;
- : ;
- : .
where , and are three messages exchanged between the UE and SN, , , and are four messages exchanged between the SN and the HN.
Case (II): the verification of fails and it is a synchronization failure. The steps of this case are as follows:
- : ;
- : ;
- : ;
- : ;
- : ;
- : .
where , and are three messages exchanged between the UE and SN, , and are three messages exchanged between the SN and the HN.
Case (III): the verification of fails and it is a MAC failure. The steps of this case are as follows:
- : ;
- : ;
- : ;
- : ;
- : ;
- : .
where , and are three messages exchanged between the UE and SN, , and are three messages exchanged between the SN and the HN.
In the above cases, denotes the session key between the SN and the HN, denotes the “Synchronization failure” indication and denotes the “MAC failure” indication.
The strand space model [28,29,30] is a well-studied formal analysis method for security protocols. In [28], Fábrega et al. studied the case of mixed protocols, where principals use secret material in more than one protocol. In such cases, the two protocols can potentially interact, forming vulnerabilities not present in either protocol alone. To find these vulnerabilities, they proposed a mixed strand space model for such cases.
As mentioned above, there are three cases in the 5G AKA protocol, so there may be interactions between these cases, forming vulnerabilities that do not exist in any single case. In order to find these vulnerabilities, we use the mixed strand space model [28] to analyze the security of the 5G AKA protocol as follows.
3.1. Mixed Strand Space for the 5G AKA Protocol
Definition 1.
A regular strand spaceis a space for case I of the 5G AKA protocol ifis the union of three kinds of strands: (1) Initiator strands,,,,,,with trace:,,. The principal associated with this strand is.computed locally is equal toandis in the correct range (i.e.,); (2) Responder strands,,,,,,,,,,,with trace:,,,,,,. The principal associated with this strand is. ,andare three messages that are not inspected by, where; (3) Server strands,,,,,,,,,,,with trace:,,,. The principal associated with this strand is.
Definition 2.
A regular strand spaceis a space for case II of the 5G AKA protocol ifis the union of three kinds of strands: (1) Initiator strands,,,,,,,with trace:,,. The principal associated with this strand is.computed locally is equal to, butis not in the correct range (i.e.,); (2) Responder strands,,,,,,,,,with trace:,,,,,. The principal associated with this strand is.,andare three messages that are not inspected by; (3) Server strands,,,,,,,,,with trace:,,. The principal associated with this strand is.
Definition 3.
A regular strand spaceis a space for case III of the 5G AKA protocol ifis the union of three kinds of strands: (1) Initiator strands,,,,,,with trace:,,. The principal associated with this strand is.computed locally is not equal to. (2) Responder strands,,,,,,,,with trace:,,,,,. The principal associated with this strand is.andare two messages that are not inspected by. (3) Server strands,,,,,,,,with trace:,,. The principal associated with this strand is.
Definition 4.
An infiltrated mixed strand spaceis a space for the 5G AKA protocol if, where penetrator strands[28,29,30].
Definition 1 gives a regular strand space for case I of the 5G AKA protocol (i.e., ), including initiator strands, responder strands and server strands for case I of the 5G AKA protocol. Definition 2 gives a regular strand space for case II of the 5G AKA protocol (i.e., ), including initiator strands, responder strands and server strands for case II of the 5G AKA protocol. Definition 3 gives a regular strand space for case III of the 5G AKA protocol (i.e., ), including initiator strands, responder strands and server strands for case III of the 5G AKA protocol. Definition 4 gives an infiltrated mixed strand space for the 5G AKA protocol, including , , and penetrator strands (i.e., ).
3.2. The Initiator’s Guarantee of the 5G AKA Protocol
Theorem 1.
Suppose: (1)is a space for the 5G AKA protocol, andis a bundle containing an initiator strand,,,,,,; (2)and, wheredenotes any authorized SN; (3)is uniquely originating in. Then,contains a unique server strand,,,,,,,,,,,and a responder strand,,,,,,,,,,,, where,,,,andis generated for. Alternatively,contains a unique server strand,,,,,,,,and a responder strand,,,,,,,,,,,,,,,,,,,,,or,,,,,,,,, where,,,andis generated for.
Proof of Theorem 1.
By assumptions (2) and (3), and are uniquely originating in , so must uniquely originate on a server strand according to Definitions 1 to 4.
- (1)
- If is a server strand of Definition 1, then , , , , , , , , , , , , where , , and . By assumption (2), , so must originate on a responder strand , , , , , , , , , , , , where and is generated for . Since , must originate on a server strand . Since is uniquely originating in , , so . Hence, , , , , , , , , , , , .
- (2)
- If is a server strand of Definition 2, then , , , , , , , , , , where , and . By assumption (2), , so must originate on an initiator strand , , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . By assumption (1) and Definition 1, on . However, on according to Definition 2. Therefore, and cannot be in the same run of the protocol, so must exist in the past run of the protocol. However, it is impossible from to because increases. That is to say, it is impossible that exists in the past run of the protocol and exists in the current run of the protocol. Hence, is not a server strand of Definition 2.
- (3)
- If is a server strand of Definition 3, then , , , , , , , , , where and . Since is uniquely originating in , originates at , where . Let . Since , is non-empty. Hence, has at least one ≤-minimal element and the sign of is positive. does not lie on a penetrator strand but must lie on a regular strand instead (Lemma 5.4 in [29]). By inspection, precedes on the regular strand and , and the regular strand containing and is a responder strand . If is a responder strand of Definition 1, then , , , , , , , , , , , , where , and is generated for . If is a responder strand of Definition 2, then , , , , , , , , , . If is a responder strand of Definition 3, then , , , , , , , , . □
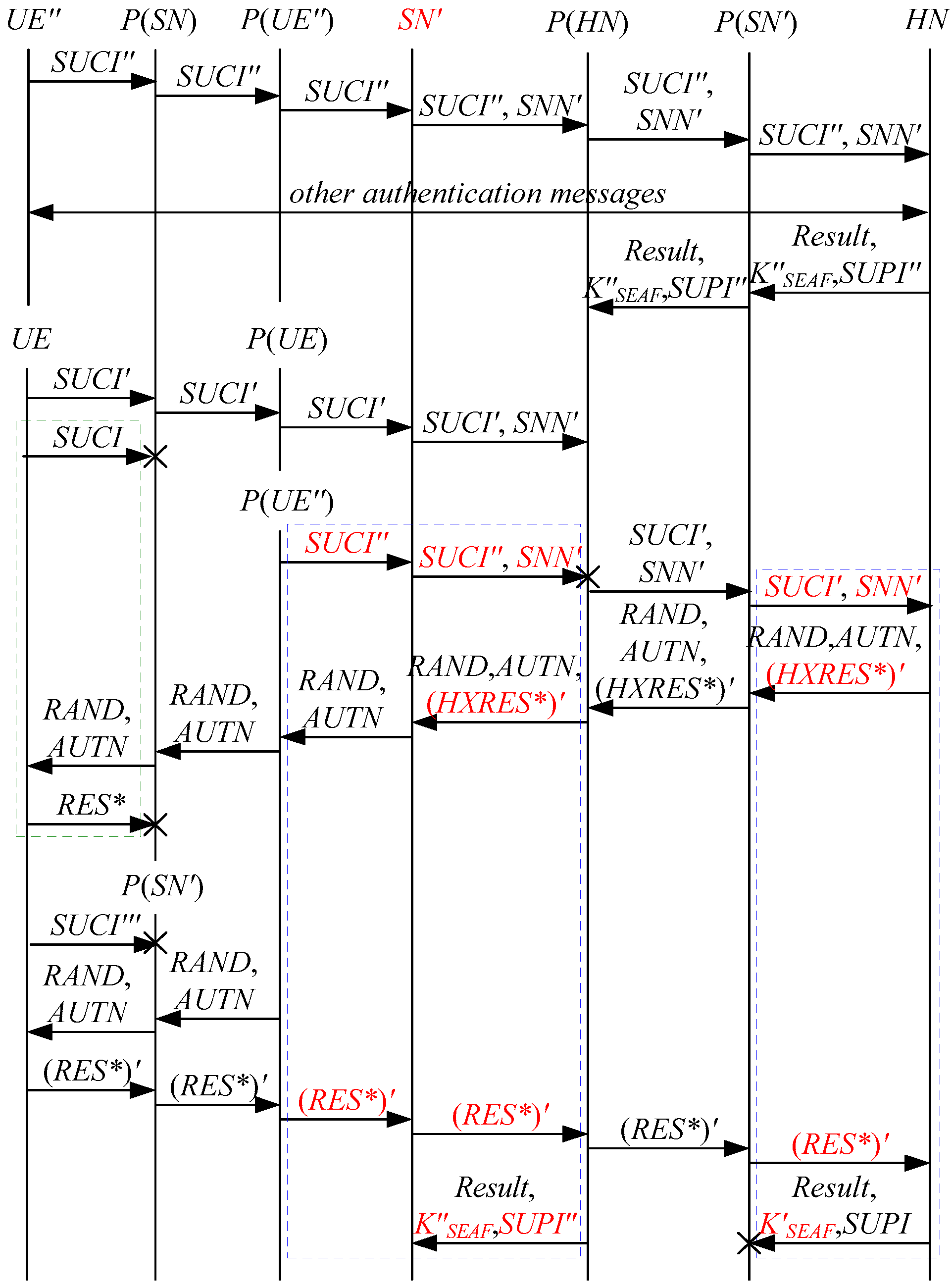
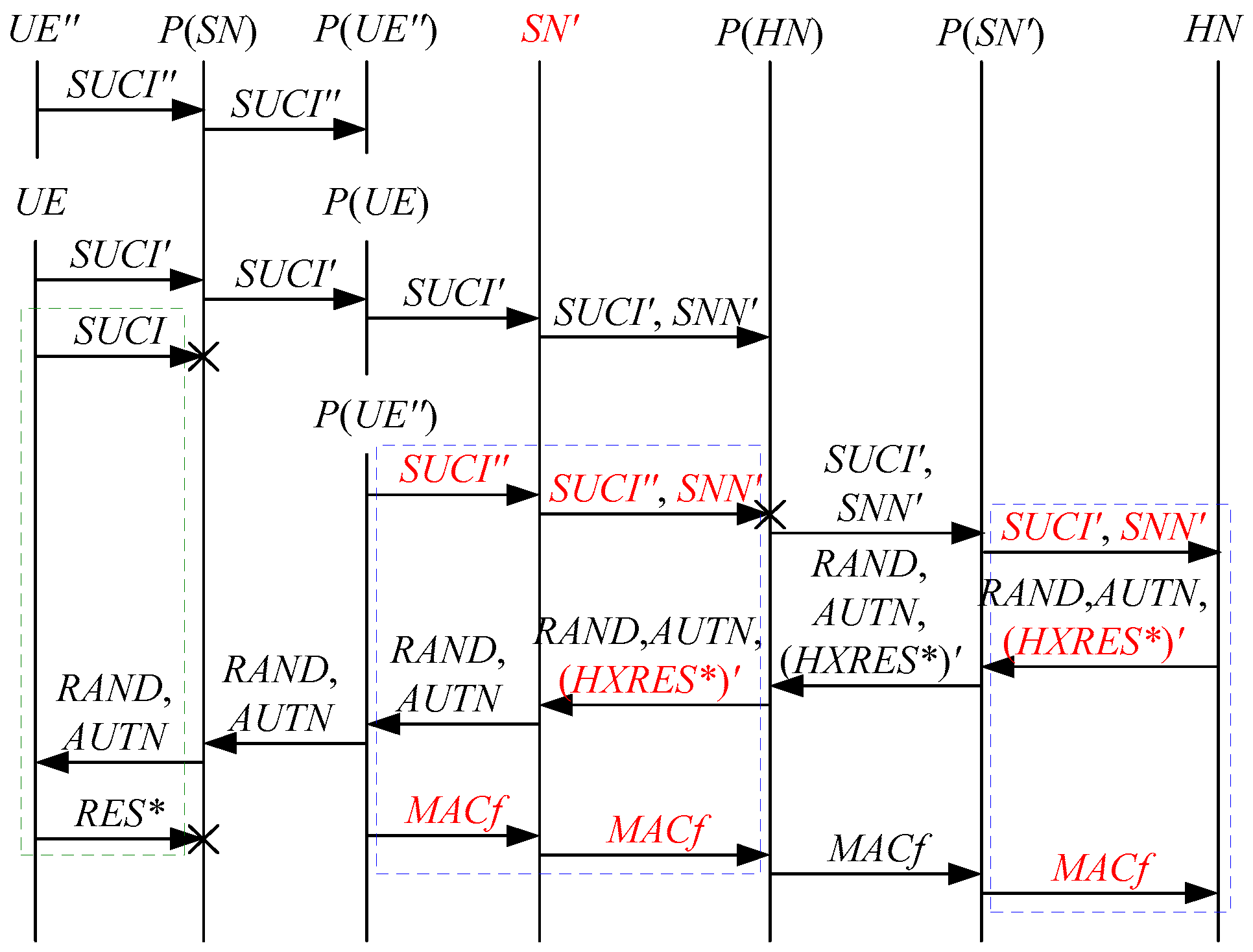
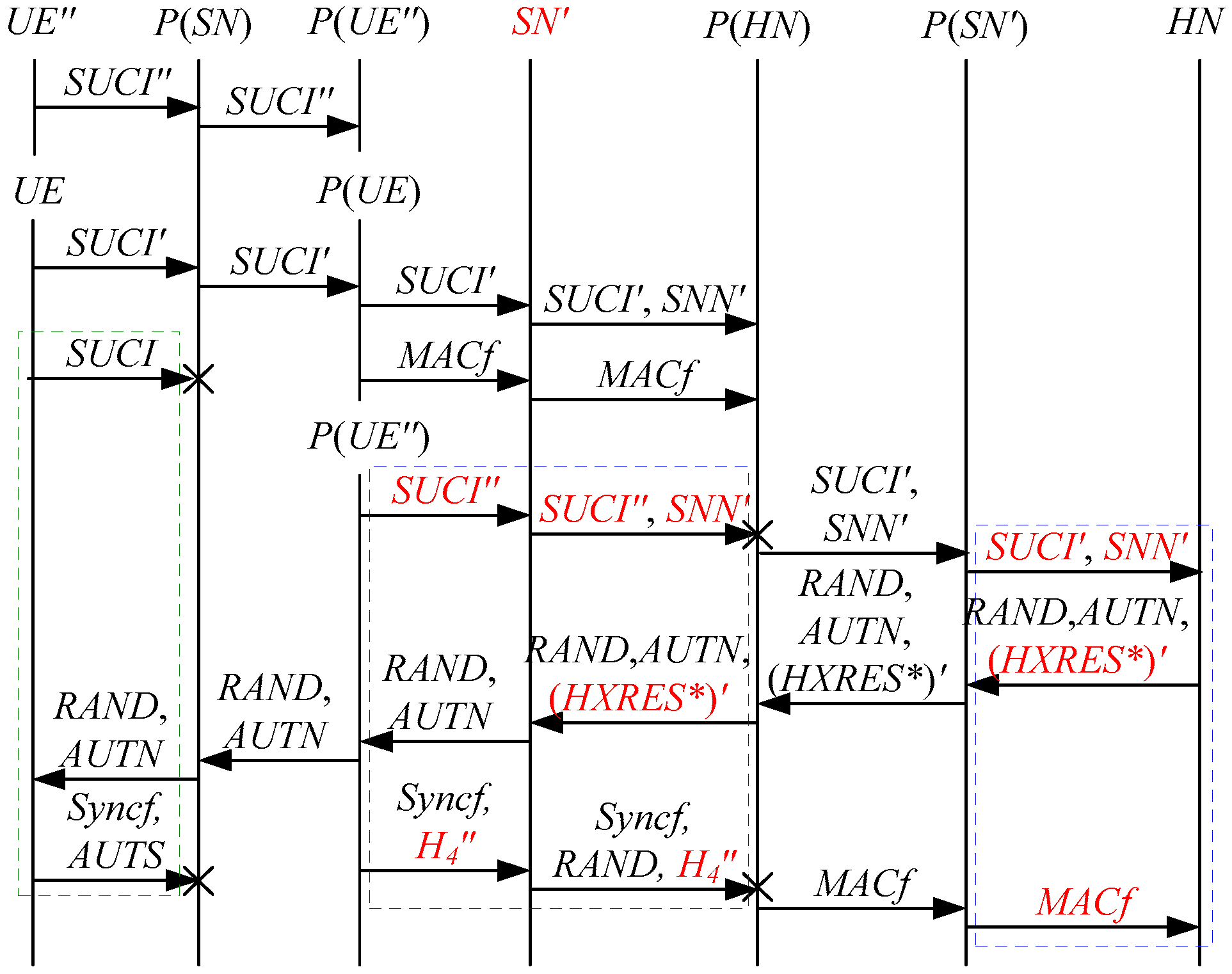
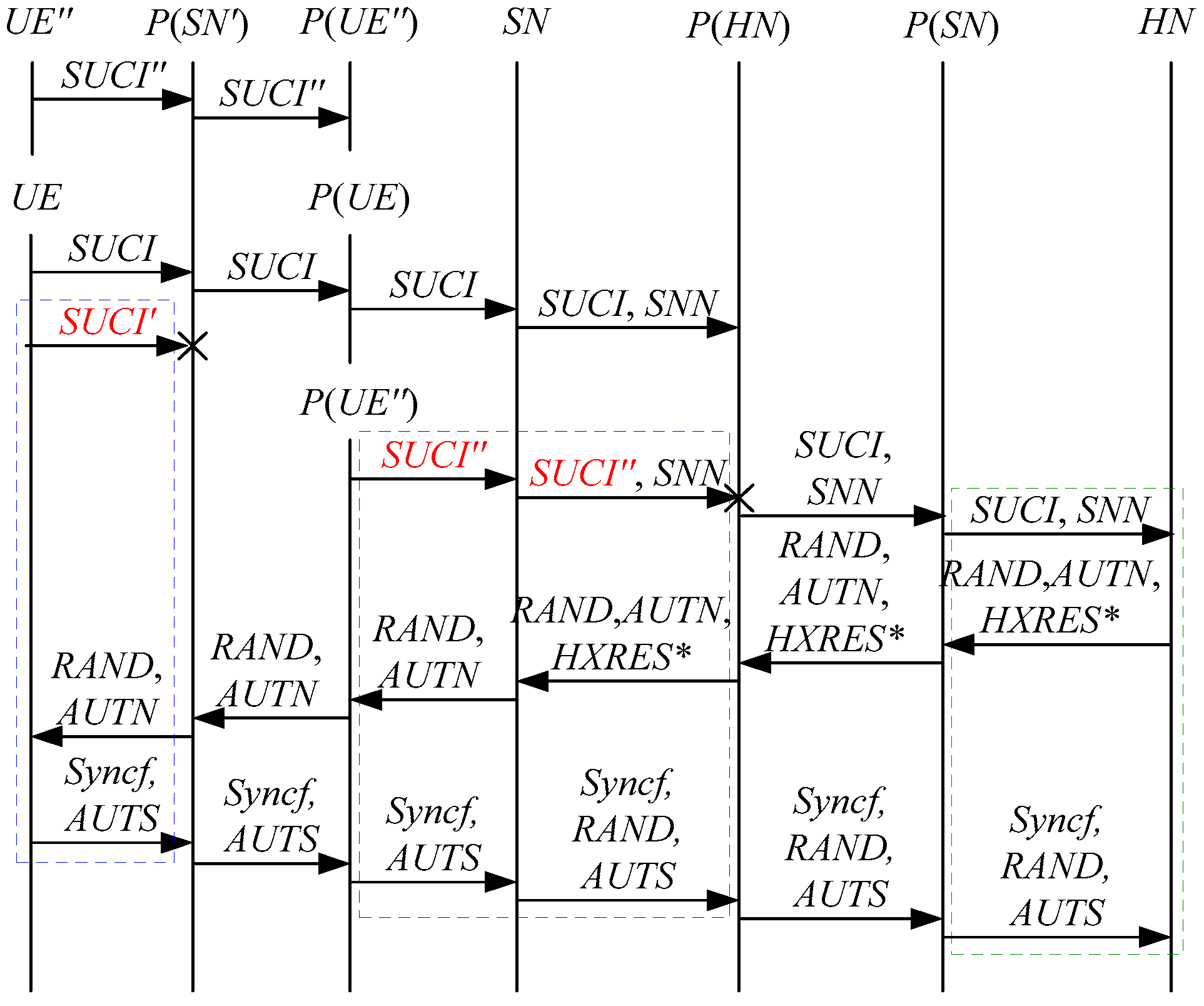
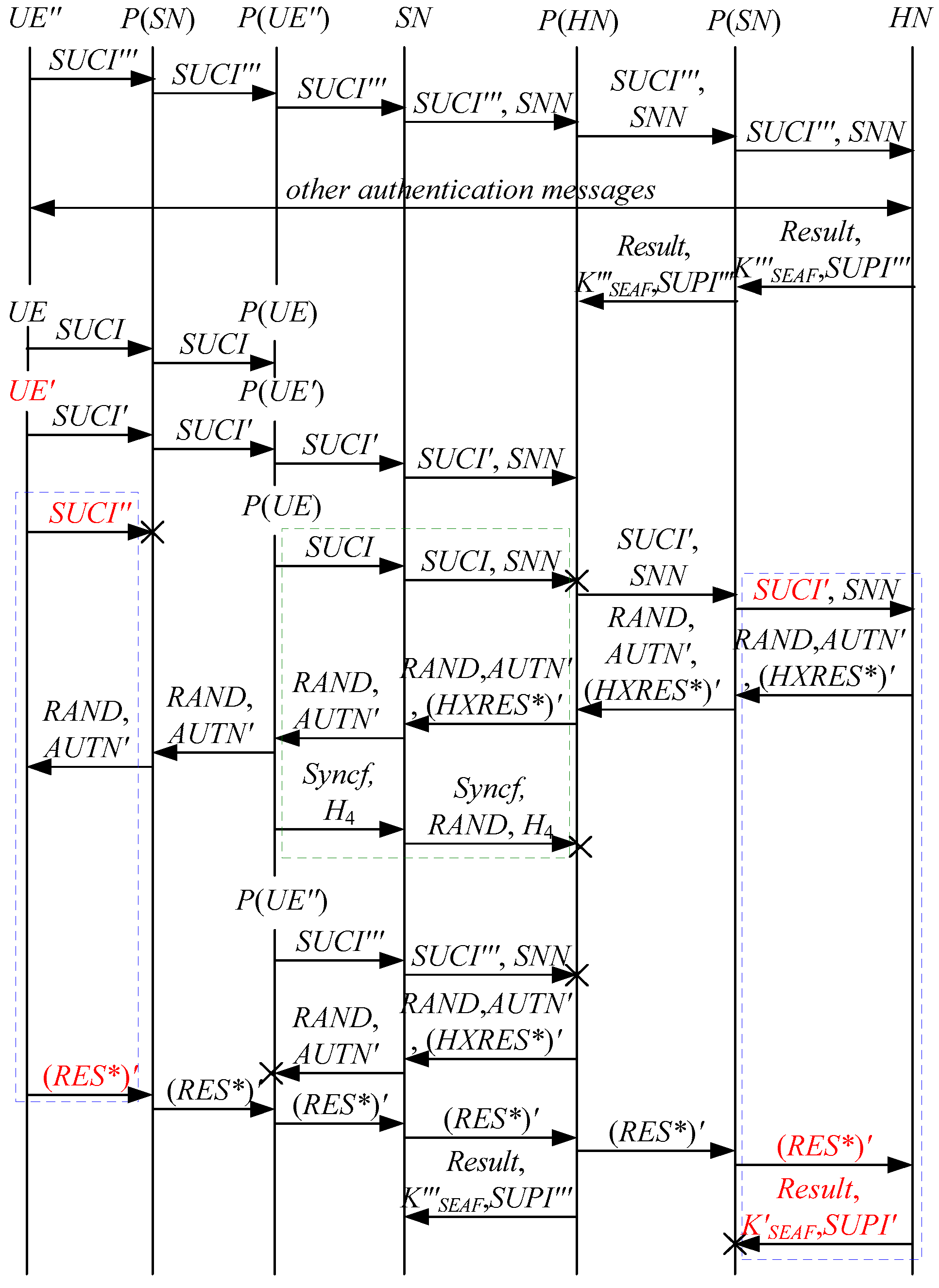
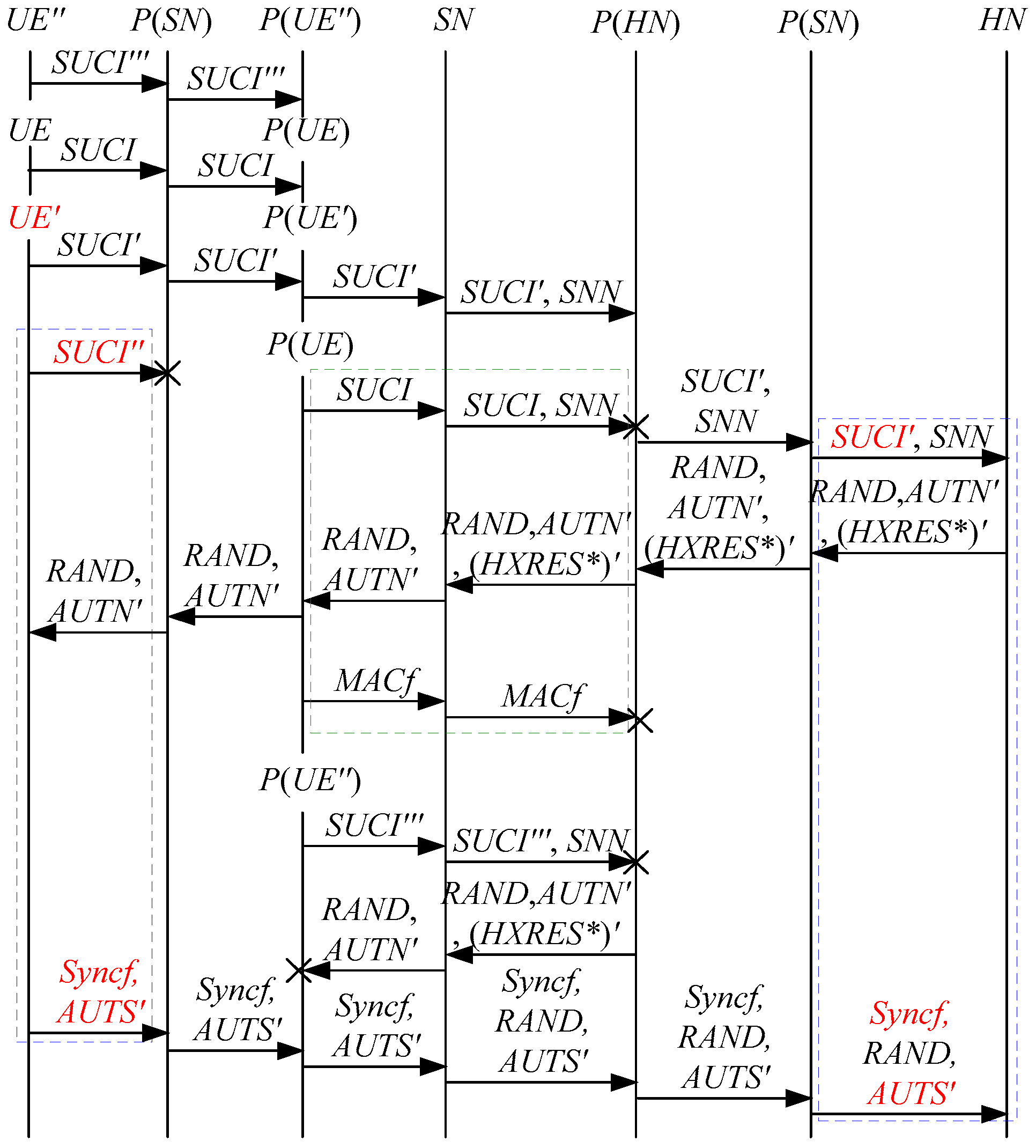
According to Theorem 1, the corresponding attack scenarios can be obtained as shown in Figure 2, Figure 3, Figure 4 and Figure 5, where the messages between the HN and the authorized SN are protected by their session key.
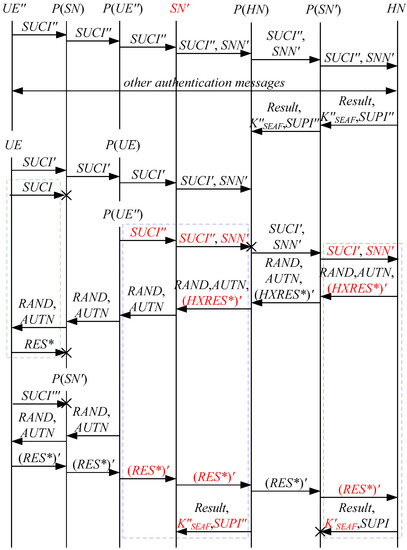
Figure 2.
The first attack scenario of the 5G AKA protocol.
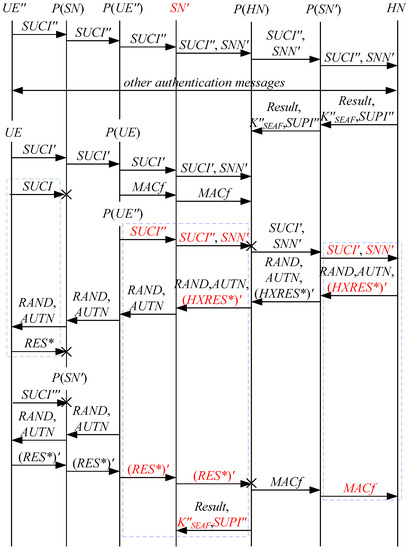
Figure 3.
The second attack scenario of the 5G AKA protocol.
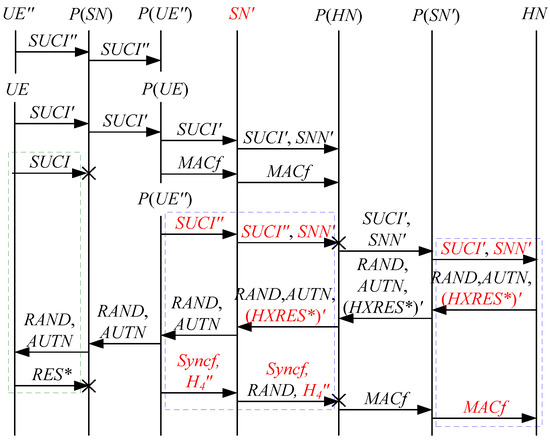
Figure 4.
The third attack scenario of the 5G AKA protocol.
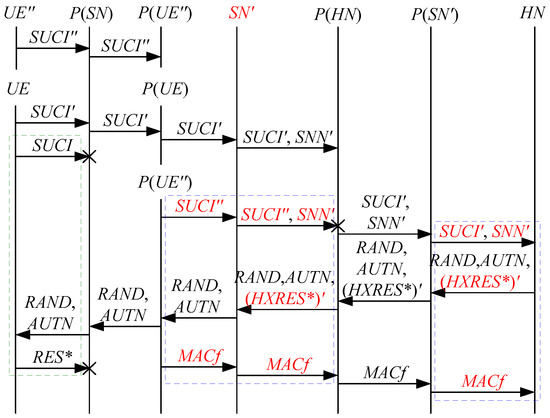
Figure 5.
The fourth attack scenario of the 5G AKA protocol.
In Figure 2, Figure 3, Figure 4 and Figure 5, the green dashed box represents the initiator strand of Theorem 1, while the blue dashed boxes represent the server strands and the responder strands of Theorem 1. The fields marked in red on the server strand and the responder strand are some fields that cannot be agreed with the UE, which are caused by MitM attacks.
According to Figure 2, Figure 3, Figure 4 and Figure 5, some specific attacks can be found as follows.
- (1)
- cannot find that and are replayed because does not contain the challenge of the UE (i.e., ), which is included in . That is to say, the replay attacks on the SN and the HN can be formed, resulting in the energy consumption ion of the SN and the HN.
- (2)
- successfully authenticates , but does not authenticate because does not contain , which makes that is included in , and , and the principal associated with the responder strand is . In [14], the authors also pointed out this security issue. That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (3)
- Both and cannot be agreed with the UE because is included in them. That is to say, the key agreement fails, resulting in a new authentication and key agreement process.
- (4)
- (5)
- In Figure 3 and Figure 4, the penetrator replays an encrypted between the SN and the HN to make authentication failure. In Figure 5, the penetrator directly sends to the SN to make authentication failure. They are called MAC failure attacks. That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (6)
- The server strand and the responder strand of Theorem 1 may exist in the past run of the protocol because they do not contain the challenge of the UE (i.e., ), which is included in . That is to say, on the UE may be a replayed message and is still in the correct range. As a result, the location privacy of the UE can be compromised by reidentifying . That is to say, the location privacy of the UE can be compromised.
Theorem 2.
Suppose: (1) is a space for the 5G AKA protocol, and is a bundle containing an initiator strand , , , , , , , ; (2) and , where denotes any authorized SN; (3) is uniquely originating in . Then, contains a unique server strand , , , , , , , , , , , and a responder strand , , , , , , , , , , , , and both and must exist in the past run of the protocol, where , , , , and is generated for . Alternatively, contains a unique server strand , , , , , , , , , and a responder strand , , , , , , , , , , where , , and . Alternatively, contains a unique server strand , , , , , , , , and a responder strand , , , , , , , , , , , , , , , , , , , , , or , , , , , , , , , where , , , and is generated for , and both and must exist in the past run of the protocol when , , , , , , , , , , , .
Proof of Theorem 2.
By assumptions (2) and (3), and are uniquely originating in , so must uniquely originate on a server strand according to Definitions 1 to 4.
- (1)
- If is a server strand of Definition 1, then , , , , , , , , , , , , where , , and . By assumption (2), . Since and , and , so . Hence, must originate on an initiator strand , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . By assumption (1) and Definition 2, on . However, on according to Definition 1. Therefore, and cannot be in the same run of the protocol, so must exist in the past run of the protocol. Because increases, it is possible from to . That is to say, it is possible that exists in the past run of the protocol and exists in the current run of the protocol. Hence, it is possible that is a server strand of Definition 1. By assumption (2), , so must originate on a responder strand , , , , , , , , , , , , where and is generated for . Since , must originate on a server strand . Since is uniquely originating in , , so . Hence, , , , , , , , , , , , . From the above, exists in the past run of the protocol and originates on , so must exist in past run of the protocol. From the above, originates on , so also must exist in the past run of the protocol.
- (2)
- If is a server strand of Definition 2, then , , , , , , , , , , where , and . By assumption (2), , so must originate on a responder strand , , , , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , , , , .
- (3)
- If is a server strand of Definition 3, then , , , , , , , , , where and . Since is uniquely originating in , originates at , where . Let . Since , is non-empty. Hence, has at least one ≤-minimal element and the sign of is positive. does not lie on a penetrator strand but must lie on a regular strand instead (Lemma 5.4 in [29]). By inspection, precedes on the regular strand and , and the regular strand containing and is a responder strand . If is a responder strand of Definition 1, then , , , , , , , , , , , , where , and is generated for . From the above, it is possible that is a responder strand of Definition 1 because it is possible from to , and both and must exist in the past run of the protocol. If is a responder strand of Definition 2, then , , , , , , , , , . If is a responder strand of Definition 3, then , , , , , , , , . □
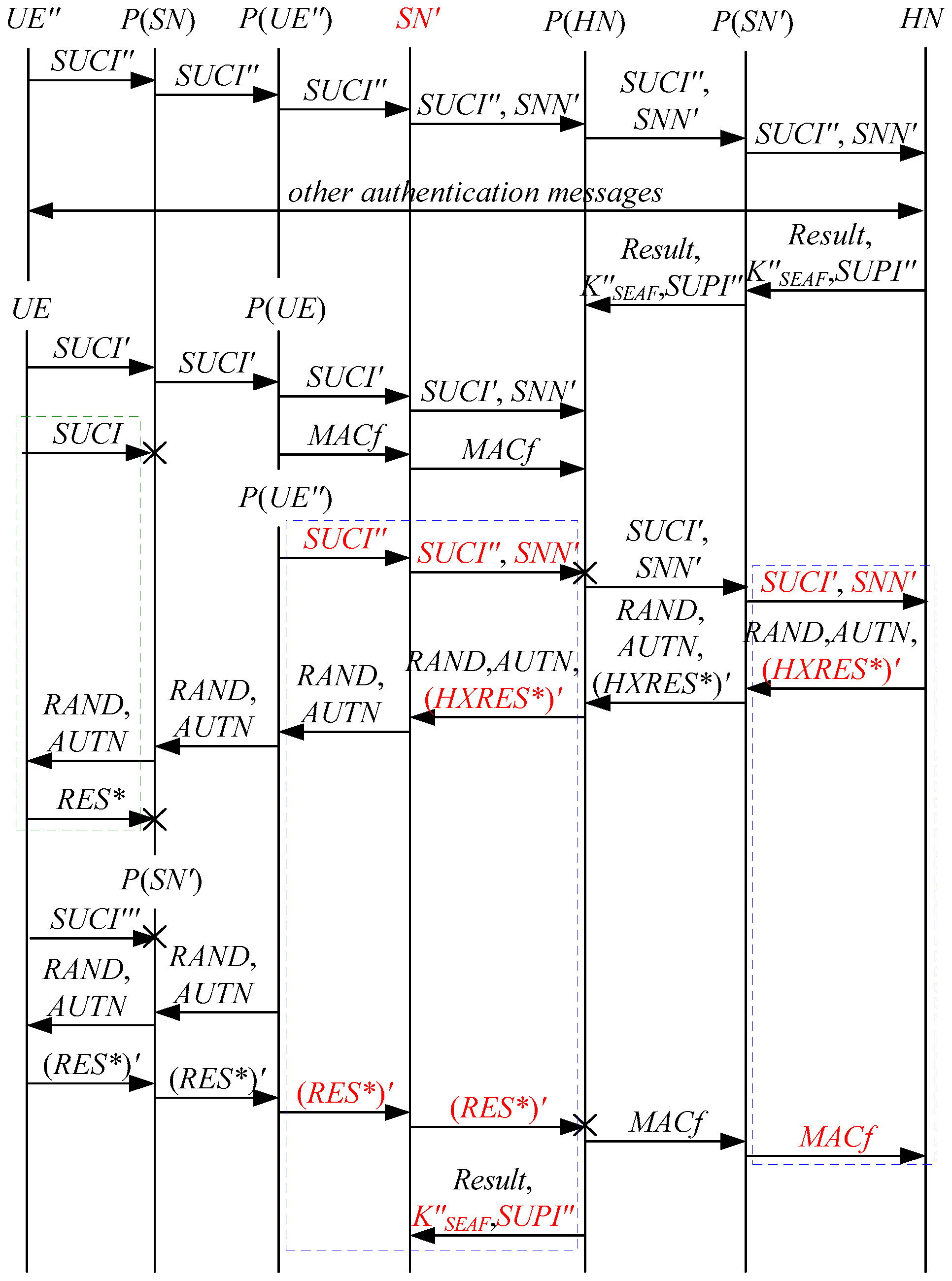
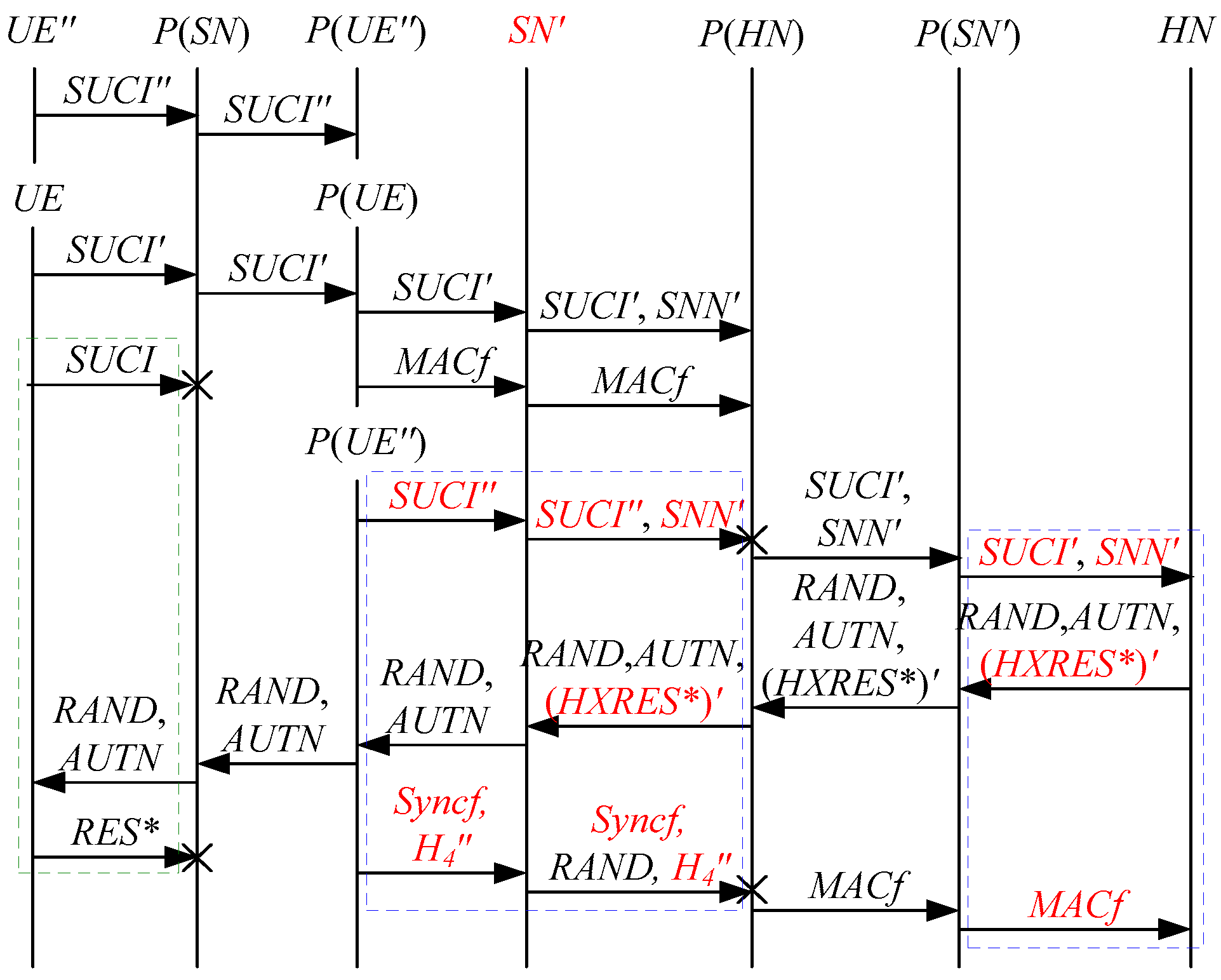
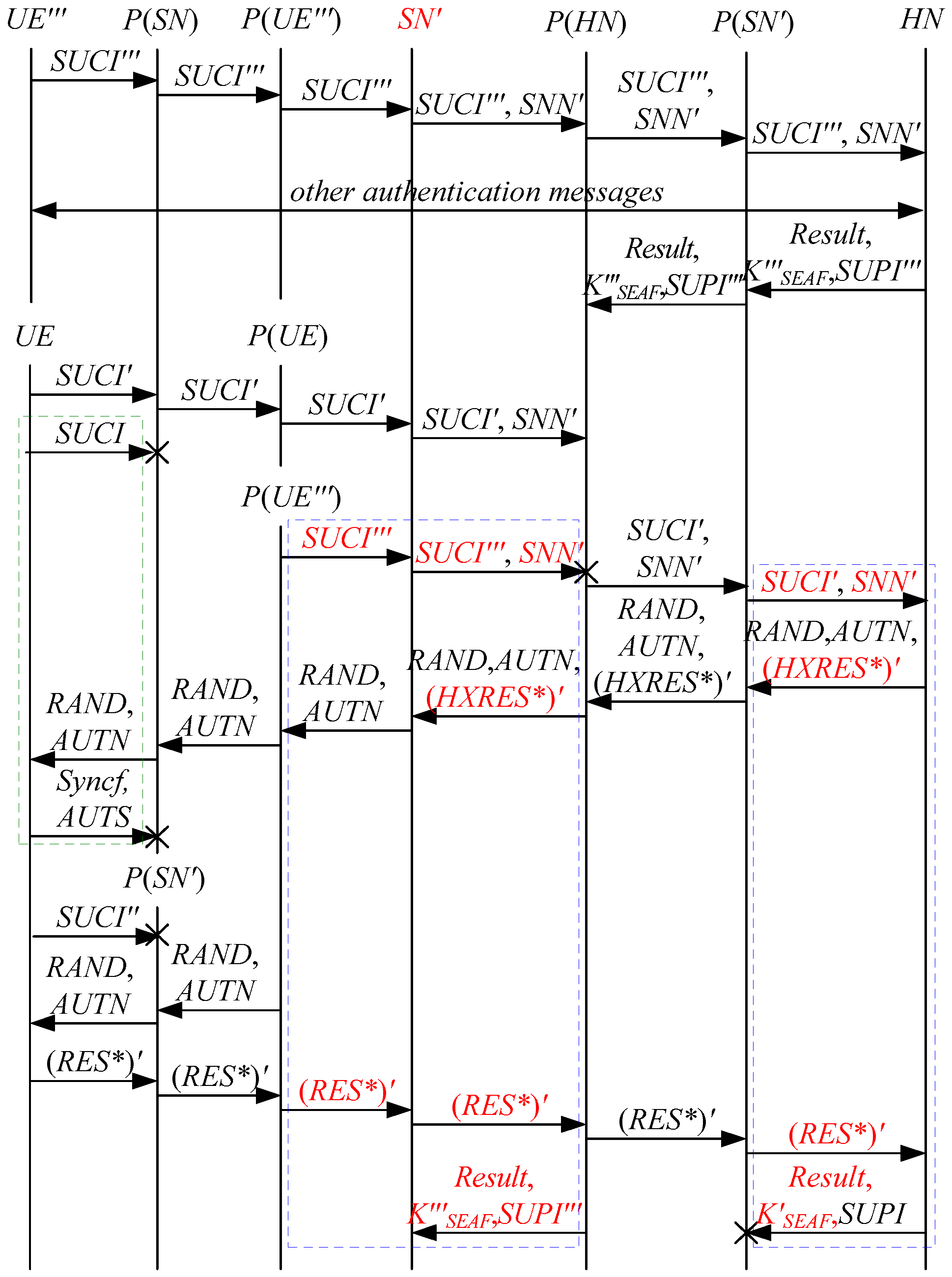
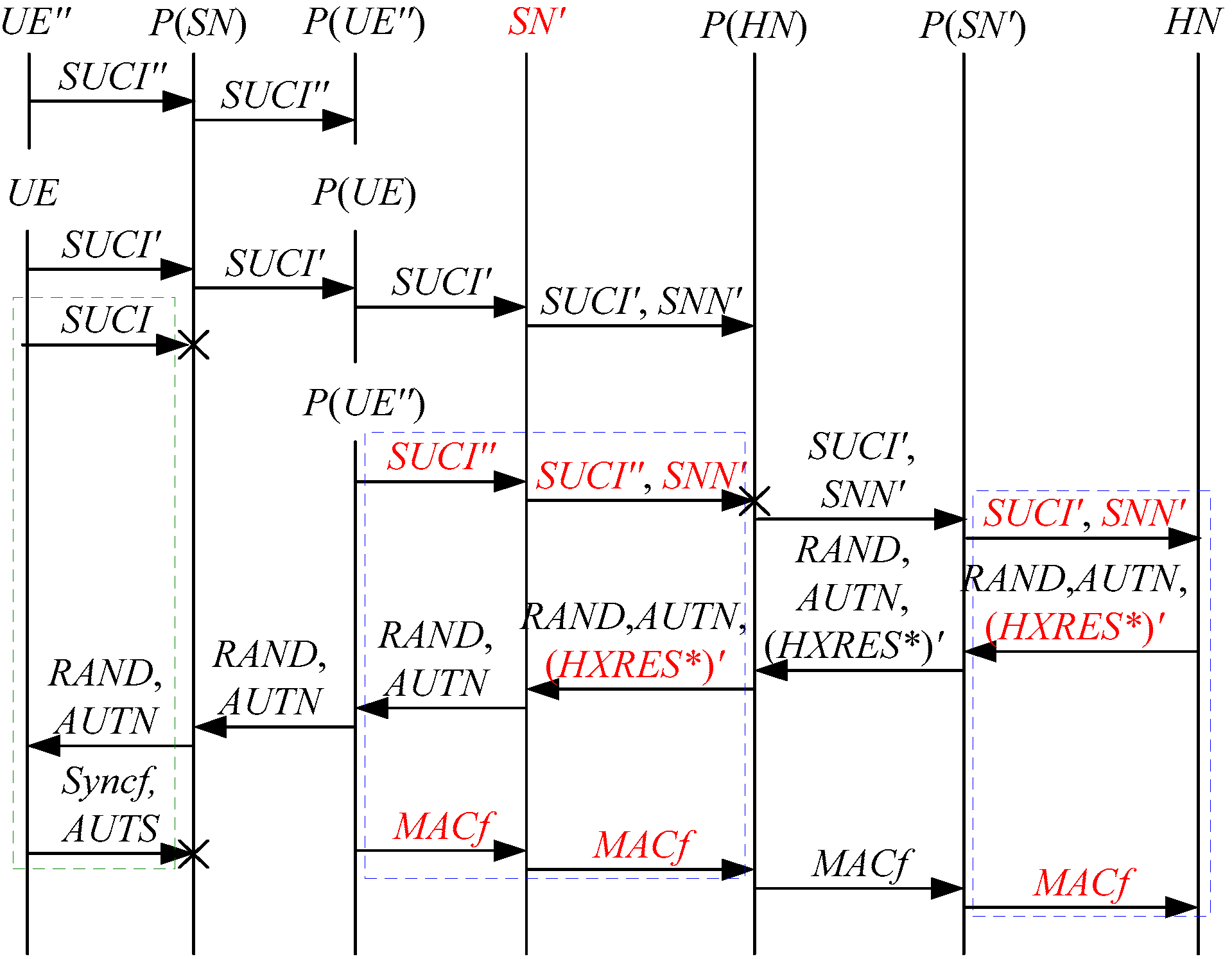
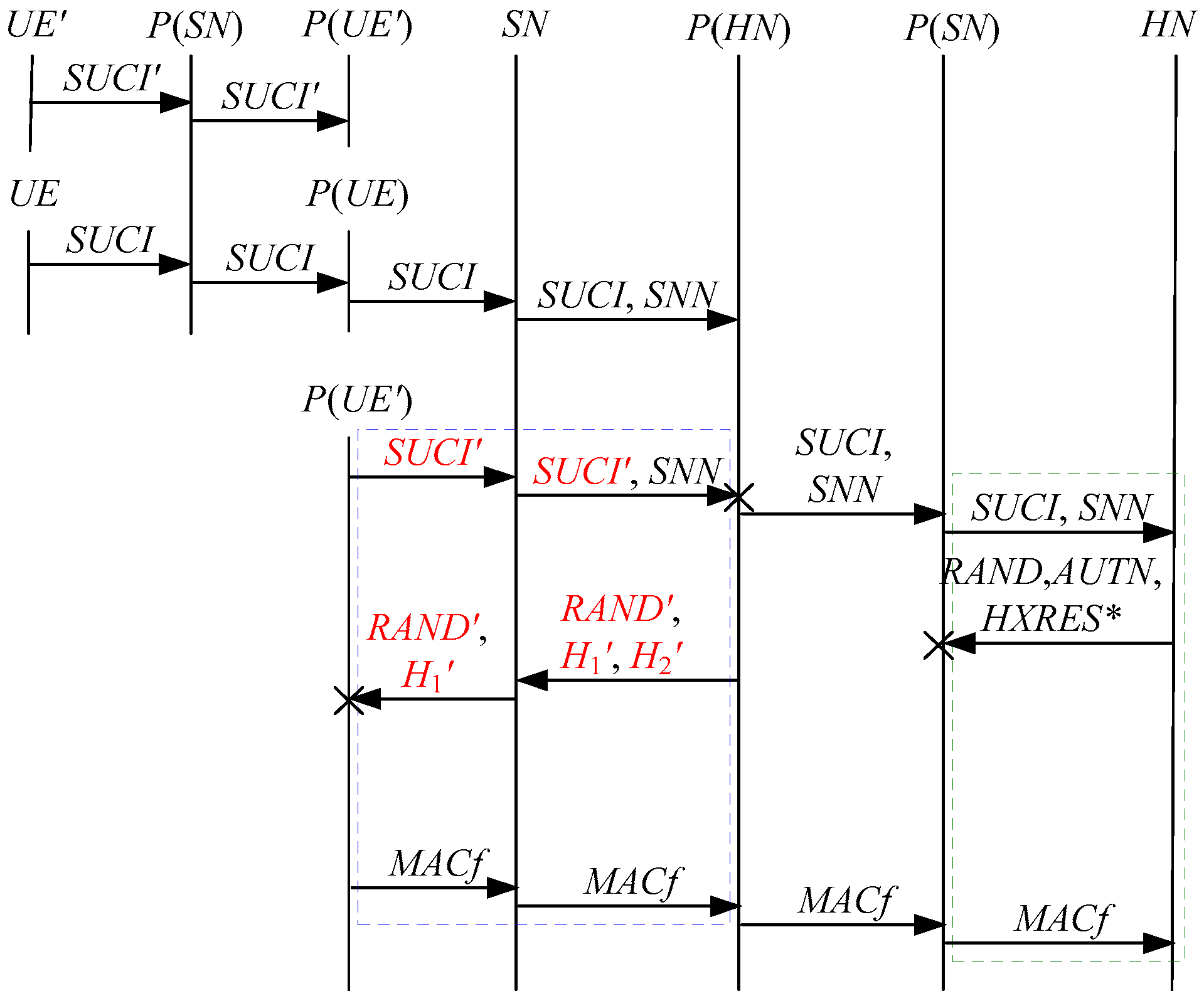
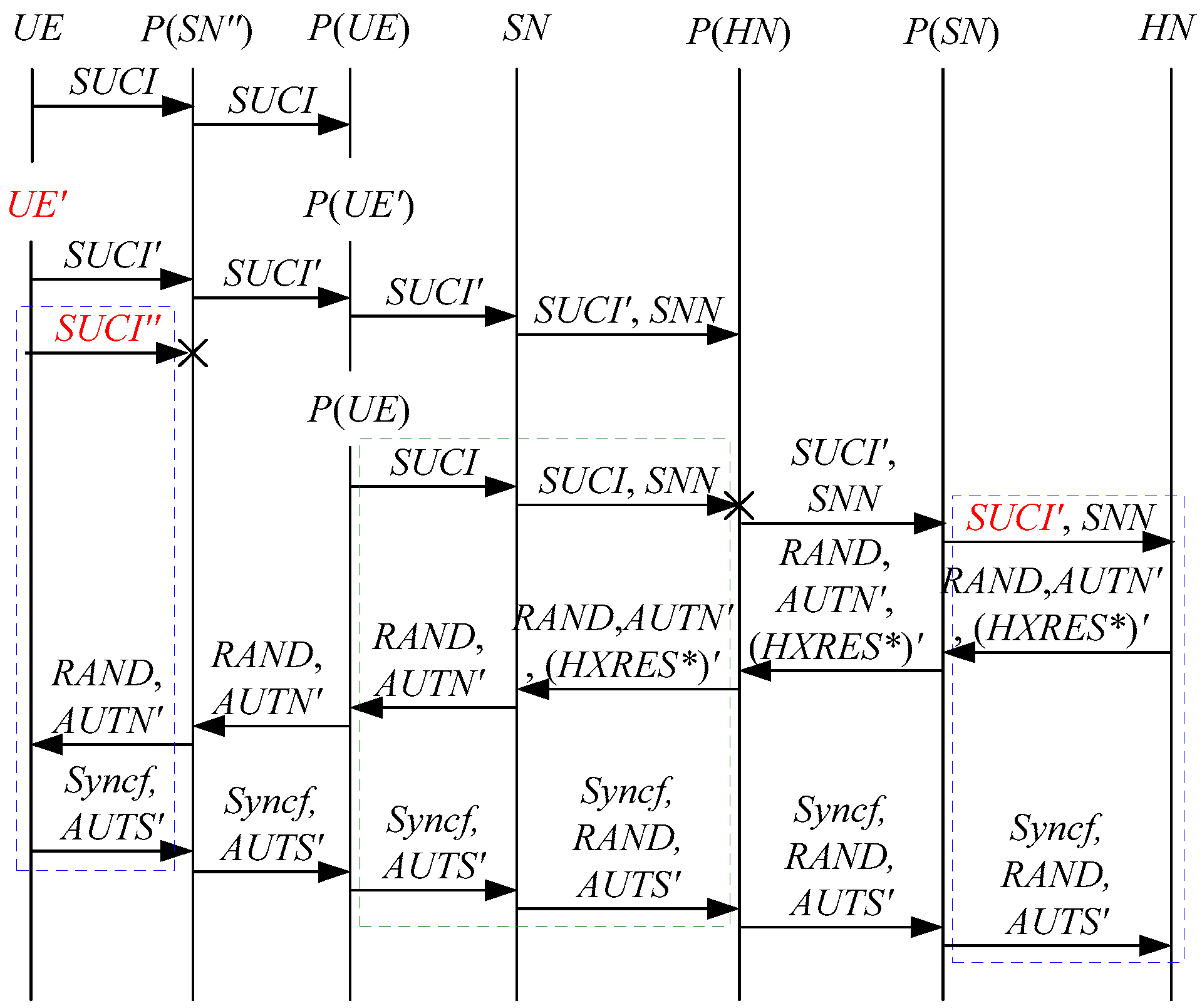
According to Theorem 2, the corresponding attack scenarios can be obtained as shown in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, where the messages between the HN and the authorized SN are protected by their session key.
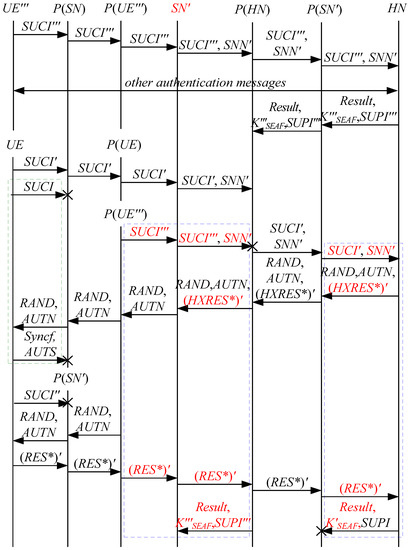
Figure 6.
The fifth attack scenario of the 5G AKA protocol.
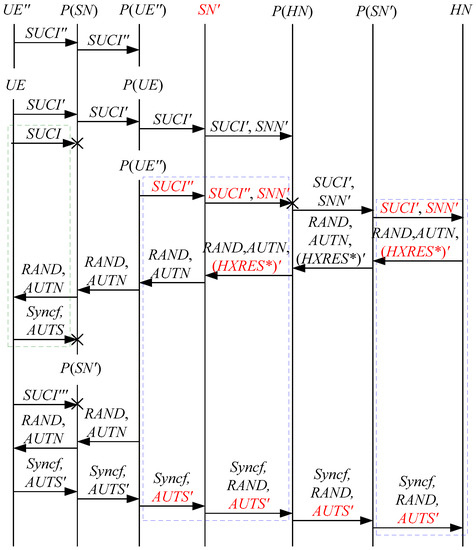
Figure 7.
The sixth attack scenario of the 5G AKA protocol.
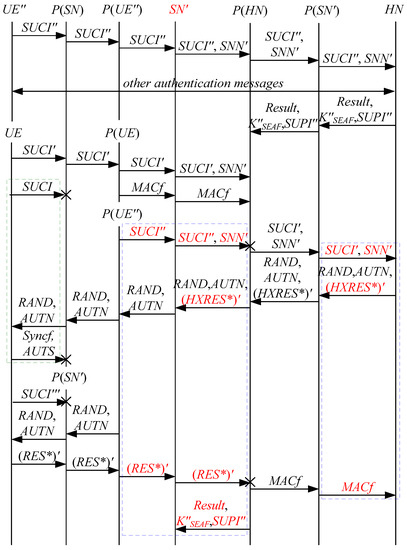
Figure 8.
The seventh attack scenario of the 5G AKA protocol.
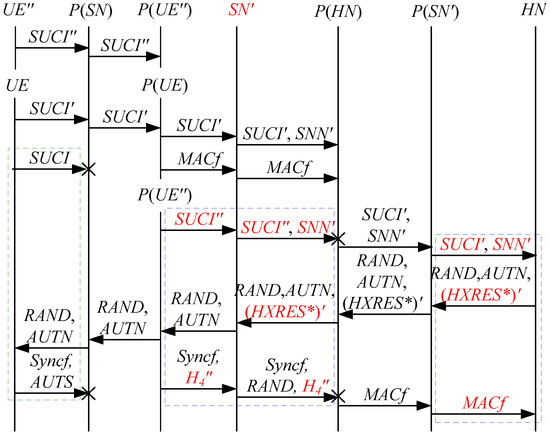
Figure 9.
The eighth attack scenario of the 5G AKA protocol.
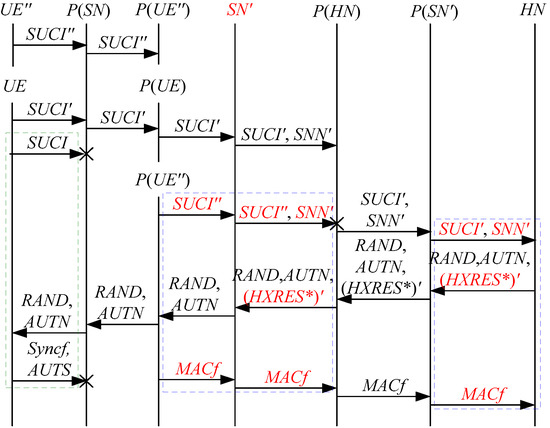
Figure 10.
The ninth attack scenario of the 5G AKA protocol.
In Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, the green dashed box represents the initiator strand of Theorem 2, while the blue dashed boxes represent the server strand and the responder strand of Theorem 2. The fields marked in red on the server strand and the responder strand are some fields that cannot be agreed with the UE, which are caused by MitM attacks.
According to Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, some specific attacks can be found as follows:
- (1)
- cannot find that and are replayed because does not contain the challenge of the UE (i.e., ), which is included in . That is to say, the replay attacks on the SN and the HN can be formed, resulting in the energy consumption ion of the SN and the HN.
- (2)
- successfully authenticates , but does not authenticate because does not contain , which means that is included in , and , and the principal associated with the responder strand is . In [14], the authors also pointed out this security issue. That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (3)
- In Figure 6, Figure 8, Figure 9 and Figure 10, there are interactions between different cases of the 5G AKA protocol, i.e., cross attacks. They are caused by the penetrators taking advantage of and . That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (4)
- In Figure 8 and Figure 9, the penetrator replays an encrypted between the SN and the HN to make authentication failure. In Figure 10, the penetrator directly sends to the SN to make authentication failure. They are called MAC failure attacks. That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (5)
- The server strand and the responder strand of Theorem 2 in Figure 6 and Figure 8 only exist in the past run of the protocol according to Theorem 2, i.e., on the initiator strand of Theorem 2 in Figure 6 and Figure 8 is a replayed message and is not in the correct range. As a result, the location privacy of the UE can be compromised by identifying . Further, the server strand and the responder strand of Theorem 2 in Figure 7, Figure 9 and Figure 10 may exist in the past run of the protocol because they do not contain the challenge of the UE (i.e., ), which is included in . That is to say, on the UE in Figure 7, Figure 9 and Figure 10 can be a replayed message and is not in the correct range. As a result, the location privacy of the UE can be compromised by identifying . In [14,15,18,24], the authors also exploited this attack. That is to say, the location privacy of the UE can be compromised.
Theorem 3.
Suppose: is a space for the 5G AKA protocol, and is a bundle containing an initiator strand , , , , , , . Then, the penetrator can complete the entire message exchange without any responder strand or server strand.
Proof of Theorem 3.
By the above assumption and Definition 3, computed locally is not equal to , so does not originate on any responder strand and server strand. □
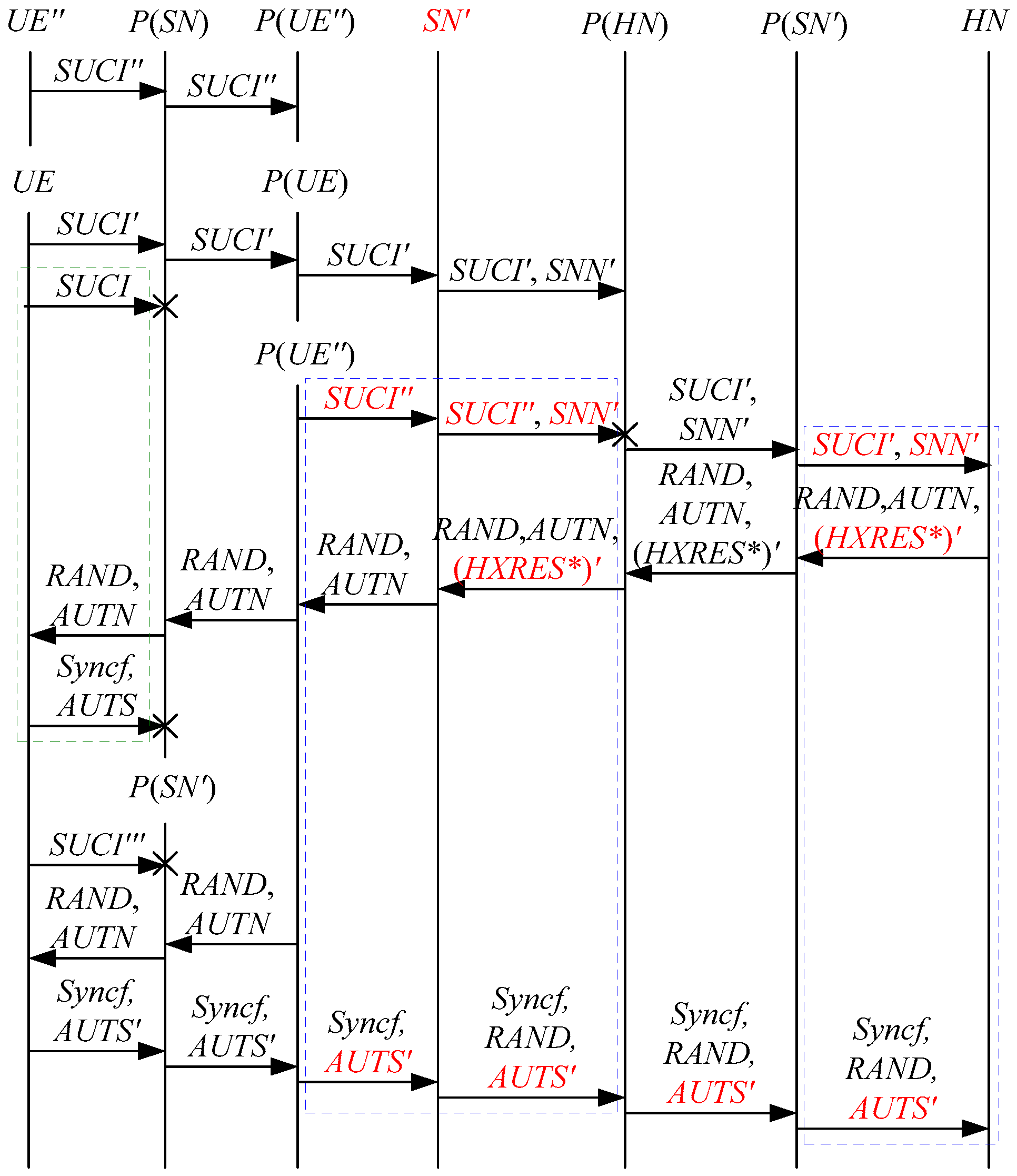
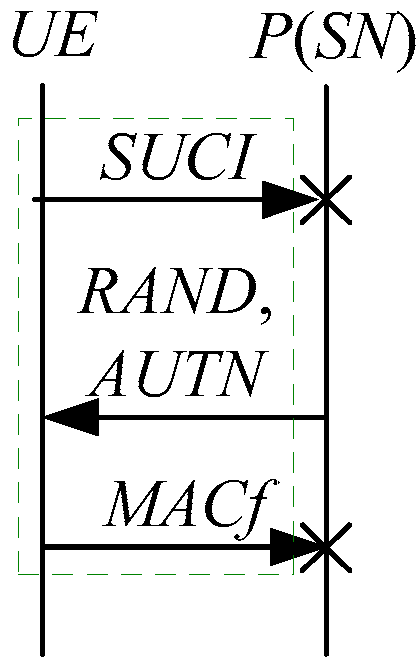
According to Theorem 3, the corresponding attack scenario can be obtained as shown in Figure 11.
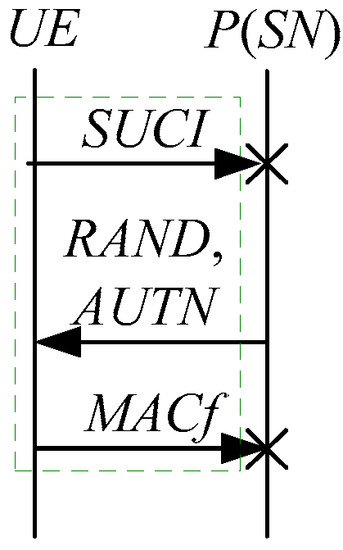
Figure 11.
The tenth attack scenario of the 5G AKA protocol.
In Figure 11, the green dashed box represents the initiator strand of Theorem 3. According to Figure 11, does not authenticate and . The penetrator can perform a masquerading attack, where is forged or tampered by . In the other words, the penetrator can forge or tamper with to make the UE respond to a “MAC failure” indication, resulting in authentication failure. This is also called MAC failure attacks. That is to say, the authentication fails, resulting in a new authentication and key agreement process.
3.3. The Server’s Guarantee of the 5G AKA Protocol
Theorem 4.
Suppose: (1) is a space for the 5G AKA protocol, and is a bundle containing a server strand , , , , , , , , , , , ; (2) and , where denotes any authorized SN; (3) is uniquely originating in . Then, contains an initiator strand , , , , , , and a responder strand , , , , , , , , , , , , where , and is generated for .
Proof of Theorem 4.
By assumption (2), . Since and , and , so . Hence, must originate on an initiator strand , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , . By assumption (2), , so must originate on a responder strand , , , , , , , , , , , , where and is generated for . Since , must originate on a server strand . Since is uniquely originating in , , so . Hence, , , , , , , , , , , , . □
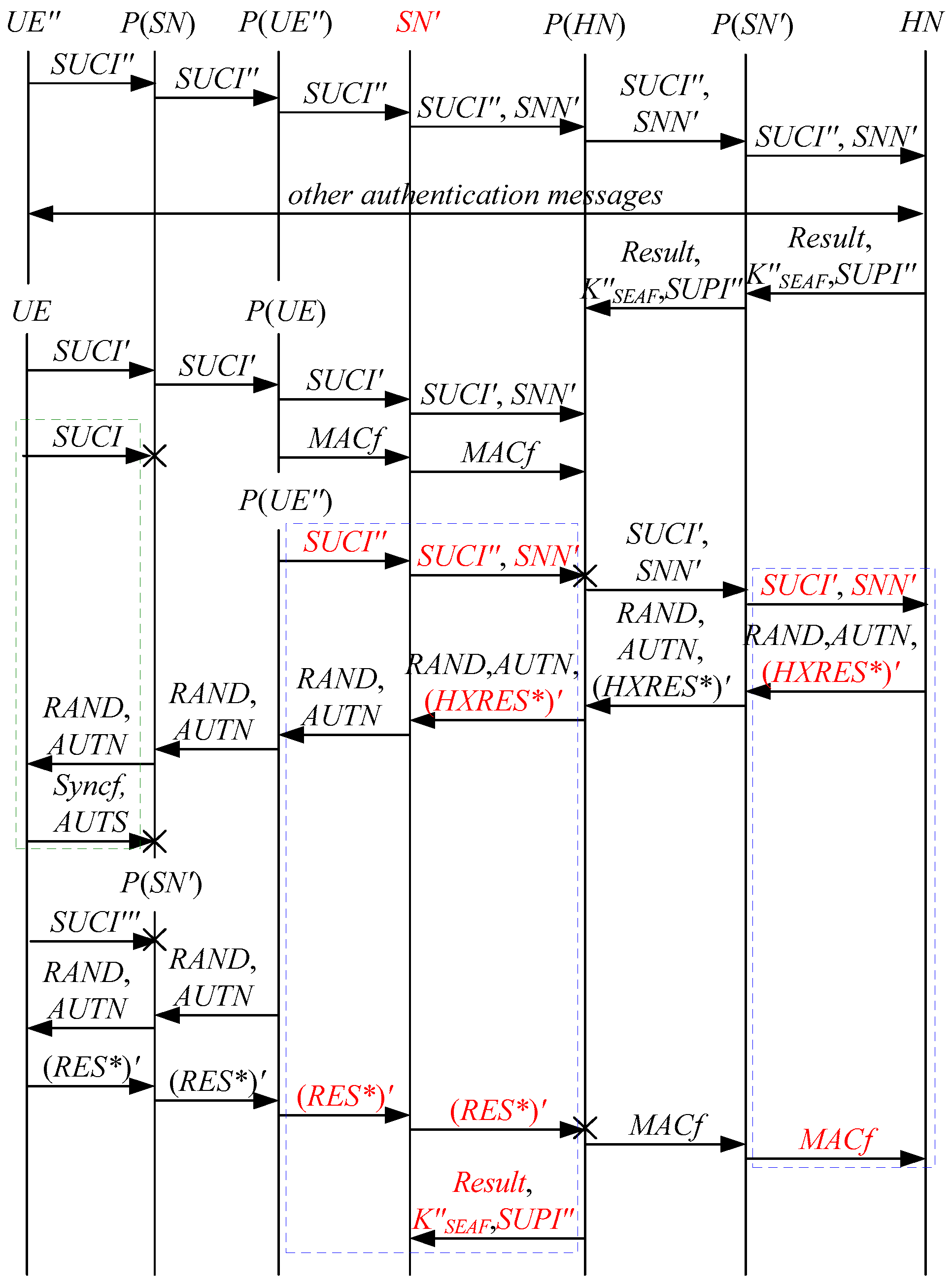
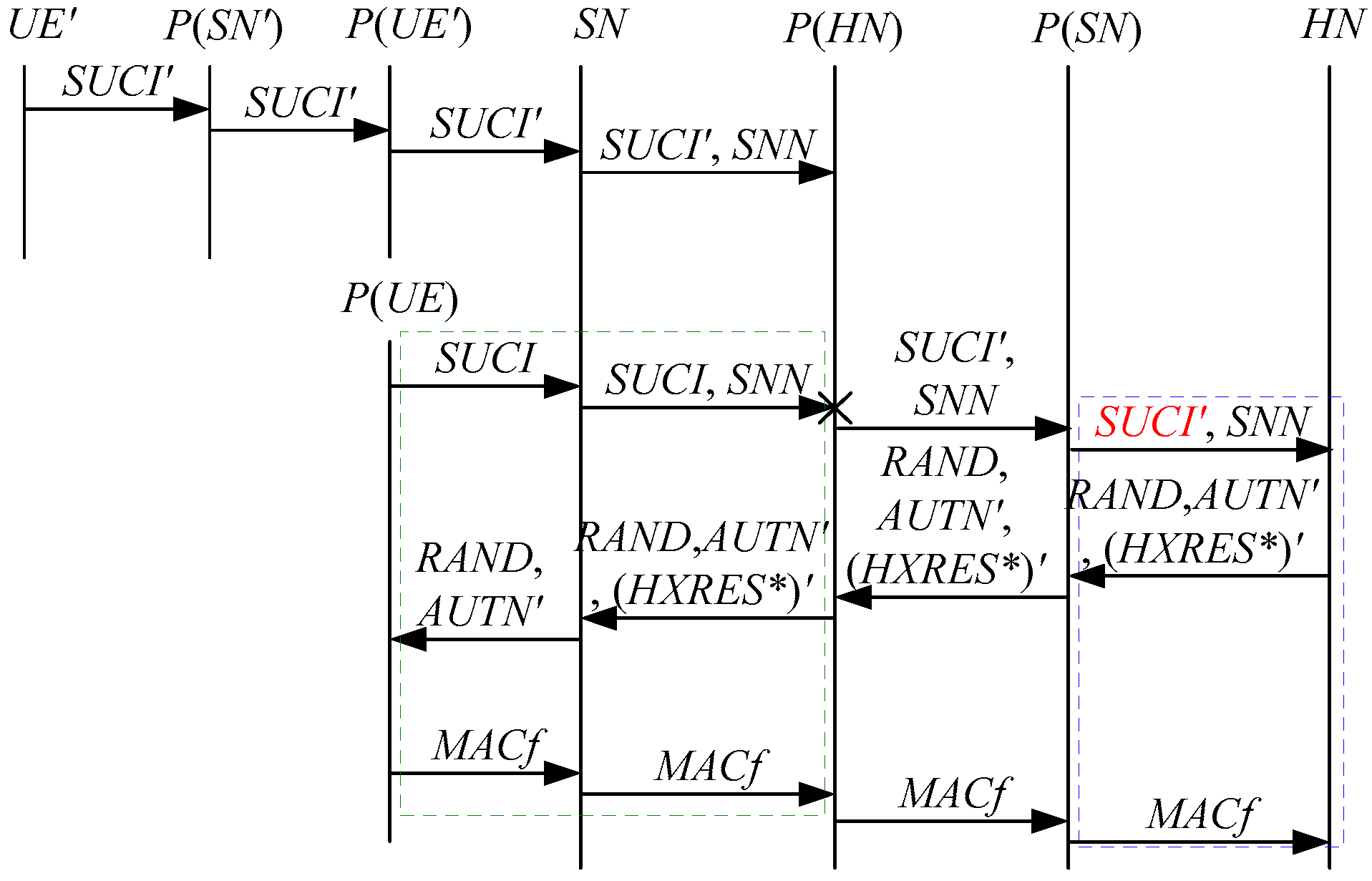
According to Theorem 4, the corresponding attack scenario can be obtained as shown in Figure 12, where the messages between the HN and the authorized SN are protected by their session key.
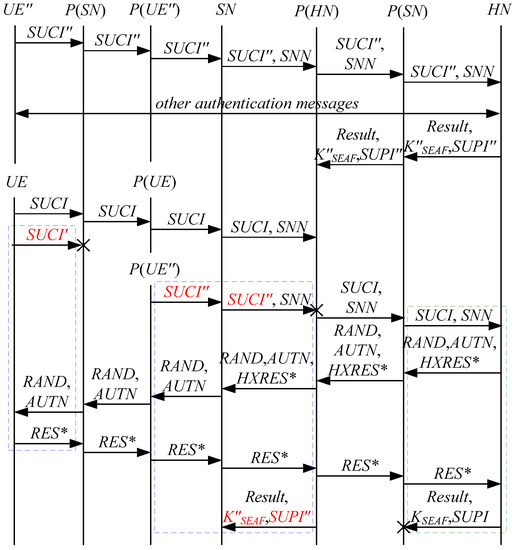
Figure 12.
The eleventh attack scenario of the 5G AKA protocol.
In Figure 12, the green dashed box represents the server strand of Theorem 4, while the blue dashed boxes represent the initiator strand and the responder strand of Theorem 4. The fields marked in red on the initiator strand and the responder strand are some fields that cannot be agreed with the HN, which are caused by MitM attacks.
According to Figure 12, successfully authenticates and , but some specific attacks can be found as follows:
- (1)
- cannot find that is replayed, which is not equal to and . This is because does not contain the challenge of the HN (i.e., ). That is to say, the replay attacks on the HN can be formed, resulting in the energy consumption ion of the HN.
- (2)
- and cannot be agreed with the HN because the HN does not send and together with , which makes that and can be a replayed key and a replayed SUPI, respectively. That is to say, the key agreement fails, resulting in a new authentication and key agreement process.
Theorem 5.
Suppose: (1) is a space for the 5G AKA protocol, and is a bundle containing a server strand , , , , , , , , , ; (2) and , where denotes any authorized SN; (3) is uniquely originating in . Then, contains an initiator strand , , , , , , , and a responder strand , , , , , , , , , , where and .
Proof of Theorem 5.
By assumption (2), , so must originate on an initiator strand , , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , , . By assumption (2), , so must originate on a responder strand , , , , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , , , , . □
According to Theorem 5, the corresponding attack scenario can be obtained as shown in Figure 13, where the messages between the HN and the authorized SN are protected by their session key.
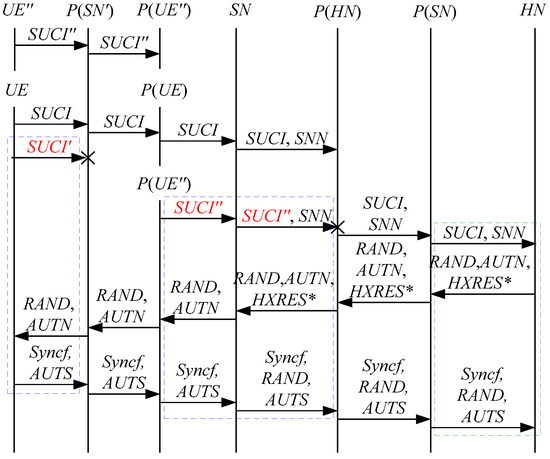
Figure 13.
The twelfth attack scenario of the 5G AKA protocol.
In Figure 13, the green dashed box represents the server strand of Theorem 5, while the blue dashed boxes represent the initiator strand and the responder strand of Theorem 5. The fields marked in red on the initiator strand and the responder strand are some fields that cannot be agreed with the HN, which are caused by MitM attacks.
According to Figure 13, successfully authenticates and . However, cannot find that is replayed, which is not equal to and . This is because does not contain the challenge of the HN (i.e., ). That is to say, the replay attacks on the HN can be formed, resulting in the energy consumption ion of the HN.
Theorem 6.
Suppose: (1) is a space for the 5G AKA protocol, and is a bundle containing a server strand , , , , , , , , ; (2) , where denotes any authorized SN. Then, contains a responder strand , , , , , , , , , where .
Proof of Theorem 6.
By assumption (2), , so must originate on a responder strand , , , , , , , , , where . □
According to Theorem 6, the corresponding attack scenario can be obtained as shown in Figure 14, where the messages between the HN and the authorized SN are protected by their session key.
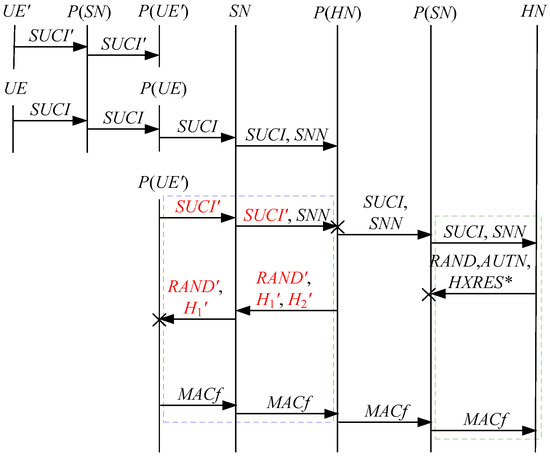
Figure 14.
The thirteenth attack scenario of the 5G AKA protocol.
In Figure 14, the green dashed box represents the server strand of Theorem 6, while the blue dashed box represents the responder strand of Theorem 6. The fields marked in red on the responder strand are some fields that cannot be agreed with the HN, which are caused by MitM attacks.
According to Figure 14, successfully authenticates , but only authenticates based on , and some specific attacks can be found as follows.
- (1)
- cannot find that is replayed, which is not equal to . This is because does not contain the challenge of the HN (i.e., ). That is to say, the replay attacks on the HN can be formed, resulting in the energy consumption ion of the HN.
- (2)
- The penetrator directly sends to the SN to make authentication failure. That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (3)
- The responder strand of Theorem 6 may exist in the past run of the protocol because it does not contain the challenge of the HN, i.e., on the HN of Theorem 6 can be a replayed message, resulting in a replay attack. In the other words, the penetrator replays an encrypted between the SN and the HN to make an authentication failure. That is to say, the authentication fails, resulting in a new authentication and key agreement process.
3.4. The Responder’s Guarantee of the 5G AKA Protocol
Theorem 7.
Suppose: (1) is a space for the 5G AKA protocol, and is a bundle containing a responder strand , , , , , , , , , , , ; (2) and , where denotes any authorized SN and denotes a pre-shared key between and any authorized ; (3) is uniquely originating in . Then, contains a unique server strand , , , , , , , , , , , and an initiator strand , , , , , , , where , , , , , and is generated for . Alternatively, contains a unique server strand , , , , , , , , and an initiator strand , , , , , , , where , , and .
Proof of Theorem 7.
By assumptions (2) and (3), and are uniquely originating in , so must uniquely originate on a server strand according to Definitions 1 to 4.
- (1)
- If is a server strand of Definition 1, then , , , , , , , , , , , , where , , , , and is generated for . By assumption (2), . Since and , and , so . Hence, must originate on an initiator strand , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , .
- (2)
- If is a server strand of Definition 2, then , , , , , , , , , , where , , , and . By Definition 1, . By assumption (2), . Since and , and , so . Hence, must originate on an initiator strand , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , . By assumption (2), , so must originate on an initiator strand , , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , , . By Definition 1, on . However, on according to Definition 2. Therefore, and cannot be in the same run of the protocol, so or must exist in the past run of the protocol. Since or exists in the past run of the protocol, must exist in the past run of the protocol. Because originates on , must exist in the past run of the protocol, so must exist in the current run of the protocol. However, it is impossible from to because increases. That is to say, it is impossible that exists in the past run of the protocol and exists in the current run of the protocol. Hence, is not a server strand of Definition 2.
- (3)
- If is a server strand of Definition 3, then , , , , , , , , , where , and . By Definition 1, . By assumption (2), . Since and , and , so . Hence, must originate on an initiator strand , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , . □
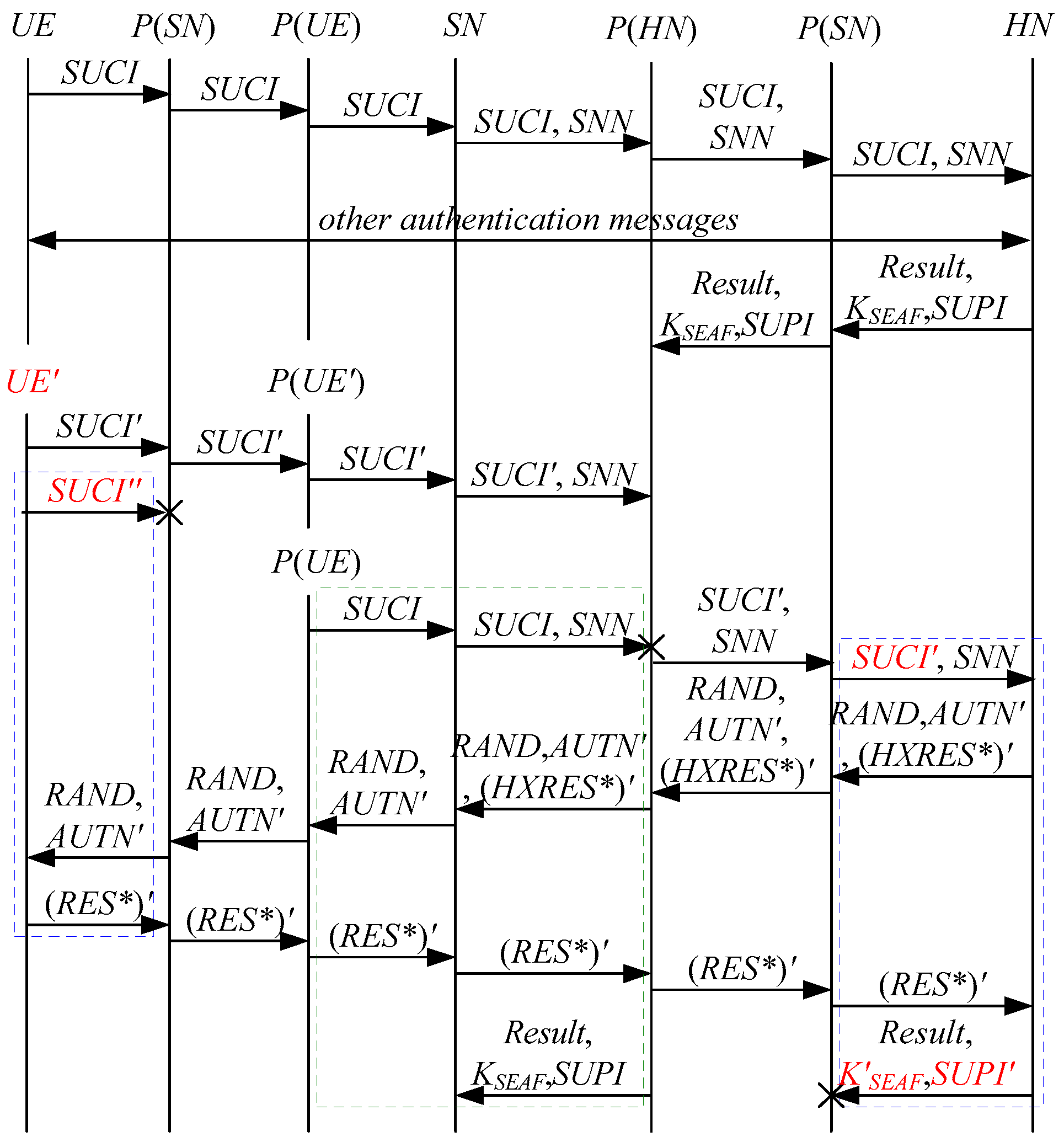
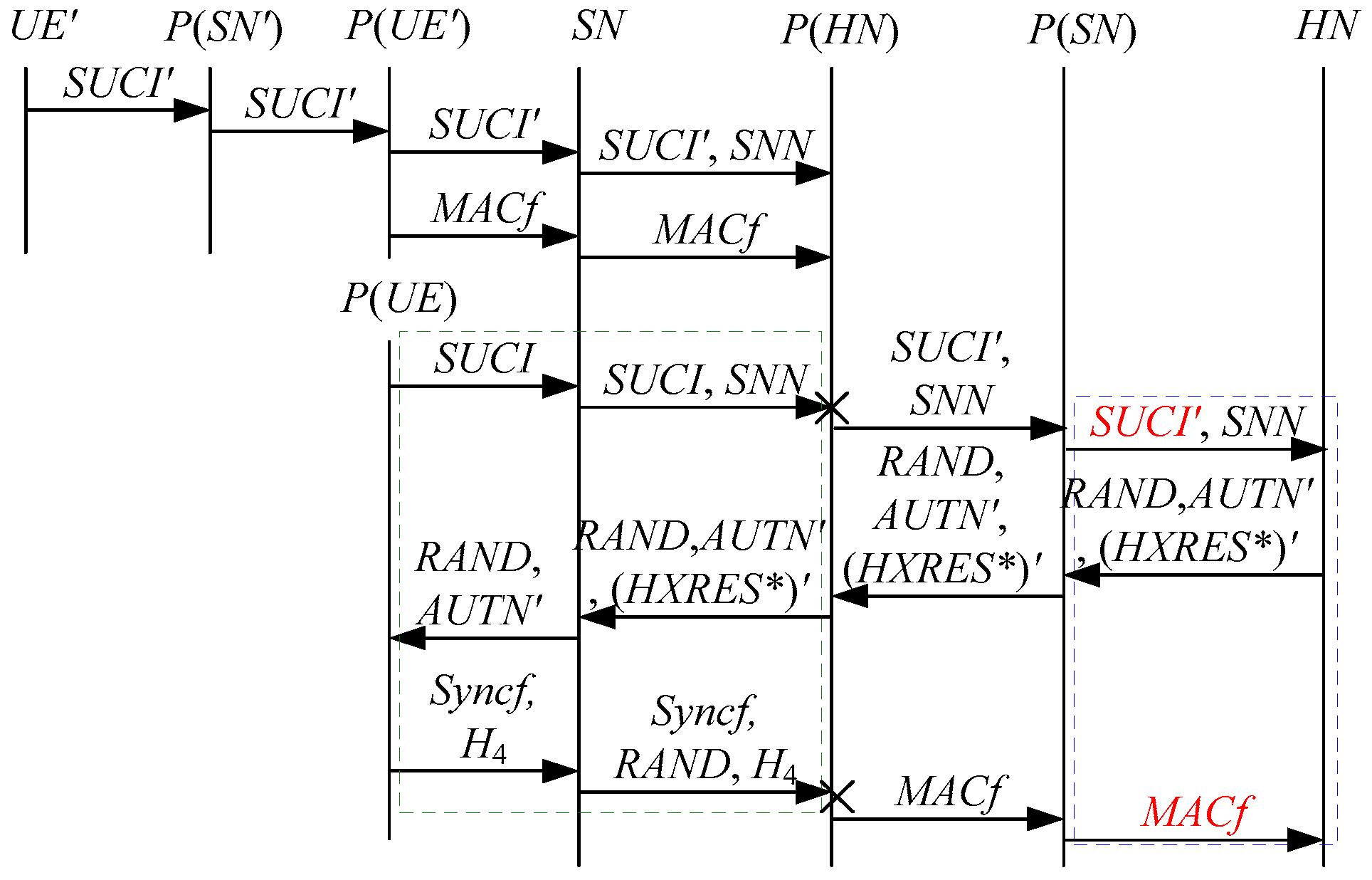
According to Theorem 7, the corresponding attack scenarios can be obtained as shown in Figure 15 and Figure 16, where the messages between the HN and the authorized SN are protected by their session key.
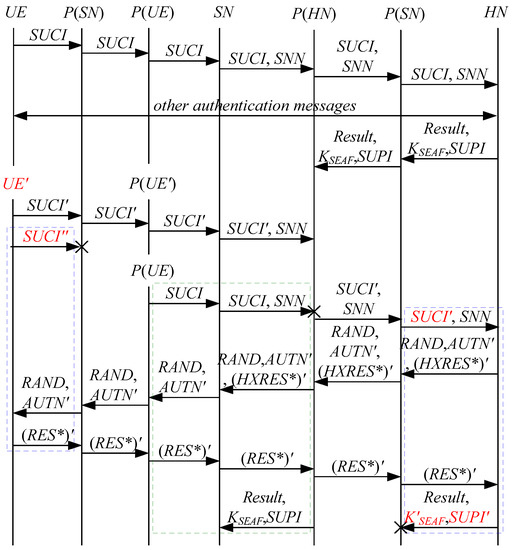
Figure 15.
The fourteenth attack scenario of the 5G AKA protocol.
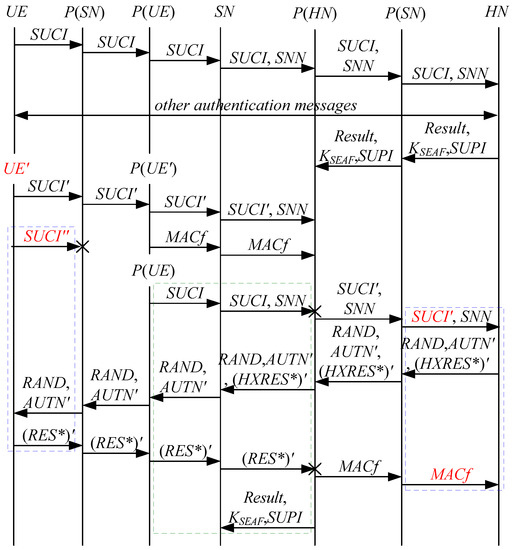
Figure 16.
The fifteenth attack scenario of the 5G AKA protocol.
In Figure 15 and Figure 16, the green dashed box represents the responder strand of Theorem 7, while the blue dashed boxes represent the initiator strand and the server strand of Theorem 7. The fields marked in red on the initiator strand and the server strand are some fields that cannot be agreed with the SN, which are caused by MitM attacks.
- (1)
- successfully authenticates , but does not authenticate . This is because cannot inspect , and , and is not sent with , which means that , and can be related to rather than . Accordingly, is included in and , and is related to . That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (2)
- In Figure 16, there are interactions between different cases of the 5G AKA protocol, i.e., cross attacks. They are caused by the penetrators taking advantage of . The penetrator replays an encrypted between the SN and the HN to make authentication failure, i.e., MAC failure attacks. That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (3)
- The initiator strand and the server strand of Theorem 7 may exist in the past run of the protocol because they do not contain the challenge of the SN, i.e., the messages received by the SN can be replayed messages. As a result, the penetrator can impersonate the UE and the HN to complete the entire 5G AKA protocol with the SN, forming DoS attacks on the SN. This results in the energy consumption ion of the SN.
Theorem 8.
Suppose: (1) is a space for the 5G AKA protocol, and is a bundle containing a responder strand , , , , , , , , , ; (2) and , where denotes any authorized SN and denotes a pre-shared key between and any authorized ; (3) is uniquely originating in . Then, contains a unique server strand , , , , , , , , , , , and an initiator strand , , , , , , , where , , , , , and is generated for . Alternatively, contains a unique server strand , , , , , , , , , and an initiator strand , , , , , , , , where , , , , and . Alternatively, contains a unique server strand , , , , , , , , , where , and .
Proof of Theorem 8.
By assumptions (2) and (3), and are uniquely originating in , so must uniquely originate on a server strand according to Definitions 1 to 4.
- (1)
- If is a server strand of Definition 1, then , , , , , , , , , , , , where , , , , and is generated for . By assumption (2), . Since and , and , so . Hence, must originate on an initiator strand , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , .
- (2)
- If is a server strand of Definition 2, then , , , , , , , , , , where , , , and . By assumption (2), , so must originate on an initiator strand , , , , , , , , where and . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , , .
- (3)
- If is a server strand of Definition 3, then , , , , , , , , , where , and . □
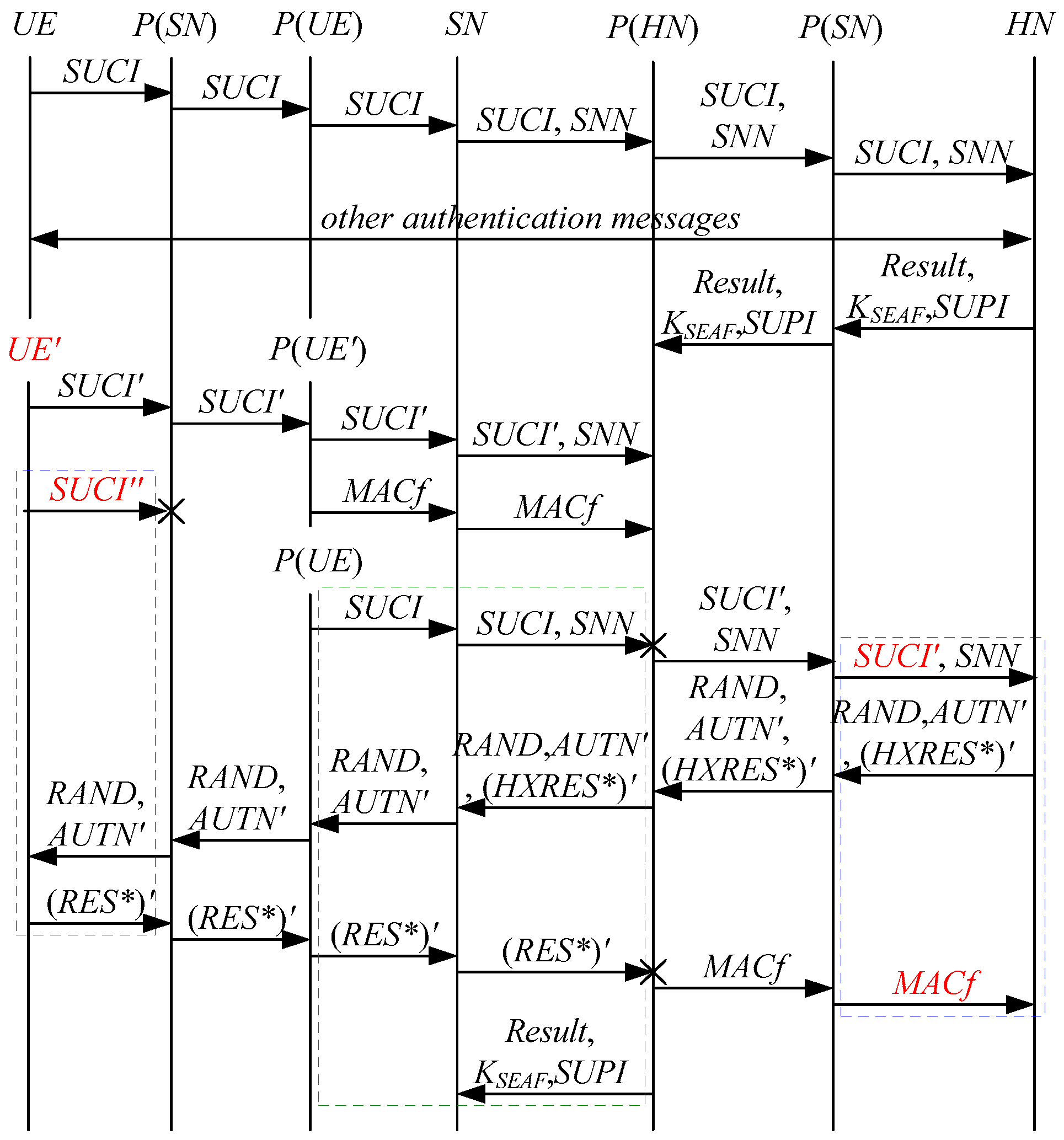
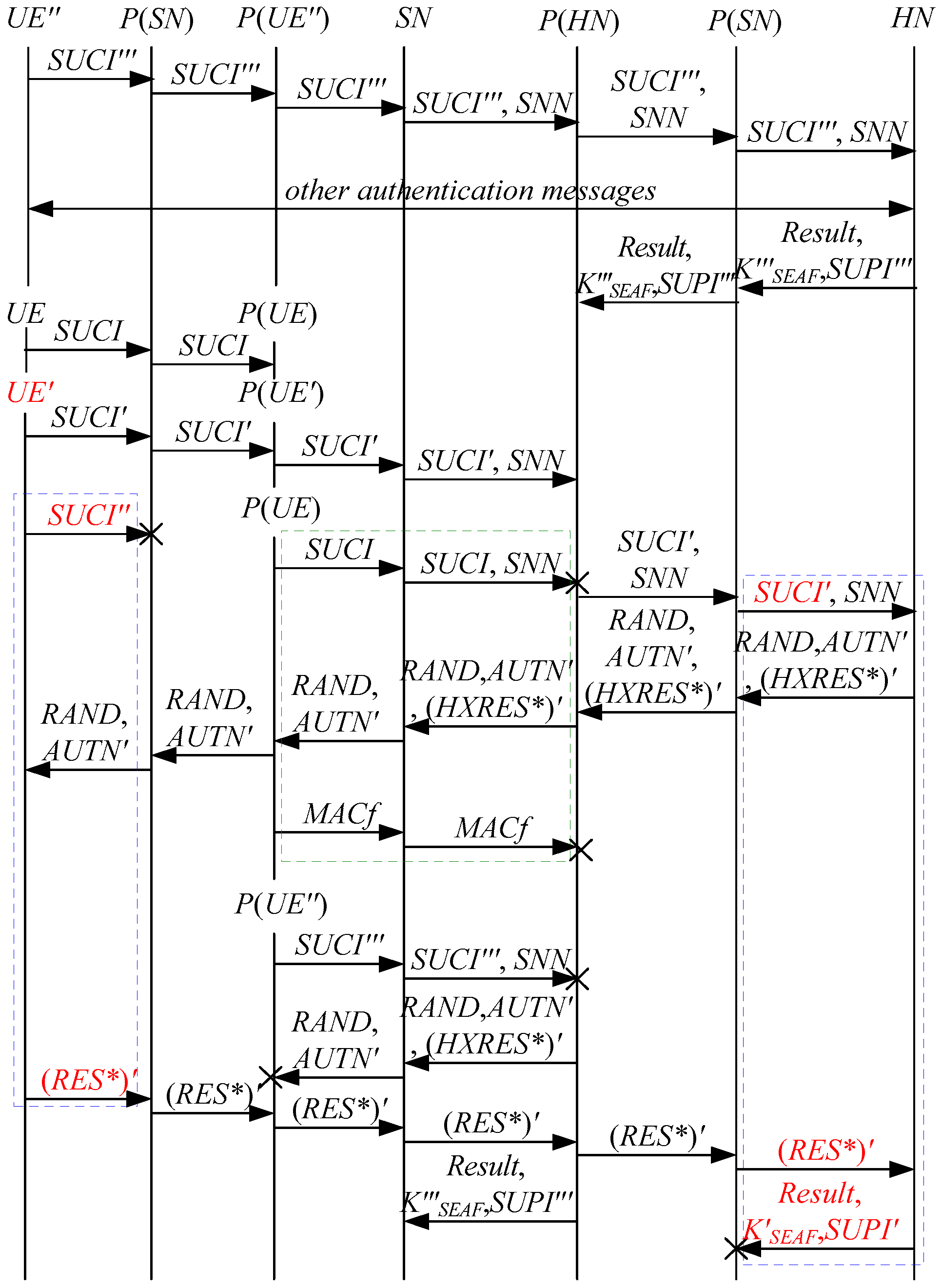
According to Theorem 8, the corresponding attack scenarios can be obtained, as shown in Figure 17, Figure 18 and Figure 19, where the messages between the HN and the authorized SN are protected by their session key.
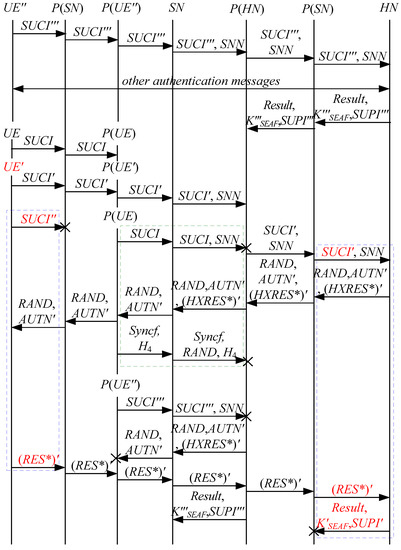
Figure 17.
The sixteenth attack scenario of the 5G AKA protocol.
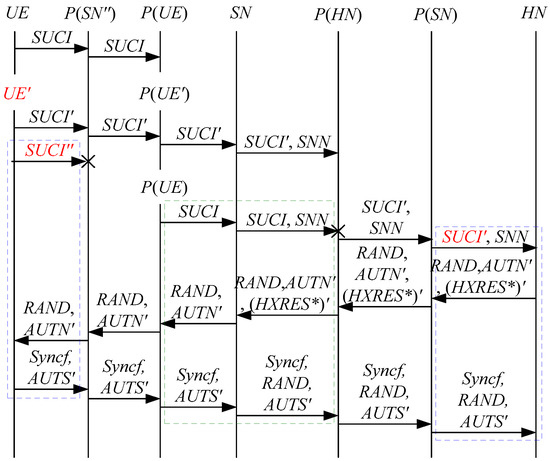
Figure 18.
The seventeenth attack scenario of the 5G AKA protocol.
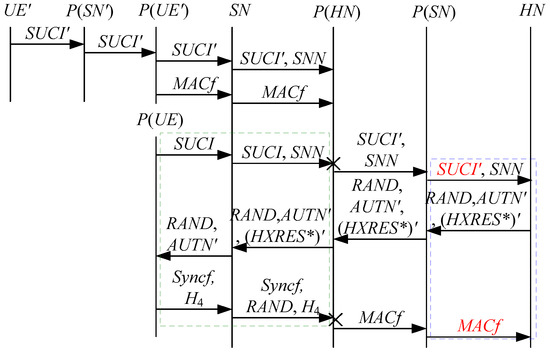
Figure 19.
The eighteenth attack scenario of the 5G AKA protocol.
In Figure 17, Figure 18 and Figure 19, the green dashed box represents the responder strand of Theorem 8, while the blue dashed boxes represent the initiator strand and the server strand of Theorem 8. The fields marked in red on the initiator strand and the server strand are some fields that cannot be agreed with the SN, which are caused by MitM attacks.
- (1)
- successfully authenticates , but does not authenticate . This is because cannot inspect , and , which means that , and can be related to rather than . Accordingly, is included in and , and is related to . That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (2)
- (3)
- In Figure 19, the penetrator replays an encrypted between the SN and the HN to make authentication failure, i.e., MAC failure attacks. That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (4)
- The initiator strand and the server strand of Theorem 8 may exist in the past run of the protocol, i.e., the messages received by the SN can be replayed messages. As a result, the penetrator can impersonate the UE and the HN to complete the entire 5G AKA protocol with the SN, forming DoS attacks on the SN. This results in the energy consumption ion of the SN.
Theorem 9.
Suppose: (1) is a space for the 5G AKA protocol, and is a bundle containing a responder strand , , , , , , , , ; (2) and , where denotes any authorized SN and denotes a pre-shared key between and any authorized ; (3) is uniquely originating in . Then, contains a unique server strand , , , , , , , , , , , and an initiator strand , , , , , , , where , , , , , and is generated for . Alternatively, contains a unique server strand , , , , , , , , , and an initiator strand , , , , , , , , where , , , , and . Alternatively, contains a unique server strand , , , , , , , , , where , , , , and .
Proof of Theorem 9.
It is the same as Theorem 8. □
According to Theorem 9, the corresponding attack scenarios can be obtained as shown in Figure 20, Figure 21 and Figure 22, where the messages between the HN and the authorized SN are protected by their session key.
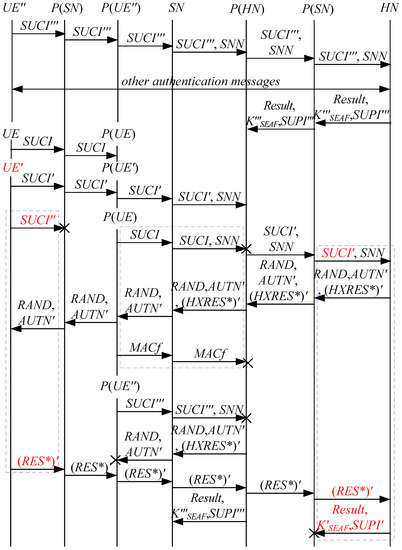
Figure 20.
The nineteenth attack scenario of the 5G AKA protocol.
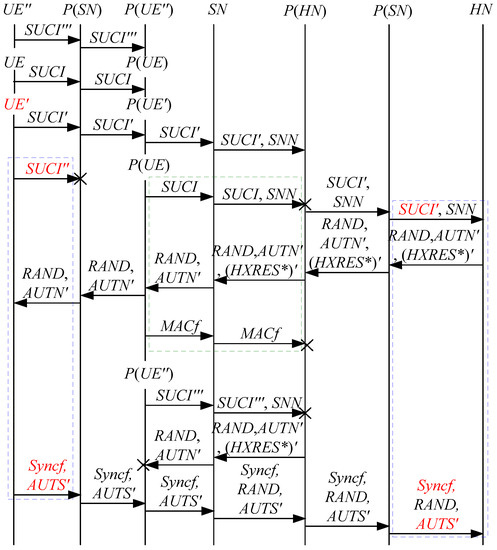
Figure 21.
The twentieth attack scenario of the 5G AKA protocol.
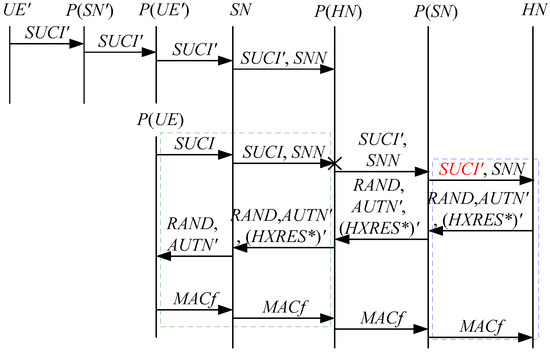
Figure 22.
The twenty-first attack scenario of the 5G AKA protocol.
In Figure 20, Figure 21 and Figure 22, the green dashed box represents the responder strand of Theorem 9, while the blue dashed boxes represent the initiator strand and the server strand of Theorem 9. The fields marked in red on the initiator strand and the server strand are some fields that cannot be agreed with the SN, which are caused by MitM attacks.
- (1)
- successfully authenticates , but does not authenticate . This is because cannot inspect , and , which makes that , and can be related to rather than . Accordingly, is included in and , and is related to . That is to say, the authentication fails, resulting in a new authentication and key agreement process.
- (2)
- (3)
- (4)
- The initiator strand and the server strand of Theorem 9 may exist in the past run of the protocol, i.e., the messages received by the SN can be replayed messages. As a result, the penetrator can impersonate the UE and the HN to complete the entire 5G AKA protocol with the SN, thus forming DoS attacks on the SN. This results in the energy consumption ion of the SN.
4. Our Proposed 5G-AKA’ Protocol and Its Security Analysis
4.1. The 5G-AKA’ Protocol
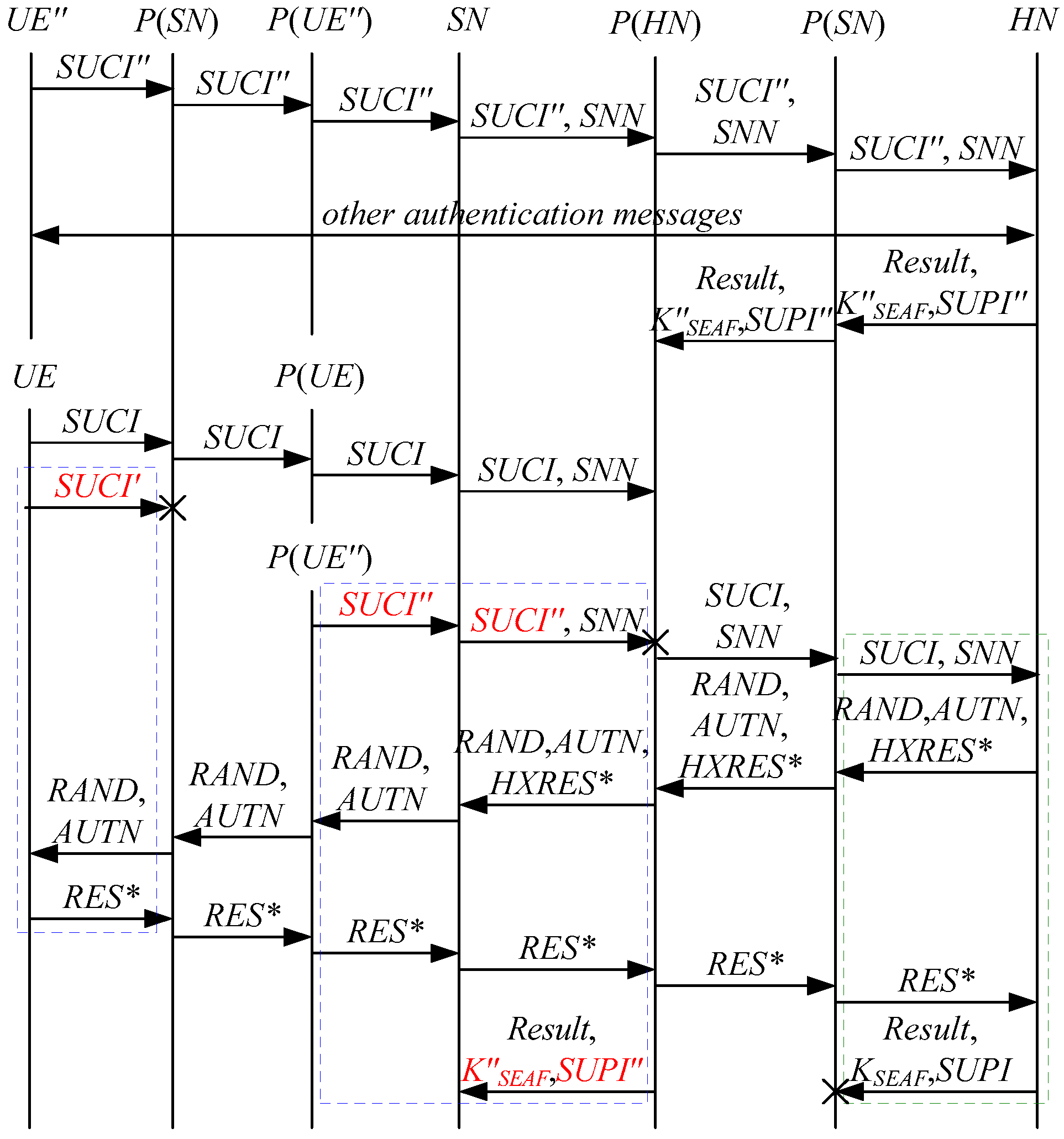
In order to overcome the above security problems of the latest version of the 5G AKA protocol, we propose a 5G-AKA’ protocol, which is illustrated in Figure 23.
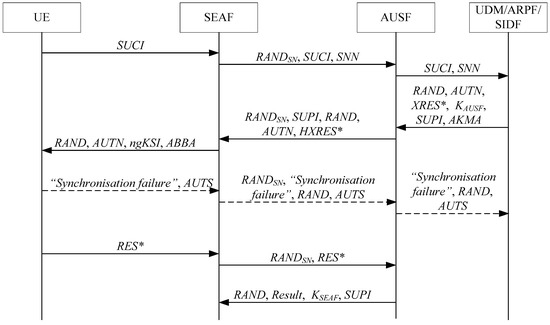
Figure 23.
Our proposed 5G-AKA’ protocol.
Compared with the latest version of the 5G AKA protocol, the main improvements of our proposed 5G-AKA’ protocol are as follows:
- To cryptographically bind and to , and protect , we replace with on the UE and the HN.where is a base key derived from .
- To prevent DoS attacks on the SN, we add the challenge–response mechanism between the SN and the HN. In detail, we add to the first three messages between the SEAF (located in the SN) and the AUSF (located in the HN) and add to the fourth message between the SEAF and the AUSF, where is an unpredictable challenge of the SEAF;
- Add to the second message between the SEAF and the AUSF, matching with in the first message between them;
- In the latest version of the 5G AKA protocol, is used to initiate a new authentication procedure for the UE. However, it causes a large number of attacks according to the above security analysis. Hence, we use a timeout mechanism on the HN instead of to initiate a new authentication procedure towards the UE. That is to say, if and are different, then the UE directly discards the receives , and the HN will initiate a new authentication procedure towards the UE when the HN does not receive an authentication response message or a synchronization failure message within a certain period of time.
According to the above descriptions, our proposed 5G-AKA’ protocol can be summarized into two cases as follows:
Case (I): the verification of succeeds and the authentication is successful. The steps of this case are as follows:
- : ;
- : ;
- : ;
- : ;
- : ;
- : ;
- : .
where , and are three messages exchanged between the UE and SN, , , and are four messages exchanged between the SN and the HN.
Case (II): the verification of fails and it is a synchronization failure. The steps of this case are as follows:
- : ;
- : ;
- : ;
- : ;
- : ;
- : .
where , and are three messages exchanged between the UE and SN, , and are three messages exchanged between the SN and the HN.
In the above cases, is replaced with . Similarly, we use the mixed strand space model [28] to analyze the security of our proposed 5G-AKA’ protocol as follows.
4.2. Mixed Strand Space for the 5G-AKA’ Protocol
Definition 5.
A regular strand space is a space for case I of the 5G-AKA’ protocol if is the union of three kinds of strands: (1) Initiator strands , , , , , , with trace: , , . The principal associated with this strand is . computed locally is equal to and is in the correct range (i.e., ); (2) Responder strands , , , , , , , , , , , , with trace: , , , , , , . The principal associated with this strand is . , and are three messages that are not inspected by , where ; (3) Server strands , , , , , , , , , , , , with trace: , , , . The principal associated with this strand is .
Definition 6.
A regular strand space is a space for case II of the 5G-AKA’ protocol if is the union of three kinds of strands: (1) Initiator strands , , , , , , , with trace: , , . The principal associated with this strand is . computed locally is equal to , but is not in the correct range (i.e., ); (2) Responder strands , , , , , , , , , , , with trace: , , , , , . The principal associated with this strand is . , and are three messages that are not inspected by ; (3) Server strands , , , , , , , , , , , with trace: , , . The principal associated with this strand is .
Definition 7.
An infiltrated strand space is a space for the 5G-AKA’ protocol if , where penetrator strands [28,29,30].
Definition 5 gives a regular strand space for case I of the 5G-AKA’ protocol (i.e., ), including initiator strands, responder strands and server strands for case I of the 5G-AKA’ protocol. Definition 6 gives a regular strand space for case II of the 5G-AKA’ protocol (i.e., ), including initiator strands, responder strands and server strands for case II of the 5G AKA protocol. Definition 7 gives an infiltrated mixed strand space for the 5G-AKA’ protocol, including , and penetrator strands (i.e., ).
4.3. The Initiator’s Guarantee of the 5G-AKA’ Protocol
Theorem 10.
Suppose: (1) is a space for the 5G-AKA’ protocol, and is a bundle containing an initiator strand , , , , , , ; (2) and ; (3) , , is uniquely originating in . Then, contains a unique server strand , , , , , , , , , , , , and a unique responder strand , , , , , , , , , , , , .
Proof of Theorem 10.
Since , according to assumption (2). Because and is uniquely originating in , must uniquely originate on a server strand according to Definitions 5 to 7.
- (1)
- If is a server strand of Definition 5, then , , , , , , , , , , , , . By assumptions (2) and (3), and are uniquely originating in , so must originate on a unique responder strand , , , , , , , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so , and . Since , must originate on a server strand . Since is uniquely originating in , , so . Since , must originate on a responder strand . Since is uniquely originating in , , so . Hence, , , , , , , , , , , , , .
- (2)
- If is a server strand of Definition 6, then , , , , , , , , , , , , where . Since , must originate on an initiator strand , , , , , , , , , so originates on . By assumptions (1) and (2), originates on . Since is uniquely originating in , . However, and , . Hence, is not a server strand of Definition 6. □
Theorem 11.
Suppose: (1) is a space for the 5G-AKA’ protocol, and is a bundle containing an initiator strand , , , , , , , ; (2) and ; (3) , , is uniquely originating in . Then, contains a unique server strand , , , , , , , , , , , and a unique responder strand , , , , , , , , , , , .
Proof of Theorem 11.
Since , according to assumption (2). Because and are uniquely originating in , must uniquely originate on a server strand according to Definitions 5 to 7.
- (1)
- If is a server strand of Definition 5, then , , , , , , , , , , , , . Since , and , so . Hence, must originate on an initiator strand , , , , , , , so originates on . By assumptions (1) and (2), originates on . Since is uniquely originating in , . However, and , . Hence, is not a server strand of Definition 5.
- (2)
- If is a server strand of Definition 6, then , , , , , , , , , , , , where . Since , must originate on an initiator strand . Since is uniquely originating in , , so and . Hence, , , , , , , , , , , , . By assumptions (2) and (3), and are uniquely originating in , so must originate on a unique responder strand , , , , , , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so , , and . Since , must originate on a responder strand . Since is uniquely originating in , , so . Hence, , , , , , , , , , , , . □
According to Theorems 10 and 11, successfully authenticates and , and all fields except on the sever strand and the responder are agreed with the UE. is unknowable to the UE because it is mainly used for the challenge–response mechanism between the SN and the HN, which does not affect the security of the 5G-AKA’ protocol. Hence, MitM attacks are prevented.
In addition, those attacks in Section 3.2 are overcome as follows:
- (1)
- Since is used to calculate , the challenge of the UE (i.e., ), the pre-shared key between the UE and the HN (i.e., ) and are included in . As a result, can find whether is replayed, successfully authenticates and , and on the UE cannot be replayed, making that the location privacy of the UE cannot be compromised.
- (2)
- Since is replaced with a timeout mechanism on the HN, MAC failure attacks are prevented. Further, on the UE cannot be replayed maliciously to generate . As a result, the penetrator cannot take advantage of and to performed cross attacks.
4.4. The Server’s Guarantee of the 5G-AKA’ Protocol
Theorem 12.
Suppose: (1) is a space for the 5G-AKA’ protocol, and is a bundle containing a server strand , , , , , , , , , , , , ; (2) and ; (3) , , is uniquely originating in . Then, contains a unique initiator strand , , , , , , and a unique responder strand , , , , , , , , , , , , .
Proof of Theorem 12.
Since , according to assumption (2). Because and , and , so . By assumption (3), is uniquely originating in , so must originate on a unique initiator strand , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , . By assumptions (2) and (3), and are uniquely originating in , so must originate on a unique responder strand , , , , , , , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so , and . Since , must originate on a server strand . Since is uniquely originating in , , so . Since , must originate on a responder strand . Since is uniquely originating in , , so . Hence, , , , , , , , , , , , , . □
Theorem 13.
Suppose: (1) is a space for the 5G-AKA’ protocol, and is a bundle containing a server strand , , , , , , , , , , , ; (2) and ; (3) , , is uniquely originating in . Then, contains a unique initiator strand , , , , , , , and a unique responder strand , , , , , , , , , , , .
Proof of Theorem 13.
Since , according to assumption (2). By assumption (3), is uniquely originating in , so must originate on a unique initiator strand , , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , , . By assumptions (2) and (3), and are uniquely originating in , so must originate on a unique responder strand , , , , , , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so , , and . Since , must originate on a responder strand . Since is uniquely originating in , , so . Hence, , , , , , , , , , , , . □
According to Theorems 12 and 13, successfully authenticates and , and all fields on the initiator strand and the responder are agreed with the HN, so MitM attacks are prevented.
In addition, those attacks in Section 3.3 are overcome as follows:
- (1)
- Although cannot find that is replayed because does not contain the challenge of the HN (i.e., ), can find whether is replayed because is used to calculate . Hence, this does not affect the security of the 5G-AKA’ protocol.
- (2)
- Since is replaced with a timeout mechanism on the HN, MAC failure attacks are prevented.
- (3)
- Since the HN sends and together with , they can be agreed with the HN.
4.5. The Responder’s Guarantee of the 5G-AKA’ Protocol
Theorem 14.
Suppose: (1) is a space for the 5G-AKA’ protocol, and is a bundle containing a responder strand , , , , , , , , , , , , ; (2) and ; (3) , , is uniquely originating in . Then, contains a unique server strand , , , , , , , , , , , , and a unique initiator strand , , , , , , .
Proof of Theorem 14.
By assumptions (2) and (3), and are uniquely originating in , so must uniquely originate on a server strand according to Definitions 5 to 7.
- (1)
- If is a server strand of Definition 5, then , , , , , , , , , , , , , where , , , , and is generated for . Since , must originate on a server strand . Since is uniquely originating in , , so . Since , must originate on a responder strand . Since is uniquely originating in , , so and according to assumption (1). As a result, , and . Hence, , , , , , , , , , , , , . Since , according to assumption (2). Because and , and , so . By assumption (3), is uniquely originating in , so must originate on a unique initiator strand , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , .
- (2)
- If is a server strand of Definition 6, then , , , , , , , , , , , , where , , and . Since , must originate on a responder strand , , , , , , , , , , , , so originates on . By assumptions (1) and (2), originates on . Since is uniquely originating in , . However, and , . Hence, is not a server strand of Definition 6. □
Theorem 15.
Suppose: (1) is a space for the 5G-AKA’ protocol, and is a bundle containing a responder strand , , , , , , , , , , , ; (2) and ; (3) , , is uniquely originating in . Then, contains a unique server strand , , , , , , , , , , , and a unique initiator strand , , , , , , , .
Proof of Theorem 15.
By assumptions (2) and (3), and and uniquely originating in , so must uniquely originate on a server strand according to Definitions 5 to 7.
- (1)
- If is a server strand of Definition 5, then , , , , , , , , , , , , , where , , , , and is generated for . Since , must originate on a unique responder strand , , , , , , , , , , , , , so originates on . By assumptions (1) and (2), originates on . Since is uniquely originating in , . However, and , . Hence, is not a server strand of Definition 5.
- (2)
- If is a server strand of Definition 6, then , , , , , , , , , , , , where , , and . Since , must originate on a responder strand . Since is uniquely originating in , , so and according to assumption (1). As a result, , and . Hence, , , , , , , , , , , , . Since , according to assumption (2). By assumption (3), is uniquely originating in , so must originate on a unique initiator strand , , , , , , , , where . Since , must originate on a server strand . Since is uniquely originating in , , so and . Hence, , , , , , , , . □
According to Theorems 14 and 15, successfully authenticates and , and all fields on the initiator strand and the responder are agreed with the HN, so MitM attacks are prevented.
In addition, those attacks in Section 3.4 are overcome as follows:
- (1)
- Since is added to the second message between the SN and the HN, and is added to the fourth message between the SN and the HN, both and on the HN can be agreed with the SN, which means that successfully authenticates and obtains the corresponding .
- (2)
- Since is replaced with a timeout mechanism on the HN, MAC failure attacks are prevented. Further, on the UE cannot be replayed maliciously to generate because . As a result, the penetrator cannot take advantage of and to performed cross attacks.
- (3)
- Since the challenge–response mechanism between the SN and the HN is added, the messages received by the SN cannot be replayed, preventing Dos attacks on the SN.
5. Discussion
5.1. Security of the 5G-AKA’ Protocol
According to the above security analysis of the latest version of the 5G AKA protocol, twenty-one attack scenarios can be obtained, where thirteen attack scenarios are related to . In our proposed 5G-AKA’ protocol, is replaced with a timeout mechanism on the HN, so the thirteen attack scenarios are eliminated. As a result, those attacks in the thirteen attack scenarios are eliminated, including MAC failure attacks.
Without considering , the comparative analysis of authentication properties [28,29,30] between the latest version of the 5G AKA protocol and our proposed 5G-AKA’ protocol is shown in Table 1.

Table 1.
The comparative analysis of authentication properties between the two protocols.
From Table 1, in the latest version of the 5G AKA protocol, only the weaker agreement can be established, and even weak agreement cannot be established in the cases of “UE to SN” and “SN to UE”, because the UE cannot authenticate the SN, and the SN cannot authenticate the UE. However, in our proposed 5G-AKA’ protocol, mutual authentication and injection agreement among the UE, the SN and the HN can be established in all cases according to the security analysis of the 5G-AKA’ protocol.
According to the above security analysis of the latest version of the 5G AKA protocol, based on those missing agreements, the penetrator can perform MitM attacks and cross attacks. Additionally, based on replayed messages, replay attacks and masquerading attacks can be performed, the location privacy of the UE can be compromised and DoS attacks on the SN can be formed. However, according to the above security analysis of the 5G-AKA’ protocol, our proposed 5G-AKA’ protocol has overcome these attacks.
In terms of secrecy properties, the keys established in the latest version of the 5G AKA protocol are secret. However, if is leaked, then the attacker can calculate and based on those messages transmitted in the past run of the protocol. As a result, the attacker can decrypt those encrypted messages transmitted in the past run of the protocol. Therefore, the latest version of the 5G AKA protocol does not provide perfect forward secrecy. However, in our proposed 5G-AKA’ protocol, is replaced with , providing perfect forward secrecy based on Diffie–Hellman exchange.
Therefore, our proposed 5G-AKA’ protocol is secure and can overcome those security problems of the latest version of the 5G AKA protocol. The comparative analysis of security properties between the 5G-AKA’ protocol and some recently improved 5G AKA protocols [22,23,24] is shown in Table 2.

Table 2.
The comparative analysis of security properties between the 5G-AKA’ protocol and some recently improved 5G AKA protocols [22,23,24].
From Table 2, only some security properties can be guaranteed in the 5G AKA protocol and these recently improved 5G AKA protocols, but all security properties can be guaranteed in our proposed 5G-AKA’ protocol.
In [22], contains the challenge of the UE (i.e., ), so the first received message of the UE cannot be a replayed message, preventing the location privacy of the UE from being compromised. However, does not contains , so the UE cannot authenticate the SN. Because the UE and the HN cannot reach an agreement in , MitM attacks can be performed. Since the MAC failure is inherited from the 5G AKA protocol, cross attacks and MAC failure attacks still exist in the protocol of [22]. The received messages of the SN do not contain the challenge of the SN (i.e., ), so these messages can be replayed messages, forming replay attacks, masquerading attacks and Dos attacks on the SN. In addition, and are encrypted, so key secrecy is provided, but perfect forward secrecy cannot be provided because and can be calculated when is leaked.
In [23], the Eph Private key and Eph Public key of the UE, the public/private key pair of the SN and the public/private key pair of the HN are used to ensure the security of the channel between the UE and the SN, the security of channel between the UE and the HN, and the security of channel between the SN and the HN. Since the first received message of the UE is encrypted by the Eph Public key of the UE, this means that the message can only be decrypted by the Eph Private key of the UE, so it cannot be a replayed message, preventing the location privacy of the UE being compromised. However, the other parts fully inherit the 5G AKA protocol, so the other attacks of the 5G AKA protocol still exist in the protocol of [23]. Similarly, perfect forward secrecy cannot be provided.
In [24], both the synchronization failure and the MAC failure are constructed as the format of , making it impossible to distinguish them, so as to prevent the location privacy of the UE from being compromised and prevent cross attacks and MAC failure attacks. However, the other parts fully inherit the 5G AKA protocol, so the other attacks of the 5G AKA protocol still exist in the protocol of [24]. Similarly, perfect forward secrecy cannot be provided.
Therefore, our proposed 5G-AKA’ protocol is better than the 5G AKA protocol, and these recently improved 5G AKA protocols in security.
5.2. Performance of the 5G-AKA’ Protocol
The comparative analysis between the 5G-AKA’ protocol and some recently improved 5G AKA protocols [22,23,24] in the number of messages, the number of fields, the amount of calculation and backward compatibility is shown in Table 3.

Table 3.
The comparative analysis between the 5G-AKA’ protocol and some recently improved 5G AKA protocols [22,23,24] in the number of messages, the number of fields, the amount of calculation and backward compatibility.
In Table 3, MN denotes the number of messages of the 5G AKA protocol. FN denotes the number of fields of the 5G AKA protocol. CA denotes the amount of calculation of the 5G AKA protocol. Note that the number of messages and the number of fields in Table 3 are the number of messages and the number of fields among the UE, the SN and the HN. ECDH denotes the generation and verification of an elliptic curve Diffie–Hellman (ECDH) exchange. PED denotes the encryption and decryption based on a public and private key pair. F denotes the generation and verification of a key function, a key derivation function, a MAC function or a hash function, which are grouped into one category because they have a similar amount of calculation [27]. According to [26], the computation overhead of the generation or verification of an ECDH exchange is 1290 us, the computation overhead of the encryption based on a public key is 2580 us, the computation overhead of the decryption based on a private key is 1750 us, the computation overhead of the hash function based on SHA-256 is 3.8 us, and the computation overhead of the MAC function based on HMAC-SHA256 is 67 us.
In our proposed 5G-AKA’ protocol, two messages related to are cut down because is replaced with a timeout mechanism on the HN. Four , one , and one are added to the messages between the SN and the HN, while two are cut down, so four fields are added. Since is replaced with on the UE and the HN, the calculation amount of one F is added. From Table 3, compared with other protocols, our proposed 5G-AKA’ protocol reduces two messages. The 5G-AKA’ protocol adds more fields than the protocols in [23] and [24], but less than the protocol in [22]. In the amount of calculation, our proposed 5G-AKA’ protocol increases the least, while the protocols in [23] and [24] increase the most because they introduce multiple public-key encryption and decryption. Hence, our proposed 5G-AKA’ protocol is efficient. Especially for the UE, only a key derivation function is added, but one field and one message are reduced.
In addition, the protocols in [23] and [24] destroys the structure of the messages instead of adding fields to the messages or extending fields in the messages, so they are not backward compatible. Our proposed 5G-AKA’ protocol only extends and adds some fields to the messages between the SN and the HN, so it is forward compatible.
6. Conclusions
In this paper, we summarize the 5G AKA protocol into three cases according to the overview of the latest version of the 5G AKA protocol and then use the mixed strand space model for mixed protocols to formally analyze the security of the 5G AKA protocol. As a result, twenty-one attack scenarios of the 5G AKA protocol are obtained, where thirteen attack scenarios are related to the MAC failure, including MAC failure attacks. Based on these attack scenarios, we find that the mutual authentication between the UE and the SN cannot be established, and only the weaker agreement can be established among the UE, the SN and the HN, resulting in MitM attacks and cross attacks. Further, by replaying some message to the UE and the SN, replay attacks and masquerading attacks can be performed, the location privacy of the UE can be compromised and DoS attacks on the SN can be formed. In addition, the 5G AKA protocol cannot provide perfect forward secrecy.
To overcome these attacks, we propose a 5G-AKA’ protocol, in which the pre-shared key between the UE and the HN is replaced with a derivation key of the pre-shared key, the challenge–response mechanism between the SN and the HN is added, the SUPI of the UE is added to the second message between the SN and the HN, and the MAC failure procedure is replaced with a timeout mechanism on the HN. According to the 5G-AKA’ protocol, we summarize the 5G-AKA’ protocol into two cases and then use the mixed strand space model for mixed protocols to formally analyze the security of the 5G-AKA’ protocol. As a result, no attack scenario is obtained.
By discussion and analysis, the 5G-AKA’ protocol can establish mutual authentication and injection agreement among the UE, the SN and the HN, and can overcome the above security problems of the latest version of the 5G AKA protocol. Therefore, the 5G-AKA’ protocol is secure. The comparative analysis of security properties between the 5G-AKA’ protocol and some recently improved 5G AKA protocols shows that the 5G-AKA’ protocol is better than these recently improved 5G AKA protocols in security. The comparative analysis between the 5G-AKA’ protocol and some recently improved 5G AKA protocols in the number of messages, the number of fields, the amount of calculation and backward compatibility shows that the 5G-AKA’ protocol is efficient, and is backward compatible with the 5G AKA protocol.
Recently, some authors also point out that the protection mechanism of SQN can be defeated due to its use of XOR in the 5G AKA protocol. This paper does not consider this security problem, and we will further study this security problem in the future.
Author Contributions
Methodology, Y.X.; formal analysis, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No.61741216, 61402367), Shaanxi Science and Technology Co-ordination & Innovation Project (No.2016KTTSGY01-03), National Key Research and Development Program (No. 2018YFC08242-04) and New Star Team Project of Xi’an University of Posts and Telecommunications.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| 3GPP | 3rd generation partnership project |
| 4G | 4th generation mobile communication technology |
| 5G | 5th generation mobile communication technology |
| ABBA | anti-bidding down between architectures |
| AKA | authentication and key agreement |
| AKMA | authentication and key management for applications |
| AMF | authentication management field |
| ARPF | authentication credential repository and processing function |
| AUSF | authentication server function |
| DoS | denial of service |
| EAP-AKA’ | improved extensible authentication protocol method for 3rd generation authentication and key agreement |
| EAP-TLS | extensible authentication protocol method for transport layer security |
| ECDH | elliptic curve Diffie–Hellman |
| EPS | evolution packet system |
| HN | home network |
| ICB | initial counter block |
| LTE | long-term evolution |
| MAC | message authentication code |
| ME | mobile equipment |
| MitM | man-in-the-middle attacks |
| PKI | public key infrastructure |
| SEAF | security anchor function |
| SIDF | subscriber identity de-concealing function |
| SN | serving network |
| SNN | serving network name |
| SQN | sequence number |
| SUCI | subscription concealed identifier |
| SUPI | subscription permanent identifier |
| TS | technical specification |
| UDM | unified data management |
| UE | user equipment |
| USIM | universal subscriber identity module |
| XOR | exclusive-or |
Notations
| the ABBA parameter | |
| , | two anonymity keys |
| the AKMA indication and routing indicator | |
| the authentication management field | |
| a dummy value of all zeros | |
| an authentication token of the HN | |
| a resynchronization parameter | |
| a base key derived from | |
| CA | the amount of calculation of the 5G AKA protocol |
| a cipher key | |
| ECDH | the generation and verification of an ECDH exchange |
| an encryption key | |
| , , | three message authentication functions |
| , , , | four key generating functions |
| F | the generation and verification of a key function or a key derivation function or a MAC function or a hash function |
| FN | the number of fields (among the UE, the SN and the HN) of the 5G AKA protocol |
| a hash function for computing MAC | |
| , , , | four messages that are not inspected by the SN |
| the HN | |
| a hashing response from | |
| a hashing expected response from | |
| an initial counter block | |
| an integrity key | |
| a long-term key between the UE and the HN | |
| a key between the UE and the access and mobility management function | |
| a key derived from and | |
| the key set of the penetrator | |
| a key derived from | |
| the session key between the SN and the HN | |
| a key derivation function | |
| a MAC of the HN | |
| the “MAC failure” indication | |
| a MAC of the UE | |
| a MAC key | |
| MN | the number of messages (among the UE, the SN and the HN) of the 5G AKA protocol |
| identifying the and the partial native security context | |
| PED | the encryption and decryption based on a public and private key pair |
| an unpredictable challenge of the HN | |
| , | two unpredictable challenges of the SEAF |
| a response | |
| a response from | |
| the authentication result | |
| an unpredictable challenge of the UE | |
| a hash function | |
| the SN | |
| the serving network name of the SN | |
| a fresh sequence number generated by the HN | |
| the highest sequence number the USIM has accepted | |
| a SUCI of the UE | |
| a SUPI of the UE | |
| the “Synchronization failure” indication | |
| the UE | |
| an ephemeral private key of the UE for Diffie-Hellman exchange | |
| an ephemeral public key of the UE for Diffie-Hellman exchange | |
| a MAC locally computed by the UE | |
| an expected response | |
| an expected response from | |
| an ephemeral private key of the HN for Diffie-Hellman exchange | |
| an ephemeral public key of the HN for Diffie-Hellman exchange |
References
- Xu, S.; Gan, Z. Review and trends of 5G security technology. Radio Commun. Technol. 2020, 46, 133–138. [Google Scholar]
- 3GPP TS 33.102: 3G Security; Security Architecture. Available online: https://www.3gpp.org/DynaReport/33102.htm (accessed on 26 January 2022).
- 3GPP TS 33.401: 3GPP System Architecture Evolution (SAE); Security Architecture. Available online: https://www.3gpp.org/DynaReport/33401.htm (accessed on 26 January 2022).
- 3GPP TS 33.501: 3GPP System Architecture Evolution (SAE); Security Architecture. Available online: https://www.3gpp.org/DynaReport/33501.htm (accessed on 26 January 2022).
- Ferrag, M.A.; Maglaras, L.; Argyriou, A.; Kosmano, D.; Janicke, H. Security for 4G and 5G cellular networks: A survey of existing authentication and privacy-preserving schemes. J. Netw. Comput. Appl. 2018, 101, 55–82. [Google Scholar] [CrossRef] [Green Version]
- Jover, R.P.; Marojevic, V. Security and protocol exploit analysis of the 5G specifications. IEEE Access 2019, 7, 24956–24963. [Google Scholar] [CrossRef]
- Ahmad, I.; Shahabuddin, S.; Kumar, T.; Okwuibe, J.; Ylianttila, M. Security for 5G and beyond. IEEE Commun. Surv. Tutor. 2019, 21, 3682–3722. [Google Scholar] [CrossRef]
- Khan, R.; Kumar, P.; Jayakody, D.N.K.; Liyanage, M. A survey on security and privacy of 5G technologies: Potential solutions, recent advancements, and future directions. IEEE Commun. Surv. Tutor. 2019, 22, 196–248. [Google Scholar] [CrossRef] [Green Version]
- Hussain, S.R.; Echeverria, M.; Karim, I.; Chowdhury, O.; Berino, E. 5GReasoner: A property-directed security and privacy analysis framework for 5G cellular network protocol. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 669–684. [Google Scholar]
- Hussain, S.R.; Echeverria, M.; Chowdhury, O.; Li, N.; Bertino, E. Privacy attacks to the 4G and 5G cellular paging protocols using side channel information. In Proceedings of the 26th Network and Distributed System Security Symposium (NDSS), San Diego, CA, USA, 24–27 February 2019; pp. 1–15. [Google Scholar]
- Khan, H.; Martin, K.M. A survey of subscription privacy on the 5G radio interface-the past, present and future. J. Informat. Secur. Appl. 2020, 53, 102537. [Google Scholar] [CrossRef]
- Security Vulnerability in 5G-AKA Draft. Available online: https://www.cs.ox.ac.uk/5G-analysis/5G-AKA-draft-vulnerability.pdf (accessed on 23 February 2022).
- Meier, S.; Schmidt, B.; Cremers, C.; Basin, D. The Tamarin prover for the symbolic analysis of security protocols. In Proceedings of the 25th International Conference on Computer Aided Verification, Saint Petersburg, Russia, 13–19 July 2013; pp. 696–701. [Google Scholar]
- Basin, D.; Dreier, J.; Hirschi, L.; Radomirovic, S.; Sasse, R.; Stettler, V. A formal analysis of 5G authentication. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, Canada, 15–19 October 2018; pp. 1383–1396. [Google Scholar]
- Liu, F.; Peng, J.; Zuo, M. Toward a secure access to 5G network. In Proceedings of the 2018 17th IEEE International Conference On Trust, Security And Privacy In Computing And Communications/12th IEEE International Conference On Big Data Science And Engineering (TrustCom/BigDataSE), New York, NY, USA, 1–3 August 2018; pp. 1121–1128. [Google Scholar]
- Borgaonkar, R.; Hirschi, L.; Park, S.; Shaik, A. New privacy threat on 3G, 4G, and upcoming 5G AKA Protocols. Proc. Priv. Enhancing Technol. 2019, 3, 108–127. [Google Scholar] [CrossRef] [Green Version]
- Cremers, C.; Dehnel-Wild, M. Component-based formal analysis of 5G-AKA: Channel assumptions and session confusion. In Proceedings of the 26th Network and Distributed System Security Symposium (NDSS), San Diego, CA, USA, 24–27 February 2019; pp. 1–15. [Google Scholar]
- Koutsos, A. The 5G-AKA authentication protocol privacy. In Proceedings of the 2019 IEEE European Symposium on Security and Privacy (EuroS & P), Stockholm, Sweden, 17–19 June 2019; pp. 464–479. [Google Scholar]
- Bana, G.; Comon-Lundh, H. Towards unconditional soundness: Computationally complete symbolic attacker. In Proceedings of the First International Conference on Principles of Security and Trust (ETAPS), Tallinn, Estonia, 24 March–1 April 2012; pp. 189–208. [Google Scholar]
- Bana, G.; Comon-Lundh, H. A computationally complete symbolic attacker for equivalence properties. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 609–620. [Google Scholar]
- Braeken, A.; Liyanage, M.; Kumar, P.; Murphy, J. Novel 5G authentication protocol to improve the resistance against active attacks and malicious serving networks. IEEE Access 2019, 7, 64040–64052. [Google Scholar] [CrossRef]
- Gharsallah, I.; Smaoui, S.; Zarai, F. A secure efficient and lightweight authentication protocol for 5G cellular networks: SEL-AKA. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 1311–1316. [Google Scholar]
- Hu, X.; Liu, C.; Liu, S.; Cheng, X. A security enhanced 5G authentication scheme for insecure channel. IEICE Trans. Inf. Syst. 2020, 103, 711–713. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Liu, C.; Liu, S.; Li, J.; Cheng, X. A vulnerability in 5G authentication protocols and its Countermeasure. IEICE Trans. Inf. Syst. 2020, 103, 1806–1809. [Google Scholar] [CrossRef]
- Edris, E.K.K.; Aiash, M.; Loo, J.K. Formal verification and analysis of primary authentication based on 5G-AKA protocol. In Proceedings of the 2020 7th International Conference on Software Defined Systems (SDS), Paris, France, 20–23 April 2020; pp. 256–261. [Google Scholar]
- Ouaissa, M.; Ouaissa, M. An improved privacy authentication protocol for 5G mobile networks. In Proceedings of the 2020 International Conference on Advances in Computing, Communication & Materials (ICACCM), Dehradun, India, 21–22 August 2020; pp. 136–143. [Google Scholar]
- Parne, B.L.; Gupta, S.; Gandhi, K.; Meena, S. PPSE: Privacy preservation and security efficient AKA protocol for 5G communication networks. In Proceedings of the 2020 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), New Delhi, India, 14–17 December 2020; pp. 1–6. [Google Scholar]
- Fábrega, F.J.T.; Herzog, J.C.; Guttman, J.D. Mixed strand spaces. In Proceedings of the 12th IEEE Computer Security Foundations Workshop, Mordano, Italy, 30–30 June 1999; pp. 72–82. [Google Scholar]
- Fábrega, F.J.T.; Herzog, J.C.; Guttman, J.D. Strand space: Proving security protocols correct. J. Comput. Secur. 1999, 7, 191–230. [Google Scholar] [CrossRef]
- Herzog, J.C. The Diffie-Hellman key-agreement scheme in the strand-space model. In Proceedings of the 16th IEEE Computer Security Foundation Workshop, Pacific Grove, CA, USA, 30 June–2 July 2003; pp. 234–247. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).