Design and Control of a Three-Level Rectifier in LCC/S-Compensated IPT for Wide Output Voltage Regulation over Various Magnetic Couplings
Abstract
:1. Introduction
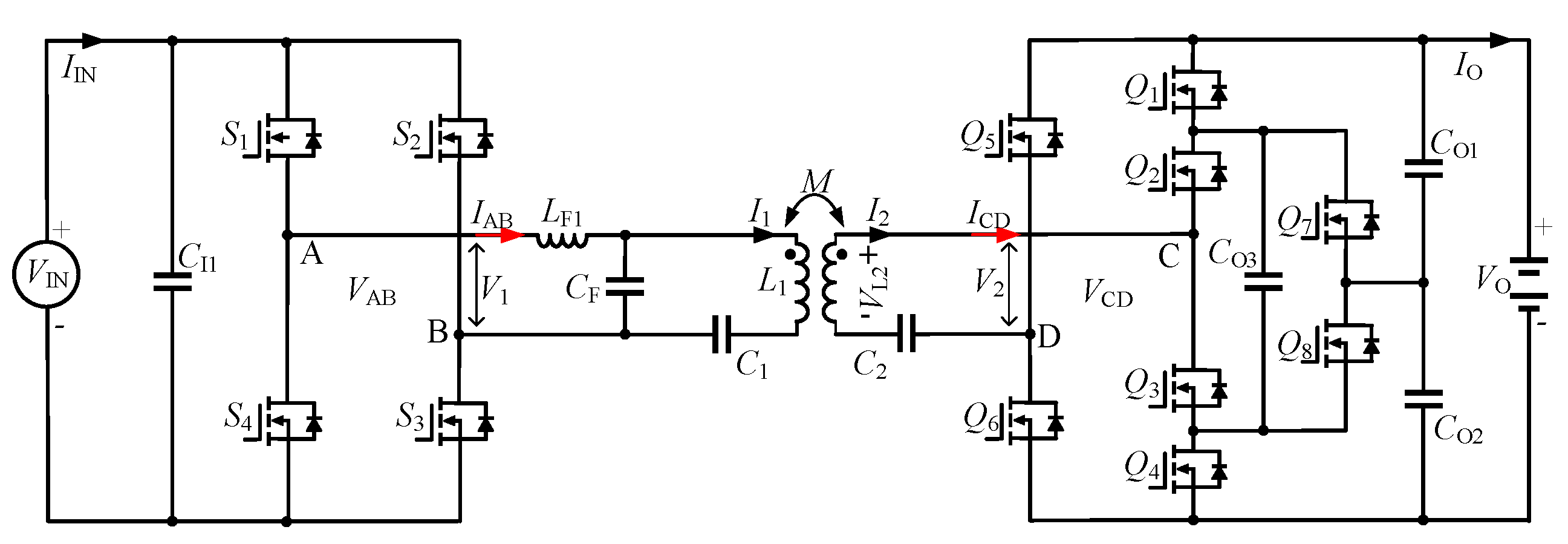
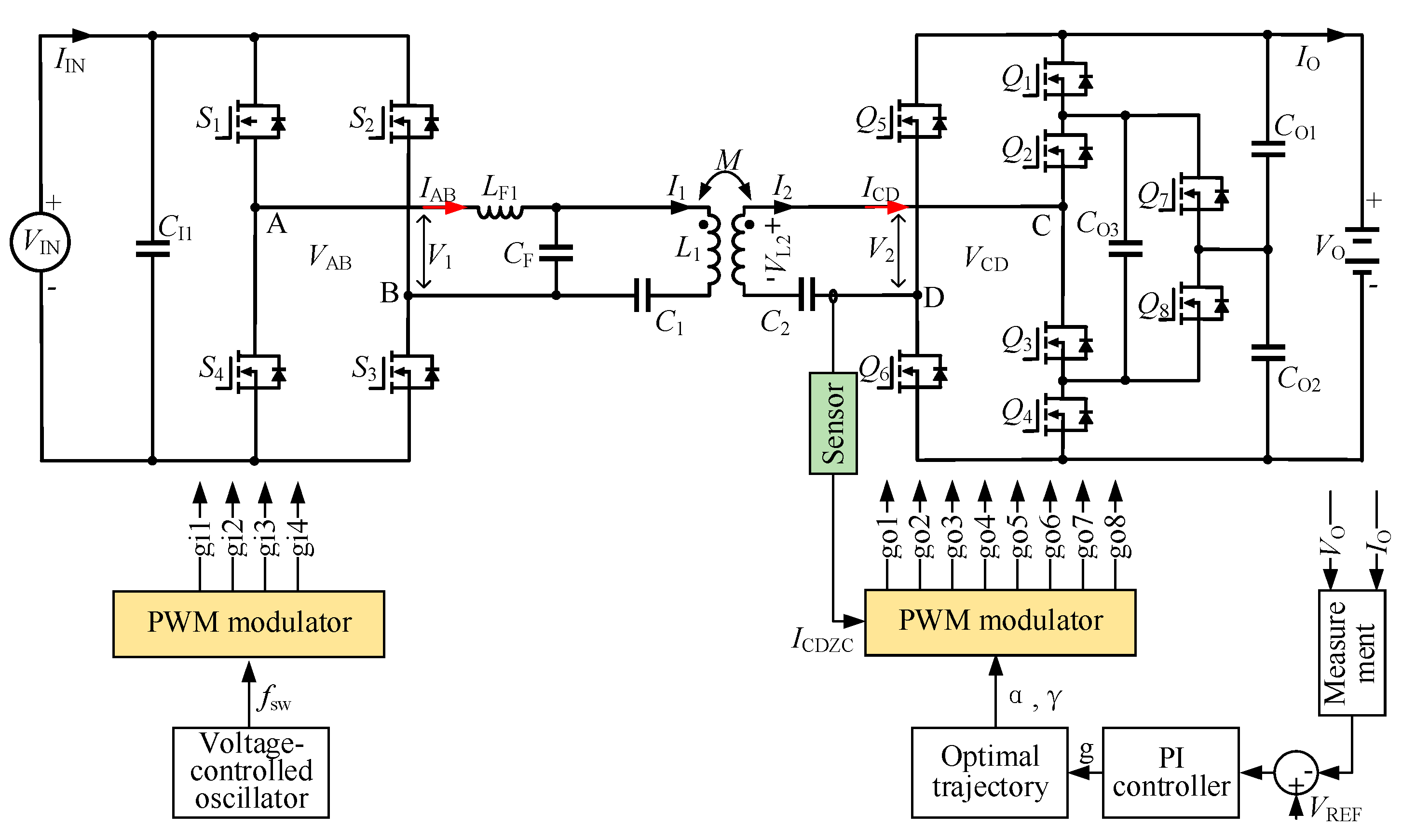
2. Analysis of the LCC/S-Compensated DAB Converter with a Three-Level Rectifier
2.1. Voltage Gain of LCC/S Compensation Network
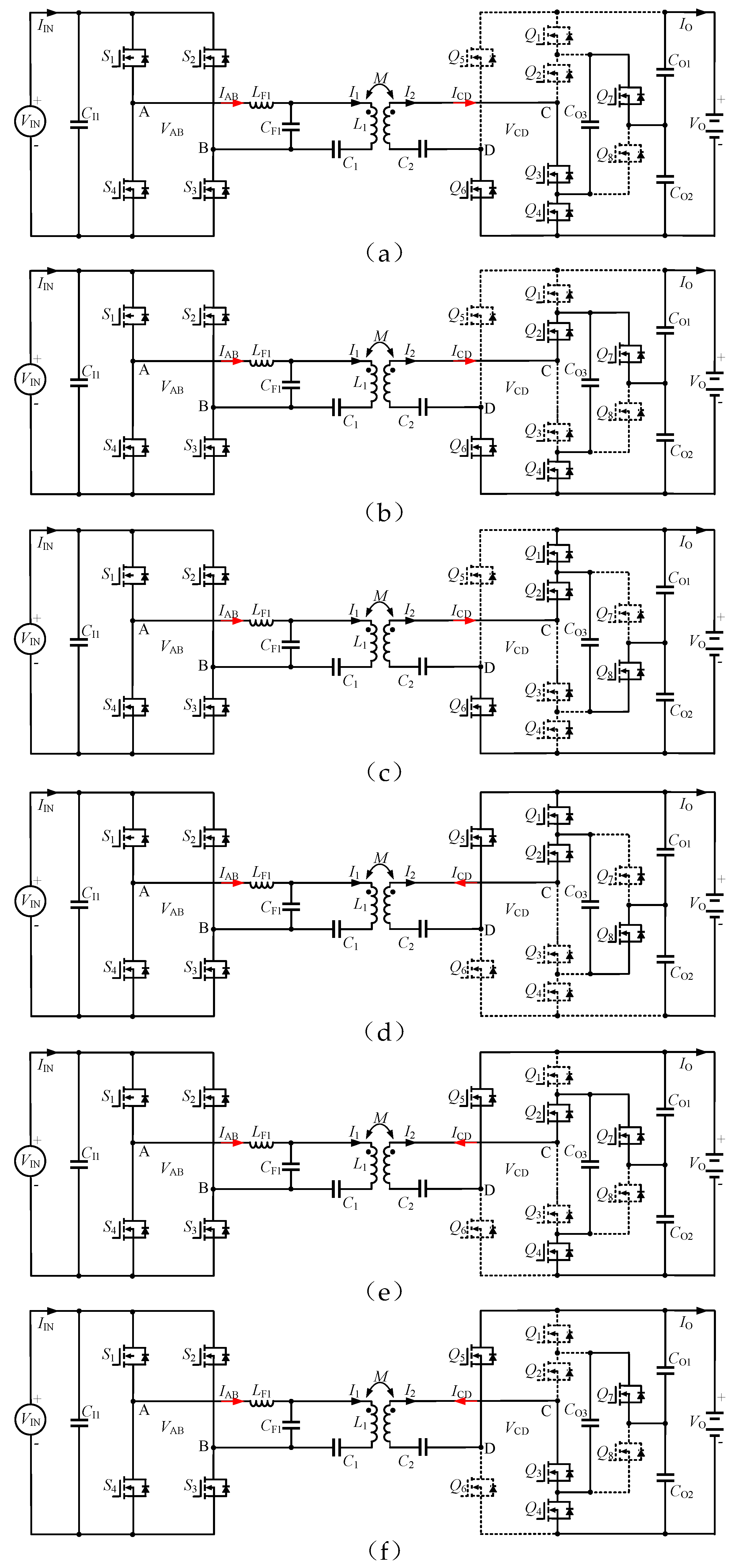
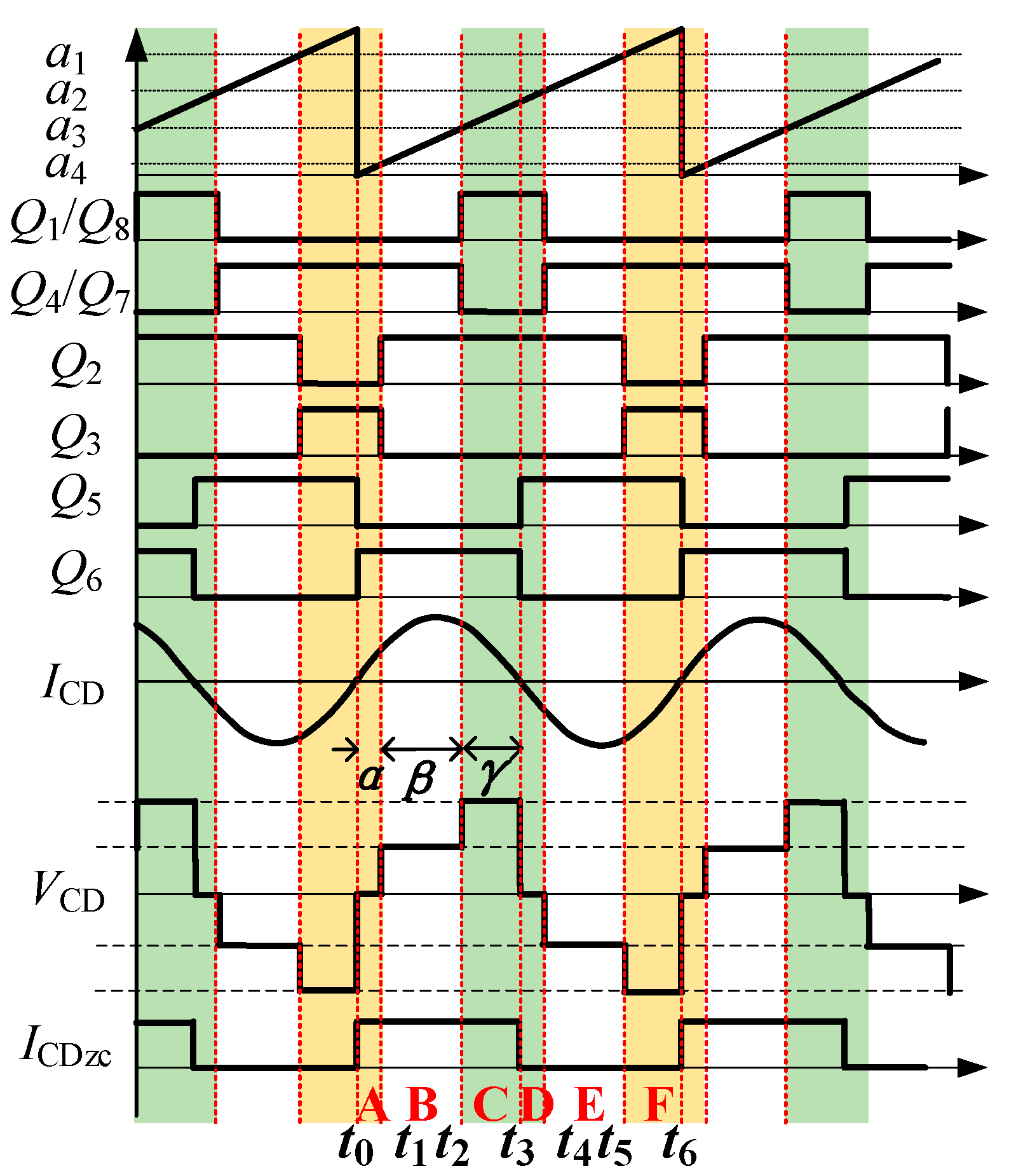
2.2. Operation of the TL Rectifier
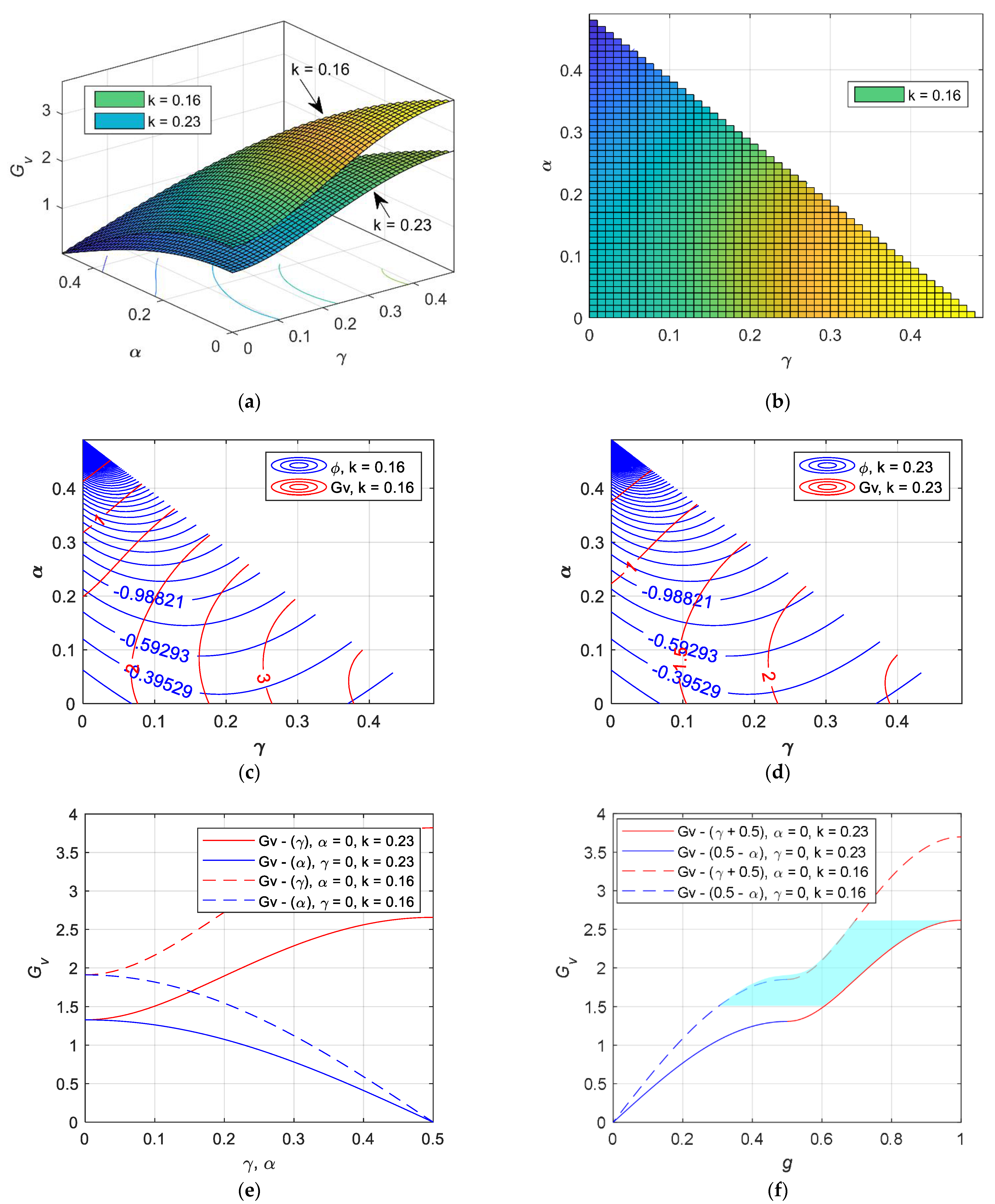
2.3. Voltage Gain of the TL Rectifier
3. Design and Implementation
3.1. Parameter Design
3.2. Primary Controller
3.3. Secondary Controller
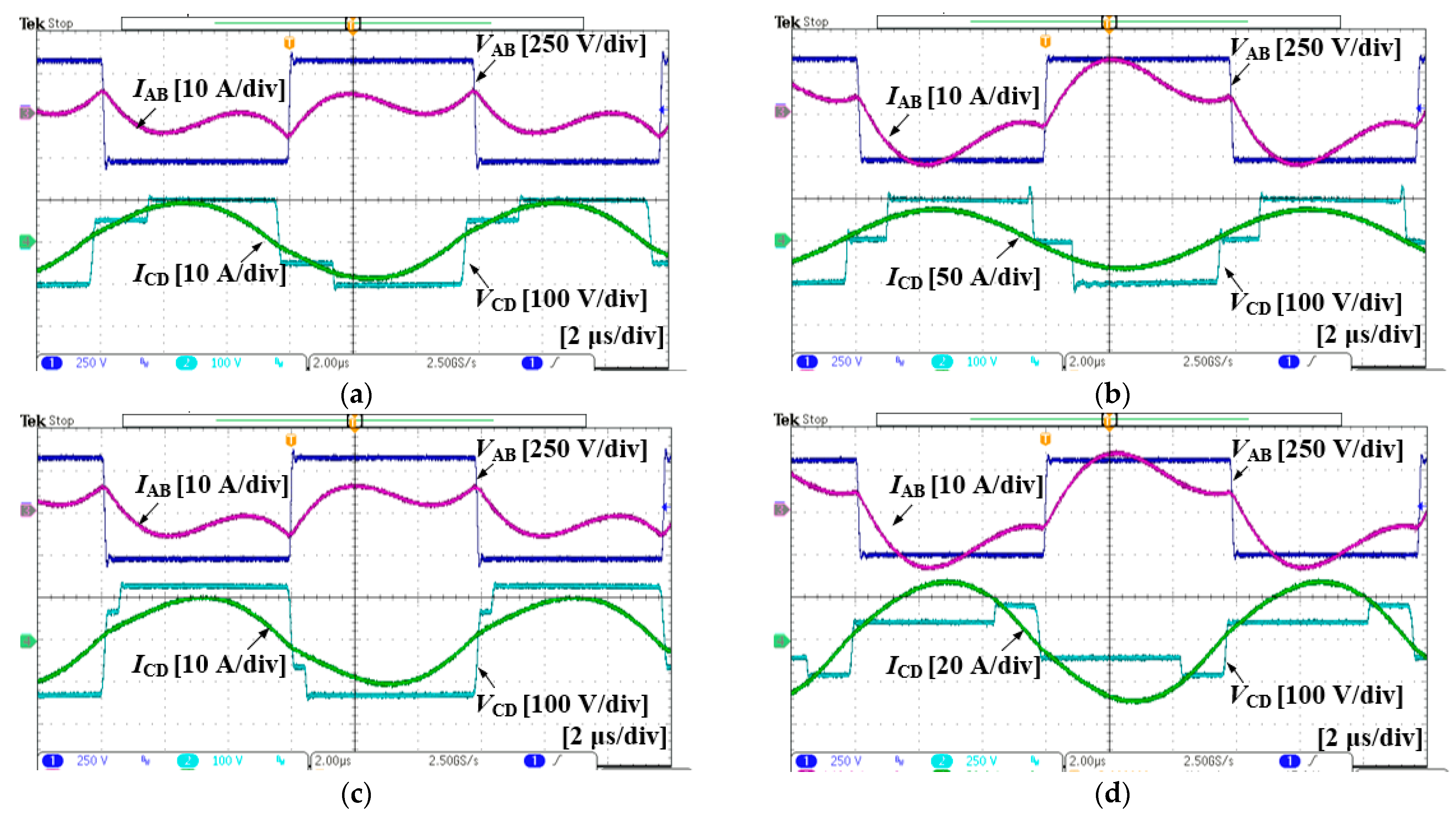
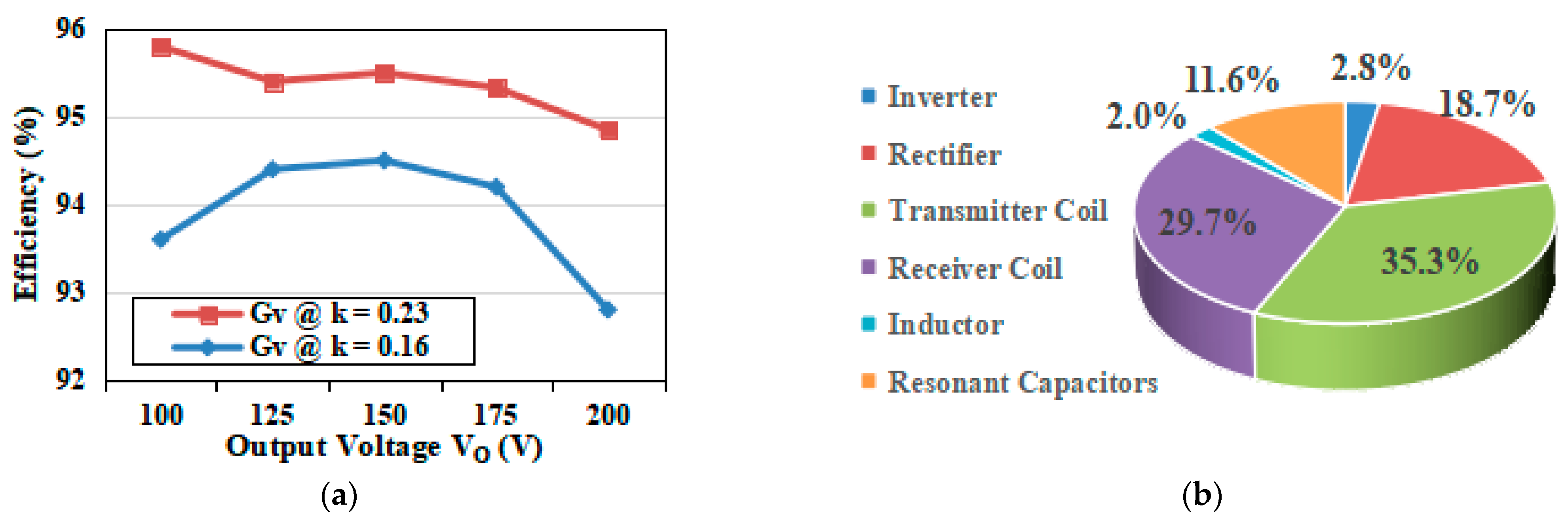
4. Experimental Verification
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, L.; Thrimawithana, D.; Madawala, U. Hybrid bidirectional wireless EV charging system tolerant to pad misalignment. IEEE Trans. Ind. Electron. 2017, 64, 7079–7086. [Google Scholar] [CrossRef]
- Qu, X.; Zhang, W.; Wong, S.; Tse, C. Design of a current-source-output inductive power transfer LED lighting system. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 306–314. [Google Scholar]
- Bito, J.; Jeong, S.; Tentzeris, M. A real-time electrically controlled active matching circuit utilizing genetic algorithms for wireless power transfer to biomedical implants. IEEE Trans. Microw. Theory Tech. 2016, 64, 365–374. [Google Scholar] [CrossRef]
- Bian, B.; Wei, Y.; Li, Y. Key Technologies for the Application of the Electric Propulsion System on the GEO Satellite Platform. Meas. Control. 2008, 41, 85–87. [Google Scholar]
- Liu, Y.; Sun, Y.; Su, M.; Zhou, M.; Zhu, Q.; Li, X. A single-phase PFC rectifier with wide output voltage and low-frequency ripple power decoupling. IEEE Trans. Power Electron. 2018, 33, 5076–5086. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wei, G.; Dong, S.; Dong, Y.; Yu, X.; Li, X. A High-Efficiency Self-Synchronous RF–DC Rectifier Based on Time-Reversal Duality for Wireless Power Transfer Applications. Electronics 2022, 11, 90. [Google Scholar] [CrossRef]
- Lu, M.; Ngo, K. Systematic design of coils in series–series inductive power transfer for power transferability and efficiency. IEEE Trans. Power Electron. 2018, 33, 3333–3345. [Google Scholar] [CrossRef]
- Cheng, B.; He, L. Realize Load-Independent Output with Soft Switching Based on Switched Capacitor for Wireless Charger System. IEEE Access 2022, 10, 10094–10104. [Google Scholar] [CrossRef]
- Simonazzi, M.; Campanini, A.; Sandrolini, L.; Rossi, C. Design Procedure Based on Maximum Efficiency for Wireless Power Transfer Battery Chargers with Lightweight Vehicle Assembly. Energies 2022, 15, 70. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Deng, J.; Nguyen, T.; Mi, C. A double-sided LCC compensation network and its tuning method for wireless power transfer. IEEE Trans. Veh. Technol. 2015, 64, 2261–2273. [Google Scholar] [CrossRef]
- Lu, J.; Zhu, G.; Lin, D.; Zhang, Y.; Jiang, J.; Mi, C. Unified Load-Independent ZPA Analysis and Design in CC and CV Modes of Higher Order Resonant Circuits for WPT Systems. IEEE Trans. Transp. Electric 2019, 5, 977–987. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Guo, Q.; Xie, S.; Yang, Y. Research on Constant Voltage/Current Output of LCC–S Envelope Modulation Wireless Power Transfer System. Energies 2022, 15, 1562. [Google Scholar] [CrossRef]
- Wu, H.; Gilchrist, A.; Sealy, K.; Bronson, D. A High Efficiency 5 kW Inductive Charger for EVs Using Dual Side Control. IEEE Trans. Indust. Inform. 2012, 8, 585–595. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Joo, D.; Lee, B. Design and Control of Inductive Power Transfer System for Electric Vehicles Considering Wide Variation of Output Voltage and Coupling Coefficient. IEEE Trans. Power Electron. 2019, 34, 1197–1208. [Google Scholar] [CrossRef]
- Stoyka, K.; Vitale, A.; Costarella, M.; Avella, A.; Pucciarelli, M.; Visconti, P. Development of a Digitally Controlled Inductive Power Transfer System with Post-Regulation for Variable Load Demand. Electronics 2022, 11, 58. [Google Scholar] [CrossRef]
- Zhang, Y.; Kan, T.; Yan, Z.; Mi, C. Frequency and Voltage Tuning of Series–Series Compensated Wireless Power Transfer System to Sustain Rated Power Under Various Conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1311–1317. [Google Scholar] [CrossRef]
- Hu, H.; Cai, T.; Duan, S.; Zhang, X.; Niu, J.; Feng, H. An optimal variable frequency phase shift control strategy for ZVS operation within wide power range in IPT systems. IEEE Trans. Power Electron. 2020, 35, 5517–5530. [Google Scholar] [CrossRef]
- Wireless Power Transfer for Light-Duty Plug-In/Electric Vehicles and Alignment Methodology. Available online: https://www.sae.org/standards/content/j2954_201904/ (accessed on 20 October 2020).
- Wang, X.; Xu, J.; Leng, M.; Ma, H.; He, S. A Hybrid Control Strategy of LCC-S Compensated WPT System for Wide Output Voltage and ZVS Range with Minimized Reactive Current. IEEE Trans. Ind. Electron. 2021, 68, 7908–7920. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, J.; Zhang, Y.; Deng, F. A Wireless Power Transfer System with Dual Switch-Controlled Capacitors for Efficiency Optimization. IEEE Trans. Power Electron. 2019, 35, 6091–6101. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.; Tian, Y.; Liu, Y. Constant Current/Voltage Charging for Primary-Side Controlled Wireless Charging System Without Using Dual-Side Communication. IEEE Trans. Power Electron. 2021, 36, 13562–13577. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, B.; Jiang, Y. Position-Independent Constant Current or Constant Voltage Wireless Electric Vehicles Charging System Without Dual-Side Communication and DC–DC Converter. IEEE Trans. Ind. Electron. 2022, 69, 7930–7939. [Google Scholar] [CrossRef]
- Iam, I.-W.; Hoi, I.-U.; Huang, Z.; Gong, C.; Lam, C.-S.; Mak, P.-I.; Da Silva Martins, R.P. Constant-Frequency and Non-Communication-Based Inductive Power Transfer Converter for Battery Charging. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 10, 2147–2162. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, J.; Wu, X.; Sheng, K.; Wang, Y. A Bidirectional Three-Level LLC Resonant Converter with PWAM Control. IEEE Trans. Power Electron. 2016, 31, 2213–2225. [Google Scholar] [CrossRef]
- Li, K.; Tan, S.; Hui, S. Overshoot Damping and Dynamics Improvement in Wireless Power Transfer Systems Via Receiver-Side Controller Design. IEEE Trans. Power Electron. 2022, 37, 2362–2371. [Google Scholar] [CrossRef]



| Symbol | Description |
|---|---|
| α | Duty cycle of zero-level voltage in the TL rectifier |
| β | Duty cycle of half-level voltage in the TL rectifier |
| γ | Duty cycle of one-level voltage in the TL rectifier |
| φ | Phase difference between ICD and VCD1 |
| Ts | Switching period |
| VAB, IAB | Inverter output voltage and current |
| VCD, ICD | Rectifier input voltage and current |
| VCD1 | Fundament component of VCD |
| ICDZC | Zero-crossing pulse signal of ICD |
| V1 | Fundament component in RMS of VAB |
| V2 | Fundament component in RMS of VCD |
| I1 | RMS current in the transmitter coil |
| I2 | RMS current in the receiver coil |
| VIN | Input DC voltage |
| VO | Output DC voltage |
| L1 | Inductance of the transmitter coil |
| L2 | Inductance of the receiver coil |
| LF | Inductance of the series resonant inductor in transmitter |
| CF | Capacitance of the parallel resonant capacitor in transmitter |
| C1 | Capacitance of the series resonant capacitor in transmitter |
| C2 | Capacitance of the series resonant capacitor in receiver |
| S1, S2, S3, S4 | Switches in the inverter |
| Q1, Q2, Q3, Q4, Q5, Q6, Q7, Q8 | Switches in the TL rectifier |
| L1 | L2 | LF | CF | C1 | C2 | VIN | VO |
|---|---|---|---|---|---|---|---|
| 44 µH | 61 µH | 32 µH | 122 nF | 222 nF | 57.5 nF | 280 V | 100–200 V |
| Reference | Compensation | No Extra DC–DC | Active Rectifier | No Wireless Feedback Communication | VO Range (V) | k Range |
|---|---|---|---|---|---|---|
| [15] | SS | × | × | × | 12 | 0.34–0.75 |
| [16] | SS | √ | × | × | 120 | 0.16–0.54 |
| [19] | LCC/S | √ | × | × | 100–180 | 0.15–0.2 |
| [20] | SS | √ | √ | × | 65–130 | 0.12 |
| [22] | SS | √ | × | √ | CC/CV | 0.1–0.43 |
| [23] | SS | √ | √ | √ | 60–170 | 0.255 |
| [25] | SS | × | × | √ | 15.3–19.2 | - |
| This study | LCC/S | √ | √ | √ | 100–200 | 0.16–0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, J.; Wang, P.; Li, J.; Chen, J.; Chen, S. Design and Control of a Three-Level Rectifier in LCC/S-Compensated IPT for Wide Output Voltage Regulation over Various Magnetic Couplings. Electronics 2022, 11, 1426. https://doi.org/10.3390/electronics11091426
Li J, Wang J, Wang P, Li J, Chen J, Chen S. Design and Control of a Three-Level Rectifier in LCC/S-Compensated IPT for Wide Output Voltage Regulation over Various Magnetic Couplings. Electronics. 2022; 11(9):1426. https://doi.org/10.3390/electronics11091426
Chicago/Turabian StyleLi, Jianting, Jinquan Wang, Puyu Wang, Jianke Li, Jingjing Chen, and Shu Chen. 2022. "Design and Control of a Three-Level Rectifier in LCC/S-Compensated IPT for Wide Output Voltage Regulation over Various Magnetic Couplings" Electronics 11, no. 9: 1426. https://doi.org/10.3390/electronics11091426
APA StyleLi, J., Wang, J., Wang, P., Li, J., Chen, J., & Chen, S. (2022). Design and Control of a Three-Level Rectifier in LCC/S-Compensated IPT for Wide Output Voltage Regulation over Various Magnetic Couplings. Electronics, 11(9), 1426. https://doi.org/10.3390/electronics11091426






