A Novel Improved Coordinate Rotated Algorithm for PWM Rectifier THD Reduction
Abstract
:1. Introduction
2. Theory and Derivation
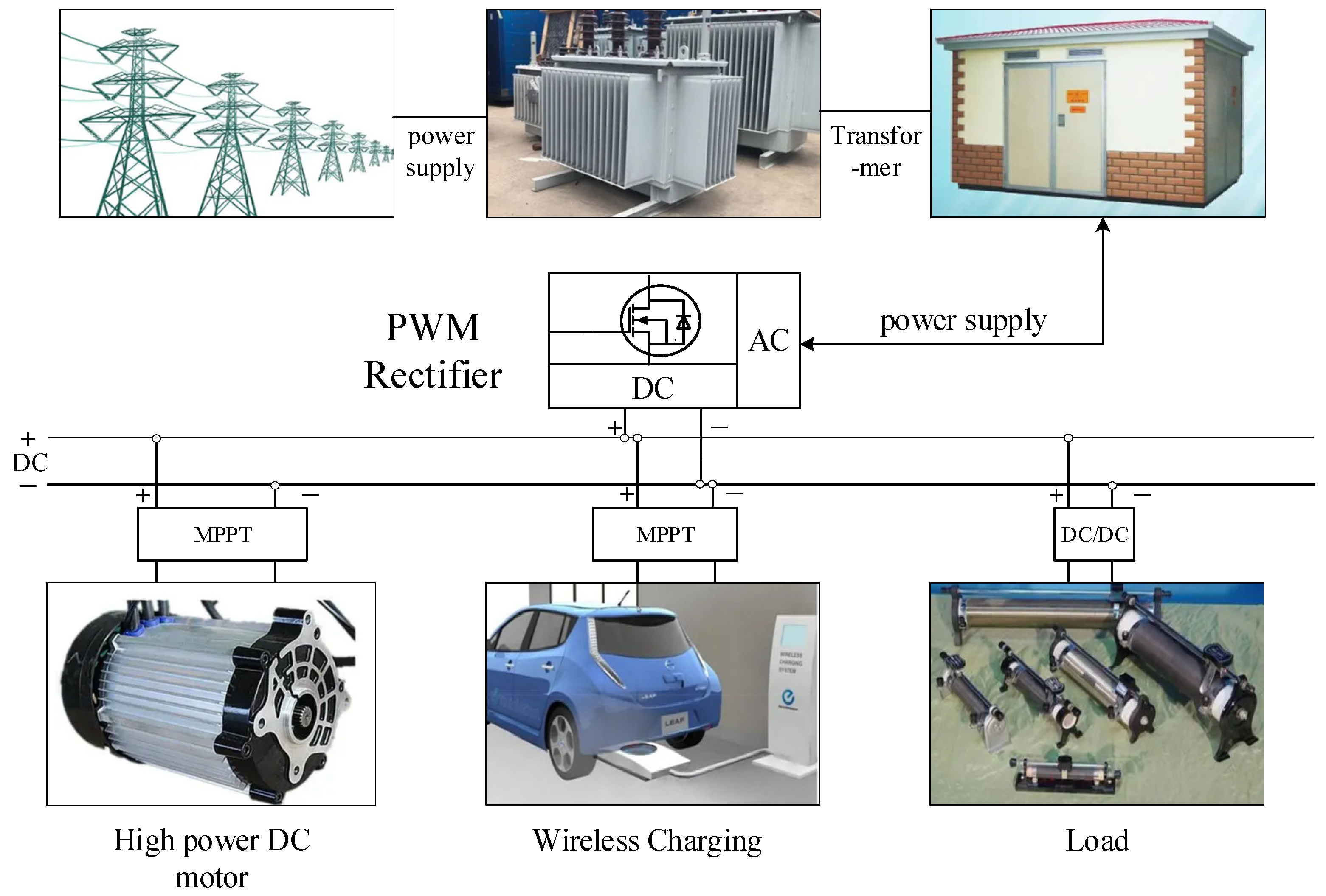
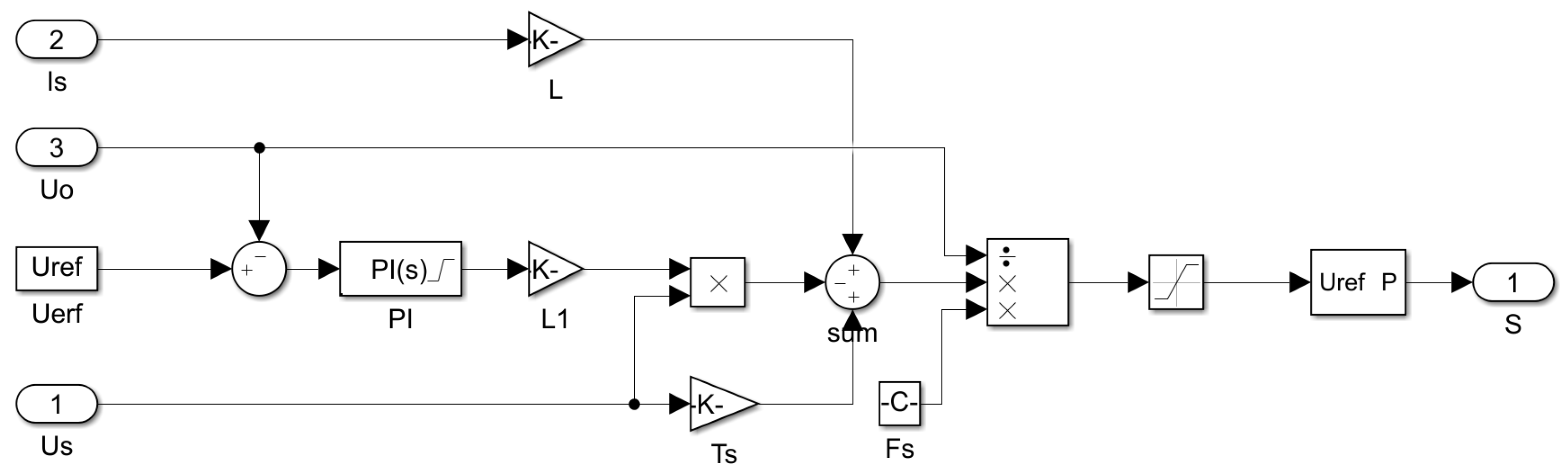
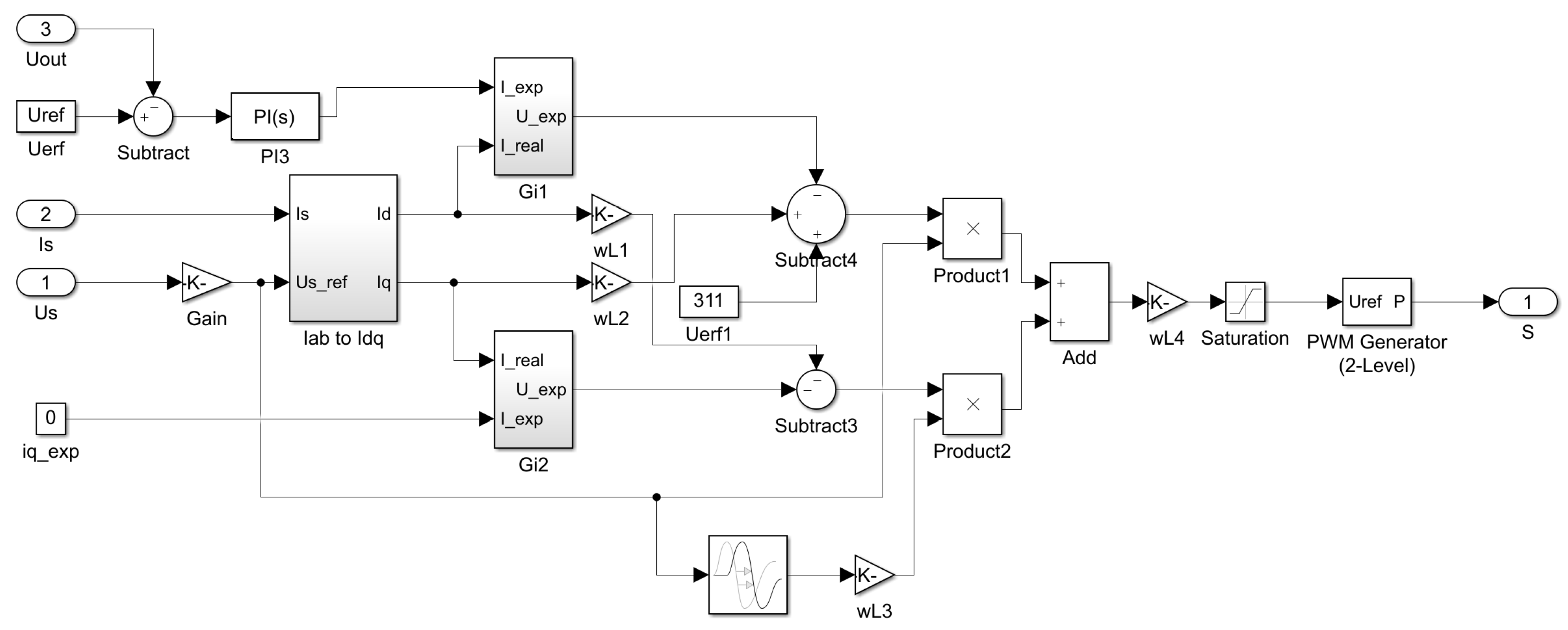
2.1. The Structure of a PWM Rectifier
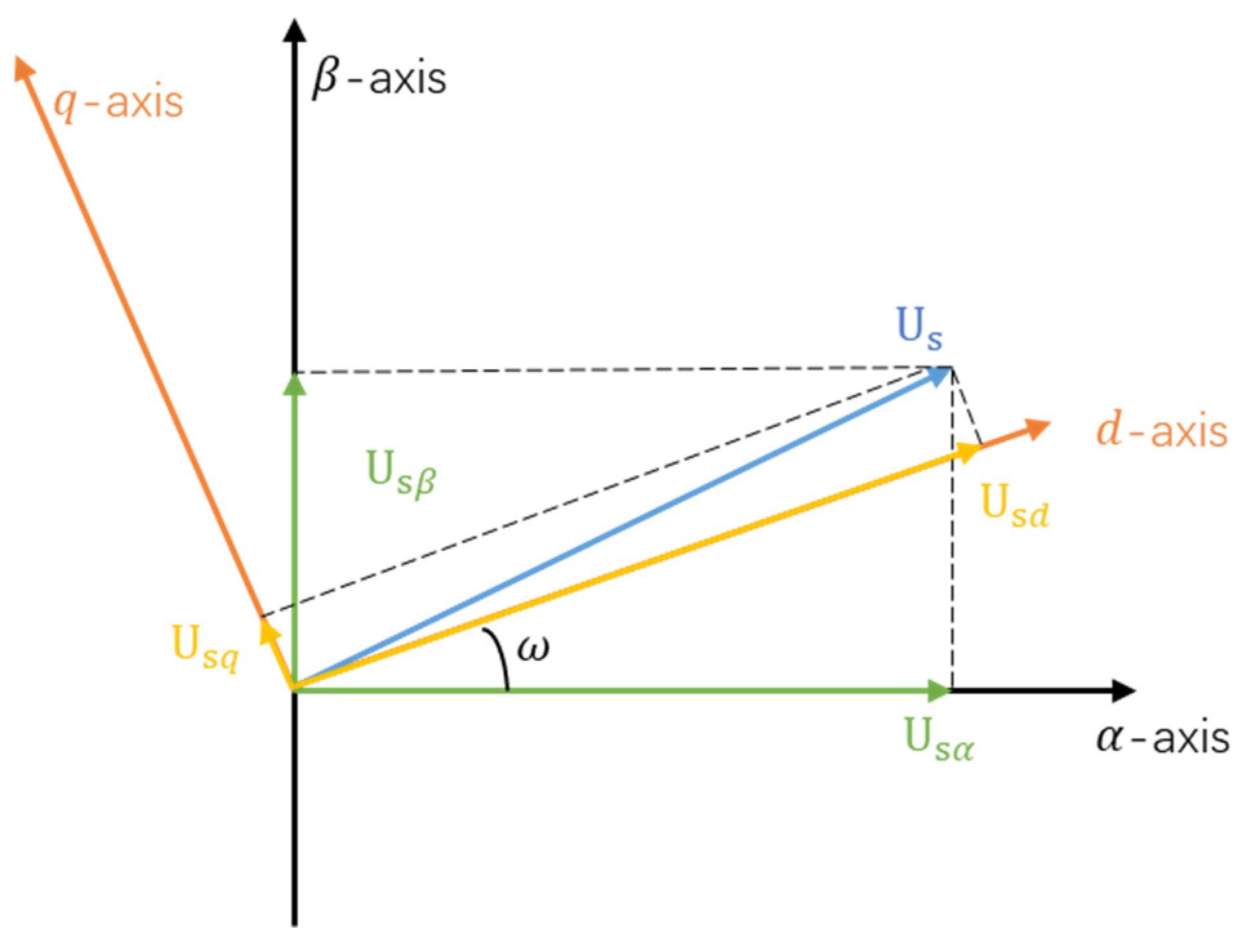
2.2. d-q Axis Current Decoupling Control
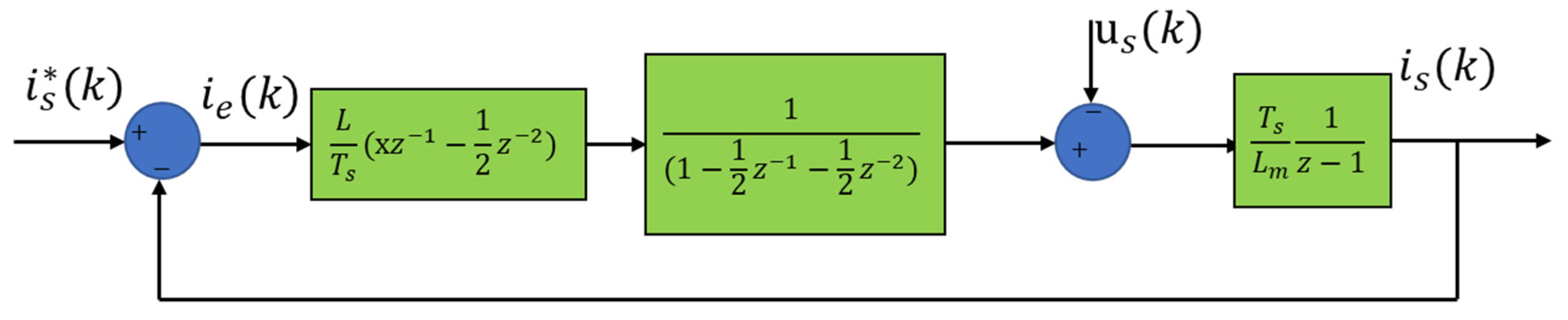
2.3. Predictive Current Control Strategy Improvement
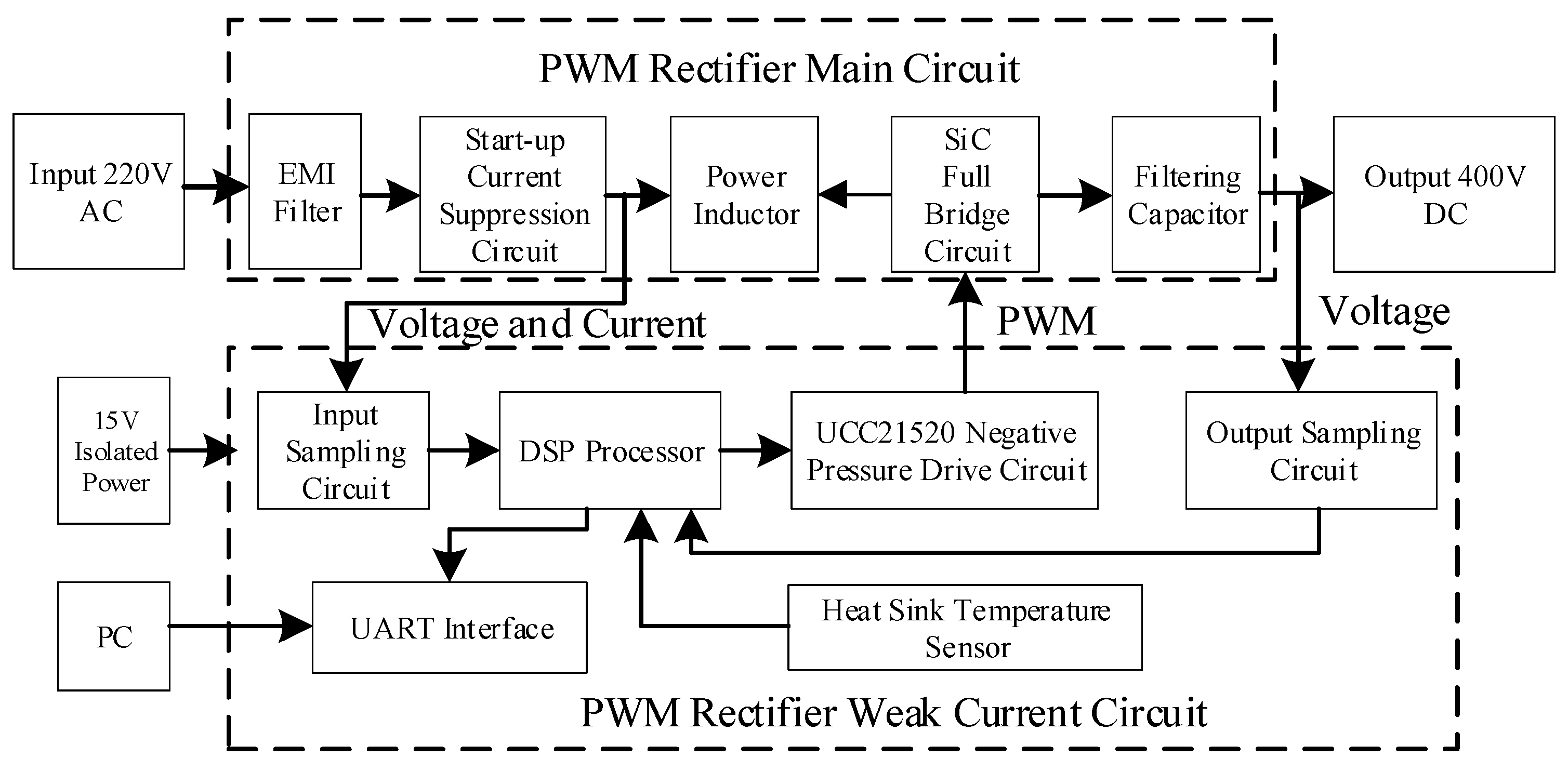
3. Circuit Component Analysis and Calculation
3.1. Analysis and Calculation of Inductance
3.2. Analysis and Calculation of Capacitance
4. Simulation and Performance Comparison
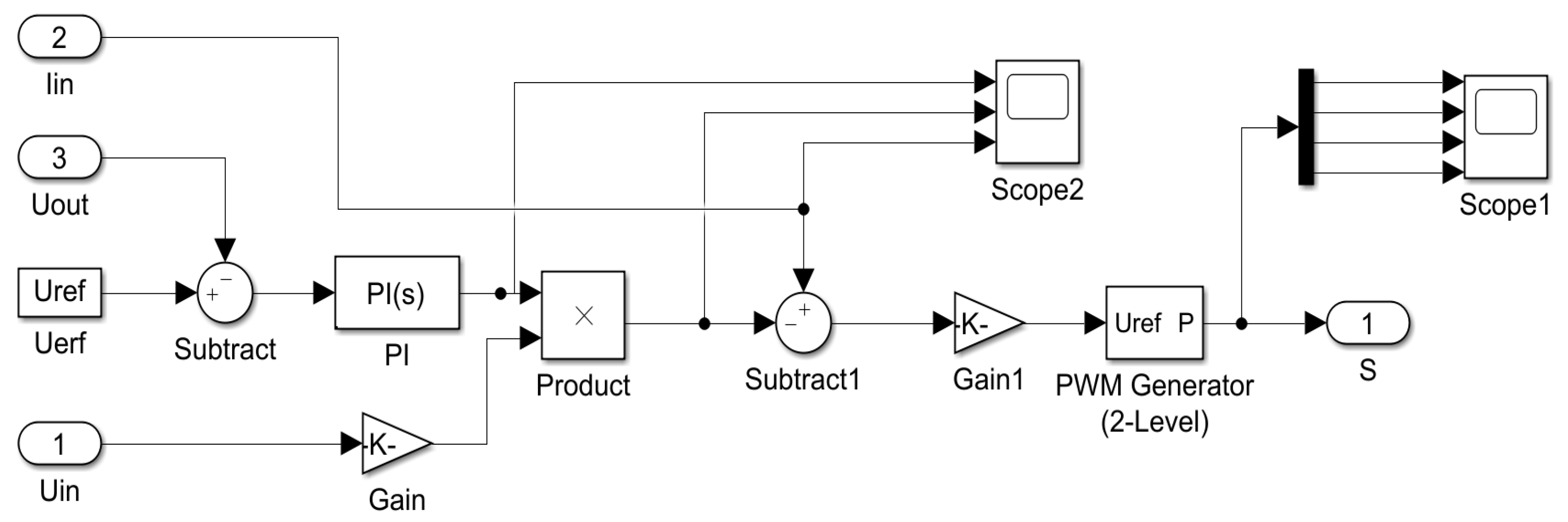
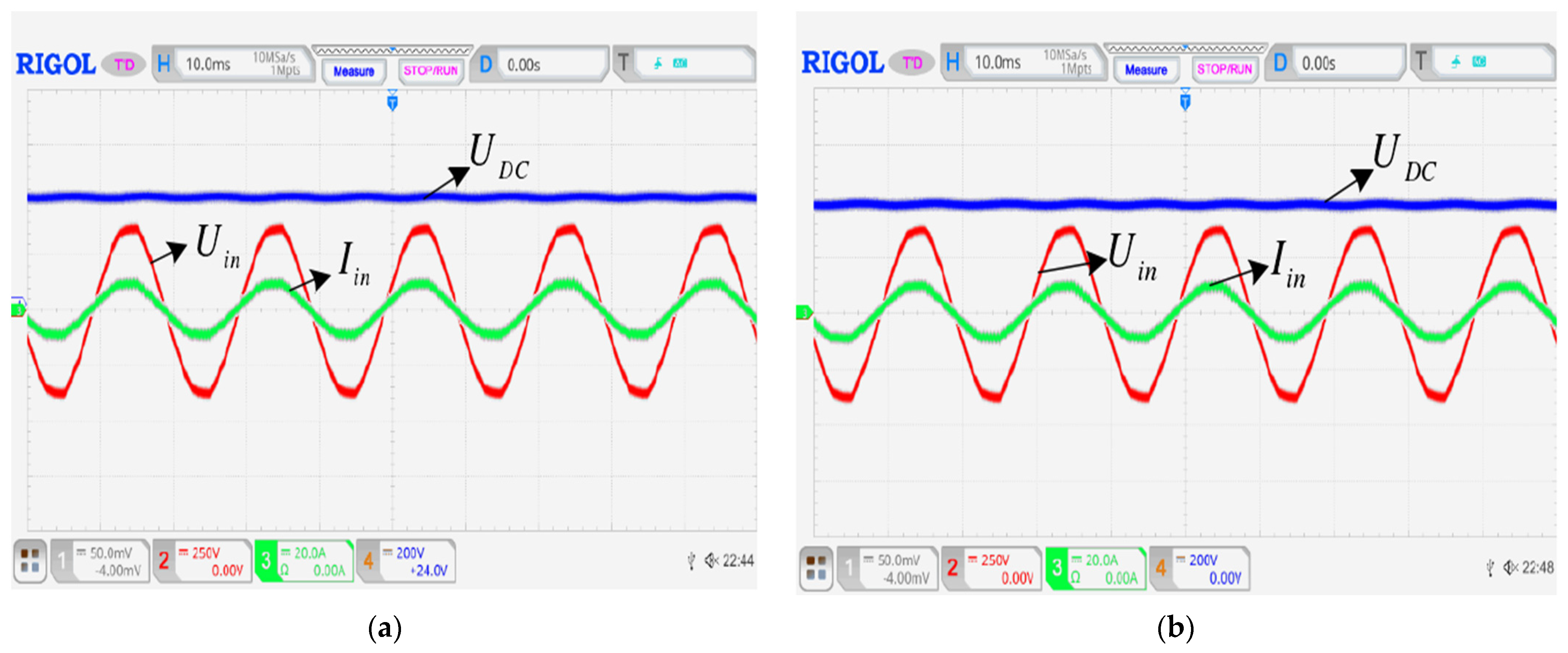
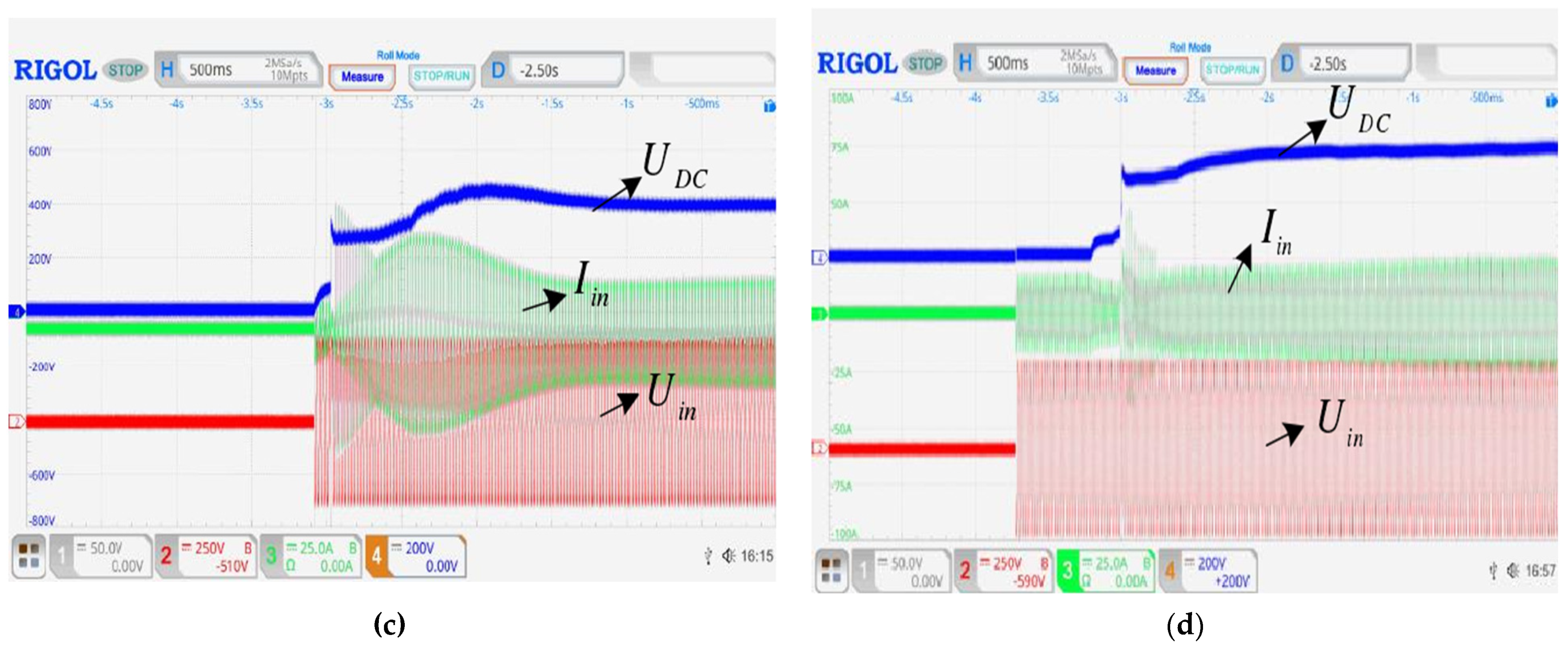
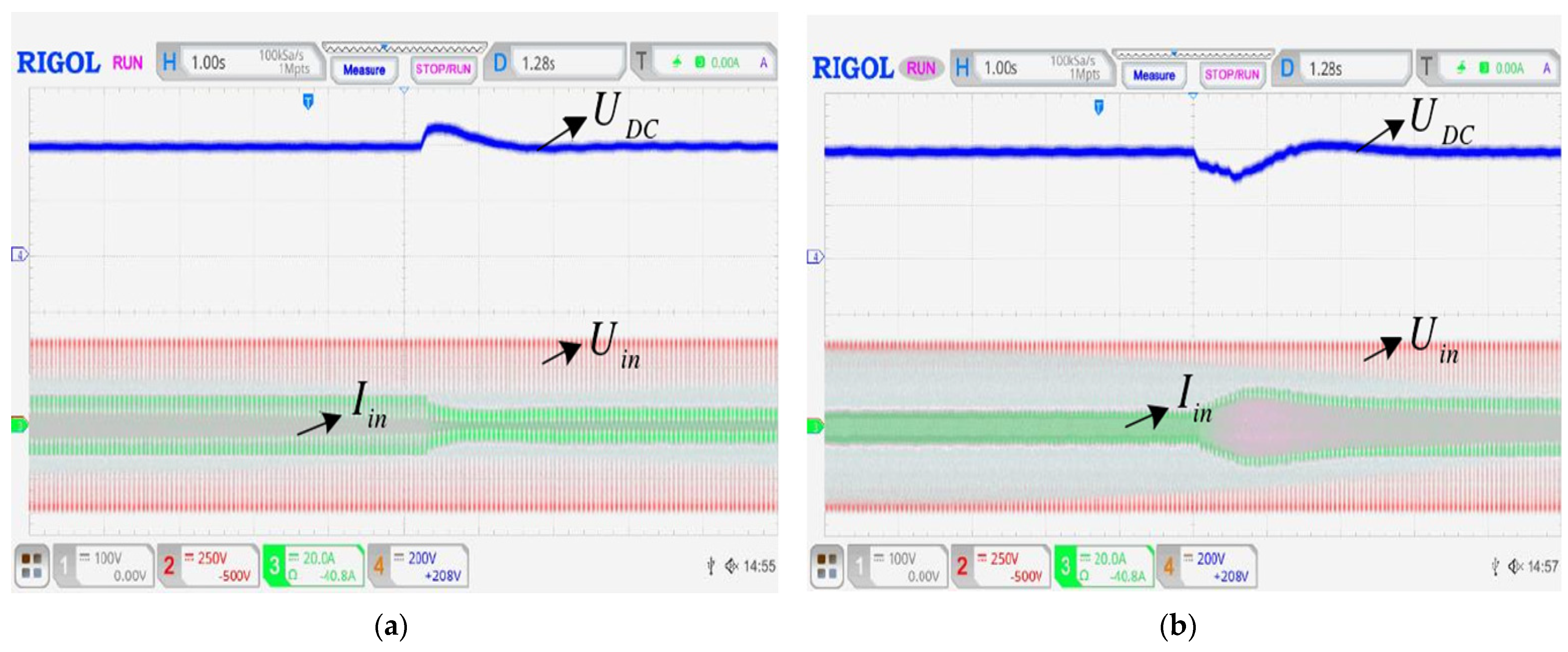
5. Experimental Results
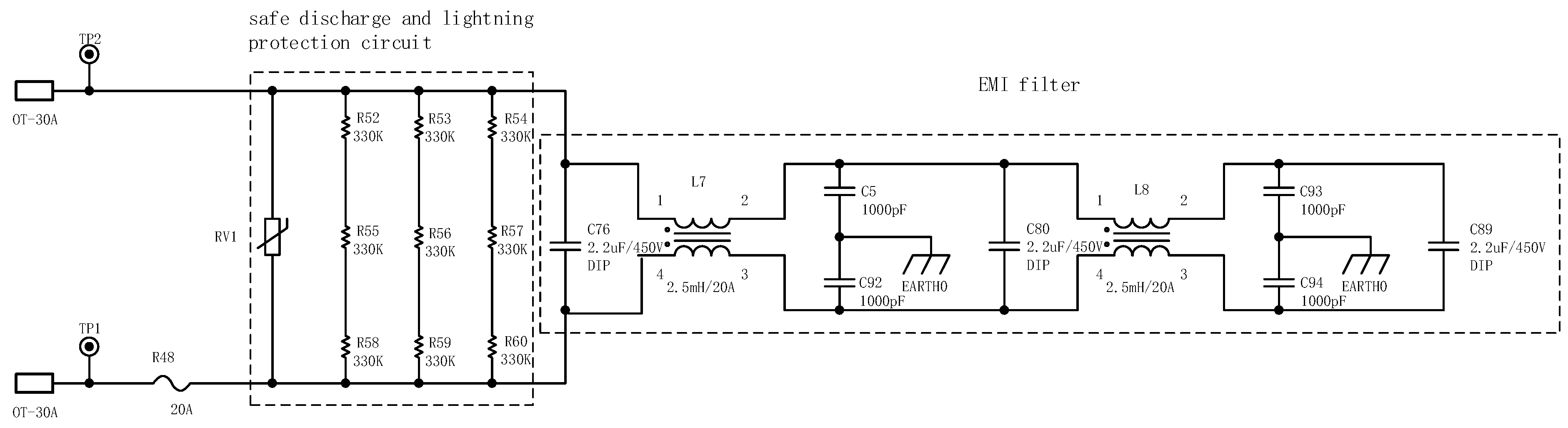
5.1. Design of Input Filtering for Harmonic Suppression
5.2. Switch Tube Parameter Selection and Drive Circuit Design
5.3. DSP Controller Selection and Control Board Design
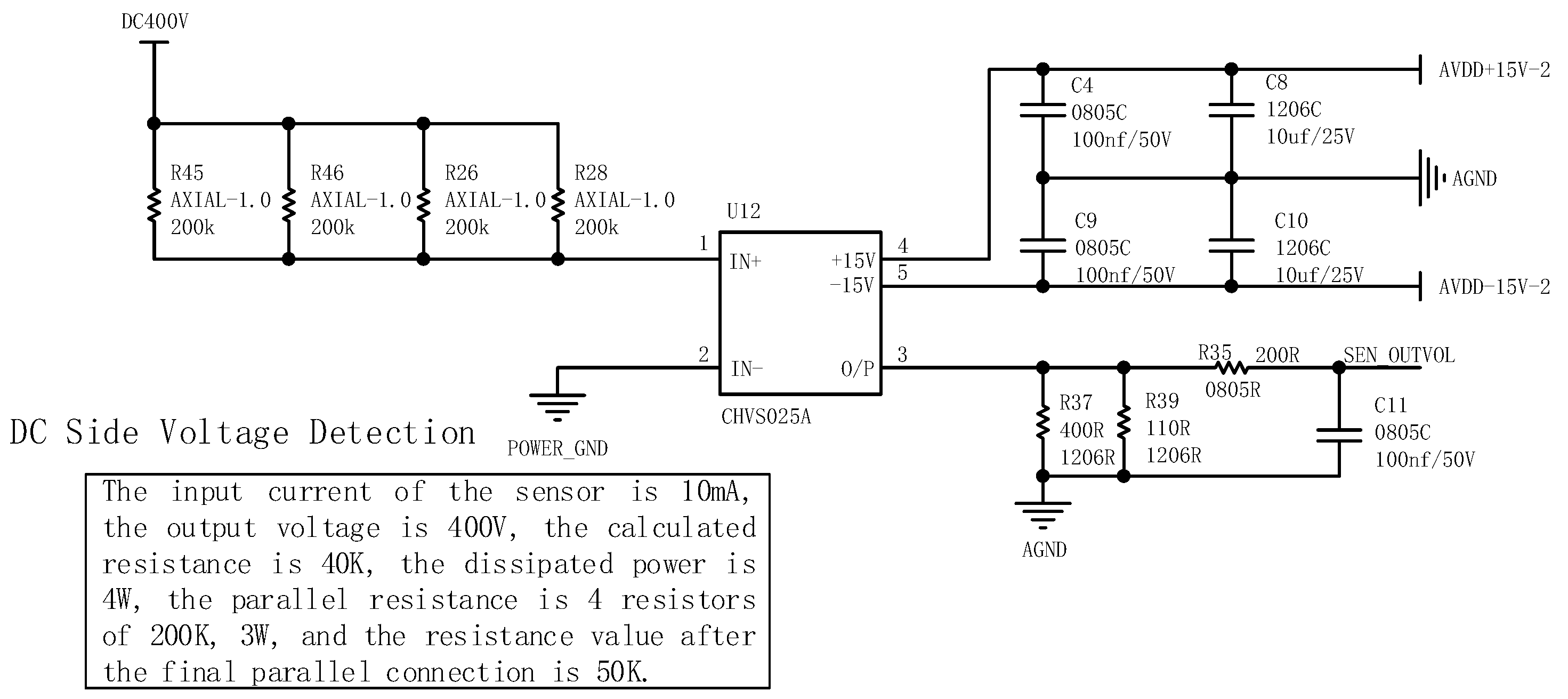
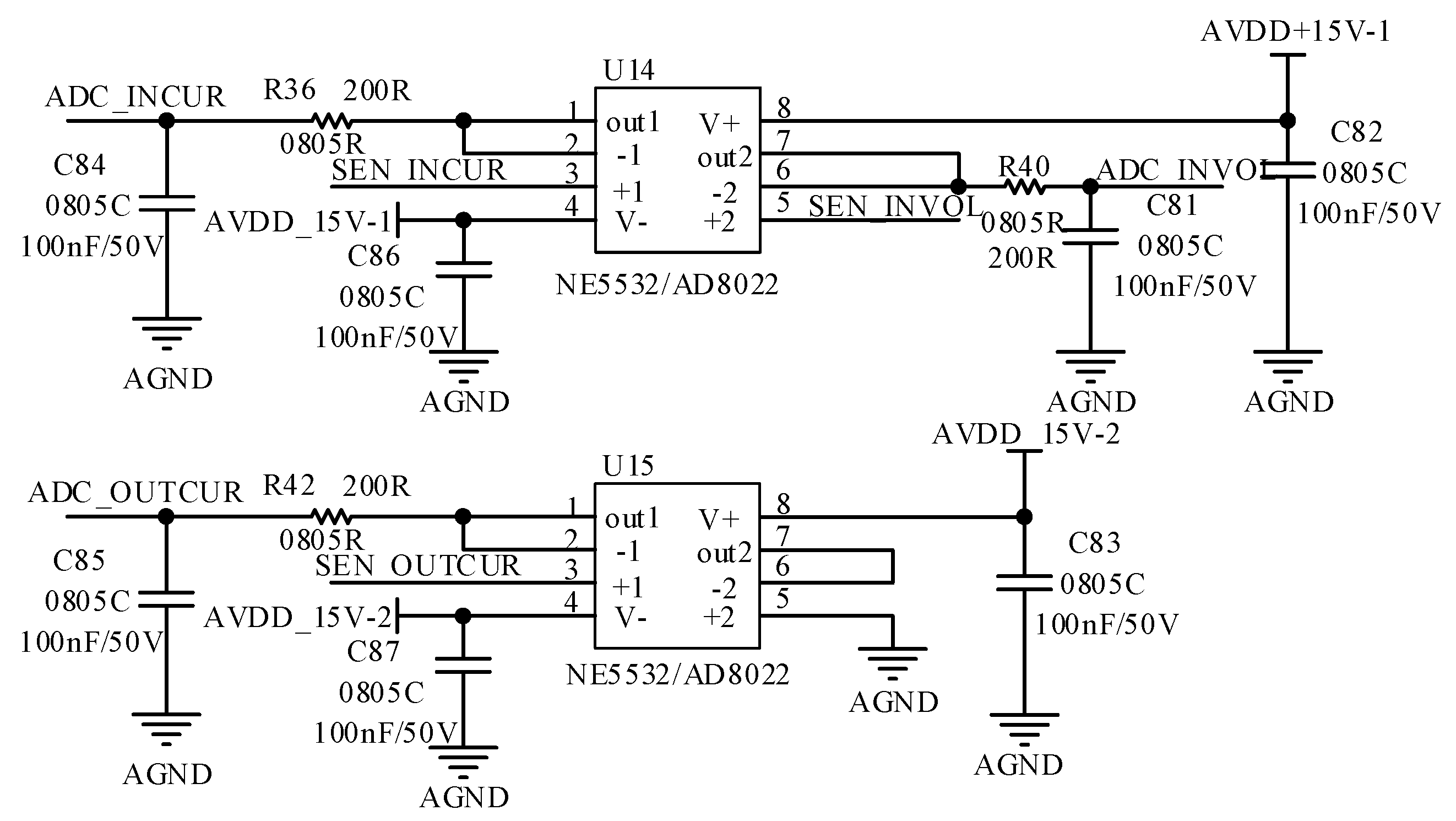
5.4. Design of Signal Sampling Circuit
5.5. Soft-Start Current-Limiting Circuit
5.6. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mao, J.; Hong, D.; Ren, R.; Li, X. The Effect of Marine Power Generation Technology on the Evolution of Energy Demand for New Energy Vehicles. J. Coast. Res. 2020, 103, 1006. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Model-Based Design of an Improved Electric Drive Controller for High-Precision Applications Based on Feedback Linearization Technique. Electronics 2021, 10, 2954. [Google Scholar] [CrossRef]
- Benedetti, D.; Agnelli, J.; Gagliardi, A.; Dini, P.; Saponara, S. Design of an Off-Grid Photovoltaic Carport for a Full Electric Vehicle Recharging. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Dini, P.; Saponara, S. Analysis, design, and comparison of machine-learning techniques for networking intrusion detection. Designs 2021, 5, 9. [Google Scholar] [CrossRef]
- Qian, Y.; Jiang, C.; Chen, C. Research on the Effects of New Energy Power Generation on Power System. In Proceedings of the International Conference on Logistics Engineering, Management and Computer Science (LEMCS 2015), Shenyang, China, 29–31 July 2015; pp. 1146–1150. [Google Scholar]
- Conlon, T.; Waite, M.; Modi, V. Assessing new transmission and energy storage in achieving increasing renewable generation targets in a regional grid. Appl. Energy 2019, 250, 1085–1098. [Google Scholar] [CrossRef]
- Cosimi, F.; Dini, P.; Giannetti, S.; Petrelli, M.; Saponara, S. Analysis and Design of a Non-linear MPC Algorithm for Vehicle Trajectory Tracking and Obstacle Avoidance. In Proceedings of the International Conference on Applications in Electronics Pervading Industry, Environment and Society, Pisa, Italy, 21–22 September 2020; pp. 229–234. [Google Scholar]
- Bernardeschi, C.; Dini, P.; Domenici, A.; Saponara, S. Co-Simulation and Verification of a Non-Linear Control System for Cogging Torque Reduction in Brushless Motors. In Proceedings of the International Conference on Software Engineering and Formal Methods, Oslo, Norway, 16–20 September 2019; pp. 3–19. [Google Scholar]
- Li, Y.; Shu, Z.; Zhu, Q. Application of Wave Power Generation in New Energy. J. Coast. Res. 2020, 105, 89–92. [Google Scholar] [CrossRef]
- Kim, S.H.; Baek, S.C.; Choi, K.B.; Park, S.J. Design and installation of 500-kW floating photovoltaic structures using high-durability steel. Energies 2020, 13, 4996. [Google Scholar] [CrossRef]
- Wu, Z.; Chang, Y.; Li, Q.; Cai, R. A Novel Method for Tunnel Digital Twin Construction and Virtual-Real Fusion Application. Electronics 2022, 11, 1413. [Google Scholar] [CrossRef]
- Benedetti, D.; Agnelli, J.; Gagliardi, A.; Dini, P.; Saponara, S. Design of a Digital Dashboard on Low-Cost Embedded Platform in a Fully Electric Vehicle. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–5. [Google Scholar]
- Coteli, R.; Acikgoz, H.; Ucar, F.; Dandil, B. Design and implementation of Type-2 fuzzy neural system controller for PWM rectifiers. Int. J. Hydrog. Energy 2017, 42, 20759–20771. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, J.S.; Lee, K.B. Sinusoidal Harmonic Voltage Injection PWM Method for Vienna Rectifier with an LCL-filter. IEEE Trans. Power Electron. 2020, 36, 2875–2888. [Google Scholar] [CrossRef]
- Pierpaolo, D.; Saponara, S. Control System Design for Cogging Torque Reduction Based on Sensor-Less Architecture. In Proceedings of the International Conference on Applications in Electronics Pervading Industry, Environment and Society, Pisa, Italy, 11–13 September 2019; pp. 309–321. [Google Scholar]
- Li, Q.; Jiang, D. Variable Switching Frequency PWM Strategy of Two-Level Rectifier for DC-link Voltage Ripple Control. IEEE Trans. Power Electron. 2017, 33, 7193–7202. [Google Scholar] [CrossRef]
- Vanco, W.E.; Silva, F.B.; Monteiro, J.; Oliveira, J.M.D.; Alves, A.C.; Júnior, C.A. Analysis of the oscillations caused by harmonic pollution in isolated synchronous generators. Electr. Power Syst. Res. 2017, 147, 280–287. [Google Scholar] [CrossRef]
- Xu, H.; Shao, Z.; Chen, F. Data-Driven Compartmental Modeling Method for Harmonic Analysis—A Study of the Electric Arc Furnace. Energies 2019, 12, 4378. [Google Scholar] [CrossRef] [Green Version]
- Alabduljabbar, A.A.; Smiai, M. A Methodology for Designing Low Power Factor Penalties in Distribution Networks. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Dini, P.; Saponara, S. Design of an observer-based architecture and non-linear control algorithm for cogging torque reduction in synchronous motors. Energies 2020, 13, 2077. [Google Scholar] [CrossRef]
- Hou, M.K.; Chen, C.H.; Cheng, M.Y. Design and analysis of a single-phase low-frequency active power factor correction circuit: A symmetric trapezoidal current waveform approach. Electr. Eng. 2016, 98, 257–270. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, P.; Wu, T.; Parhi, K.K.; Zeng, X.; Chen, Y. A low-power twiddle factor addressing architecture for split-radix FFT processor. Microelectron. J. 2021, 117, 105276. [Google Scholar] [CrossRef]
- Xu, D.P.; Jiang, Y.W.; Kwon, J.H.; Hwang, S.M. Analysis of the Effects of Electromagnetic Circuit Variables on Sound Pressure Level and Total Harmonic Distortion in a Balanced Armature Receiver. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Cogging torque reduction in brushless motors by a nonlinear control technique. Energies 2019, 12, 2224. [Google Scholar] [CrossRef] [Green Version]
- Dutta, A.; Koley, K.; Saha, S.K.; Sarkar, C.K. Impact of temperature on linearity and harmonic distortion characteristics of underlapped FinFET. Microelectron. Reliab. 2016, 61, 99–105. [Google Scholar] [CrossRef]
- Akbari, A.; Danesh, M.; Khalili, K. A method based on spindle motor current harmonic distortion measurements for tool wear monitoring. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 5049–5055. [Google Scholar] [CrossRef]
- Barbie, E.; Rabinovici, R.; Kuperman, A. Closed-Form Analytic Expression of Total Harmonic Distortion in Single-Phase Multilevel Inverters with Staircase Modulation. IEEE Trans. Ind. Electron. 2019, 67, 5213–5216. [Google Scholar] [CrossRef]
- Hu, H.; He, Z.; Gao, S. Harmonic distortion degradation and filter optimization based on sensitivity studies with considering resonance issue. IEEJ Trans. Electr. Electron. Eng. 2015, 10, 512–520. [Google Scholar] [CrossRef]
- Wang, R.; Li, C.; Han, X.; Liu, C. Carrier-based PWM modulation strategy for dual-output two-stage matrix converter. IET Power Electron. 2019, 12, 2135–2145. [Google Scholar] [CrossRef]
- Ranjan, R.K.; Mazumdar, K.; Pal, R.; Chandra, S. Generation of square and triangular wave with independently controllable frequency and amplitude using OTAs only and its application in PWM. Analog. Integr. Circuits Signal Processing 2017, 92, 1–13. [Google Scholar] [CrossRef]
- Liu, B.; Zha, Y.; Zhang, T.; Chen, S. Triple-state hysteresis direct power control for three phase PWM rectifier. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 2–5 August 2015; pp. 783–789. [Google Scholar]
- Li, Y.; Zhao, H. A Space Vector Switching Pattern Hysteresis Control Strategy in VIENNA Rectifier. IEEE Access 2020, 8, 60142–60151. [Google Scholar] [CrossRef]
- Liu, Y.C.; Ge, X.; Tang, Q.; Deng, Z.; Gou, B. Model predictive current control for four-switch three-phase rectifiers in balanced grids. Electron. Lett. 2016, 53, 44–46. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Li, B.; Liu, J. Robust predictive current control of PWM rectifier under unbalanced and distorted network. IET Power Electron. 2021, 14, 797–806. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Electro-Thermal Model-Based Design of Bidirectional On-Board Chargers in Hybrid and Full Electric Vehicles. Electronics 2021, 11, 112. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Design of adaptive controller exploiting learning concepts applied to a BLDC-based drive system. Energies 2020, 13, 2512. [Google Scholar] [CrossRef]
- Bernardeschi, C.; Dini, P.; Domenici, A.; Palmieri, M.; Saponara, S. Formal verification and co-simulation in the design of a synchronous motor control algorithm. Energies 2020, 13, 4057. [Google Scholar] [CrossRef]
- Renjini, G. Comparison between Peak and Average Current Mode Control of Improved Bridgeless Flyback Rectifier with Bidirectional Switch. In Proceedings of the 2015 International Conference on Technological Advancements in Power and Energy (TAP Energy), Vallikavu, India, 24–26 June 2015; pp. 254–259. [Google Scholar]
- Xiao, D.; Alam, K.S.; Akter, M.P.; Shakib, S.S.I.; Zhang, D.; Rahman, M.F. Modulated model predictive control for four-leg inverters with online duty ratio optimization. IEEE Trans. Ind. Appl. 2020, 56, 3114–3124. [Google Scholar] [CrossRef]
- Mei, J.; Miao, H.; Huang, C.; Xu, Y.; Ma, T.; Hu, Q.; Chen, W. Hybrid one-cycle control scheme for fault-tolerant modular multilevel rectifiers. Int. J. Electron. 2017, 104, 1483–1499. [Google Scholar] [CrossRef]
- Nguyen-Van, T.; Abe, R.; Tanaka, K. Digital adaptive hysteresis current control for multi-functional inverters. Energies 2018, 11, 2422. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.A.; Chang, E.C.; Tseng, C.H.; Chung, T.Y. A single-stage LED tube lamp driver with power-factor corrections and soft switching for energy-saving indoor lighting applications. Appl. Sci. 2017, 7, 115. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Zhang, J.; Wu, X. An Improved Variable On-Time Control Strategy for a CRM Flyback PFC Converter. IEEE Trans. Power Electron. 2016, 32, 915–919. [Google Scholar] [CrossRef]
- Malekanehrad, M.; Adib, E. Bridgeless Single-Phase Step-Down PFC Converter. IET Power Electron. 2016, 9, 2631–2636. [Google Scholar] [CrossRef]
- Narasimhulu, V.; Kumar, D.V.A.; Babu, C.S. Computational intelligence based control of cascaded H-bridge multilevel inverter for shunt active power filter application. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 1–9. [Google Scholar] [CrossRef]



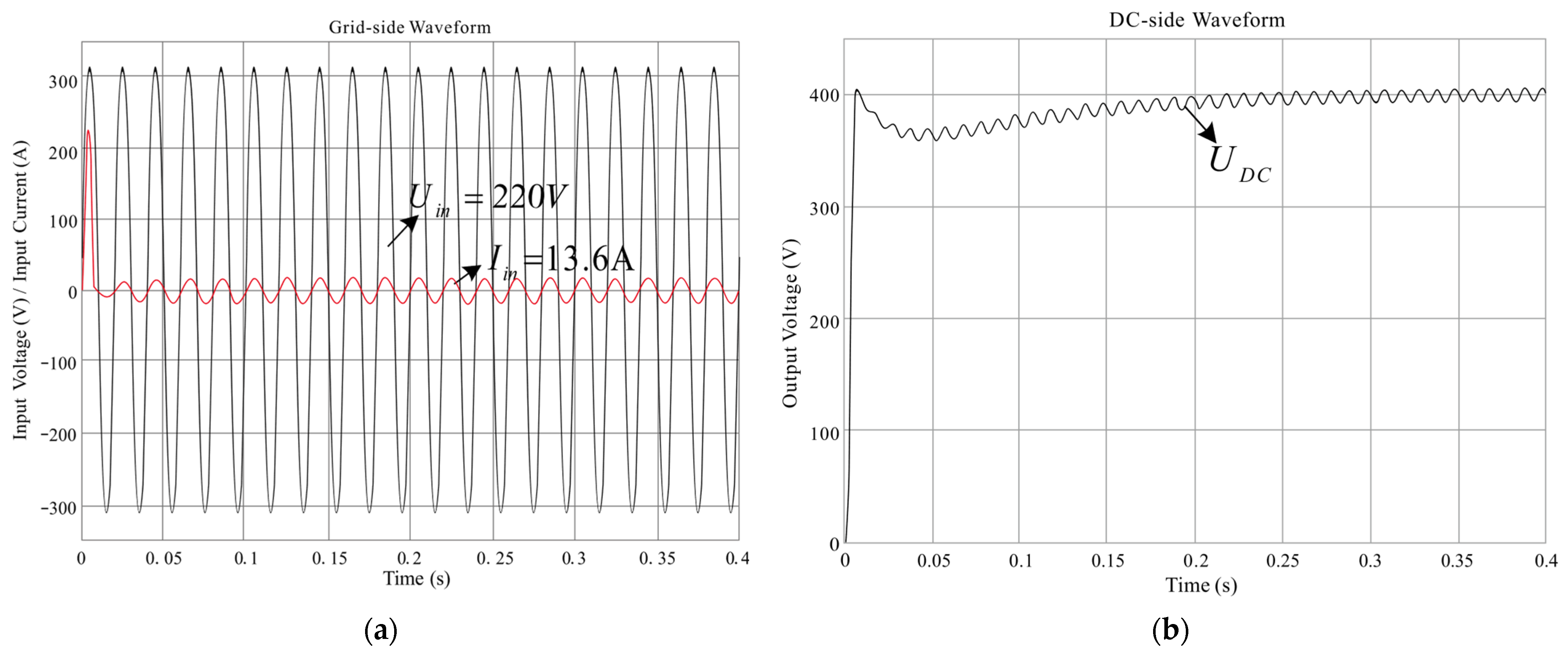

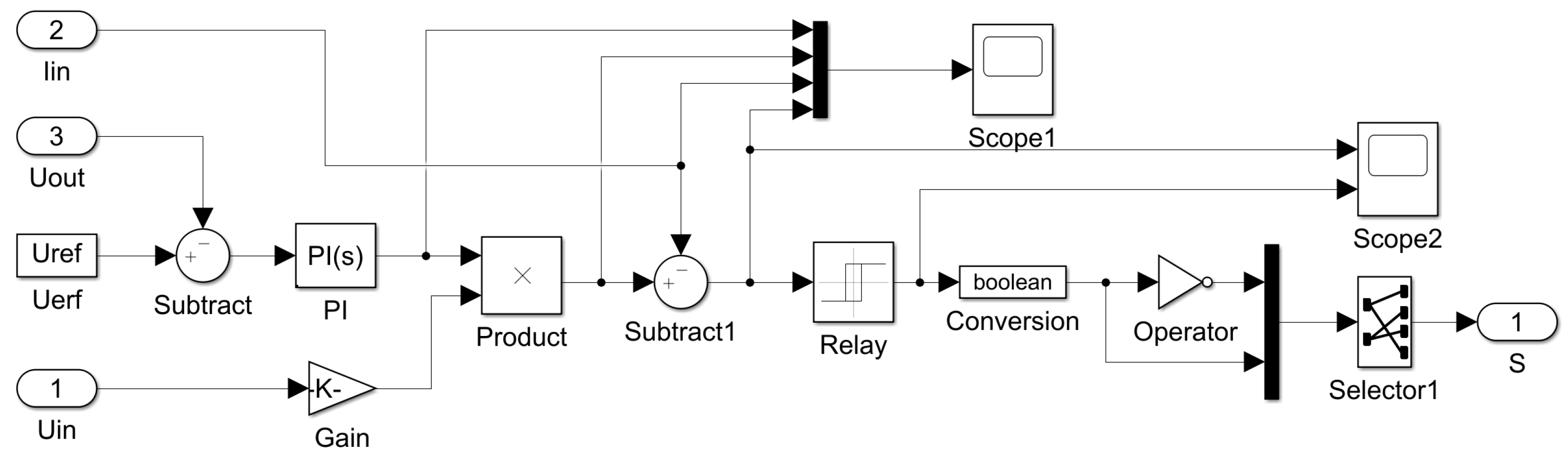
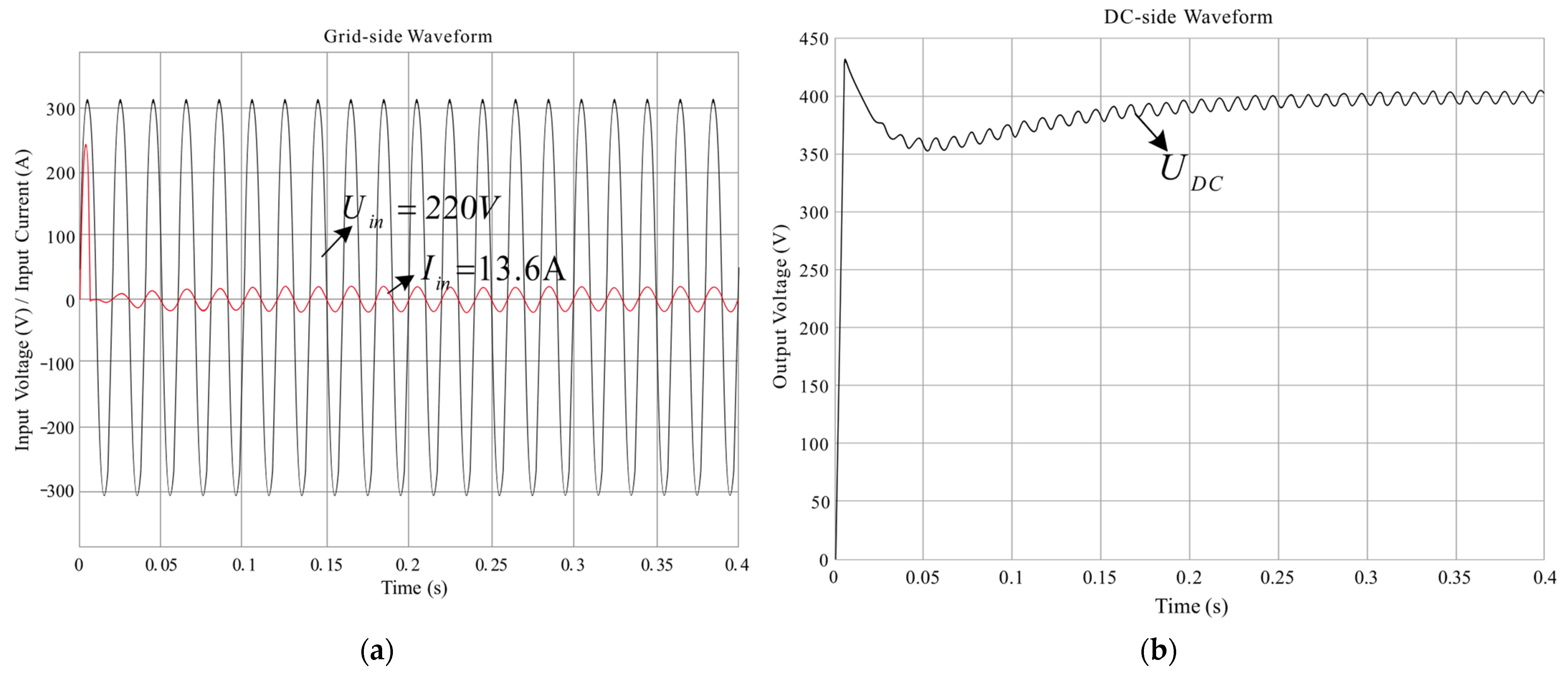
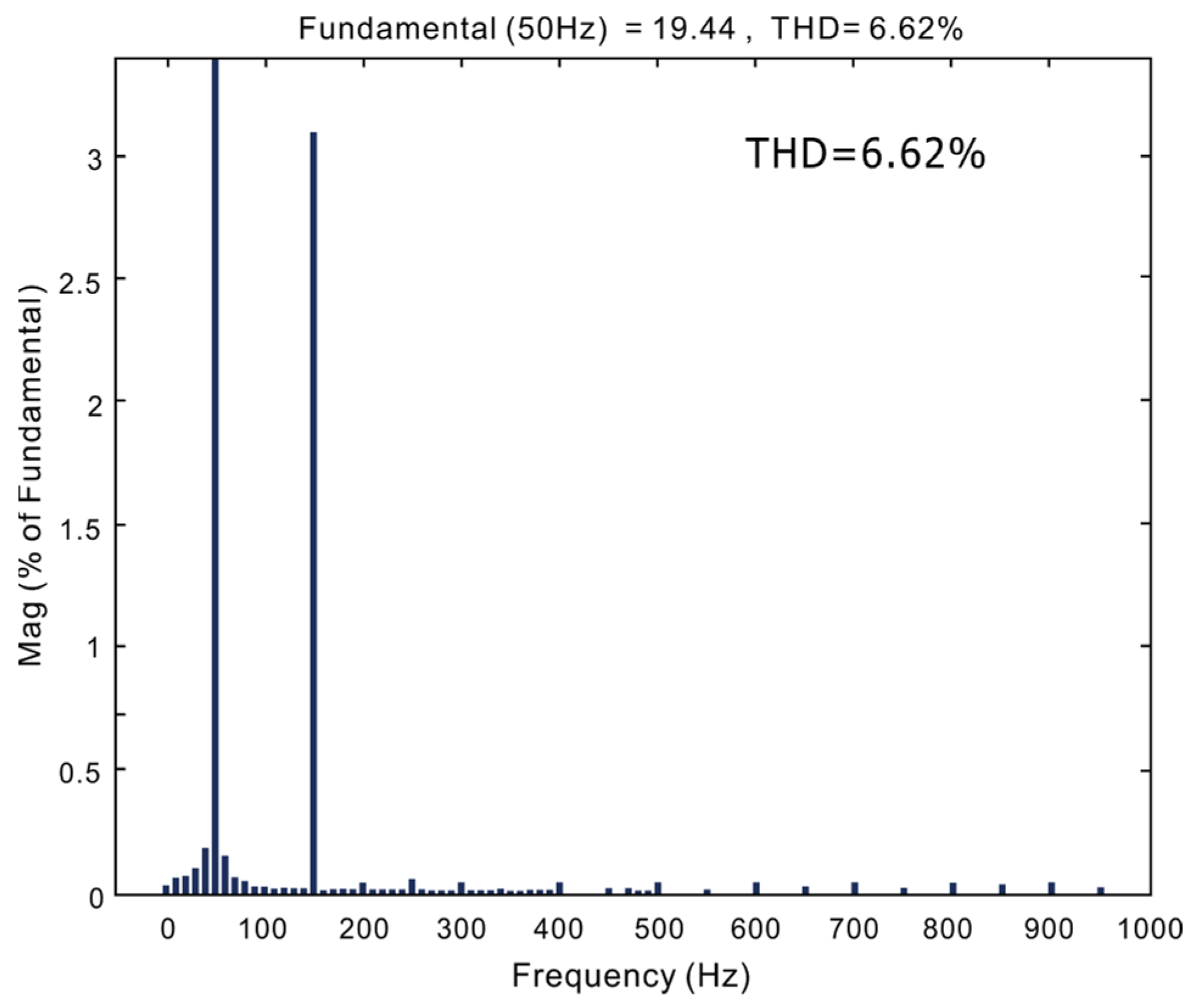











| Circuit Parameters | Value |
|---|---|
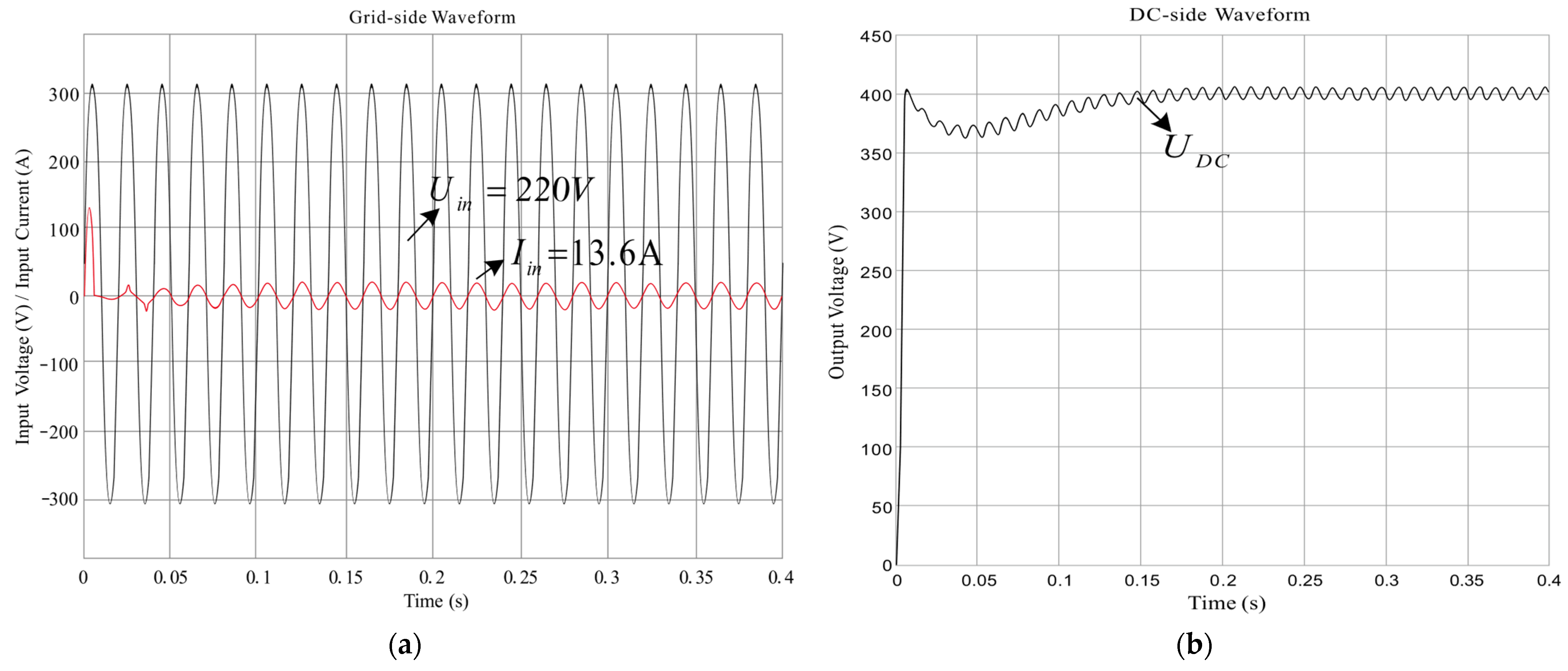
| Grid-side Voltage Uin | 220 VAC/50 Hz |
| DC-side Voltage UDC | 400 VDC |
| Grid-side Inductor L | 820 μH |
| DC-side Capacitor C | 2000 μF |
| Circuit Equivalent Resistor R | 0.2 Ω |
| Switching Frequency F | 100 kHz |
| Rated Output Power PDC | 3000 W |
| Control Algorithm | THD at Grid-Side L of 820 μH | THD at Grid-Side L of 410 μH |
|---|---|---|
| Triangle wave method | 3.53% | 4.16% |
| Hysteresis current method | 6.62% | 8.76% |
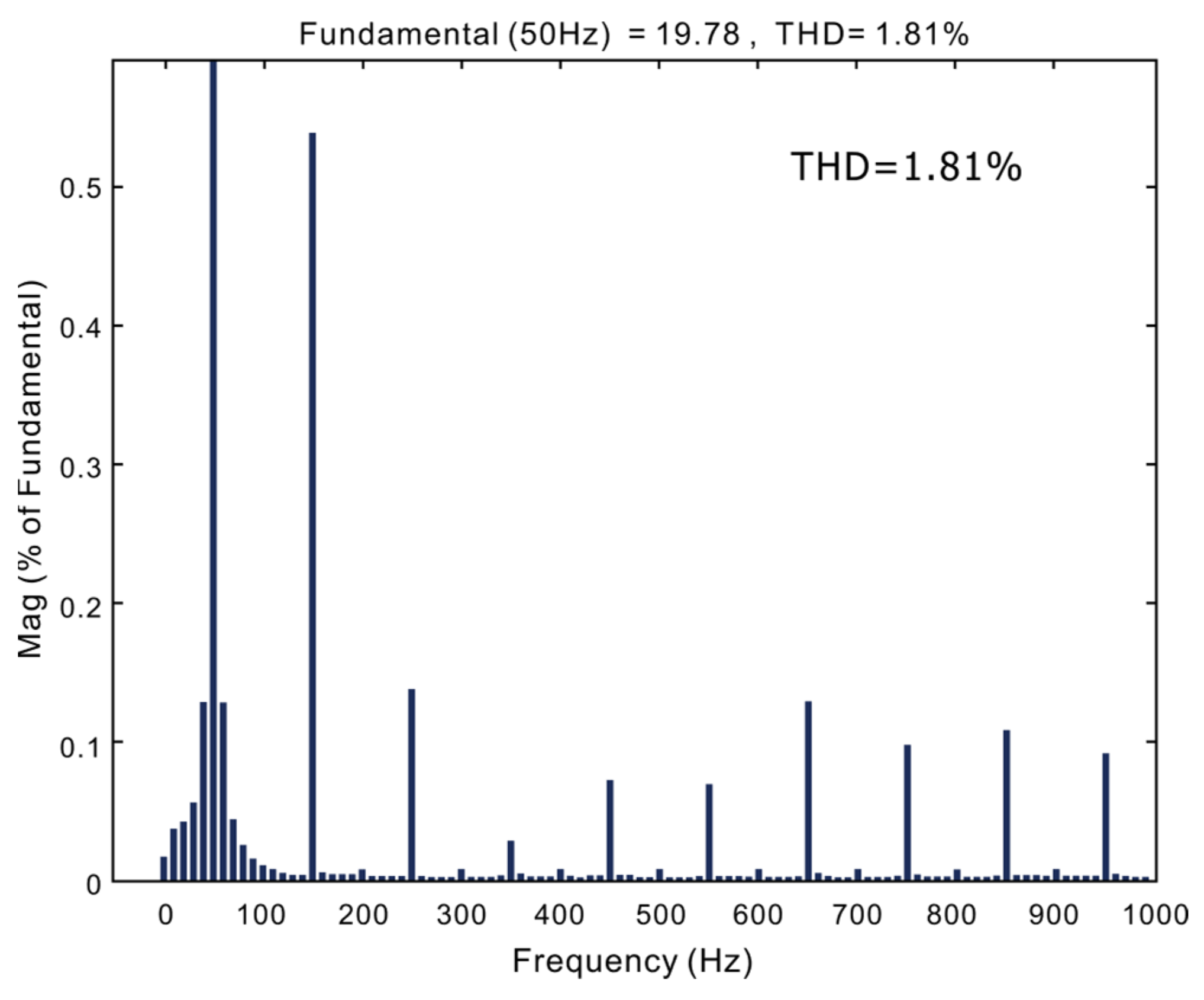
| Predictive current method | 1.86% | 5.26% |
| Proposed method | 1.81% | 2.57% |
| Operating Condition | tr | Ts,5% | Omax | e∞ |
|---|---|---|---|---|
| 220 Vrms and 50 Hz, 400 V | 0.02 s | 0.08 s | 2.3% | <1% |
| 110 Vrms and 60 Hz, 400 V | 0.11 s | 0.24 s | 8.1% | <1% |
| 220 Vrms and 50 Hz, 500 V | 0.02 s | 0.09 s | 3.3% | <1% |
| 110 Vrms and 60 Hz, 500 V | 0.14 s | 0.30 s | 6.7% | <1% |
| VAC (V) | IAC (A) | PAC (W) | PF | VDC (V) | IDC (A) | PDC (W) | Efficiency (%) | THD |
|---|---|---|---|---|---|---|---|---|
| 240.1 | 2.884 | 678.4 | 0.9916 | 399.88 | 1.667 | 666.5 | 96.25% | 6.39% |
| 240.05 | 5.179 | 1243.5 | 0.9965 | 399.89 | 3.004 | 1201.3 | 96.61% | 5.06% |
| 240.0 | 7.819 | 1876.5 | 0.9986 | 399.93 | 4.54 | 1815.7 | 96.76% | 4.72% |
| 239.78 | 10.430 | 2500.8 | 0.9987 | 400.14 | 6.052 | 2421.5 | 96.83% | 4.21% |
| 239.54 | 12.989 | 3111.5 | 0.999 | 400.04 | 7.538 | 3015.4 | 96.91% | 3.92% |
| 239.41 | 14.193 | 3398.0 | 0.9992 | 400.02 | 8.241 | 3296.7 | 97.02% | 3.57% |
| Parameters | Simulated Results | Measured Results |
|---|---|---|
| Input Voltage | 85~240 VAC | 110~240 VAC |
| Frequency | 47~63 Hz | 50 Hz |
| THD | 1.81% | 3.57% |
| Power Factor | 0.9997 | 0.9992 |
| Output Voltage | 380~420 VDC | 380~420 VDC |
| Output Voltage Ripple | 15.2 V | 18 V |
| Maximum Power | 3 kW | 3296 W |
| Peak Efficiency | 98.1% | 97.02% |
| Method | Input Voltage | Frequency | THD | Power Factor | Output Voltage | Output Voltage Ripple | Maximum Power |
|---|---|---|---|---|---|---|---|
| CMC [38] | 90~140 VAC | 35 Hz | >8% | / | 12 VDC | 1.2 V | 30 W |
| OCC [39] | 60 VAC | 60 Hz | 6.2% | 99.8% | 150 VDC | 6 V | 1275 W |
| MDR [40] | 50~110 VAC | 60 Hz | 3.8% | / | 140 VDC | 4 V | 980 W |
| HCC [41] | 110~220 VAC | 50/60 Hz | / | / | 100~150 VDC | / | 150 W |
| DBB [42] | 100~120 VAC | 60 Hz | 6.86% | 94.16% | 60 VDC | / | 18 W |
| VOT [43] | 90~264 VAC | 50 Hz | 4.7% | 98% | 24 VDC | / | 60 W |
| PFC [44] | 110 VAC | 60 Hz | 3.5% | 99.5% | 24 VDC | / | 80 W |
| CI [45] | 254 VAC | / | 4.48% | 98.69% | 1080 VDC | / | 4000 W |
| Proposed | 110~240 VAC | 50 Hz | 3.57% | 99.92% | 380~420 VDC | 18 V | 3296 W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Wang, Z.; Wang, C.; Zhu, Y.; Cao, X. A Novel Improved Coordinate Rotated Algorithm for PWM Rectifier THD Reduction. Electronics 2022, 11, 1435. https://doi.org/10.3390/electronics11091435
Zhu Y, Wang Z, Wang C, Zhu Y, Cao X. A Novel Improved Coordinate Rotated Algorithm for PWM Rectifier THD Reduction. Electronics. 2022; 11(9):1435. https://doi.org/10.3390/electronics11091435
Chicago/Turabian StyleZhu, Yuying, Zuming Wang, Chenyi Wang, Yuyu Zhu, and Xin Cao. 2022. "A Novel Improved Coordinate Rotated Algorithm for PWM Rectifier THD Reduction" Electronics 11, no. 9: 1435. https://doi.org/10.3390/electronics11091435





