Dielectric-Loaded Miniaturized Cavity Bandpass Filter with Improved Power Capacity
Abstract
:1. Introduction
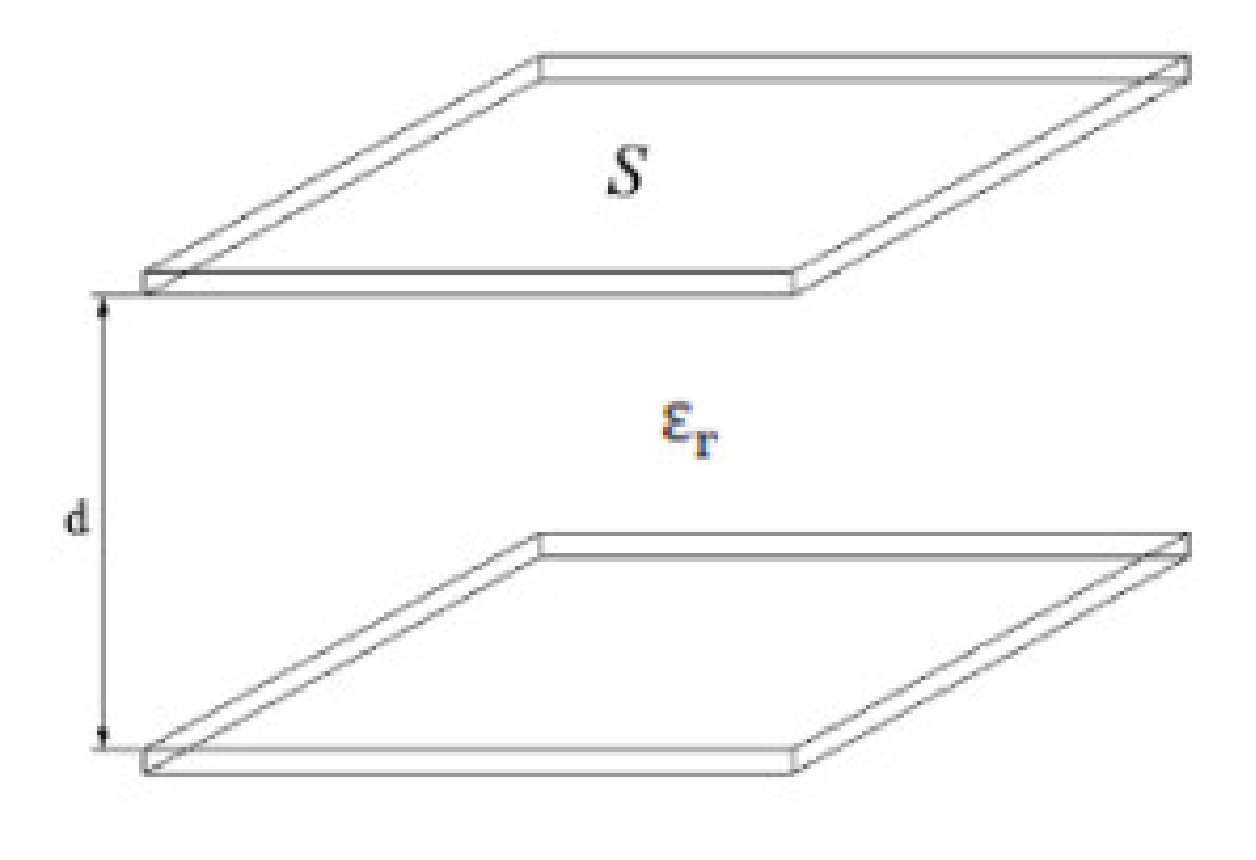
2. Dielectric-Loaded Metal Resonator
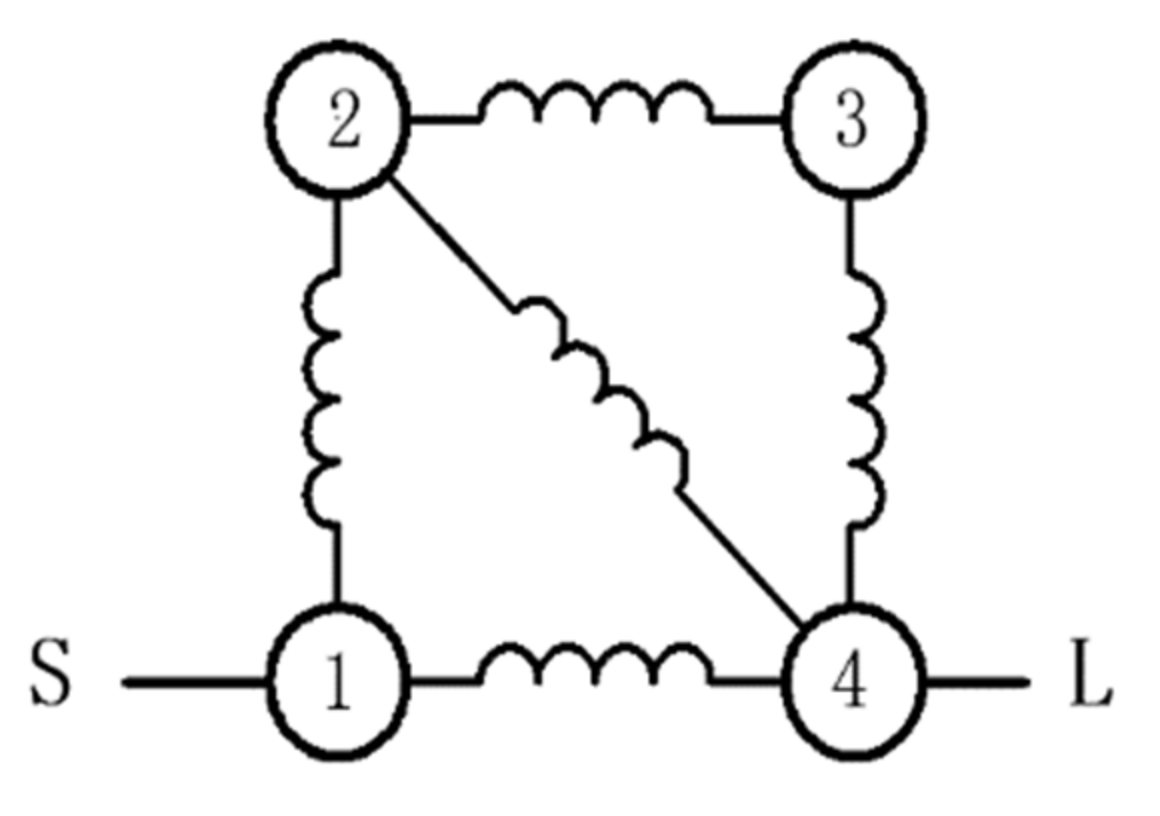
3. Design of Generalized Chebyshev Filter
4. Theory of Filter Power Capacity
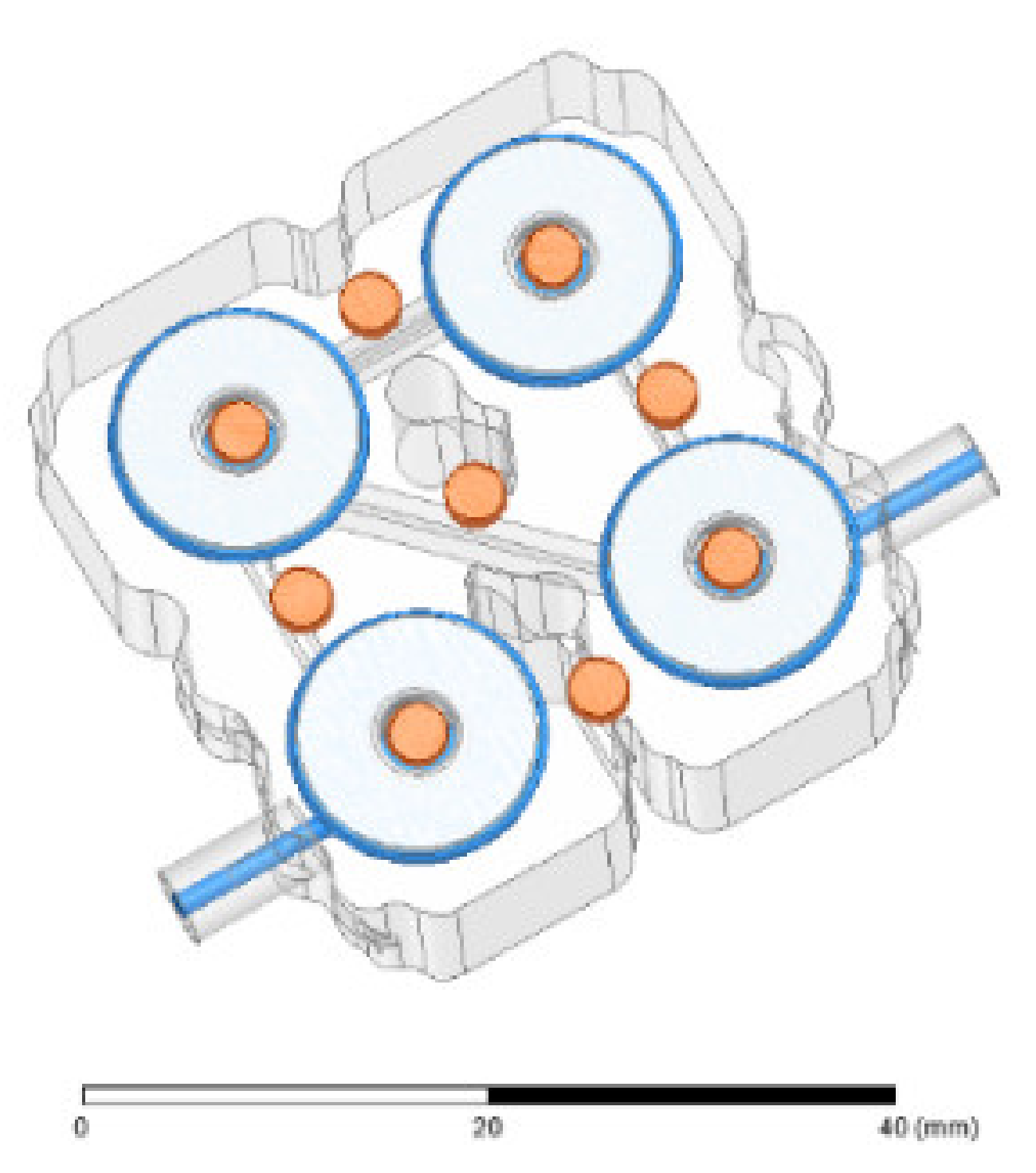
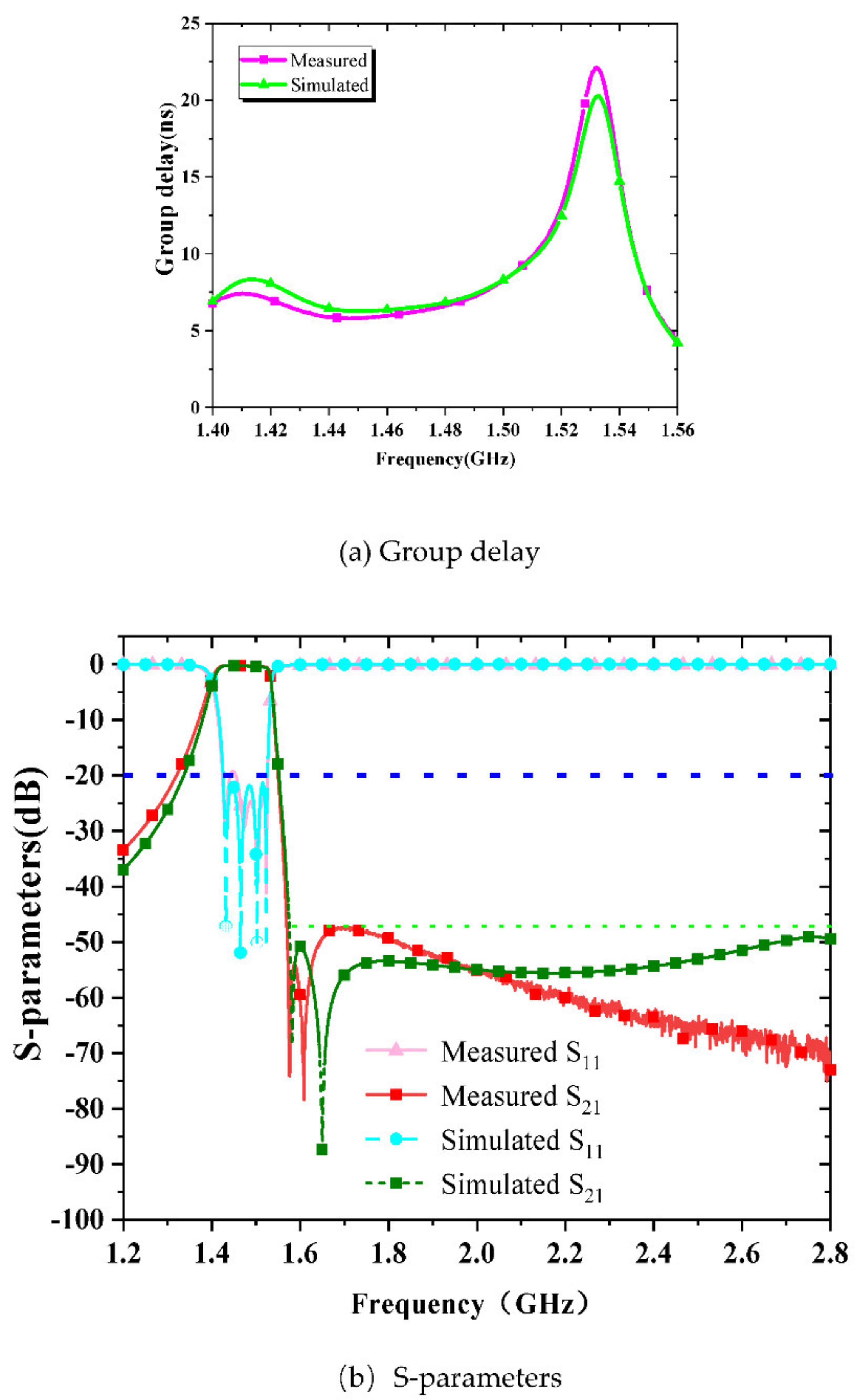
5. Experimental Results of Dielectric-Loaded Miniaturized Cavity Bandpass Filter
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Laplanche, E.; Delhote, N.; Périgaud, A.; Tantot, O.; Verdeyme, S.; Bila, S.; Pacaud, D.; Carpentier, L. Tunable Filtering Devices in Satellite Payloads: A Review of Recent Advanced Fabrication Technologies and Designs of Tunable Cavity Filters and Multiplexers Using Mechanical Actuation. IEEE Microw. Mag. 2020, 21, 69–83. [Google Scholar] [CrossRef]
- Rong, C.; Xu, Y.; Xia, M.; Luo, Y.; Ou, R. Broadband class E GaN power amplifier design in S band with low-pass match. In Proceedings of the 2014 IEEE International Conference on Communiction Problem-Solving, Beijing, China, 5–7 December 2014; pp. 372–375. [Google Scholar] [CrossRef]
- Maity, S.; Ghosal, R.; Gupta, B. Modal Charts of Cylindrical Dielectric Resonators [Application Notes]. IEEE Microw. Mag. 2021, 23, 54–71. [Google Scholar] [CrossRef]
- Shahid, I.; Thalakotuna, D.; Karmokar, D.K.; Mahon, S.J.; Heimlich, M. Periodic Structures for Reconfigurable Filter Design: A Comprehensive Review. IEEE Microw. Mag. 2021, 22, 38–51. [Google Scholar] [CrossRef]
- Doumanis, E.; Goussetis, G.; Vuorio, J.; Hautio, K.; Amper, O.; Kuusmik, E.; Pallonen, J. Tunable Filters for Agile 5G New Radio Base Transceiver Stations [Application Notes]. IEEE Microw. Mag. 2021, 22, 26–37. [Google Scholar] [CrossRef]
- Mao, C.X.; Zhang, Y.; Zhang, X.Y.; Xiao, P.; Wang, Y.; Gao, S. Filtering Antennas: Design Methods and Recent Developments. IEEE Microw. Mag. 2021, 22, 52–63. [Google Scholar] [CrossRef]
- Widaa, A.; Höft, M. Miniaturized Dual-Band Dual-Mode TM-Mode Dielectric Filter in Planar Configuration. IEEE J. Microw. 2022, 2, 326–336. [Google Scholar] [CrossRef]
- Deng, J.Y.; Yuan, D.D.; Yin, J.Y.; Sun, D.; Guo, L.X.; Ma, X.H.; Hao, Y. Ultracompact Bandpass Filter Based on Slow Wave Substrate Integrated Groove Gap Waveguide. IEEE Trans. Microw. Theory Tech. 2022, 70, 1211–1220. [Google Scholar] [CrossRef]
- Zhao, D.; Lin, F.; Sun, H.; Zhang, X.Y. A Miniaturized Dual-Band SIW Filtering Antenna with Improved Out-of-Band Suppression. IEEE Trans. Antennas Propag. 2022, 70, 126–134. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, G.; Liu, Z.; Tang, W.; Yang, J. Compact Balanced Bandpass Filter Based on Equilateral Triangular Patch Resonator. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 90–93. [Google Scholar] [CrossRef]
- Feng, T.; Ma, K.; Wang, Y. A Miniaturized Bandpass Filtering Power Divider Using Quasi-Lumped Elements. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 70–74. [Google Scholar] [CrossRef]
- Qin, T.; Lin, X.Q.; Fan, Y.L. Analysis, Design, and Implementation of Miniaturized Multimode Waveguide Filters Based on Epsilon-Near-Zero Channel Concept. IEEE Trans. Microw. Theory Tech. 2021, 69, 3598–3606. [Google Scholar] [CrossRef]
- Sekiya, N.; Kobayashi, S. Compact, Low Loss, and High Power Handling HTS Dual-Mode Double-Strip Resonator Filter with New Feeding Structure. IEEE Trans. Appl. Supercond. 2019, 29, 1500804. [Google Scholar] [CrossRef]
- Sekiya, N. Design of Compact and High-Power HTS Double-Strip Dual-Mode Patch Resonator Filter for Transmit Filter Applications. IEEE Trans. Appl. Supercond. 2017, 27, 1501804. [Google Scholar] [CrossRef]
- Setsune, K.; Enokihara, A. Elliptic-disc filters of high-T/sub c/superconducting films for power-handling capability over 100 W. IEEE Trans. Microw. Theory Tech. 2000, 48, 1256–1264. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, R.; Vetury, R.; Shealy, J. 40.6 Watt, High Power 3.55 GHz Single Crystal XBAW RF Filters for 5G Infrastructure Applications. In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Free, C.E.; Aitchison, C.S. “RF Filters”, RF and Microwave Circuit Design: Theory and Applications; Wiley: Hoboken, NJ, USA, 2022; pp. 209–237. [Google Scholar] [CrossRef]
- Shan, Q.; Chen, C.; Wu, W. Design of an UWB bandpass filter with a notched band using asymmetric loading stubs. In Proceedings of the 2016 IEEE International Conference on Microwave and Millimeter Wave Technology (ICMMT), Beijing, China, 5–8 June 2016; pp. 410–412. [Google Scholar] [CrossRef]
- Zhou, P.; Shi, Y.; Tang, W. Multi-Mode and Ultra-Wideband Common-Mode Filter Based on Asymmetric Short-Stub Loaded Resonator. In Proceedings of the 2019 IEEE MTT-S International Wireless Symposium (IWS), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Aidoo, M.W.; Song, K. Reconfigurable Dual-Band Bandpass Filter Using Stub-Loaded Stepped-Impedance Resonators. In Proceedings of the 2019 16th International Computer Conference on Wavelet Active Media Technology and Information Processing, Chengdu, China, 14–15 December 2019; pp. 434–437. [Google Scholar] [CrossRef]
- Li, H.-Y.; Xu, J.-X.; Zhang, X.Y. Miniaturized Balanced Filtering Power Dividers with Arbitrary Power Division Ratio Using Multi-Mode Dielectric Resonator in Single Cavity. IEEE Trans. Circuits Syst. II Express Briefs 2022. [Google Scholar] [CrossRef]
- Zheng, D.; Wu, K. Generalized Design Considerations of Leaky-Wave Antennas Based on Multi-Mode Resonator (MMR) Concept. In Proceedings of the 2021 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (APS/URSI), Singapore, 4–10 December 2021; pp. 641–642. [Google Scholar] [CrossRef]
- Zhao, G.; Li, M.; Zhao, R.; Tu, Z.; Yan, Y.; Mo, X. Highly Selective UWB Bandpass Filter with Dual Notch Bands Using Stub Loaded Multiple-mode Resonator. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; pp. 1299–1309. [Google Scholar] [CrossRef]
- Luo, B.; Li, Q.-Q.; Zhang, J.-b.; Yang, H. A Novel Design of 5G Band Multi-Mode Dielectric Filter with Symmetrical Zeros. In Proceedings of the 2021 IEEE 3rd International Conference on Frontiers Technology of Information and Computer (ICFTIC), Greenville, SC, USA, 12–14 November 2021; pp. 683–686. [Google Scholar] [CrossRef]
- Xu, L.; Yu, W.; Qin, W.; Chen, J.X. Design of Dual-Channel Filter Based on Dual-Mode Dielectric Resonators. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 45–49. [Google Scholar] [CrossRef]
- Fathi, P.; Aliasgari, J.; Karmakar, N.C. Wireless Rotation Sensor Using Dual-layered Two-fold Spiral Resonator. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 789–792. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, J. Differential Dual-Band Filters with Flexible Frequency Ratio Using Asymmetrical Shunt Branches for Wideband CM Suppression. IEEE Trans. Microw. Theory Tech. 2017, 65, 4606–4615. [Google Scholar] [CrossRef]
- Huong, T.T.T.; Tuan, A.D.; Thao, T.T.; Vu, V.Y. A Novel Resonator Structure to Improve Power Handling Capacity in Iris Coupled Cavity Filter. In Proceedings of the 2019 International Conference on Advanced Technologies for Communications (ATC), Hanoi, Vietnam, 17–19 October 2019; pp. 98–102. [Google Scholar] [CrossRef]
- Wu, Y.; Fourn, E.; Besnier, P.; Quendo, C. Direct Synthesis of Multiband Bandpass Filters with Generalized Frequency Transformation Methods. IEEE Trans. Microw. Theory Tech. 2021, 69, 3820–3831. [Google Scholar] [CrossRef]
- Musonda, E.; Hunter, I.C. Exact Design of a New Class of Generalized Chebyshev Low-Pass Filters Using Coupled Line/Stub Sections. IEEE Trans. Microw. Theory Tech. 2015, 63, 4355–4365. [Google Scholar] [CrossRef] [Green Version]
- Kuo, J.; Ng, C.L. Explicit Solution to Exact Synthesis of Cross-Coupled Quadruplet Filter with a Real-Frequency Zero Pair. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 141–143. [Google Scholar] [CrossRef]
- Zeng, L.Y.; Yang, Y.; Wu, Y.; Yu, M.; Peng, J.; Liang, D. Exploiting Redundancy in Direct Synthesis for Inline Filters. IEEE Trans. Microw. Theory Tech. 2021, 69, 4489–4498. [Google Scholar] [CrossRef]
- Nwajana, A.O.; Dainkeh, A.; Yeo, K.S.K. Substrate integrated waveguide (SIW) bandpass filter with novel microstrip-CPW-SIW input coupling. J. Microw. Optoelectron. Electromagn. Appl. 2017, 16, 393–402. [Google Scholar] [CrossRef]
- Cai, C.; Wang, J.; Zhu, L.; Wu, W. A New Approach to Design Microstrip Wideband Balun Bandpass Filter. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 116–118. [Google Scholar] [CrossRef]
- Circuit Modelling of Bandpass/Channel Filter with Microstrip Implementation. Available online: http://section.iaesonline.com/index.php/IJEEI/article/view/2466 (accessed on 31 March 2022).
- Hu, S.; Hu, Y.; Zheng, H.; Zhu, W.; Gao, Y.; Zhang, X. A Compact 3.3–3.5 GHz Filter Based on Modified Composite Right-/Left-Handed Resonator Units. Electronics 2020, 9, 1. [Google Scholar] [CrossRef] [Green Version]
- Saeed, R. A compact microstrip low-pass filter with ultra wide stopband using compact microstrip resonant cells. Int. J. Microw. Wirel. Technol. 2017, 9, 1023–1027. [Google Scholar]
- Zhang, P.; Liu, L.; Chen, D.; Weng, M.-H.; Yang, R.-Y. Application of a stub-loaded square ring resonator for wideband bandpass filter design. Electronics 2020, 9, 176. [Google Scholar] [CrossRef] [Green Version]
- Jung, E.-Y.; Hwang, H.-Y. A balun-BPF using a dual-mode ring resonator. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 652–654. [Google Scholar] [CrossRef]






| Relative Permittivity | 1.0 | 2.1 | 10 |
| Resonant Frequency f (MHz) | 1726.9 | 1472.3 | 1008.4 |
| Ref. | (GHz) | Filter Order | Size | IL 1 (dB) | RL 2 (dB) | FBW 3 | GD 4 (ns) |
|---|---|---|---|---|---|---|---|
| [33] | 1.684 | none | 0.21 × 0.63 | 1.3 | 22 | 4.00% | none |
| [34] | 1.000 | none | 0.59 × 0.32 | 3 | 10 | 30.00% | none |
| [35] | 2.600 | 3 | 0.16 × 0.09 | 1.8 | 25 | 3.00% | none |
| [38] | 4.500 | 2 | 0.28 × 0.09 | 3.0 | 10.0 | 60.00% | ≤0.4 |
| [36] | 3.350 | 2 | 0.12 × 0.09 | 2.4 | 20.0 | 5.97% | ≤2.5 |
| [39] | 2.450 | 2 | 0.15 × 0.13 | 2.4 | 20.0 | 1.63% | none |
| This work | 1.475 | 4 | 0.19 × 0.08 | 0.49 | 20.0 | 6.10% | ≤21.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rong, C.; Xu, Y.; Zhang, Y. Dielectric-Loaded Miniaturized Cavity Bandpass Filter with Improved Power Capacity. Electronics 2022, 11, 1441. https://doi.org/10.3390/electronics11091441
Rong C, Xu Y, Zhang Y. Dielectric-Loaded Miniaturized Cavity Bandpass Filter with Improved Power Capacity. Electronics. 2022; 11(9):1441. https://doi.org/10.3390/electronics11091441
Chicago/Turabian StyleRong, Chuicai, Yun Xu, and Yuming Zhang. 2022. "Dielectric-Loaded Miniaturized Cavity Bandpass Filter with Improved Power Capacity" Electronics 11, no. 9: 1441. https://doi.org/10.3390/electronics11091441
APA StyleRong, C., Xu, Y., & Zhang, Y. (2022). Dielectric-Loaded Miniaturized Cavity Bandpass Filter with Improved Power Capacity. Electronics, 11(9), 1441. https://doi.org/10.3390/electronics11091441





