A New Fast Logarithm Algorithm Using Advanced Exponent Bit Extraction for Software-Based Ultrasound Imaging Systems

Abstract

Ultrasound B-mode imaging provides anatomical images of the body with a high resolution and frame rate. Recently, to improve its flexibility, most ultrasound signal and image processing modules in modern ultrasound B-mode imaging systems have been implemented in software. In a software-based B-mode imaging system, an efficient processing technique for calculating a logarithm instruction is required to support its high computational burden. In this paper, we present a new method to efficiently implement a logarithm operation based on exponent bit extraction. In the proposed method, the exponent bit field is first extracted and then some algebraic operations are applied to improve its precision. To evaluate the performance of the proposed method, the peak signal-to-noise ratio (PSNR) and the execution time were measured. The proposed efficient logarithm operation method substantially reduced the execution time, i.e., eight times, compared to direct computation while providing a PSNR of over 50 dB. These results indicate that the proposed efficient logarithm computation method can be used for lowering the computational burden in software-based ultrasound B-mode ultrasound imaging systems while improving or maintaining the image quality.

1. Introduction

A medical ultrasound imaging system can show the anatomical structure of the body in real time. The reconstruction of ultrasound images has traditionally been implemented using hardware-based signal and image processing engines. Recently, to enhance their computational flexibility, research on software-based ultrasound imaging systems has been actively conducted with various advanced computing technologies [1,2,3]. For software-based ultrasound systems, an efficient software implementation method is necessary for supporting the complex signal and image processing blocks demanding high computational power.

In ultrasound B-mode imaging, log compression has been widely used for emphasizing weak scattering signals on the same scale as strong specular reflections [4]. In log compression, the envelope signal, after receive beamforming and quadrature demodulation, is transformed by applying a logarithm operation. Since the computation of logarithm operations generally requires complex floating operation on software-based ultrasound imaging systems, it takes a longer execution time. Therefore, to implement a computationally efficient software-based ultrasound imaging system, it is necessary to minimize the execution time of the logarithm operation.

To lower the computational complexity in logarithm operations, various approximation methods, such as a look-up table (LUT) and Taylor’s series, have been proposed [5,6]. In this study, to further lower this computational complexity, a new approximation method, in which the exponent bits of IEEE 754 floating-point envelope data are utilized, is presented. The IEEE 754 floating-point format is the standard notation used to represent floating-point data in computers [7]. According to this notation, certain bits are assigned to indicate the exponent of a given floating point value. In this study, those bits for exponent are used to approximate the logarithm operation. In addition, to further lower the execution time for logarithm operations, single instruction and multiple data (SIMD) programming techniques were applied. The feasibility of the proposed logarithm approximation method was demonstrated by implementing it with an ARM Corted-A9 processor (Arm Holdings PLC, Cambridge, UK) embedded in a commercial system-on-chip (SoC) board (XC7Z020-CLG484-1, Xilinx Inc., San Jose, CA, USA).

2. Methods

2.1. IEEE 754 Format

Computers generally use the floating-point standard notation for real numbers. Currently, the most widely used floating-point standard is the IEEE 754 standard. As shown in Figure 1, this standard uses 3 bit fields for one real number expression [7].

Each bit field represents the sign, exponent, and mantissa of the real number. Thus, a certain real number (i.e., $v$) can be expressed by the following [7]:

$$v={\left(-1\right)}^S\times 2^{E-bias}\times \left(1+2^{1-p}\times T\right)$$

(1)

where bias is a constant determined by the standard, and 127 is used for the C language float type on a 64-bit AP. When the given real number v is positive—such as the envelope signal in ultrasound B-mode imaging—Equation (1), after taking the log of both sides, can be rewritten by the following:

$${log}_2\left(v\right)=\left(E-bias\right)+{log}_2\left(1+2^{1-p}\ast T\right)$$

(2)

where T is composed of p—1 bits. Since the second term on the right side of Equation (2) is less than 1, after applying a rounding down operation (i.e., RoundDown), Equation (2) can be represented by the following:

$$RoundDown({log}_2\left(v\right))=E-bias$$

(3)

As shown in Equation (3), therefore, if a real number is expressed based on the IEEE 754 standard, the exponent bit has an approximate relation to the result of the logarithm operation. In the proposed logarithm approximation method, these relationships are utilized.

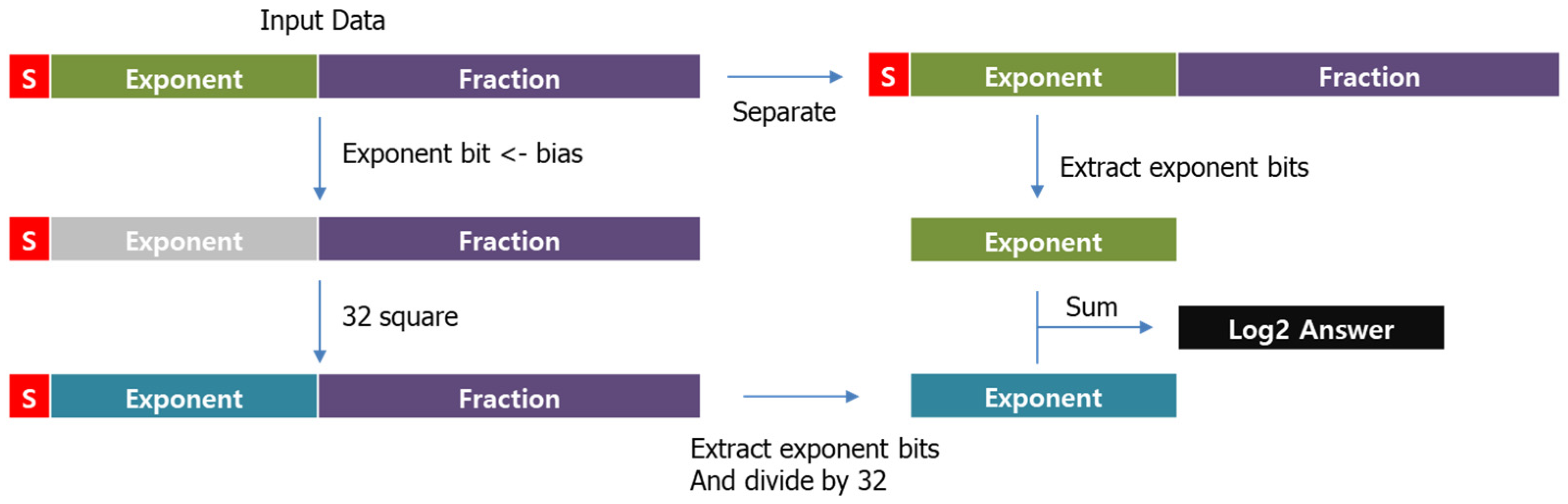
2.2. Proposed Method: Logarithm Computation with Advanced Exponent Bit Extraction

The log compression process in ultrasound B-mode imaging requires several considerations compared to a general logarithm operation. First, since the ultrasound B-mode imaging system performs log compression on the envelope of the received signal, the input is always positive. In addition, log-compressed signals are expressed as an eight-bit integer for display after applying a discard operation [8]. Therefore, it is possible to approximate the logarithm operation to show an appropriate level of accuracy without considering the sign. By considering these characteristics, in the proposed method, before extracting the exponent bit in Equation (3), additional processes are needed for improving its accuracy and running speed on an AP.

Figure 2 shows the block diagram of the processing modules in the proposed method. Here, input floating-point data are first parallelized for fast processing of operations. Then, the exponent bit of each data piece is separated to prevent overflow in the following processing steps. To enhance the numerical accuracy of the proposed method, an additional power operation is performed on the separated mantissa. Finally, the logarithm operation is completed by extracting the exponent bit. Each step in the proposed method will be explained in the following sub-sections.

2.3. Data-Level Parallelization

Since the proposed method performs powering operations on the input number, the iterative multiplication operation of the input data takes the main computing time. Therefore, to utilize SIMD operations supported in modern APs, multiple input data are merged to form a single vector register, and these multiple data can be processed in one instruction processing time [9]. Thus, the multiplication operation is processed through data-level parallelism, and the efficiency of the operation can be increased.

2.4. Exponent Bit Separation

The proposed method raises the parallelized input data to the power of the data to enhance the numerical resolution. Due to this powering operation, an overflow issue may occur in the 32-bit floating-point precision range. Moreover, the use of the 64-bit double precision data type may result in a performance drop due to a low data parallelization ratio. Therefore, by separating the exponent bit field, overflow in the subsequent power operation can be prevented. By taking the N square operation on both sides, Equation (1) can be rewritten as follows:

$$v^N=2^{N\times \left(E-bias\right)}\times {\left(1+2^{1-p}\times T\right)}^N$$

(4)

As indicated in Equation (4), as N increases, the number of power terms of two becomes too large for the single precision representation. However, the second term on the right-hand side is less than the Nth power of two. Therefore, by separating the exponent bit field of the parallelized input data, the power is performed only on the second term on the right side. The bias in Equation (4) is written to the exponent part to make the semantic value of the exponent part 0, and then, only the remaining mantissa part is N-times squared. In addition, the separated exponent part is multiplied by N. By doing so, the operation equivalent to the N square of the input data can be performed in the single precision expression.

2.5. Precision Enhancement

In ultrasound B-mode imaging systems, the result of the log operation is converted into decibel units to recontract an image [10,11]. Thus, the envelope signal (v) in Equation (1) can be represented in decibel units by

$$dB\left(v\right)=20lo{g}_{10}\left(v\right)$$

(5)

However, since the exponent bit extracted by Equation (3) is a round-down value after applying a $lo{g}_2()$ operation, Equation (5) can be rewritten as

$$dB\left(v\right)\approx RoundDown(lo{g}_2\left(v\right))\times {\log }_{10}2\times 20=\left(E-bias\right)\times {\log }_{10}2\times 20$$

(6)

Then, in ultrasound B-mode imaging systems, the dynamic range (DR) of the signal in Equation (6) is typically limited to be displayed, e.g., 40–60 dB. For a given DR value, when the maximum decibel value of the signal to be expressed by ultrasound B-mode imaging systems is assumed to be $d{B}_{max}$, Equation (6) can be rewritten as

$$\max \left(\min \left(\frac{RoundDown\left(lo{g}_2\left(v\right)\right)\times 20{log}_{10}2-d{B}_{max}}{DR}, 0\right)+1,0\right)$$

(7)

From Equation (7), all signals within the DR to be expressed are mapped from 0 to 1. Regarding this value, in order to display it on a display using a n-bit integer data type, the brightness value of each pixel is calculated by remapping the result of Equation (7) to $0~\left(2^n-1\right)$ as

$$\max \left(\min \left(\frac{RoundDown\left(lo{g}_2\left(v\right)\right)\times 20{log}_{10}2-d{B}_{max}}{DR}, 0\right)+1,0\right)\times \left(2^n-1\right)$$

(8)

The pixel brightness value calculated by Equation (8) has a discrete value. This is because the brightness value of the pixel was derived from the value of Equation (3) having a discrete value. In addition, the discrete interval is changed as the value of Equation (3), in which one is a discrete interval, is multiplied by a certain number.

The discrete spacing of pixel values is the total product of coefficients multiplied by the $lo{g}_2()$ truncated value in Equation (8) as follows:

$$\frac{20{log}_{10}2\times \left(2^n-1\right)}{DR}$$

(9)

As seen in Equation (9), this is independent of $d{B}_{max}$. In general, since the ultrasound B-mode imaging system uses eight as value of n and 60 as the value of DR, the quantized discrete interval of the image output calculated by substituting this value into Equation (9) is 25.68. According to the change of the envelope signal, the brightness of each pixel shows only a discrete change of 25.68 in 256 steps and has quantization error. The detained change of soft tissues appears as a numerical difference smaller than this discrete interval of 25.68 on the display. Therefore, such low numerical resolution is insufficient to express detailed changes in soft tissues.

As a solution to the quantization error issue, before extracting the exponent bit, as shown in Equation (4), the envelope signal (v) is N squared and then compensated by division after the round down operation so that the size of the discretization step in Equation (9) can be reduced. Thus, Equation (6) can be rewritten as

$$dB\left(v\right)\approx RoundDown(lo{g}_2\left(v^N\right))/N\times {\log }_{10}2\times 20$$

(10)

Then, Equation (8) representing the brightness value of a pixel can be represented by

$$\max \left(\min \left(\frac{RoundDown\left(lo{g}_2\left(v^N\right)\right)/N\times 20{log}_{10}2-d{B}_{max}}{DR}, 0\right)+1,0\right)\times \left(2^n-1\right)$$

(11)

Finally, Equation (9) showing the size of the pixel brightness value quantization interval is given as

$$\frac{20{log}_{10}2\times \left(2^n-1\right)}{DR\times N}$$

(12)

As seen in Equation (12), N reduces the output quantization error. However, since the input must be multiplied by the size of N, the complexity of the operation and the size of N are inversely proportional. Therefore, it is necessary to select an appropriate N value.

In this study, 32 was selected as the value of N as a compromised value of these trade-off relationship. This is in consideration of the characteristics of a display monitor, in which brightness values for each pixel are stored and expressed as an integer data type. In addition, when N is larger than 32, the size of the pixel brightness value quantization interval in Equation (12) is smaller than 1 so that all integer data can be used on the display without a gap. However, since the exponent bit separation technique in Section 2.4 is used, only the separated mantissa (fraction bit) is raised to the power of 32. The exponent bit must be multiplied by 32, but, as shown in Equation (9), it is divided by 32 again so that it is not necessary to multiply by 32.

2.6. Exponent Bit Extraction

Now, the input real number is divided into an exponent part separated by exponent bit separation and a mantissa part to the power of 32. Meanwhile, if a real number is multiplied by 32 and then log2 is taken, it is expressed by the following:

$${\log }_2{v}^{32}=32\left(E-bias\right)+{\log }_2{\left(1+2^{1-p}\ast T\right)}^{32}$$

(13)

Then, after performing rounding and dividing by 32, Equation (5) can be represented by the following:

$$fix({\log }_2{v}^{32})/32=\left(E-bias\right)+fix({\log }_2{\left(1+2^{1-p}\ast T\right)}^{32})/32$$

(14)

The first term on the right side of Equation (6) is the exponential part separated by exponent bit separation. Then, the second term is equivalent to the mantissa of the input after being powered, exponent-bit-extracted, and divided by 32. Therefore, by adding two values, it is possible to approximate the logarithm operation more accurately and efficiently. All these operations are performed by the SIMD pipeline as described in Figure 3.

2.7. Experimental Setup

To evaluate the efficiency and accuracy of the proposed method, phantom experiments were conducted. In the experiment, two phantom data pieces were obtained by the Vantage™ Research Ultrasound Systems (Verasonics Inc., Kirkland, WA, USA) from two tissue mimicking phantoms (CIRS, SUN NUCLEAR, Louisa, VA, USA). These data were processed with the system-on-chip (SoC) evaluation board (XC7Z020-CLG484-1, Xilinx Inc.) equipped with an ARM Cortex-A9 AP (Arm Holdings PLC, Cambridge, UK). The SIMD operation was implemented with the NEON intrinsic provided by the ARM processor. The code implementing the proposed method was compiled by the GNU compiler collection (GCC).

The accuracy was compared with the log function provided by the math library of the GCC. In addition, the peak signal-to-noise-ratio (PSNR) was computed as follows [12]:

$$PSNR=10{\log }_{10}\left(\frac{MA{X}_i^2}{MSE}\right)$$

(15)

where MAX_i is the maximum value of the image and MSE is the mean squared error between two images from the reference and proposed methods. The processing time was also measured by using the time measurement function of the ARM processor for input data with 192 scanlines and 512 samples.

3. Experiment Results

Figure 4 shows the ultrasound B-mode images from two tissue mimicking phantoms when using the reference (i.e., math library in GCC) and the proposed bit extraction methods along with the Taylor series approximation method. As shown in Figure 4, under visual assessment, it is difficult to identify the difference among the three logarithm computation methods.

For quantitative comparison, the PSNR values for the Taylor series approximation and proposed bit extraction methods were computed, as described in Equation (5). As summarized in

Table 1. Comparison of PSNR values of Taylor series approximation and proposed bit extraction methods with two phantom data sets.

Case	1	2
Taylor series approximation method	96.3 dB	99.6 dB
Proposed bit extraction method	55.2 dB	58.2 dB

, the proposed bit extraction method presented 55.2 dB and 58.2 dB for ultrasound B-mode images when using a convex array probe and a linear array probe, respectively. Although the PNSR values from the proposed bit extraction method are lower than those from the Taylor series approximation method (i.e., 96.3 dB and 99.6 dB), as demonstrated in Figure 4, the proposed bit extraction method is suitable for being used in ultrasound B-mode imaging.

The execution times for the approximation methods, including the Taylor series approximation and proposed bit extraction methods, were compared with the reference method as summarized in

Table 2. Comparison of computation times from the reference, Taylor’s series approximation, and proposed bit extraction methods.

	Reference (GCC)	Taylor Series (SIMD)	Bit Extraction (SIMD)
Time (ms)	23.9	10.1	2.8

. The proposed bit extraction method was eight-fold faster than the reference where the built-in function (i.e., log10) in GCC was utilized. Moreover, it outperformed the Taylor series approximation method, at 2.8 ms vs. 10.1 ms, respectively. Both approximation methods (i.e., Taylor series and bit extraction) were implemented by utilizing SIMD operations in the ARM AP.

4. Conclusions

In this study, the log compression of ultrasound B-mode imaging was able to be optimized by using advanced exponent bit extraction. When validating its feasibility using an ARM Cortex-A9 AP, the performance of the proposed bit extraction method outperformed the reference and Taylor’s series methods in terms of execution time. Moreover, the proposed bit extraction method showed a PSNR value over 55 dB, which is reasonable in ultrasound B-mode imaging. Thus, the proposed efficient logarithm computation method based on bit extraction can enhance the performance of software-based ultrasound B-mode imaging systems while preserving image quality.