Few-Shot Learning Based on Double Pooling Squeeze and Excitation Attention
Abstract
:1. Introduction
- We propose a novel few-shot learning method based on double pooling squeeze and excitation attention (dSE) in order to improve the discriminative ability of the model. In order to improve the robustness of the model, we also designed a new loss function.
- We propose a novel attention module (dSE), which adopts two types of pooling. Different from the conventional few-shot learning methods employing image-level or pixel-level features, we innovatively used the pixel-level and channel-level informative local feature description to represent each image with image-to-class measures.
- Experiments on four common few-shot benchmark datasets with two different backbones demonstrate that our proposed method shows more excellent classification accuracy compared to other state-of-the-art methods. More importantly, our results on more challenging fine-grained datasets are superior to those of other methods.
2. Related Work
2.1. Few-Shot Learning
2.2. Attention Mechanism
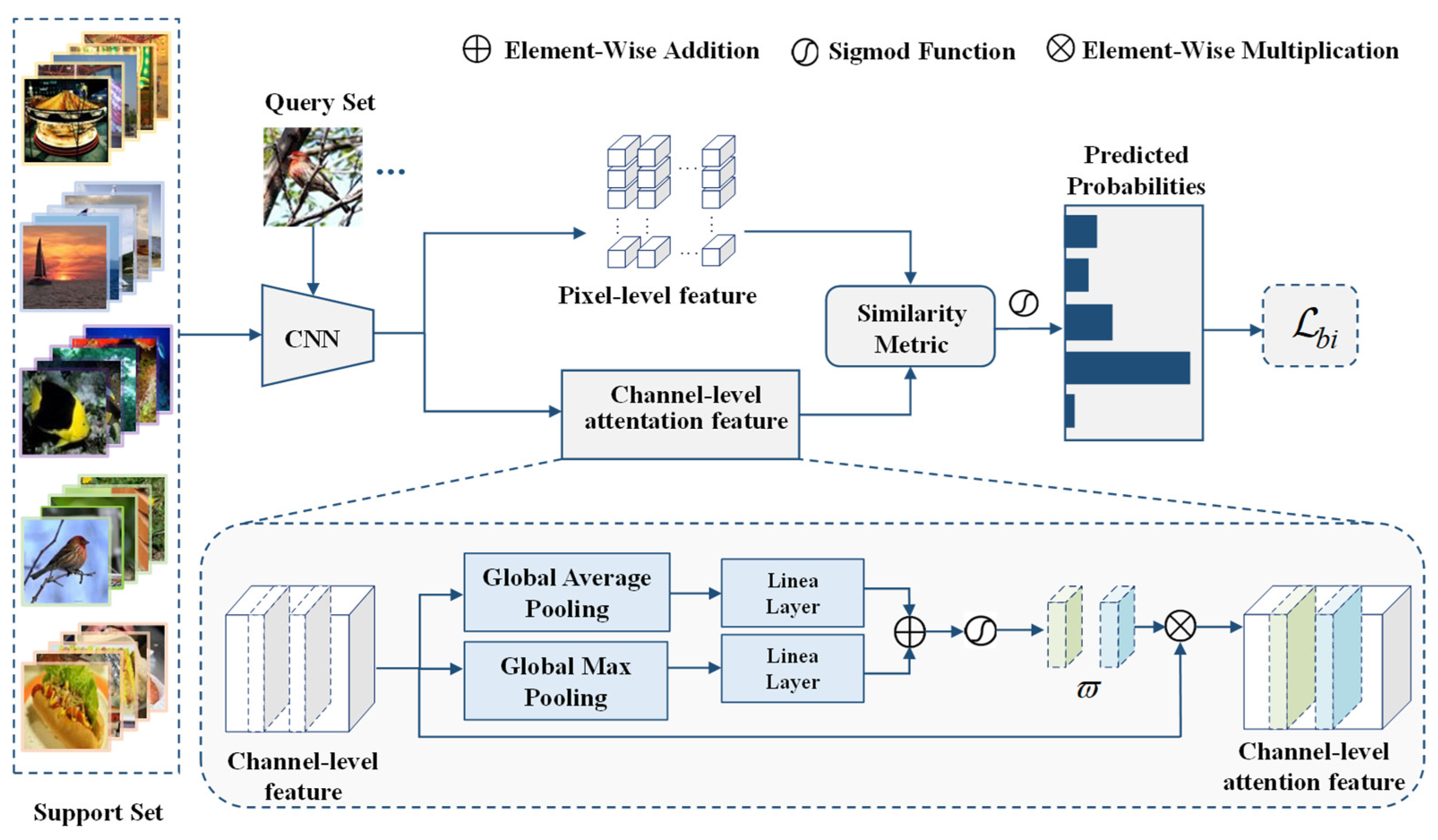
3. Methodology
3.1. Problem Definition
3.2. Multi-Feature-Embedded Representation
3.2.1. Pixel-Level Feature Representation
3.2.2. Channel-Level dSE Attention Module
3.3. Similarity Metric
3.4. The Loss Function
4. Experiments
4.1. Datasets
4.2. Implementation Details
4.3. Experiments on Common Few-Shot Classification Datasets
4.3.1. Experimental Results on miniImageNet
4.3.2. Experimental Results on tieredImageNet
4.3.3. Experimental Results on CIFAR-FS
4.3.4. Experimental Results on FC100
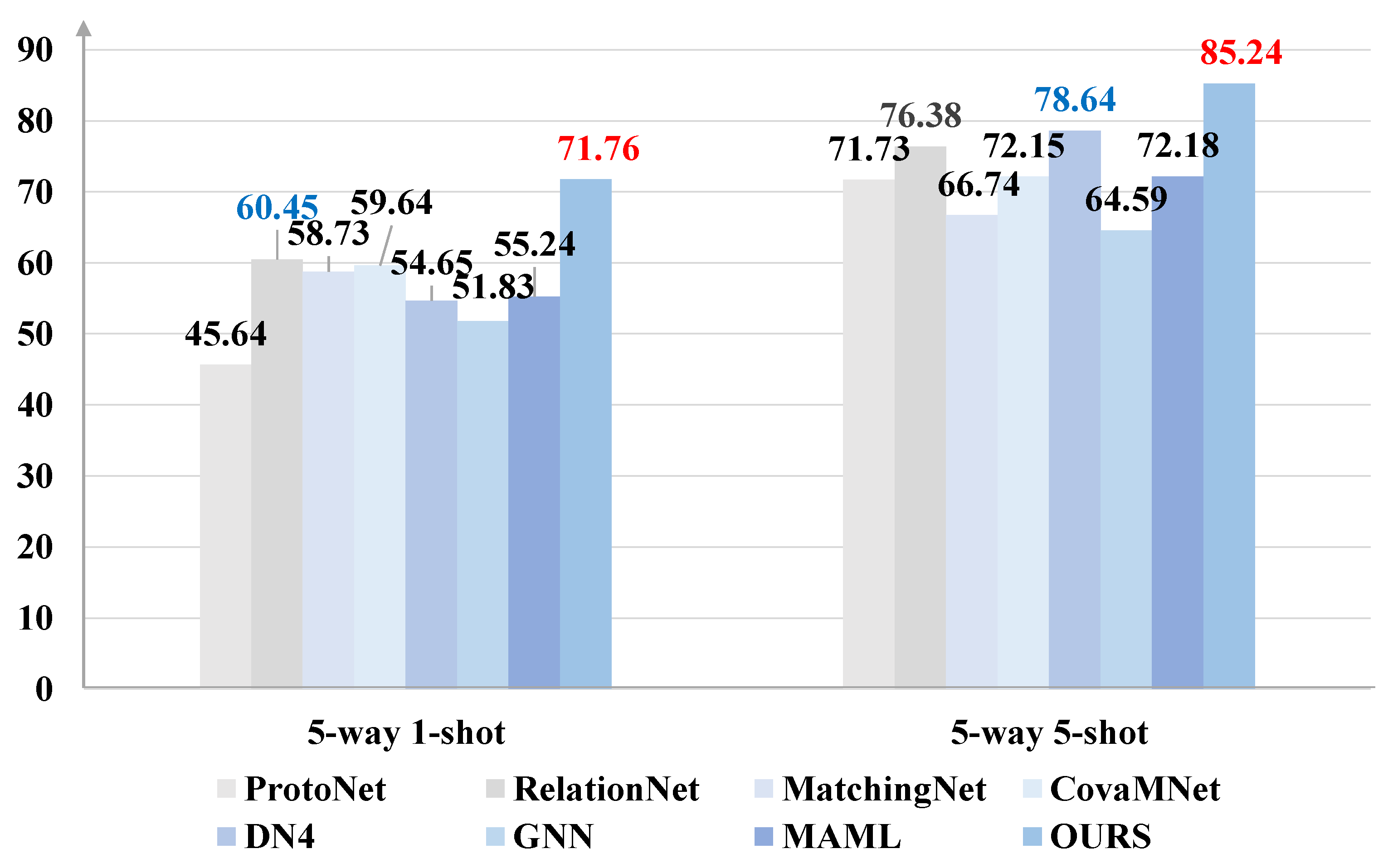
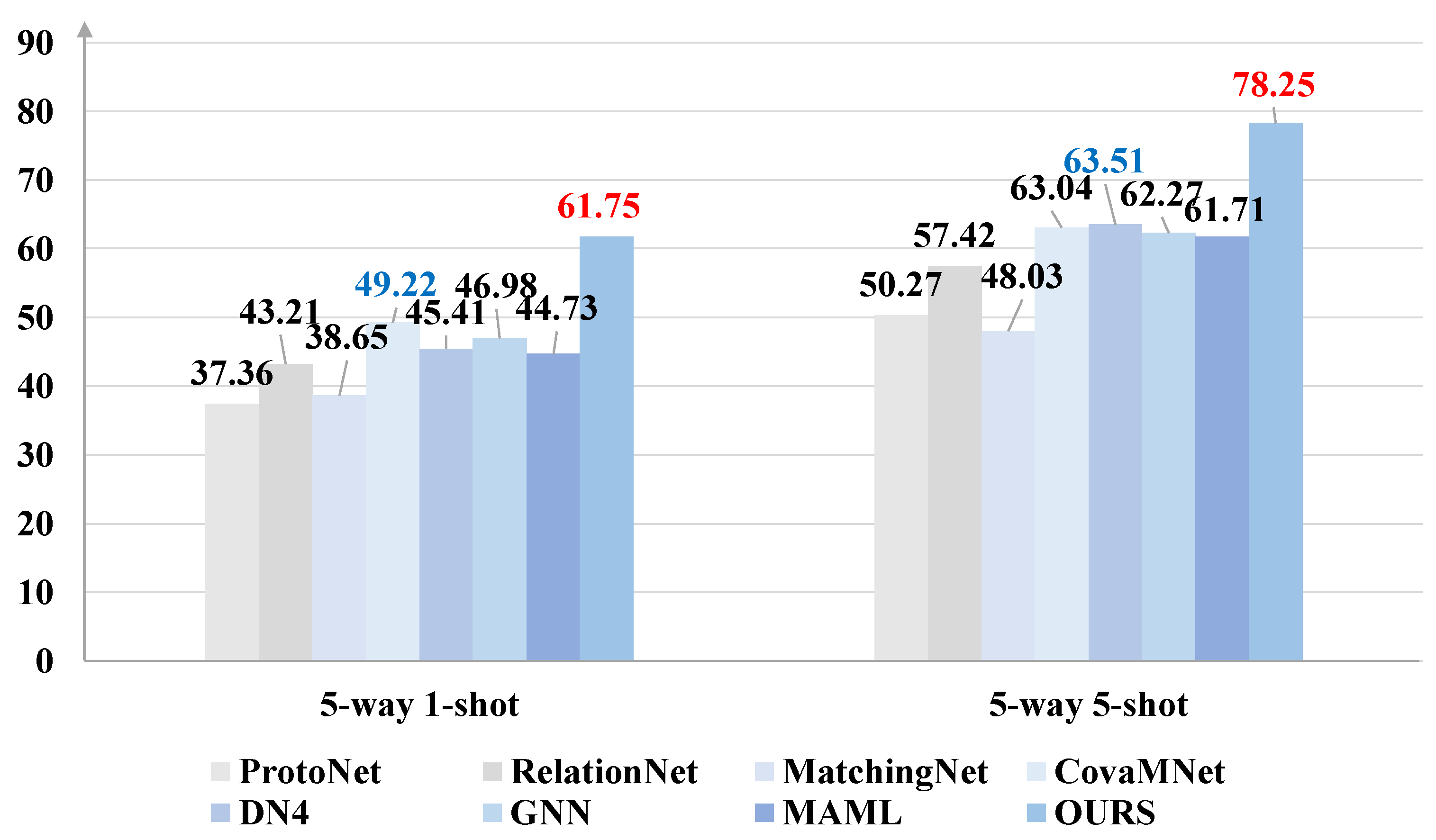
4.4. Experiments on the Fine-Grained Few-Shot Classification Datasets
4.5. Experiments on Fine-Grained Few-Shot Classification Datasets
4.5.1. Effectiveness of Different Components
4.5.2. Effectiveness of Attention Mechanism dSE
5. Experimental Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wertheimer, D.; Hariharan, B. Few-shot learning with localization in realistic settings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6558–6567. [Google Scholar]
- Lifchitz, Y.; Avrithis, Y.; Picard, S.; Bursuc, A. Dense classification and implanting for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9258–9267. [Google Scholar]
- Xu, W.; Xu, Y.; Wang, H.; Tu, Z. Attentional constellation nets for few-shot learning. In Proceedings of the International Conference on Learning Representations, Virtual, 3–7 May 2021. [Google Scholar]
- Kang, D.; Kwon, H.; Min, J.; Cho, M. Relational embedding for few-shot classification. In Proceedings of the IEEE/CVF In-ternational Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 8822–8833. [Google Scholar]
- Cao, K.; Brbic, M.; Leskovec, J. Concept learners for few-shot learning. arXiv 2020, arXiv:2007.07375. [Google Scholar]
- Li, H.; Eigen, D.; Dodge, S.; Zeiler, M.; Wang, X. Finding task-relevant features for few-shot learning by category traversal. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1–10. [Google Scholar]
- Chen, H.; Li, H.; Li, Y.; Chen, C. Multi-level metric learning for few-shot image recognition. In Proceedings of the International Conference on Artificial Neural Networks, Bristol, UK, 6–9 September 2022; Springer: Cham, Switzerland, 2022; pp. 243–254. [Google Scholar]
- Sell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4080–4090. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D. Matching networks for one shot learning. Adv. Neural Inf. Process. Syst. 2016, 29, 3630–3638. [Google Scholar]
- Li, W.; Wang, L.; Xu, J.; Huo, J.; Gao, Y.; Luo, J. Revisiting local descriptor based image-to-class measure for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7260–7268. [Google Scholar]
- Huang, H.; Wu, Z.; Li, W.; Huo, J.; Gao, Y. Local descriptor-based multi-prototype network for few-shot learning. Pattern Recognit. 2021, 116, 107935. [Google Scholar] [CrossRef]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the ICML Deep Learning Workshop, Lille, France, 6–11 July 2015; Volume 2. [Google Scholar]
- Simon, C.; Koniusz, P.; Nock, R.; Harandi, M. Adaptive subspaces for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4136–4145. [Google Scholar]
- Zhang, C.; Cai, Y.; Lin, G.; Shen, C. Deepemd: Differentiable earth mover’s distance for few-shot learning. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.H.; Hospedales, T.M. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1199–1208. [Google Scholar]
- Li, W.; Xu, J.; Huo, J.; Wang, L.; Gao, Y.; Luo, J. Distribution consistency based covariance metric networks for few-shot learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8642–8649. [Google Scholar]
- Zheng, Y.; Wang, R.; Yang, J.; Xue, L.; Hu, M. Principal characteristic networks for few-shot learning. J. Vis. Commun. Image Represent. 2019, 59, 563–573. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Mishra, N.; Rohaninejad, M.; Chen, X.; Abbeel, P. A simple neural attentive meta-learner. arXiv 2017, arXiv:1707.03141. [Google Scholar]
- Lee, K.; Maji, S.; Ravichandran, A.; Soatto, S. Meta-learning with differentiable convex optimization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10657–10665. [Google Scholar]
- Lu, X.; Wang, W.; Ma, C.; Shen, J.; Shao, L.; Porikli, F. See more, know more: Unsupervised video object segmentation with co-attention siamese networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3623–3632. [Google Scholar]
- Lu, X.; Wang, W.; Shen, J.; Crandall, D.; Luo, J. Zero-shot video object segmentation with co-attention siamese networks. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2228–2242. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Liu, Y.; Dong, X.; Lu, X.; Khan, F.S.; Hoi, S.C. Distilled Siamese Networks for Visual Tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 8896–8909. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Jiang, Z.; Kang, B.; Zhou, K.; Feng, J. Few-shot classification via adaptive attention. arXiv 2020, arXiv:2008.02465. [Google Scholar]
- Lim, J.S.; Astrid, M.; Yoon, H.J.; Lee, S.I. Small object detection using context and attention. In Proceedings of the 2021 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Jeju Island, South Korea, 13–16 April 2021; pp. 181–186. [Google Scholar]
- Li, T.; Li, Z.; Luo, A.; Rockwell, H.; Farimani, A.B.; Lee, T.S. Prototype memory and attention mechanisms for few shot image generation. In Proceedings of the International Conference on Learning Representations, Virtual Event, Austria, 3–7 September 2021. [Google Scholar]
- Yang, L.; Li, L.; Zhang, Z.; Zhou, X.; Zhou, E.; Liu, Y. Dpgn: Distribution propagation graph network for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 13390–13399. [Google Scholar]
- Oh, J.; Yoo, H.; Kim, C.; Yun, S.Y. BOIL: Towards representation change for few-shot learning. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Ye, H.J.; Hu, H.; Zhan, D.C.; Sha, F. Few-shot learning via embedding adaptation with set-to-set functions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8808–8817. [Google Scholar]
- Chen, Z.; Ge, J.; Zhan, H.; Huang, S.; Wang, D. Pareto self-supervised training for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2021; pp. 13663–13672. [Google Scholar]
- Wertheimer, D.; Tang, L.; Hariharan, B. Few-shot classification with feature map reconstruction networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2021; pp. 8012–8021. [Google Scholar]
- Zhou, Z.; Qiu, X.; Xie, J.; Wu, J.; Zhang, C. Binocular mutual learning for improving few-shot classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 8402–8411. [Google Scholar]
- Xie, J.; Long, F.; Lv, J.; Wang, Q.; Li, P. Joint Distribution Matters: Deep Brownian Distance Covariance for Few-Shot Classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 7972–7981. [Google Scholar]
- Zhang, M.; Zhang, J.; Lu, Z.; Xiang, T.; Ding, M.; Huang, S. IEPT: Instance-level and episode-level pretext tasks for few-shot learning. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 September 2020. [Google Scholar]
- Afrasiyabi, A.; Lalonde, J.F.; Gagné, C. Mixture-based feature space learning for few-shot image classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 9041–9051. [Google Scholar]
- Xu, C.; Fu, Y.; Liu, C.; Wang, C.; Li, J.; Huang, F.; Xue, X. Learning dynamic alignment via meta-filter for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Montreal, QC, Canada, 10–17 October 2021; pp. 5182–5191. [Google Scholar]
- Kim, J.; Kim, H.; Kim, G. Model-agnostic boundary-adversarial sampling for test-time generalization in few-shot learning. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 599–617. [Google Scholar]
- Liu, Y.; Schiele, B.; Sun, Q. An ensemble of epoch-wise empirical bayes for few-shot learning. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 404–421. [Google Scholar]
- Zhang, C.; Ding, H.; Lin, G.; Li, R.; Wang, C.; Shen, C. Meta navigator: Search for a good adaptation policy for few-shot learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 9435–9444. [Google Scholar]
- Wu, J.; Zhang, T.; Zhang, Y.; Wu, F. Task-aware part mining network for few-shot learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 8433–8442. [Google Scholar]






| Method | Backbone | 5-way–1-shot | 5-way–5-shot |
|---|---|---|---|
| BOIL [32] | Conv-64F | 49.61 ± 0.16 | 66.45 ± 0.37 |
| ProtoNet [8] | Conv-64F | 49.42 ± 0.78 | 68.20 ± 0.66 |
| CovaMNet [16] | Conv-64F | 51.19 ± 0.76 | 67.65 ± 0.63 |
| DN4 [10] | Conv-64F | 51.24 ± 0.74 | 71.02 ± 0.64 |
| DSN [13] | Conv-64F | 51.78 ± 0.96 | 68.99 ± 0.69 |
| FEAT [33] | Conv-64F | 55.15 ± 0.20 | 71.61 ± 0.16 |
| OURS | Conv-64F | 59.42 ± 0.51 | 77.36 ± 0.73 |
| PSST [34] | ResNet-12 | 64.05 ± 0.49 | 80.24 ± 0.45 |
| ConstellationNet [5] | ResNet-12 | 64.89 ± 0.23 | 79.95 ± 0.37 |
| FRN [35] | ResNet-12 | 66.45 ± 0.19 | 82.83 ± 0.13 |
| DeepEMD [14] | ResNet-12 | 65.91 ± 0.82 | 79.74 ± 0.56 |
| BML [36] | ResNet-12 | 67.04 ± 0.63 | 83.63 ± 0.29 |
| Meta DeepBDC [37] | ResNet-12 | 67.34 ± 0.43 | 84.46 ± 0.28 |
| OURS | ResNet-12 | 69.64 ± 0.44 | 87.95 ± 0.53 |
| Method | Backbone | 5-way–1-shot | 5-way–5-shot |
|---|---|---|---|
| ProtoNet [8] | Conv-64F | 48.67 ± 0.87 | 69.57 ± 0.75 |
| BOIL [32] | Conv-64F | 49.35 ± 0.26 | 69.37 ± 0.12 |
| DN4 [10] | Conv-64F | 53.37 ± 0.86 | 74.45 ± 0.70 |
| CovaMNet [16] | Conv-64F | 54.98 ± 0.90 | 71.51 ± 0.75 |
| IEPT [38] | Conv-64F | 58.25 ± 0.48 | 75.63 ± 0.46 |
| OURS | Conv-64F | 61.47 ± 0.83 | 79.56 ± 0.64 |
| RelationNet [15] | ResNet-12 | 58.99 ± 0.86 | 75.78 ± 0.76 |
| DSN [13] | ResNet-12 | 67.39 ± 0.82 | 82.85 ± 0.56 |
| MixtFSL [39] | ResNet-12 | 70.97 ± 1.03 | 86.16 ± 0.67 |
| FEAT [33] | ResNet-12 | 70.80 ± 0.23 | 84.79 ± 0.16 |
| DeepEMD [14] | ResNet-12 | 71.16 ± 0.87 | 83.95 ± 0.58 |
| RENet [4] | ResNet-12 | 71.61 ± 0.51 | 85.28 ± 0.35 |
| DMF [40] | ResNet-12 | 71.89 ± 0.52 | 85.96 ± 0.35 |
| OURS | ResNet-12 | 75.25 ± 0.64 | 89.21 ± 0.46 |
| Method | Backbone | 5-way–1-shot | 5-way–5-shot |
|---|---|---|---|
| ProtoNet [8] | Conv-64F | 55.50 ± 0.70 | 72.00 ± 0.60 |
| ConstellationNet [5] | Conv-64F | 69.30 ± 0.30 | 82.70 ± 0.20 |
| OURS | Conv-64F | 69.70 ± 0.42 | 87.56 ± 0.44 |
| MetaOpt Net [20] | ResNet-12 | 72.00 ± 0.70 | 84.20 ± 0.50 |
| MABAS [41] | ResNet-12 | 73.51 ± 0.92 | 85.49 ± 0.68 |
| RENet [4] | ResNet-12 | 74.51 ± 0.46 | 86.60 ± 0.32 |
| OURS | ResNet-12 | 77.12 ± 0.40 | 92.85 ± 0.30 |
| Method | Backbone | 5-way–1-shot | 5-way–5-shot |
|---|---|---|---|
| MetaOptNet [20] | ResNet-12 | 41.10 ± 0.60 | 55.50 ± 0.60 |
| ProtoNet [8] | ResNet-12 | 41.54 ± 0.76 | 57.08 ± 0.76 |
| E3BM [42] | ResNet-12 | 43.20 ± 0.30 | 60.20 ± 0.30 |
| ConstellationNet [5] | ResNet-12 | 43.80 ± 0.20 | 59.70 ± 0.20 |
| MixtFSL [39] | ResNet-12 | 44.89 ± 0.63 | 60.70 ± 0.60 |
| Meta Navigator [43] | ResNet-12 | 46.40 ± 0.81 | 61.33 ± 0.71 |
| DeepEMD [14] | ResNet-12 | 46.47 ± 0.78 | 63.22 ± 0.71 |
| TPMN [44] | ResNet-12 | 46.93 ± 0.71 | 63.26 ± 0.74 |
| OURS | ResNet-12 | 50.32 ± 0.73 | 71.55 ± 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Su, J.; Wang, Y.; Zhang, J.; Zhong, Y. Few-Shot Learning Based on Double Pooling Squeeze and Excitation Attention. Electronics 2023, 12, 27. https://doi.org/10.3390/electronics12010027
Xu Q, Su J, Wang Y, Zhang J, Zhong Y. Few-Shot Learning Based on Double Pooling Squeeze and Excitation Attention. Electronics. 2023; 12(1):27. https://doi.org/10.3390/electronics12010027
Chicago/Turabian StyleXu, Qiuyu, Jie Su, Ying Wang, Jing Zhang, and Yixin Zhong. 2023. "Few-Shot Learning Based on Double Pooling Squeeze and Excitation Attention" Electronics 12, no. 1: 27. https://doi.org/10.3390/electronics12010027
APA StyleXu, Q., Su, J., Wang, Y., Zhang, J., & Zhong, Y. (2023). Few-Shot Learning Based on Double Pooling Squeeze and Excitation Attention. Electronics, 12(1), 27. https://doi.org/10.3390/electronics12010027






