Stability Analysis for Single-Lane Traffic with a Relay Controller in a Closed Loop
Abstract
1. Introduction
2. Control System Configuration
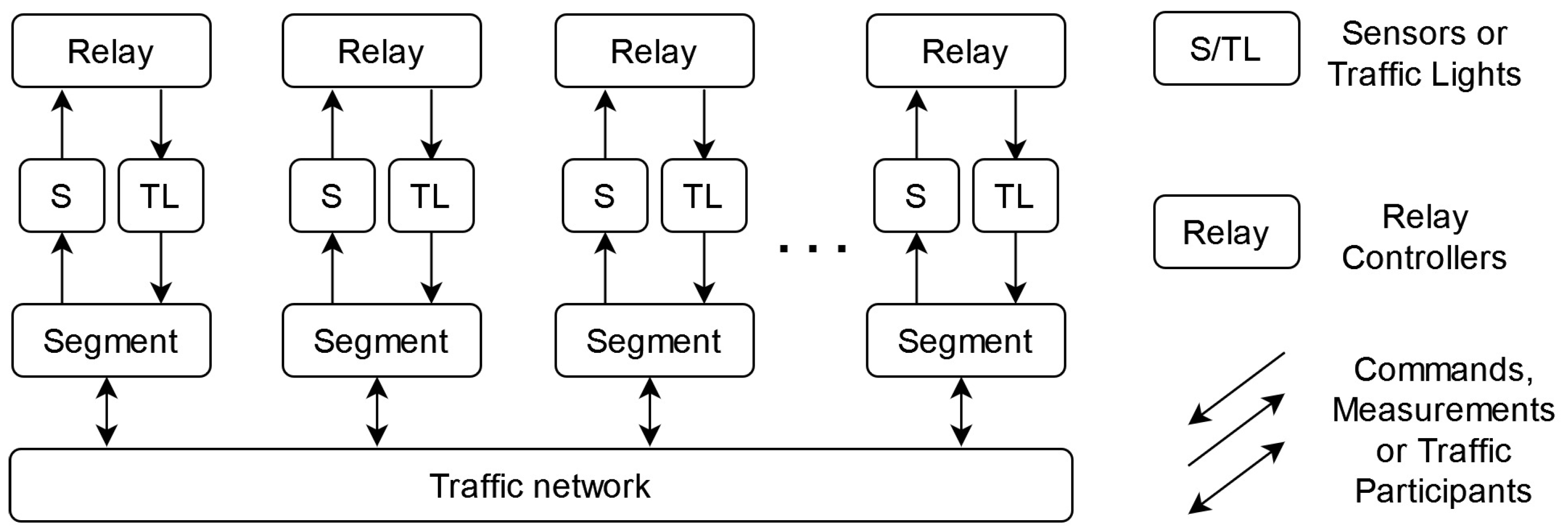
2.1. Context: The Decentralized Traffic Network
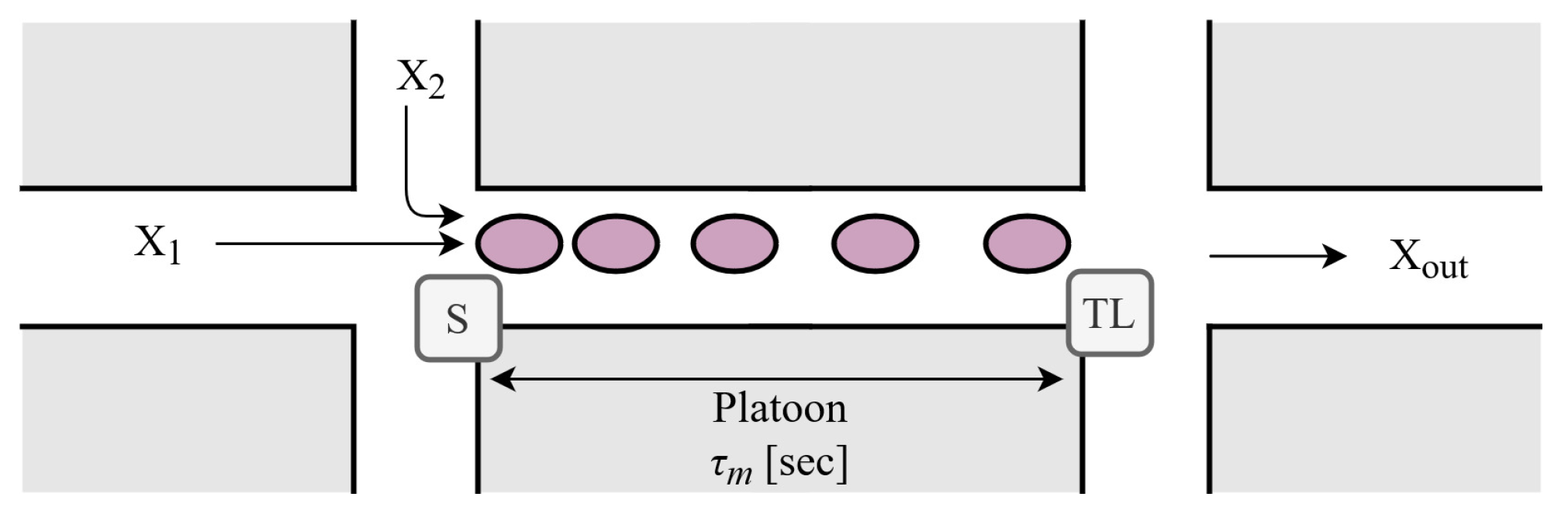
2.2. Dynamics of Vehicles as a String of Traffic Participants
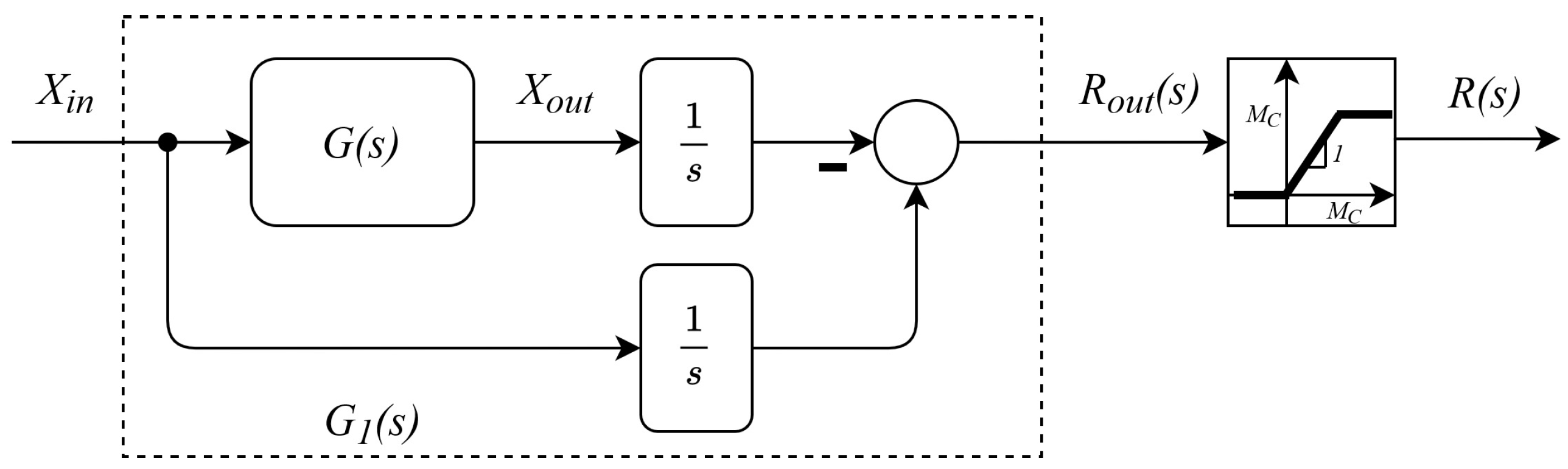
2.3. Road Segment Model
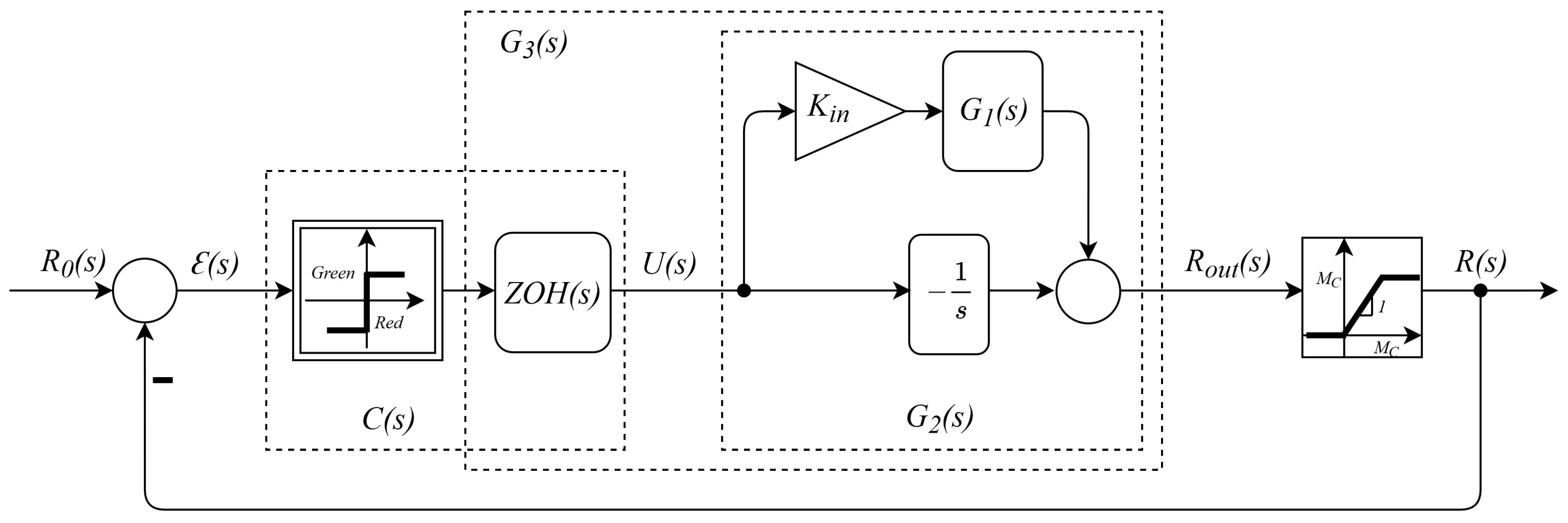
2.4. Closed-Loop Structure for the Single-Lane Road Segment
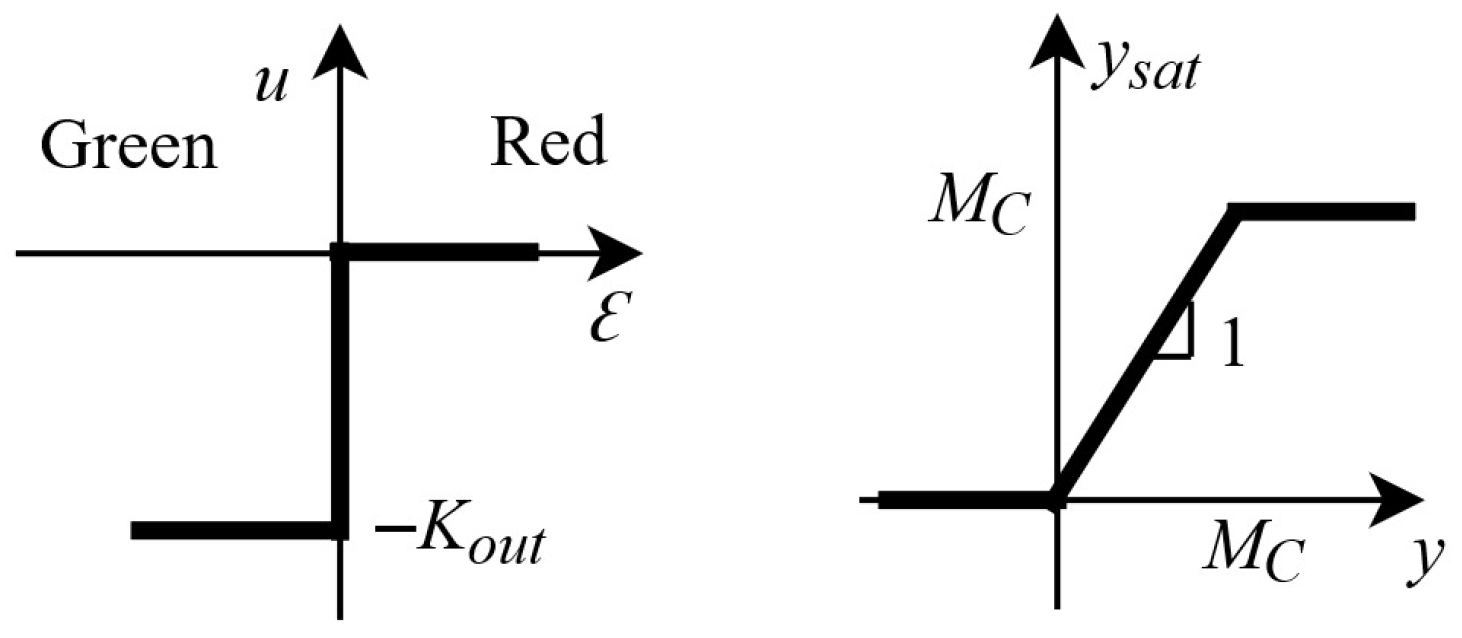
2.5. Controller Model
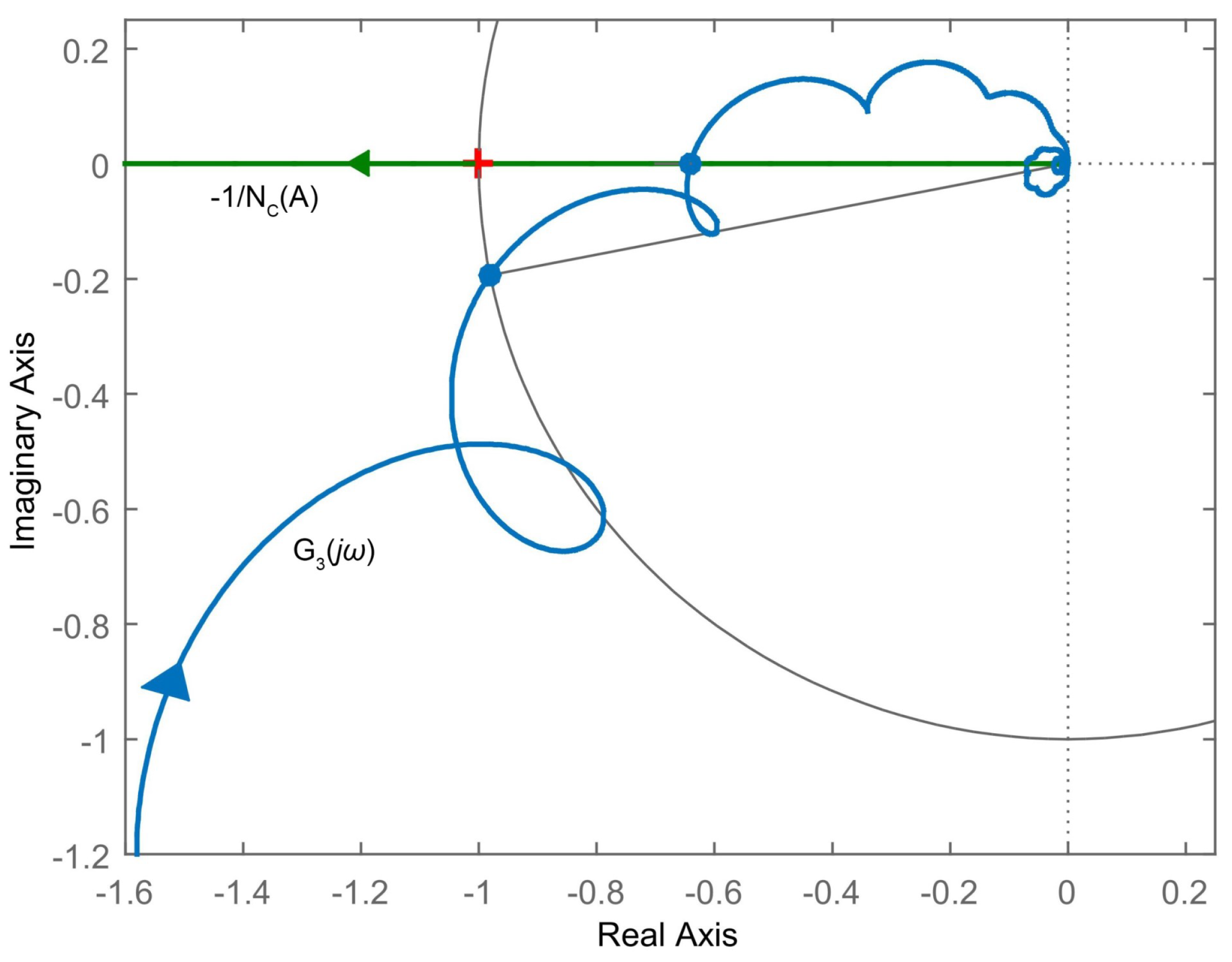
3. Stability Analysis
4. Case Study
4.1. Time Response
4.2. Frequency Response and Stability Conditions
4.3. Network Example
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Figueiredo, L.; Jesus, I.; Machado, J.T.; Ferreira, J.R.; De Carvalho, J.M. Towards the development of intelligent transportation systems. In Proceedings of the 2001 IEEE Intelligent Transportation Systems Proceedings, Oakland, CA, USA, 25–29 August 2001; pp. 1206–1211. [Google Scholar]
- Psaraki, V.; Pagoni, I.; Schafer, A. Techno-economic assessment of the potential of intelligent transport systems to reduce CO2 emissions. IET Intell. Transp. Syst. 2012, 6, 355–363. [Google Scholar] [CrossRef]
- Ferreira, E.D.; Subrahmanian, E.; Manstetten, D. Intelligent agents in decentralized traffic control. In Proceedings of the 2001 IEEE Intelligent Transportation Systems Proceedings, Oakland, CA, USA, 25–29 August 2001; pp. 705–709. [Google Scholar]
- Sims, A.G.; Dobinson, K.W. The Sydney coordinated adaptive traffic (SCAT) system philosophy and benefits. IEEE Trans. Veh. Technol. 1980, 29, 130–137. [Google Scholar] [CrossRef]
- Hunt, P.; Robertson, D.; Bretherton, R.; Winton, R. SCOOT—A Traffic Responsive Method of Coordinating Signals; Transport and Road Research Laboratory: Wokingham, UK, 1981. [Google Scholar]
- Head, K.L.; Mirchandani, P.B.; Sheppard, D. Hierarchical Framework for Real-Time Traffic Control; Number 1360; Transportation Research Board: Washington, DC, USA, 1992. [Google Scholar]
- Luyanda, F.; Gettman, D.; Head, L.; Shelby, S.; Bullock, D.; Mirchandani, P. ACS-Lite algorithmic architecture: Applying adaptive control system technology to closed-loop traffic signal control systems. Transp. Res. Rec. 2003, 1856, 175–184. [Google Scholar] [CrossRef]
- Gartner, N.H. OPAC: A Demand-Responsive Strategy for Traffic Signal Control; Number 906; Transportation Research Record: Washington, DC, USA, 1983. [Google Scholar]
- Aoyama, K.I. Universal traffic management system (UTMS) in Japan. In Proceedings of the VNIS’94-1994 Vehicle Navigation and Information Systems Conference, Yokohama, Japan, 31 August–2 September 1994; pp. 619–622. [Google Scholar]
- UTMS Socitey of Japan. Available online: https://utms.or.jp/english/ (accessed on 25 November 2022).
- Madeleine, E.Z.; Dafflon, B.; Gechter, F.; Contet, J.M. Vehicle platoon control with multi-configuration ability. Procedia Comput. Sci. 2012, 9, 1503–1512. [Google Scholar]
- Chen, D.; Zhao, M.; Sun, D.; Zheng, L.; Jin, S.; Chen, J. Robust H∞ control of cooperative driving system with external disturbances and communication delays in the vicinity of traffic signals. Phys. A Stat. Mech. Its Appl. 2020, 542, 123385. [Google Scholar] [CrossRef]
- Hao, W.; Ma, C.; Moghimi, B.; Fan, Y.; Gao, Z. Robust optimization of signal control parameters for unsaturated intersection based on tabu search-artificial bee colony algorithm. IEEE Access 2018, 6, 32015–32022. [Google Scholar] [CrossRef]
- Jin, L.; Amin, S. Analysis of a stochastic switching model of freeway traffic incidents. IEEE Trans. Autom. Control 2018, 64, 1093–1108. [Google Scholar] [CrossRef]
- Cenedese, C.; Cucuzzella, M.; Scherpen, J.; Grammatico, S.; Cao, M. Highway Traffic Control via Smart e-Mobility—Part I: Theory. arXiv 2021, arXiv:2102.09354. [Google Scholar]
- Yu, H.; Diagne, M.; Zhang, L.; Krstic, M. Bilateral boundary control of moving shockwave in LWR model of congested traffic. IEEE Trans. Autom. Control 2020, 66, 1429–1436. [Google Scholar] [CrossRef]
- Reveliotis, S.; Masopust, T. Efficient liveness assessment for traffic states in open, irreversible, dynamically routed, zone-controlled guidepath-based transport systems. IEEE Trans. Autom. Control 2019, 65, 2883–2898. [Google Scholar] [CrossRef]
- Yi, J.; Lin, H.; Alvarez, L.; Horowitz, R. Stability of macroscopic traffic flow modeling through wavefront expansion. Transp. Res. Part B Methodol. 2003, 37, 661–679. [Google Scholar] [CrossRef]
- Tang, T.Q.; Huang, H.J.; Zhang, Y.; Xu, X.Y. Stability analysis for traffic flow with perturbations. Int. J. Mod. Phys. C 2008, 19, 1367–1375. [Google Scholar] [CrossRef]
- Haddad, J.; Geroliminis, N. Stability analysis of traffic control in two-region urban cities. In Proceedings of the Swiss Transportation Research Conference (STRC), Ascona, Switzerland, 11–13 May 2011; pp. 1–29. [Google Scholar]
- Viscotel, l.A.; Patrascu, M. Design of Stabilizing Predictor-based Controller for Closed Loop Traffic Control with Real-Coded Genetic Algorithms. In Proceedings of the 2021 20th European Control Conference (ECC), Delft, The Netherlands, 29 June–2 July 2021. [Google Scholar]
- Constantinescu, V. Contributions to Modelling and Control in Urban Intelligent Transportation Systems. Ph.D. Thesis, University Politehnica of Bucharest, Bucharest, Romania, 2019. [Google Scholar]
- Chedjou, J.C.; Kyamakya, K. A review of traffic light control systems and introduction of a control concept based on coupled nonlinear oscillators. In Recent Advances in Nonlinear Dynamics and Synchronization; Springer: Cham, Switzerland, 2018; pp. 113–149. [Google Scholar] [CrossRef]
- Ion, A.; Constantinescu, V.; Patrascu, M. Agent based simulation applied to the design of control systems for emergency vehicles access. In Proceedings of the 14th International Conference on ITS Telecommunications, Copenhagen, Denmark, 2–4 December 2015; pp. 50–54. [Google Scholar]
- Bertolotti, T. Generative and Demonstrative Experiments. In Model-Based Reasoning in Science and Technology; Springer: Berlin/Heidelberg, Germany, 2014; pp. 479–498. [Google Scholar]
- Berceanu, C.; Patrascu, M. Initial Conditions Sensitivity Analysis of a Two-Species Butterfly-Effect Agent-Based Model. In Multi-Agent Systems EUMAS 2022; Lecture Notes in Computer Science; Baumeister, D., Rothe, J., Eds.; Springer: Cham, Switzerland, 2022; Volume 13442, pp. 60–78. [Google Scholar]
- Robertson, D.I. Transyt: A Traffic Network Study Tool; Road Reserch Laboratory, Ministry of Transport: Crowthorne, UK, 1969.
- Axhausen, K.W.; Korling, H.G. Some measurements of Robertson’s platoon dispersion factor. Transp. Res. Rec. 1987, 1112, 71–77. [Google Scholar]
- Vander Velde, W.E. Multiple-Input Describing Functions and Nonlinear System Design; McGraw Hill: New York, NY, USA, 1968. [Google Scholar]
- Fendrich, O. Describing functions and limit cycles. IEEE Trans. Autom. Control 1992, 37, 486–487. [Google Scholar] [CrossRef]
- Usai, E. Describing Function Analysis of Nonlinear Systems; University of Cagliari, Italy: Cagliari, Italy, 2008. [Google Scholar]
- Dashkovskiy, S.; Feketa, P. Zeno phenomenon in hybrid dynamical systems. PAMM 2017, 17, 789–790. [Google Scholar] [CrossRef]
- Åström, K.J.; Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]

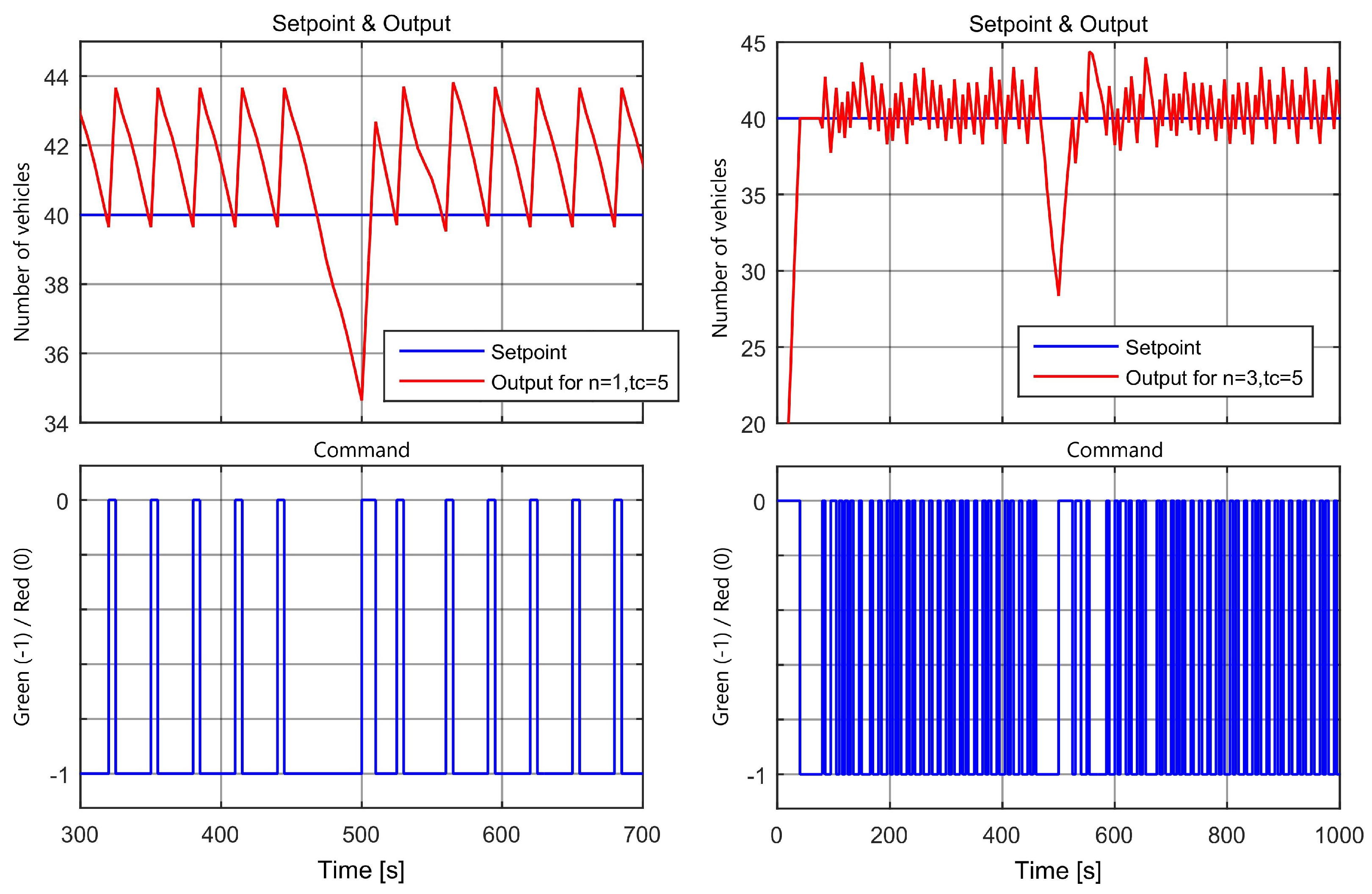


| n | Max. | Max. Green | Closed Loop Stable? | |||
|---|---|---|---|---|---|---|
| (Vehicles) | (Sec) | (Vehicles) | Vehicles | (Sec) | Other Remarks | |
| 5…10 | 1…4.5 | 5…8 | 0…5 | 9…17 | 15…65 | Yes |
| 5…10 | 1…4.5 | 5…8 | 50 | 9…14 | 15…55 | Yes, however the segment stays empty with green light in some cases. |
| 40 | 1…3 | 5 | 0…50 | 44 | 15…55 | Yes |
| 1 | 1…3 | 5 | 0 | 5 | 25 | Yes |
| 1 | 1…3 | 5 | 5…50 | 5 | 40 | Yes, however the segment stays empty with green light in some cases. |
| 10…70 | 1…3 | 5…20 | 0…50 | 14…83 | 25…100 | Often stable. Saturation in some cases. |
| 10 | 5 | 5 | 0…50 | 54 | Always green | Output is permanently saturated to constant value. |
| 10 | 6 | 5 | 0…50 | 54 | Mostly green | Wide oscillations, high waiting times. |
| n | CL Stable? | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 5 | 1.01 | 0.48 | 0.013 | 0.06 | 0.06 | 0.08 | Y |
| 0.5 | 5 | 1.1 | 4.95 | 0.145 | 0.06 | 0.06 | 0.08 | Y |
| 1 | 5 | 1.24 | 8.58 | 0.27 | 0.06 | 0.06 | 0.08 | Y * |
| 1 | 15 | 0.34 | −35 | 19 | 0.17 | 0.17 | 0.23 | N |
| 1 | 30 | 0.24 | −64 | 30 | 0.33 | 0.33 | 0.42 | N |
| 1 | 60 | 0.08 | −58 | 9.47 | 0.58 | 0.59 | 0.73 | N * |
| 1.5 | 5 | 1.4 | 9.2 | 0.3 | 0.06 | 0.06 | 0.08 | Y * |
| 2 | 5 | 1.56 | 12.7 | 0.44 | 0.06 | 0.06 | 0.08 | Y * |
| 2 | 60 | 0.05 | −30 | 9.6 | 0.59 | 0.59 | 0.73 | N |
| 2.2 | 5 | 1.64 | 14 | 0.48 | 0.06 | 0.06 | 0.08 | Y |
| 3 | 5 | 0.12 | 8.85 | 0.56 | 0.06 | 0.06 | 0.08 | N |
| 3.5 | 45 | 0.04 | −10 | 52 | 0.47 | 0.47 | 0.59 | N |
| 3.6 | 50 | 0.04 | 20.6 | 3.46 | 0.51 | 0.51 | 0.64 | N |
| 4 | 30 | 0.04 | −76 | 30 | 0.33 | 0.33 | 0.43 | N * |
| 5 | 40 | 0.026 | −16.4 | 45.6 | 0.43 | 0.43 | 0.55 | N * |
| 5 | 60 | 0.023 | 32.9 | 3.9 | 0.59 | 0.60 | 0.74 | N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patrascu, M.; Constantinescu, V. Stability Analysis for Single-Lane Traffic with a Relay Controller in a Closed Loop. Electronics 2023, 12, 5. https://doi.org/10.3390/electronics12010005
Patrascu M, Constantinescu V. Stability Analysis for Single-Lane Traffic with a Relay Controller in a Closed Loop. Electronics. 2023; 12(1):5. https://doi.org/10.3390/electronics12010005
Chicago/Turabian StylePatrascu, Monica, and Vlad Constantinescu. 2023. "Stability Analysis for Single-Lane Traffic with a Relay Controller in a Closed Loop" Electronics 12, no. 1: 5. https://doi.org/10.3390/electronics12010005
APA StylePatrascu, M., & Constantinescu, V. (2023). Stability Analysis for Single-Lane Traffic with a Relay Controller in a Closed Loop. Electronics, 12(1), 5. https://doi.org/10.3390/electronics12010005







