Magnetic Interference Compensation Using the Adaptive LMS Algorithm

Abstract

The aim of this study is to evaluate the method for the compensation of magnetic field interference from the mains, which consists primarily of components with a frequency of 50 (60) Hz and its multiples. The setup compensates for the interfering field using three Helmholtz coils, magnetic field sensors, a digital processing unit, and power amplifiers. The processing unit implements an adaptive least-mean-square (LMS) algorithm to calculate the currents through coils that are necessary for compensation. The prototype fully compensates for interfering with the magnetic field at 50, 150, 250, and 350 Hz down to the noise level of the sensor arrangement within 20 s and reduces higher harmonics. The overall reduction in the rms value of the interfering field is better than 28 dB, and a significantly better reduction is achieved in the frequency range from 0 Hz to 400 Hz.

1. Introduction

Cold atoms have emerged as a powerful platform for quantum technologies, including quantum simulation, information processing, and metrology [1,2]. In many cases, these technologies rely on the precise control of the interactions between cold atoms, which is achieved by controlling the magnetic field [3]. In some cases, however, minimizing the magnetic field is crucial for avoiding perturbations of the delicate quantum coherences of atoms. Therefore, it is essential to achieve the desired level of control and accuracy of the magnetic field in experiments.

In quantum memories, which are devices that store and retrieve light [4], even a small residual magnetic field (of less than 1 mG) can cause collapses and revivals of the retrieved light, leading to limited usability [5]. In addition, magnetic field gradients can cause a loss of atomic spin coherences, reducing storage times. In atomic magnetometry, the presence of stray magnetic fields, originating from various sources such as Earth’s magnetic field, environmental magnetic fields, and magnetic fields generated by the experimental setup itself, can cause systematic errors that limit their sensitivity and accuracy [6].

If magnetic traps are used for cold atom trapping and cooling, magnetic field fluctuations can induce transitions between internal spin states, leading to decoherence and loss of the atoms. Magnetic field fluctuations can also result in fluctuations in the trap position, leading to heating of the trapped atoms [7]. In experiments with Bose–Einstein condensates, where a sudden change from a repulsive to an attractive interaction can create matter-wave solitons [8] or a periodic modulation of the interaction can lead to the emission of matter-wave jets [9,10], the precise control over the interaction is required. This translates into the need for precise magnetic field control at the sub-mG level.

Due to the extreme importance of having a static magnetic field with a value close to zero or with an appropriate gradient, several interfering magnetic field compensation systems have been presented in the past. Traditionally, three orthogonally mounted Helmholtz coils are used to generate a magnetic field that opposes the interfering one, thus compensating it. The simplest attempts compensate for the DC component only, therefore the Earth’s magnetic field. A more complex solution is presented in [11] and offers a three-axis control system incorporating a PID (“proportional–integral–differential”) regulator. The field is sensed by a combination of fluxgate sensors and pick-up coils. The reported cancellation is in the range of 100:1 for an ideal stray field, and less for a non-homogenous field.

Another solution is presented in [12]. The hardware for this compensation scheme is like the above; the authors find the interfering field to be stable in time over several hours, and they measure it in advance to find its shape within one period of the mains. Next, they feed the Helmholtz coils with a current that is manually shaped to compensate for the interfering field, and the compensating current is synchronized with the mains. The rms value of the interfering field is reduced to about one tenth, depending on the axis observed.

A PID regulator is also implemented in [13]. A PC computer is used for digital processing of the PID algorithm, and this limits the speed of the cancellation system to about 100 Hz. The reported magnetic interference with the cancellation active is 370 μG rms in the frequency range between 10 and 100 Hz and about 10 μG rms at lower frequencies.

A combination of PID regulation and fuzzy logic is used to compensate for the interfering magnetic field in [14]. The compensation settles to an optimal value in about 60 s depending on the parameters used in the algorithm. The compensating system aims to achieve long-term stability of the magnetic field, and only this is reported; no results are given on the rejection of main’s interference.

2. Materials and Methods

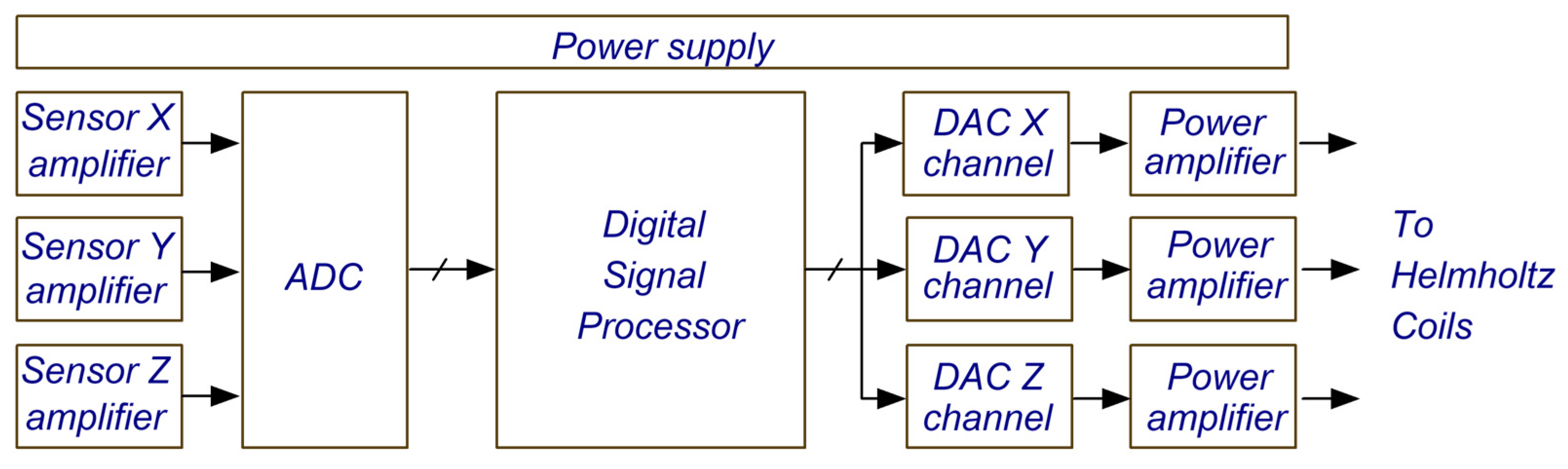
The presented system for magnetic field compensation consists of three orthogonally mounted magnetic field sensors with associated analog-to-digital (ADC) converter, digital signal processor (DSP), three digital-to-analog converter (DAC) channels with associated power amplifiers, three orthogonally mounted Helmholtz coils, and a power supply (Figure 1). The system can run independently, and all operational parameters can be set using front panel switches in combination with digital and analog input control signals. The system can be connected to a PC for enhanced handling. The LabVIEW software running on the PC visualizes the digitized magnetic field as sensed by sensors in all three axes and allows for detailed system set-up.

Three high-sensitivity magneto-resistive sensors, type HMC1001, are used to sense magnetic field within the center of the Helmholtz coils. Sensors are mounted orthogonally to each other and are aligned with the axes of the Helmholtz coils, allowing them to sense X, Y, and Z components of the magnetic field, respectively. Differential signals from sensors are amplified by instrumentational amplifiers (a pair of OPA2189) with a gain of 300, and resulting signals are digitized using LTC2373-18, four-channel, 18-bit ADC with sampling frequency of 5 kHz. Each instrumentational amplifier implements second-order RC low-pass filtering to limit the analog bandwidth to the Nyquist range of the ADC. The ADC is connected to the processor using a serial peripheral bus (SPI). The HMC1001 sensors require reset pulse after being exposed to overloading magnetic field, and three power drivers NCP81074A serve this purpose. The arrangement has sensitivity of 10 µG/LSB (least significant bit).

A high-performance ARM Cortex m microprocessor type STM32H743 was selected as the digital signal processing unit. In order to avoid the production of a dedicated printed circuit board, a Nucleo series DEMO board is used. The processor runs at 400 MHz clock frequency, and the demo board includes memory, input/output connections, and bus interfaces required for the purpose.

The interfering magnetic field can have any direction and is compensated using three orthogonally mounted Helmholtz coils. The following discussion applies to each of the three Helmholtz coils.

A Helmholtz coil arrangement consists of two square cross-section coils mounted at a specified distance. The two coils can be connected in series and driven by a single DAC stage and power amplifier to achieve homogenous magnetic field within the arrangement. However, the two coils can also be driven individually to produce a gradient in the magnetic field. In order to achieve both options stated above, two DAC stages and two power amplifiers are planned for the future, with one set per coil. For the time being, the two coils are connected in series, and one DAC stage and one power amplifier per axis are implemented.

Each DAC stage consists of two 18-bit DAC chips AD5870. One is used for coarse manual compensation of the DC magnetic field at present, and the other is used to implement adaptive interference compensation of the AC magnetic field. Both DAC chips are driven by SPI bus. Outputs of the two DAC chips are summed and low-pass filtered before entering the power output amplifier. It has been calculated that a current of up to 2 A should suffice to compensate for Earth’s magnetic field and interference fields. The primary source of magnetic interference components is the mains; therefore, frequency components of 50 Hz and its multiples are expected, and their expected amplitude is less than 10 mG. It has been determined that components above 600 Hz have negligible amplitude and effect on planned experiments, and considering the expected amplitude of the compensating current and the inductance of the Helmholtz coils, the output amplifier was designed. The output amplifier is built around a power operational amplifier OPA548, supplied by ±24 V, and is connected as a current driver; the feedback signal for the operational amplifier (OP) is a voltage drop over a small value resistor connected in series with the coil. The output current of the OP is limited to 2 A using a current-set resistor.

When the system for compensation of magnetic field is fully functional, it will consist of 3 times 2 times 2; therefore, 12 DAC chips and 6 power output stages. At present, six DAC chips and three power output stages are implemented, allowing three Helmholtz sets of coils, where each set consists of two coils connected in series.

The compensating algorithm implemented in the DSP requires a reference signal providing the frequency/phase of the interfering magnetic field; in our case, it is 50 Hz, which is the same as the main’s frequency. Such reference signal cannot be generated within the processor since the frequency of the mains may not be exactly 50 Hz and is not stable. Instead, the reference signal is derived from the mains using an optocoupler and a comparator to achieve a clean square-wave reference, which is passed to the processor for additional filtering and shaping.

The software of the processing unit implements a well-known “Least Mean Square (LMS) adaptive algorithm”, described, for instance, in [15] Chapter 6 and [16] Chapter 10. The universality of this algorithm was demonstrated already in [17] (Chapters 9 to 12: adaptive modelling in FIR digital filter synthesis, adaptive equalization of telephone channels, multiple reference noise cancelling, cancelling 60 Hz interference in electrocardiography, cancelling donor heart interference in heart-transplant electrocardiography, and cancelling noise in speech analysis, to list just a few) and in [18] Chapter 10: adaptive filtering of ocular artefacts from the human EEG, adaptive telephone echo cancellation, and fetal monitoring. The algorithm and its implementation are briefly reviewed here for one axis only and for the sinusoidal shape of the interfering field.

The magnetic sensor periodically probes the field within the interior of the Helmholtz coils and provides the error signal e_k representing this field for every successive measurement (k subscript stands for the successive measurement count); this is the field that needs to be compensated. The compensation is achieved by generating an opposite field by sending the current with a correct amplitude and phase through the pair of Helmholtz coils. The correct current can be derived from a periodically sampled reference signal x_k, which must have the same frequency as the interfering signal, using a finite impulse response digital filter (FIR filter). Such filter can only alter the amplitude and phase of a reference signal x, and the alteration depends on the filter core w_k(i). Interfering magnetic field and compensating field are then added within the Helmholtz coil and sensed by the magnetic sensor as the error signal. If the average value of the error signal e_k from the sensor is non-zero, filter core w_k(i) of the FIR filter must be adjusted to achieve better nulling. Once the average reading from the sensor becomes zero, the interfering field is optimally compensated, and the filter core w_k(i) should remain as is.

The filter core w_k+1(i) should be updated for every successive measurement k based on the current filter core w_k(i), the current error signal e_k, current and several past values of the reference signal x, and an arbitrarily selected LMS gain factor μ defining the speed of the adaptation algorithm. The adaptation algorithm itself can be divided into the following:

(a)

Initially set the filter core w₀(i) to an arbitrary fixed value, i.e., 0; there are N elements in the filter core, and initialize all past readings of reference signal x to 0.

(b)

Compute the output of the FIR filter as follows:

$$n_k={\displaystyle \sum }_{i=0}^{N-1}{w}_k\left(i\right) x_{k-i}$$

(1)

(c)

Apply the calculated output to the pair of Helmholtz coils and measure the error signal $e_k$ using magnetic sensor.

(d)

Update filter core as ($i=\left\{0 to N-1\right\}$):

$$w_{k+1}\left(i\right)=w_k\left(i\right)+2\mu e_k{x}_{k-i}$$

(2)

(e)

Repeat from step (b).

The algorithm requires N past values of reference signal x. These are available in a circular buffer created in memory of the DSP. The filter core length N is arbitrarily selected as 128 elements.

The software implemented in the DSP follows the block diagram given in Figure 2. The initialization phase defines variables and configures processor peripheral modules. After the initialization, the processor enters an infinite loop where it checks and responds to flags sent from interrupt routines.

Timer TIM4 is used to issue an interrupt every 200 μs; on this interrupt, the field-measuring ADC is instructed to make four consecutive measurements for three axes of magnetic field and one additional reference measurement (step c above). The results are stored in a circular buffer, and a flag is raised to activate adaptive LMS processing within the main loop.

Timer TIM3 is used to issue an interrupt every 500 μs; on this interrupt, the reference signal is being processed. A square-wave signal coming from the main’s zero-crossing detector is reshaped to include only the first few harmonics of the main’s signal and thus allows the LMS compensation for those harmonics only. The reshaped signal is stored in a separate circular buffer and is available to the LMS algorithm as reference signal x_i.

The reshaping is performed in two steps: first, a sawtooth signal is created by counter TIM 17, which becomes reset on every rising edge of the main’s synchronized square wave and increments for the rest of the main’s period. The content of this counter follows a sawtooth wave shape, which includes all harmonics (odd and even) of the main’s frequency, and violates the Nyquist criteria. The second step is the low-pass filtering of this sawtooth using an IIR (Infinite Impulse Response) filter. The filter is a fourth-order Chebyshev-type with a corner frequency of 400 Hz and 1 dB ripple. The derived reference signal is suitable for compensation of magnetic interference for all odd and even harmonics of the mains up to frequency of 400 Hz. Since magnetic interference consists mainly of odd harmonics, the sawtooth signal can be modified on user’s command into a triangular shape, which only consists of main’s frequency and odd harmonics. When such triangular signal is filtered using the same IIR filter, the system only compensates for interference with the main’s frequency and odd harmonics.

The main program starts the LMS processing after a flag is received from TIM4 interrupt routine and calculates results of three FIR filters (step b above) for each of the three axes, then combines these results with manual preset values for DC field compensation, and reshapes them into a suitable form to be sent to 12 DACs using a DMA transfer protocol. Additionally, it updates filter cores for all three axes (step d above). Finally, when enough past field measurement results are accumulated, it initiates a DMA transfer to send them to a PC for visualization.

The software on a PC intercepts packages of results sent from processor and visualizes measurement results. Additionally, it allows detailed control of the processing parameters.

The schematic diagrams for the hardware and source files, both for the DSP and PC, are available in [19].

3. Results

The experimental results were obtained to evaluate the quality of magnetic field interference compensation. For this purpose, a set of three, orthogonally mounted Helmholtz coils was prepared. All coils have a square cross-section with a side measuring 350 mm and have 10 turns of a wire with a diameter of 0.4 mm. The three-dimensional magnetic field sensor was placed in the center of the coils. The following tests were performed without any magnetic shielding around the coils in a normal laboratory environment with several mains-supplied instruments around.

The random noise of the electronics was evaluated first. For this purpose, the three magnetic sensors were shorted; therefore, the resulting noise was caused by the amplifier and ADC only. The timing diagram of this noise and its spectrum for one axis are only presented in Figure 3. The RMS value obtained was 19.5 μG, and the noise floor in the range from 0 Hz to 500 Hz was 4 μG rms.

Next, the short circuits from the sensors were removed, and the DC current through the coils was manually set to compensate for the Earth’s magnetic field. Intentionally, the compensating current was set in such a way that the three traces on the computer screen did not overlap. Figure 4 shows the timing diagram of the obtained signal at all three axes and the corresponding amplitude spectra. An individual component has an amplitude of about 3 mG peak-to-peak. By combining contributions from all three axes, the effective value of the interference magnetic field was 1.46 mG. The spectrum reveals strong contributions at a frequency of 50 Hz and odd harmonics. The effective amplitude at 50 Hz was about 1 mG rms and about 300 μG rms at 150 Hz. Further harmonics decreased in amplitude, fell below 100 μG rms. and above 500 Hz, and were therefore about 40 dB below the component at 50 Hz. The noise floor was practically the same as the one with the magnetic field sensors shorted.

Different shapes of the interfering components suggest that there are several sources of interfering magnetic field present, each of them with a unique combination of harmonic components.

Finally, the adaptive LMS algorithm was activated to compensate for the interfering field in Figure 4. The resulting timing diagram and spectrum after about 20 s of adaptation are presented in Figure 5. The first four components in the spectrum were completely compensated for; there was no sign of interference at 50 Hz, 150 Hz, 250 Hz, and 350 Hz. The component at 450 Hz was reduced to about one-half, while the higher harmonics remained as they were. The resulting effective value of the interfering signal in a frequency range from 0 Hz to 1 kHz was about 53 μG, which is about 28 dB better than without the compensation. The compensation in the frequency range from 0 Hz to 400 Hz was significantly better since all the peaks in this range were at the noise floor.

The adaptation procedure for the LMS algorithm requires some time, which strongly depends on the LMS gain factor μ. For the small factor μ, the adaptation process takes a longer time, and the compensation is more precise, while for the larger factor μ, the adaptation is faster but more sensitive to random (not periodic in nature) interfering signals. Since the aim of this experiment was to compensate for interference from the mains, the smaller factor μ is superior. Figure 6 shows the behavior of the rms value of the interfering magnetic field during adaptation; it dropped from about 1.4 mG rms for more than 20 dB in a few seconds and continued dropping to the forementioned −28 dB within 20 s.

4. Discussion

The described magnetic field compensation system implements the LMS adaptation algorithm and is best used by following these steps:

(a)

The DC magnetic field is to be compensated manually first; for this step, the adaptation algorithm should be disabled. The DC compensation is performed by manually setting DC currents for all three Helmholtz coils while observing the readouts from the three magnetic field sensors in a timing diagram on the PC screen (when all six coils are implemented, a desired magnetic field gradient will be set in this step).

(b)

The adaptation for the LMS algorithm is to be enabled next. This allows the system to learn and compensate for magnetic interference from the mains by adapting the filter core w(i). The adaptation takes about 20 s, and the current shape of the field within the Helmholtz coils can be observed on the PC screen.

(c)

After about 20 s, the compensation system learns about the interference field and is able to compensate it without any additional information, providing the interfering field from the mains does not change. Therefore, the adaptation can now be disabled by setting the factor μ to zero. This freezes the filter core w(i).

(d)

The physics experiment can now be started within the DC and AC compensated magnetic fields.

(e)

After the experiment is finished, the adaptation can be re-enabled, and the compensation system can adjust the filter core w(i) again to interference, which may have been altered since the last adaptation. The manual DC compensation can also be adjusted if needed. The use continues with the above step (c).

The results shown in Figure 5 show a complete cancellation of the main’s interference for 50 Hz, and the first three odd harmonics of this frequency. The system can compensate for interference at all frequencies that are also present in the reference signal. When the reference signal is a square wave as obtained from the zero-crossing detector of the mains, theoretically, all odd harmonics can be compensated. However, such a reference signal violates the Nyquist range and hinders digital processing. To avoid problems, the square-wave signal is digitally reformatted within the processor into a sawtooth signal and filtered to contain only a selected number of odd and even harmonic components. For this experiment, the decision was made to compensate harmonics up to about 500 Hz. Higher harmonics could be compensated for by widening the band-pass range of the filter for the reference signal; at higher frequencies, some phase compensation should also be implemented digitally to avoid over-compensation and instability.

Manual compensation of the DC magnetic field (mainly the Earth’s field) will be replaced by an integral regulator implemented in the DSP in the final version of the system. The manual intervention is planned to set the desired level of the magnetic field and its gradient only. The integration of this new functionality, in combination with the demonstrated method for compensation of magnetic field interference in the frequency range up to 400 Hz, would yield a complete and robust solution to address the critical needs of magnetic interference compensation and magnetic field cancellation in cold atom experiments and quantum technologies.

The present system implements only one three-dimensional magnetic field sensor. This is sufficient for a homogenous magnetic field in the vicinity of the physical experiment. However, the field is not homogenous, and the measurement at one point in space is not sufficient. Once the system is complete, it will have more detectors strategically placed around the physical experiment, and their readouts will be combined into a single three-dimensional result.

As can be seen from Figure 3 and Figure 5, the noise floor within the range from 0 Hz to 500 Hz is practically the same for inputs to the amplifiers that are shorted or connected to the magnetic sensor. The noise is therefore mainly caused by the amplifier; the sensor does not worsen the noise. A better amplifier with less noise is to be implemented. The current sensitivity of the magnetic field detection of 10 μG/LSB suffices.

The sampling rate of the ADC is set to 5 kHz. This rate is selected to allow sufficient processing time for the selected microcontroller and, simultaneously, to set the Nyquist frequency far above the expected highest harmonic of the interference field. With this, the available processing time is only 200 μs, and a sizeable chunk of this time is wasted on the preparation of data for DACs. The results obtained by the adaptive LMS algorithm are to be sent to DAC using DMA transfer, and this requires the reformatting of results into a matrix of consecutive logic levels for the microcontroller port where DACs are wired. This reformatting basically limits the sampling rate. It would be beneficial to implement the LMS algorithm in a field programmable gate array (FPGA), where chunks of the LMS algorithm and reformatting processes can be implemented in separate logic blocks that operate simultaneously.

5. Conclusions

The classical LMS algorithm, as described in the literature, was implemented to reduce magnetic interference from the mains. A contemporary microprocessor and low-noise analog components were used in the hardware. The details of the implementation are provided in [19]. Special care was taken in the preparation of the reference signal, which must be synchronous with the mains and have the same frequency and constant phase. The harmonics represented in the reference signal were selected using a suitable IIR filtering of the signal coming from a main’s zero-crossing detector. The resulting cancellation of the interfering mains-synchronous components is more than adequate for our experiments involving cold atoms since the cancellation of the main’s harmonics in the frequency range from 50 Hz to 400 Hz was close to 40 dB.

The described approach involves learning time intervals when the interfering signal is annulled. When the learning is finished, it becomes disabled, and as long as the interfering signal does not change, the annulment is valid, and additional magnetic fields from other sources can be activated to suit the requirements of the experiment with cold atoms. This approach satisfies our needs for experimenting with cold atoms and quantum technologies.