1. Introduction
With the continuous progress of modern technology, the 5G era has arrived. Thanks to the unceasing innovation in communication and network technology, VoIP (Voice over Internet Protocol) communication technology has gained widespread popularity compared to the 4G era. Applications such as WeChat, Skype, and various conference software have become widely used among the general public. VoIP has attracted market and public attention due to its ability to fully exploit network bandwidth, minimize call costs, and facilitate the implementation of value-added services. Moreover, with the recent outbreak of COVID-19, offline meetings have shifted to online platforms, and traditional classrooms have transitioned to online classrooms. Consequently, VoIP communication technology has garnered increased significance.
However, it is worth mentioning that during VoIP communication, not only does the near-end microphone capture the speech of the near-end speaker, but it also records the sound played by the near-end speaker, causing the far-end speaker to potentially hear the echo of their speech. Moreover, due to speech encoding, decoding, and the transmission of data over the network, there may be varying levels of time delays that further contribute to the generation of echo, causing inconvenience for speakers. Therefore, in line with the continuous development of the VoIP industry, echo cancellation has emerged as a prominent research focus and a crucial area for improvement to enhance the quality of communication processes and enhance user experience.
There are two main types of echo in VoIP communication: circuit echo and acoustic echo. Due to the two to four wire conversion of the switch, circuit echo is generated on the network side [
1]. However, due to the advancement of echo cancellation technology, circuit echo has been effectively reduced and canceled. As a result, the focus of echo cancellation has shifted from circuit echo to acoustic echo.
It is very difficult to cancel acoustic echo. There are several main reasons: (1) the communication process mainly takes place in enclosed environments such as conference rooms, where the sound emitted by the speaker will be reflected repeatedly and then captured by the microphone, mixing with the speech of the near-end speaker. This process results in a long tail of the echo, and the corresponding echo path [
2] has a long impulse response. Therefore, to achieve echo cancellation, it is necessary to increase the order of the adaptive filter. (2) During communication, it is impossible to guarantee absolute silence in the environment. Noise caused by personnel movement or other forms of interference can disrupt the propagation of sound, leading to significant fluctuations in the pulse response of the acoustic echo. Therefore, the acoustic echo path is not stable. The rapid changes in the echo path require the echo cancellation process to have a fast convergence speed [
3] and good tracking performance. However, algorithms with fast convergence speeds are closely related to computational complexity. The echo cancellation filter used to cancel echo has a high order, and conventional fast algorithms often cannot effectively solve the problem. (3) During the VoIP communication process, environmental noise can affect echo cancellation. Additionally, in situations with high background noise, echo cancellation not only needs to handle the echo, but also needs to consider the background noise, making filter design extremely challenging.
In summary, the main research challenge in echo cancellation currently lies in dealing with the acoustic echo. The noise, reverberation, and variations in echo paths significantly increase the complexity of acoustic echo cancellation. Developing an efficient echo cancellation system can greatly enhance the user experience during VoIP communication.
For acoustic echo, it can be classified into two types: linear echo and non-linear echo. Linear echo refers to the echo produced by sound waves propagating in a straight path in space, while non-linear echo refers to the non-linear effect generated by sound waves propagating in space [
4]. Linear echo can be effectively canceled using traditional methods. These methods primarily rely on adaptive filtering techniques, such as the Least Mean Square (LMS) algorithm [
2], Normalized Least Mean Square (NLMS) algorithm [
3], Recursive Least Squares (RLS) algorithm [
5], and Blocked Frequency Domain Adaptive Filter (PBFDAF) [
4]. Diniz et al. [
2] propose a method that involves utilizing LMS adaptive filters to replicate the echo path and subsequently subtracting the estimated echo signal from the input signal, thereby achieving effective echo cancellation. This algorithm is straightforward, dependable, and widely applicable; however, it utilizes instantaneous values instead of expected values in its calculation during the iteration process. As a consequence, this approach introduces errors into the calculation process, which are affected by the input signal and subsequently evolve as the input signal changes. When assessing the performance of the adaptive filtering algorithm, the LMS algorithm may introduce uncertainty in the rate of convergence, which ultimately leads to numerous uncertain factors in echo and unstable echo cancellation.
To address this issue, Slock et al. [
3] replace the LMS algorithm with the NLMS algorithm to simulate the echo path, accompanied by the incorporation of normalization operations into the LMS algorithm. This modification aims to ensure algorithm convergence through normalization, thereby enhancing the overall convergence effect. Nevertheless, it is important to note that this algorithm possesses significant drawbacks in terms of convergence rate and steady-state error.
Duttweiler et al. [
6] introduce the proposition normalized Least Mean Square (PNLMS) algorithm as a means to emulate the echo path. This algorithm effectively modifies the filter weight in proportion to the sparse character of the echo path (sparse character describes the phenomenon where there are fewer significant signal components present on the echo path during the transmission of acoustic signals), which enhances convergence speed and minimizes steady-state error for the sparse echo path. However, the performance of this algorithm might diminish for the non-sparse echo path. Liu et al. [
1] propose the improvement normalized Least Mean Square (IPNLMS) algorithm to address the issue of performance degradation in the non-sparse echo path. In comparison to the PNLMS algorithm, this method effectively enhances the convergence rate when dealing with the non-sparse echo path; however, the steady-state error and computational complexity also increase as a result.
Speex is an open source audio codec, mainly used for real-time audio communication [
7]. Its echo cancellation part is based on NLMS and implemented using a multi-delay block filter [
8] in the frequency domain. It has the advantages of efficient echo suppression, low latency, and cross platform support, making it widely used in real-time communication applications.
For linear echo, adaptive filters can already achieve good cancellation effects. However, when it comes to nonlinear echo, adaptive filters often fall short in achieving the desired effect due to the presence of reverberation and complex acoustic characteristics (such as distortion, non-linear resonance, and interference effect [
9]). In order to address the intricate non-linear relationship between inputs and outputs, deep neural networks (DNNs) are increasingly utilized for echo cancellation tasks. A DNN is a neural network with multiple layers. It is introduced by Hinton et al. [
10], which effectively tackles the problem of gradient explosion and vanishing in multi-layer neural networks, thereby enabling the creation of truly deep networks. As deep learning technology evolves, DNNs are able to more effectively extract deep data information. Compared to shallow neural networks, DNNs possess stronger capabilities in expressing non-linear relationships.
UNet [
11] is a network model that follows a symmetrical U-shaped structure. It is typically an encoder–decoder structure. The first half of UNet is responsible for feature extraction and continuously reducing the input size, typically achieved through convolution and down-sampling operations. The latter half aims to restore the original input size. Apart from convolution, the crucial steps of this process include up-sampling and skip connections. Skip connections concatenate the location information of the bottom layer with the semantic information of the deep layer to achieve better results. Because the network structure of UNet has local connectivity characteristics, it can be used for speech signal processing. Choi et al. [
12] improve UNet by proposing Tiny Recurrent UNet (TRUNet), and propose phase-aware
-sigmoid mask (PHM) for speech enhancement. Fu et al. [
13] build a network framework based on UNet and Conformer [
14] to enhance speech and cancel echo.
In the field of speech signal processing, the self-attention mechanism can capture long-range dependencies in the input, and dynamically adjust focus to distinct regions. However, the simple self-attention approach presents significant challenges due to its high computational complexity, rendering it impractical for speech processing tasks. To alleviate this problem, Zhang et al. [
15] propose a axial self-attention (ASA) for acoustic echo cancellation. ASA can reduce the need for memory and computation, making it more suitable for speech signals. Consequently, many scholars are still working hard to find effective strategies to mitigate the complexity of self-attention.
The acoustic echo cancellation system based on DNN primarily operates in the time-frequency domain and relies on spectral masking for its main processing [
16]. Spectral masking refers to the process of multiplying the spectrum of the original signal with the mask element by element in the time-frequency domain to obtain the mask corrected spectrum. The mask can take various forms, such as ideal binary mask (IBM), ideal ratio mask (IRM), and complex ideal ratio mask (cIRM) [
17].
One-step methods are the simplest application of DNN in acoustic echo cancellation systems, which simultaneously solve linear and non-linear echo. Westhausen et al. [
18] proposes the dual signal transformation LSTM [
19] network (DTLN), which successfully achieves both linear and non-linear echo cancellation. The network is comprised of two key blocks, each consisting of two LSTM layers and a fully connected layer. The prediction of the mask is accomplished using the sigmoid activation function. The input feature is the normalized logarithmic power spectrum of the near and far end microphones connected in series. This structure has high modeling ability and can further improve echo cancellation ability by stacking models.
In addition to one-step methods, more research is focused on using adaptive filters to process linear echo and neural networks to process non-linear echo. Lukas et al. [
20] propose a non-linear echo cancellation model that utilizes a recurrent neural network (RNN), which can achieve better real-time echo cancellation performance while using lower computing resources. Similarly, Ma et al. [
21] also propose an echo cancellation model based on the RNN denoising network model, but they introduce a separate branch for the far-end reference speech within the network. The input of the model consists of two components: the linear filtering output (residual signal) and the far-end reference speech. The output comprises three components: near-end speech voice activity detection (VAD), far-end speech VAD, and clean near-end speech. Since the far-end reference speech is incorporated as an input, this model exhibits superior cancellation performance. In addition to networks that perform calculations in the real domain, there are also networks that perform calculations in the complex domain. The complex domain is an extension of the real domain, which includes all numbers in the form of
. Zhang et al. [
22] propose F-T-LSTM based on phase and time-frequency information in the complex domain. This model can fully utilize the phase information of speech and achieve better cancellation performance with fewer parameters and smaller time delay.
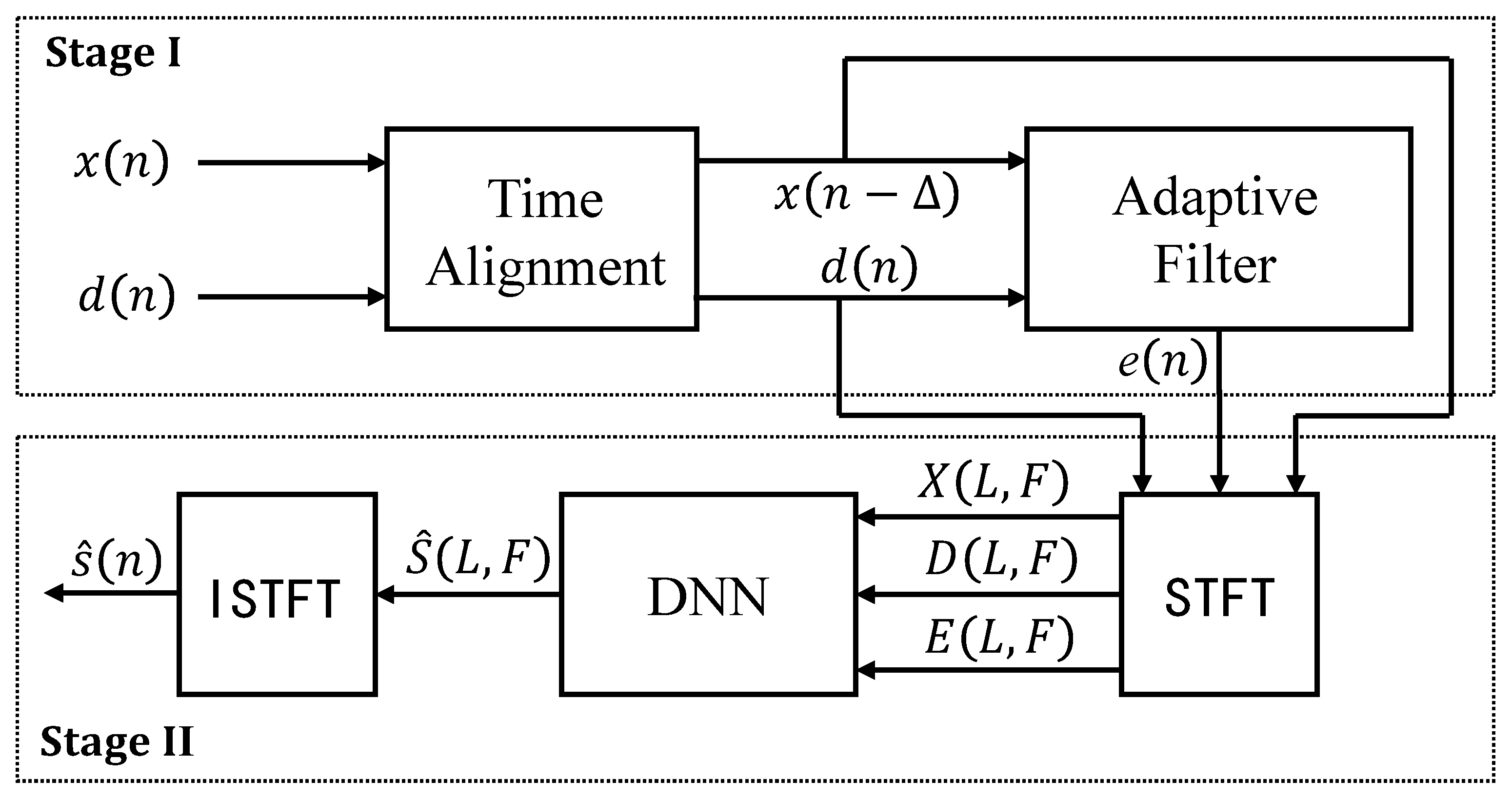
In this work, inspired by the above technologies and theories, we use adaptive filters to cancel linear echo and DNNs to cancel non-linear echo, constructing a multi-stage acoustic echo cancellation model. In the linear echo cancellation stage, the inputs of the adaptive filter are far-end reference speech and near-end microphone signal. In the non-linear echo cancellation stage, the inputs of DNNs are the complex spectra of the far-end reference speech, the near-end microphone signal and the output of the adaptive filter, and the output is the complex spectrum of the estimated near-end speech. Our contributions are summarized as follows:
To select a more suitable adaptive filter, we conduct a performance comparison on various adaptive filters using the same dataset. After evaluation, we opt for the Speex algorithm as the initial component of our multi-stage acoustic echo cancellation model.
Due to the delay between the far-end reference speech and near-end microphone signal, we use the Generalized Cross Correlation Phase Transformation (GCC-PHAT) algorithm for delay estimation. Then we perform delay compensation on the far-end reference speech to achieve better linear echo cancellation performance.
With the aim of canceling non-linear echo, we propose Multi-Scale Time-Frequency UNet (MSTFUNet) as the second component of the multi-stage acoustic echo cancellation model. MSTFUNet is based on UNet and achieves good echo cancellation performance.
To address the issue of high computational complexity and difficulty in handling speech tasks of simple self-attention. We propose Improved Time-Frequency Self-Attention (ITFSA), which can effectively extract time-frequency speech information.
In the process of encoding and decoding in UNet, much detailed information is lost. To alleviate this issue, we introduce the Channel and Time-Frequency Attention (CTFA) module to connected each encoder and decoder. This module is capable of extracting information in both channel and time-frequency dimensions at multiple scales.
In the following sections, we will provide a detailed introduction to our proposed technical terms.
The remaining sections of this paper are organized as follows: In
Section 2, we provide a detailed explanation of the signal model and the various components of our proposed model.
Section 3 introduces the datasets utilized in our experiments, along with the implementation details.
Section 4 showcases the outcomes of our experiments, accompanied by a thorough analysis. Lastly,
Section 5 concludes this paper by drawing final remarks based on our findings.