Proof of Concept of the Use of the Parametric Effect in Two Media with Application to Underwater Acoustic Communications
Abstract
1. Introduction
Approaches
2. Nonlinear Acoustic: Parametric Transduction Generation
- Shock distance: In cases where a finite-amplitude harmonic wave of a given frequency propagates, its profile changes progressively (deforms) due to the difference in propagation velocity of its parts so that the points with higher pressure (crests) move faster than those of lower pressure (valleys) [8]. Thus, this profile becomes more abrupt in the propagation until it reaches a “sawtooth” shape when the wave travels the known shock distance, as depicted in Figure 1. In the frequency domain, this phenomenon results in the appearance of harmonics and subharmonics, or distortion.Figure 1. Scheme for interpreting shock distance.The shock distance is calculated as follows. Let u be the amplitude of the particle velocity in the wave. It can then be shown that the phase velocity of the acoustic wave crest is , and the phase velocity of the trough is , where is the small-signal sound speed, and is the nonlinearity coefficient of the medium. Initially, the crest of the wave is separated from its trough by a distance , and the crest takes time T to reach the trough [19,24,25], as in Equation (1):This equation does not strictly define the shock distance , which was obtained by considering the distance at which the wavefront becomes vertical at zero crossing [19,26]. Then it can be shown in Equation (2) thatwhere k is the wave number, and M is the acoustic Mach number , where v is the local wave velocity.In the context of the parametric effect, the formation of shock waves is important because it acts as a mechanism for transferring energy between different frequency components of sound waves. This means that shock waves can affect the amplitude and phase of other waves in the medium, generating new frequencies or changing the amplitude of existing ones.
- Absorption distance: As the wave propagates, each frequency that appears in the medium is absorbed with different intensities by the medium so that the higher frequencies are absorbed with different intensities. (harmonics) will decay faster than the difference frequency ; therefore, the latter will be able to propagate over greater distances. Consequently, the nonlinear generation of new frequencies is limited to a distance concerning the transducer called interaction distance or “absorption length”. Thus, this process can be visualized as the interaction of a set of virtual acoustic sources (array) contained along the absorption length [27] as depicted in Figure 2.Figure 2. Scheme for interpreting absorption distance.
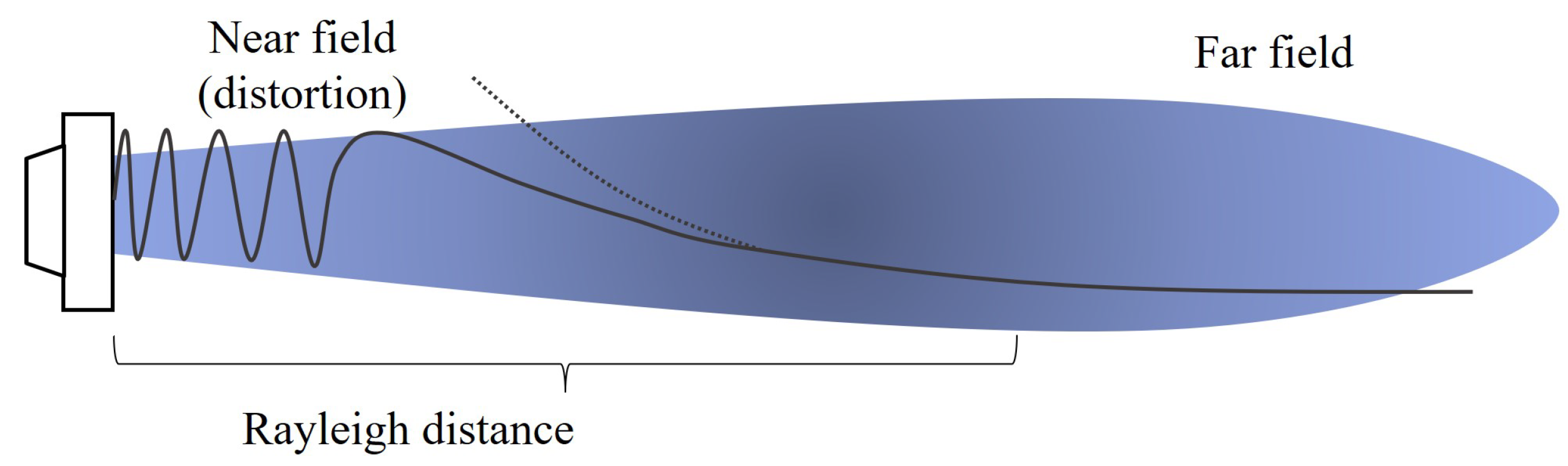
- Rayleigh distance: This is the boundary that separates the near field from the far field. Therefore, it is the distance from which the wave can be considered to change from behaving as a plane wave to a spherical wave. From this distance, the wave attenuates 6 dB when doubling the distance to the source [28]. When studying an emission phenomenon, it is imperative to consider the proximal field of the transducer. This consideration requires the inclusion of the main radiated frequencies, which are predominantly enclosed within a cylindrical boundary defined by the Rayleigh distance and the transducer surface area. Conversely, in the far field, the onset of spherical radiation divergence is evident. Energy propagation occurs at an accelerated rate [27,29], as shown in Figure 3.Figure 3. Scheme for interpreting Rayleigh distance.This Rayleigh distance [19] is given by the Equation (4):where a is the diameter of the active zone of the emitting transducer. Once the above distances are taken into account, mathematical models are used to help predict the behavior of the acoustic field of secondary frequencies [30]. One such model, used in the present study, is discussed below.
3. Theoretical Analysis: Westervelt Model
3.1. Problem Formulation
- Continuity equation: This is a mathematical expression that states that the total mass of a gas cube of volume must remain constant in the face of volume variation, so it is also called the mass conservation equation. Is expressed as follows in Equation (5):where is the partial derivative in each of the Cartesian coordinates; is the mass density; and is the velocity vector associated with the motion of the fluid particles.
- Navier–Stokes equation is derived from the law of conservation of momentum (Newton’s Second Law) for viscous fluids in Equation (6):where is the pressure; the bulk viscosity; and the shear viscosity. The term is called “the convective” or “transport acceleration” term.
3.2. Analytical Solution of the Problem
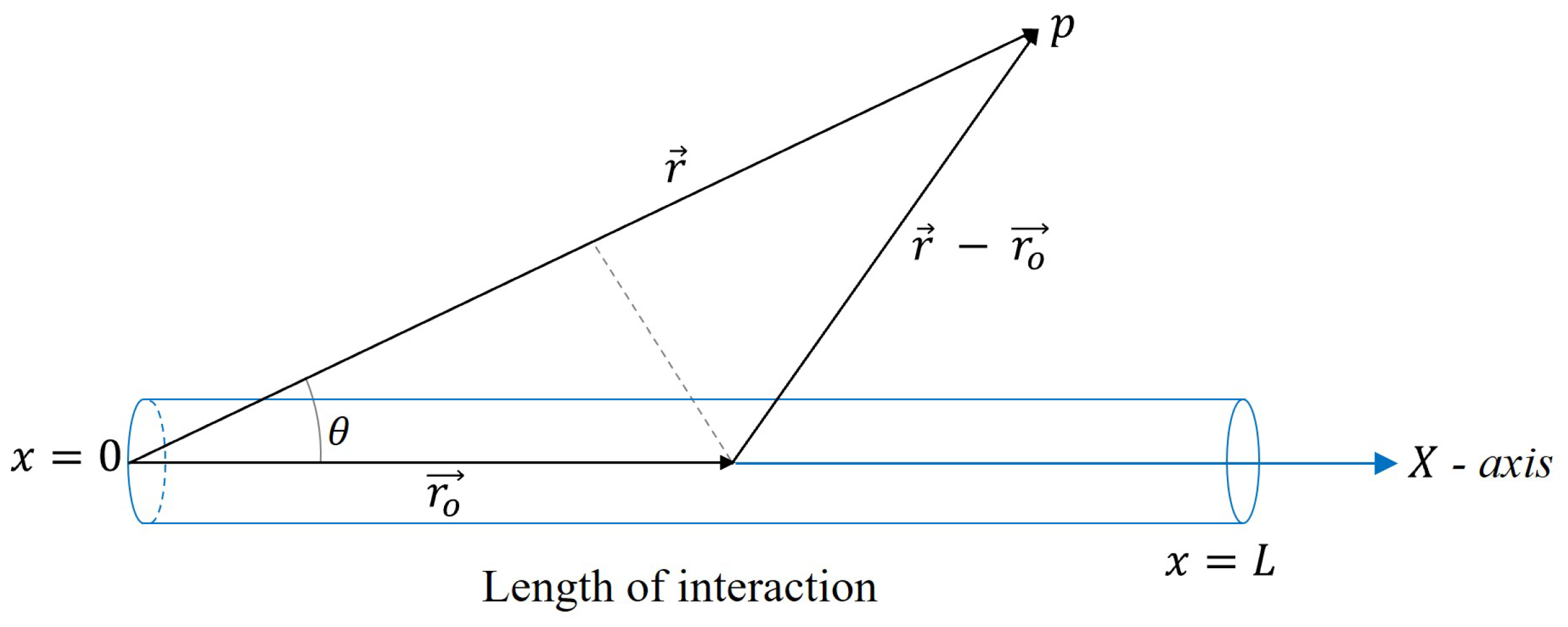
- Amplitude modulation: This technique was studied by Berktay in 1965 [4]. It is a general method for the nonlinear generation of an audible frequency from ultrasonic frequencies. It consists of emitting a primary ultrasonic wave modulated in amplitude by an audible frequency, which is demodulated in the medium through nonlinear effects. This process is called self-demodulation [20,34,35]. The pressure wave of the primary beam exciting the medium is shown in Equation (10):where is the pressure amplitude of the carrier wave; is the absorption coefficient of the carrier signal ; and is the modulation envelope defined by the modulating wave, the frequency of which is small compared with that of the carrier signal.By substituting the equation of the primary field (10) in Equation (9) and integrating gives the pressure distribution of the parametric frequency along the radiation axis at a distance r in the far field [36] by the following Equation (11):where A is a constant related to the amplitude , the absorption of the medium , and the cross-sectional area of the transducer a. is the envelope of the function.For convenience, Equation (11) is rewritten as follows:This development based on the Berktay and Smith equation [36] provides a valuable approximation for steering near-axis beams. According to this equation, the demodulated signal is proportional to the second derivative with respect to time of the squared envelope of the carrier signal. This acoustic model is widely used in parametric source preprocessing [37,38]. It should be noted that the characteristics of the self-demodulated wave are influenced by the primary waves, and the amplitude of the difference frequency is proportional to the square of the carrier frequency.
- Nonlinear interaction of two monochromatic waves: This interaction is also called the scattering of sound by sound [2], where the primary wave is expressed by the following Equation (14):where, after some trigonometric calculations, we obtain Equation (15):Thus, the primary wave is equivalent to a carrier wave of frequency amplitude-modulated by the half-wave difference frequency . These developments show that both techniques are related such that, the nonlinear interaction of two monochromatic waves is a particular case of the amplitude modulation method.
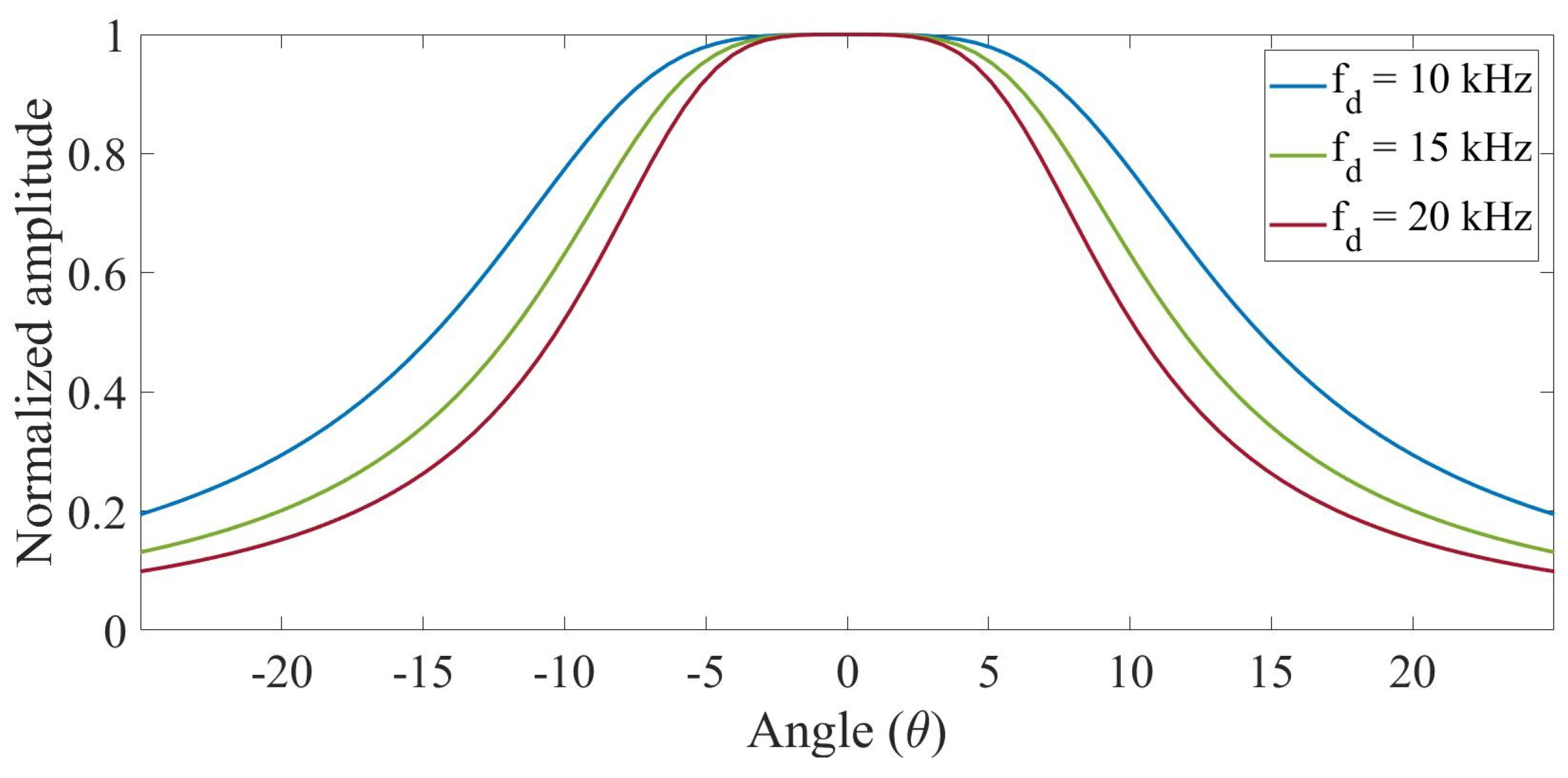
- Directivity: The parameter sets the directivity of the parametric such that the closer the mean primary and difference frequencies are the closer the directivity of the difference frequency will be to f. Furthermore, for the same ratio , the higher the absorption of the medium, the lower the directivity of the parametric since the primary frequency does not propagate sufficiently for the parametric to acquire greater directivity [27]. Figure 5 shows the directivity of parametric signals in air with a mean carrier frequency of 200 kHz and different difference frequencies of 10, 15 and 20 kHz and a transducer diameter of 33 mm.
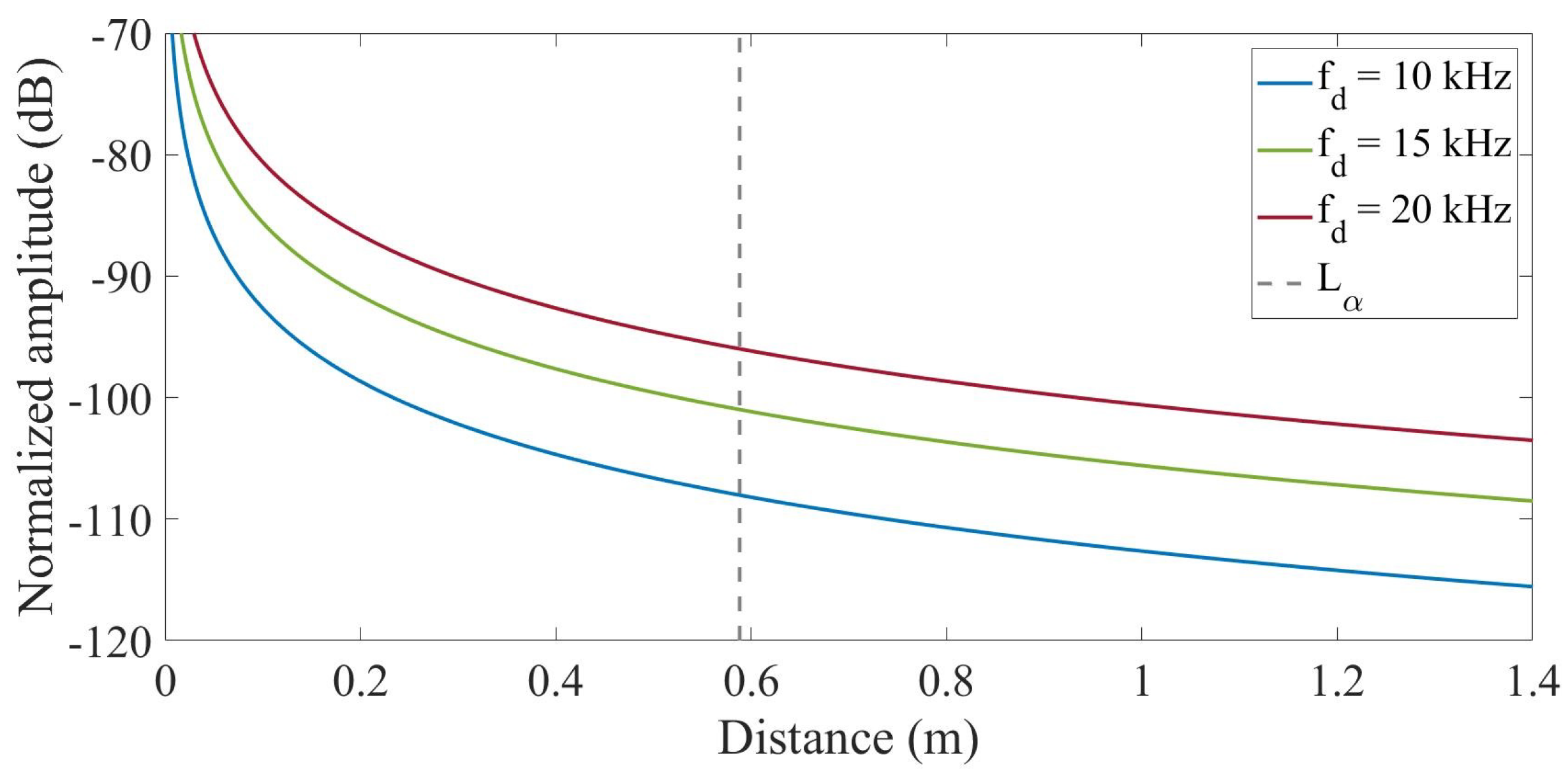
- Attenuation: Once the parametric is formed (a necessary condition since it is a far-field solution), its attenuation is inversely proportional to the distance, which occurs with the primary beam, except that it has more absorption than the secondary beam. Figure 6 shows the behavior of the parametric with the same frequencies as in Figure 5. The gray vertical line in red marks the absorption distance for which Westervelt’s theory is applicable.
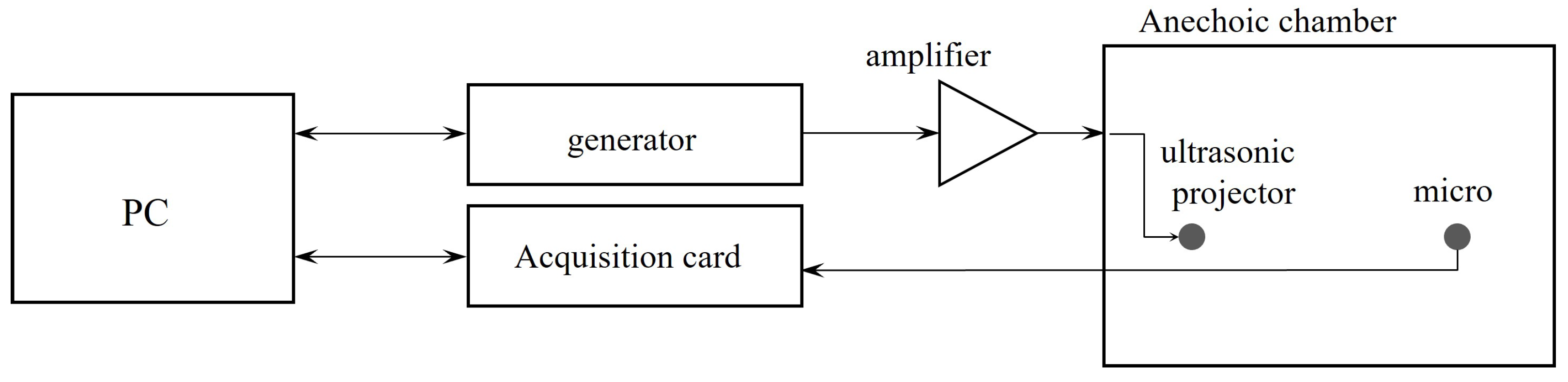
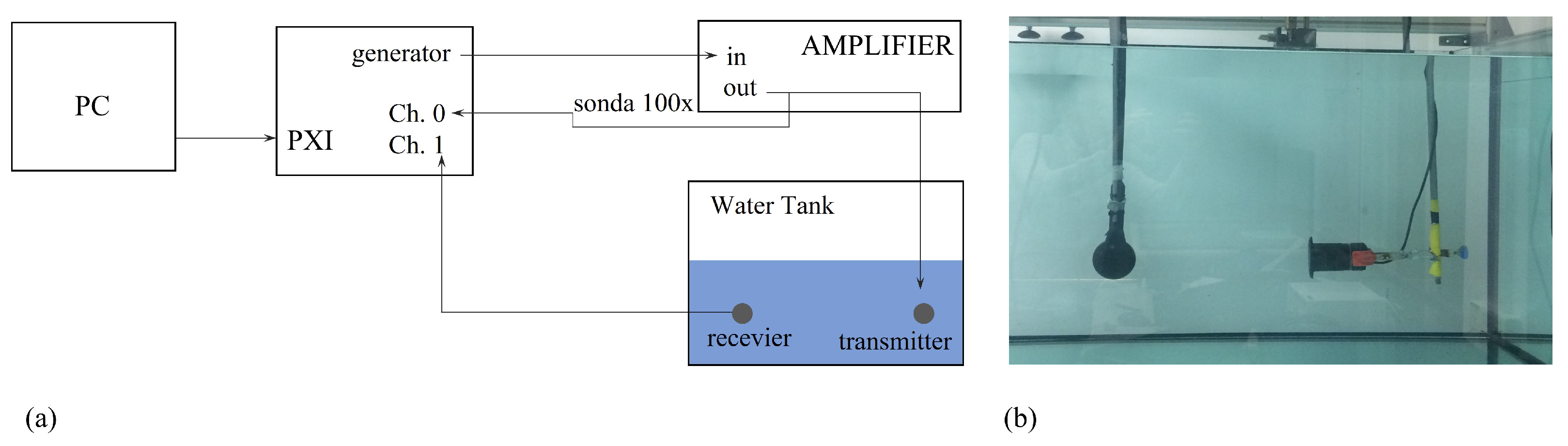
4. Experimental Set-Up
4.1. Air Measurements
4.2. Water Measurements
5. Analysis and Results of Measurements in Air and Water
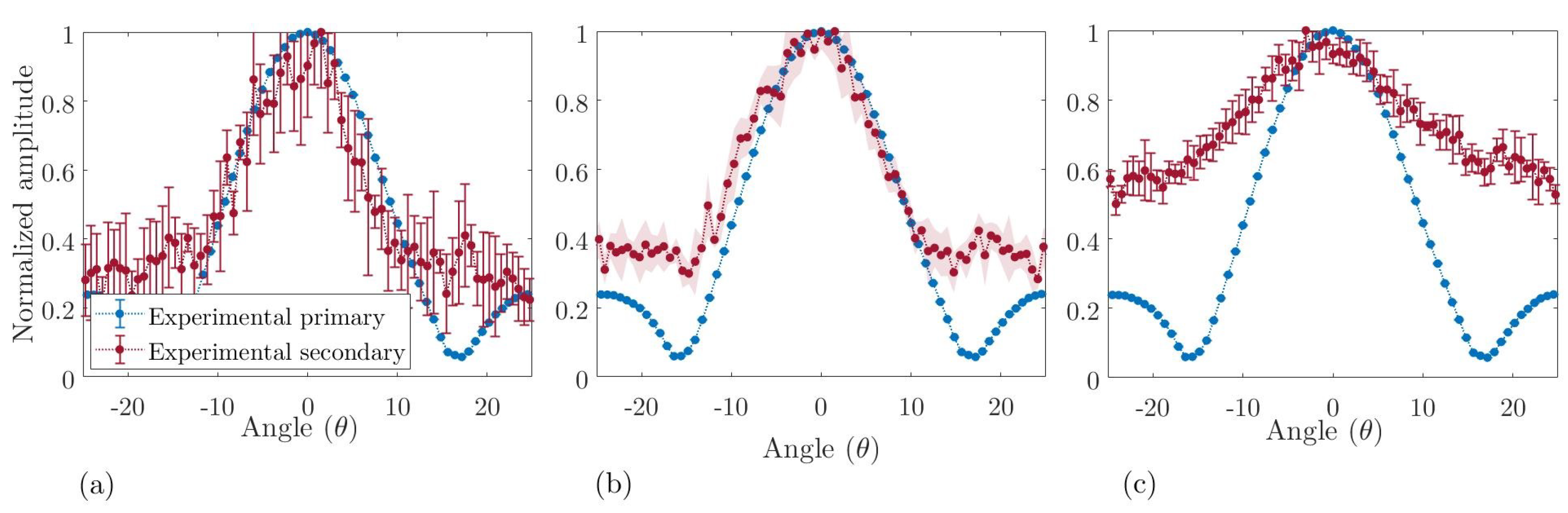
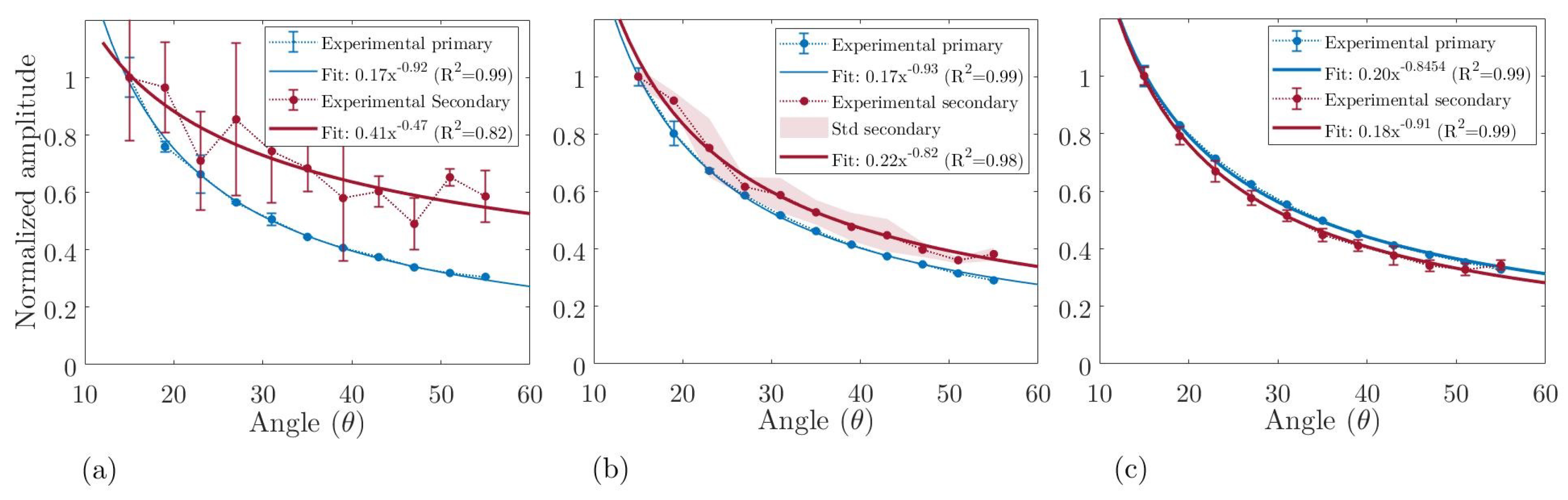
5.1. Directivity and Attenuation in Air
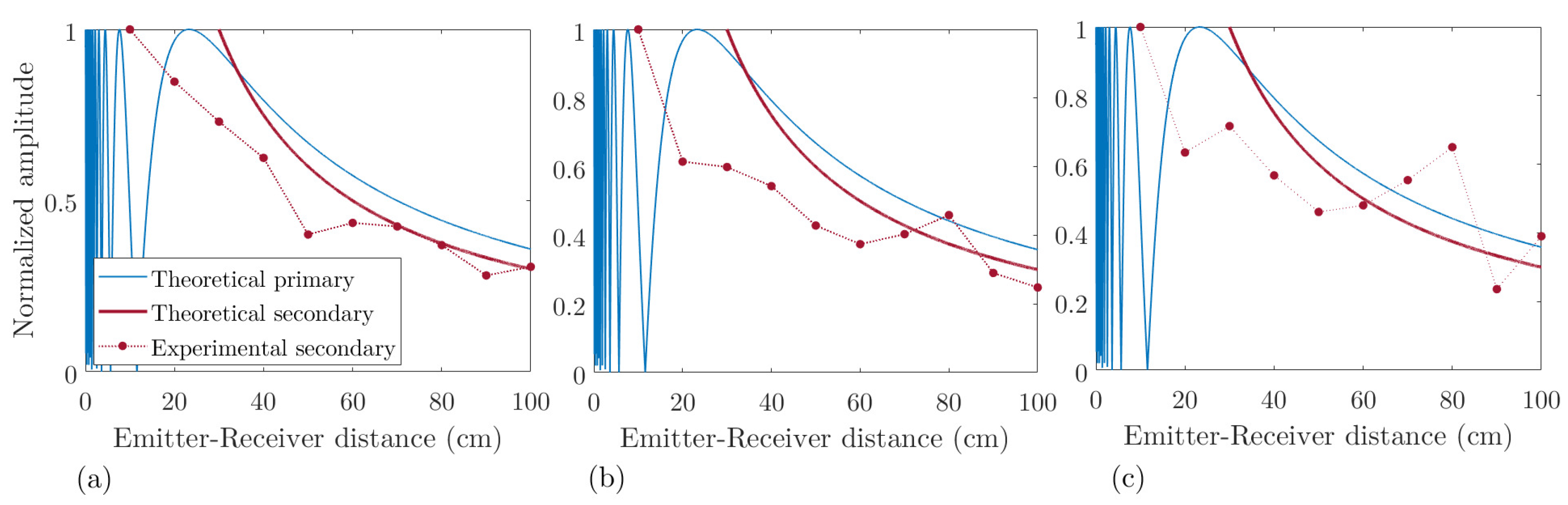
5.2. Directivity and Attenuation in Water
6. Applications to Underwater Acoustic Communications
- E(t): This is the modulating signal that contains the information to be transmitted.
- y(t): Is the carrier signal that supports the frequency shift of the modulating signal; often of the sine type, i.e., .
- x(t): Is the modulated signal resulting from the modulation process, the product of the carrier and the modulating signal; that is,
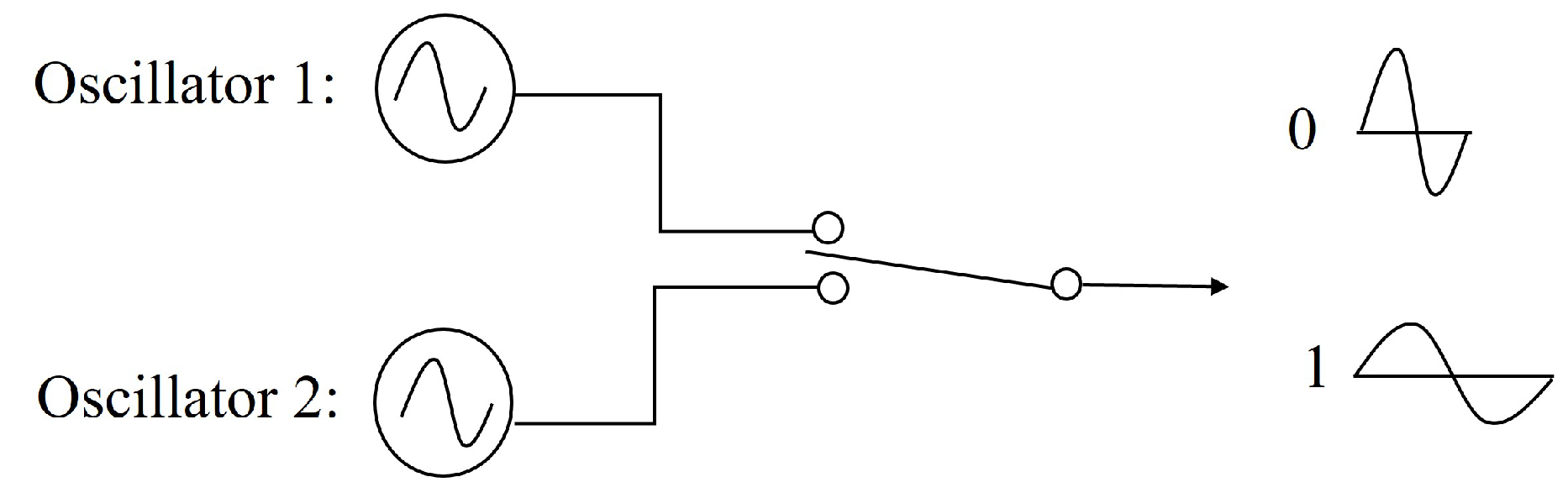
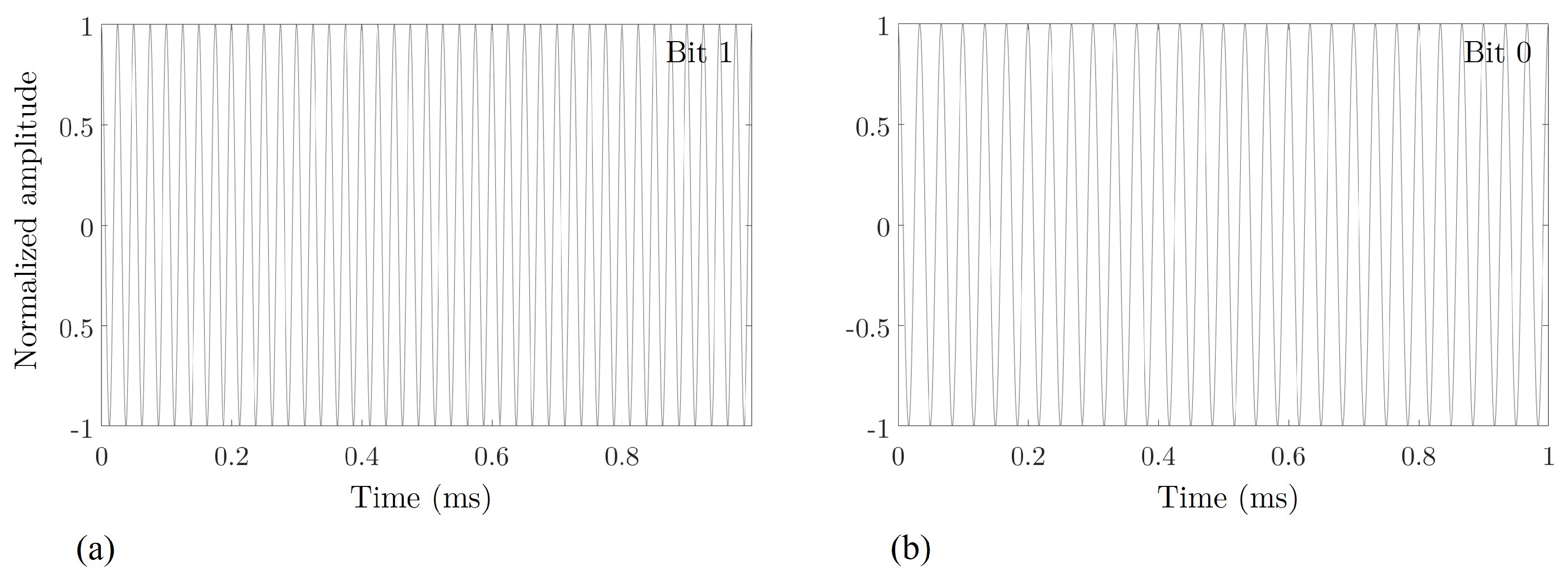
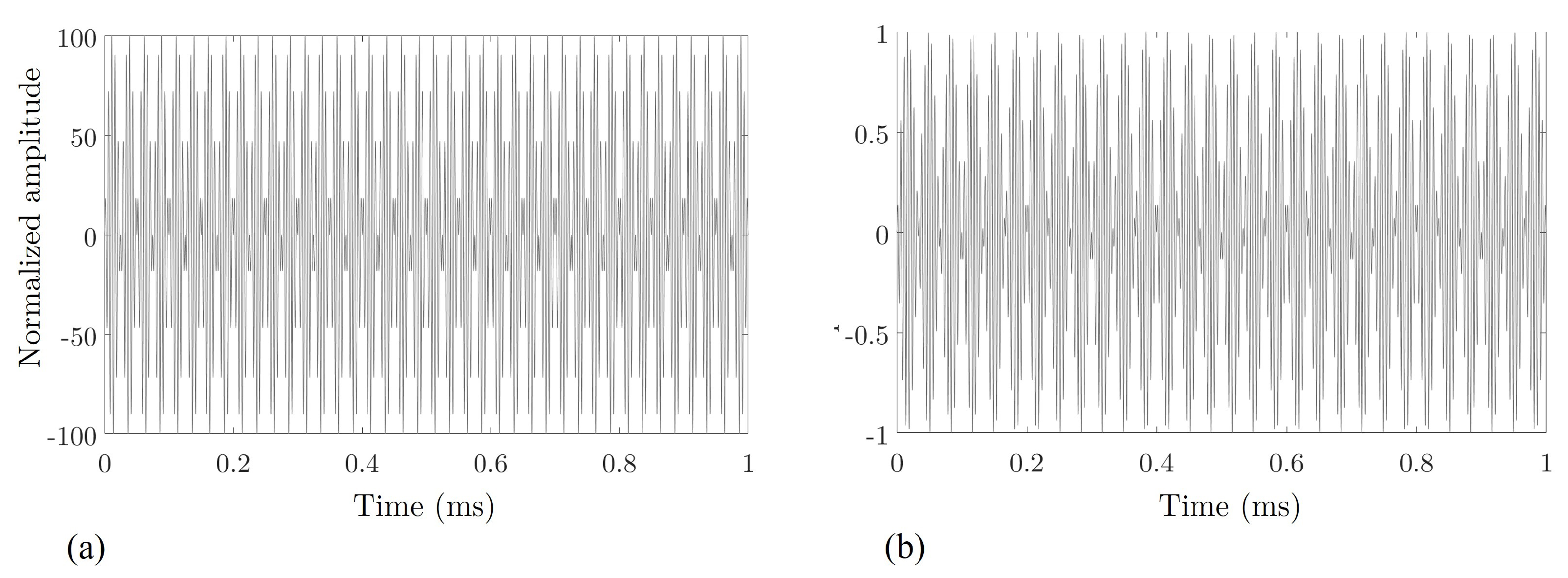
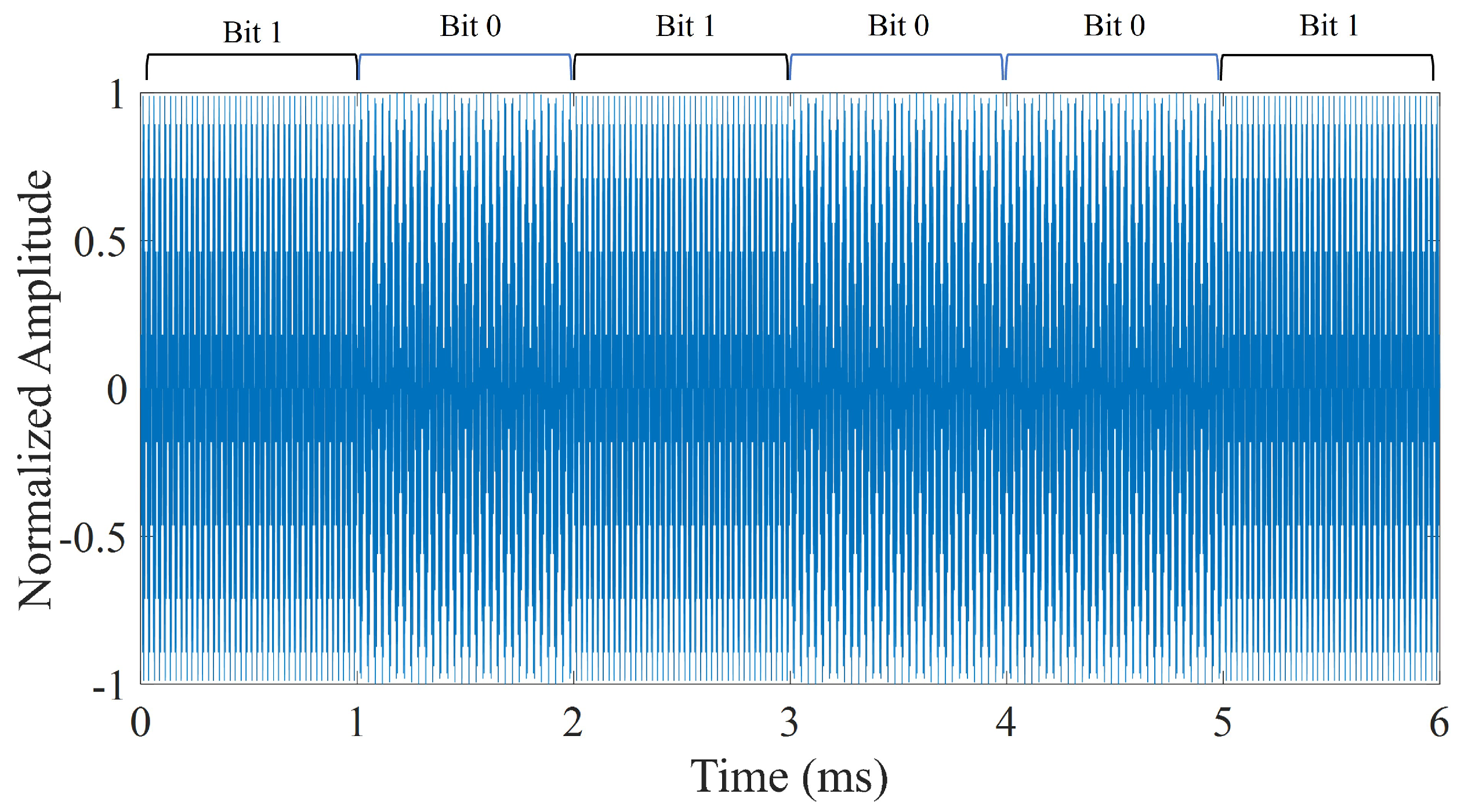
Frequency Shift Keying Modulation: Signal Processing
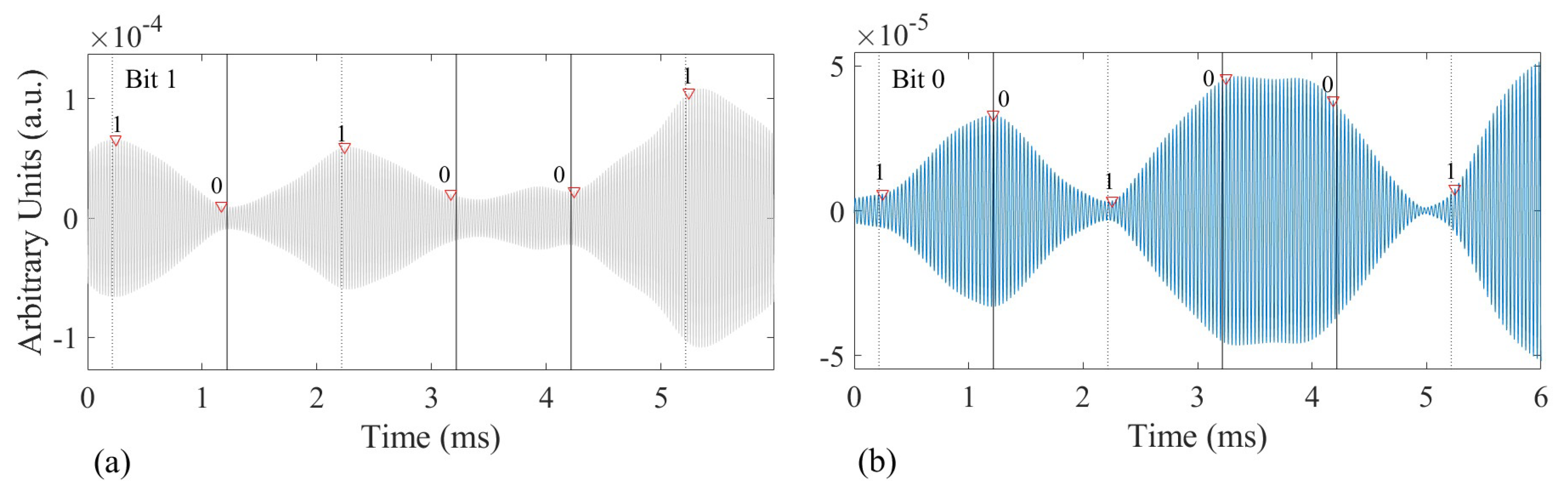
7. Bit Detection by Cross-Correlation Method and Results
8. Conclusions
8.1. For Measurements in Air
8.2. For Measurements in Water
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Edrich, J. 3.2. Parametric Amplifiers. In Methods in Experimental Physics; Elsevier: Amsterdam, The Netherlands, 1976; pp. 225–245. [Google Scholar] [CrossRef]
- Westervelt, P.J. Scattering of Sound by Sound. J. Acoust. Soc. Am. 1957, 29, 199–203. [Google Scholar] [CrossRef]
- Westervelt, P.J. Parametric Acoustic Array. J. Acoust. Soc. Am. 1963, 35, 535–537. [Google Scholar] [CrossRef]
- Berktay, H. Possible exploitation of non-linear acoustics in underwater transmitting applications. J. Sound Vib. 1965, 2, 435–461. [Google Scholar] [CrossRef]
- Berktay, H.O.; Leahy, D.J. Farfield performance of parametric transmitters. J. Acoust. Soc. Am. 1974, 55, 539–546. [Google Scholar] [CrossRef]
- Bennett, M.B.; Blackstock, D.T. Parametric array in air. J. Acoust. Soc. Am. 1975, 57, 562–568. [Google Scholar] [CrossRef]
- Yoneyama, M.; Fujimoto, J.; Kawamo, Y.; Sasabe, S. The audio spotlight: An application of nonlinear interaction of sound waves to a new type of loudspeaker design. J. Acoust. Soc. Am. 1983, 73, 1532–1536. [Google Scholar] [CrossRef]
- Pompei, F.J. Sound from Ultrasound: The Parametric Array as an Audible Sound Source. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2002. [Google Scholar]
- Mellen, R.H.; Browning, D.G.; Konrad, W.L. Parametric Sonar Transmitting Array Measurements. J. Acoust. Soc. Am. 1971, 49, 932–935. [Google Scholar] [CrossRef]
- Mikulka, J.; Hladky, D.; Sliz, J. Parametric array as a source of audible signal. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016. [Google Scholar] [CrossRef]
- Hwang, Y.; Ahn, H.; Nguyen, D.N.; Kim, W.; Moon, W. An underwater parametric array source transducer composed of PZT/thin-polymer composite. Sens. Actuators A Phys. 2018, 279, 601–616. [Google Scholar] [CrossRef]
- Li, H.; Ma, J.; Zhu, J.; Chen, B. Numerical and Experimental Studies on Inclined Incidence Parametric Sound Propagation. Shock Vib. 2019, 2019, 2984191. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, S.H.; Li, W. Parametric Acoustic Array and Its Application in Underwater Acoustic Engineering. Sensors 2020, 20, 2148. [Google Scholar] [CrossRef]
- Yu, S.; Liu, B.; Yu, K.; Yang, Z.; Kan, G.; Zong, L. Application of a parametric array over a mid-frequency band (4–10 kHz) –measurements of bottom backscattering strength. Ocean Eng. 2023, 280, 114914. [Google Scholar] [CrossRef]
- Konrad, W.L. Design and Performance of Parametric Sonar Systems. Technical Report. 1975. Available online: https://apps.dtic.mil/sti/citations/tr/ADA016242 (accessed on 20 July 2023).
- Pederson, T.B. A parametric sonar performance calculator. Le J. Phys. Colloq. 1979, 40, C8-137–C8-139. [Google Scholar] [CrossRef]
- Godø, O.R.; Foote, K.G.; Dybedal, J.; Tenningen, E.; Patel, R. Detecting Atlantic herring by parametric sonar. J. Acoust. Soc. Am. 2010, 127, EL153–EL159. [Google Scholar] [CrossRef] [PubMed]
- Quazi, A.; Konrad, W. Underwater acoustic communications. IEEE Commun. Mag. 1982, 20, 24–30. [Google Scholar] [CrossRef]
- Kopp, L.; Cano, D.; Dubois, E.; Wang, L.; Smith, B.; Coates, R. Potential performance of parametric communications. IEEE J. Ocean. Eng. 2000, 25, 282–295. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, G.; Yin, J.; Zhang, X.; Han, X. A modulation method of parametric array for underwater acoustic communication. Appl. Acoust. 2019, 145, 305–313. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, G.; Tang, S.; Yin, J.; Guo, L.; Sheng, X.; Li, M. Directional bionic underwater communication method using a parametric acoustic array and recursive filtering. Appl. Acoust. 2022, 191, 108665. [Google Scholar] [CrossRef]
- Coates, R.; Zheng, M.; Wang, L. “BASS 300 PARACOM”: A “model” underwater parametric communication system. IEEE J. Ocean. Eng. 1996, 21, 225–232. [Google Scholar] [CrossRef]
- Campo Valera, M.M.; Felis Enguix, I. Propiedades y aplicaciones del efecto paramétrico en aire y agua. In Proceedings of the IV Jornadas JAAS Acústica, Audio y Sonido 2018, Buenos Aires, Argentina, 15–16 August 2018. [Google Scholar]
- Hamilton, M.F.; Blackstock, D.T. Nonlinear Acoustics; Academic Press: San Diego, CA, USA, 1998; Volume 237. [Google Scholar]
- Campo-Valera, M.; Rodríguez-Rodríguez, I.; Rodríguez-Rodríguez, J. Conceptos Básicos de la Ciencia del Sonido en el Mar; UMA Editorial: Málaga, Spain, 2023; p. 104. [Google Scholar] [CrossRef]
- Villó-Pérez, I.; Alcover-Garau, P.M.; Campo-Valera, M.; Toledo-Moreo, R. A novel 1D-FDTD scheme to solve the nonlinear second-order thermoviscous hydrodynamic model. Commun. Nonlinear Sci. Numer. Simul. 2022, 118, 107015. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics; Universidad de California: San Diego, CA, USA, 1999; p. 560. [Google Scholar]
- Jiménez, V.Y. Análisis, Modelado e Igualación No Lineal de Arrays Paramétricos Acústicos. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2016. [Google Scholar]
- Lurton, X. An Introduction to Underwater Acoustics: Principles and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Kite, T.D.; Post, J.T.; Hamilton, M.F. Parametric array in air: Distortion reduction by preprocessing. J. Acoust. Soc. Am. 1998, 2, 1091–1092. [Google Scholar] [CrossRef]
- Blackstock, D.T. Approximate Equations Governing Finite-Amplitude Sound in Thermoviscous Fluids. General Dynamics GD/E Report GD-1463-52. 1963. Available online: https://apps.dtic.mil/sti/citations/AD0415442 (accessed on 20 July 2023).
- Bjørnø, L. Introduction to nonlinear acoustics. Phys. Procedia 2010, 3, 5–16. [Google Scholar] [CrossRef]
- Berktay, H.O.; Shooter, J.A. Nearfield effects in end-fire line arrays. J. Acoust. Soc. Am. 1973, 53, 550–556. [Google Scholar] [CrossRef]
- Cervenka, P.; Alais, P. Fourier formalism for describing nonlinear self-demodulation of a primary narrow ultrasonic beam. J. Acoust. Soc. Am. 1990, 88, 473–481. [Google Scholar] [CrossRef]
- Li, S.W. Pre-processing methods for parametric array to generate wideband difference frequency signals. In Proceedings of the OCEANS 2008, Quebec City, QC, Canada, 15–18 September 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Berktay, H.; Smith, B. End-fire array of virtual acoustic sources produced by the interaction of cylindrically spreading acoustic waves. Electron. Lett. 1965, 1, 202. [Google Scholar] [CrossRef]
- Garay, G. Propagación Acústica No Lineal en un Medio de Múltiple Scattering. Master’s Thesis, Universidad de la República, Montevideo, Uruguay, 2018. [Google Scholar]
- Campo-Valera, M.; Felis-Enguix, I.; Villó-Pérez, I. Signal Processing for Parametric Acoustic Sources Applied to Underwater Communication. Sensors 2020, 20, 5878. [Google Scholar] [CrossRef] [PubMed]
- Couch, L.W.; Elizondo, R.J.R.; Ruiz, J.L.C. Sistemas de Comunicación Digitales y Analógicos; Pearson Educación: London, UK, 2008; Volume 7. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W.; Buck, J.R. Tratamiento de Señales en Tiempo Discreto; Pearson Educación: London, UK, 2011. [Google Scholar]
- Adrián-Martínez, S.; Bou-Cabo, M.; Felis, I.; Llorens, C.D.; Martínez-Mora, J.A.; Saldaña, M.; Ardid, M. Acoustic signal detection through the cross-correlation method in experiments with different signal to noise ratio and reverberation conditions. In Proceedings of the Ad-hoc Networks and Wireless: ADHOC-NOW 2014 International Workshops, ETSD, MARSS, MWaoN, SecAN, SSPA, and WiSARN, Benidorm, Spain, 22–27 June 2014; Revised Selected Papers 13. Springer: Berlin/Heidelberg, Germany, 2015; pp. 66–79. [Google Scholar]

| Variables | Description |
|---|---|
| Difference frequency | |
| Shock distance | |
| Small-signal sound speed | |
| Nonlinearity coefficient | |
| Nonlinear parameter | |
| Wavelength of the primary frequency | |
| k | Wave number |
| M | Mach number |
| v | Local wave velocity |
| Absortion length | |
| Attenuation coefficient | |
| Rayleigh distance | |
| a | Diameter of the active zone of the emitting transducer |
| Partial derivative | |
| Absolute mass density | |
| Absolute velocity vector | |
| p | Absolute pressure |
| Bulk viscosity | |
| Shear viscosity | |
| Acoustic quantities | |
| Pressure distribution of the parametric frequency | |
| Pressure wave of the primary wave | |
| Carrier frequency | |
| Envelope defined by the modulating wave | |
| Parametric frequency (twice of the ) | |
| Acoustic field of the difference frequency | |
| Digital modulation |
| Primary Freq. (kHz) | Difference Freq. (kHz) | Secondary Freq. (Param) (kHz) |
|---|---|---|
| = 197, = 207 | 10 | 20 |
| = 195.5, = 209.5 | ∼15 | 30 |
| = 190, = 210 | 20 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campo-Valera, M.; Rodríguez-Rodríguez, I.; Rodríguez, J.-V.; Herrera-Fernández, L.-J. Proof of Concept of the Use of the Parametric Effect in Two Media with Application to Underwater Acoustic Communications. Electronics 2023, 12, 3459. https://doi.org/10.3390/electronics12163459
Campo-Valera M, Rodríguez-Rodríguez I, Rodríguez J-V, Herrera-Fernández L-J. Proof of Concept of the Use of the Parametric Effect in Two Media with Application to Underwater Acoustic Communications. Electronics. 2023; 12(16):3459. https://doi.org/10.3390/electronics12163459
Chicago/Turabian StyleCampo-Valera, María, Ignacio Rodríguez-Rodríguez, José-Víctor Rodríguez, and Luis-Jorge Herrera-Fernández. 2023. "Proof of Concept of the Use of the Parametric Effect in Two Media with Application to Underwater Acoustic Communications" Electronics 12, no. 16: 3459. https://doi.org/10.3390/electronics12163459
APA StyleCampo-Valera, M., Rodríguez-Rodríguez, I., Rodríguez, J.-V., & Herrera-Fernández, L.-J. (2023). Proof of Concept of the Use of the Parametric Effect in Two Media with Application to Underwater Acoustic Communications. Electronics, 12(16), 3459. https://doi.org/10.3390/electronics12163459