A Novel Compact Gysel Power Divider with Bandpass Filtering Responses
Abstract
:1. Introduction
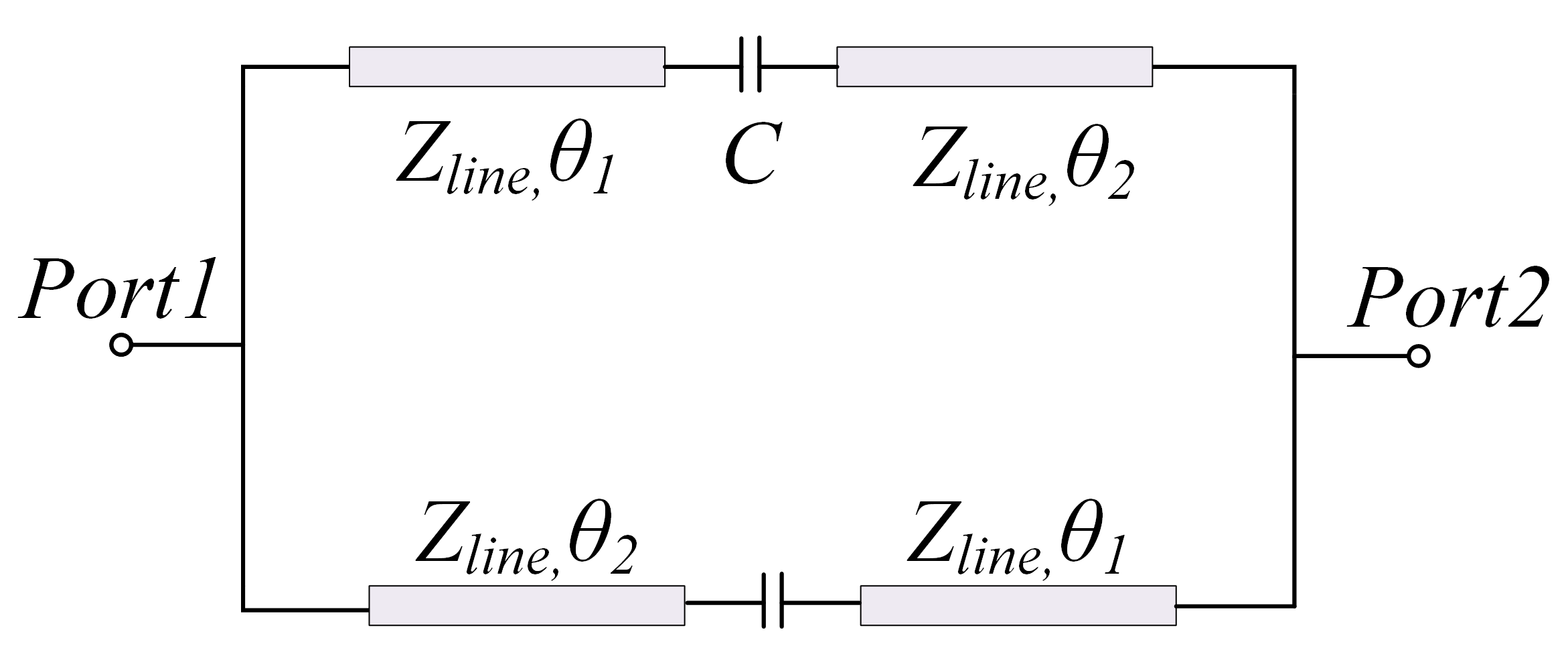
2. Design of the Proposed Compact Gysel FPD
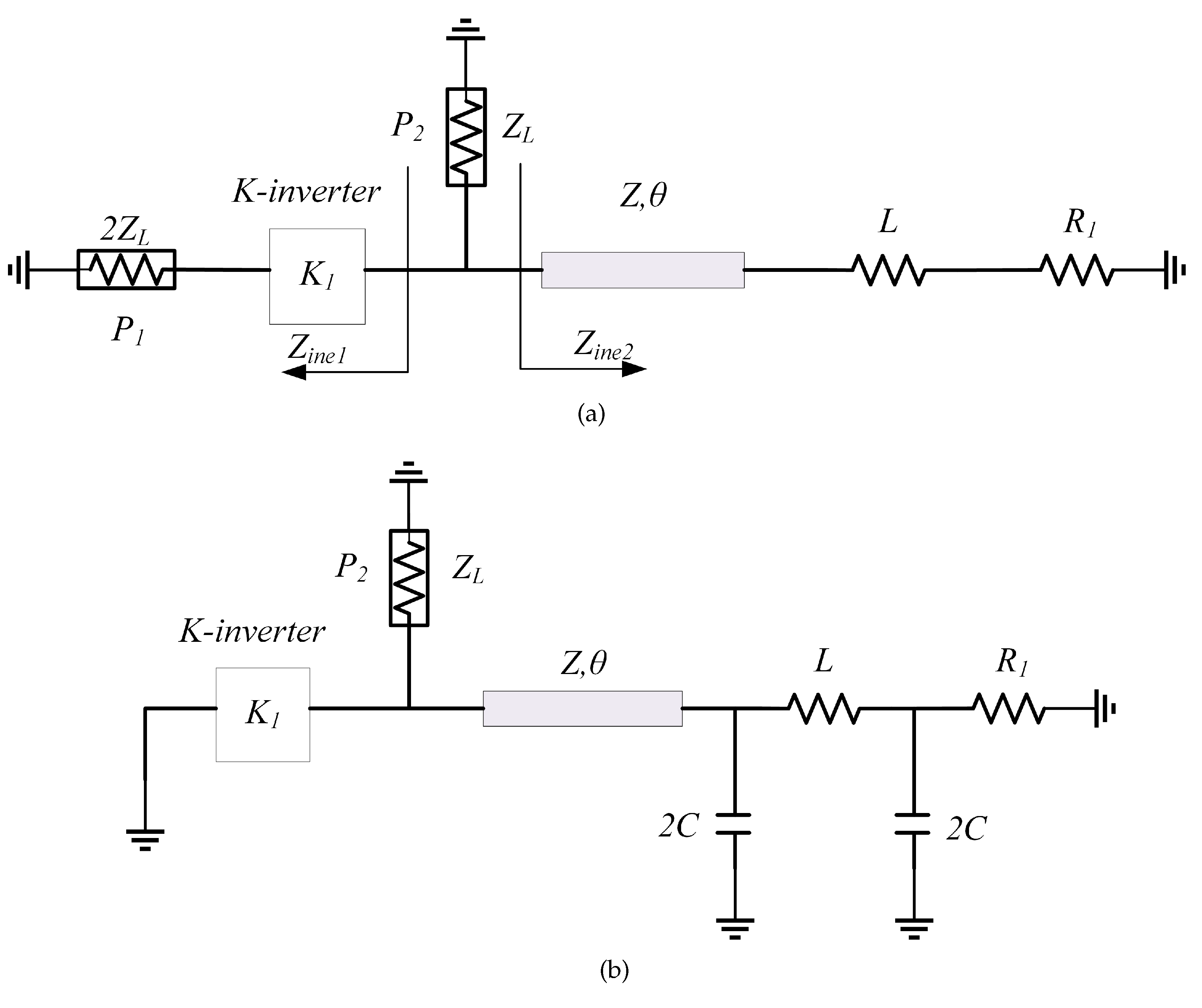
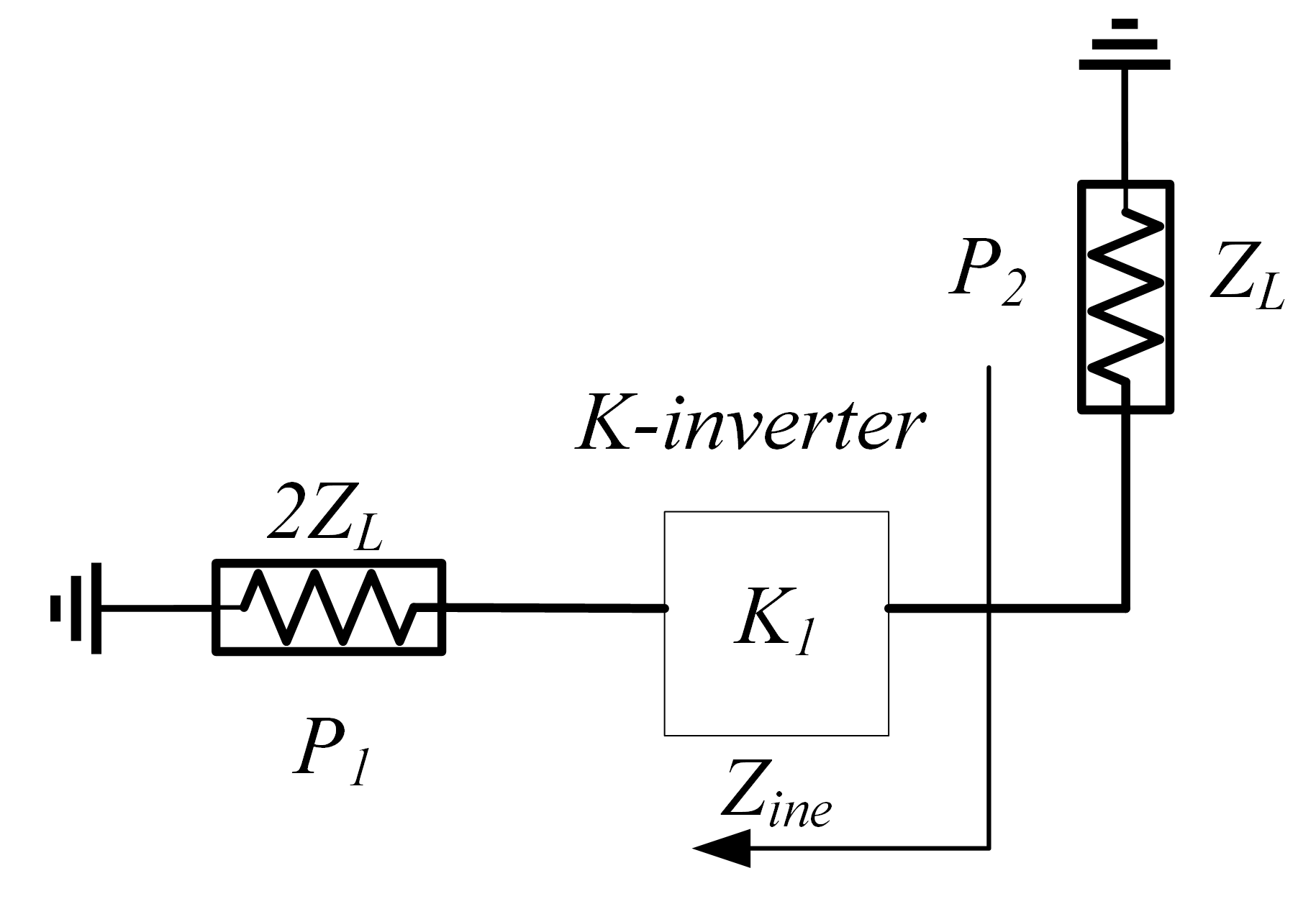
2.1. Analysis of the K-Inverter
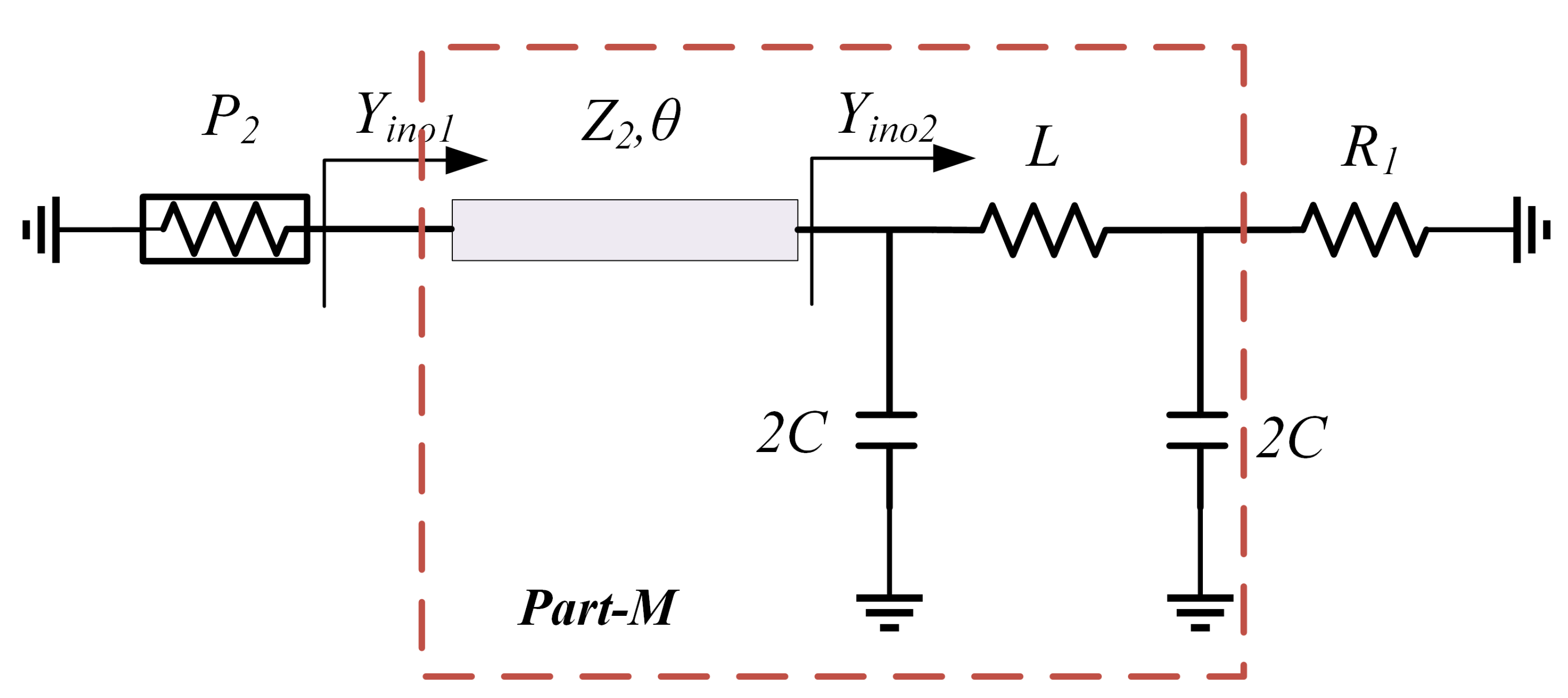
2.2. Analysis of the Even Mode
2.3. Analysis of the Odd Mode
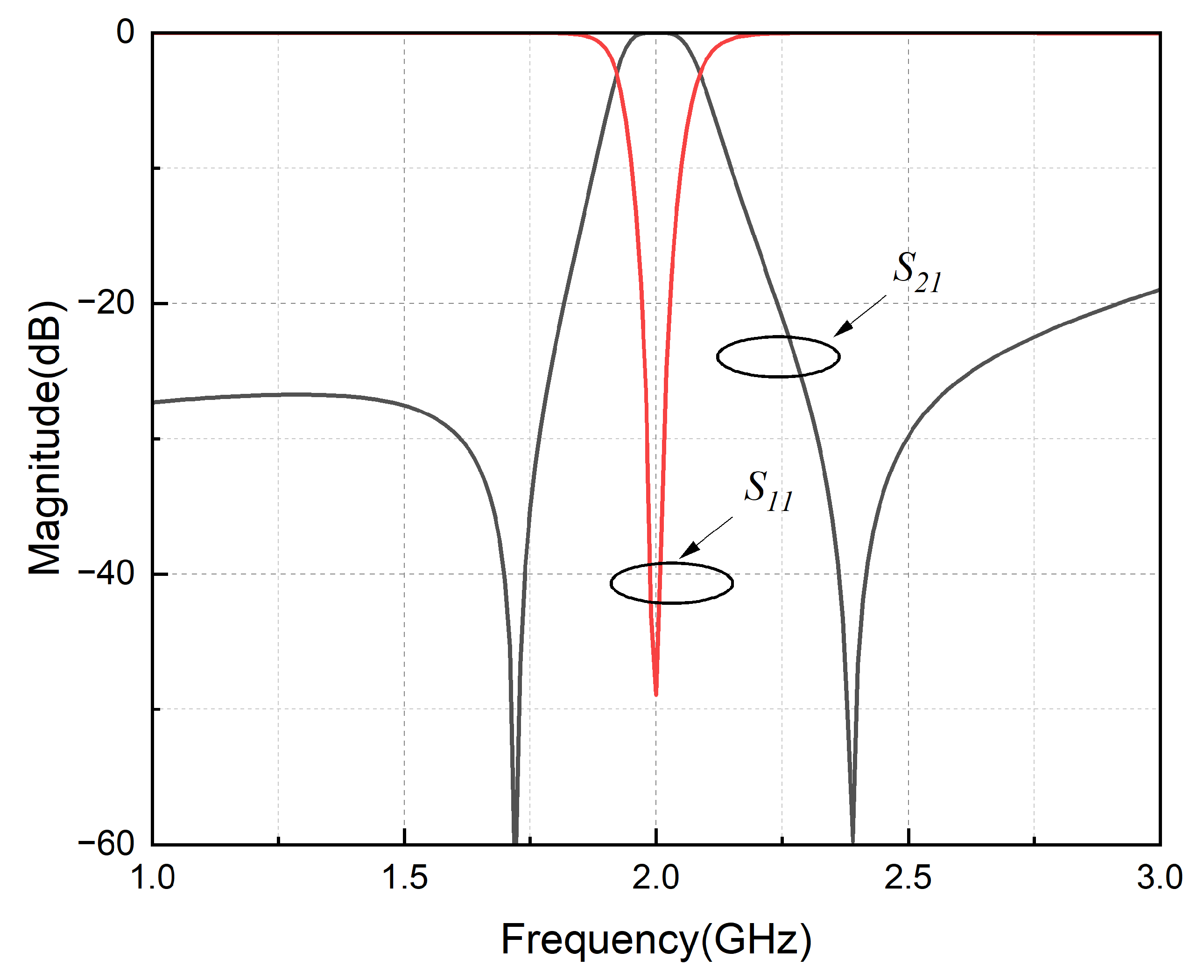
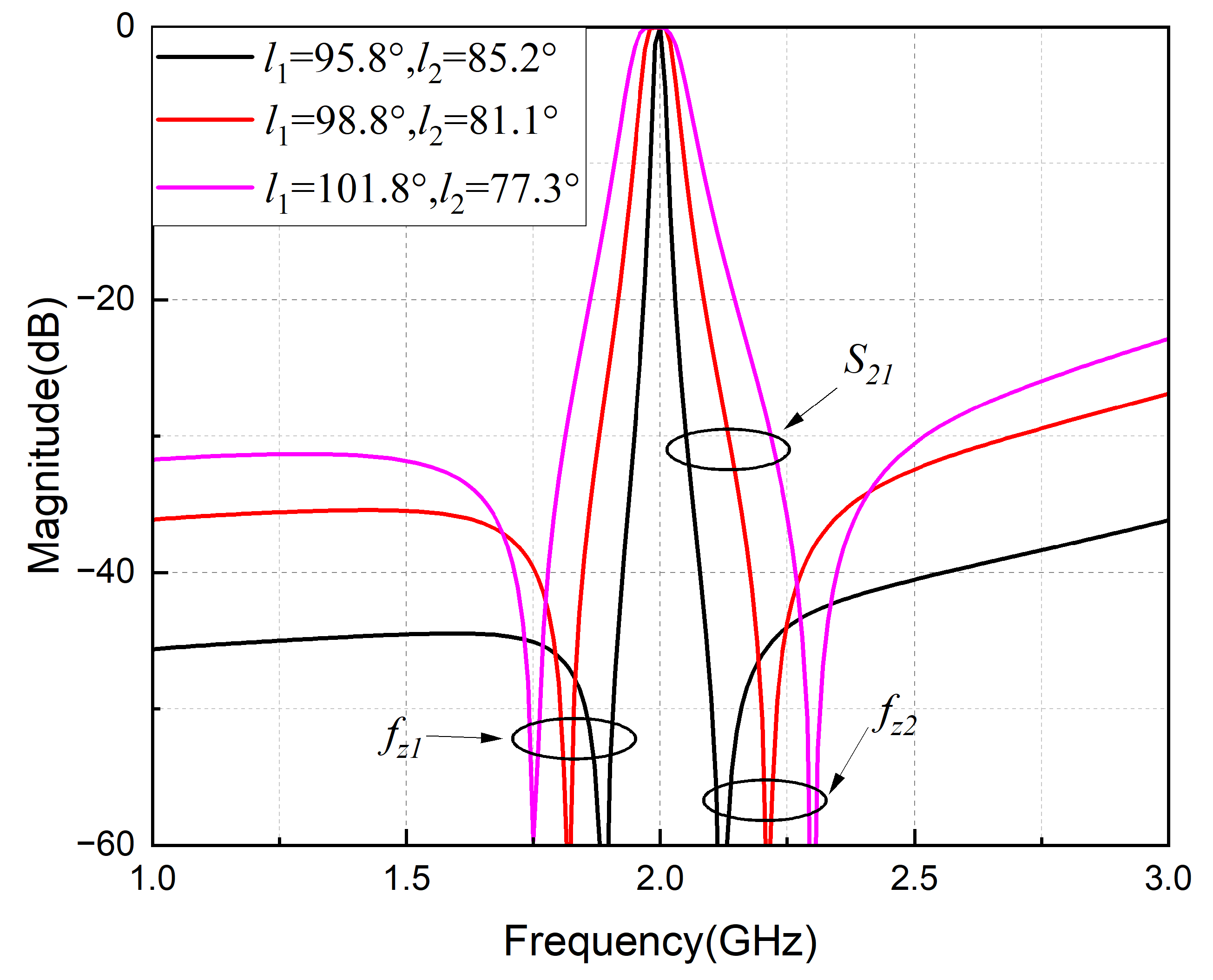
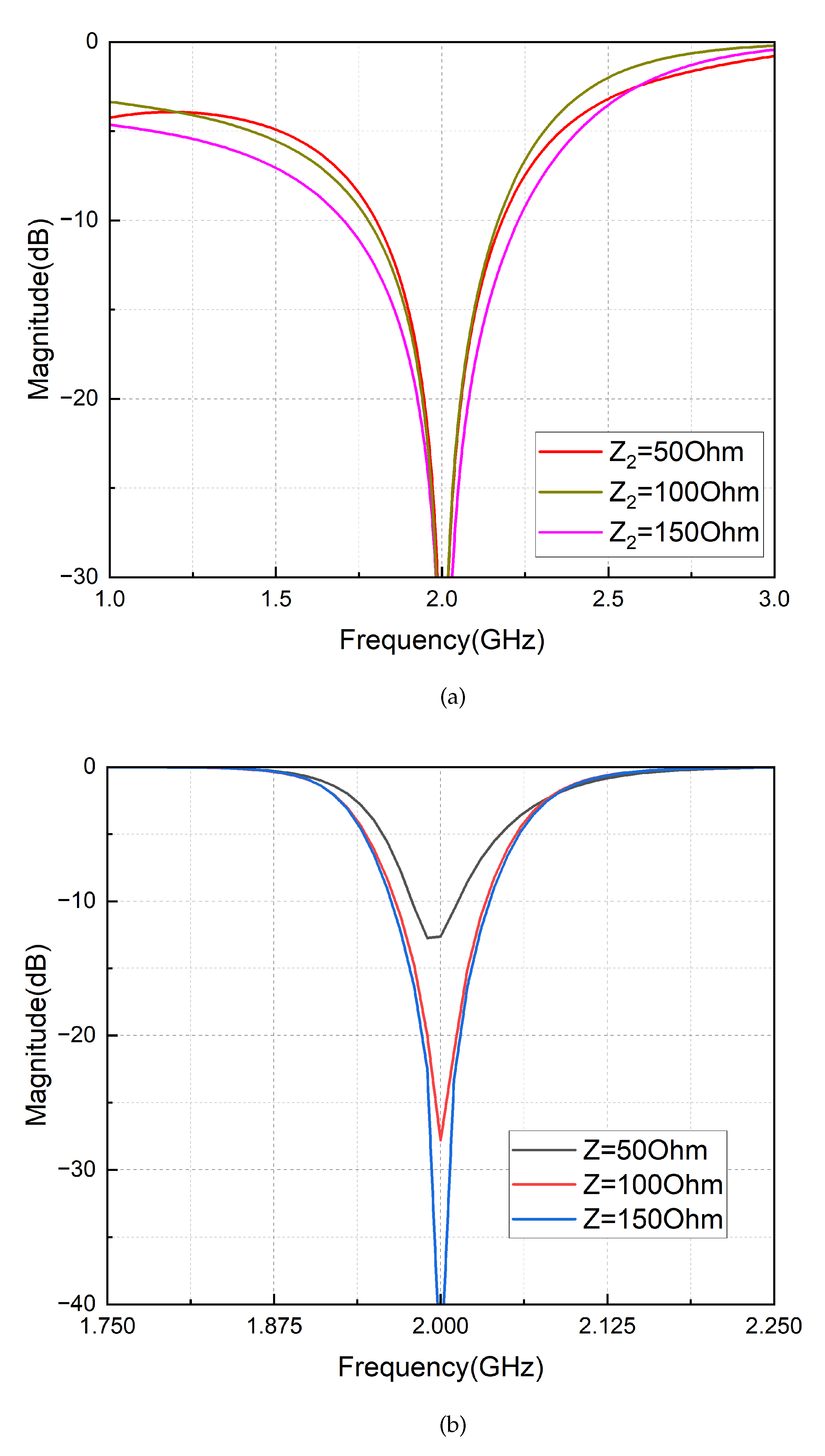
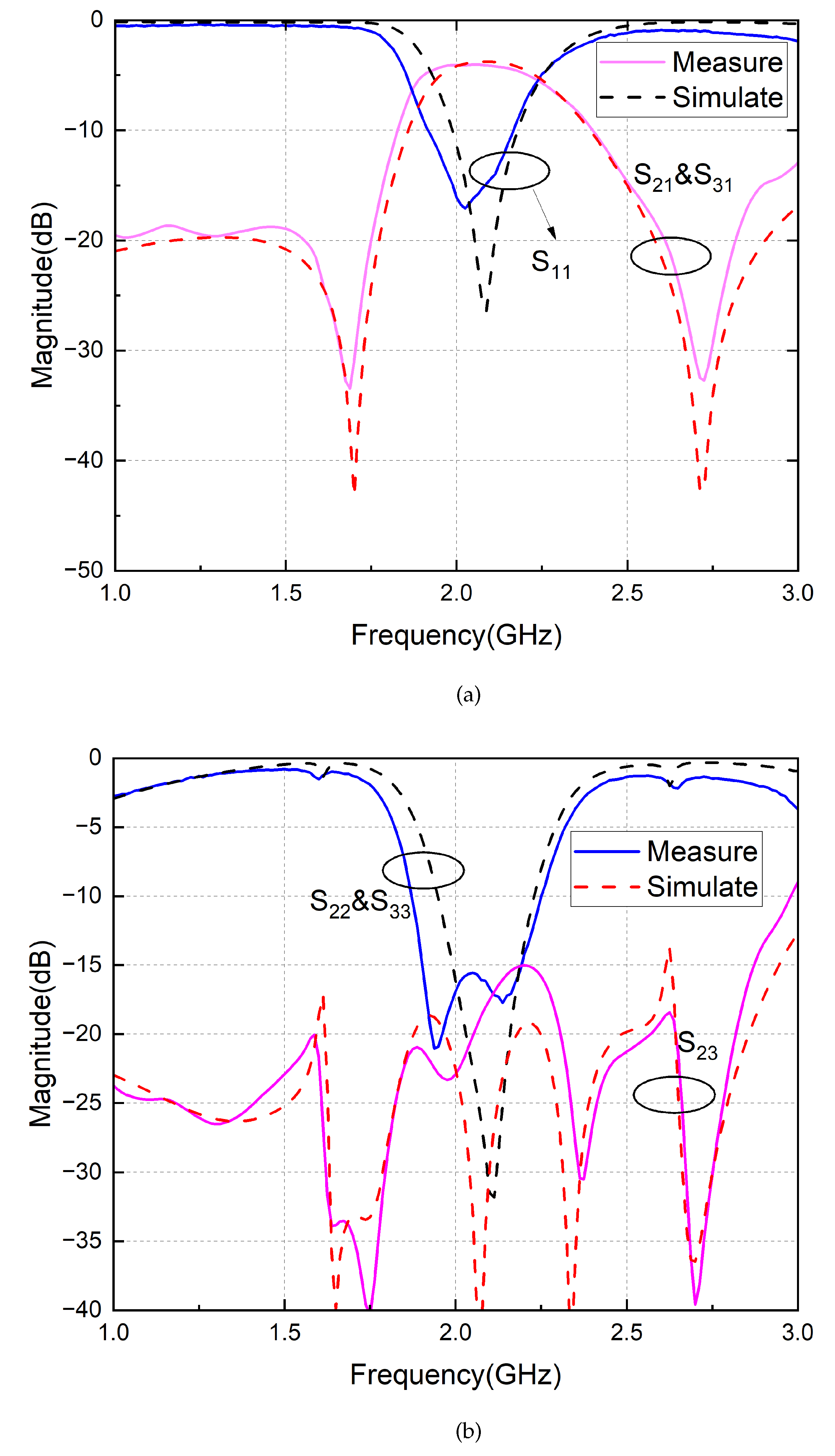
3. Simulation and Measurement of the Circuit
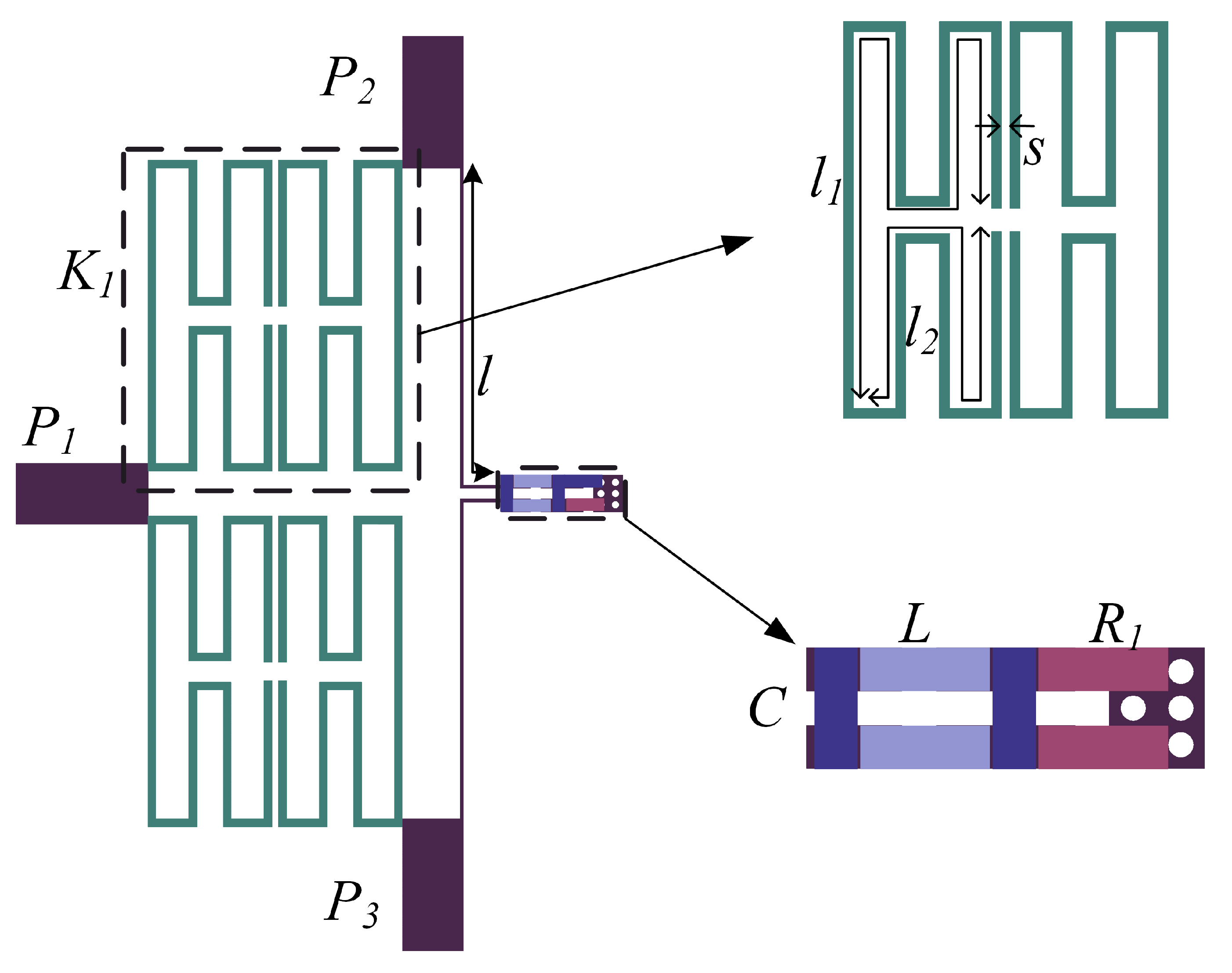
3.1. Design Procedure
- Determine the required index and frequency of the device, adjust the length and coupling strength of the two transmission lines in the filtering structure by Equations (1a) and (2), and match the equivalent impedance of the structure to 70.7 [12].
- Take the equivalent impedance of the microstrip line to 150 or other values. Based on the existing frequency, use Equation (7) to calculate the inductance value, Equation (12) to calculate the capacitance value, Equation (14) to calculate the electrical length of the lines, and Equation (21) to calculate the resistance value.
- Substitute each part into the structure to complete the design.
3.2. Simulated and Measured Results
3.3. Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chau, W.M.; Hsu, K.W.; Tu, W.H. Filter-Based Wilkinson Power Divider. IEEE Microw. Wireless Compon. Lett. 2014, 24, 239–241. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, S.; Zhu, L. 2n-Way Wideband Filtering Power Dividers with Good Isolation Enhanced by a Modified Isolation Network. IEEE Trans. Microw. Theory Tech. 2022, 70, 3177–3187. [Google Scholar] [CrossRef]
- Wang, D.; Guo, X.; Wu, W. Wideband Unequal Power Divider with Enhanced Power Dividing Ratio, Fully Matching Bandwidth, and Filtering Performance. IEEE Trans. Microw. Theory Tech. 2022, 70, 3200–3212. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, Y.; Zhang, T.; Che, W.; Xue, Q. N-Way Gysel Power Divider with Arbitrary Power-Dividing Ratio. IEEE Trans. Microw. Theory Tech. 2019, 67, 659–669. [Google Scholar] [CrossRef]
- Nemati, R.; Karimian, S.; Shahi, H.; Masoumi, N.; Safavi-Naeini, S. Multisection Combined Gysel–Wilkinson Power Divider with Arbitrary Power Division Ratios. IEEE Trans. Microw. Theory Tech. 2021, 69, 1567–1578. [Google Scholar] [CrossRef]
- Wen, P.; Ma, Z.; Liu, H.; Zhu, S.; Ren, B.; Song, Y.; Wang, X.; Ohira, M. Dual-Band Filtering Power Divider Using Dual-Resonance Resonators with Ultrawide Stopband and Good Isolation. IEEE Microw. Wireless Compon. Lett. 2019, 29, 101–103. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, L.; Sun, S. Proposal and Design of a Power Divider with Wideband Power Division and Port-to-Port Isolation: A New Topology. IEEE Trans. Microw. Theory Tech. 2020, 68, 1431–1438. [Google Scholar] [CrossRef]
- Wang, X.; Ma, Z.; Xie, T.; Ohira, M.; Chen, C.P.; Lu, G. Synthesis Theory of Ultra-Wideband Bandpass Transformer and its Wilkinson Power Divider Application with Perfect in-Band Reflection/Isolation. IEEE Trans. Microw. Theory Tech. 2019, 67, 3377–3390. [Google Scholar] [CrossRef]
- Shao, C.; Li, Y.; Chen, J.X. Compact dual-band microstrip filtering power divider using T-junction structure and quarter-wavelength SIR. Electron. Lett. 2017, 53, 434–436. [Google Scholar] [CrossRef]
- Zhao, X.L.; Gao, L.; Zhang, X.Y.; Xu, J.X. Novel Filtering Power Divider with Wide Stopband Using Discriminating Coupling. IEEE Microw. Wireless Compon. Lett. 2016, 26, 580–582. [Google Scholar] [CrossRef]
- Yu, X.; Sun, S. A Novel Wideband Filtering Power Divider with Embedding Three-Line Coupled Structures. IEEE Access 2018, 6, 41280–41290. [Google Scholar] [CrossRef]
- Wang, K.X.; Zhang, X.Y.; Hu, B.J. Gysel Power Divider with Arbitrary Power Ratios and Filtering Responses Using Coupling Structure. IEEE Trans. Microw. Theory Tech. 2014, 62, 431–440. [Google Scholar] [CrossRef]
- Shen, G.; Che, W.; Xue, Q.; Feng, W. Novel Design of Miniaturized Filtering Power Dividers Using Dual-Composite Right-/Left-Handed Resonators. IEEE Trans. Microw. Theory Tech. 2018, 66, 5260–5271. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y.; Wu, C.T.M. High-Selectivity and Miniaturized Filtering Wilkinson Power Dividers Integrated with Multimode Resonators. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 1990–1997. [Google Scholar] [CrossRef]
- Song, K. Compact filtering power divider with high frequency selectivity and wide stopband using embedded dual-mode resonator. Electron. Lett. 2015, 51, 495–497. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, J.; Zhu, L.; Wu, W. Dual-Band Filtering Power Divider with High Selectivity and Good Isolation. IEEE Microw. Wireless Compon. Lett. 2016, 26, 774–776. [Google Scholar] [CrossRef]
- Chen, M.T.; Tang, C.W. Design of the Filtering Power Divider with a Wide Passband and Stopband. IEEE Microw. Wireless Compon. Lett. 2018, 28, 570–572. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Wang, K.X.; Hu, B.J. Compact Filtering Power Divider with Enhanced Second-Harmonic Suppression. Microw. Wireless Compon. Lett. 2013, 23, 483–485. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, C.; Zhou, K.; Wu, W. Compact dual-band filtering power divider based on SIW triangular cavities. Electron. Lett. 2018, 54, 1072–1074. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, J.; Li, J.L. Design of compact wideband filtering power divider with extended isolation and rejection bandwidth. Electron. Lett. 2016, 52, 1387–1389. [Google Scholar] [CrossRef]
- Mandal, A.; Moyra, T.; Paul, P. Compact Low-pass Filtering-response Wilkinson Power Divider with Wide Harmonic Suppression. In Proceedings of the 2023 IEEE 13th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 8–11 March 2023; pp. 1243–1249. [Google Scholar] [CrossRef]
- Huang, F.; Zhu, L. Balanced-to-Unbalanced Filtering In-Phase Power Divider Based on 2-D Patch Resonator. IEEE Microw. Wirel. Technol. Lett. 2023, 33, 399–402. [Google Scholar] [CrossRef]


| Circuit | Freq | IL | ISO | Size | Type |
|---|---|---|---|---|---|
| (GHz) | (dB) | (dB) | () | ||
| [11] | 3.00 | 3.6 | 16.5 | 0.5 × 0.38 | Wilkinson |
| [12] | 1.96 | 3.9 | 19 | 0.21 × 0.28 | Gysel |
| [14] | 3.50 | 3.9 | 25 | 0.17 × 0.30 | Wilkinson |
| [15] | 2.41 | 4.2 | 17 | 0.45 × 0.45 | Wilkinson |
| [20] | 2.15 | 4.3 | 17 | 0.59 × 0.295 | Wilkinson |
| [21] | 2.25 | 4.3 | / | 0.38 × 0.21 | Wilkinson |
| [22] | 4 | 4.38 | 23 | 0.88 × 0.97 | Wilkinson |
| This work | 2.08 | 4.0 | 23 | 0.150.25 | Gysel |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Chen, Z.; Wang, K. A Novel Compact Gysel Power Divider with Bandpass Filtering Responses. Electronics 2023, 12, 3578. https://doi.org/10.3390/electronics12173578
Wu Z, Chen Z, Wang K. A Novel Compact Gysel Power Divider with Bandpass Filtering Responses. Electronics. 2023; 12(17):3578. https://doi.org/10.3390/electronics12173578
Chicago/Turabian StyleWu, Zeyu, Zihao Chen, and Kaixu Wang. 2023. "A Novel Compact Gysel Power Divider with Bandpass Filtering Responses" Electronics 12, no. 17: 3578. https://doi.org/10.3390/electronics12173578
APA StyleWu, Z., Chen, Z., & Wang, K. (2023). A Novel Compact Gysel Power Divider with Bandpass Filtering Responses. Electronics, 12(17), 3578. https://doi.org/10.3390/electronics12173578








