An Analytical Model of a System with Compression and Queuing for Selected Traffic Flows
Abstract
:1. Introduction
2. Resources and Traffic in Communications Networks
2.1. Resources of the Network
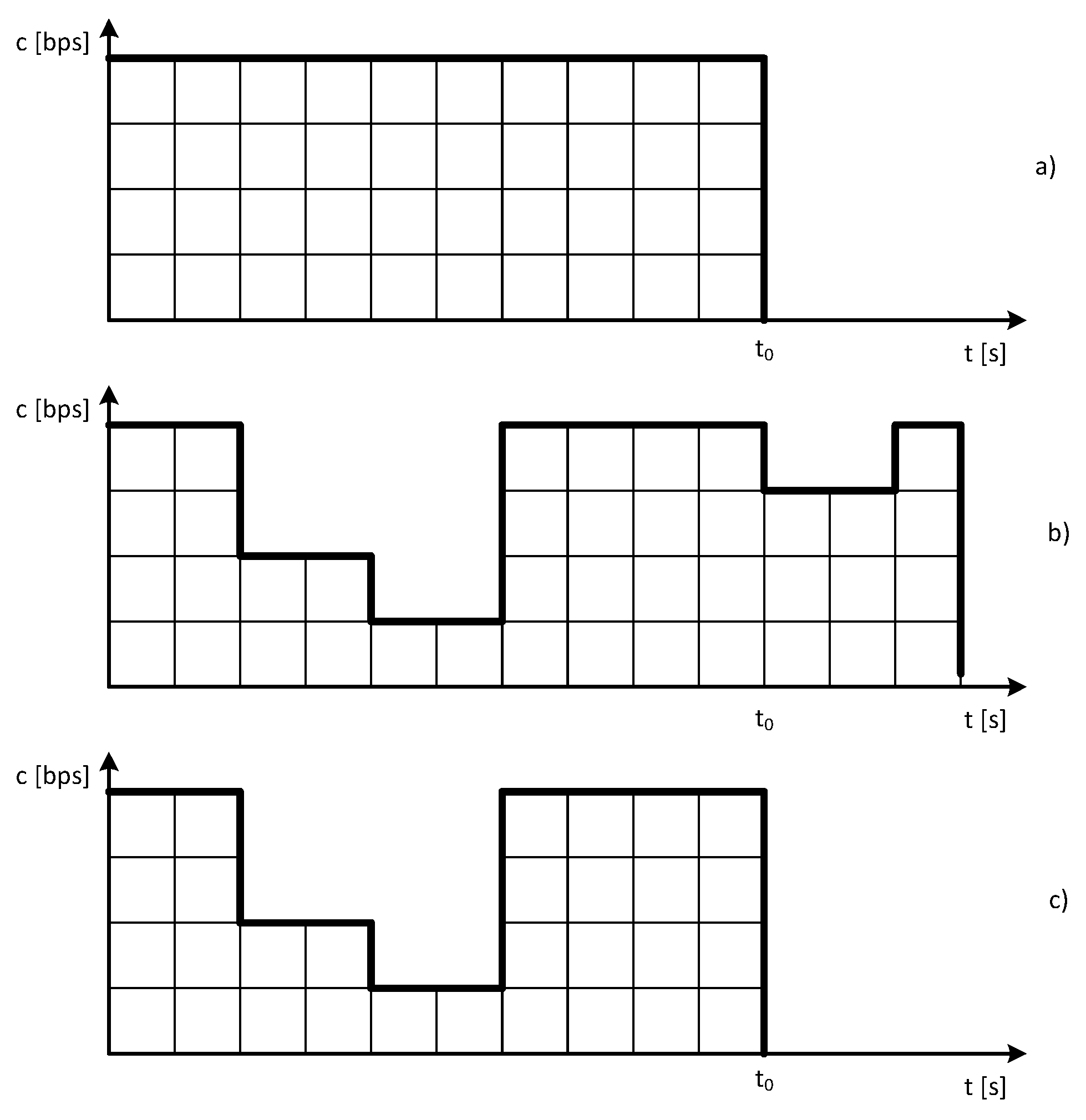
2.2. Traffic in Communications Networks
- Stream traffic
- -
- Call arrival intensity of new calls—;
- -
- Intensity of service process (the inverse of the time needed to transmit data)—;
- -
- The number of demanded resources .
- Elastic traffic
- -
- Call arrival intensity of new calls—;
- -
- Intensity of service process (the inverse of the time needed to transmit data)—;
- -
- Number of demanded resources .
- Adaptive traffic
- -
- Call arrival intensity of new calls—;
- -
- Intensity of service process (the inverse of the time needed to transmit data)—;
- -
- Number of demanded resources .
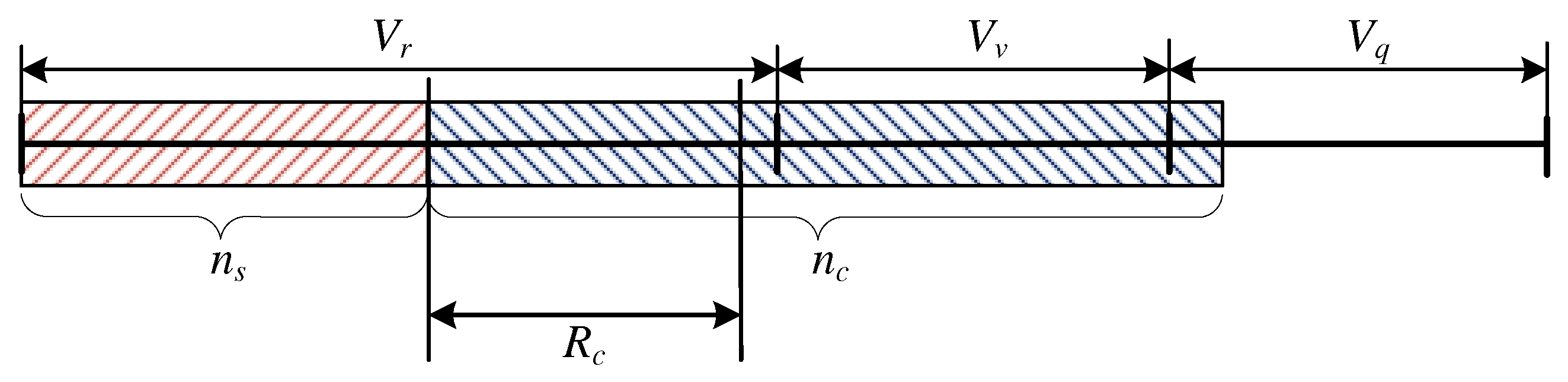
2.3. Structure and Working Principle of the Queuing System
3. Analytical Model
3.1. Analysis of the Service Process at the Macrostate Level
- ,
- ,
- .
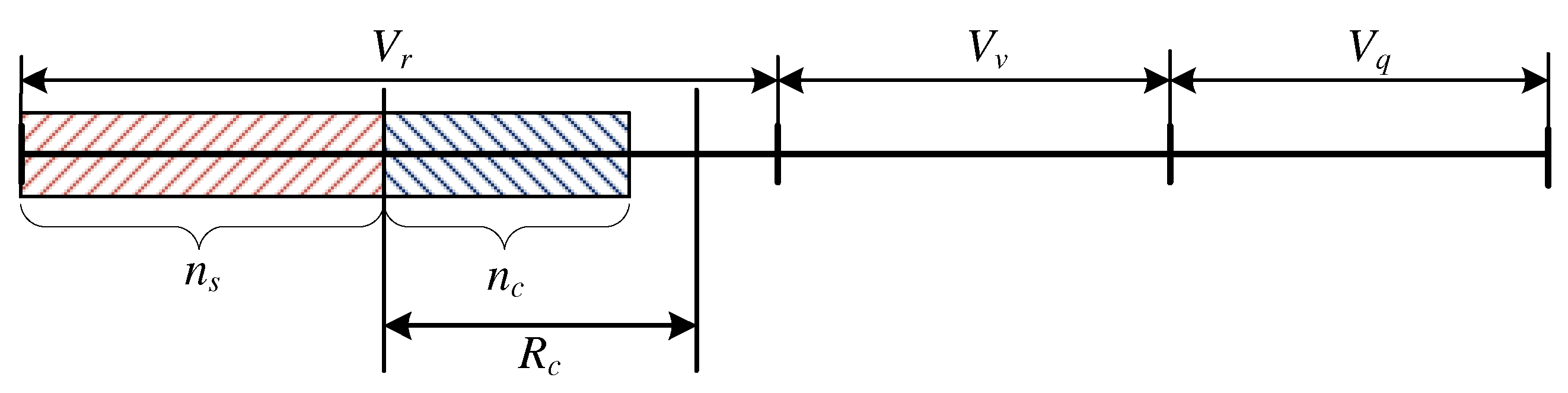
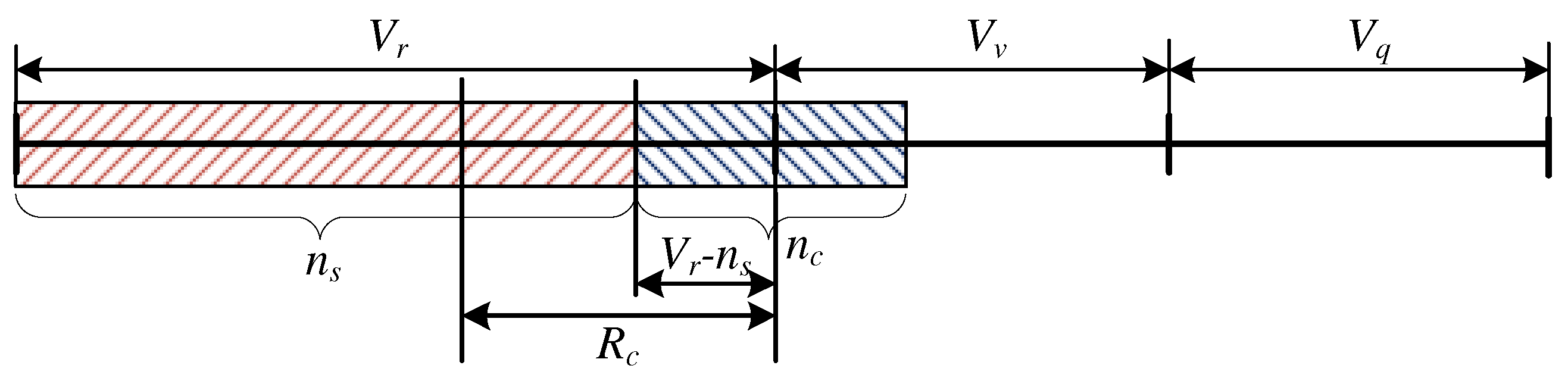
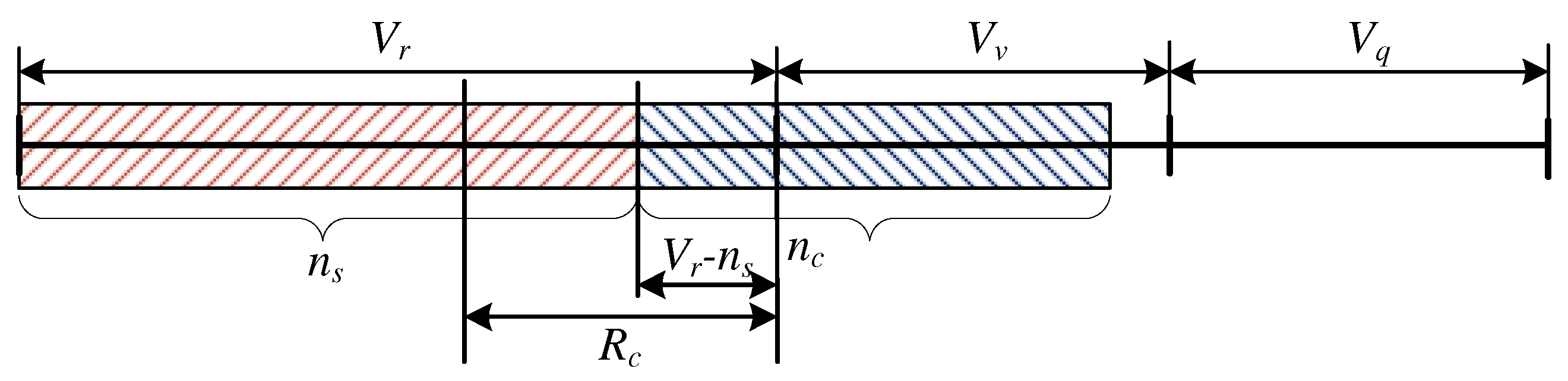
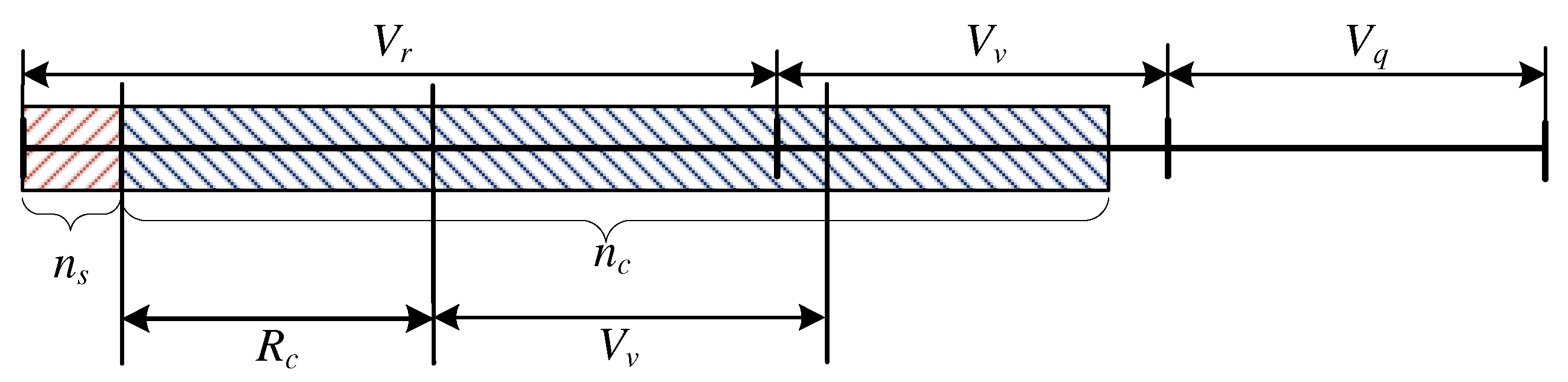
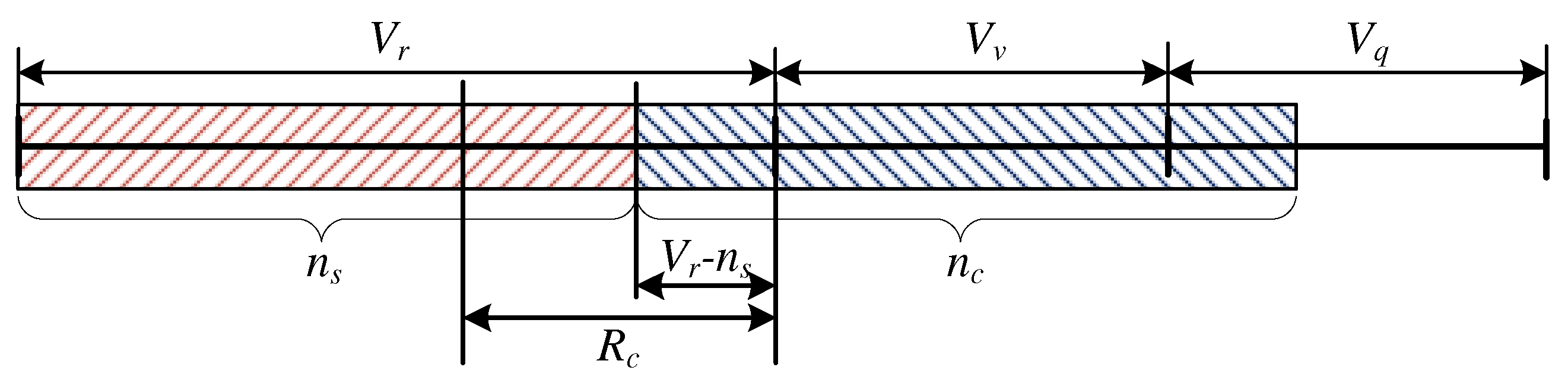
3.1.1. Occupation of the System:
- and ,
- and ,
- and ,
- and .
Case Study: and
Case Study: and
Case Study: and
Case Study: and
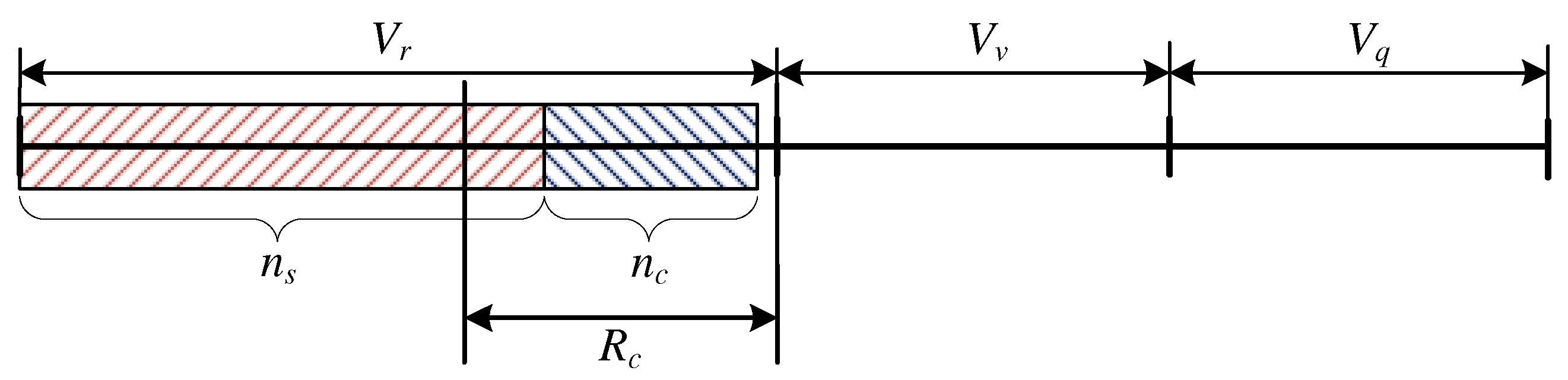
3.1.2. System Occupancy:
- and ,
- and ,
- and ,
- and .
Case Study: and
Case Study: and
Case Study: and
Case Study: and
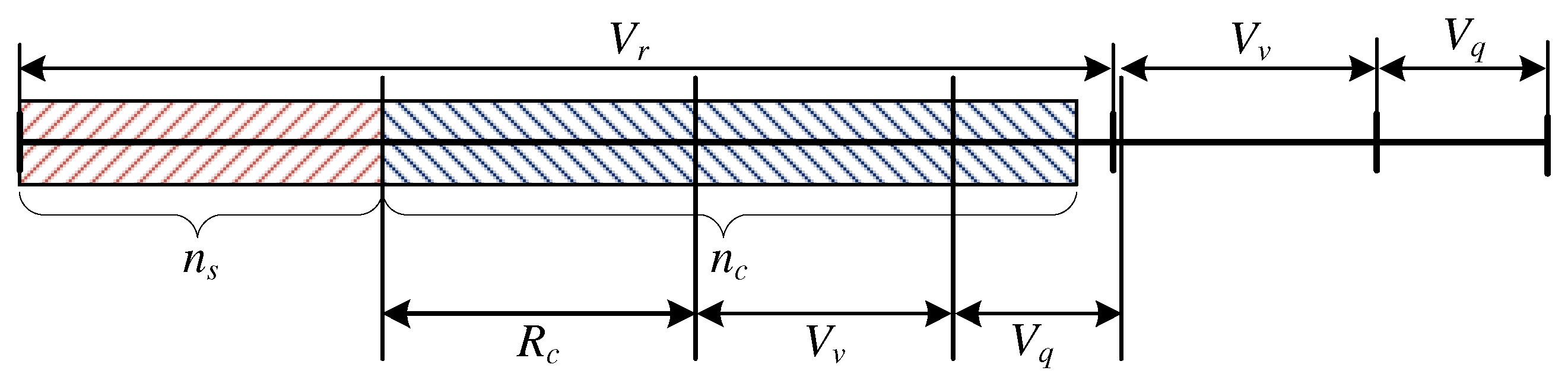
3.1.3. Occupancy of the System:
- and ,
- and .
The Case Study: and
The Case Study: and
3.2. System Characteristics
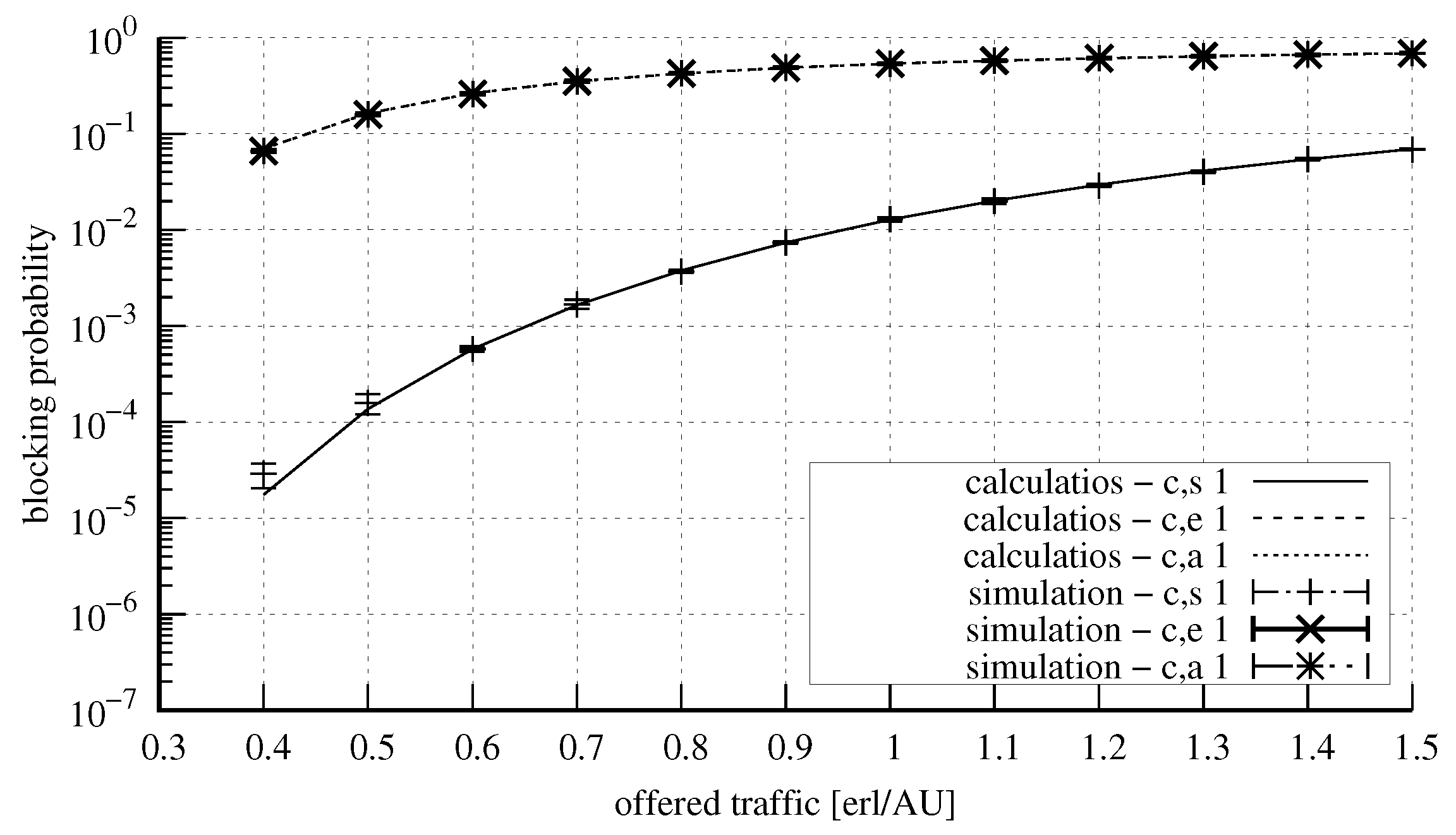
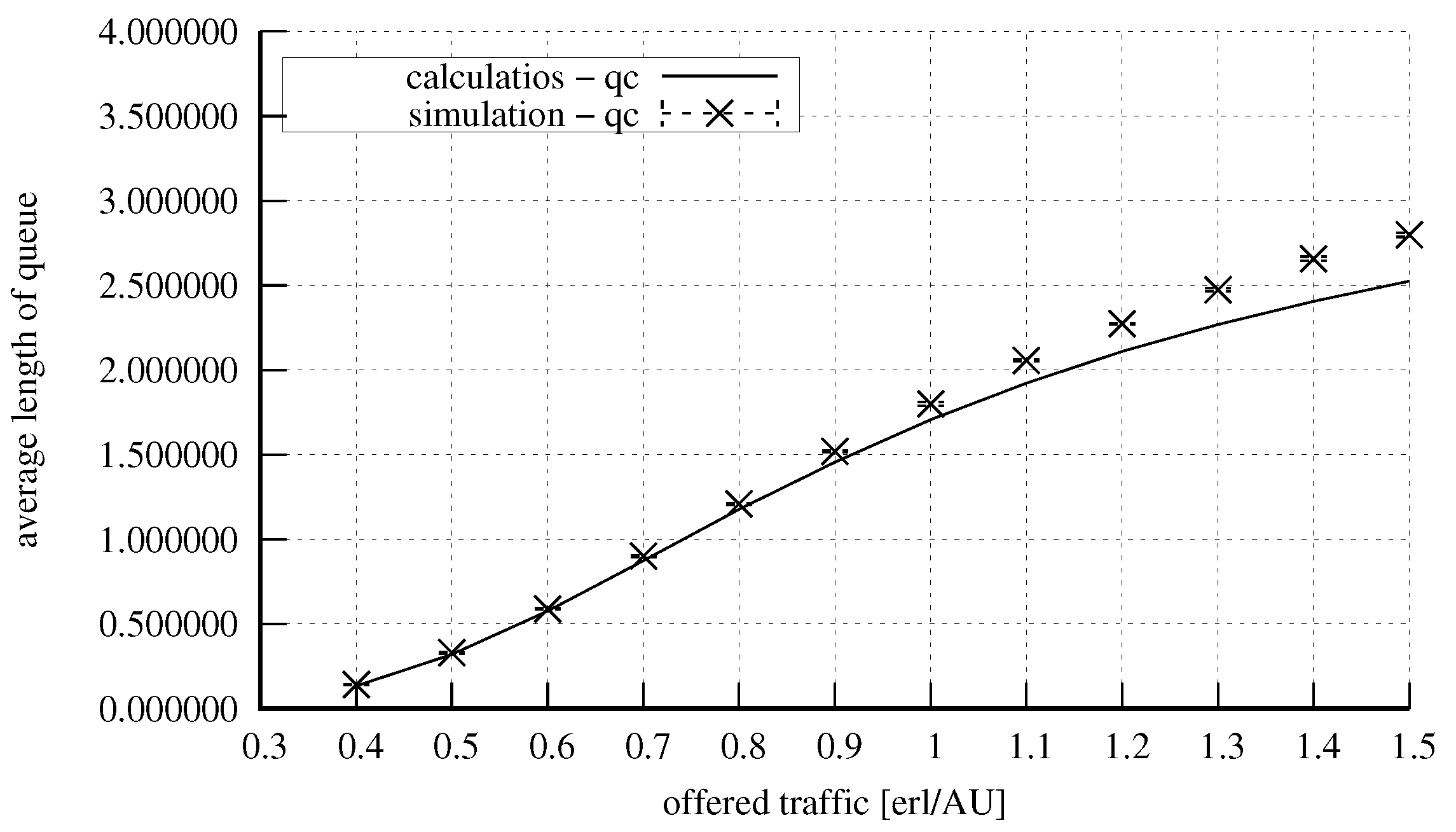
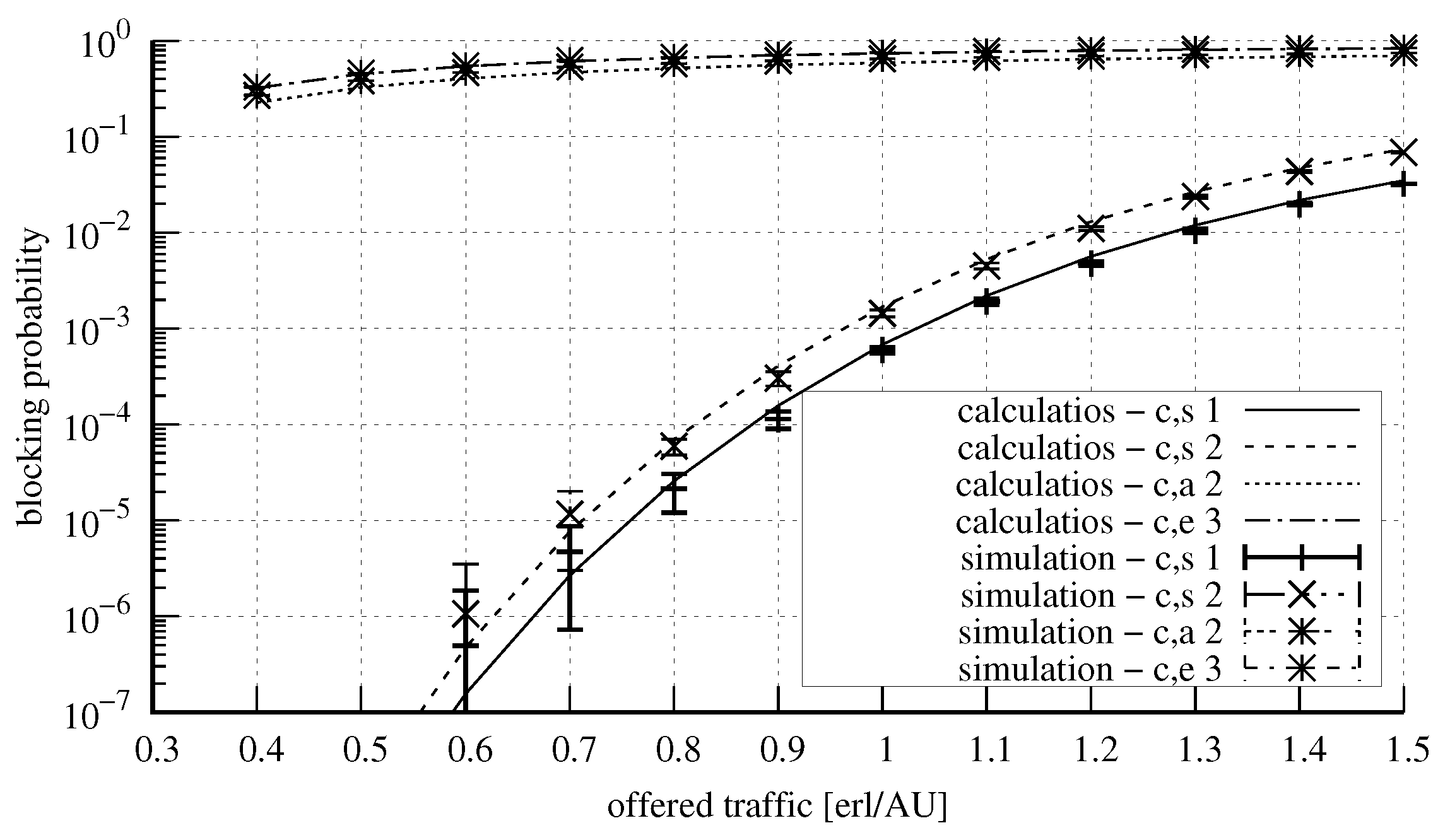
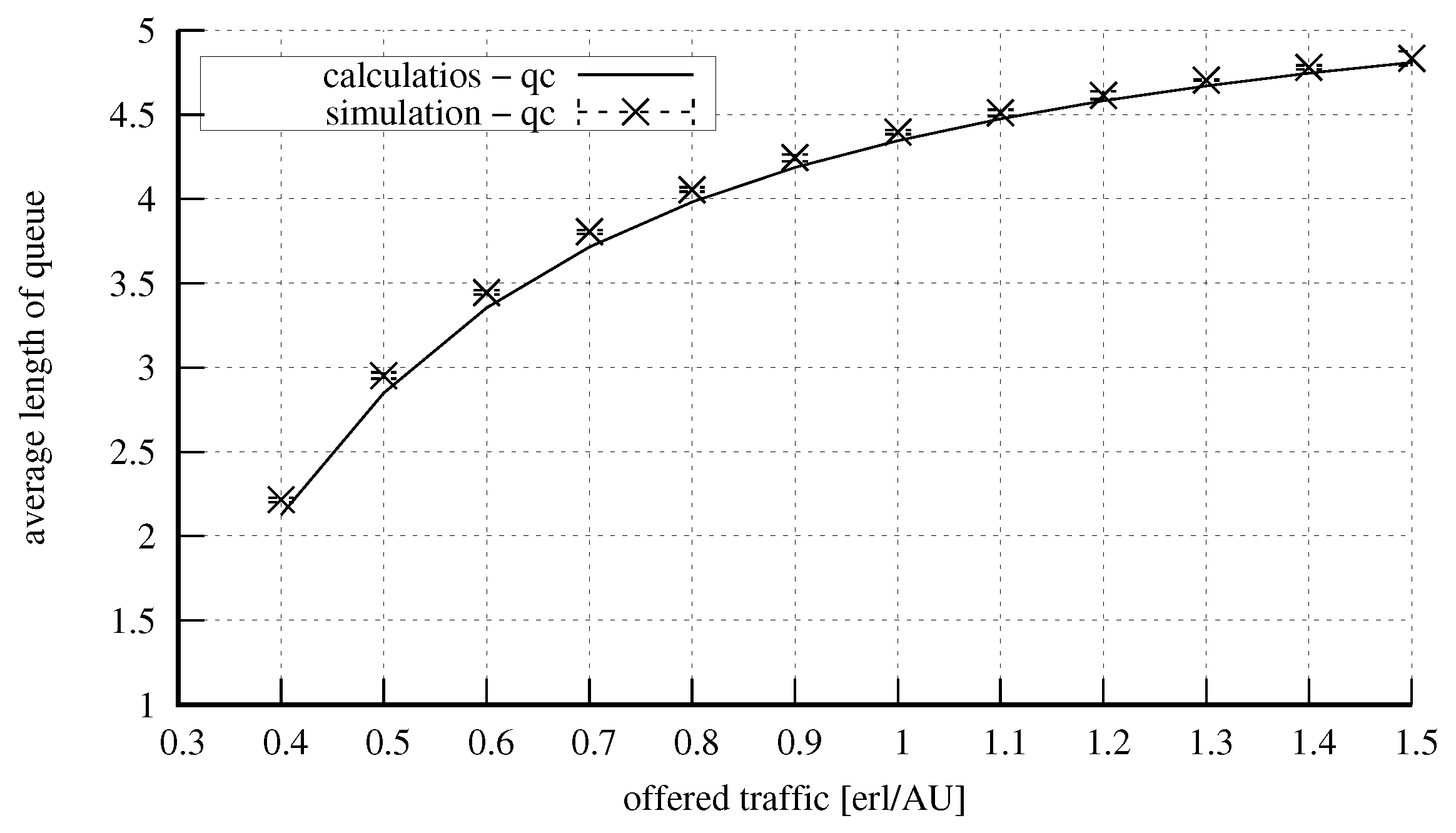
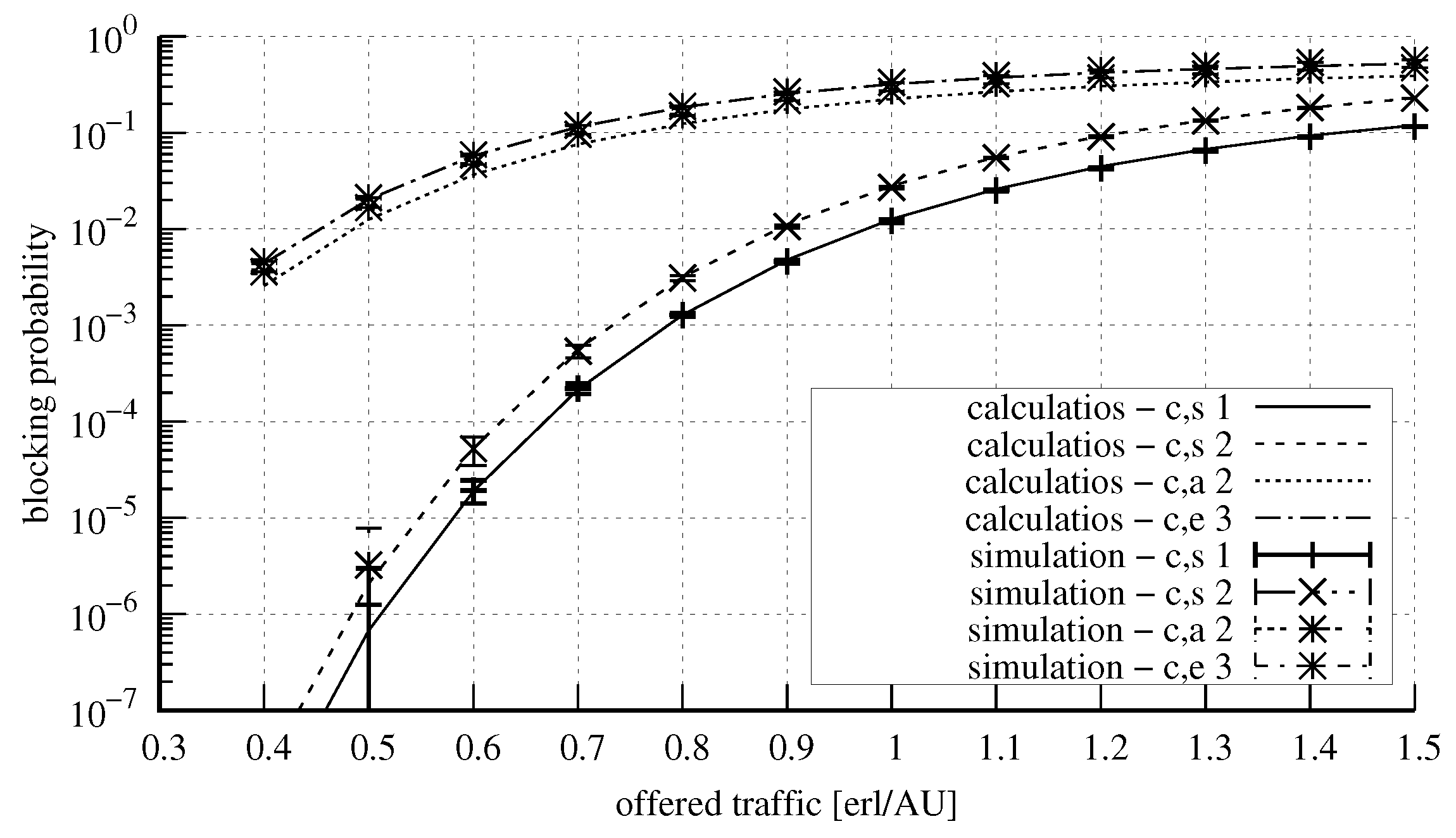
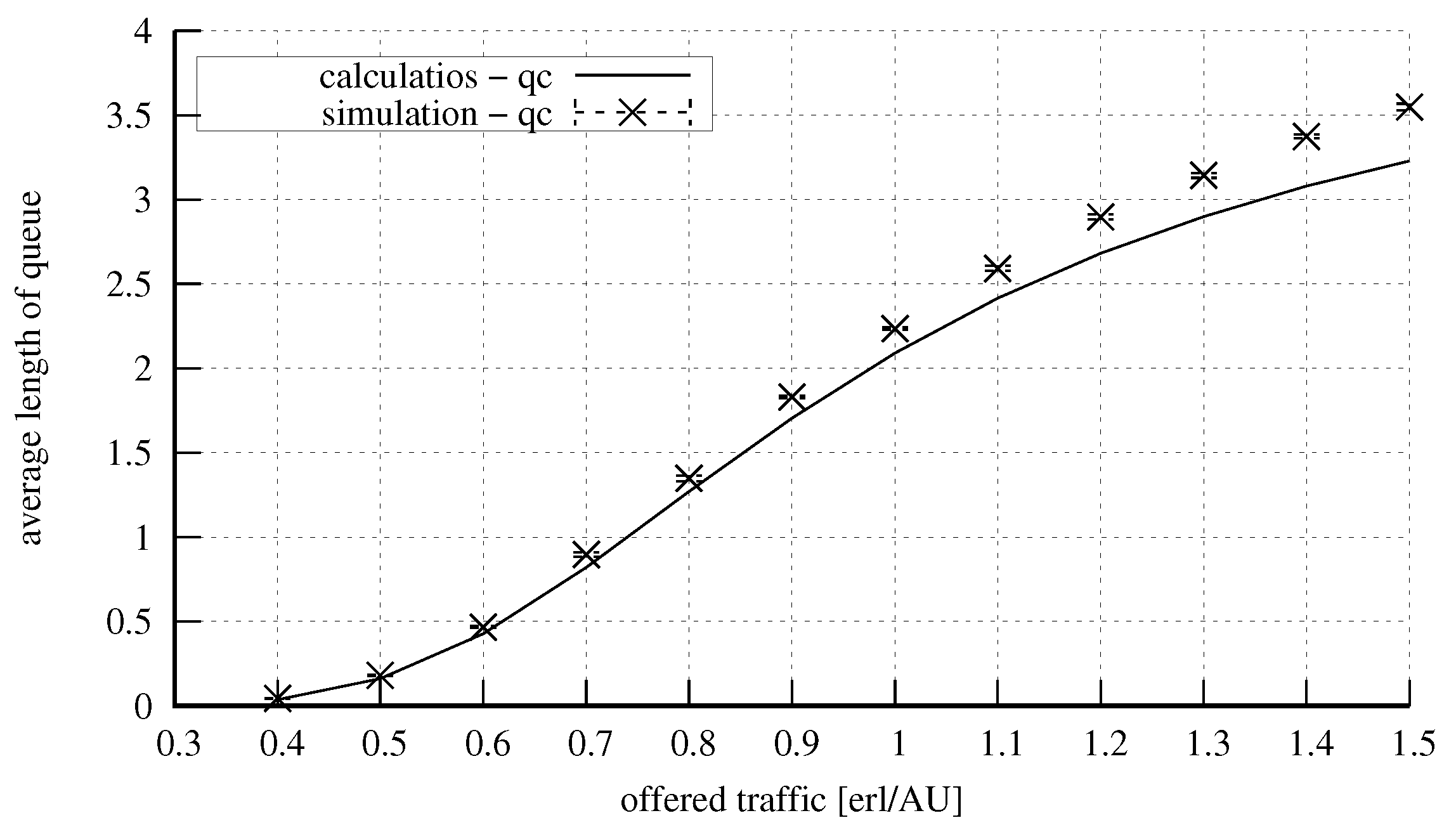
4. Numerical Results
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xia, L.; Zhao, M.; Tian, Z. 5G Service Based Core Network Design. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference Workshop (WCNCW), Marrakech, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next Generation 5G Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Tataria, H.; Shafi, M.; Molisch, A.F.; Dohler, M.; Sjöland, H.; Tufvesson, F. 6G Wireless Systems: Vision, Requirements, Challenges, Insights, and Opportunities. Proc. IEEE 2021, 109, 1166–1199. [Google Scholar] [CrossRef]
- Stamatelos, G.M.; Koukoulidis, V.N. Reservation-based Bandwidth Allocation in a Radio ATM Network. IEEE/ACM Trans. Netw. 1997, 5, 420–428. [Google Scholar] [CrossRef]
- Rácz, S.; Gerő, B.P.; Fodor, G. Flow level performance analysis of a multi-service system supporting elastic and adaptive services. Perform. Eval. 2002, 49, 451–469. [Google Scholar] [CrossRef]
- Bonald, T.; Virtamo, J. A recursive formula for multirate systems with elastic traffic. IEEE Commun. Lett. 2005, 9, 753–755. [Google Scholar] [CrossRef]
- Logothetis, M.; Moscholios, I.D. Efficient Multirate Teletraffic Loss Models Beyond Erlang; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Hanczewski, S.; Stasiak, M.; Weissenberg, J. A Queueing Model of a Multi-Service System with State-Dependent Distribution of Resources for Each Class of Calls. IEICE Trans. Commun. 2014, E97-B, 1592–1605. [Google Scholar] [CrossRef]
- Weissenberg, J.; Weissenberg, M. Model of a Queuing System with BPP Elastic and Adaptive Traffic. IEEE Access 2022, 10, 130771–130783. [Google Scholar] [CrossRef]
- Ericsson. Ericsson Mobility Report; Technical Report; Ericsson: Hong Kong, China, 2021. [Google Scholar]
- Głąbowski, M. Modelling of State-dependent Multi-rate Systems Carrying BPP Traffic. Ann. Telecommun. 2008, 63, 393–407. [Google Scholar] [CrossRef]
- Głąbowski, M.; Sobieraj, M. Compression mechanism for multi-service switching networks with BPP traffic. In Proceedings of the 2010 7th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP 2010), Newcastle Upon Tyne, UK, 21–23 July 2010; pp. 816–821. [Google Scholar] [CrossRef]
- McArdle, C.; Tafani, D.; Barry, L.P. Overflow traffic moments in channel groups with Bernoulli-Poisson-Pascal (BPP) load. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 2403–2408. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kmiecik, D.; Stasiak, M. On Increasing the Accuracy of Modeling Multi-Service Overflow Systems with Erlang-Engset-Pascal Streams. Electronics 2021, 10, 508. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, X.; Horiguchi, S. Recursive Formula for the Moments of Queue Length in the M/M/1 Queue. IEEE Commun. Lett. 2008, 12, 690–692. [Google Scholar] [CrossRef]
- Isijola-Adakeja, O.A.; Ibe, O.C. M/M/1 Multiple Vacation Queueing Systems With Differentiated Vacations and Vacation Interruptions. IEEE Access 2014, 2, 1384–1395. [Google Scholar] [CrossRef]
- Foruhandeh, M.; Tadayon, N.; Aïssa, S. Uplink Modeling of K-Tier Heterogeneous Networks: A Queuing Theory Approach. IEEE Commun. Lett. 2017, 21, 164–167. [Google Scholar] [CrossRef]
- Czachorski, T. Queueing Models of Traffic Control and Performance Evaluation in Large Internet Topologies. In Proceedings of the 2018 IEEE 13th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT), Lviv, Ukraine, 11–14 September 2018; Volume 1, p. 1. [Google Scholar] [CrossRef]
- Andonov, V.; Poryazov, S.; Otsetova, A.; Saranova, E. A Queue in Overall Telecommunication System with Quality of Service Guarantees. In Proceedings of the Future Access Enablers for Ubiquitous and Intelligent Infrastructures, Sofia, Bulgaria, 28–29 March 2019; Poulkov, V., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 243–262. [Google Scholar]
- Chydzinski, A. Per-flow structure of losses in a finite-buffer queue. Appl. Math. Comput. 2022, 428, 127215. [Google Scholar] [CrossRef]
- Cisco. Cisco Annual Internet Report (2018–2023); Technical Report; Cisco: San Jose, CA, USA, 2020. [Google Scholar]
- Kelly, F.P.; Zachary, S.; Ziedins, I. (Eds.) Stochastic Networks: Theory and Applications, Notes on Effective Bandwidth; Oxford University Press: Oxford, UK, 1996; pp. 141–168. [Google Scholar]
- Guerin, R.; Ahmadi, H.; Naghshineh, M. Equivalent capacity and its application to bandwidth allocation in high-speed networks. IEEE J. Sel. Areas Commun. 1991, 9, 968–981. [Google Scholar] [CrossRef]
- Bonald, T.; Roberts, J.W. Internet and the Erlang Formula. SIGCOMM Comput. Commun. Rev. 2012, 42, 23–30. [Google Scholar] [CrossRef]
- Hanczewski, S.; Stasiak, M.; Weissenberg, J. A Model of a System With Stream and Elastic Traffic. IEEE Access 2021, 9, 7789–7796. [Google Scholar] [CrossRef]
- Hanczewski, S.; Stasiak, M.; Weissenberg, J. Queueing model of a multi-service system with elastic and adaptive traffic. Comput. Netw. 2018, 147, 146–161. [Google Scholar] [CrossRef]
- Tyszer, J. Object-Oriented Computer Simulation of Discrete-Event Systems; Springer: New York, NY, USA, 2012. [Google Scholar]





| Area: | |||
|---|---|---|---|
| 1 | 1 | ||
| — | |||
| — | |||
| Area: | |||
| — | |||
| — | |||
| Area: | |||
| — | |||
| — | |||
| Area: | |||
|---|---|---|---|
| — | |||
| — | |||
| Area: | |||
| — | |||
| — | |||
| Area: | |||
| — | |||
| — | |||
| Area: | |||
|---|---|---|---|
| 0 | 0 | ||
| 0 | — | ||
| — | |||
| Area: | |||
| — | 0 | ||
| 0 | 0 | ||
| — | |||
| Area: | |||
| — | |||
| — | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanczewski, S.; Stasiak, M.; Weissenberg, J. An Analytical Model of a System with Compression and Queuing for Selected Traffic Flows. Electronics 2023, 12, 3601. https://doi.org/10.3390/electronics12173601
Hanczewski S, Stasiak M, Weissenberg J. An Analytical Model of a System with Compression and Queuing for Selected Traffic Flows. Electronics. 2023; 12(17):3601. https://doi.org/10.3390/electronics12173601
Chicago/Turabian StyleHanczewski, Sławomir, Maciej Stasiak, and Joanna Weissenberg. 2023. "An Analytical Model of a System with Compression and Queuing for Selected Traffic Flows" Electronics 12, no. 17: 3601. https://doi.org/10.3390/electronics12173601
APA StyleHanczewski, S., Stasiak, M., & Weissenberg, J. (2023). An Analytical Model of a System with Compression and Queuing for Selected Traffic Flows. Electronics, 12(17), 3601. https://doi.org/10.3390/electronics12173601






