A Multi-Robot-Based Architecture and a Trust Model for Intelligent Fault Management and Control Systems

Abstract

One of the most important challenges in robotics is the development of a Multi-Robot-based control system in which the robot can make intelligent decisions in a changing environment. This paper proposes a robot-based control approach for dynamically managing robots in such a widely distributed production system. A Multi-Robot-based control system architecture is presented, and its main features are described. Such architecture facilitates the reconfiguration (either self-reconfiguration ensured by the robot itself or distributed reconfiguration executed by the Multi-Robot-based system). The distributed reconfiguration is facilitated through building a trust model that is based on learning from past interactions between intelligent robots. The Multi-Robot-based control system architecture also addresses other specific requirements for production systems, including fault flexibility. Any out-of-control fault occurring in a production system results in the loss of production time, resources, and money. In these cases, robot trust is critical for successful job completion, especially when the work can only be accomplished by sharing knowledge and resources among robots. This work introduces research on the construction of trust estimation models that experimentally calculate and evaluate the trustworthiness of robots in a Multi-Robot system where the robot can choose to cooperate and collaborate exclusively with other trustworthy robots. We compare our proposed trust model with other models described in the literature in terms of performance based on four criteria, which are time steps analysis, RMSD evaluation, interaction analysis, and variation of total feedback. The contribution of the paper can be summarized as follows: (i) the Multi-Robot-based Control Architecture; (ii) how the control robot handles faults; and (iii) the trust model.

1. Introduction

A Multi-Robot-based control system is an emerging solution that is gaining popularity [1]. Today there are a wide variety of research activities that have been approved in this spirit [2]. In this paper, we are particularly interested in the architecture and behavior of intelligent robots that work together, especially in the event of a fault. Usually, the detection of faulty components is manual and time-consuming [3,4]. Nowadays, pattern classification [5,6], fuzzy logic [7,8], expert systems [9,10] as well as causal analysis such as knowledge-based representation [11] represent a centralized approach of the solution. However, these approaches suffer from having to handle massive data [12]. To overcome these limits (computation time, massive data, and scalability), Multi-Robot-based Control System has been proposed because of the need for decentralized data handling and decision-making [13]. In particular, we are interested in robots that are cooperative, dependent on each other, and communication reliable.

In the Multi-Robot-based control system, robots need to know information about the environment through sensors [14] and need also to execute some commands through actuators [15]. The robots can be affected by many fault types: (i) faults affecting the robot perception (which means sensors) [16], (ii) faults affecting the robot’s actions on the environment (which means actuators) [17], and (iii) faults affecting the robot behavior. The fault detection can be endogenous (i.e., the robot identifies a fault in itself) or exogenous (i.e., the robot perceives a fault in another one). In this paper, we are interested only in endogenous fault detection [18].

In our Multi-Robot-based control system, the robots coordinate their behavior together to detect and identify a fault that can occur in the system [19]. On the one hand, the robots are independent, which means they can make their own decisions without interfering with others. On the other hand, the robots are dependent on each other, which means a robot sometimes needs help from the other robot to achieve its goals [20,21]. The Multi-Robot task planning can be performed online or offline. Online task planning means that the robots search for the solution during the task execution [22]. Offline task planning means that the robots already determine the solution before the task execution [23]. In this paper, we are interested in online Multi-Robot task planning.

Additionally, Multi-Robot cooperation can be centralized or distributed. A centralized approach means that a specific robot plays a particular role as a coordinator between all robots [24]. A distributed approach means that all the robots must cooperate to find a convenient solution for the whole system [25]. In this work, distributed cooperation is adopted.

Though its importance, few research papers have considered treating faults by endogenous Multi-Robots in a distributed and open system with online task planning.

The primary goal of this research is to create a decision-making framework in a Multi-Robot system that is founded on the concept of trust, where robots can only cooperate and collaborate with other trustworthy robots. Because of the unknown faults involved, trust is a key factor in any collaboration, especially in a highly dynamic and unpredictable environment where robots are expected to work. In this paper, we present research on the development of trust assessment models that tentatively ascertain and assess the reliability of robots in the Multi-Robot framework where the robot can decide to participate and team up solely with other reliable robots.

Our main contributions consist of defining the following items:

(i)

The Multi-Robot-based Control Architecture by presenting in detail the main components and methods. Such architecture facilitates the reconfiguration (either self-reconfiguration ensured by the robot itself or distributed reconfiguration executed by the Multi-Robot-based system). For this first contribution, we use the finite state machine to represent the architecture.

(ii)

The Multi-Robot-based control system architecture also addresses other specific requirements for production systems, including fault flexibility.

(iii)

Trust Model: The distributed reconfiguration is facilitated through building a trust model that is based on learning from past interactions between intelligent robots. Our proposed model outperformed the trust models described in the literature in terms of performance.

The remainder of this paper is organized as follows: Section 2 presents the state of the art on the related works. Section 3 introduces the Multi-Robot-based Control Architecture. Section 4 describes how the control Robot handles faults. In Section 5, we introduce the Trust Model. In Section 6, we compare our proposed trust model with other models described in the literature in terms of performance based on four criteria, which are time steps analysis, RMSD evaluation, interaction analysis, and variation of total feedback.

Finally, the conclusions and future work are summarized in the Section 7.

2. Related Works

SPORAS is a reputation mechanism proposed by [26] for a weakly connected environment where agents have a common goal. With this methodology, the reputation value is calculated by combining user opinions. The rating numbers are collected using two of the most recent agents. In addition, this model offers a new recursive reputation scoring procedure depending on previous reputation scores at a given point in time; the more recent ratings carry greater weight. However, this approach has two major shortcomings. Firstly, SPORAS only collects the most recent reviews between two users. Secondly, users with extremely high reputation scores are notified after each update. Users with low scores have significantly fewer score changes when using a reputation-based trust.

In [27], the authors presented a reliability–reputation model called TRR, which integrates agent societies and evaluates agent reputation based on trustworthiness. In this approach, an agent’s reputation is determined by ratings given by other agents who have interacted with them before, as well as the trustworthiness of those rating agents. Trusted agents receive higher scores, while less trusted agents have a lower impact on the reputation score.

The REGRET model [28] derives ontological interactions from diverse sources. Consequently, each element of the reputation score must be evaluated separately, considering individual or societal dimensions. These reputation values are subsequently consolidated to form the ontological reputation. An advantage of the REGRET model is that it calculates reputation by considering the number of agents and the frequency of interactions among rating agents.

Based on a review of the literature, each model used distinct variables to evaluate an agent’s reputation. For instance, the TRR model emphasized the importance of considering the reliability of rating agents, where a trustworthy evaluator’s presented value was deemed accurate. In contrast, TRR assigned equal weight to all interactions, overlooking the significance of recent contacts that reflect an agent’s recent behavior. On the other hand, SPORAS incorporated the passage of time in reputation assessment and placed greater emphasis on recent interactions. The REGRET model, however, pointed out that both TRR and SPORAS overlooked the impact of the number of agents rating a single agent and the frequency of interactions among rating agents. Consequently, each model prioritizes different variables in the calculation of an agent’s reputation.

In [29], the authors created the trust score model, which calculates trustworthiness in the form of a direct trust score using a combined logic and q-learning rule framework. In [30], the authors examined the use of a trust framework in Multi-Robot soccer to see how trust affects action choice. The choice of timing analysis to include in the confidence assessment, particularly in real-world scenarios, is one of the most common errors found in the trust assessment model literature [31]. A majority of trust evaluation techniques rely on a statistical or heuristic approach to develop a trust evaluation algorithm, which may not be appropriate for analyzing the behavior of complex agents.

In [32], the authors proposed a trust estimation model in which an agent’s trust in MAS is experimentally evaluated. To estimate trust, the proposed approach uses temporal difference learning, which involves the concept of Markov games and heuristics. In [33], the authors developed a trust-based Multi-Robot control system to increase the efficiency of robot collaboration through recognition and cooperation only with trusted robots. In [34], the authors proposed a trust-based navigation control algorithm that determines a robot’s trustworthiness based on its service and uses this information to determine the robot’s waypoint to avoid deadlocks. In a mobile and collaborative smart factory, [35] proposed a trust-based team-building paradigm for efficient automated guided vehicle (AGV) teams. In [36], the authors’ approach is founded on introducing a basic trust model within a competitive multi-agent system, assuming that an agent’s trust measure reflects their expertise, under the condition that an ample number of competitive interactions are executed. In [37], the authors proposed several agents possessing specific expertise, represented as a real value ranging from 0 to 1. To simplify the simulation, each agent has only one type of service. The agent is asked to provide a service of type T, where T represents one of the available service types.

The work described in this article is built on previous work reported in [27,36] by enhancing efficiency and offering an innovative model that addresses the problems of the previous model. The proposed trust model provides several contributions to reduce uncertainty and enhance performance, as described below:

-

The proposed trust model and algorithm offer a viable approach to reducing uncertainty in heterogeneous robot networks.

-

The trust model formalizes reputation in self-governing networks of robots.

-

It demonstrates that reputation can be effectively utilized even in the absence of a central authority or external calibration.

-

The simulation results showcase the model’s essential features, including improved performance compared to the reference models.

3. The Multi-Robot-Based Control Architecture

Every Intelligent Robot existing in our Multi-Robot system has its specific Goal to accomplish and can produce a plan (which is constituted of tasks) related to this goal. This strategy permits the Intelligent Robot to choose a suitable plan of tasks to be performed.

In Figure 1, we represent a subset of the ontology modeling the Goal, Task Planner, and Fault Handling (only the concepts and roles related to behavior composition are shown). Each Intelligent Robot is assumed to have its own Goals. To ensure a defined Goal, a set of Plans can be proposed. A Plan is related to a set of Tasks. Each Task has some inputs that are Events and uses some Resources. An Intelligent Robot can subscribe to a specific Task. An Intelligent Robot can send or receive a message. The different classes of planning, perception, treating faults, object, space, context, and reconfiguration, as well as how these classes are related to one another, are referred to as semantics for robot knowledge.

In Figure 1, the ontology classes and their hierarchies are drawn in rectangles, while relationships between classes are connected with black solid arrows, where:

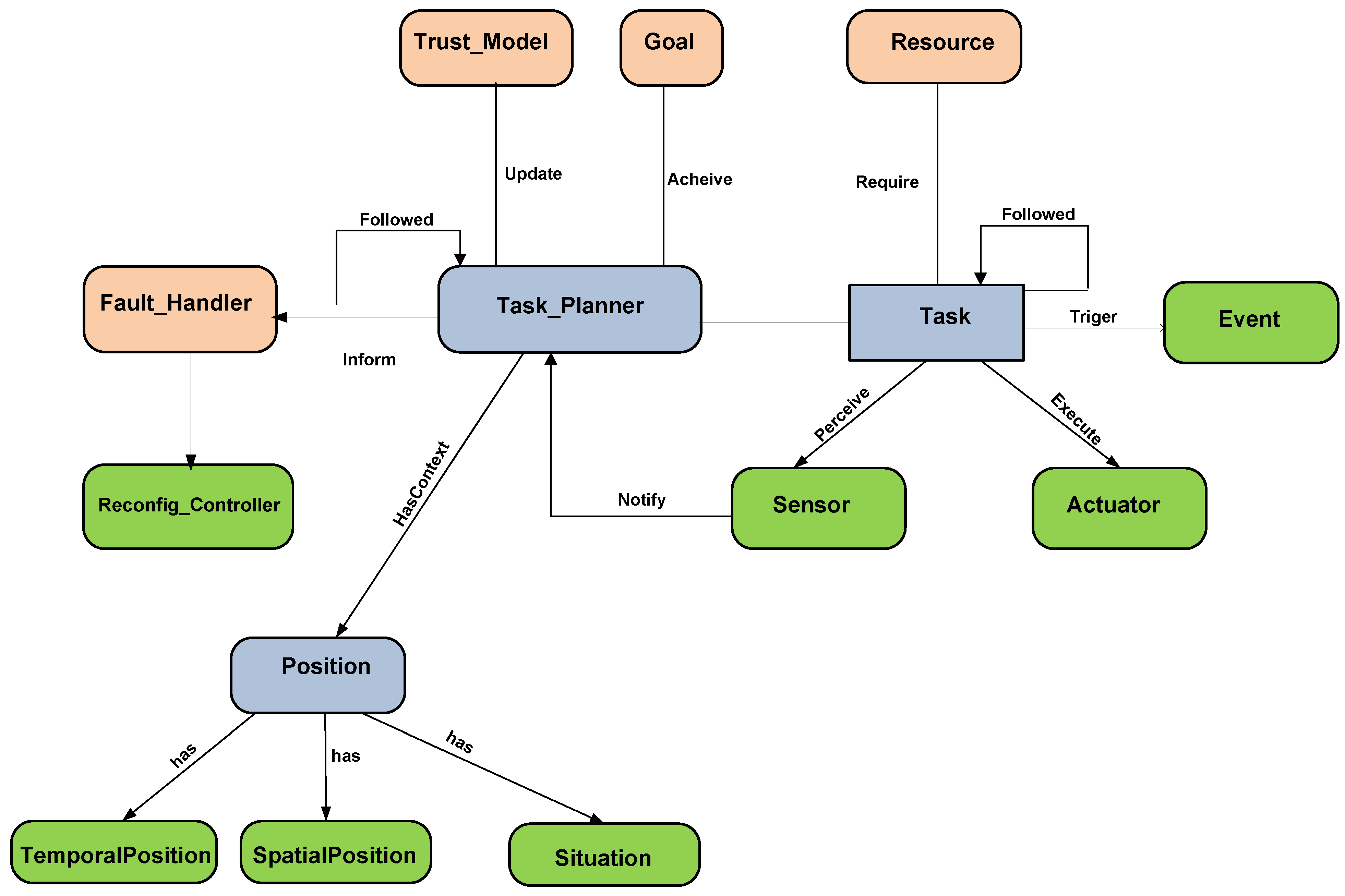
• Goal: represents the high-level objectives or desired outcomes that the intelligent robot aims to achieve in the manufacturing system. Based on the state of the environment, the intelligent robot can execute the goal with the acheiveGoal method or abort it with cancelGoal method (in case of major modification on the environment). The intelligent robot can check the state of execution through the getStateExecution method. As usual, the isConsistentWith method permits attesting the consistency between two Goals or more and the getUtility method allows selecting the most convenient Goal.
• Task Planner: represents the sequences of actions and decisions designed to accomplish specific goals. They provide a structured framework for the robot to follow to achieve its objectives. Task plans outline the steps, dependencies, and priorities involved in executing the required tasks. The intelligent robot arranges task sequences and executes tasks following a specific plan that permits it to achieve a specific goal.
• Fault_Handler: The intelligent robot has to control the system and discover any fault that can occur based on its symptoms to determine its type and save the occurrence time associated with this fault. To accomplish this, the intelligent robot uses various sensors, monitoring devices, and data analysis techniques. It continuously gathers data from the system, such as sensor readings, machine outputs, or environmental parameters, and analyzes them to detect anomalies or deviations from expected behavior.
• Trust_Model: used to establish and evaluate trust relationships among different entities within the intelligent system. It defines the criteria and factors that contribute to trustworthiness, such as reliability, credibility, past performance, or reputation. Each robot assesses the trustworthiness of the other robot based on various factors such as past interactions, observed behavior, and reliability.
• Reconfig_Controller: whenever a fault occurs, the intelligent robot has to decide the right reconfiguration to ensure that the whole system is still working right.
• Task: a robot’s suitable action selection process.
• Event: the intelligent robot receives notifications about any event that occurs in the environment
• Resource: each intelligent robot needs some resources to execute a task (for example, workpiece).
• Sensor: a robot uses its sensors to perceive objects and models the world in which it lives.
• Position: refers to a certain environmental circumstance that surrounds robots and can reveal information about a robot’s suitable movement selection process. To support such cognitive capacities, our model is provided by the context, which consists of three classes of knowledge: Situation, TemporalPosition, SpatialPosition. The basic knowledge that an intelligent robot must access for localization and navigation is represented by context, temporal position, and spatial position. They represent a perceived environment.
• Actuator: the flexible robot can execute the task using the actuator. For each actuator, we must propose a behavior to judge the requests to it.

3.1. How to Calculate the Distance

We consider a set of R robots in a two-dimensional, square, grid-like environment.

The robot initially holds many parameters such as

🗸

The current node position at time t;

🗸

The start node position;

🗸

The goal node position.

The robot calculates the distance through the following formula:

$$\mathrm{d}(\mathrm{V}1, \mathrm{V}2)=k\sqrt{{\displaystyle \sum _{i=1}^n{\left|V_{1i}-V_{2i}\right|}^k}}$$

where the distance d between two robot nodes in dimensional space.

The parameter k determines the metric:

🗸

k = 1, Manhattan distance

🗸

k = 2, Euclidean distance

🗸

k $\to \infty$, dominance distance (only the feature with the largest difference is taken into account).

3.2. Robot Behavior

• Movement behavior

Each robot has four degrees of freedom represented by its set of actions {up, down, left, right}.

If the robot must move from the current node position to the goal node position, the robot plans to move, testing several candidate paths before selecting the best one.

• Communication Behavior

At every step, a robot exchanges its local position and shares its knowledge with all other agents.

• Collision avoidance behavior

The main robot behavior is the collision avoidance strategy, which means avoiding any obstacle (it can be another robot or any object existing in the environment) that the robot can encounter in its path.

3.3. Model

In our scenario, we have a collection of R robots located in a two-dimensional square grid environment. Each robot has four actions it can take, specifically moving up, down, left, or right. The robots all start from the same location and are outfitted with a radio transceiver that allows them to communicate with other robots within a certain range of their current position.

The parameters used by our model are

R: Set of robots

r: robot (r ∈ R)

Ac_r: Set of actions of a robot r, Ac_r = {up, left, down, right}

G_r: Set of goals to be achieved by a robot r

Ac: Set of joint actions of R agents, Ac = R × Ac

ac_rⁱ: i-th joint action of the robot, aci ∈ Ac

P^s_r: Starting point of robot r

Pⁱ_r: Location of robot r at the time i

P^g_r: Goal position of robot r

KindT: A robot that can be considered as usually trustworthy, often trustworthy, often untrustworthy, or usually untrustworthy. KindT = {UT, OT, OU, UU}

Prob_r: Probability of lying assigned to robot r

Th_r: Threshold for a robot r to consider another robot as trustworthy (under this value, it is considered untrustworthy).

The process aims to minimize coverage time and redundancy while ensuring that the robots fully achieve their goals. The robots aim to determine the most efficient path from the origin to the destination point while avoiding obstacles. This can be expressed as an objective function:

$$\min (P_r^s,P_r^g)=d(P_r^s-P_r^1)+{\displaystyle \sum _{i=1}^{n-1}d(P_r^i,P_r^{i+1})}+d(P_r^n+P_r^g)$$

(1)

The fitness function, denoted by Equation (1), evaluates the solution domain, where P_r^s represents the starting point, P_r^g is the goal point, Pi is the ith point that the robot moves to, and d(P_rⁱ, P_rⁱ⁺¹) represents the Euclidean distance between P_rⁱ and P_rⁱ⁺¹.

4. Intelligent Robot Handling Faults

Potential faults can manifest within both physical and virtual components of the robotic system, subsequently permeating through and interrupting the sense–think–act cycle inherent to the system. Consequently, these faults exert a notable adverse influence on the system’s capacity to successfully achieve its intended objectives [38].

Hardware faults can potentially manifest in any physical element of the robotic system, specifically sensors and actuators. Software faults could impact the program such as unexpected conditions. The communication faults may alter the interaction between the different intelligent robots.

A faulty sensor in a Multi-Robot system refers to a sensor component that is not functioning as intended or providing accurate readings. Such a sensor may produce erroneous or inconsistent data, leading to incorrect perceptions of the environment [39,40]. In a Multi-Robot system where multiple robots collaborate and make decisions based on sensor information, a faulty sensor can disrupt the overall performance and coordination of the system.

A faulty actuator represents an actuator that is not performing its intended functions correctly. This can manifest as reduced precision, responsiveness, or even complete failure in executing movements or tasks [41,42].

Faulty software in a Multi-Robot system corresponds to software components or programs that exhibit incorrect behavior or fail to function as expected. Such faults can arise due to errors in code, algorithm design, or interactions between software modules [43,44].

Faulty communication in a Multi-Robot system refers to disruptions or errors that occur during the exchange of information between robots or between robots and a central control unit. This can lead to incomplete, delayed, or corrupted data transmission, hindering effective collaboration and coordination among robots [45,46].

At this juncture, it becomes pivotal to discern significant research voids in a comprehensive manner, encompassing all facets of fault detection, including the recognition of faulty sensors, actuators, software, and communication. To the best of our knowledge, research papers that comprehensively address fault detection in robotic systems across the domains of hardware, software, and interaction are currently unavailable in the publicly accessible literature. Our contribution entails the development of an intelligent system endowed with the capacity to proficiently manage a set of faults that can affect hardware, software, or interaction. The proposed solution is predicated upon a reconfiguration paradigm strategically delineated across three hierarchical levels: the goal level, the plan level, and the task level.

When studying Multi-Robot system, an important topic is to identify which faults could happen in the system. It is important to define at the beginning which faults can be taken into consideration. Firstly, we introduce the different kinds of faults that can occur in the system. After that, we will present how the faults are treated by self-reconfiguration. Finally, we present the different levels of reconfigurations.

4.1. Types of Faults

Belief refers to the robot’s perception or understanding of its environment, tasks, and actions. When an intelligent robot operates, it relies on its beliefs about the world to make decisions and take actions. These beliefs are based on the information the system has gathered through sensors, planning, and reasoning processes. “Unbelief” in this context could refer to the robot’s lack of accurate understanding or perception of its environment and capabilities due to the presence of faults. The robot’s ability to make informed decisions and take appropriate actions is compromised when its beliefs do not align with reality. This mismatch between belief and reality, caused by the various faults, can lead to unexpected and potentially undesirable behavior in the intelligent robot system. By considering that a fault can affect an Intelligent Robot [38], we define a list of faults that can happen such as actuator fault, behavior fault, and sensor fault (Figure 2).

Table 1. The typical faults related to Figure 2.

Event	Meaning
T	Fault alarm
M1	Actuator fault
M2	Behavior fault
M3	Sensor fault
A1	Communication fault
A2 (resp. A3)	Actuator A2 (resp. A3) is broken
A4 (resp. A5, A6)	Behavior A4 (resp. A5, A6) is incorrect
A7 (resp. A8, A9)	Sensor A7 (resp. A8, A9) is broken

explains the event meaning related to Figure 2.

➢

We consider the following fault that concern the behavior of an Intelligent Robot:

• Action fault: the Intelligent Robot does not execute the action well. In this case, the robot’s belief about its ability to perform the action correctly might be misaligned with reality, leading to faulty behavior.
• Plan fault: the Intelligent Robot generates a plan that does not reach the goal.
• Unexpected condition: the Intelligent Robot faces an abnormal condition. In such cases, the robot’s beliefs about its environment might not align with the actual conditions, leading to unanticipated behavior.

NB: The process of deciding on faulty intelligent robots is beyond the scope of this paper.

➢

The different faults that concern the actuator:

• Blocked off: the actuator does not execute any request.
• Blocked on: the actuator is always activated even without request.

In these cases, the robot’s belief about the actuator’s state might not match the actual state, leading to incorrect actions or lack of actions.

4.2. Faults Handling Using Self-Reconfiguration

For each kind of fault, we save data about the fault regarding the fault type, the occurrence time, and the treatment time. Therefore, we have a queue denoted by Queue^Agent to save the faults affecting the behavior, the perception, and the execution of Intelligent Robots (where N^A represents the number of all faults saved in Queue^Agent).

The various steps involved in the robot’s self-reconfiguration for fault handling are illustrated in Figure 3.

• The sensor informs the Planner Task of the occurred fault.
• The Planner Task asks the Fault Handler for fault recovery.
• The Fault Handler requests reconfiguration from the Reconfiguration Controller.
• The Reconfiguration Controller treats the request and takes the decision.
• The Reconfiguration Controller asks Fault Handler to apply the reconfiguration.
• The Fault Handler applies the reconfiguration.
• The Fault Handler asks Planner Task to be reconfigured.
• The Planner Task is reconfigured consequently, and the fault is recovered.

4.3. Order of Reconfigurability

The reconfigurability level (RL) is deployed to represent the different kinds of reconfigurable layers in an automated, self-configured Multi-Robot-based control system. RL can be used as a reconfiguration complexity indicator. The higher RL leads to more reconfigurability, which would cost more in function of time and resources required for the reconfiguration.

Multi-Robot-based control system can be reconfigured in three levels:

RL₁: At the task level, the Multi-Robot-based control system can only change the task due to a simple fault. For example, instead of moving right, move left due to an obstacle.

RL₂: At the plan level, the Multi-Robot-based control system includes all the reconfigurations in the first level, plus reconfiguring the Task planner, which means it is possible to change the planning for a specific fault occurring.

RL₃: At the goal level, the Multi-Robot-based control further changes the goal. This is accomplished only if the goal cannot be achieved due to some circumstances (some faults happen and do not allow the goal to be ensured).

Running Example. The Multi-Robot-based control system considers many scenarios in case faults happen to physical components such as sensors, actuators, or machines (Figure 4). In the first level, we consider three goals (Goal 1, Goal 2, and Goal 3). In the second level, there are some task planners related to each goal. Let us say three task planners (TaskPlanner1, TaskPlanner2, and TaskPlanner3). In the third level, there are some tasks defined for each task planner. We consider, for example, five tasks (Task1, ..., Task5).

Due to faults that may happen, the intelligent control system incorporates a reconfiguration mechanism that encompasses three levels: goal reconfiguration, plan task reconfiguration, and task reconfiguration. At the goal level, the system transitions from one goal to another, while at the plan task level, it switches between different plan tasks. Furthermore, at the task level, specific tasks are modified or substituted with alternative tasks to achieve the desired reconfiguration.

We denote in the following by (i) n_Goal the number of possible Goals implementing the system.R_i denotes a particular Goal where i ∈ [1, n_Goal].

(ii) n_{Plan i} the number of possible plans related to a specific goal R_i, and let Ri,j (where i ∈ [1, n_Goal] and j ∈ [1, n_{Plan i}]) be a state of Ri representing a particular Plan.

(iii) n_{Task i,j} the number of all possible tasks related to Ri,j (i denotes a specific goal and j represents a specific plan).

We denote R_i,j,k where i represents the goal, j represents the Plan, and k represents the Task (i ∈ [1, n_Goal], j ∈ [1, n_{Plan i}] and k ∈ [1, n_{Task i j}]). If we move from R_i,j,k to R_i,j,l that means the reconfiguration concerns only the task level. If we move from R_i,m,k to R_i,n,p that means the reconfiguration concerns two levels, meaning the plan level as well as the task level. If we move from R_i,m,k to R_j,n,p that means the reconfiguration is applied on three levels (goal, plan, and task).

5. Faults Handling Using Trust Model

5.1. Generic Trust Model

The proposed framework architecture of the trust estimation model is depicted in Figure 1. The trust estimation model comes into action once two robots interact. When a robot, labeled as “j,” discovers an objective that belongs to another robot, labeled as “i,” robot j initiates the interaction by transmitting the location information to robot i. Robot i subsequently explores the target location and obtains observations from the environment in return. The observations function as the outcome of the interaction between robot j and robot i and are then employed as input for the trust model. Additionally, robot i seeks the trust estimate of robot j from other robots to incorporate it into its present trust update calculation (See Algorithm 1).

Algorithm 1: Exploring the environment

1: Get_Current_Node  // the current robot position 2: Get_Goal_Node  // is the goal position 3: while current_node  <> goal_node do    updateWorld(time)    If data available from other agents      if node has been visited      choose arbitrary action in {acri}       else      check for current trust on agent ‘j’     if trustworthiness > Threshold       explore new node       get environment data through sensor       Update the trust on agent ‘j’      End if       End if    End if End do end

Running Example

In this running example, we consider three robots RB1, RB2, and RB3. RB1 is designated as the leader but has a sensor flaw that causes it to misclassify zones as blue. The environment used was a 6 × 12 grid cell world where every cell measured 20 cm × 20 cm. The grid cell was partitioned into a blue zone and a green zone, with the blue zone representing the objective locations that the robots needed to find, while the green zone was intended to mistake the agents. The robots were aware of the positions of the zones in the grid cell but not the color distribution, and they were required to determine the blue zones’ positions.

The general goal involves robots finding blue zones as targets within a resource constraint of ten locations. It follows a game of tag format, with RB1 as the leader and each subsequent robot verifying information and updating the trustworthiness estimates of the previous robot. RB1 has a sensor flaw programmed into it, and RB2 and RB3 must evaluate RB1’s trustworthiness to determine if it should continue to lead. RB1 sends location information to RB2, which verifies the information and updates its trustworthiness estimate of RB1. In this case, two scenarios are possible: the first one, where robot RB1 sends the correct information to robot RB2, and the second scenario where robot RB1 sends the wrong information to robot RB2. If robot RB2 relies on the information provided by RB1 and goes to the target location, it might end up finding nothing there. This results in a waste of time and resources. Therefore, the robots need to establish a level of trust with each other to improve the decision-making process.

RB2 then sends the information to RB3, which investigates and assesses the credibility of both RB1 and RB2. After verifying RB1’s misclassification, RB2 moves on to explore the closest target area that RB1 has not yet explored. RB3 reached the same conclusion as RB2 that RB1 cannot be trusted after a certain number of mistakes. After RB1 was proven to be reliable, RB2 and RB3 took action on excluding RB1 and dynamically rearranged the exploration teams.

5.2. Trust Model Presentation

In this section, we present two methods (tFeedB [36] and TRR [27]) with our proposed method (tReconf) based on the trust model.

5.2.1. First Method (tFeedB)

Let us consider two robots P and Q [36]; robot P attributes a trust value to robot Q that reflects P’s subjective assessment of another robot’s trustworthiness. It stems from P’s previous direct experience with Q. Firstly, the trust measure assigned to any other robot is null since the robot has not interacted with other robots and hence has no knowledge of the environment. Now, we will go through how a robot’s trust measure is calculated and updated with other robots.

Take, for example, the ith step for robot P. Due to some fault, robot P requires certain reconfiguration in this situation. As a result, P considers soliciting the help of another robot Q. After P has forwarded the request to Q and Q has responded, P assesses the quality of the response (feedback). Every feedback is a number in the range {0,1}. A feedback value of 0 (1, resp.) indicates the response’s refusal (acceptation, resp.). Let FB1, ..., FBs represent the feedback that evaluates the quality of Q’s answers to the request R1, ..., RN.

At the ith step, the trust measure Trust_i(P, Q) assigned by P to Q is computed as

$$Trus{t}_i(P,Q)=\alpha \ast Trus{t}_{i-1}(P,Q)+(1-\alpha )\ast \frac{{\displaystyle \sum _{j=1}^{N}F{B}_j}}{N}$$

(2)

where Trust_i−1(P, Q) is the previous value of trust assigned by P to Q, and α is a real value in the range [0, 1] reflecting the significance given to previous reliability evaluations concerning the current evaluation. α indicates the weight of the past evaluations when updating the trust (it indicates the significance given to the past concerning the current moment). N is used to denote the number of interactions or requests that have occurred between robot P and robot Q over time, and it helps contextualize the trust-building process between the two robots. If it is the first interaction of P with Q, no previous evaluation may be used for updating the trust. The feedback includes an assessment of the response’s quality, which informs P about the quality of the contributions made by the robots who were contacted to generate the response.

5.2.2. Second Method (TRR)

Step 1: Reputation

The authors take [27] into account Q’s reputation in the community as can be seen by P, as well as services that fit into the category. A reputation, noted by Reputation(P, Q), is a measured value that has robot P upon robot Q. The authors hypothesized that a weighted mean of all the trust values Reputation(C, Q) that every robot C (different from P and Q) related to Q is used to calculate the reputation Reputation(P, Q) that a robot P attributes to another robot Q. In other words, we suppose that the trust that C has in Q is reflected by the recommendation that each robot C makes to robot P regarding robot Q. The trust measure Reputation(P, C) is used to weigh this suggestion from C, taking into account P’s trust in C. In the present stage, the intelligent robot P receives some recommendations from the other robots in response to past recommendation requests.

The function Reputation(P, C) is calculated roughly as follows:

$$Reputation(P,Q)=\frac{{\displaystyle \sum _{C\ne P,Q}^{}Trust(P,C)\ast Trust(C,Q)}}{{\displaystyle \sum _{C\ne P,Q}^{}Trust(P,C)}}$$

(3)

Step 2: Trust

$$Trus{t}_i(P,Q)=\alpha \ast Trus{t}_{i-1}(P,Q)+(1-\alpha )\ast reputation(P,Q)$$

(4)

We presume that each community robot can have his or her reliability model, independent of the other robots, and we will not go into depth about this model here.

The authors suggest that the coefficient α is not constant, but rather depends on (i) the number of encounters that P and Q have had in the past about the category’s services, and (ii) P’s expertise in evaluating the category’s services. To make things easier, we will treat the coefficient α as a constant.

Furthermore, when the Equation (3) is taken into consideration, the Formula (4) above becomes:

$$Trus{t}_i(P,Q)=\alpha \ast Trus{t}_{i-1}(P,Q)+(1-\alpha )\ast \frac{{\displaystyle \sum _{C\ne P,Q}^{}Trust(P,C)\ast Trust(C,Q)}}{{\displaystyle \sum _{C\ne P,Q}^{}Trust(P,C)}}$$

(5)

5.2.3. Our Method (tReconf)

Robot P can utilize its feedback to update its internal trust model for the system’s robots. The overall process that leads to responding to the requested reconfiguration is logically distributed into three phases: (i) robot P submits a reconfiguration request to robot Q and requires its collaboration; (ii) Q responds to the service request; (iii) P updates its internal trust model (using the feedback).

Step 1: Computation of FeedB(rec, P, Q) value: each feedback FeedB(rec, P, Q) is a real number in the range [0;1], indicating the quality of the reconfiguration offered by robot Q to robot P regarding the reconfiguration rec. A feedback value of such that FeedB(rec, P, Q) = 0 means that the reconfiguration is bad in quality terms while FeedB(rec, P, Q) = 1 means that the reconfiguration is perfectly good.

Step 2: The reconfiguration reliability that robot P attributes to the reconfigurations supplied by robot Q is represented by RecfgR(P, Q). P modifies its RecfgR mappings based on this feedback noted FeedB(P, Q). We recall that reliability is a measure of a robot’s trust in another robot, with RecfgR(P, Q) = 0 indicating that Q is completely unreliable and RecfgR(P, Q) = 1 indicating that Q is completely trustworthy.

We specifically chose to compute Q’s actual reliability in its reconfiguration with P by averaging all the Q feedbacks. As a result, if we consider Trust(Q, C), and the feedback for Q concerning a reconfiguration rec is FeedB(rec, P, Q), the current reconfiguration reliability RecfgR(P, Q) is computed as follows: if we consider Trust(Q, C), and the feedback for Q concerning a reconfiguration rec is FeedB(rec, P, Q), the evaluation made by P is Trust(P, Q)*FeedB(rec, P, Q). We obtain an estimate of Q’s precise value by averaging all the relevant reconfigurations where |Reconfig(P, Q)| denotes the total number of reconfigurations provided by Q at the previous step to robot P.

$$\mathrm{Re}cfgR(P,Q)=\frac{{\displaystyle \sum _{rec\in \mathrm{Re}config(P)}Trust(P,Q)\ast FeedB(rec,P,Q)}}{\left|reconfig(P,Q)\right|}$$

(6)

Running example:

In Figure 5, an example is represented in which robot P must evaluate the reconfiguration reliability of robot Q (RecfgR). Robot Q ensures three reconfigurations provided to robot P represented by rec1 (resp. rec2 and rec3). We note also that robot P has evaluated the trust to Q in each step and obtains the following values 0.3 (resp. 0.5 and 0.7) that robot P assigns to robot Q. Robot P evaluates the reconfiguration ensured by robot P by assigning the FeedB measure 0.6 (resp. 0.9, 0.5). Consequently, the reconfiguration reliability that assigns robot P to robot Q is

$$\mathrm{Re}cfgR(P,Q)=\frac{0.3\ast 0.6+0.5\ast 0.9+0.7\ast 0.5}{3} = 0.33$$

Step 3: Trust(P, Q): when P calculates the whole trust score to assign to Q, it considers both the contributions of reconfiguration reliability RecfgR(P, Q) and previous reputation Trust_i−1(P, Q). The percentage of importance to give to the reconfiguration reliability is represented by the value $(1-\alpha )\ast \mathrm{Re}cfgR(P,Q)$.

$$Trus{t}_i(P,Q)=\alpha \ast Trus{t}_{i-1}(P,Q)+(1-\alpha )\ast \mathrm{Re}cfgR(P,Q)$$

(7)

α is a real value in the range [0;1] that represents the relevance that P assigns to previous reliability evaluations following the existing evaluation. In other words, α permits the assessment of the value placed on memory (trust) in comparison to the present reconfiguration reliability RecfgR.

Moreover, we take into consideration Equation (6), and the Formula (7) above becomes

$$Trus{t}_i(P,Q)=\alpha Trus{t}_{i-1}(P,Q)+(1-\alpha )\frac{{\displaystyle \sum _{rec\in \mathrm{Re}config(P)}Trust(P,Q)\ast FeedB(rec,P,Q)}}{\left|reconfig(P,Q)\right|}$$

(8)

6. Experimental Results

We consider three robots called RB1, RB2, and RB3 that must explore space and gather a specific number of colored balls. The robots must swiftly find all the target-colored cells that have been assigned to them. In particular, RB1 (resp. RB2, RB3) must gather ten blue (resp. red, yellow) balls. The agents are aware of where the balls are. They must scavenge the surroundings to locate their balls. A robot will inform the appropriate robot if it comes across a ball that belongs to another robot. For instance, if RB1 discovers a red ball belonging to RB2, then RB1 will inform RB2 about the location of the ball. The given scenario describes a situation where robot RB1 can mistakenly provide inaccurate information to robot RB2 while exploring an environment to collect specific-colored balls. This could happen due to faulty or damaged sensors, high uncertainty, or a highly dynamic environment that differs from initial observations.

The robots in the environment are working individually to find their cells, but they can collaborate to speed up the process. This collaboration involves sharing information about cells found by other robots. For instance, if Robot RB1 finds a cell that belongs to Robot RB3, it will share the cell’s location information with Robot RB3. Robot RB3 will then verify the cell color by exploring the location shared by Robot RB1. If the cell’s color matches Robot RB3’s objectives, the interaction is successful.

At the beginning, each trustee robot is randomly assigned one of five profiles. The robots explore the environment to achieve their objectives of finding their respective cells and may work collaboratively to expedite the time it takes to complete their objectives. If a robot shares correct information, the trust in that robot increases, and if they repeatedly share incorrect information, the trust decreases over time. The generated trust values range from 0.0 to 1.0, with 0.5 representing neutral trust. A decrease of up to 10% from the neutral trust is considered an acceptable reduction in trust level before a robot’s trustworthiness is questioned, and the minimum trust value is set to 0.2 for the simulation.

Since cooperation and communication are allowed, if one robot comes across a colored cell that belongs to another robot, the location data can be communicated. However, there is a potential that a sensor error will cause the incorrect robot to receive the cell location information. All the robots are unaware of the possibility of the sensor malfunction, which is coded in a probabilistic mode. The predicted trust levels for each robot range from 1.0 to 0.2, with higher values indicating more real trustworthiness. The objective of robots is to reach their goals within a limited number of steps and avoid collisions. In case of a collision, the robots are returned to their previous positions. The game ends after all robots have reached their goals. The goal yields a reward of 100, while a collision results in a penalty of −10. In all other scenarios, the reward is set at −1 to incentivize taking fewer steps.

By comparing the performance of the established trust models tReconf to two other models previously discussed in the literature, namely tFeedB [36] and TRR [27], the models’ effectiveness is assessed. The reason for selecting these three models for the comparative study is that they employ similar principles in evaluating trustworthiness.

The simulation involves a set of trustor and trustee robots that engage in interactions for a duration of 85 rounds. Each robot in the simulation is programmed with a probability of experiencing sensor malfunction, which causes it to incorrectly identify the color of the grid cell. This probability of malfunction can be associated with the probability of lying.

Table 2. The probability of a sensor’s failure to correctly identify the color of a cell.

Robot	Sensor Malfunction Probability	Trustworthiness
RB1	0.1	0.9
RB2	0.4	0.6
RB3	0	1

presents the probabilities of the sensor malfunction occurring, which were determined using arithmetic reasoning based on three different levels of robot credibility: fully trustworthy, fully untrustworthy, and partially trustworthy.

In the following section, we compare tReconf with tFeedB [36] and TRR [27] based on four criteria, which are time steps analysis, RMSD evaluation, interaction analysis, and variation of total feedback.

6.1. Time Steps Analysis

The term “time steps” is used in this study to describe how many cells the robots must pass through to accomplish their goals. The trust model utilized in the decision-making framework is thought to be more effective the fewer time steps a robot needs to take to accomplish its goal. A robot should have some degree of trust in the sender robot when receiving shared information from another robot before exploring the area they have been sent to. The receiving robot would experience fewer time steps overall if the sender were to always communicate accurate location information. If the sender is dishonest and the receiver robot nevertheless complies with their instructions, the time steps would increase because of non-value-added procedures. Shorter completion times would result from the accurate identification of trustworthy robots by a reliable trust evaluation model.

When a robot shares information with another robot (e.g., RB3 sharing information with RB2), the receiving robot (RB2) moves toward the target location to identify the grid cell, and the number of cells crossed to reach the target location is added to the total time steps taken to complete the objective. In situations where there is a high level of trust among robots, positive outcomes are almost guaranteed for each interaction, and every time step is considered value-added and contributes to achieving the objectives. Conversely, if a robot follows false information from an untrustworthy source, the likelihood of a negative outcome increases, and the time steps taken during such an instance are not considered value-added. Instead, they only serve to prolong the time required to complete the objectives.

According to Figure 6, it is evident that the tReconf model outperforms other models in terms of time steps due to its utilization of a trust model that ensures precise outcomes. The tReconf model selectively relies on trustworthy agents while disregarding messages from less reliable sources. In contrast, the tFeedB model struggles to accurately identify trustworthy agents, resulting in a higher number of time steps required. However, the TRR model emerges as a satisfactory solution, as its outcomes exhibit a reasonable level of performance.

6.2. RMSD Evaluation

The study assesses the trust models’ effectiveness and accuracy using two methods: time steps analysis and RMSD analysis. The time steps analysis measures the trust models’ effectiveness in accelerating the robot’s achievement of simulation objectives. The RMSD method calculates the difference between expected and actual trustworthiness values to evaluate the accuracy of the trust models. A lower RMSD value indicates a more precise trustworthiness estimation. The study uses the RMSD analysis to assess the trust models’ effectiveness in accurately estimating robots’ trustworthiness. The actual trustworthiness values are obtained from Table 2, while the trustworthiness estimates generated by the model at the end of the simulation are the predicted values. A lower RMSD value indicates higher estimation accuracy for trustworthiness.

Table 3. Comparison between tReconfig, tFeedB, and TRR trust models based on RMSD values.

TRUST	tReconf	tFeedB	TRR
T1,2	0.015	0.031	0.026
T1,3	0.009	0.025	0.034
T2,1	0.027	0.042	0.008
T2,3	0.006	0.028	0.033
T3,1	0.008	0.064	0.051
T3,2	0.015	0.031	0.019

displays the calculated RMSD values from simulation trials.

In comparison to the two literature models, the results in Table 3 demonstrate that our method tReconf has the lowest RMSD values, indicating superior accuracy in trustworthiness estimation. However, when evaluating entirely trustworthy robots, tFeedB [36] is the worst.

6.3. Interaction Analysis

To accurately distinguish between trustworthy and untrustworthy robots, a trust decision-making framework must have the right number of contacts with other robots. Only those trustworthy robots would produce value-added interactions in the future, which might speed up the completion of the target.

RB1 and RB3 are predicted to interact more than RB2, which has greater malfunction probabilities, based on the communication sensor malfunction probabilities.

The following inferences can be made from

Table 4. Comparison between tReconfig, tFeedB, and TRR trust models based on the average number of interactions.

Interaction	tReconf	tFeedB	TRR
I1,2	10	25	15
I1,3	53	35	47
I2,1	24	26	18
I2,3	32	23	35
I3,1	48	37	43
I3,2	7	28	11

:

-

The tReconf model operates as anticipated, with more interactions being seen with the RB1 and RB3 trustworthy robots and fewer interactions being seen with the RB2 robot. Since RB3 is more reliable than RB1, there are more interactions with RB3.

-

The TRR model functions also as expected, exhibiting a higher number of interactions with the trustworthy robots RB1 and RB3, while fewer interactions are observed with the RB2 robot.

-

However, with tFeedB model, there are fewer contacts with RB1 and RB3 than anticipated because trustworthiness cannot be reliably determined by tFeedB models.

6.4. Variation of Total Feedback versus Percentage of Unreliable Robots

In this subsection, we explain several tests we conducted to assess the efficacy of our tReconf strategy in identifying the best-suited candidates for reconfiguration. The competing robots’ behavior is simulated in our prototype. Each simulated actor has a distinct skill to which the simulator assigns a real value between [0, 1]. For the sake of simplicity, we have assumed that only one reconfiguration type exists in this scenario.

Figure 7 illustrates the results in terms of the variation in total feedback from tFeedB, TRR, and tReconf robots versus the different percentages of unreliable robots P. We ran some tests with different percentages of unreliable robots P. We performed the following: We looked at nine different robot populations, each with a size of N = 150 robots and a different proportion P of unreliable robots. 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, and 90% are the nine P values we examined. We fixed the value of parameter α to 0.41, with the tFeedB, TRR, and tReconf robots participating in the game.

The results are shown in Figure 7 in terms of the results of tFeedB, TRR, and tReconf robots vs. the percentage of unreliable robots P.

Based on Figure 7, we conclude that the TfeedB approach reaches its maximum bank amount for P = 20%, and the performance of tFeedB solutions for other p-values drops. The reasons for this are (i) the TfeedB robot is not able to correctly distinguish unreliable robots, and (ii) it suffers unnecessary costs while asking for recommendations when the population is reliable (P < 50%). In contrast to the TfeedB approach, TRR gradually learns to distinguish trusted robots, which reduces the cost of referrals. Furthermore, reliability in TRR is determined by the number of interactions between the trustor and the trustee. Moreover, Figure 7 shows that the performance of TRR is not significantly affected by the presence of unreliable robots. The approach TRR is a good solution as it provides good results in all cases (when all robots are reliable as well as when most of them are unreliable). This can be explained by the fact that TRR is based on the two parameters of reliability and reputation. Whenever the reputation is weak, the choice is based on reliability. Whenever reliability is reduced, the decision is based on reputation. Another advantage of this approach is that the reputation is calculated over all the community, not only restricted between two robots. The major disadvantage of TRR is that it does not take into consideration the quality of the solution ensured by the chosen robot Q, as does our solution tReconf.

If we consider the tReconf approach, it starts with acceptable results and gradually surpasses the other solutions, especially when the percentage of unreliable robots is important (more than 50%). In our approach tReconf, we give more importance to the past interactions between robots P and Q as well as the trust that has robot P in Q. That is why, even when most robots are unreliable, the choice of robot P is based on its own experience, which means that P should choose the best robot that previously interacts with it successfully (by calculating the updated feedback that has P on Q). Therefore, the solution is not affected by the high percentage of unreliable robots in this case. The only disadvantage that has our approach tReonf is that robot P does not need to contact all the other robots to decide on the best robot to choose to ensure the reconfiguration. In some cases, this is not sufficient, and robot P needs to consider the reputation of robot Q in the whole community not only calculated by robot P itself.

7. Conclusions

In this paper, we consider treating faults by endogenous Multi-Robots in a distributed and open framework with online task planning. The essential objective of this research is to make a decision-making framework in a Multi-Robot framework that is established on the concept of belief, where robots can only coordinate and collaborate with other reliable robots. Because of the faults that may occur, trust may be a key factor in any collaboration, particularly in a highly dynamic and unpredictable environment where robots are anticipated to work. In this, we present our contribution to the trust model that discovers and evaluates the reliability of robots in a Multi-Robot system where the robot can choose to take part and group up exclusively with other dependable robots. Our main contributions comprise defining (i) the Multi-Robot-based Control Architecture by presenting in detail the main components and methods. Such architecture facilitates the reconfiguration (either self-reconfiguration ensured by the robot itself or distributed reconfiguration executed by the Multi-Robot-based system). For this first contribution, we use the finite state machine to represent the architecture. (ii) The Multi-Robot-based control system architecture also addresses other specific requirements for production systems, including fault flexibility. (iii) Trust Model: The distributed reconfiguration is facilitated through building a trust model tReconf that is based on learning from past interactions between intelligent robots. It should be noted that this paper focuses on proposing a new trust model tReconf and discussing its potential benefits rather than providing specific formulas or algorithms for calculating trust. We compare tReconf with tFeedB [36] and TRR [27] based on four criteria, which are time steps analysis, RMSD evaluation, interaction analysis, and variation of total feedback. Our proposed model outperformed the trust models described in the literature in terms of performance.

Our future work will be the following. Our methodology can be expanded to include human-computer interaction. Our Multi-Robot-based control system can be ameliorated to allow robots to participate in multiple collaborations at the same time. This work is part of our work on cloud, fog, and edge computing (see, for example, [47]). The problem considered in this paper is a typical candidate for application of cloud, fog, and edge computing because the robots need to maintain the knowledge about the other robots, the environment, the knowledge about trust, etc., and make decisions in real-time. This requires maintaining global and local knowledge and decision-making with trade-offs between the decision time and accuracy. Future research will consider these aspects of robot-based intelligent control systems.