Nonlinear Multi-Object Differential Game Simulation Model in LabVIEW
Abstract
:1. Introduction
1.1. State of Knowledge
1.2. Study Objectives
1.3. Article Content
2. Differential Game Mathematical Model
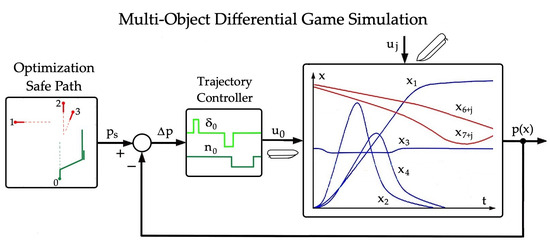
2.1. Game Control Process
- Control of the object with no information available on the disturbances operating on such an object. In this case, we have only the state equations of the object and a set of acceptable steering actions. Such a control should be then determined as to ensure the minimal functional, under a condition that the disturbance tends to its maximum; in this case, the differential game should be solved with a min max optimum condition.
- Synthesis of the multi-layer hierarchical systems. One of the essential hierarchical languages for the steering systems of various nature and methods of determining optimal control is the theory of games including common interests and the right to the first turn.
- Control of the object encountering a greater number of the moving objects of different quality index and final goals. An example, in this case, may be a process of ship control in collision situations when encountering a greater number of the moving or non-moving objects (vessels, underwater obstructions, shore line, etc.), which is a differential game with many participants.
2.2. Ship Kinematics and Dynamics as Control Objects
2.3. State Equations
3. Ship Differential Game Model in LabVIEW
- A graphical interface, the desktop;
- A structure diagram;
3.1. State Equation Models
3.2. State Equation Computer Simulation
3.3. Simulator Desktop
4. Simulation Studies
- Cooperative game safe control, taking into account the COLREG rules of preventing ship collisions at sea (Figure 15);
- Non-cooperative game safe control, in situations of a subjective erroneous assessment of the navigational situation or in restricted visibility conditions at sea (Figure 16);
- Optimal non-game safe control, with unchanged values of the course and speed of the ship (Figure 17).
5. Conclusions
- The modeling of various navigational situations in terms of the risk of collision resulting from the subjectivity of the assessment of the maneuvering situation and the state of visibility at sea;
- The degree of cooperation between ships to be obtained;
- The assessment of the size of a safe trajectory deviation of a ship from an initial direction as well as the largest non-cooperative control and the smallest cooperation of ships to avoid collisions;
- The feasibility of a previously determined safe trajectory of a ship to be checked, based on the algorithm of the positional or matrix games;
- The synthesis of new control algorithms using artificial intelligence methods;
- The practical training of navigators to prevent ship collisions at sea.
Funding
Data Availability Statement
Conflicts of Interest
References
- Marden, J.R.; Shamma, J.S. Game theory and control. Annu. Rev. 2018, 1, 105–134. [Google Scholar] [CrossRef]
- Sani, M.; Robu, B.; Hably, A. Limited information model predictive control for pursuit-evasion games. In Proceedings of the 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 13–17 December 2021; pp. 265–270. [Google Scholar] [CrossRef]
- Gong, Z.; He, B.; Liu, G.; Zhang, X. Solution for Pursuit-Evasion Game of Agents by Adaptive Dynamic Programming. Electronics 2023, 12, 2595. [Google Scholar] [CrossRef]
- Guo, X.; Guo, A.; Zhao, S. Null-Space-Based Multi-Player Pursuit-Evasion Games Using Minimum and Maximum Approximation Functions. Electronics 2022, 11, 3729. [Google Scholar] [CrossRef]
- Lisowski, J. A Synthesis of Algorithms Determining a Safe Trajectory in a Group of Autonomous Vehicles Using a Sequential Game and Neural Network. Electronics 2023, 12, 1236. [Google Scholar] [CrossRef]
- Isaacs, R. Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization; Dover Publications: New York, NY, USA, 1999; ISBN 0-486-40682-2. [Google Scholar]
- Mikulski, L.; Kropiowska, D. Usage of a zero-sum differential game in the optimal control of an object described by a nonlinear model. Tech. Trans. Civ. Eng. 2018, 9, 109122. [Google Scholar]
- Yanan, L.; Gerolamo, C.; Franck, G.; Domenico, C.; Etienne, B. Differential game theory for versatile physical interaction. Nat. Mach. Intell. 2019, 1, 36–43. [Google Scholar] [CrossRef]
- Gajarsky, J.; Gorsky, M.; Kreutzer, S. Differential Games, Locality, and Model Checking for FO Logic of Graphs. In Proceedings of the 30th EACSL Annual Conference on Computer Science Logic, Gottingen, Germany, 14–19 February 2022. [Google Scholar] [CrossRef]
- Sani, M.; Hably, A.; Robu, B.; Dumon, J.; Meslem, N. Experiments on the control of differential game of target defense. In Proceedings of the ECC—21st European Control Conference, Bucharest, Romania, 13–16 June 2023; Available online: https://hal.science/hal-04153630 (accessed on 5 August 2023).
- Gammoudi, N.; Zidani, H. A differential game control problem with state constraints. Math. Control Relat. Fields 2023, 13, 554–582. [Google Scholar] [CrossRef]
- Mylvaganam, T.; Sassano, M.; Astolfi, A. A differential game approach to multi-agent collision avoidance. IEEE Trans. Autom. Control 2017, 62, 4229–4235. [Google Scholar] [CrossRef]
- Turetsky, V.; Hayoun, S.Y.; Shima, T.; Tarasyev, A. On the value of differential game with asymmetric control constraints. IFAC-PapersOnLine 2018, 51, 799–804. [Google Scholar] [CrossRef]
- Ougolnitsky, G.; Usov, A. Spatially Distributed Differential Game Theoretic Model of Fisheries. Mathematics 2019, 7, 732. [Google Scholar] [CrossRef]
- Gong, Z.; He, B.; Hu, C.; Zhang, X.; Kang, W. Online Adaptive Dynamic Programming-Based Solution of Networked Multiple-Pursuer and Single-Evader Game. Electronics 2022, 11, 3583. [Google Scholar] [CrossRef]
- Li, Y.; Hu, X. A differential game approach to intrinsic formation control. Automatica 2022, 136, 110077. [Google Scholar] [CrossRef]
- Engwerda, J. Min-Max Robust Control in LQ-Differential Games. Dyn. Games Appl. 2022, 12, 1221–1279. [Google Scholar] [CrossRef]
- Cappello, D.; Mylvaganam, T. Distributed Differential Games for Control of Multi-Agent Systems. IEEE Trans. Control Netw. Syst. 2022, 9, 635–646. [Google Scholar] [CrossRef]
- Wang, X.; Ma, Z.; Mao, L.; Sun, K.; Huang, X.; Fan, C.; Li, J. Accelerating Fuzzy Actor–Critic Learning via Suboptimal Knowledge for a Multi-Agent Tracking Problem. Electronics 2023, 12, 1852. [Google Scholar] [CrossRef]
- Kaklis, D.; Varlamis, I.; Giannakopoulos, G.; Varelas, T.J.; Spyropoulos, C.D. Enabling digital twins in the maritime sector through the lens of AI and industry 4.0. Int. J. Inf. Manag. Data Insights 2023, 3, 00178. [Google Scholar] [CrossRef]
- Gkerekos, C.; Lazakis, I. A novel, data-driven heuristic framework for vessel weather routing. Ocean. Eng. 2020, 197, 106887. [Google Scholar] [CrossRef]
- Lisowski, J. The dynamic game theory methods applied to ship control with minimum risk of collision. Risk Anal. V Simul. Hazard Mitig. 2006, 91, 293–302. [Google Scholar] [CrossRef]
- Lisowski, J. Game Control Methods Comparison when Avoiding Collisions with Multiple Objects Using Radar Remote Sensing. Remote Sens. 2020, 12, 1573. [Google Scholar] [CrossRef]
- Gierusz, W. Simulation Model of the Shiphandling Training Boat “Blue Lady”. IFAC Proc. Vol. 2001, 34, 255–260. [Google Scholar] [CrossRef]
- Lisowski, J. Synthesis of a Path-Planning Algorithm for Autonomous Robots Moving in a Game Environment during Collision Avoidance. Electronics 2021, 10, 675. [Google Scholar] [CrossRef]
- NI. State-Space Model Definitions (Advanced Signal Processing Toolkit or Control Design and Simulation Module). Available online: https://www.ni.com/docs/en-US/bundle/labview-advanced-signal-processing-toolkit-api-ref/page/lvsysidconcepts/modeldefinitionsss.html (accessed on 24 July 2023).
- NI. Estimating and Validating a State-Space Model (Advanced Signal Processing Toolkit or Control Design and Simulation Module). Available online: https://www.ni.com/docs/en-US/bundle/labview-control-design-and-simulation-module/page/lvsysidconcepts/case_study_ssest.html (accessed on 25 July 2023).
- NI. Defining a Cost Function (Control Design and Simulation Module). Available online: https://www.ni.com/docs/en-US/bundle/labview-control-design-and-simulation-module/page/lvsimconcepts/sim_c_costfunc.html (accessed on 25 July 2023).
- Wang, E.; Hoshino, H.; Ramanan, D.; Kitani, K. Joint Metrics Matter: A Better Standard for Trajectory Forecasting; Cornell University: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
















 : speed V0 of ship 0 reduced by 25%.
: speed V0 of ship 0 reduced by 25%.
 : speed V0 of ship 0 reduced by 25%.
: speed V0 of ship 0 reduced by 25%.
| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| a1 (m−1) | 41.4 | a10 (s−1) | 0.93 |
| a2 (m−2) | 0.19 | b1 (m−2) | 113 |
| a3 (m−1) | 62.0 | b2 (m−1) | 1.55 |
| a4 (m−1) | 44.2 | b3 (s−1) | 1.45 |
| a5 | 6.93 | b4 (s−1) | 1.36 |
| a6 | 31.8 | b4+j (s−1 m−1) | 10.0 |
| a7 (m−1) | 89.0 | b5+j (s m−2) | 0.80 |
| a8 | 44.1 | b6+j (m−1) | 95.2 |
| a9 | 44.3 |
| Ship j | Speed Vj (kn) | Course ψj (deg) | Coordinate Xj (nm) | Coordinate Yj (nm) |
|---|---|---|---|---|
| 0 | 20.0 | 0 | 0 | 0 |
| 1 | 14.5 | 090 | −5.2 | 7.3 |
| 2 | 16.2 | 180 | 1.1 | 8.4 |
| 3 | 16.0 | 200 | 1.6 | 7.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisowski, J. Nonlinear Multi-Object Differential Game Simulation Model in LabVIEW. Electronics 2023, 12, 3848. https://doi.org/10.3390/electronics12183848
Lisowski J. Nonlinear Multi-Object Differential Game Simulation Model in LabVIEW. Electronics. 2023; 12(18):3848. https://doi.org/10.3390/electronics12183848
Chicago/Turabian StyleLisowski, Józef. 2023. "Nonlinear Multi-Object Differential Game Simulation Model in LabVIEW" Electronics 12, no. 18: 3848. https://doi.org/10.3390/electronics12183848
APA StyleLisowski, J. (2023). Nonlinear Multi-Object Differential Game Simulation Model in LabVIEW. Electronics, 12(18), 3848. https://doi.org/10.3390/electronics12183848