Detection of Weak Fault Signals in Power Grids Based on Single-Trap Resonance and Dissipative Chaotic Systems
Abstract
:1. Introduction
2. Detection Principle Based on Stochastic Resonance
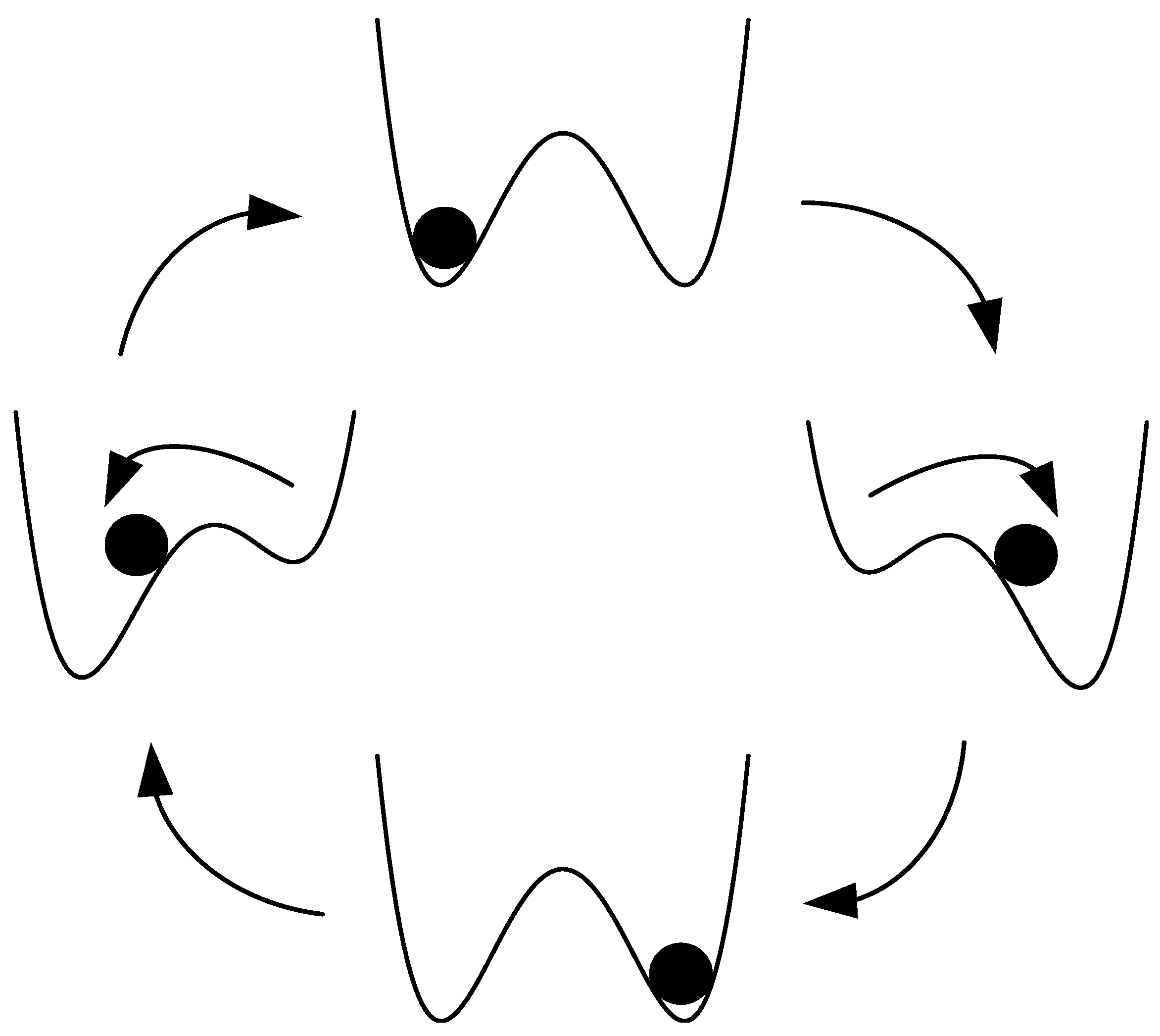
2.1. Fundamentals of Stochastic Resonance
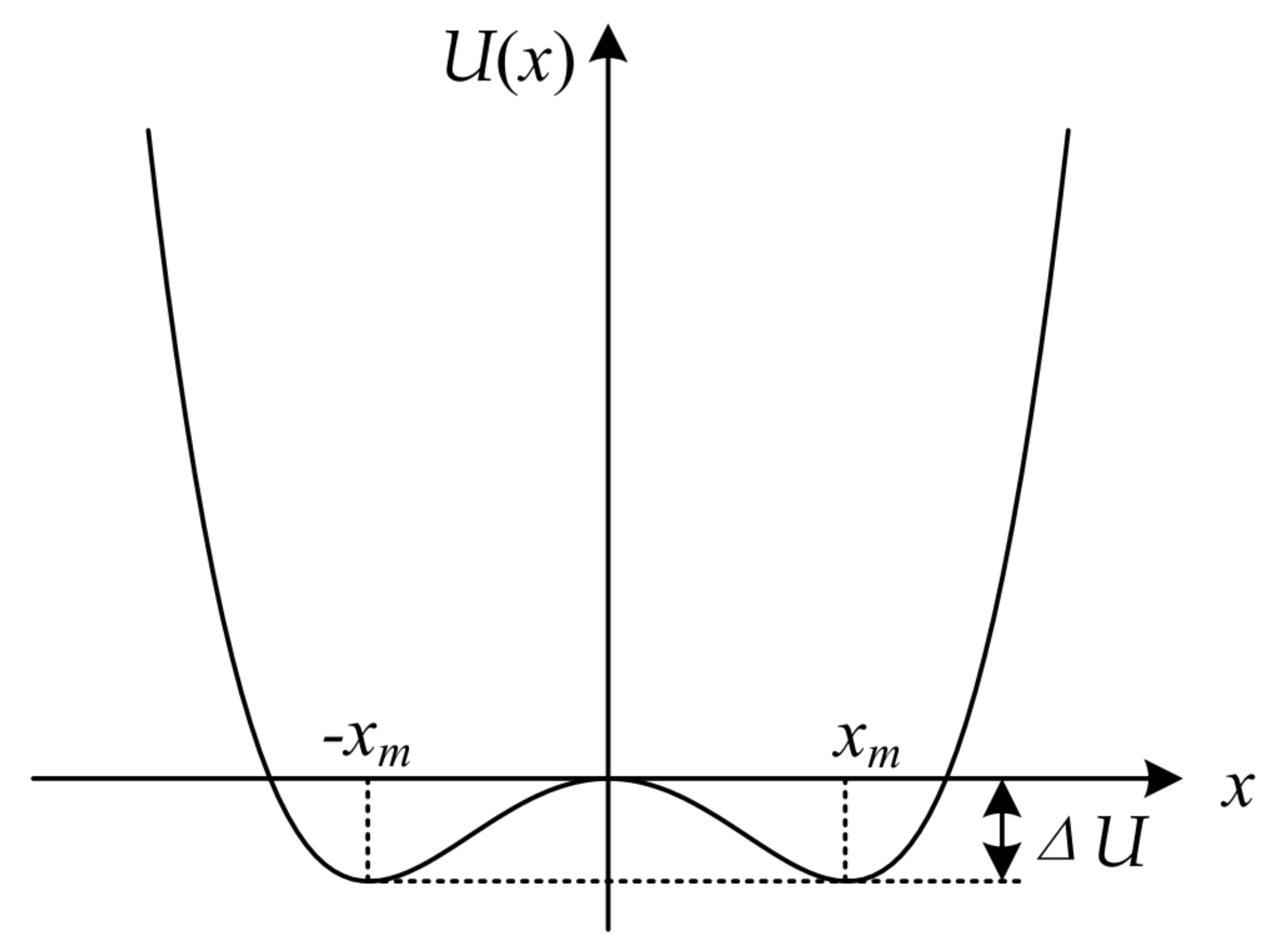
2.2. A Single-Trap Approximate Model of Stochastic Resonance
2.3. Nonlinear Distortion and Restoration of Stochastic Resonance
2.4. Stochastic Resonance Frequency Detection Model for Engineering Signals
2.5. Cascaded Stochastic Resonance Frequency Detection Model
3. Periodic Amplitude Detection of Dissipative Chaotic Systems
3.1. Yang System
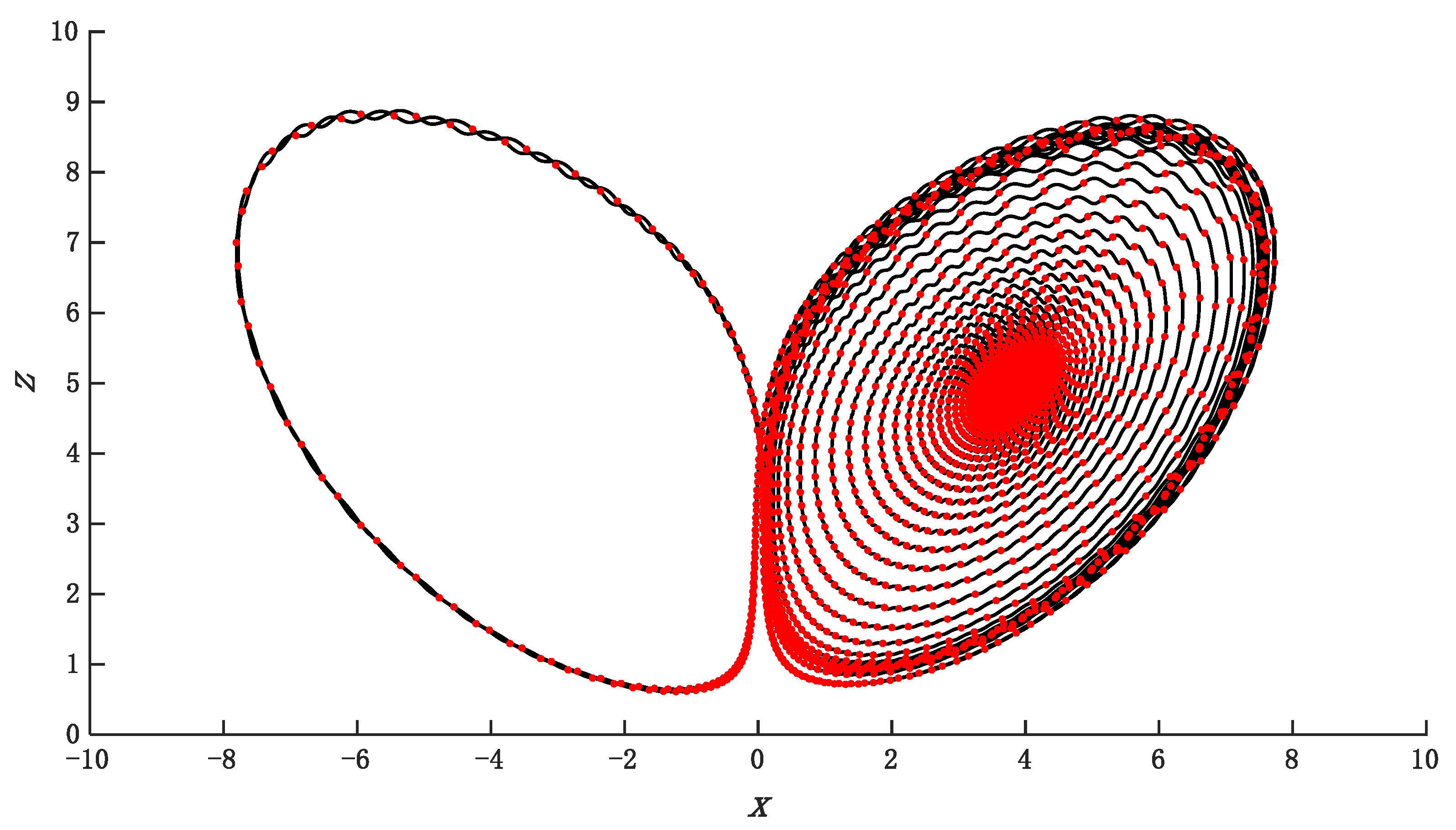
3.2. Chen System
4. Simulation and Experiment
4.1. Steady State Harmonic Amplitude Detection Simulation
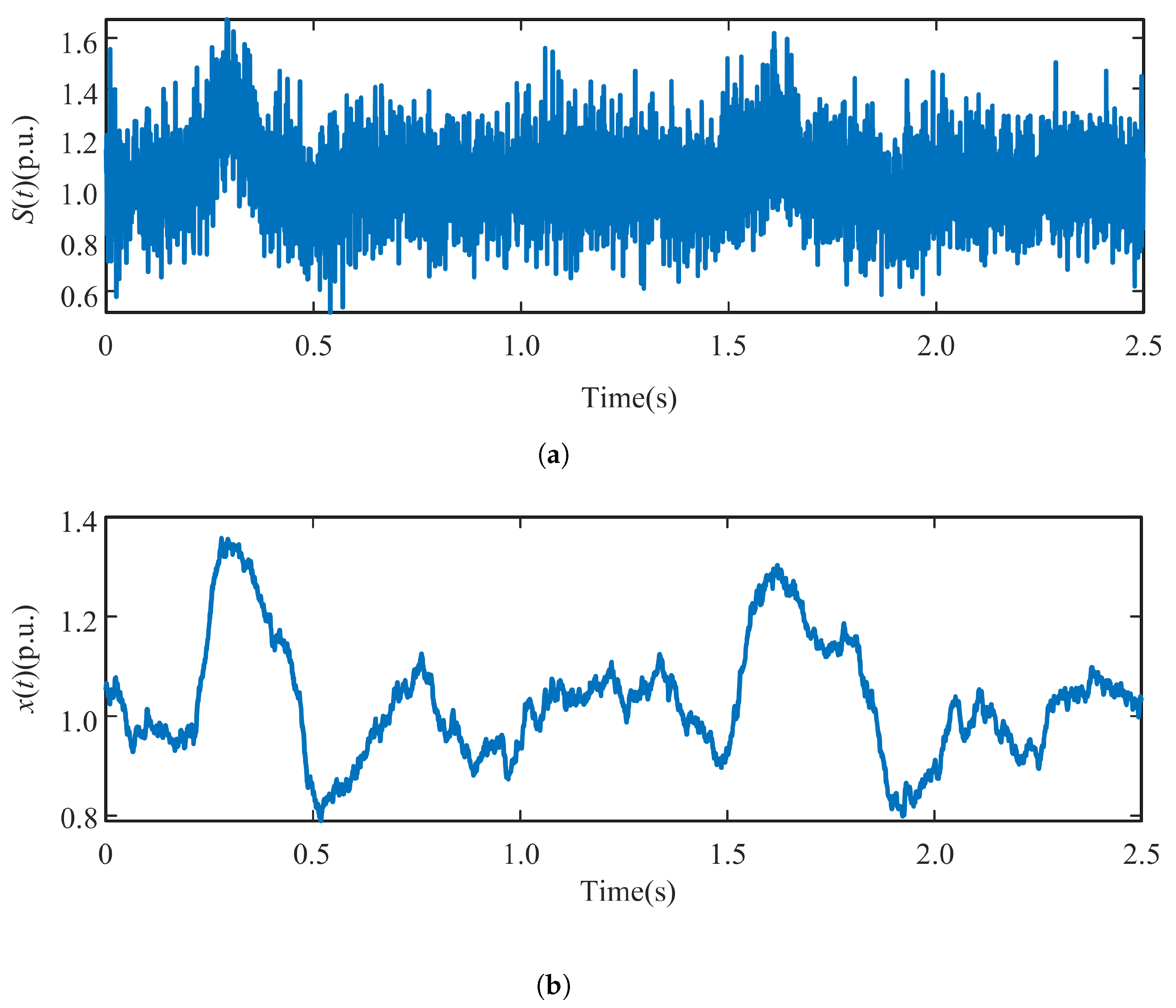
4.2. Detection Experiment of DC Transmission Line Voltage Fluctuation
4.3. Motor Speed Sensor Signal Detection Experiment
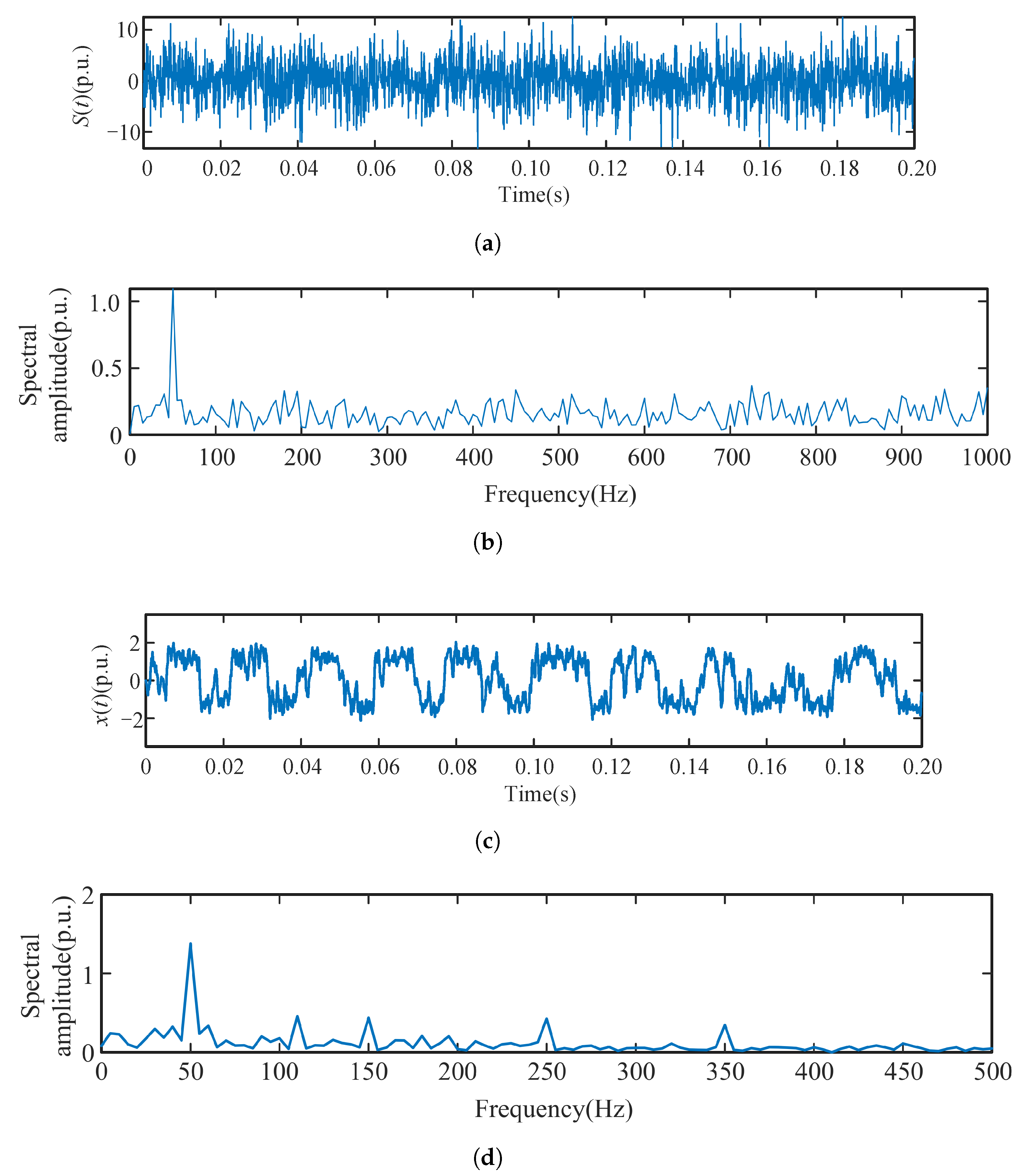
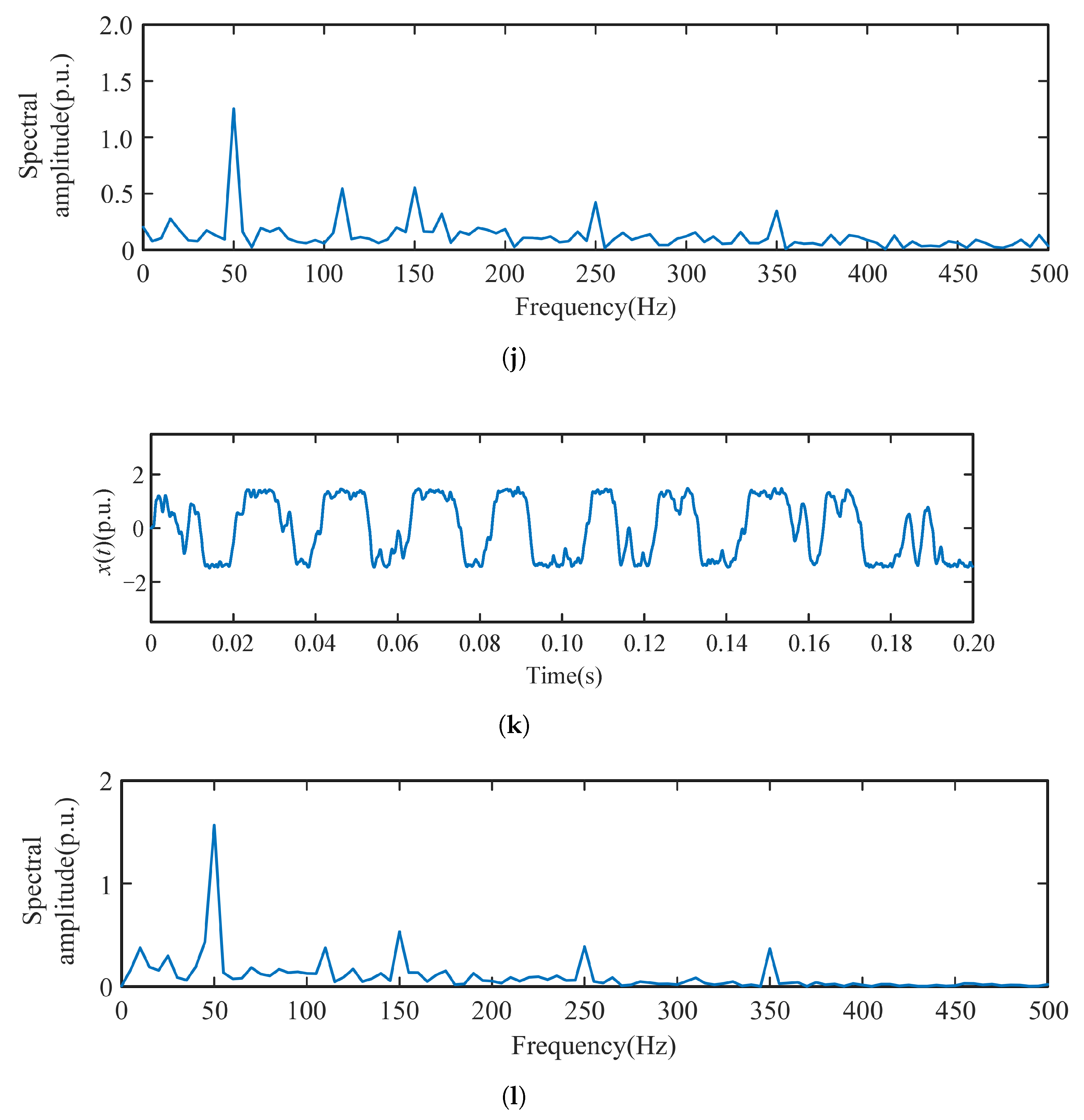
4.4. Low Frequency Oscillation Signal Detection Experiment
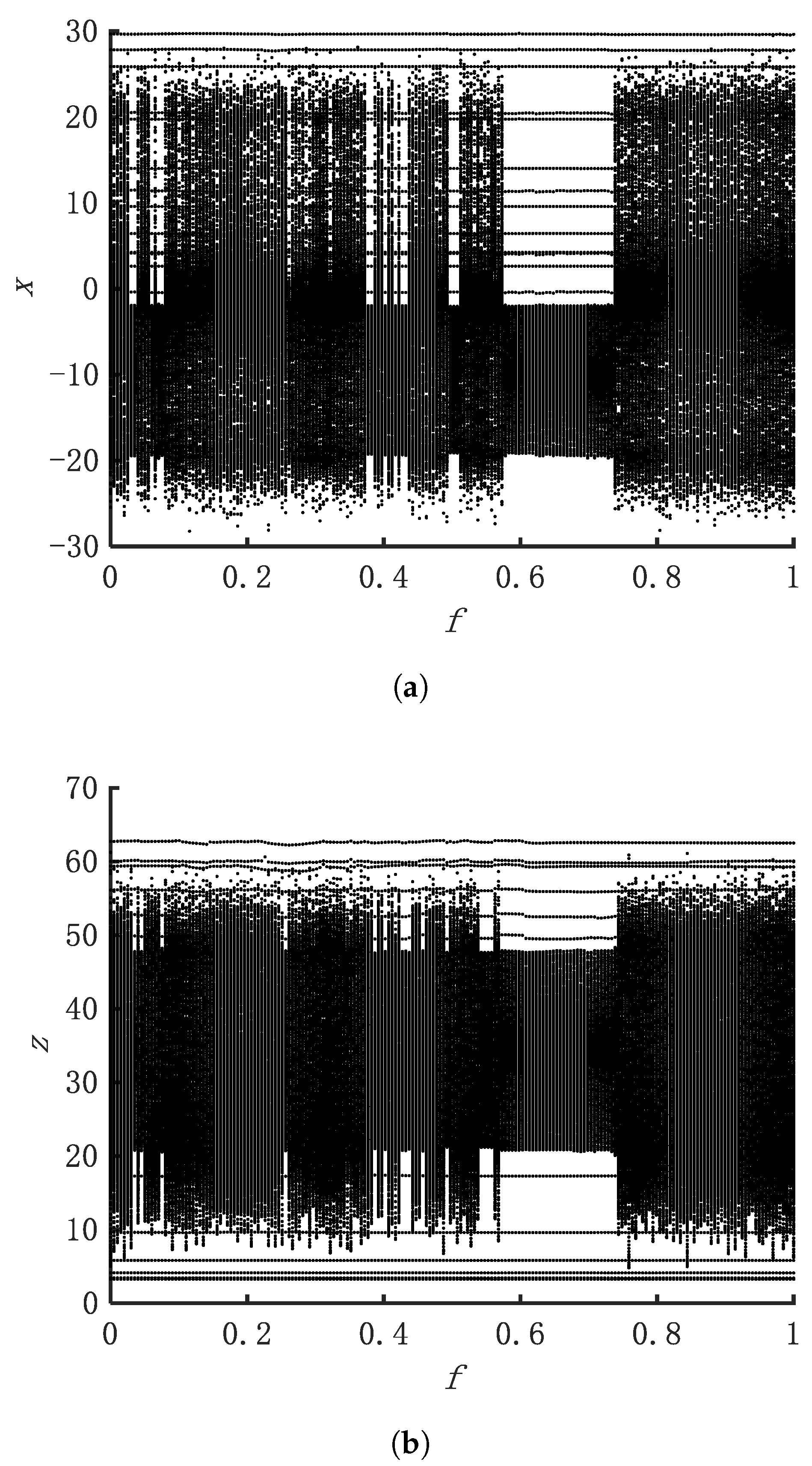
4.5. Real-Time Analysis of Weak Harmonic Chaos Detection Methods
5. Conclusions
- (1)
- The single-trap approximate model of bistable stochastic resonance has good detection performance for common fault signals in power systems such as impulse signals, non-periodic signals, low-frequency oscillation signals and periodic harmonic signals. Correlation detection technology can maximize the advantages of the single-trap stochastic resonance method. Compared with the classical time–frequency domain signal detection method, the method in this paper has a higher detection accuracy and efficiency.
- (2)
- The Yang system exhibits sensitive detection and a strong anti-noise ability in environments with poor signal-to-noise ratios. It can provide amplitude detection with a relative error of no more than 0.508% in an extreme noise environment of −100 dB, providing a good solution for power systems. A new approach is provided to ensure the reliable harmonic signal detection in extremely noisy environments.
- (3)
- The Chen system has extremely high sensitivity in environments with poor signal-to-noise ratios, and has an anti-noise ability that greatly exceeds that of the classical time–frequency domain analysis method, achieving a relative error of no more than 0.0102% in the highly noisy environment of −60 dB. It presents a new method for high-precision harmonic amplitude detection in highly noisy power system environments.
- (4)
- The Yang system follows some general rules of chaotic systems for weak harmonic detection. Increasing the system’s chaotic capacity can improve the system’s resistance to random noise and periodic noise, but it will reduce the detection accuracy of weak harmonic signals. The chaotic capacity is also the degree of confusion in the bifurcation diagram of the system. Since both the Yang and Chen systems can be considered as evolving from the Lorenz system, this conclusion is applicable to all dissipative “Lorenz-like systems”. According to engineering noise environments and engineering precision requirements, the system chaos capacity is modified by modifying the system equations to obtain the best system suitable for the current noise environment so as to obtain the best comprehensive detection performance.
- (5)
- Compared with non-dissipative chaotic systems such as Duffing systems, dissipative chaotic systems have a higher detection accuracy and anti-noise performance, but the detection efficiency is slightly reduced. Dissipative chaotic systems are more suitable for extremely noisy environments and engineering scenarios that require a high detection accuracy, while non-dissipative chaotic systems are more suitable for engineering scenarios that generally require precision and real-time detection performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maria, F.; Dimitrios, R.; Stefanos, P. Decision Support System for Emergencies in Microgrids. Sensors 2022, 22, 9457. [Google Scholar]
- Miao, M.; Yong, L.; Wang, Z.; Ou, L.; Fang, L.; Kwang, L.; Yi, T. An Emergency Energy Management for AC/DC Micro-grids in Industrial Park. IFAC-PapersOnLine 2018, 51, 251–255. [Google Scholar] [CrossRef]
- Xu, Y.; Du, Y.; Li, Z.; Xi, L.; Liu, Y. Harmonic Parameter Online Estimation in Power System Based on Hann Self-Convolving Window and Equidistant Two-Point Interpolated DFT. MAPAN 2019, 35, 69–79. [Google Scholar] [CrossRef]
- Chen, L.; Chen, G. Harmonic Detection and Control of Power System Based on Improved EEMD Algorithm. In Proceedings of the 2015 3rd International Conference on Advances in Energy and Environmental Science, Zhuhai, China, 25–26 July 2015. [Google Scholar]
- Wei, W.; Liu, Z.; Lin, C.; Sha, W. Harmonic Detection of Power System Based on SVD and EMD. In Proceedings of the 2013 Ninth International Conference on Computational Intelligence and Security, Emei Mountain, China, 14–15 December 2013; pp. 185–189. [Google Scholar]
- Qi, D.; Wang, W.; Quan, G.; Long, Q.; Jin, Y. Power system harmonic detection based on second-order synchrosqueezing wavelet transform. Int. J. Power Energy Syst. 2018, 38, 144–151. [Google Scholar] [CrossRef]
- Fan, C.; Chen, D.; Fan, L. Research of two phase flow signal denoising based on fractional wavelet transform. In Proceedings of the 2018 IEEE 7th Data Driven Control and Learning Systems Conference (DDCLS), Enshi, China, 25–27 May 2018; pp. 698–703. [Google Scholar]
- Nan, W.; Zhao, H. A Variable Step Size LMS Adaptive Filtering Algorithm Based on Maximum Correntropy Criterion for Identification of Low Frequency Oscillation Modes. IFAC-PapersOnLine 2019, 52, 163–167. [Google Scholar] [CrossRef]
- Raman, L.K.; Gopal, Y.; Birla, D.; Lalwani, M. Effect of fault classification and detection in transmission line using wavelet detail coefficient. Int. J. Comput. Aided Eng. Technol. 2022, 17, 288. [Google Scholar] [CrossRef]
- Benzi1, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A Math. Gen. 1981, 14, L453. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Marchesoni, F.; Menichella-Saetta, E.; Santucci, S. Stochastic Resonance in Bistable Systems. Phys. Rev. Lett. 1989, 62, 349–352. [Google Scholar] [CrossRef]
- Gang, H.; Nicolis, G.; Nicolis, C. Periodically forced Fokker–Planck equation and stochastic resonance. Phys. Rev. A 1990, 42, 2030–2041. [Google Scholar] [CrossRef]
- Huang, D.; Yang, J.; Zhang, J.; Liu, H. An improved adaptive stochastic resonance with general scale transformation to extract high-frequency characteristics in strong noise. Int. J. Mod. Phys. B 2018, 32, 1850185. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Wu, J. SSR detection method based on normalized adaptive stochastic resonance. In Environmental Science and Information Application Technology; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Han, D.; Su, X.; Shi, P. Weak Fault Signal Detection of Rotating Machinery Based on Multistable Stochastic Resonance and VMD-AMD. Shock Vib. 2018, 2018, 4252438. [Google Scholar] [CrossRef]
- Hong-Yan, X.; Wei, X. The neural networks method for detecting weak signals under chaotic background. Acta Phys. Sin. 2007, 56, 3771–3776. [Google Scholar] [CrossRef]
- Kumar, P.; Narayanan, S.; Gupta, S. Bifurcation analysis of a stochastically excited vibro-impact Duffing-Van der Pol oscillator with bilateral rigid barriers. Int. J. Mech. Sci. 2017, 127, 103–117. [Google Scholar] [CrossRef]
- Hou, J.; Yan, X.P.; Li, P.; Hao, X.H. Weak wide-band signal detection method based on small-scale periodic state of Duffing oscillator. Chin. Phys. B 2018, 27, 030702. [Google Scholar] [CrossRef]
- Liu, X.C.; Li, P.P. Weak Signal Detection Based on the Nonlinear Dynamic Model. Appl. Mech. Mater. 2012, 157, 887–891. [Google Scholar] [CrossRef]
- Zhao, H.; Lin, Y.; Dai, Y. Hidden Attractors and Dynamics of a General Autonomous van der Pol-Duffing Oscillator. Int. J. Bifurc. Chaos 2014, 24, 1450080. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, Y.; Zhang, X. Weak signal detection based on Mathieu-Duffing oscillator with time-delay feedback and multiplicative noise. Chaos Solitons Fractals 2020, 137, 109832. [Google Scholar] [CrossRef]
- Hu, N.; Wen, X. The application of Duffing oscillator in characteristic signal detection of early fault. J. Sound Vib. 2003, 268, 917–931. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, S. Application of van der Pol–Duffing oscillator in weak signal detection. Comput. Electr. Eng. 2015, 41, 1–8. [Google Scholar]
- Yang, Q.; Dong, K.; Song, J.; Jin, F.; Mo, W.; Hui, Y. A Weak Signal Detection Method Based on Memristor-Based Duffing-Van der pol Chaotic Synchronization System. In Proceedings of the 13th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 4–7 June 2021. [Google Scholar]
- Xiao, F.; Yan, G.; Zhang, X. Effect of signal modulating noise in bistable stochastic dynamical systems. Chin. Phys. 2003, 12, 946. [Google Scholar]
- Peter, J.; Peter, H. Amplification of small signals via stochastic resonance. Phys. Rev. A 1991, 44, 8032–8042. [Google Scholar]
- Yong, L.; Tai, W.; Yan, G.; Zhen, W. Study of the property of the parameters of bistable stochastic resonance. Acta Phys. Sin. 2007, 56, 30. [Google Scholar]
- Li, H.; Bao, R.; Xu, B.; Zheng, J. Intrawell stochastic resonance of bistable system. J. Sound Vib. 2004, 272, 155–167. [Google Scholar] [CrossRef]
- Yim, M.Y.; Liu, K.L. Linear response and stochastic resonance of subdiffusive bistable fractional Fokker–Planck systems. Phys. A Stat. Mech. Its Appl. 2006, 369, 329–342. [Google Scholar] [CrossRef]
- Guo, L.; Guang, W.; Jin, W.; Xue, W. A Novel Underwater Location Beacon Signal Detection Method Based on Mixing and Normalizing Stochastic Resonance. Sensors 2020, 50, 1292. [Google Scholar]
- Leng, Y.; Wang, T. Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise. Acta Phys. Sin. 2003, 52, 2432–2437. [Google Scholar] [CrossRef]
- Wang, M.J.; Zeng, Y.C.; Chen, G.H.; He, J. Nonresonant parametric control of Chen’s system. Acta Phys. Sin. 2011, 60, 10509. [Google Scholar] [CrossRef]
- Yue, L.; Bao, Y.; Yao, S. Chaos-based weak sinusoidal signal detection approach under colored noise background. Acta Phys. Sin. 2003, 52, 526. [Google Scholar] [CrossRef]

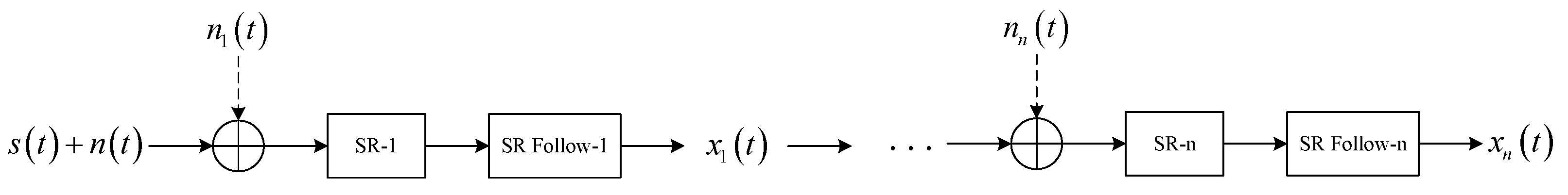










| Harmonic Order | Theoretical Value (Hz) | Detected Value (Hz) | SR Error (%) | VMD Error (%) | EEMD Error (%) | SST Error (%) |
|---|---|---|---|---|---|---|
| (a) SNR = −20 dB | ||||||
| 1 | 50 | 50 | 0 | 0.02 | 0.11 | 0 |
| 2.2 | 110 | 110 | 0 | 0.07 | 0.06 | 0.03 |
| 3 | 150 | 150 | 0 | 0.04 | 0.15 | 0.08 |
| 5 | 250 | 250 | 0 | 0.12 | 0.13 | 0.08 |
| 7 | 350 | 350 | 0 | 0.17 | 0.19 | 0.11 |
| (b) SNR = −30 dB | ||||||
| 1 | 50 | 50 | 0 | 0.12 | 0.32 | 0.07 |
| 2.2 | 110 | 110 | 0 | 0.17 | 0.43 | 0.11 |
| 3 | 150 | 150 | 0 | 0.23 | 0.39 | 0.19 |
| 5 | 250 | 250 | 0 | 0.27 | 0.51 | 0.28 |
| 7 | 350 | 350 | 0 | 0.43 | 0.71 | 0.29 |
| Harmonic Order | Actual Value/p.u. | Detection Value/p.u. | Relative Error/% |
|---|---|---|---|
| (a) SNR = 20 dB, Yang system | |||
| 1 | 1.0 | 1.0 | 0 |
| 2.2 | 0.15 | 0.15 | 0 |
| 3 | 0.25 | 0.25 | 0 |
| 5 | 0.2 | 0.2 | 0 |
| 7 | 0.1 | 0.1 | 0 |
| (b) SNR = 20 dB, Chen system | |||
| 1 | 1.0 | 1.0 | 0 |
| 2.2 | 0.15 | 0.15 | 0 |
| 3 | 0.25 | 0.25 | 0 |
| 5 | 0.2 | 0.2 | 0 |
| 7 | 0.1 | 0.1 | 0 |
| (c) SNR = −20 dB, Yang system | |||
| 1 | 1.0 | 1.0 | 0 |
| 2.2 | 0.15 | 0.15 | 0 |
| 3 | 0.2498 | 0.25 | 0 |
| 5 | 0.2 | 0.2 | 0 |
| 7 | 0.1 | 0.1 | 0 |
| (d) SNR = −20 dB, Chen system | |||
| 1 | 1.0 | 1.0 | 0 |
| 2.2 | 0.15 | 0.15 | 0 |
| 3 | 0.25 | 0.25 | 0 |
| 5 | 0.2 | 0.2 | 0 |
| 7 | 0.1 | 0.1 | 0 |
| (e) SNR = −60 dB, Yang system | |||
| 1 | 1.0 | 1.0 | 0 |
| 2.2 | 0.15 | 0.15 | 0 |
| 3 | 0.25 | 0.25 | 0 |
| 5 | 0.2 | 0.2 | 0 |
| 7 | 0.1 | 0.1 | 0 |
| (f) SNR = −60dB, Chen system | |||
| 1 | 1.0 | 1.0000122 | 0.00122 |
| 2.2 | 0.15 | 0.1499985 | 0.001 |
| 3 | 0.25 | 0.25 | 0 |
| 5 | 0.2 | 0.2000036 | 0.0018 |
| 7 | 0.1 | 0.0999898 | 0.0102 |
| (g) SNR = −100 dB, Yang system | |||
| 1 | 1.0 | 1.00207 | 0.207 |
| 2.2 | 0.15 | 0.14983 | 0.113 |
| 3 | 0.2498 | 0.25127 | 0.508 |
| 5 | 0.2 | 0.19972 | 0.14 |
| 7 | 0.1 | 0.09981 | 0.19 |
| (h) SNR = −100 dB, Chen system | |||
| 1 | 1.0 | 1.0204031 | 2.0403 |
| 2.2 | 0.15 | 0.1517132 | 1.1421 |
| 3 | 0.25 | 0.2449147 | 2.0341 |
| 5 | 0.2 | 0.2040105 | 2.0053 |
| 7 | 0.1 | 0.0966392 | 3.3608 |
| Detection Value/s | Monitoring Center Data Value/s | |||
|---|---|---|---|---|
| First | Second | First | Second | |
| (a) Disturbance moment | ||||
| Experimental data | 0.2992 (+) | 1.6021 (+) | 0.3 (+) | 1.6 (+) |
| 0.4998 (−) | 1.8968 (−) | 0.5 (−) | 1.9 (−) | |
| Detection Value/p.u. | Monitoring Center Data Value/p.u. | |||
| First | Second | First | Second | |
| (b) Voltage fluctuation | ||||
| Experimental data | 0.3504 (+) | 0.1849 (+) | 0.348 (+) | 0.186 (+) |
| 0.1129 (−) | 0.1062 (−) | 0.112 (−) | 0.107 (−) | |
| Detection Value/s | Monitoring Center Data Value/s | |||
|---|---|---|---|---|
| First | Second | First | Second | |
| (a) Disturbance moment | ||||
| Experimental data | 0.2992 (+) | 1.6007 (+) | 0.3 (+) | 1.6 (+) |
| 0.5001 (−) | 1.8993 (−) | 0.5 (−) | 1.9 (−) | |
| Detection Value/p.u. | Monitoring Center Data Value/p.u. | |||
| First | Second | First | Second | |
| (b) Voltage fluctuation | ||||
| Experimental data | 0.3491 (+) | 0.1853 (+) | 0.348 (+) | 0.186 (+) |
| 0.1121 (−) | 0.1072 (−) | 0.112 (−) | 0.107 (−) | |
| Method | Window Interpolate FFT | VMD | EEMD | Empirical Wavelet Transform | Single-Trap Stochastic Resonance | Yang System | Chen System |
|---|---|---|---|---|---|---|---|
| Time taken (s) | 1.032 | 2.3814 | 7.5216 | 2.0105 | 0.4393 | 1.0492 | 1.1377 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Qi, X.; Yuan, Z.; Tang, X.; Li, Z. Detection of Weak Fault Signals in Power Grids Based on Single-Trap Resonance and Dissipative Chaotic Systems. Electronics 2023, 12, 3896. https://doi.org/10.3390/electronics12183896
Sun S, Qi X, Yuan Z, Tang X, Li Z. Detection of Weak Fault Signals in Power Grids Based on Single-Trap Resonance and Dissipative Chaotic Systems. Electronics. 2023; 12(18):3896. https://doi.org/10.3390/electronics12183896
Chicago/Turabian StyleSun, Shuqin, Xin Qi, Zhenghai Yuan, Xiaojun Tang, and Zaihua Li. 2023. "Detection of Weak Fault Signals in Power Grids Based on Single-Trap Resonance and Dissipative Chaotic Systems" Electronics 12, no. 18: 3896. https://doi.org/10.3390/electronics12183896
APA StyleSun, S., Qi, X., Yuan, Z., Tang, X., & Li, Z. (2023). Detection of Weak Fault Signals in Power Grids Based on Single-Trap Resonance and Dissipative Chaotic Systems. Electronics, 12(18), 3896. https://doi.org/10.3390/electronics12183896





