A Hierarchical Control Strategy Based on Dual-Vector Model Predictive Current Control for Railway Energy Router

Abstract

The multiport and multidirectional energy flow of railway energy routers (RERs) poses a significant challenge when integrating photovoltaic (PV) systems and energy storage systems (ESSs). To address this issue, this paper proposes an improved hierarchical control strategy for RERs with a reference signal generation layer and an inverter control layer. In the reference signal generation layer, a time-segmentation energy allocation strategy based on a state machine is proposed to manage the multidirectional energy flow in RERs resulting from PV systems and ESSs while minimizing peak power demand. In the inverter control layer, a dual-vector model predictive current control (MPCC) strategy is designed for back-to-back inverters. The dual-vector MPCC strategy eliminates the need for individual PWM blocks, thereby enhancing RER current-tracking accuracy and efficiency. The prominent advantage of the dual-vector MPCC strategy is its ability to achieve high current-tracking accuracy while minimizing active power losses. Simulations and hardware-in-the-loop experiments are conducted to validate the feasibility and effectiveness of the proposed method.

1. Introduction

Railways have become a crucial component of the national economy, with China’s railways operating over 150,000 km, including 40,000 km of high-speed railways. Electrified railways commonly utilize traction transformers to convert three-phase grid AC voltage into a single-phase AC-27.5 kV traction power supply system. However, this unique configuration leads to issues such as negative-sequence current and power factor. The energy demand for electrified railways is large. For instance, the total electricity consumption in 2022 alone was as high as 787 billion kWh [1]. To achieve the vision of “carbon neutrality”, it becomes pragmatic to optimize the energy structure of electrified railways and seamlessly integrate new energy sources. On the other hand, electrified railways generate massive regenerative braking energy (RBE) during operation [2]. Unrecycled RBE directly flows to the upstream power grid, which not only leads to a large amount of energy waste but also causes power quality deterioration in the upstream power grid [3,4]. Consequently, enhancing the recovery and reuse rate of RBE emerges as a potent strategy for achieving energy conservation, emission reduction, and the optimization of the energy consumption structure.

To handle these issues, railway energy routers (RERs), which integrate both photovoltaic (PV) systems and energy storage systems (ESSs) into the traction power supply system via back-to-back converters, have been proposed [5,6]. Most of the existing RER research mainly focuses on RER topology [7,8,9], compensation principle [10,11,12], or energy allocation strategy [13,14,15], while fewer studies have delved into the realm of control strategies. Most of these studies have traditionally focused on conventional RERs that lack integration with PV systems and ESSs. However, the multiport and multidirectional energy flow of RERs necessitates a fresh perspective when integrating PV systems and ESSs. Traditional control methods can no longer satisfy the RER requirements. Consequently, the adoption of a layered approach involving energy allocation strategies and device control layers becomes imperative.

For energy allocation, the scheme proposed in [5,13] integrates PV systems with the DC link of back-to-back converters, offering the capability to absorb new energy locally and enhance the flexibility and reliability of the traction power supply system. But these research studies only discuss the architecture design and lack in-depth research on energy management. Deng et al. [6,10,11] propose methods to recycle RBE by integrating ESSs into the DC link of back-to-back converters. These methods solve the problem that RBE returns to the upstream grid when surplus energy exists. But these research studies only discuss the case of integrating ESSs alone. These methods are not suitable for the case of integrating PV systems and ESSs together. The purposes of an energy allocation strategy are peak shaving and valley filling, which in turn reduce the electricity bill. Many of the aforementioned studies employ a traditional peak-shaving energy allocation strategy, capable of reducing energy charges but not both energy charges and power demand charges.

For device control, as a core component of RERs, the control of back-to-back converters determines the quality of RERs. The control methods for converters mainly include the following: (1) Hysteresis control [16,17,18,19], which has a large tracking error and large current ripple. (2) Proportional–integral (PI) control [20], which is simple and easy to use but has large overshoot during the DC-side voltage transition stage and a slow response speed. The steady-state tracking error of the AC-side compensation current is large, which causes errors between the active power/reactive power of back-to-back converter compensation and the reference command value. (3) Proportion resonance (PR) control [21,22], which requires a fundamental wave controller and multiple harmonic controllers and increases the economic cost. (4) Sliding-mode variable structure control [23], which can achieve the fast and accurate tracking of the compensation current but is prone to chattering. The model predictive control technology has been widely used in grid-connected converter control in recent years because of its simple principle, no modulation unit, high robustness, good current-tracking effect, and strong applicability in various nonlinear systems [24,25]. Therefore, this paper designs a dual-vector model predictive current control (MPCC) strategy for back-to-back converters.

To solve the problem of the multiport and multidirectional energy flow of RERs when PV systems and ESSs are integrated, this paper proposes an improved hierarchical control strategy with a reference signal generation layer and a converter control layer.

In the reference signal generation layer, a time-segmentation energy allocation strategy is proposed to solve the multidirectional energy flow brought by PV systems and ESSs, as well as to reduce the maximum power demand.

In the converter control layer, a dual-vector MPCC strategy for back-to-back converters that has flexible control and does not need a separate PWM block is presented. The method improves the current-tracking accuracy and efficiency of RERs.

The remainder of this paper is organized as follows: The structure of RERs is introduced in Section 2. The four operation modes and the time-segmentation energy allocation strategy are analyzed in Section 3. An improved hierarchical control strategy for RERs with a reference signal generation layer and a converter control layer is constructed in Section 4. Simulation verification and HIL experiments are presented in Section 5. Finally, the conclusion is presented in Section 6.

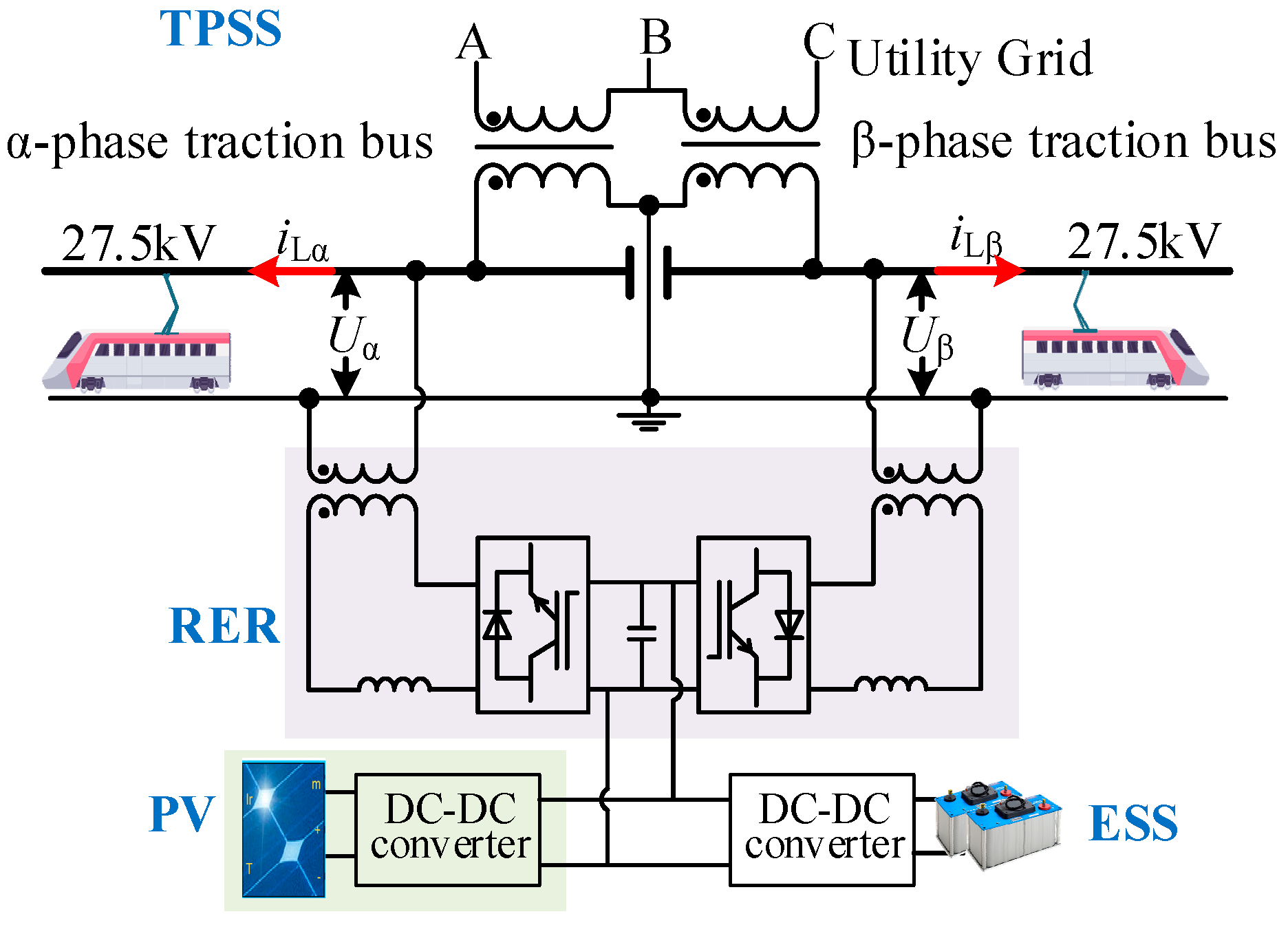
2. System Structure of RERs

The topology of RERs is illustrated in Figure 1. Two-phase traction buses with 27.5 kV voltage are connected to a three-phase grid through a V/V traction transformer. The back-to-back inverter is composed of two single-phase voltage source inverters (VSC_α/VSC_β), whose AC sides are connected to the traction buses via step-down transformers T_α and T_β, respectively. The inverters are interconnected by a buffer capacitor on the DC side. The PV system and ESS are integrated into the traction power supply system through the back-to-back inverter’s DC bus.

3. Results of Operating Modes and Time-Segmentation Energy Allocation Strategy for RERs

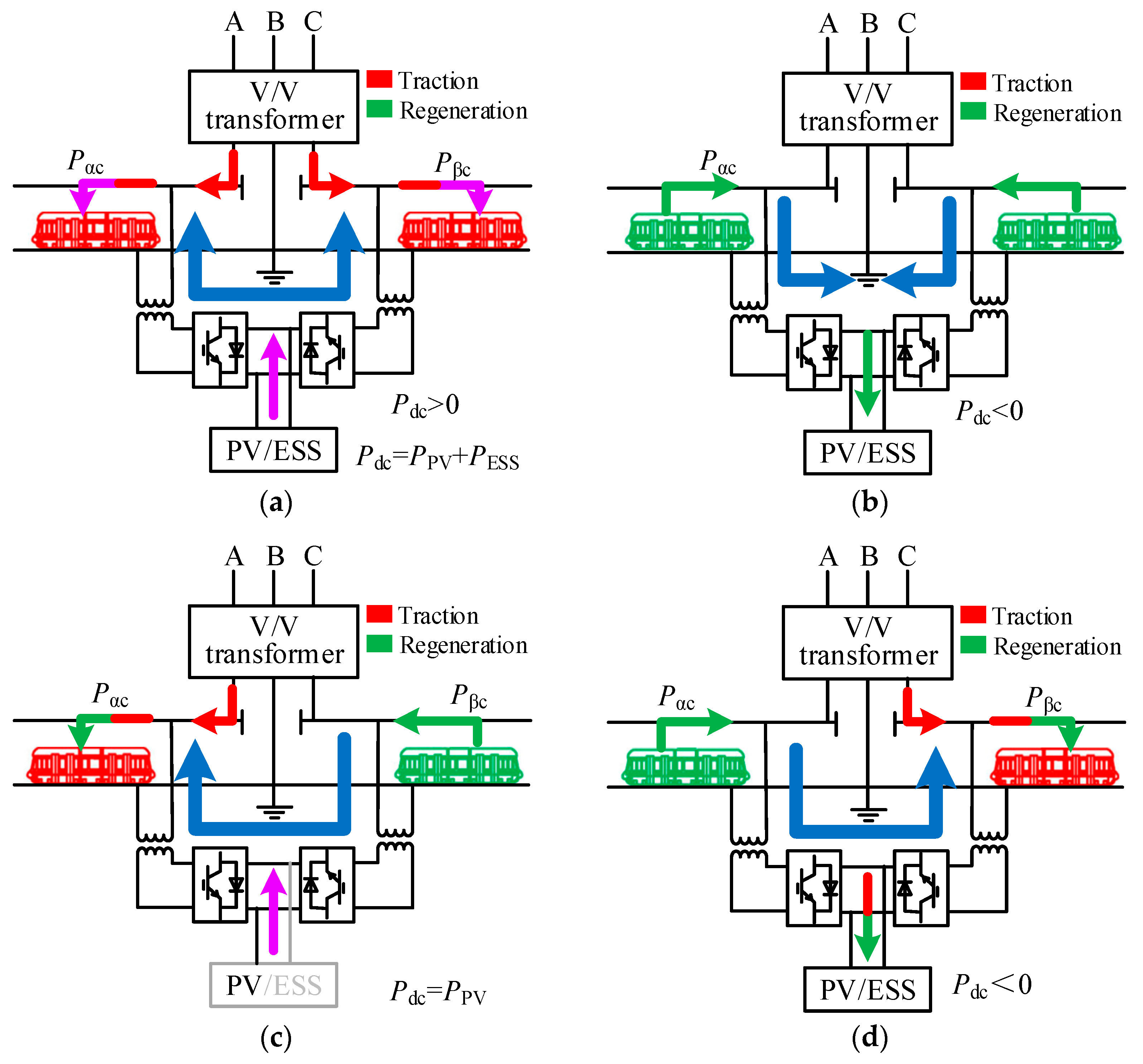
3.1. Four Operating Modes of RERs

As shown in Figure 1, many uncertain factors lead to the complexity of energy flow, e.g., whether the two feeder loads are in traction state or in regenerative braking state, whether the PV system is in working state or not, whether the ESS is charging or discharging. For ease of analysis, four typical modes are summarized in Figure 2.

P_g represents the active power of the upstream utility grid; P_PV represents the power generated by the PV system; P_ESS represents the power of the ESS regardless of charging or discharging; P_Lα, P_Lβ denote the active power of α/β traction loads, respectively; P_cα and P_cβ (Q_cα and Q_cβ) denote the active (reactive) power compensated by VSC_α and VSC_β, respectively; SOC_min, SOC_max denote the upper and lower state-of-charge (SOC) limits of the ESS, respectively. P_H represents the value of peak-clipping power. P_low represents the value of valley-filling adjustment power.

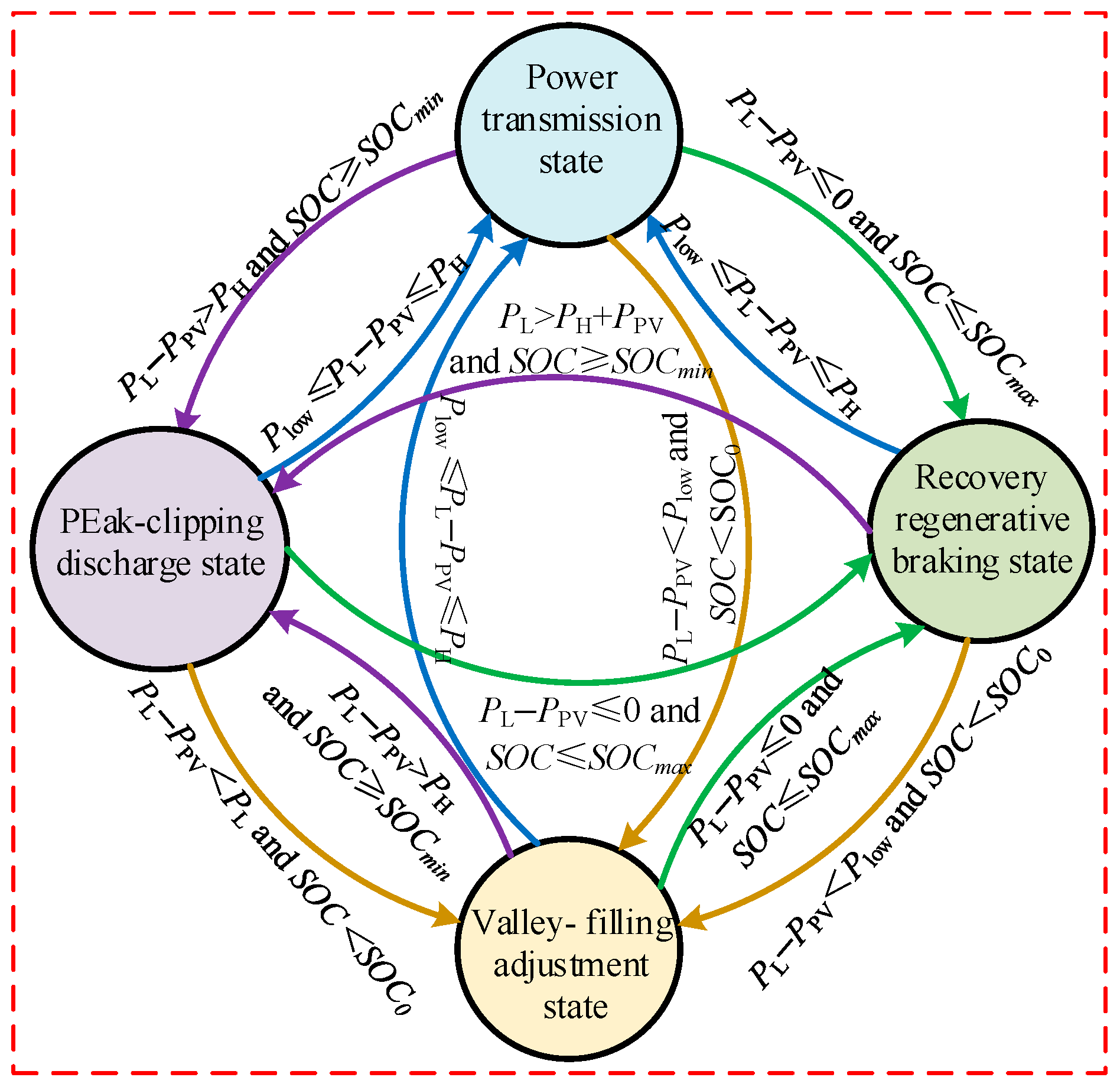
• Mode 1: peak-clipping discharge state. In this situation, the loads satisfy (P_Lα + P_Lβ − P_PV) ≥ P_H, and the ESS satisfies SOC > SOC_min. Then, the ESS is in discharge state. The power generated by the PV system or ESS is distributed to both traction buses through the RER. Then, a certain amount of active power is transferred from one traction bus to the other to achieve power balance. Meanwhile, the reactive power of each bus is independently compensated.
• Mode 2: recovery regenerative braking state. As shown in Figure 2, the loads meet (P_Lα + P_Lβ − P_PV) < 0, and the ESS satisfies SOC < SOC_max. The ESS enters the charging state. RBE is first absorbed by the load on the same traction bus, and the remaining part is transferred to the other traction bus to be absorbed by the RER. Then, the unconsumed RBE is absorbed by the ESS, and the part that cannot be absorbed is fed back to the upstream utility grid. The energy generated by the PV system is first absorbed by the load, and the excess energy is absorbed by the ESS (if the ESS is still capable), otherwise it is discarded.
• Mode 3: power transmission state. In this scenario, the ESS does not work. The SOC of the ESS exceeds the effective threshold, or the loads meet P_low ≤ (P_Lα + P_Lβ − P_PV) < P_H, whether in traction state or in regenerative braking state.
• Mode 4: valley-filling adjustment state. In this mode, the loads meet 0 ≤ (P_Lα + P_Lβ − P_PV) < P_low. Specifically, if the instantaneous SOC(t) is less than the initial SOCSOC (SOCSOC₀), the ESS enters the charging state, otherwise it enters the standby state. The SOC values should be the same during the alternation of the daily cycle to keep the ESS continuously working.

3.2. Time-Segmentation Energy Allocation Strategy

The energy allocation strategy is the optimal approach to solve the control problem of the multiport and multidirectional energy flow when the PV system and the ESS are integrated in an RER. In China, railways have a two-part tariff policy. To reduce the electricity tariff, this subsection proposes a time-segmentation energy allocation strategy, which divides the 24 h into peak-shaving-valley-filling mode, and maximum demand mode. The peak-shaving-valley-filling mode uses lower peak–valley values to minimize the energy charge. The maximum demand mode uses higher peak–valley values to reduce the demand as much as possible, thus reducing the power demand charge. As shown in Figure 3, the time-segmentation energy management strategy is divided into the following three steps:

• Data processing: This step involves initializing variables, detecting data, and calculating the traction load. The initialized variables include the threshold values of the SOC (SOC_min, SOC_max), the initial value of the SOC (SOC₀), the rated capacity of the inverter (S_max), and the maximum discharge power of the ESS (P_BM).
• Judge mode: First, based on the historical measured data, the time period, t ∈ (t₁, t₂), in which the maximum demand is probable to appear is estimated and set as the maximum demand mode. Then, different peak-valley values are set for the maximum demand mode, and the peak-shaving-valley-filling mode, respectively.
• Judge state: Based on the instantaneous power of the traction load and PV system, and the instantaneous SOC(t) of the ESS, as well as the peak and valley values obtained in the previous step, the system operation status is judged in real time. Specifically, it is divided into peak-clipping discharge state, recovery regenerative braking state, power transmission state, and valley-filling adjustment state. The specific judgment process is shown in Figure 3, and the transition relationships among different operation states are shown in Figure 4.

4. Hierarchical Control Strategy

The dual intermittency and volatility of PV sources and traction load cause difficulties in system control. Employing an energy allocation strategy is an effective way to solve this problem. This paper constructs a hierarchical control strategy for RERs, as shown in Figure 5, which is divided into reference signal generation layer and converter control layer. To achieve the stable operation of the three-port system of an RER, one port needs to work in master mode to stabilize the DC bus voltage and maintain the energy balance of the RER, while the remaining ports work in slave mode to manage their own output power and complete the corresponding power flow scheduling tasks. In this paper, the ESS works in master mode, and the PV system and the converters on both sides work in slave mode.

4.1. Reference Signal Generation

At the reference signal generation layer, the energy storage output is first calculated based on the time-segmentation energy allocation strategy shown in Figure 3. Then, the reference power of the RER is calculated based on the compensation principle [5].

Finally, according to second-order generalized integrator (SOGI), the αβ0 stationary reference frame is fabricated on the single-phase inverter. After coordinate transformation, the active power and reactive power of the single-phase voltage source converter in the dq0 rotating reference frame can be expressed as

$$[P Q]=[e_d{i}_d e_d{i}_q]$$

(1)

Therefore, the reference-current instructions of the back-to-back inverter can be obtained and are

$$i_{\mathrm{c}\mathsf{\alpha }\mathrm{ref}}=\sqrt{2}\left(\frac{P_{\mathrm{c}\mathsf{\alpha }\mathrm{ref}}}{U_{\mathsf{\alpha }}}\right)\sin (\omega t)+\sqrt{2}\left(\frac{Q_{\mathrm{c}\mathsf{\alpha }\mathrm{ref}}}{U_{\mathsf{\alpha }}}\right)\cos (\omega t)$$

(2)

$$i_{\mathrm{c}\mathsf{\beta }\mathrm{ref}}=\sqrt{2}\left(\frac{P_{\mathrm{c}\mathsf{\beta }\mathrm{ref}}}{U_{\mathsf{\beta }}}\right)\sin (\omega t-\frac{\pi }{3})+\sqrt{2}\left(\frac{Q_{\mathrm{c}\mathsf{\beta }\mathrm{ref}}}{U_{\mathsf{\beta }}}\right)\cos (\omega t-\frac{\pi }{3})$$

(3)

where U_α and U_β denote the root-mean-square values of U_α and U_β, respectively.

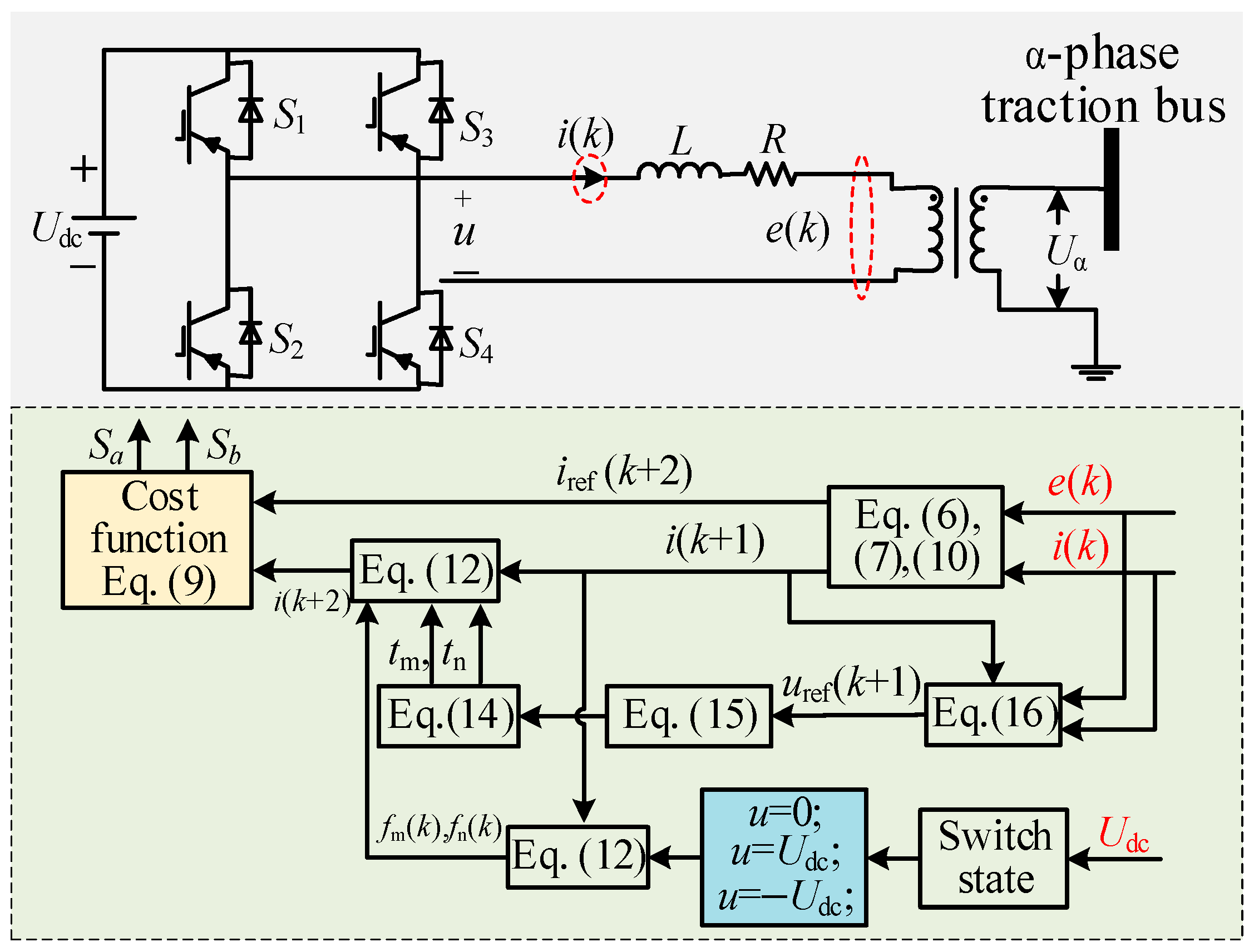
4.2. Modeling and Control of Back-to-Back Inverter

Due to the buffer effect of the intermediate DC capacitor, VSC_α/VSC_β of the back-to-back inverter can be controlled independently, even when active power exchange is present. This paper takes VSC_α as an example to design a current controller, because VSC_α and VSC_β have the same structure and function. A dual-vector MPCC strategy is proposed for back-to-back converters to accurately track the reference current and acquire stable and rapid control capability. The basic principle is to seek the voltage vector that minimizes the current-tracking error as the output voltage of the voltage source converter.

Figure 6 shows an equivalent circuit of the single-phase voltage source converter. L (R) denotes the inductor (resistor) of the circuit; u and i denote the output voltage and current of VSC_α, respectively; e denotes the output voltage of the grid.

Referring to Figure 6, the following equation can be obtained as

$$L\frac{di}{dt}=u-Ri-e$$

(4)

The current derivative in the continuous-time domain is described in Equation (4). Correspondingly, the current derivative in the discrete domain is replaced by the first-order forward Euler approximation method with a sampling period T_s, which can be expressed as follows:

$$\frac{di(k+1)}{dt}=\frac{i(k+1)-i(k)}{T_{\mathrm{s}}}$$

(5)

Then, in the discrete-time domain, the output current dynamics can be described as

$$i(k+1)=i(k)+\frac{T_{\mathrm{s}}}{L}\left[u(k)-e(k)-Ri(k)\right]$$

(6)

In MPCC, according to (6), the three different output voltages produced by VSC_α can predict three different future output currents. At each sampling time point, the voltage that minimizes the cost function is selected from three possible voltages as the output voltage. And the cost function is defined as the absolute error between the present current and the future reference current. Due to the cost function, the actual output current generated by the optimal output voltage is forced to approach the future reference current in the next step. The one-step future reference current (i_ref(k + 1)) can be calculated using the Lagrange extrapolation formula.

$$i_{\mathrm{ref}}(k+1)=3i_{\mathrm{ref}}(k)-3i_{\mathrm{ref}}(k-1)+i_{\mathrm{ref}}(k-2)$$

(7)

where i_ref(k) denotes the present reference current; i_ref(k − 1) denotes the one-step past reference current; i_ref(k − 2) denotes the two-step past reference current.

Due to the large amount of calculation for model predictive control, the control program has an unavoidable calculation delay in practice. Therefore, the output current of the one-step delay is obtained by dynamically moving the output current one step forward in (6), which can be described as shown in (8).

$$i(k+2)=i(k+1)+\frac{T_{\mathrm{s}}}{L}\left[u(k+1)-e(k+1)-Ri(k+1)\right]$$

(8)

where i(k + 2) denotes the two-step future current; u(k + 1) denotes three different possible voltage vectors output by VSC_α; considering that the grid voltage changes slowly, e(k + 1) is approximately equal to e(k), i.e., e(k + 1) ≈ e(k).

At every sampling instant, the cost function that evaluates the absolute errors between the two-step future reference current (i_ref(k + 2)) and the predicted output currents is described as

$$g=\left|i_{\mathrm{ref}}(k+2)-i(k+2)\right|$$

(9)

Also, i_ref(k + 2) can be calculated using the Lagrange extrapolation formula.

$$i_{\mathrm{ref}}(k+2)=3i_{\mathrm{ref}}(k+1)-3_{\mathrm{ref}}(k)+i_{\mathrm{ref}}(k-1)$$

(10)

Due to the fact that VSC_α can only produce three different output voltages (i.e., u_out1 = 0; u_out2 = U_dc; u_out3 = −U_dc), a large current error is generated. And the delay compensation increases the current error and distortion. Although current with high-quality waveforms and smaller errors can be achieved by increasing the sampling frequency, a greater cost is needed in practice. Therefore, this paper proposes a dual-vector MPCC strategy that considers all possible future combinations produced by two voltages of VSC_α (i.e., (u_out1, u_out1), (u_out1, u_out2), (u_out1, u_out3), (u_out2, u_out1), (u_out2, u_out2), (u_out2, u_out3), (u_out3, u_out1), (u_out3, u_out2), (u_out2, u_out2)).

The sampling period is assigned to two variable time intervals, corresponding to the first and second voltages in a voltage combination. At every sampling instant, the error between the actual current and the reference current is reduced by changing the variable time interval. The virtual voltage can be expressed as

$$u_{mn}=\frac{t_{\mathrm{m}}}{T_s}{u}_{\mathrm{out}m}+\frac{t_{\mathrm{n}}}{T_s}{u}_{\mathrm{out}n}$$

(11)

where u_outm, u_oun (m, n = 1, 2, 3) denote three different possible output voltages, respectively; t_m and t_n correspond to the working time of the first voltage (u_outm) and the second voltage (u_outn) during the kth sampling period, respectively, satisfying t_m + t_n = T_s.

Therefore, another way of expressing the two-step future output current is

$$i(k+2)=i(k+1)+f_{\mathrm{m}}(k)t_m+f_n(k)t_n$$

(12)

where f_m(k) and f_n(k) denote the derivatives of the output current produced by the first voltage (u_outm) and the second voltage (u_outn) during the kth sampling period, respectively. They can be expressed as

$$f_j(k)=\frac{u_{\mathrm{out}j}-e(k)-Ri(k+1)}{L},j\in (m,n)$$

(13)

To simplify the algorithm, modulation model predictive control is used to calculate the vector application time. The basic idea is that the larger the objective function corresponding to the corresponding vector, the larger the control error. Therefore, its action time should be as short as possible. The distribution of t_m and t_n satisfies

$$\{\begin{array}{l}{t}_m=\frac{G_n}{G_m+G_n}{T}_s\\ t_n=\frac{G_m}{G_m+G_n}{T}_s\end{array}$$

(14)

where G_m and G_n denote the voltage cost function of the first voltage (u_outm) and the second voltage (u_outn) during the kth sampling period, respectively, which are defined as

$$G_p=\left|u_{ref}(k+1)-u_{outp}\right|,p\in (m,n)$$

(15)

where u_ref(k + 1) denotes the one-step future reference voltage value, which can be calculated using the deadbeat algorithm as

$$u_{\mathrm{ref}}(k+1)=\frac{L\left[i_{\mathrm{ref}}(k+2)-i(k+1)\right]}{T_{\mathrm{s}}}+Ri(k+1)+e(k+1)$$

(16)

According to (11) and (14)~(16), the virtual vector that minimizes Equation (9) can be solved; then, dual-vector MPCC can be realized.

Figure 6 describes the flow diagram of the dual-vector MPC method.

Comparing the conventional MPCC strategy and the dual-vector MPC method, Figure 7 shows the output current waveforms of VSC_α with the same sampling frequency. It can be seen that steady-state current error and current ripple can be reduced by utilizing the dual-vector MPC method without increasing the sampling frequency.

4.3. Control of DC/DC Converter

ESSs play an important role in balancing power and adjusting the DC bus voltage for RERs. In this paper, the voltage outer loop is used to generate a reference value for the current inner loop to maintain DC bus voltage stability and manage the charge and discharge of the ESS, as shown in Figure 5b.

Because the output characteristics are influenced by the environment and climate, a PV system should have two modes: maximum power point tracking (MPPT) mode and non-working mode. To effectively use renewable energy, it generally works in MPPT mode. However, when the environmental factors change so that the PV system cannot continuously supply power, the working mode is turned to non-working mode. The DC/DC converter control structure of the PV system is shown in Figure 5c.

5. Analysis of Simulations and Experiments

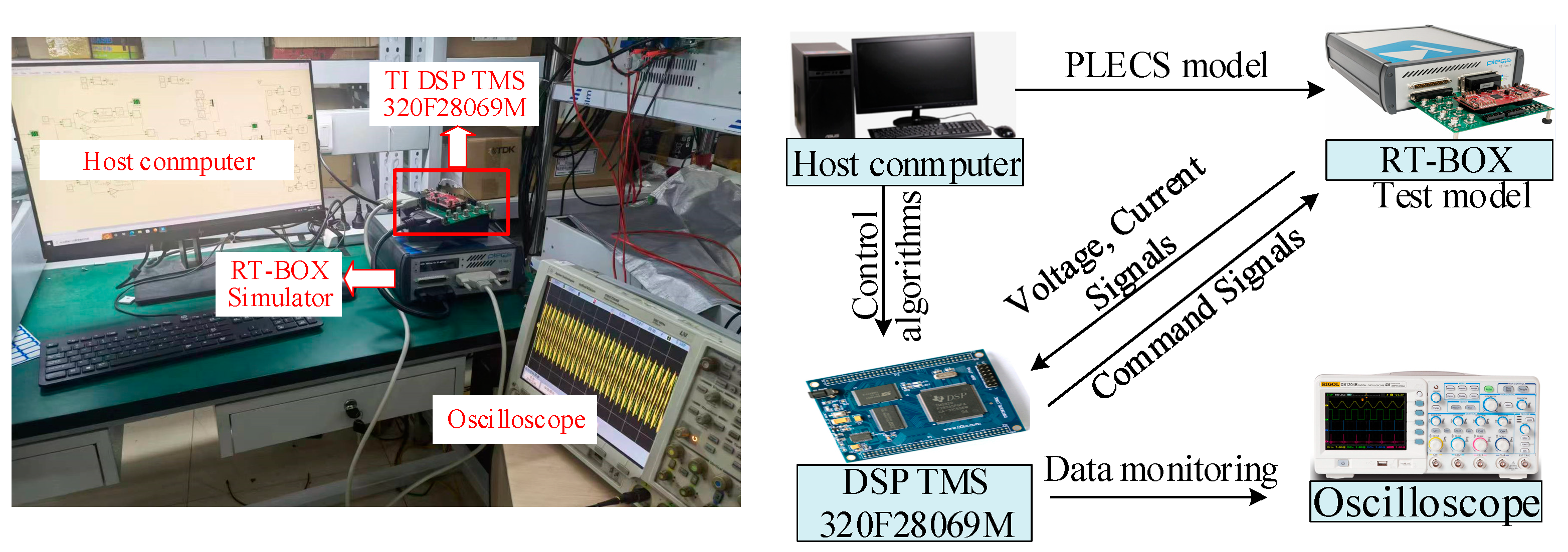
5.1. HIL Experimental Verification

In this section, to verify the correctness and effectiveness of the proposed method, an HIL simulation platform consisting of a real controller (TMS320F28335 DSP) and a virtual controlled object is built, as depicted in Figure 8. An RER model and a traction power supply system model are both implemented in the RT-BOX simulator using PLECS software 4.7.5. The voltage and current signals of the converter are transmitted to the DSP controller through the A/D conversion unit. Then, the hierarchical control strategy presented in Section 4 is implemented using the DSP controller. Finally, the control signals are transmitted to the built RER from the D/A conversion unit to the control converters.

In this subsection, the data of four typical moments are selected to constitute two dynamic operating conditions to verify the correctness of the proposed dual-vector MPCC strategy. The HIL platform parameters are specified in

Table 1. HIL experimental parameters.

Item	Parameter	Value
Three-phase power grid	Phase-to-phase voltage (kV)	220
	Short-circuit capacity (MVA)	2000
V/V transformer	Transformer ratio (kV/kV)	220/27.5
Back-to-back inverter	Transformer ratio (kV/kV)	27.5/2
	Nominal capacity (MVA)	12
	DC bus voltage (V)	4000
ESS	Energy storage medium type	Lithium–iron–phosphate battery
	Nominal capacity (kWh)	1000
	Nominal power (MVA)	10
PV system	Nominal power (MVA)	5

.

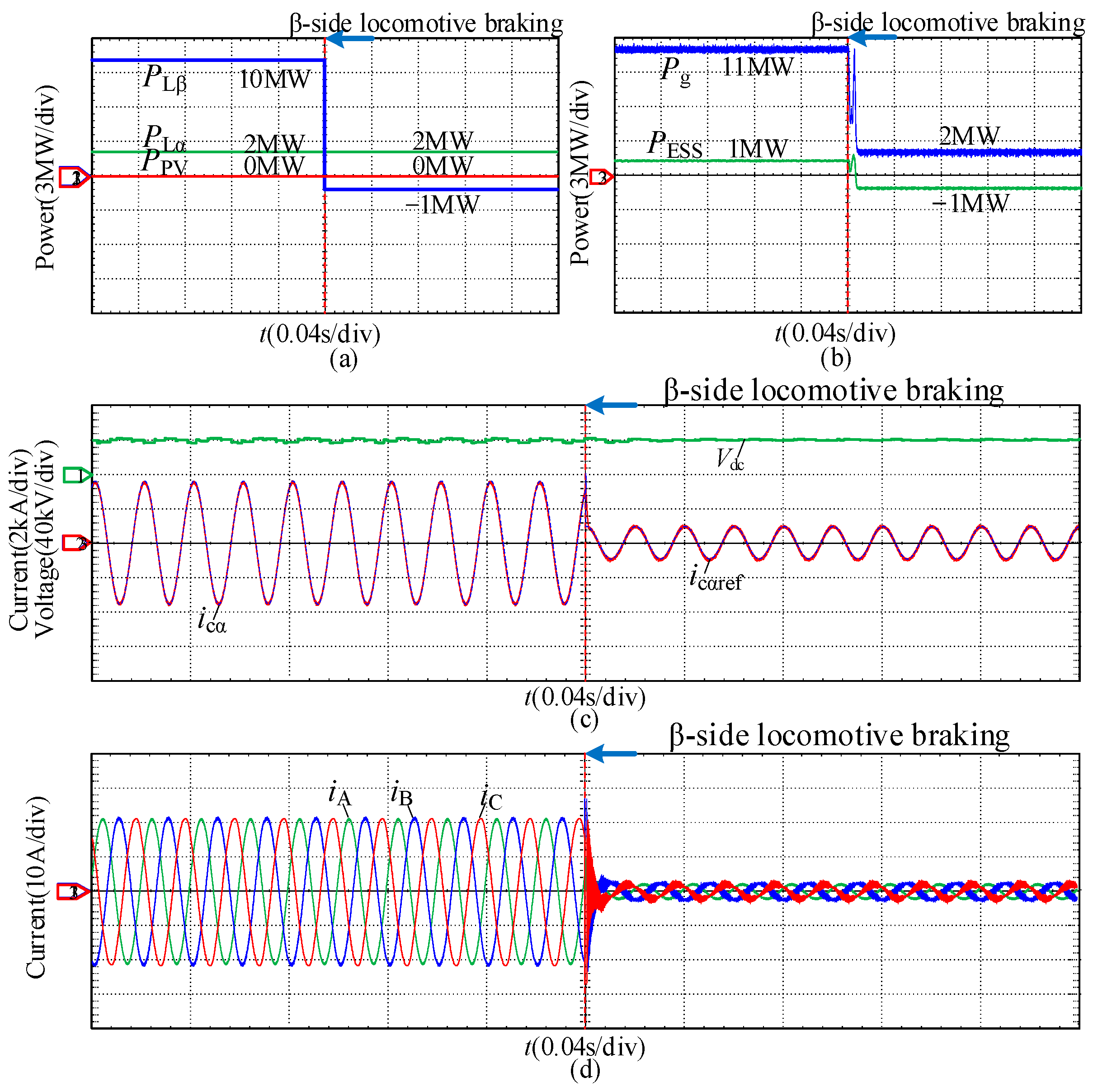
• Power transmission state and recovery regenerative braking state: The experimental waveforms are described in Figure 9.

Before β-side locomotive braking, the loads are −1 MW and 7 MW, respectively, and the system is in power transmission state. The 1 MW active power generated by the PV system is absorbed; the ESS does not work; and the consumption of the upper-grid power is 5 MW. After β-side locomotive braking, the load changes to −1 MW, and the system is in recovery regenerative braking state. The ESS is in charging state, absorbing the regenerative braking energy of the two traction buses. The 1 MW active power generated by the PV system is directly absorbed by the ESS, and no energy is fed back to the upper grid. The DC bus voltage of the RER introduced in Figure 9c remains around its reference value, which ensures the normal operation of the RER. The result of converter α tracking the reference current shows that the dual-vector MPC method can ensure the accurate tracking of current. As shown in Figure 9d, when the RER works in power transmission state, the grid-side currents of the traction transformer are almost symmetric; when the RER works in recovery regenerative braking mode, the primary-side currents of the traction transformer almost become 0.

2.

Peak-clipping discharge state and valley-filling adjustment state: The experimental waveforms are described in Figure 10.

Before β-side locomotive braking, the loads are 2 MW and 10 MW, respectively, and the system is in peak-clipping discharge state. The ESS is in discharging state, providing 1 MW active power to the traction bus; the PV system does not work; and the consumption of the upper-grid power is equal to the preset peak value (11 MW). After β-side locomotive braking, the load changes to −1 MW, and the system is in valley-filling adjustment state. The ESS is in charging state, acting as a load and consuming 1 MW active power, absorbing the regenerative braking energy of the two traction buses. The whole system consumes upper-grid power equal to the preset valley value (2 MW). The DC bus voltage of the RER introduced in Figure 10c remains around its reference value, which ensures the normal operation of the RER. The result of converter α tracking the reference current shows that the dual-vector MPC method can ensure the accurate tracking of current. As shown in Figure 10d, the grid-side currents of the traction transformer are almost symmetric.

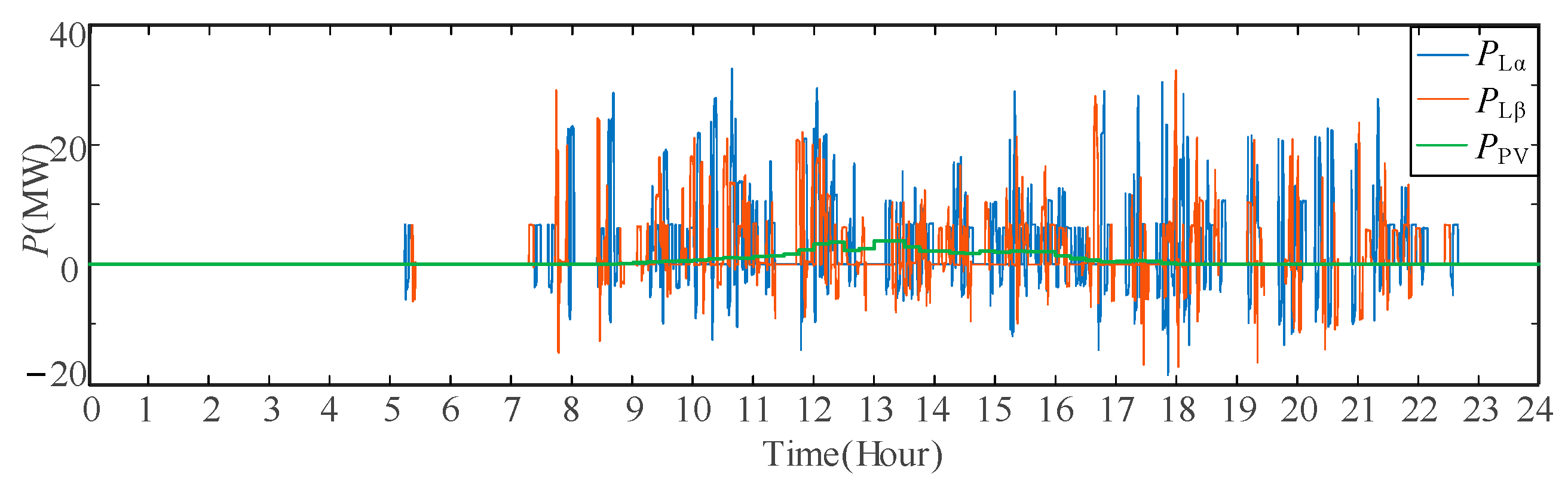
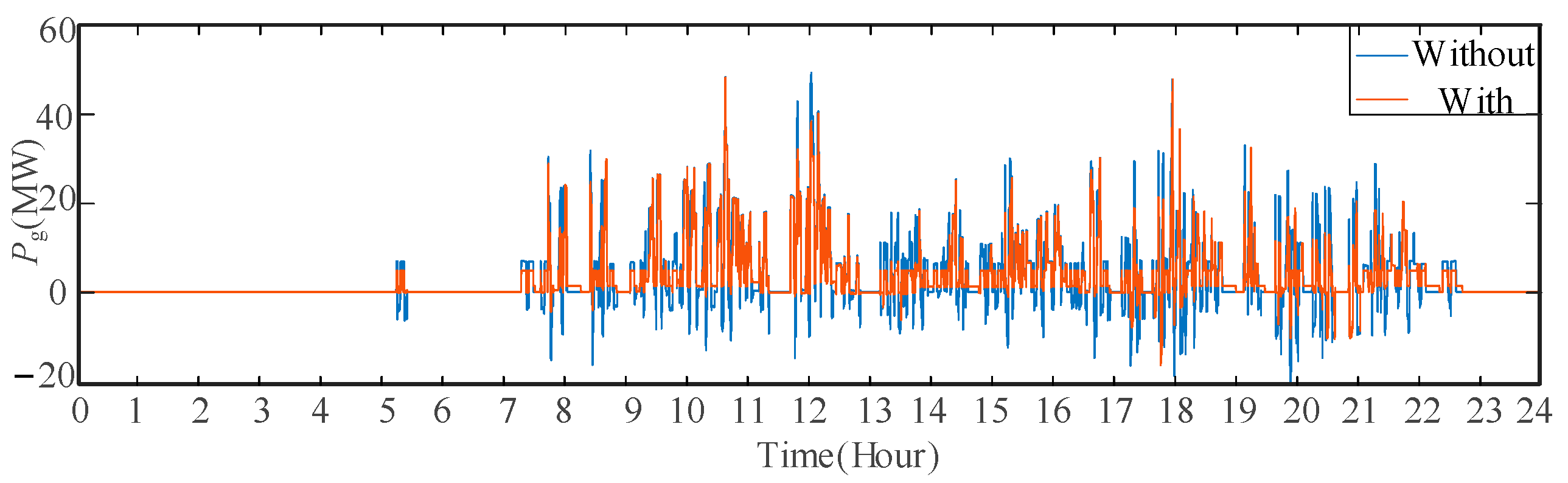
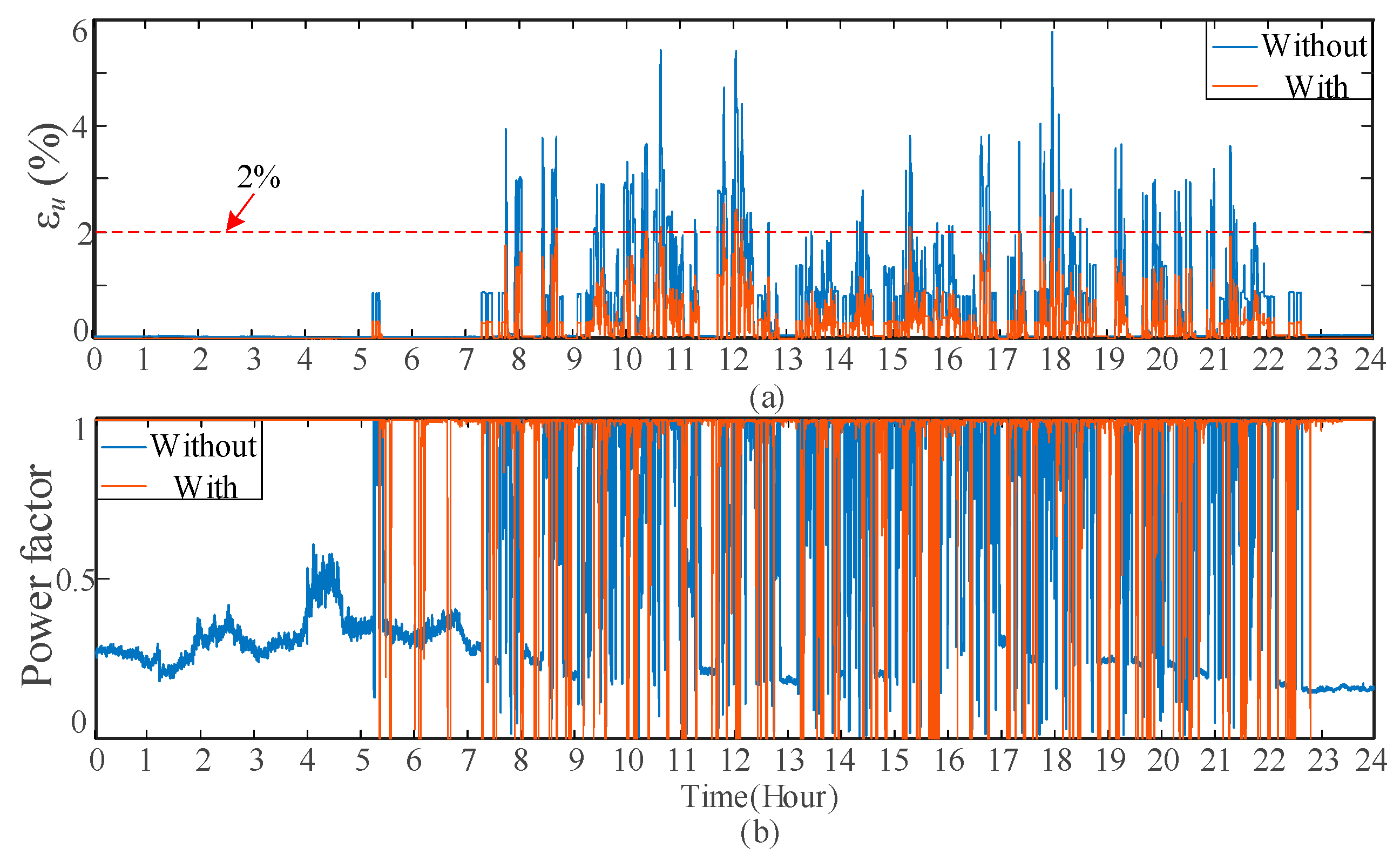
5.2. Typical Daily Measured Load Data Verification

Considering the daily periodicity of train operation, this section selects the typical daily measured load data of a traction substation in a high-speed railway section (sampling interval: 1 s/time). Correspondingly, the PV system selects the measured power generation data of the PV power station near the traction substation during a typical summer day (sampling interval: 1 min/time) to further evaluate the engineering capability of the RER.

Figure 11 shows typical daily field data of a traction substation. The traction load of the two arms is quite different, and 16.27 MWh RBE is returned to the upstream grid every day, accounting for 19.82% of the traction energy. It means that the traction substation is suitable for installing an RER system.

Based on a professional economic analysis, the specific parameters of the RER system are as follows: the rate capacity of the RER is 11 × 2 MVA; the capacity of the ESS battery is 1000 kWh; and the PV installed capacity is 1 MWp.

Figure 12 shows the changes in total active power on the traction side without and with RER deployment. Thanks to the addition of a PV system and an ESS, the power consumed by the traction is obviously decreased after RER deployment. The total traction power is reduced from 85.1 MWh to 71.8 MWh, and its rate of decrease is 15.63%. The energy recovery efficiency of RBE is 86.81%. The consumption of the PV system is 5.45 MWh, and the consumption rate is 68.76%.

Figure 13 shows the instantaneous SOC of the ESS. The SOC does not exceed the limit and can be restored to SOC₀ during the alternation of the day cycle, ensuring ESS state consistency.

In Figure 14, it is easily inferred that the voltage imbalance degree shows an overall downward trend after RER deployment, and its 95% probability value decreases from 2.83% to 1.24%, which meets the 2% international standard. On the other hand, without RER deployment, the probability of the instantaneous power factor being equal to 1 is 33.89%, while with RER deployment, it is 75%. The power factor shows an overall increasing trend, and the average value rises from 0.61 to 0.91.

5.3. Comparison with Previous Works

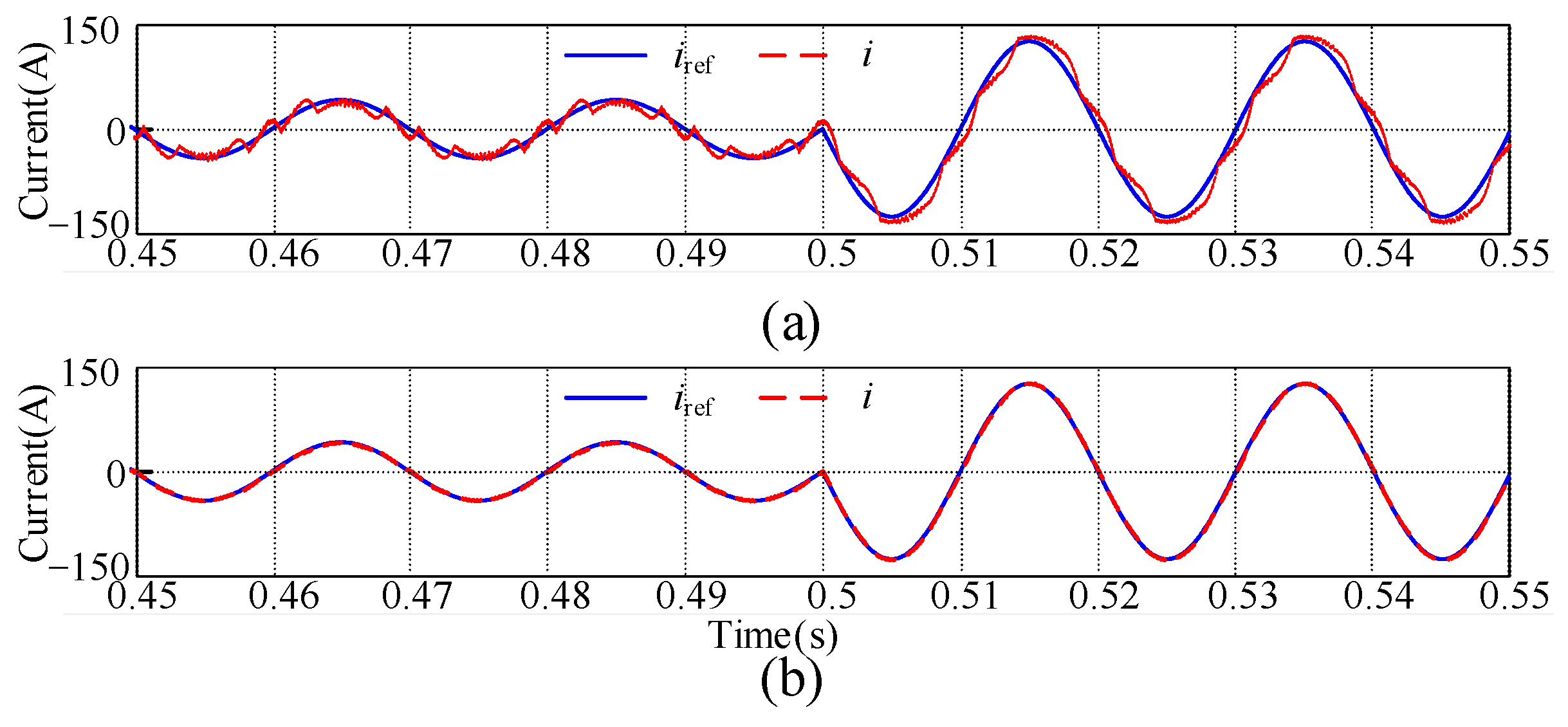
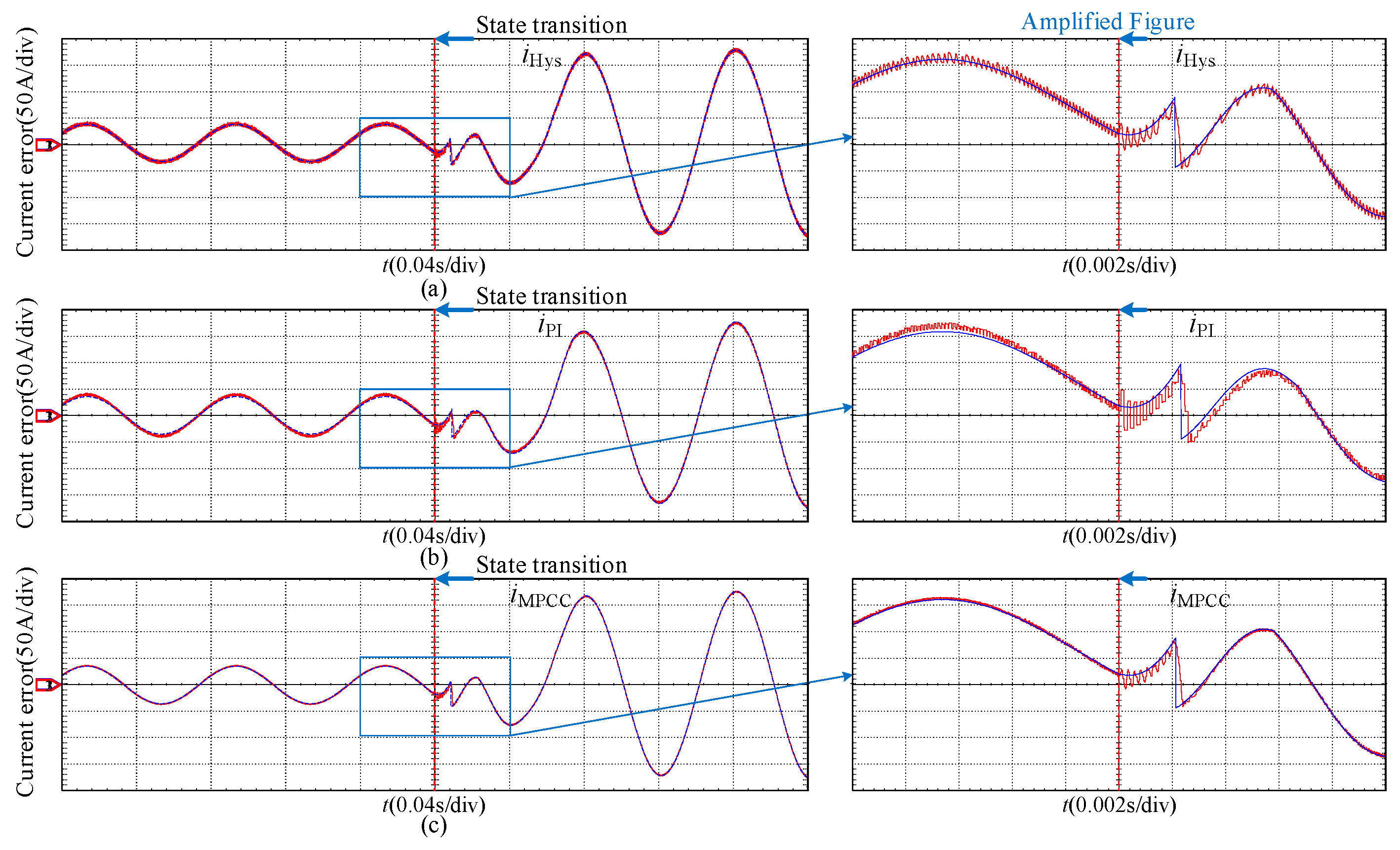
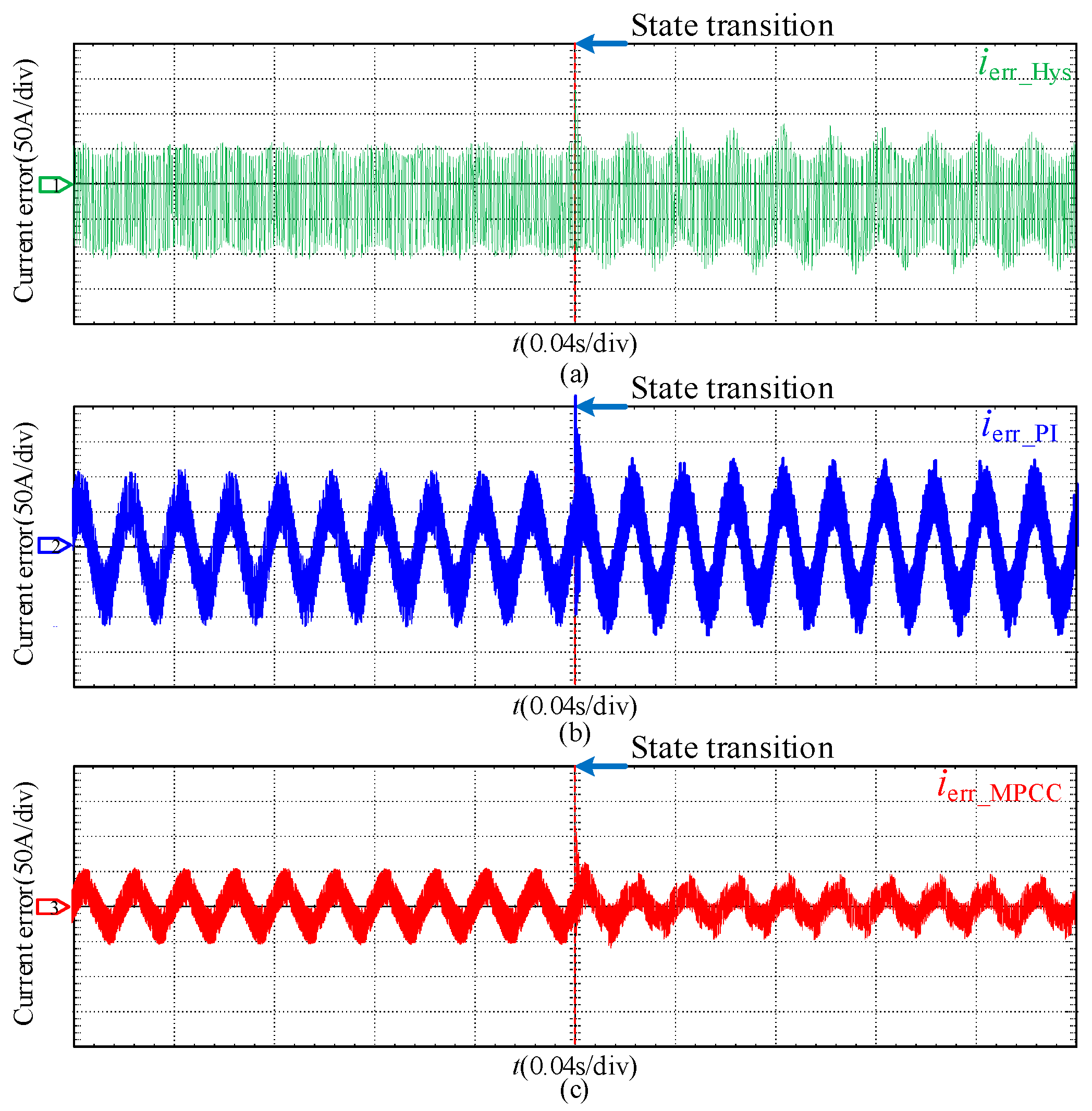
• Comparison of different control strategies: hysteresis control [16,17,18,19], PI control [20], and the proposed dual-vector MPCC strategy. The specific operating conditions involve transitioning from recovery regenerative braking state to peak-clipping discharge state. Figure 15 illustrates the current of inverter α following the application of three different control strategies. It can be observed that during transient processes, when employing the proposed dual-vector MPCC strategy, there is high precision in tracking the reference current with minimal current deviation. Figure 16 shows the current-tracking error when three different control strategies are adopted for converter α. It can be observed that the current error is minimized when employing the dual-vector MPCC strategy. Therefore, the current-tracking error can be employed effectively, and current-tracking accuracy can be improved by using the proposed dual-vector MPCC strategy.
• Comparison of the proposed time-segmentation energy allocation strategy with the previous strategy:

  Table 2. Simulation results with different energy allocation strategies.

  Scheme	Device Capacity		Threshold		RBE Utilization Rate (%)	PV Absorption Rate (%)	Power Quality		Maximum Demand with/without Access (MW)
  	BTB-RER (MVA)	ESS (kWh)	Peak PH (MW)	Valley Plow (MW)			95% εu *	Power Factor
  Without any devices	---	---	---	---	---	---	2.83	0.61	21.23
  traditional peak-shaving energy allocation strategy [7,10]	11 × 2	1000	4.74	1.42	87.46	68.69	1.21	0.908	20.06 (↓5.51%)
  The proposed time-segmentation energy allocation strategy	11 × 2	1000	4.74 29.4 (11–13 h)	1.42 2.37 (11–13 h)	86.81	68.76	1.24	0.91	19.03 (↓10.36%)

  * The 95% probability value of voltage imbalance degree.

  shows the simulation results with different energy allocation strategies. With the time-segmentation energy management strategy, the power demand reduction rate increases from 5.51% to 10.36% with the same RBE recovery rate, PV consumption rate, and power quality improvement effect. The results suggest that the time-segmentation energy allocation strategy proposed in this paper can simultaneously reduce the maximum demand and PV consumption, and recover regenerative braking energy, as well as improve power quality.

6. Conclusions

In this paper, a hierarchical control strategy for RERs is proposed. The feasibility and effectiveness of the proposed scheme are verified with the analysis of typical scenarios, comparative studies, and field cases. The paper is concluded as follows.

(1) This paper proposes an improved hierarchical control strategy with a reference signal generation layer and a converter control layer that realize on-site consumption of PV energy, RBE recycling and reuse, and peak shaving and valley filling on the grid side to stabilize grid load fluctuations. Meanwhile, power quality problems such as reactive power compensation and negative-sequence voltage imbalance are solved.

(2) Compared with the existing PI control and hysteresis control, the dual-vector MPCC strategy of back-to-back converters for RERs has high current-tracking accuracy and low active power loss. Additionally, it has flexible control and does not need a separate PWM block.

(3) The simulation of typical daily measured load data validate that the proposed time-segmentation energy allocation strategy can achieve peak shaving and valley filling, as well as reduce maximum power demand.

The fact is that with the installed capacity of ESSs, the recovery rate of RBE and the utilization rate of PV systems increase, but this brings more problems, such as cost and site selection. Hence, how to optimally configure the installed capacity of ESSs to maximize the benefits is another research focus.