Abstract
The Proportional-Integral-Derivative (PID) controller, a fundamental element in industrial control systems, plays a pivotal role in regulating an extensive array of controlled objects. Accurate and rapid adaptive tuning of PID controllers holds significant practical value in fields such as mechatronics, robotics, and automatic control. The three parameters of the PID controller exert a substantial influence on control performance, rendering the tuning of these parameters an area of significant interest within related research fields. Numerous tuning techniques are widely employed to optimize its functionality. Nonetheless, their adaptability and control stability may be constrained in situations where prior knowledge is inadequate. In this paper, a multi-phase focused PID adaptive tuning method is introduced, leveraging the deep deterministic policy gradient (DDPG) algorithm to automatically establish reference values for PID tuning. This method constrains agent actions in multiple phases based on the reward thresholds, allowing the output PID parameters to focus within the stable region, which provides enhanced adaptability and maintains the stability of the PID controller even with limited prior knowledge. To counteract the potential issue of a vanishing gradient following action constraints, a residual structure is incorporated into the actor network. The results of experiments conducted on both first-order and second-order systems demonstrate that the proposed method can reduce the tracking error of a PID controller by 16–30% compared with the baseline methods without a loss in stability.
1. Introduction
In this section, the characteristics and control methods of PID controllers are introduced, leading to the introduction of the methods for controlling PID controllers using reinforcement learning. Related works are also discussed here. Finally, the main contributions are summarized in light of the above content.
1.1. Motivation
PID controllers are widely used in industrial process control, with over 90% of applications relying on this simple yet highly effective controller design [1,2]. PID controllers are typically designed by tuning the parameters , , and [3]. However, as linear controllers, PID controllers have limitations in achieving sophisticated control [4] because of parameter tuning often relying on the guidance of empirical data [5], which makes accurate PID parameter tuning difficult for complex systems. Developing adaptive parameter tuning PID controllers that can adapt to multiple task scenarios has become one of the key research topics in the field of control [6,7].
PID parameters can be optimized using two main methods: classical tuning methods and optimization methods [8,9]. Classical methods often rely on heuristic tuning or model construction to address specific engineering challenges [10]. However, these methods, such as the Ziegler–Nichols method [11] and the Cohen–Coon method [12], make assumptions about the underlying model or attempt to estimate the best approximation of the PID parameters [13]. Therefore, small deviations from the model assumptions may result in significant discrepancies between the predicted and actual system behavior. Optimization methods can obtain optimal PID parameters by precisely modeling the problem. Studies [14,15,16] show that optimization methods can obtain optimal PID parameters by accurately modeling the problem. Nevertheless, an accurate model is often difficult to obtain in practical engineering problems. As a consequence, developing PID adaptive tuning methods that can adapt to a wide range of task scenarios remains a major research challenge in the control field.
Neural network techniques, which provide a high-dimensional mapping relationship between inputs and outputs as supervised learning issues, are important techniques for PID adaptive tuning. Neural networks have been shown to outperform some other intelligent methods in terms of PID adaptive tuning [17,18]. However, again, collecting the right data labels can be challenging in actual engineering problems [19].
To address the limitations in supervised learning, this paper attempts to apply reinforcement learning (RL)—a model-free method—to PID adaptive tuning, as it allows agents to identify optimal behavior through trial-and-error interactions with the environment [20,21]. Unlike neural network methods, RL methods do not require labeled data; instead, agents interact with environments and modify their exploration policies through reward functions to find the optimal policy. Our goal is to utilize an agent that is allowed to explore freely in the environment to determine the optimal PID parameters without the use of an engineering model. However, the instability and windup phenomena [22] caused by the use of a truly random exploration are obviously unacceptable. Therefore, many studies guide the exploration of the agent by pre-setting empirical PID parameters based on engineering experience as reference values. In this work, the aim is to automatically establish and modify PID reference values throughout the execution process to ensure stability in the absence of prior knowledge. PID parameter tuning is characterized by its continuous correspondence with tracking performance [11] within the boundary conditions, where a small change in parameters does not cause a significant change in control effect. This feature provides guidance for balancing exploration and exploitation when using RL to solve the problem of PID adaptive tuning. When the PID output reaches a certain level of control, the agent’s policy is constrained and guided, which helps to further improve the performance of the PID controller without causing output oscillation.
1.2. Related Works
Recently, RL-based methods have been widely applied in the field of PID parameter tuning. The authors of [23] proposed the application of RL to PID controller design to improve the performance of agents in OpenAI, and the average total number of control steps per episode from episode 5000 to episode 6000 was reduced by more than 5%. The authors of [24] developed an RL-based PID tuning method called continuous actor–critic learning automata (CACLA) for human-in-the-loop physical assistive control. In another study [25], the authors addressed the problem of simultaneously outputting multiple parameters in PID controllers based on an RL framework. Ref. [26] proposed an expert agent-based system based on RL for self-adapting multiple low-level PID controllers in mobile robots.
Nevertheless, in the above-cited works, the agent’s policy is more focused on exploration in the early phases of iteration, resulting in excessive PID output amplitude and integral saturation, which can destabilize the system. Aiming at the closed-loop stability of RL-based PID tuning methods, the authors of [27] expressed a PID controller as a shallow neural network of the actor network, and improved the stability of the PID controller. The results show that the moving average of the number of time steps per episode before the PI controller was reduced by nearly 50%. Ref. [10] proposed an RL-based stability-preserving PID adaptive tuning framework that guarantees the controller’s stability in the entire closed-loop process and found that this approach reduced the MSE tracking error by more than 10% compared with other methods. However, this method requires a known set of PID parameters as reference values to guide the agent’s exploration. Ref. [19] initialized all the PID parameters to 0 without prior knowledge based on simultaneous calculation of the policy and value function using the RBF network, but this method lacks universality as the network topology is tailored to a specific system.
Based on the analysis presented above, the aim of our research is to develop an RL-based PID adaptive tuning framework that can be applied to various systems with limited prior knowledge while ensuring PID controller stability and improved tracking performance. To mitigate the risk of instability, this paper intends to regulate the action of the agent by constraining its exploration, drawing inspiration from the theory of constraint reinforcement learning [28]. This is achieved by imposing instantaneous constraints on the agent’s actions, a technique for which a theoretical framework has been proposed in the literature [29]. By incorporating explicitly constrained or softly penalized constraint violations [30], the agent can achieve the desired result while avoiding unstructured exploration.
1.3. Main Contributions
In this work, a multi-phase focused deep deterministic policy gradient (MF-DDPG) framework for PID adaptive tuning was proposed. The method ensures the stability of the PID controller in the closed-loop system under limited prior knowledge conditions by focusing on the agent actions in phases, while achieving fast convergence performance and better control effect. The main contributions of our work can be summarized as:
- To balance exploration and exploitation in RL-based PID adaptive tuning, a multi-phase focused PID parameter adaptive tuning framework was proposed based on RL. To ensure the agent’s output PID parameters remain within the stable region, the agent’s action exploration is constrained to remain close to a corresponding reference value of the PID parameters during each phase, a reference value that is then adjusted when the agent performance satisfies a preset reward threshold condition. In this framework, the PID parameter search space is continuously refined from coarse to fine across the training phases, leading to a near-monotonic improvement in the PID parameters’ performance.
- To solve the problem of obtaining a reference value for PID adaptive tuning under the constraint of limited prior knowledge, a mechanism to automatically determine a reference value of the PID parameters was introduced in the multi-phase focusing process. At each phase, the agent automatically establishes a reference value of the PID parameters based on the current phase’s reward threshold and explores within a certain range around this reference value. The reference values established in different phases provide a baseline for the tracking performance of the PID controller, ensuring that the PID controller continuously focuses on improving control performance. The proposed method achieves impressive control performance without prior knowledge of the precise reference values of the PID parameters.
- To address the challenge of a vanishing gradient, which can arise when constraining the output of the actor net of the proposed algorithm, a residual structure was added to the actor net. After applying multi-phase action constraints, the numerical space of the output for the actor net in RL is compressed, leading to a small range of output changes that may cause the gradient to vanish during back-propagation, hindering agent exploration. To overcome this issue, a residual structure was introduced from the shallow layer to the deeper layer of the actor net, preventing the gradient from vanishing and enabling the agent to maintain a certain level of exploration even after multiple action constraints.
1.4. Paper Organization
The outline of the paper is as follows. Section 2 describes the preliminary stages of our work. Section 3 is the description of the proposed MF-DDPG framework for adaptive PID tuning, and the stability maintaining mechanism of the framework. Section 4 provides the experimental results and analysis of the method. Section 5 is the conclusion of the work.
2. Preliminary Work
In this section, the principles and structure of PID controllers are introduced, as well as the foundational knowledge related to reinforcement learning algorithms. Building upon this foundation, the multi-phase focused framework is introduced and a detailed analysis is provided of its principles and workflow.
2.1. PID Control
PID controllers can be divided into two main types: series PID and parallel PID controllers [11]. In series PID controllers, the parameters are coupled, whereas in parallel PID controllers, the three PID parameters are decoupled. The latter approach offers easier tuning and wider applicability. Therefore, this paper primarily focuses on parallel PID controllers:
where is the difference between the setpoint and the output . Equation (1) represents the PID control system in continuous form; however, in many applications, PID controllers are stated in terms of discrete time conditions, as demonstrated in (2):
where and are the integrated and differentiated errors of a discrete PID controller, respectively, in which . This paper focuses on investigating PID controllers based on Equation (2) and more specifically, how to address the integral saturation issue during the adjustment of PID controllers. Actuator saturation is a common problem that can cause instability in PID controllers. When a PID controller saturates, it can become an open-loop system [27], causing system errors to accumulate and leading to a loss of stability known as “windup”. To mitigate the effects of windup, many studies have employed anti-windup techniques [22]. These techniques involve setting upper and lower bounds for the controller’s output to prevent the accumulation of integral terms by accounting for saturation, as shown below:
According to (3), when the output is lower than the lower bound, the controller will take as the output, and when the output is higher than the upper bound, it will take as the output. This may prevent a build up in the integrator incremental error accumulation [27]. Naturally, this is a fundamental technique for preventing integral saturation, and this paper will further develop it, as will be covered in more depth later.
2.2. Deep Deterministic Policy Gradient Algorithm
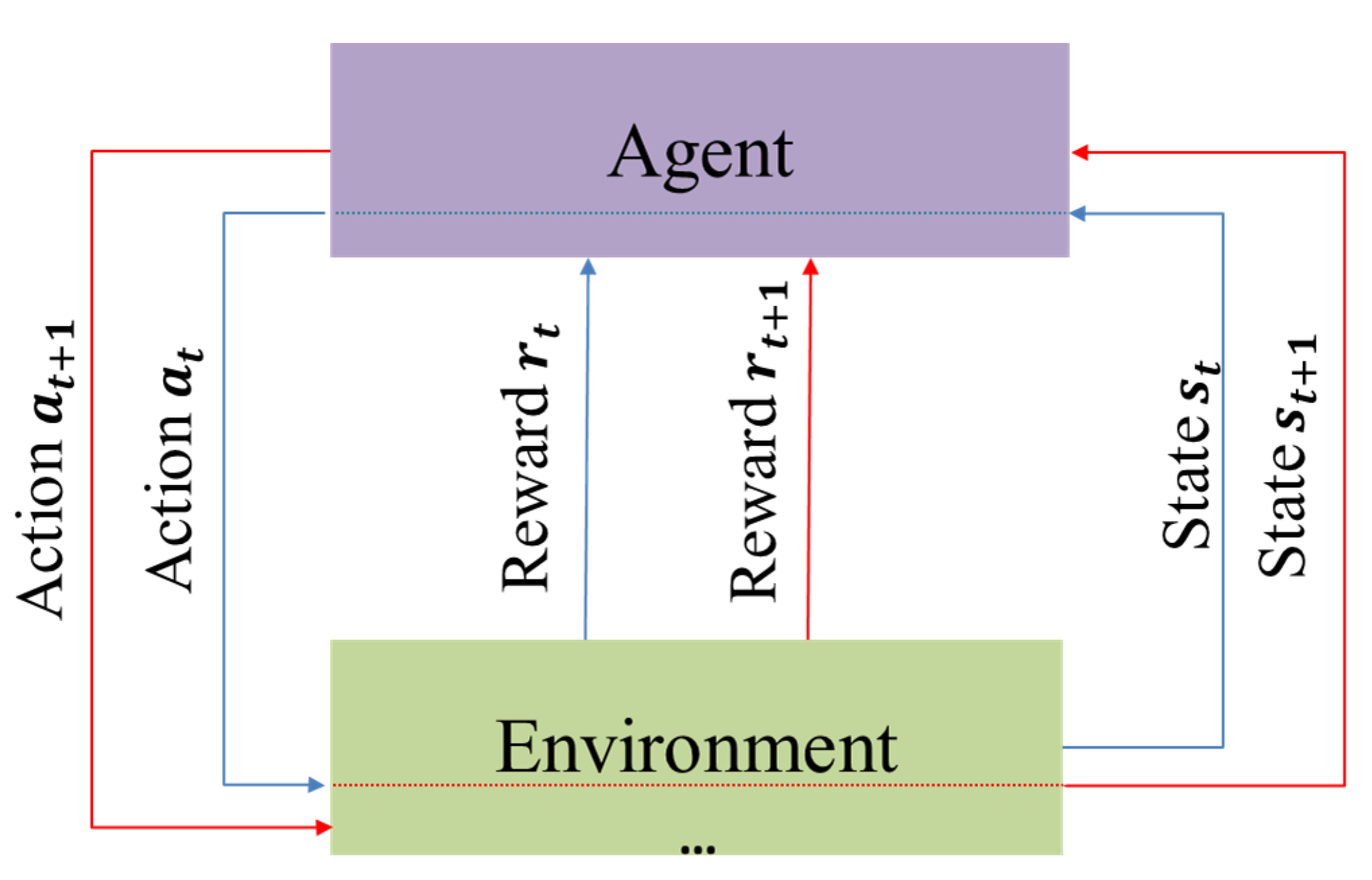
The Markov Decision Process (MDP) is the foundation of RL [31], which defines a mathematical model of sequential decision-making where the current state depends only on the preceding state and action [32]. The MDP definition is satisfied for PID tuning as the PID output error from the previous step is the input for the next step. RL consists of four components: state , action , policy, and reward . PID parameter tuning is equivalent to an agent’s random exploration of the environment, where various reward functions correspond to the outputs of different parameters. The policy maps the state and action to an action probability distribution , while the agent receives a reward for the action it took in the current state . The transition from one state to the next state occurs with a certain transition probability based on the action taken in the current state (Figure 1). Here, t represents the time step during an episode with a duration of T, where the agent takes one step at each time step. The , , and corresponds to the state, action, and reward values, respectively, resulting from the interaction between the agent and the environment at time t. The goal of RL is to maximize the return by identifying the optimal parameters.
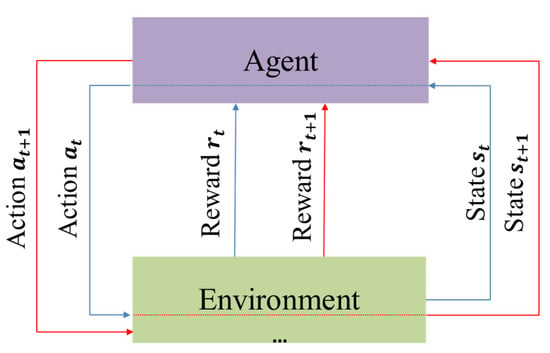
Figure 1.
Iterative interaction between agents and environments.
In the context of RL, a policy can be categorized into two forms: deterministic or stochastic. For the PID parameter tuning problem, the parameters output by the agent are in continuous vector form, making it more appropriate to use a deterministic policy [33]. Therefore, in the current work, the deep deterministic policy gradient (DDPG) algorithm was used as the foundation of the research framework. The paper defines the cumulative reward over a policy trajectory with a finite number of steps, and aims to maximize the expected cumulative discounted reward starting from a certain state:
where represents the trajectory of the sampled policy, is the discounted return starting at . In order to maximize , the policy is parameterized with and solved by a neural network. Equation (4) can be rewritten as
Through gradient ascent, the optimization objective becomes
where is the learning rate. A policy-based method provides a more direct solution than a value-based method. However, due to the strong randomness of the policy and significant variance in the network updating process, it can be difficult to obtain the best solution. To estimate the action value function, a critic network is used in a value-based optimization network. With parameterized value function approximation, the actor parameter is used for the policy network, while the critic parameter is used for the value network, forming an Actor–Critic (AC) structure. According to the policy gradient theorem [34], the policy parameters can be updated by following the gradient of the expected reward with respect to the policy parameters
where represents the value function of action in state [31,35]. For a deterministic policy given as , every action value is computed by
without sampling from stochastic policies, where is stochastic noise introduced to encourage exploration. The DDPG algorithm is commonly used to facilitate agent exploration in continuous action spaces. The algorithm establishes Q-value nets and corresponding target nets for the critic network, as well as policy nets and corresponding target nets for the actor network. To reduce correlations between samples, a replay buffer is utilized to store previously sampled data . For updating the networks’ parameters, a random batch N of transition experiences is selected from . Based on the method outlined in [33], the critic network is updated by minimizing the MSE loss of
where is computed by target nets. The actor network is updated by
The networks iteratively update the parameters according to (9) and (10) until convergence.
3. Multi-Phase Focused PID Adaptive Tuning with DDPG
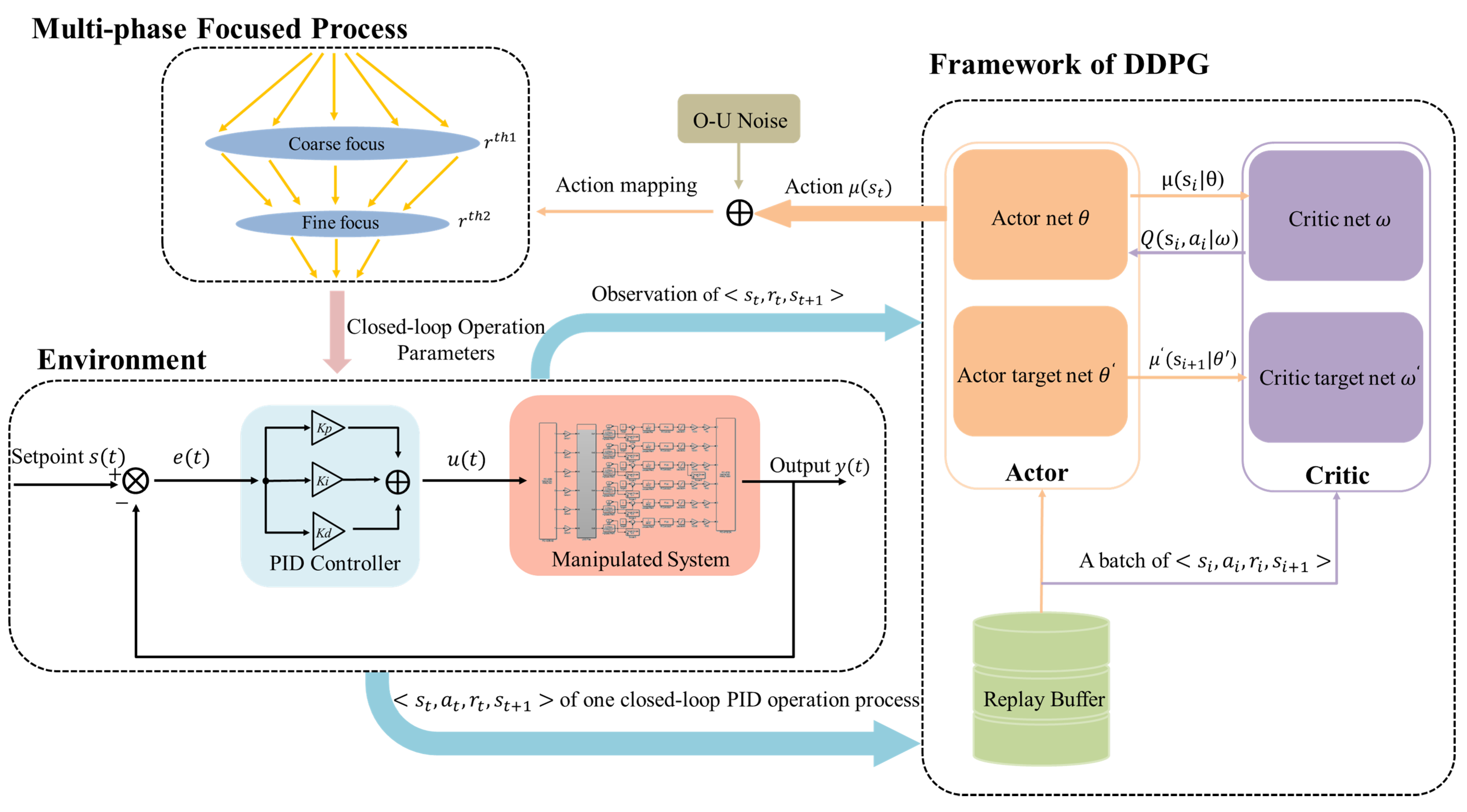
In this section, the methodology for utilizing MF-DDPG to automatically update the parameters of PID controllers is introduced and the proposed method for PID adaptive tuning using RL is described. Figure 2 illustrates the framework of the proposed method, showing the coupling mechanism between the PID controller and the multi-phase focused RL algorithm. The proposed method is based on multi-phase action constraints that restrict the agents’ exploration to a maximum within the stable region by imposing constraints and gradually focusing actions. This method requires only approximate knowledge of the PID parameters’ range, without the need to establish a reference value for them. The reference value is automatically determined along with the switching of the corresponding phases.
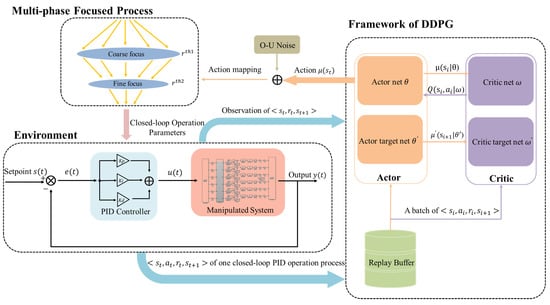
Figure 2.
Illustration of the multi-phase focused PID adaptive tuning with DDPG. The DDPG algorithm framework is the basis of the whole algorithm. The agent calculates through the actor net, determines whether the constraint condition of phase-switching is satisfied after action mapping, and outputs the corresponding action as PID control parameters. After the PID performs the whole closed-loop control process, the output tuple is stored in the replay buffer and the process enters the next episode.
- Environment and agent: The PID closed-loop control operation serves as the environment for the agent, and each step where the PID controller completes a full closed-loop control is an interaction between the agent and the environment. The resulting experience data are stored in the replay buffer. By iteratively learning the agent’s initial random exploration policy, RL aims to eventually learn the environment’s distribution and guide the agent’s exploration towards the optimal policy. To update the critic and actor networks, a set of experience data are randomly selected from the replay buffer every K iterations. The updated actor network then computes the next action based on the current state of the agent, which corresponds to the parameters of the subsequent PID closed-loop operation.
- State and action: The state represents the information obtained by the interaction between the agent and the environment. The agent obtains the reward by evaluating the current state . In the PID control problem, many studies [36,37] take the entire episodic trajectories of inputs and outputs of t-th closed-loop operationandas the state, where L represents the maximum number of time steps of the episodic trajectories. Yet this will introduce the problem of overly high-dimensional inputs to the RL networks. In another study [10], episodic data are described as a state customized to equal the time step, reducing the input dimension, but still potentially resulting in information redundancy. Our observations show that the early stages of the control process exhibit significant output fluctuations, while the output value stabilizes progressively towards the setpoint in the later stages, known as the tuning characteristic of PID control. To capture the impact of the episode’s setting, the time frame with the most pronounced output fluctuations was selected, representing the state of each episode with the first H steps of the closed-loop process. Additionally, in the early stages of exploration, the agent frequently explores the unstable interval of PID parameters, leading to excessive closed-loop operation amplitude and output oscillation, making the output oscillation in the first H steps more noticeable. To address this issue, the system’s output from the previous H steps was normalized and used as the state representation. This simplifies the agent state and reduces network dimension while preserving the observed environmental information. In each episode, the action is the episodic PID parameters , and action is used to guide the episodic PID closed-loop operation.
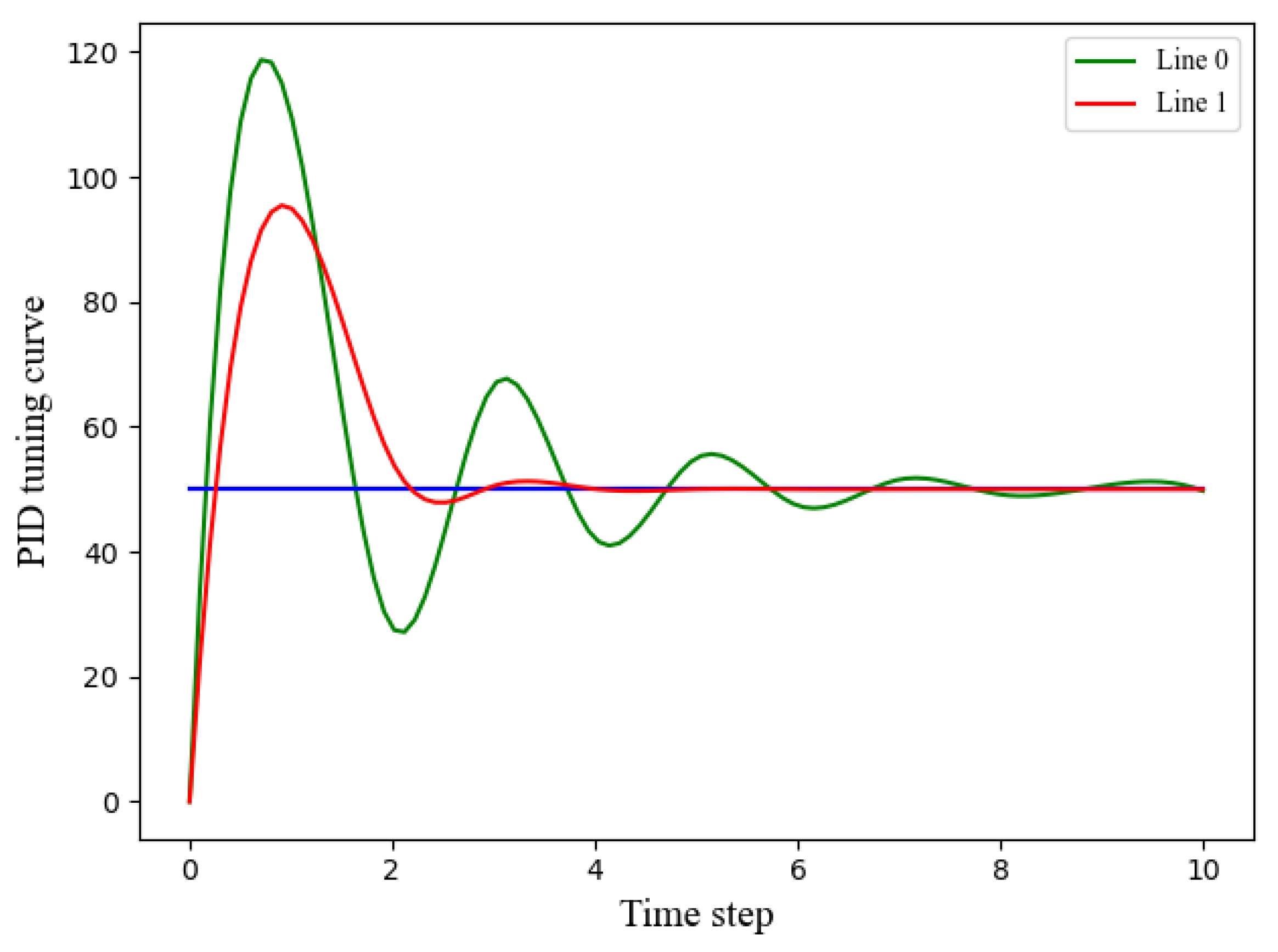
- Reward: To ensure effective control, the reward function of the PID controller should be designed to have a positive correlation with its performance. In particular, the amplitude of the system output should be minimized, as illustrated in Figure 3, and the output should converge to the setpoint rapidly. Accordingly, our reward function incorporates both the time steps and the error of the complete closed-loop trajectories. The reward function is described aswhere , represents the n-th step of the t-th episodic closed-loop operation. The weights of the error and time step in the reward function are denoted by and , respectively. By adjusting these weights, this paper can comprehensively consider trajectory-based metrics of both the error and the number of time steps N during the PID tuning process. This enables us to utilize a trade-off between output amplitude and time steps in reward design. A smaller amplitude of the output corresponds to a shorter time interval and a higher reward. It is worth noting that all rewards are less than 0.
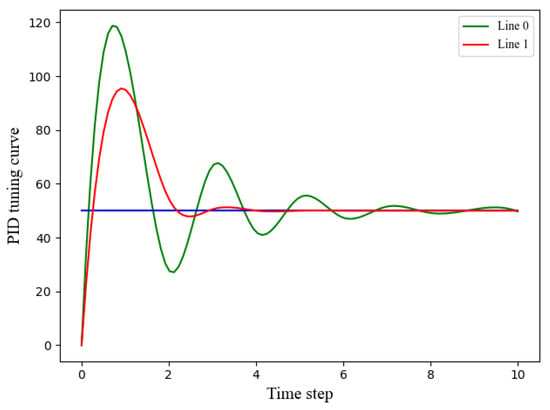 Figure 3. Illustration of the PID tuning curve. Line 1 has better performance than Line 0.
Figure 3. Illustration of the PID tuning curve. Line 1 has better performance than Line 0.
The proposed method utilizes the anti-windup method described in (3) to establish an initial upper and lower bound for the vectors of and , respectively, for the PID parameters. However, the output of the activation layer of the actor net does not necessarily fall within the range of PID parameters, and directly constraining the actions through normalization [38] compresses the action space and restricts the agent from fully exploring the environment. Therefore, it is necessary to establish a comprehensive mapping between the action interval and . We define
were O-U noise [35] is used as . and are the upper and lowed bounds of the activation function, respectively. To ensure comprehensive exploration by the agent and guarantee stability of the closed-loop process, a linear mapping relationship between the activation function output interval and the PID parameter interval can be established. This linear relationship, represented by Equation (14), can be viewed as adding an analogous linear activation layer to the actor network, thus leaving the calculation in DDPG unaffected. This is regarded as the first phase of agent exploration. However, this mapping alone may not ensure stability, and thus, the paper further constrains actions based on various thresholds to ensure stability of PID adaptive tuning with RL. These thresholds are established based on the reward function, and in this study, two thresholds, and , are set with being smaller than , and the reference values for the PID controller are automatically established each time the reward satisfies the criteria, allowing the agent to continue exploring within a specific range of the reference values until the algorithm converges. The reference value of the PID parameters is initialized as
At the beginning of the algorithm, the agent takes actions according to (14) and obtains the episodic tuple of experience . Once at , if this satisfies , then the reference value is set as
Once the new reference value of the PID parameters has been established, the action constraints are switched to initiate the second phase of exploration. For , and , the corresponding exploration ranges , and are set, respectively. The range of PID parameters in the second phase is
where . Then the new mapping of the action to the PID parameters is
Equation (18) indicates that the agent explores within a certain range of the current reference value which guarantees a baseline performance and further ensures the stability of PID closed-loop control based on the first phase. Similar to (14), the in (18) also satisfies a linear relationship with the of the actor network. By setting the threshold , the agent is able to explore in the stable region of PID parameters. To obtain better parameters and a more stable closed-loop tuning region, further constraining the agent’s exploration space in the stable region is proposed based on the second phase. If the reward at satisfies , then is set as
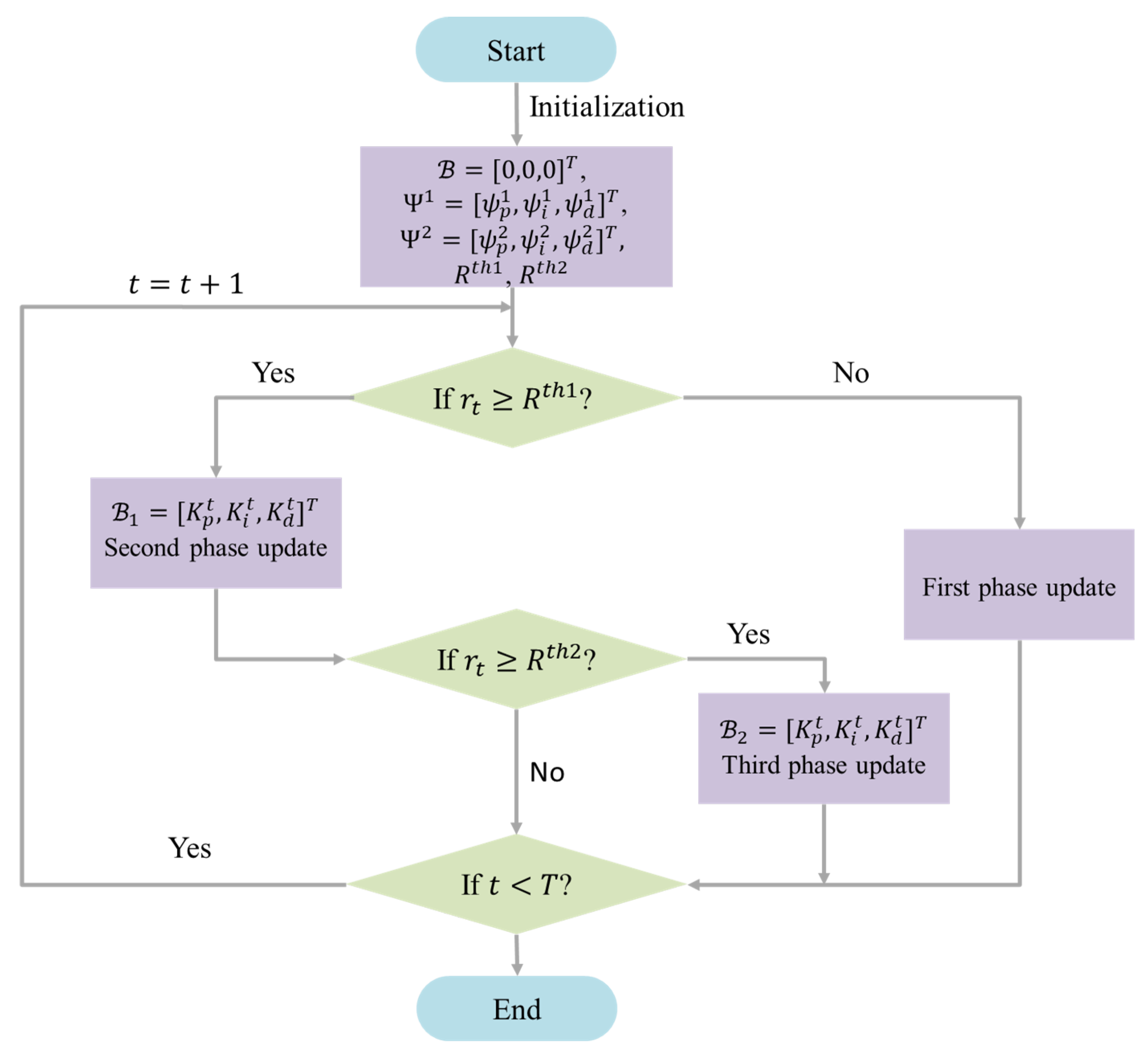
and the exploration range is . The constraint on the agent’s action will then repeat (17) and (18) until convergence. The process of constraining the actions in phases is similar to the focusing process of a camera. By focusing on the action through constraints corresponding to , the PID parameters are stabilized within the stable region, which corresponds to “coarse focusing”. Further constraints are applied to the action when the threshold of are met, so that the PID parameters are limited to smaller parameter range, achieving a more refined control effect. This process corresponds to “fine focusing”. Figure 4 illustrates the overall flowchart of the algorithm, and Algorithm 1 provides the pseudo-code of the proposed algorithm.
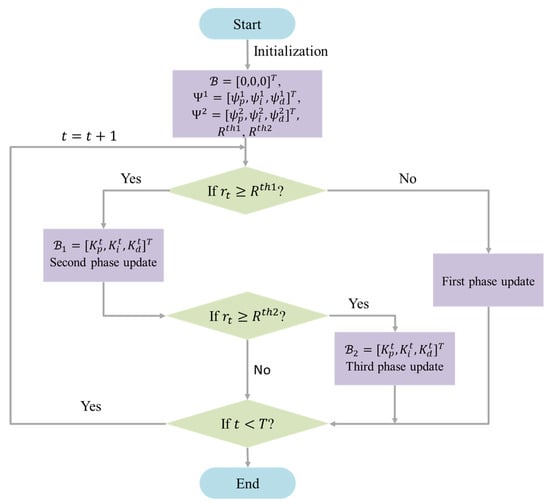
Figure 4.
Flow chart of multi-phase action constraint PID tuning with RL.
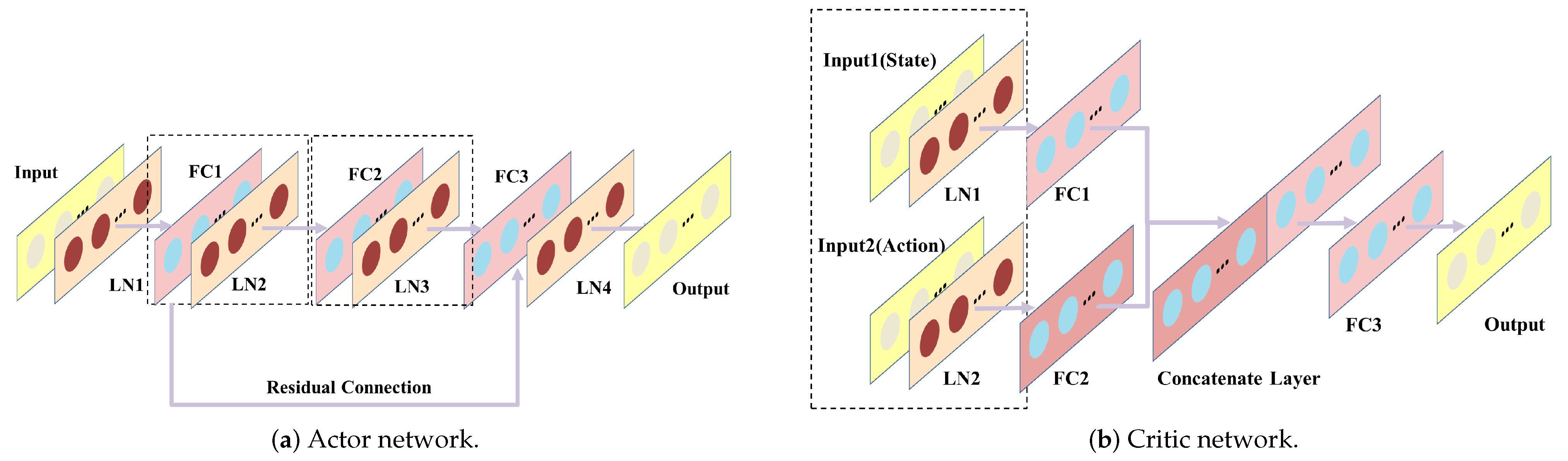
To reflect the proposed approach, corresponding modifications to the actor net and critic net in the DDPG framwork were made. Before the action switching phases of exploration, the agent may enter the unstable region of the PID, resulting in a large output amplitude that could cause the agent to fall into the saturated region of the activation function [39], as previously explained. To mitigate this issue during computation, a normalization layer [40] was added before each layer of the network. Based on the principle of gradient back-propagation [41] in neural networks, after focusing actions through multiple phases, the output of the neural network changes very little, and, as a result, the gradient update of the hidden layer can become very slow, particularly for shallow neural networks, where the gradient can vanish entirely. To address this issue, a residual structure was added from the first fully connected layer to the third fully connected layer for the actor net (the actor net has a total of three fully connected layers). The network structure is depicted in Figure 5. To represent the mapping relationship of two layers in a network, denoted by where X is the output of the shallow network, a basic shortcut was incorporated as a residual connection [42]. This results in the mapping relationship becoming , and during gradient back-propagation, the partial derivative of with respect to the shallow network parameters will not be 0, thus avoiding the issue of gradients vanishing.
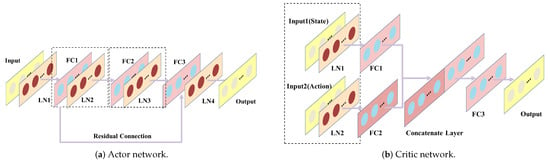
Figure 5.
The structure of the actor and critic networks. is a normalization layer, is a fully connected layer.
Remark 1.
The proposed method circumvents the need for direct action constraints and instead regulates the threshold setting through the reward function. Directly constraining the trajectory of a closed-loop process to ensure exploration in the stable region is challenging due to the lack of prior knowledge. The reward function, which is positively correlated with the stability of PID adaptive tuning and incorporates both amplitude and time considerations, is used to adjust the threshold value. As a result, this method allows for flexible and adaptable threshold setting based on the reward function.
| Algorithm 1 Multi-phase Focused DDPG-based PID Adaptive Tuning Algorithm |
|
4. Experimental Results and Analysis
In this section, experimental validations of the proposed algorithm using both first-order and second-order systems are conducted. The analysis of the experimental results demonstrates that the algorithm adequately achieves adaptive tuning of PID controllers and significantly improves their performance.
4.1. Experiment Settings
In this section, the validation of the proposed method is presented using a first-order system and a second-order system. The first-order system is modeled by
and the second-order system is modeled by
with initial condition . The RL algorithm parameters used in the experiments are presented in Table 1. To ensure a fair comparison, the PID parameter ranges for the first-order system and the second-order system were set to and , respectively, based on their tuning characteristics. The algorithm parameters were initialized based on the PID range, and the PID parameters interval was kept within the predetermined range. Table 2 shows the proposed algorithm’s parameters. The sample time for the first-order system and the second-order system were set to 1 s and 0.01 s, respectively. At each sample, the system performs a closed-loop operation to determine the error and system output . The second-order system has 50 times more closed-loop data in each episode than the first-order system due to the different sampling rates. To facilitate further analysis, the reward weights of the two systems, and , were adjusted so that the rewards were of the same order of magnitude. The paper also set the same exploration interval for and since the first-order and second-order systems were not sensitive to differential setting of the exploration range before and after the action range switching. Moreover, the exploration rate for was increased significantly over the rates for and to facilitate the experiment, as has a smaller range than and . Further parameter settings were made based on the PID tuning experience model and the benchmark of the DDPG model.

Table 1.
Parameters used for DDPG algorithm.

Table 2.
Parameters of multi-phase focused PID adaptive tuning algorithm.
4.2. Threshold Selection Experiment
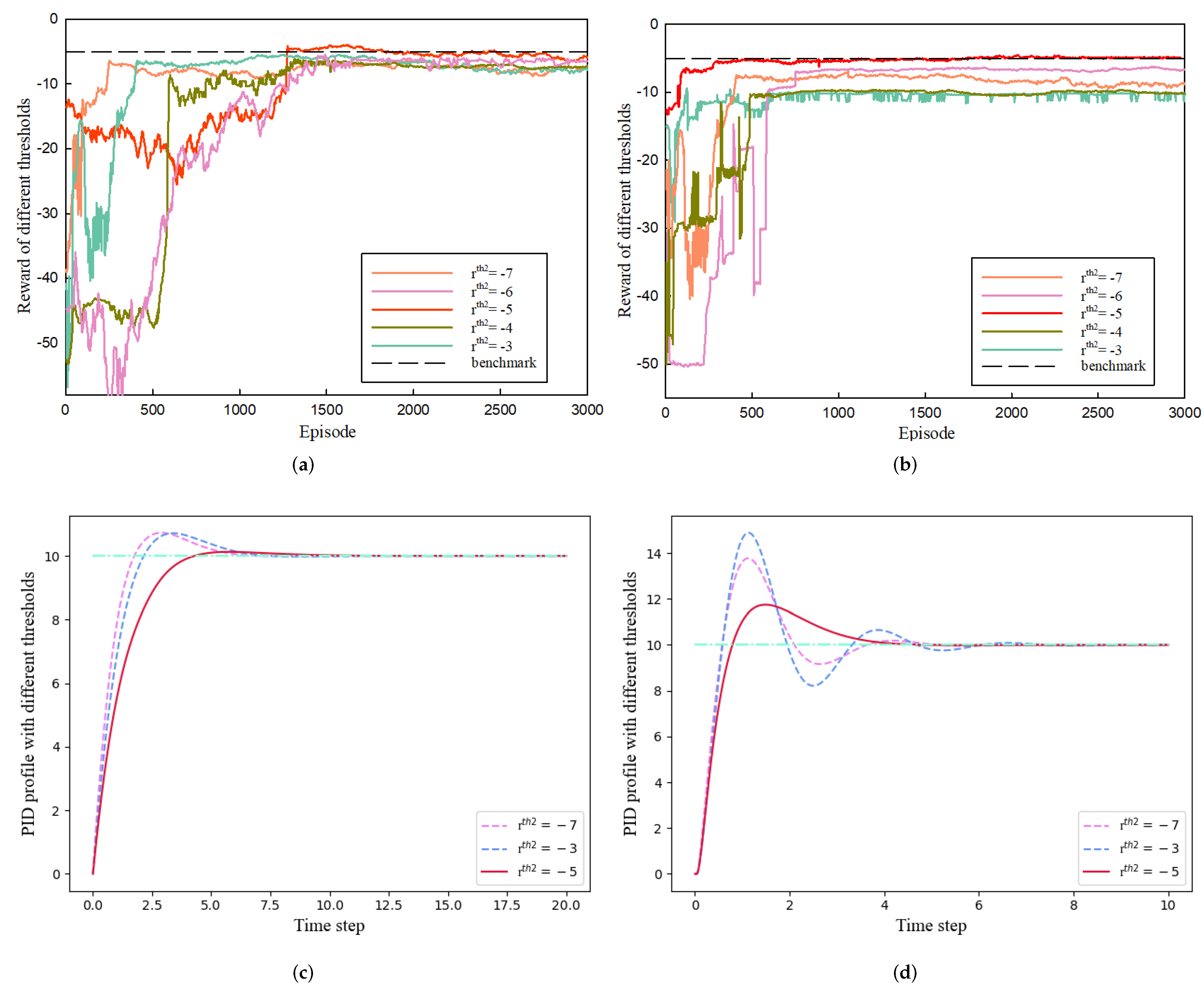
In this section, the impact on the proposed method of changing the thresholds is explored. The proposed method uses and as the threshold values to switch the PID reference values when the running reward surpasses these thresholds. Therefore, how these thresholds are set can significantly impact the algorithm’s performance. When action constraint is not employed, the rewards of both systems converge to around −10, as confirmed in the main experiment. To guarantee the algorithm’s fundamental performance, = −10 was set, while should be within the range . To determine the optimal threshold value, the threshold between −7 and −3 was set to in the experiments. Figure 6 displays the outcomes. The top row shows the reward curves for various values across the complete episodes, where “benchmark” represents the reward = −5. When is set to −5, the reward function in the first-order system converges to −5, indicating that the algorithm has switched constraints during the three phases, and the PID output remains within a stable range. However, when = −7 or −6, the agent’s exploration is limited, resulting in the reward converging around the corresponding threshold. Conversely, the running reward cannot meet the conditions when = −4 or −3, causing the reward to stagnate at a lower level. This issue is further highlighted in the optimal PID tracking curve in the lower left plot for a first-order system with various and is also shown in Figure 6’s upper and lower right plots for second-order systems. In the experiments, the threshold selection step size was set to 1. This choice was made because the reward function’s design ensured that variations in the reward value within a range of 1 or less would not have a significant impact on the final PID control performance. Therefore, the step size for threshold design in this experiment is deemed reasonable. Thus, setting to −5 is the optimal choice.
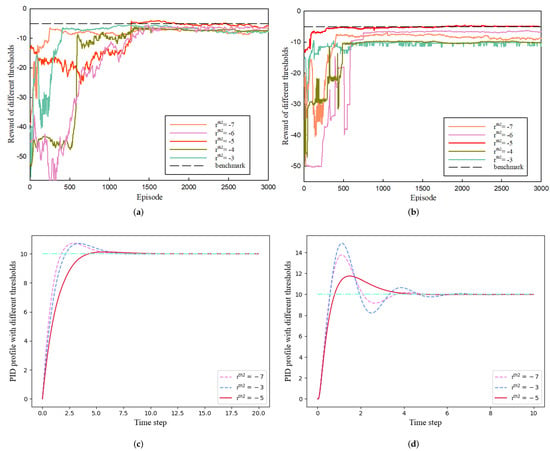
Figure 6.
Comparison of running reward and PID tracking performance under different settings. (a) Reward of different in first-order system. (b) Reward of different in second-order system. (c) Optimal PID curves corresponding to different of first-order system (Blue line corresponds to setpoint). (d) Optimal PID curves corresponding to different of second-order system.
4.3. Experimental Analysis
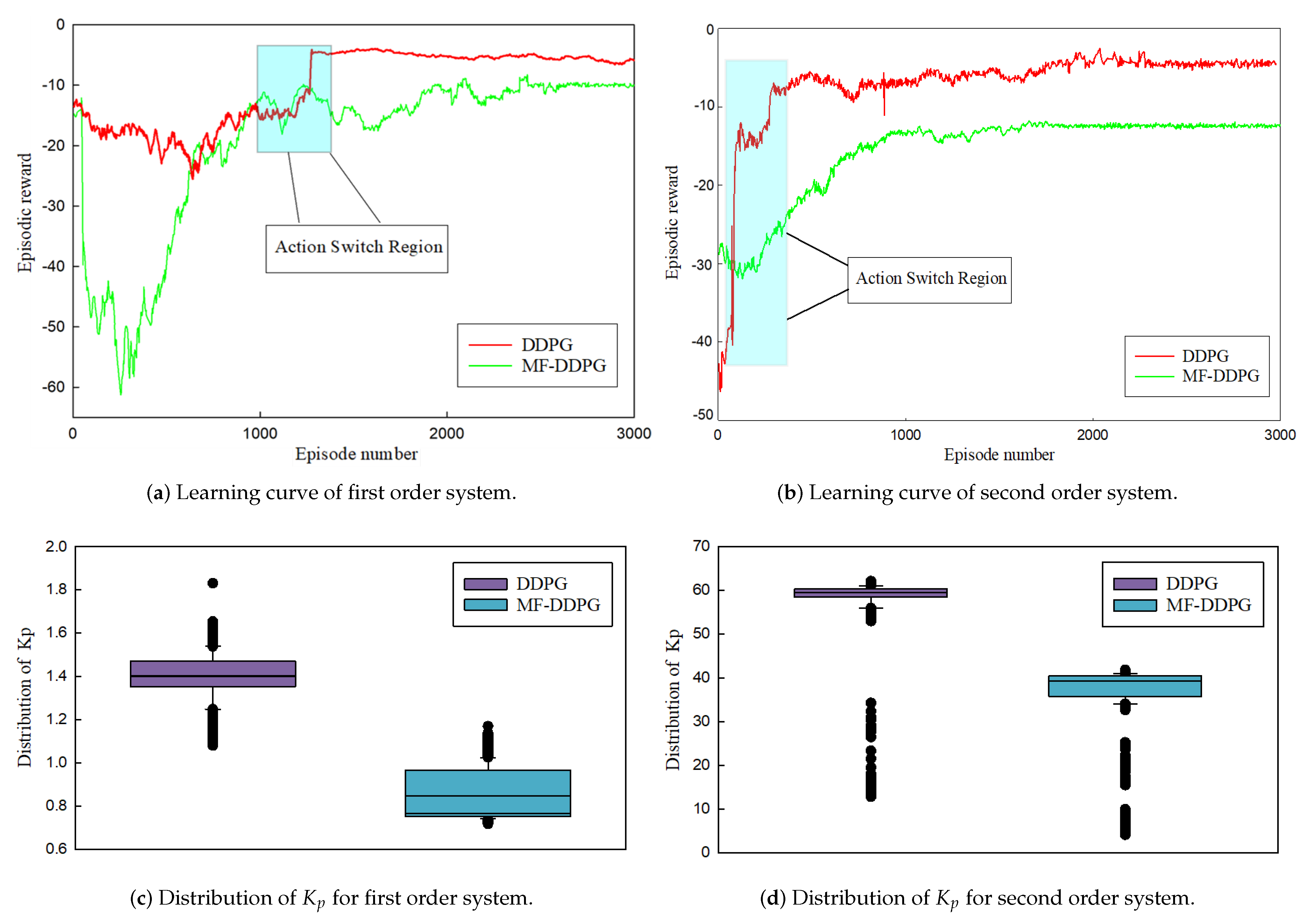
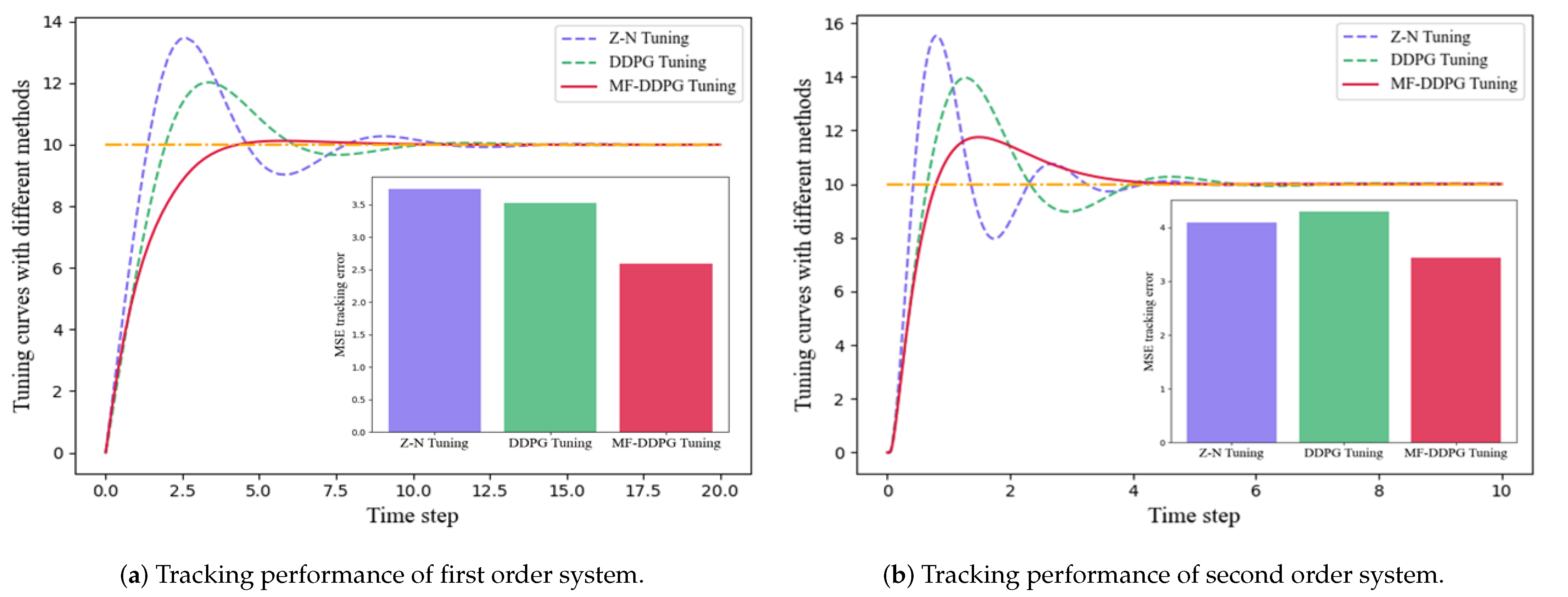
In this section, we present a comparative analysis of the performance of the MF-DDPG PID adaptive tuning method against existing methods. Figure 7 shows a comparison between the proposed method and the DDPG-based PID tuning method, which serves as the baseline in this study. The top row shows the learning curves of the two methods in both the first-order and second-order systems, with the average reward of our proposed method plotted in red and that of the DDPG method in green. In the absence of action constraint, the learning curves of both systems converge to around −10. However, the proposed method achieves a higher average reward in both systems, indicating the superior stability and performance of the proposed method. Notably, the reward curve of MF-DDPG displays a notable rise when the action constraint is satisfied, which validates the capability of the proposed method. The PID parameter ranges of both methods were also examined over the entire episode to further demonstrate the efficacy of the proposed method. The bottom row of Figure 7 illustrates the distribution range of the parameter in the two systems, ranging from 25% to 75%. The parameter exploration interval of MF-DDPG is more concentrated, with less variance than that of the baseline method. This implies that the action value changes do not disrupt the exploration process but instead lead to the agent’s actions being more focused on the stable region of the PID parameters, thereby enhancing the stability of the closed-loop system. Furthermore, the PID tracking performance of various methods was explored. Of the numerous PID tuning methods available in the literature, the DDPG-based method and the Ziegler–Nichols method [11] were chosen for the comparison. The results are presented in Figure 8 and Table 3, with the mean square error (MSE) employed to measure the tracking performance of the PID controllers. the proposed method achieves the lowest MSE in both the first-order and second-order systems, with performance improvements of 16–30% compared to the baseline methods. These findings demonstrate the effectiveness of the MF-DDPG PID tuning method and the closed-loop stability it offers, confirming that it can rapidly track the setpoint while maintaining the smallest PID amplitude during the entire closed-loop process.
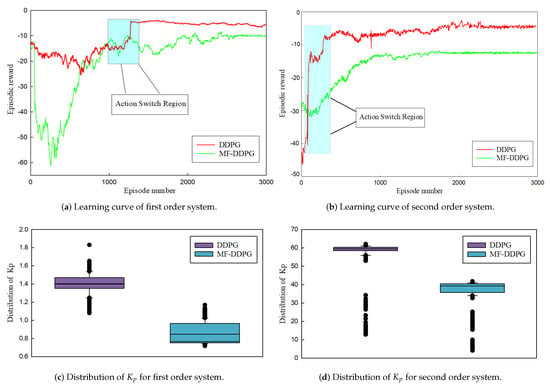
Figure 7.
Comparison of the tuning results with Algorithm 1 and DDPG.
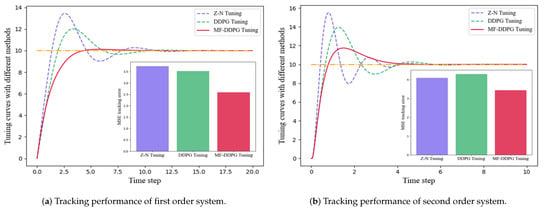
Figure 8.
Comparison of Ziegler–Nichols method, DDPG-based method, and multi-phase focused method represented by purple, green, and red bars, respectively (Orange line corresponds to setpoint).

Table 3.
MSE of different methods (In parentheses is the improvement of MF-DDPG over different methods in terms of tracking MSE).
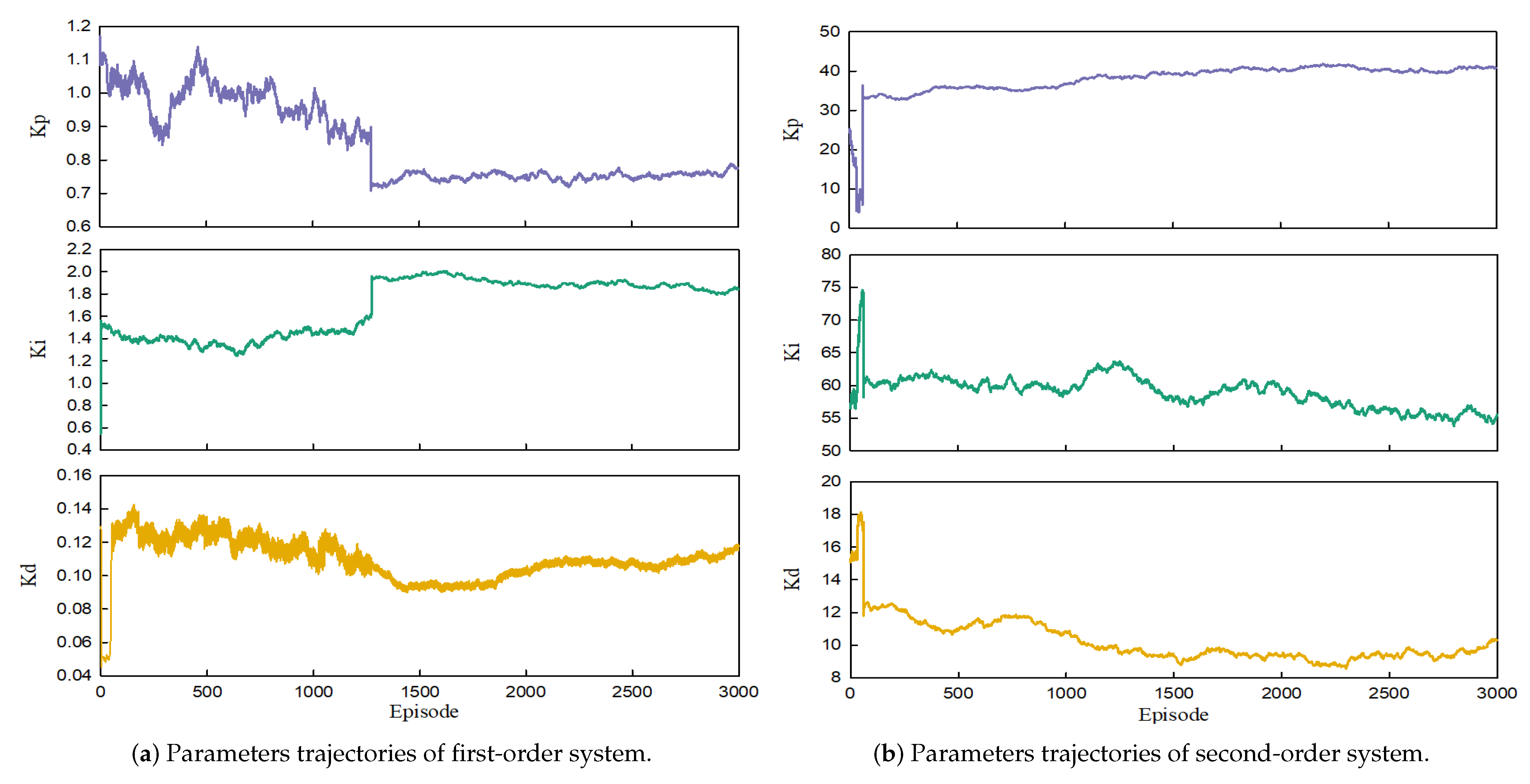
Additional experiments were conducted to investigate the changes in the three PID parameters during the switching of action constraints. The outcomes are displayed in Figure 9, which illustrates the trajectories of , , and during the entire process. The three parameters , , and exhibit significant variations during the initial stages of the algorithm’s execution. This behavior indicates that the agent is in a phase of random exploration. However, once the rewards meet the threshold conditions, the range of variations for these PID parameters stabilizes rapidly, with only minor fluctuations. It can be observed that the PID parameters enter a stable range throughout the whole episode, as , , and essentially stabilize within a small interval following the action constraint switching. These results demonstrate that the interval of the parameters can be focused after switching with multiple action constraints, regardless of how big or small the initial interval of the three parameters is. This ensures that the agents’ actions are more likely to be exploitative in the following episode, which is also beneficial for the stability of PID tracking.
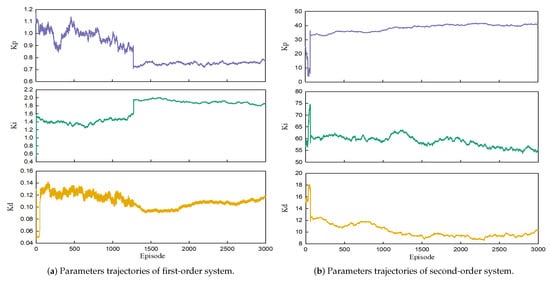
Figure 9.
Trajectories of the parameters.
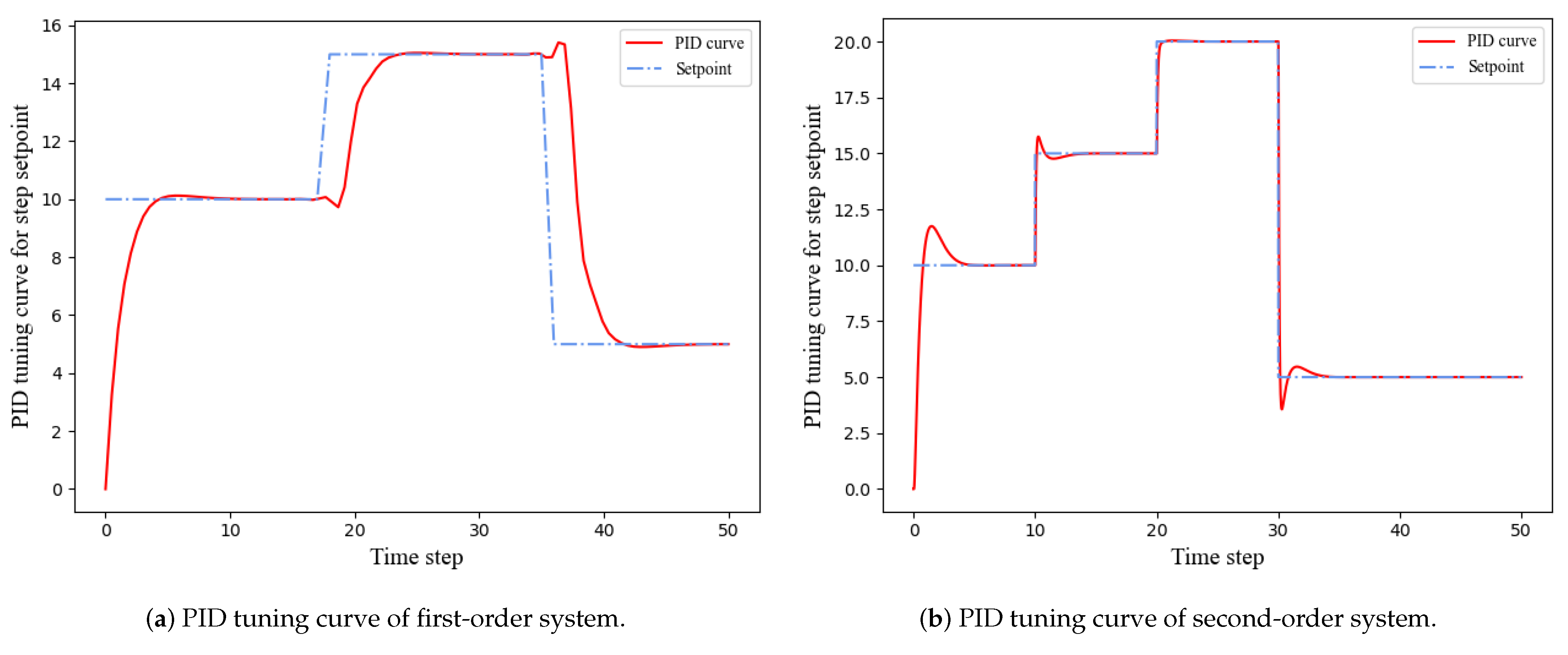
The performance of the proposed method was evaluated by examining its ability to maintain consistent setpoint tracking when the setpoint is varied, which is a crucial criterion. To verify the PID adaptive tracking capability of MF-DDPG, step signals were applied to the setpoints of the two systems. Figure 10 illustrates that the proposed method is capable of quickly and stably tracking the new setpoints without experiencing significant oscillations. The PID outputs remain consistently within a stable range. Notably, the second-order system’s higher sampling frequency results in a lower PID output delay than that of the first-order system. This experiment demonstrates that our PID parameter tuning method can generate stable tracking effects and has an excellent adaptive tuning capability.
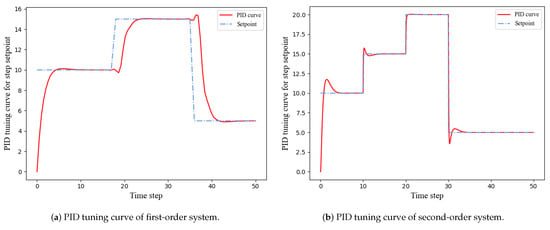
Figure 10.
PID tracking performance with varying setpoint.
4.4. Ablation Experiment
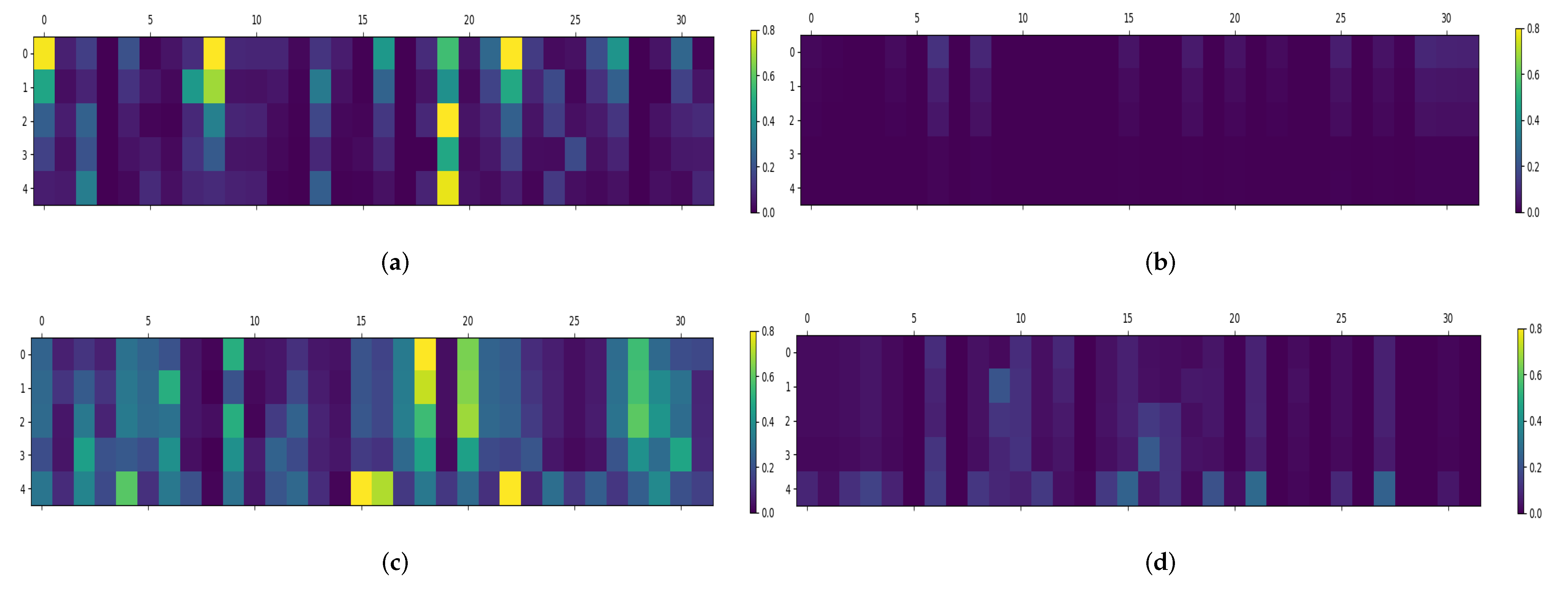
A residual structure was applied to the actor network to overcome the problem of a vanishing gradient resulting from the reduction in the action space following the switching of action constraints. To validate the effectiveness of the residual structure, the paper monitored the actor network’s gradient updates throughout the entire learning process. Specifically, the paper focused on the first fully-connected () layer and computed the mean episodic value matrix of the absolute gradients for layer across all episodes, as illustrated in Figure 11. The results demonstrate that actor networks with residual structures have higher average gradients compared to those without, since the gradients of actor networks without residual structures become very small after switching actions, resulting in slow parameter updates. Moreover, the compressed output action space of the actor network limits agent exploration, making it less ideal for learning. However, with the residual structure, the gradients of the actor network do not vanish even when the action space is focused by multiple action constraints. As shown in Figure 11, the gradients of the actor network’s shallow network persist with the residual structure, indicating that the reduction in action space does not negatively impact the parameter updates of the actor network. This is advantageous for updating PID output parameters and achieving a more balanced trade-off between exploration and exploitation.
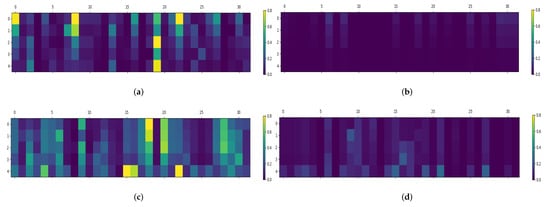
Figure 11.
Comparison of the gradients of actor networks. (a) Gradient of layer in actor network with residual structure for first-order system. (b) Gradient of layer in actor network without residual structure for first-order system. (c) Gradient of layer in actor network with residual structure for second-order system. (d) Gradient of layer in actor network without residual structure for second-order system.
4.5. Comparison with Existing PID Tuning Methods
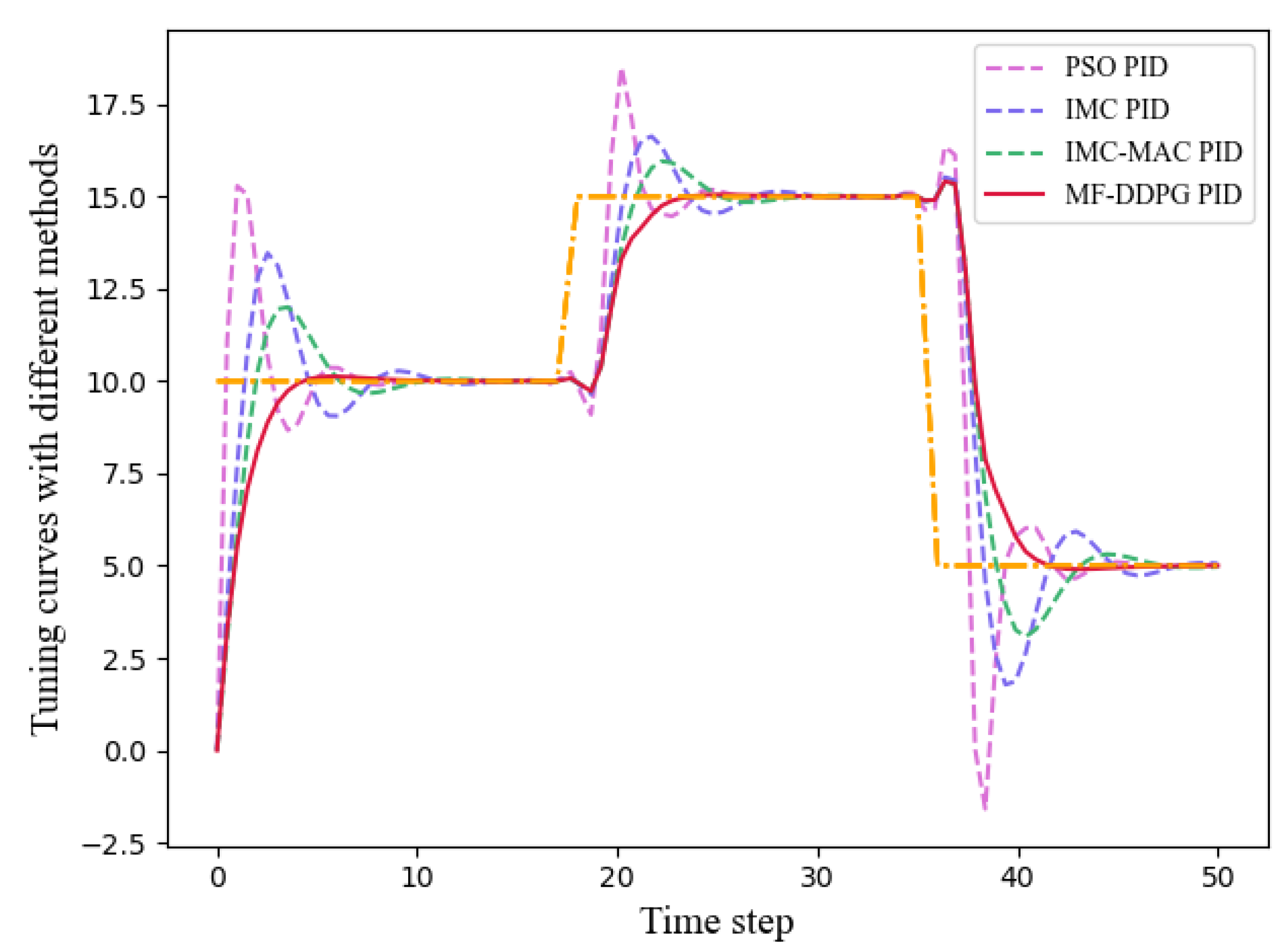
In this section, a comparative analysis of the proposed PID adaptive tuning algorithm and several mainstream PID control algorithms is carried out, evaluating the performance of different algorithms in PID adaptive tuning. The paper selects the particle swarm optimization (PSO) tuning method [14], internal model control (IMC) tuning method, and the IMC–Maclaurin (IMC-MAC) closed-loop tuning method [43] for comparison with the proposed MF-DDPG tuning method. The PID controller is applied to a first-order system, as described in Equation (20) (similar considerations apply to second-order systems). The setpoint of the PID controller is designed to be variable, and under the control of the different methods, the respective PID control performance is compared. The results are illustrated in Figure 12. Compared to the PID controllers controlled by the other algorithms, the PID controller controlled by MF-DDPG demonstrates rapid and stable tracking of variable setpoints, with minimal oscillations in the tracking curve when setpoints change. Table 4 records the MSE for different tracking curves. Experimental results indicate that, in comparison to mainstream PID adaptive tuning algorithms, the MF-DDPG algorithm continues to exhibit advantages.
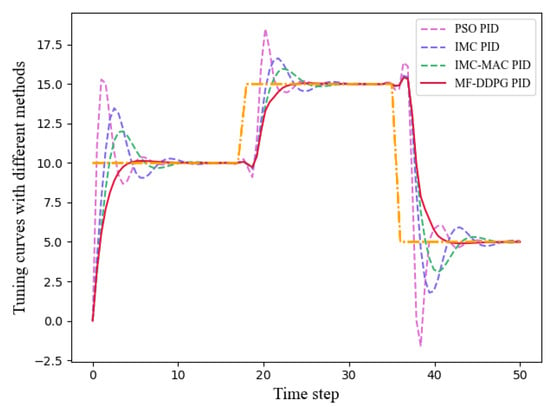
Figure 12.
Comparison of different methods for PID adaptive tuning.

Table 4.
MSE of PID tracking curves with different methods.
5. Conclusions
A novel RL-based PID adaptive tuning method was proposed that utilizes multi-phase action constraints. Building on the existing PID adaptive tuning method, this work extends the method by independently exploring parameters using an RL-based algorithm to obtain a finer range of PID parameters. By establishing reference values for PID parameters based on reward thresholds and controlling the agent’s exploration process as a constraint condition, the proposed method can determine more optimal PID tuning parameters with limited prior knowledge while ensuring closed-loop stability during the PID parameter discovery phase. To address the issue of a vanishing gradient caused by the switching of action scale and to expand the agent’s action space, this paper redesigns the reward function and state based on existing literature and adds a residual structure to the actor network. The results of experiments conducted on both first-order and second-order systems demonstrate that our proposed method exhibits a substantial improvement in performance when compared to baseline methods.
In the future, the method will be expanded to nonlinear complex systems to acquire appropriate PID parameters while maintaining system stability.
Author Contributions
Conceptualization, X.R. and Y.D.; methodology, Y.D. and X.Z.; software, X.W. and X.L.; validation, Y.D., X.W. and X.Z.; formal analysis, Y.D. and X.R.; writing—original draft preparation, Y.D. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (Grant No. 2021ZD0140301).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- García-Martínez, J.R.; Cruz-Miguel, E.E.; Carrillo-Serrano, R.V.; Mendoza-Mondragón, F.; Toledano-Ayala, M.; Rodríguez-Reséndiz, J. A PID-Type Fuzzy Logic Controller-Based Approach for Motion Control Applications. Sensors 2020, 20, 5323. [Google Scholar] [CrossRef] [PubMed]
- Boubertakh, H.; Tadjine, M.; Glorennec, P.-Y.; Labiod, S. Tuning Fuzzy PD and PI Controllers Using Reinforcement Learning. ISA Trans. 2010, 49, 543–551. [Google Scholar] [CrossRef] [PubMed]
- Borase, R.P.; Maghade, D.K.; Sondkar, S.Y.; Pawar, S.N. A Review of PID Control, Tuning Methods and Applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Yu, D.L.; Chang, T.K.; Yu, D.W. A Stable Self-Learning PID Control for Multivariable Time Varying Systems. Control Eng. Pract. 2007, 15, 1577–1587. [Google Scholar] [CrossRef]
- Lee, D.; Lee, S.J.; Yim, S.C. Reinforcement Learning-Based Adaptive PID Controller for DPS. Ocean Eng. 2020, 216, 108053. [Google Scholar] [CrossRef]
- Wang, L.; Barnes, T.J.D.; Cluett, W.R. New Frequency-Domain Design Method for PID Controllers. IEE Proc.-Control Theory Appl. 1995, 142, 265–271. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. The Future of PID Control. Control Eng. Pract. 2001, 9, 1163–1175. [Google Scholar] [CrossRef]
- Bucz, Š.; Kozáková, A. Advanced Methods of PID Controller Tuning for Specified Performance. PID Control Ind. Process. 2018, 73–119. [Google Scholar]
- Bansal, H.O.; Sharma, R.; Shreeraman, P.R. PID Controller Tuning Techniques: A Review. J. Control Eng. Technol. 2012, 2, 168–176. [Google Scholar]
- Lakhani, A.I.; Chowdhury, M.A.; Lu, Q. Stability-Preserving Automatic Tuning of PID Control with Reinforcement Learning. arXiv 2021, arXiv:2112.15187. [Google Scholar]
- Ziegler, J.G.; Nichols, N.B. Optimum Settings for Automatic Controllers. J. Dyn. Syst. Meas. Control 1993, 115, 220–222. [Google Scholar] [CrossRef]
- Cohen, G.H.; Coon, G.A. Theoretical consideration of retarded control. Trans. Am. Soc. Mech. Eng. 1953, 75, 827–834. [Google Scholar] [CrossRef]
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A. Process Dynamics and Control; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- GirirajKumar, S.M.; Jayaraj, D.; Kishan, A.R. PSO Based Tuning of a PID Controller for a High Performance Drilling Machine. Int. J. Comput. Appl. 2010, 1, 12–18. [Google Scholar] [CrossRef]
- Chiha, I.; Liouane, H.; Liouane, N. A Hybrid Method Based on Multi-Objective Ant Colony Optimization and Differential Evolution to Design PID DC Motor Speed Controller. Int. Rev. Model. Simul. (IREMOS) 2012, 5, 905–912. [Google Scholar]
- Sarkar, B.K.; Mandal, P.; Saha, R.; Mookherjee, S.; Sanyal, D. GA-Optimized Feedforward-PID Tracking Control for a Rugged Electrohydraulic System Design. ISA Trans. 2013, 52, 853–861. [Google Scholar] [CrossRef]
- Lazar, C.; Carari, S.; Vrabie, D.; Kloetzer, M. Neuro-Predictive Control Based Self-Tuning of PID Controllers. In Proceedings of the 12th European Symposium on Artificial Neural Networks, Bruges, Belgium, 28–30 April 2004; p. 395. [Google Scholar]
- Iplikci, S. A Comparative Study on a Novel Model-Based PID Tuning and Control Mechanism for Nonlinear Systems. Int. J. Robust Nonlinear Control 2010, 20, 1483–1501. [Google Scholar] [CrossRef]
- Guan, Z.; Yamamoto, T. Design of a Reinforcement Learning PID Controller. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 1354–1360. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Astrom, K.J.; Rundqwist, L. Integrator Windup and How to Avoid It. In Proceedings of the 1989 American Control Conference, Pittsburgh, PA, USA, 21–23 June 1989; IEEE: Pittsburgh, PA, USA, 1989; pp. 1693–1698. [Google Scholar]
- Qin, Y.; Zhang, W.; Shi, J.; Liu, J. Improve PID Controller through Reinforcement Learning. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; IEEE: Xiamen, China, 2018; pp. 1–6. [Google Scholar]
- Zhong, J.; Li, Y. Toward Human-in-the-Loop PID Control Based on CACLA Reinforcement Learning. In Proceedings of the International Conference on Intelligent Robotics and Applications, Shenyang, China, 8–11 August 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 605–613. [Google Scholar]
- Carlucho, I.; De Paula, M.; Acosta, G.G. An adaptive deep reinforcement learning approach for MIMO PID control of mobile robots. ISA Trans. 2020, 102, 280–294. [Google Scholar] [CrossRef]
- Carlucho, I.; De Paula, M.; Acosta, G.G. Double Q-PID algorithm for mobile robot control. Expert Syst. Appl. 2019, 137, 292–307. [Google Scholar] [CrossRef]
- Lawrence, N.P.; Stewart, G.E.; Loewen, P.D.; Forbes, M.G.; Backstrom, J.U.; Gopaluni, R.B. Optimal PID and Antiwindup Control Design as a Reinforcement Learning Problem. IFAC-PapersOnLine 2020, 53, 236–241. [Google Scholar] [CrossRef]
- Liu, Y.; Halev, A.; Liu, X. Policy Learning with Constraints in Model-Free Reinforcement Learning: A Survey. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 19–27 August 2021; International Joint Conferences on Artificial Intelligence Organization: Montreal, QC, Canada, 2021; pp. 4508–4515. [Google Scholar]
- Le, H.; Voloshin, C.; Yue, Y. Batch Policy Learning under Constraints. In Proceedings of the 36th International Conference on Machine Learning PMLR, Long Beach, CA, USA, 10–15 June 2019; pp. 3703–3712. [Google Scholar]
- Bohez, S.; Abdolmaleki, A.; Neunert, M.; Buchli, J.; Heess, N.; Hadsell, R. Value Constrained Model-Free Continuous Control. arXiv 2019, arXiv:1902.04623. [Google Scholar]
- Watkins, C.J.C.H.; Dayan, P. Q-Learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Norris, J.R. Markov Chains; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning PMLR, Beijing, China, 21–26 June 2014; pp. 387–395. [Google Scholar]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Adv. Neural Inf. Process. Syst. 1999, 12, 1057–1063. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Shin, J.; Badgwell, T.A.; Liu, K.-H.; Lee, J.H. Reinforcement Learning—Overview of Recent Progress and Implications for Process Control. Comput. Chem. Eng. 2019, 127, 282–294. [Google Scholar] [CrossRef]
- Spielberg, S.; Tulsyan, A.; Lawrence, N.P.; Loewen, P.D.; Gopaluni, R.B. Deep Reinforcement Learning for Process Control: A Primer for Beginners. arXiv 2020, arXiv:2004.05490. [Google Scholar]
- Bhatia, A.; Varakantham, P.; Kumar, A. Resource Constrained Deep Reinforcement Learning. Proc. Int. Conf. Autom. Plan. Sched. 2019, 29, 610–620. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning PMLR, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Panda, R.C.; Yu, C.-C.; Huang, H.-P. PID Tuning Rules for SOPDT Systems: Review and Some New Results. ISA Trans. 2004, 43, 283–295. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).