Vulnerable Area Identification of Islanded Combined Electrical and Heat Networks Based on Static Sensitivity Analysis
Abstract
:1. Introduction
2. CEHN Model
2.1. EN Model
2.2. DHN Model
2.2.1. Hydraulic Model
2.2.2. Thermal Model
2.3. Combined Heat and Power Units
3. Static Sensitivity Matrix of the Islanded CEHN
4. The Power Flow Calculation Method for Islanded CEHN
4.1. Decomposition Power Flow Models of EN and DHN
| Algorithm 1 Islanded CEHN power flow calculation |
| Input: EN: Network topology; Line impedance; Known active power, reactive power, voltage magnitude and voltage phase angle. DHN: Network topology; Pipe length, diameter, and roughness; Known heat power; Supply temperature of the source and return temperature of the load Output: EN: Voltage magnitude and voltage phase angle; Jacobian matrix. DHN: Pipe mass flow rate; Supply temperature and return temperature; Jacobian matrix. |
| Initialize variables do do Calculation of hydraulic vector of mismatches Calculation of hydro-thermal Jacobi matrix Update pipe mass flow rate Calculation of nodal supply and return temperatures |
| Calculation of heat power of CHP unit 1 Calculation of electrical power of CHP unit 1 do Calculation of electrical vector of mismatches Calculation of electrical Jacobi matrix Update voltage magnitude and voltage phase angle Calculation of electrical power of CHP unit 2 Calculation of heat power of CHP unit 2 Output data |
4.2. Combined Heat and Power Units
5. Case Study
5.1. Introduction of the Network
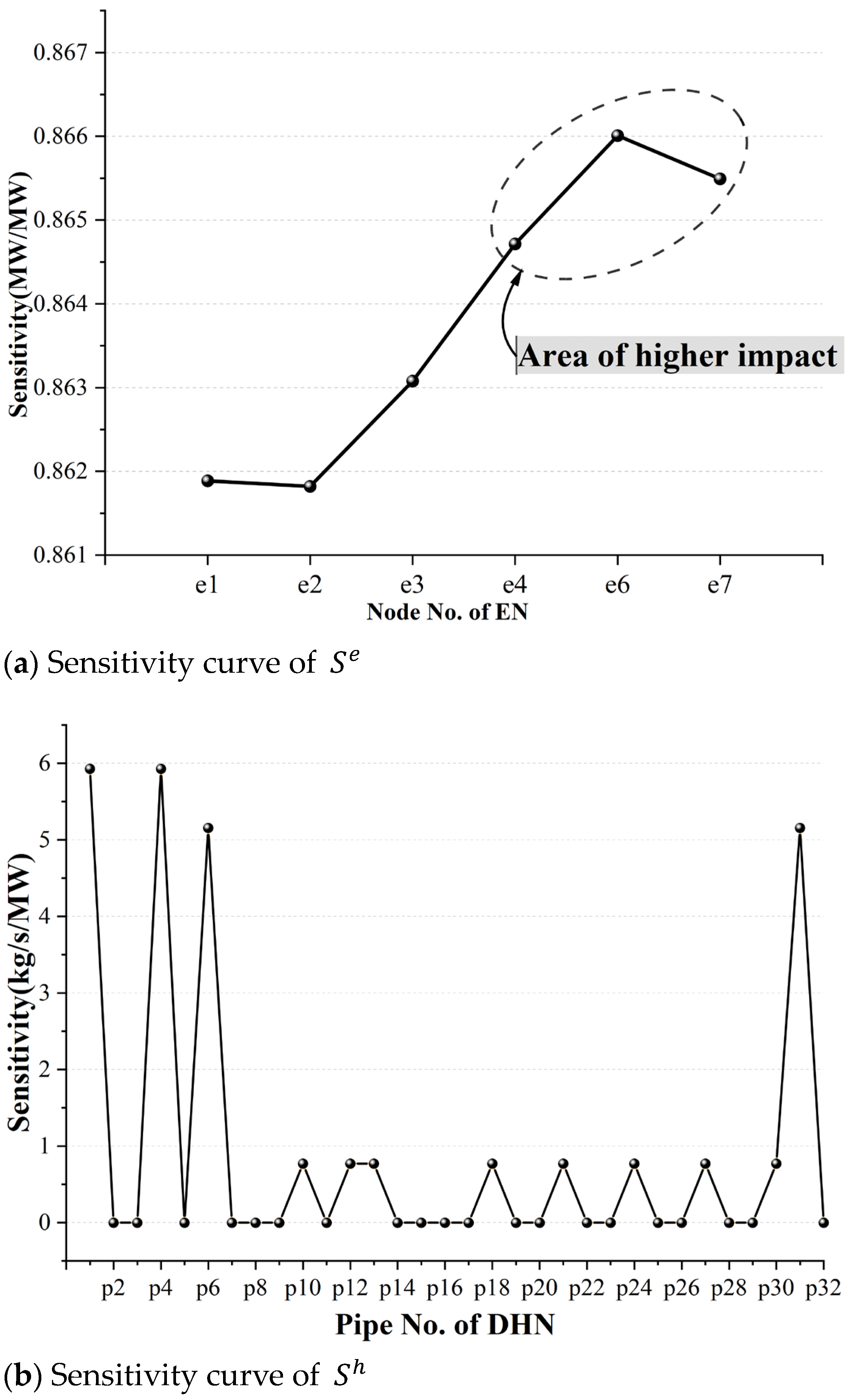
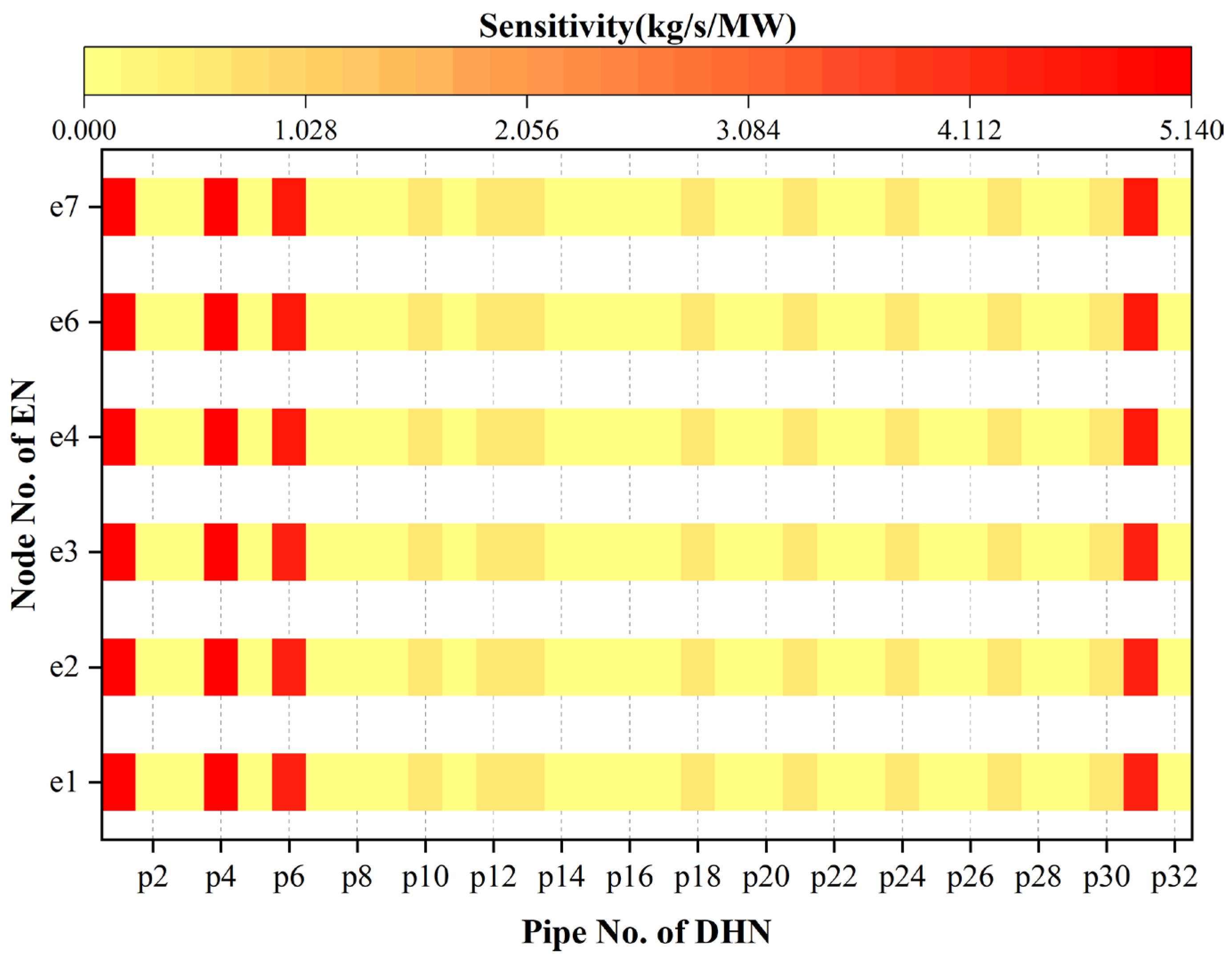
5.2. Calculation and Analysis of the Static Sensitivity
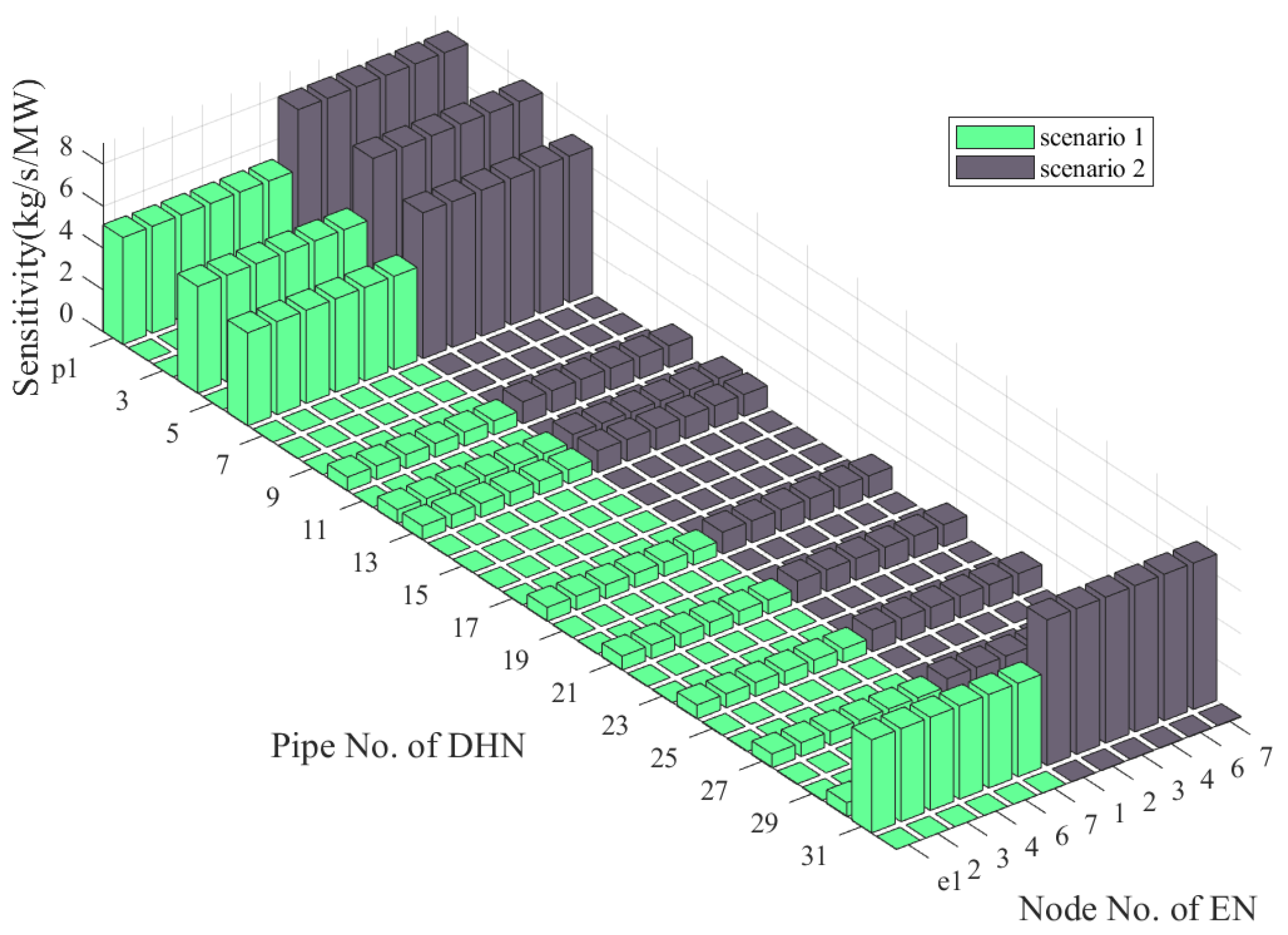
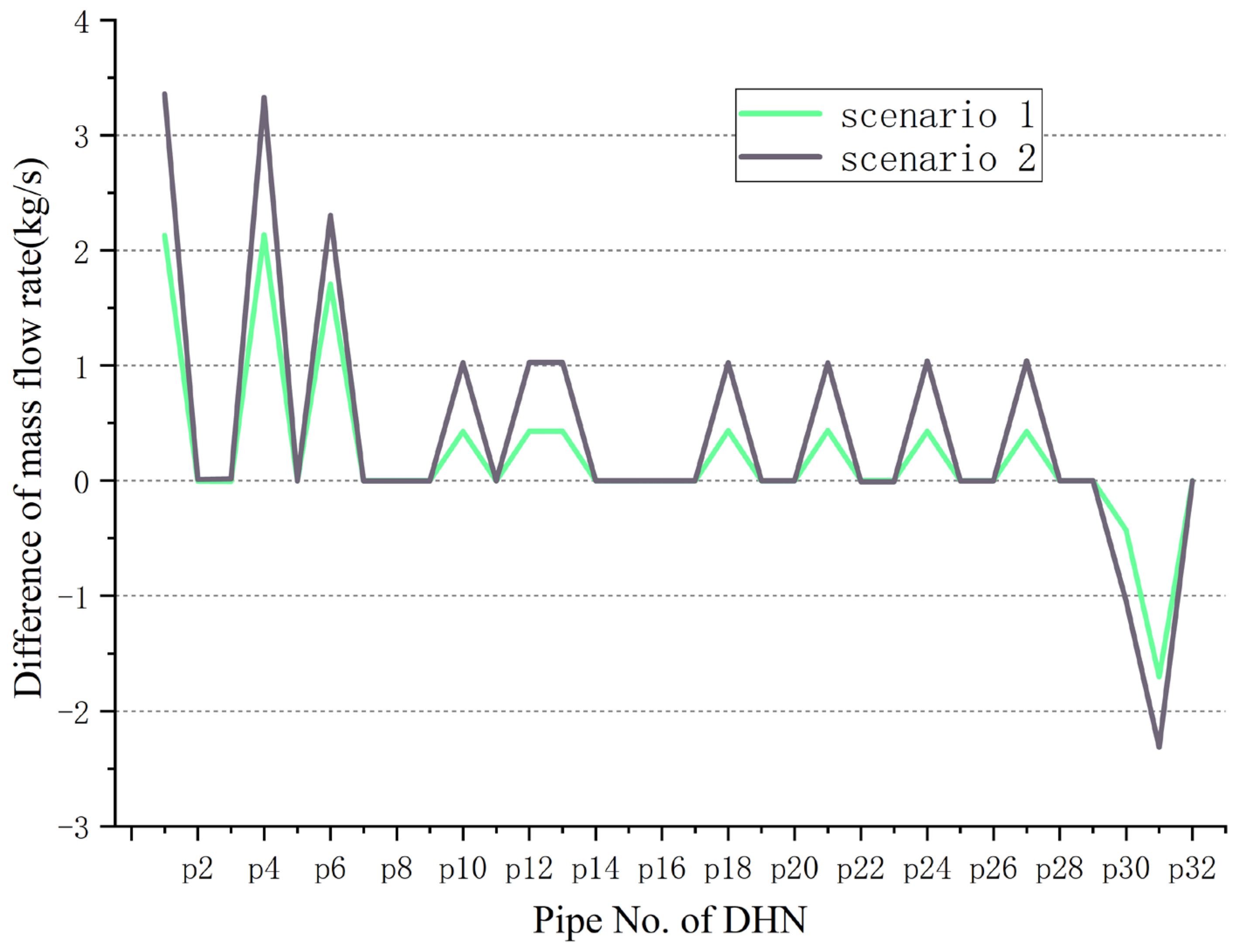
5.3. Stability Enhancement Effect of Simultaneous Use of Different Types of CHP Units in an Islanded CEHN
6. Conclusions
- The mass flow rate to node power injection sensitivity can reflect the DHN mass flow rate security margin.
- Based on the value of the elements in the sensitivity matrix, the vulnerable areas of the islanded CEHN can be quickly identified, which can avoid extensive power flow calculations.
- Two CHP units with contrary heat-to-electric ratio characteristics are used at the EN slack node and the DHN slack node, which can reduce the sensitivity of the islanded CEHN and improve the system stability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Coordinate (Row, Column) | Value | Coordinate (Row, Column) | Value |
|---|---|---|---|
| (2, 1) | 0.1662 | (14, 18) | −0.1633 |
| (2, 2) | −0.1662 | (14, 18) | −0.1633 |
| (3, 2) | 0.1644 | (19, 18) | 0.1630 |
| (2, 3) | −0.1662 | (32, 18) | 0.1682 |
| (4, 3) | 0.1655 | (19, 19) | −0.1630 |
| (2, 4) | −0.1662 | (20, 19) | 0.1600 |
| (5, 4) | 0.1651 | (19, 20) | −0.1630 |
| (5, 5) | −0.1651 | (21, 20) | 0.1600 |
| (6, 5) | 0.1606 | (19, 21) | −0.1630 |
| (5, 6) | −0.1651 | (22, 21) | 0.1624 |
| (7, 6) | 0.1658 | (32, 21) | 0.2557 |
| (32, 6) | −1.0814 | (22, 22) | −0.1624 |
| (7, 7) | −0.1658 | (23, 22) | 0.1597 |
| (8, 7) | 0.1625 | (22, 23) | −0.1624 |
| (7, 8) | −0.1658 | (24, 23) | 0.1602 |
| (9, 8) | 0.1639 | (22, 24) | −0.1624 |
| (7, 9) | −0.1658 | (25, 24) | 0.1663 |
| (10, 9) | 0.1612 | (32, 24) | 0.0477 |
| (5, 10) | −0.1651 | (25, 25) | −0.1663 |
| (11, 10) | 0.1647 | (26, 25) | 0.1639 |
| (32, 10) | 0.2936 | (25, 26) | −0.1663 |
| (11, 11) | −0.1647 | (27, 26) | 0.1641 |
| (12, 11) | 0.1623 | (25, 27) | −0.1663 |
| (11, 12) | −0.1647 | (28, 27) | 0.1668 |
| (13, 12) | 0.1639 | (32, 27) | 6.0557 |
| (32, 12) | 0.4071 | (28, 28) | −0.1668 |
| (13, 13) | −0.1639 | (29, 28) | 0.1651 |
| (14, 13) | 0.1633 | (1, 29) | 0.1650 |
| (32, 13) | 0.9648 | (28, 29) | −0.1668 |
| (14, 14) | −0.1633 | (28, 30) | 0.1668 |
| (15, 14) | 0.1628 | (30, 30) | −0.1687 * |
| (15, 15) | −0.1628 | (32, 30) | −0.0320 |
| (16, 15) | 0.1602 | (7, 31) | 0.1658 |
| (15, 16) | −0.1628 | (30, 31) | −0.1687 * |
| (17, 16) | 0.1598 | (32, 31) | 0.1494 |
| (14, 17) | −0.1633 | (11, 32) | 0.1647 |
| (18, 17) | 0.1603 | (31, 32) | −0.1690 |
| Coordinate (Row, Column) | Value | Coordinate (Row, Column) | Value |
|---|---|---|---|
| (1, 1) | 3.2357 | (3, 8) | −1.0029 |
| (2, 1) | −2.0024 | (8, 8) | 2.6010 |
| (7, 1) | −1.2334 | (10, 8) | 3.2849 |
| (9, 1) | −6.6334 | (11, 8) | 2.0511 |
| (10, 1) | 4.1066 | (1, 9) | 6.3175 |
| (1, 2) | −2.0037 | (2, 9) | −3.9113 |
| (2, 2) | 3.6055 | (7, 9) | −2.4065 |
| (8, 2) | −1.6020 | (9, 9) | 3.0818 |
| (9, 2) | 4.1060 | (10, 9) | −1.9072 |
| (10, 2) | −7.3915 | (1, 10) | −3.9106 |
| (3, 3) | 2.3921 | (2, 10) | 7.0395 |
| (4, 3) | −1.3934 | (8, 10) | −3.1292 |
| (8, 3) | −0.9991 | (9, 10) | −1.9084 |
| (11, 3) | −4.9043 | (10, 10) | 3.4340 |
| (12, 3) | 2.8512 | (3, 11) | 4.6729 |
| (3, 4) | −1.3892 | (4, 11) | −2.7172 |
| (4, 4) | 3.2726 | (8, 11) | −1.9565 |
| (6, 4) | −1.8838 | (11, 11) | 2.2797 |
| (11, 4) | 2.8532 | (12, 11) | −1.3280 |
| (12, 4) | −6.7094 | (3, 12) | −2.7200 |
| (14, 4) | 3.8559 | (4, 12) | 6.3952 |
| (5, 5) | 1.2299 | (6, 12) | −3.6759 |
| (6, 5) | −1.2300 | (11, 12) | −1.3243 |
| (13, 5) | −2.5215 | (12, 12) | 3.1198 |
| (14, 5) | 2.5214 | (14, 12) | −1.7959 |
| (4, 6) | −1.8792 | (5, 13) | 2.4038 |
| (5, 6) | −1.2299 | (6, 13) | −2.4042 |
| (6, 6) | 3.2025 | (13, 13) | 1.1727 |
| (12, 6) | 3.8582 | (14, 13) | −1.1728 |
| (13, 6) | 2.5215 | (4, 14) | −3.6786 |
| (14, 6) | −6.3842 | (5, 14) | −2.4041 |
| (1, 7) | −1.2320 | (6, 14) | 6.0870 |
| (7, 7) | 1.2334 | (12, 14) | −1.7917 |
| (9, 7) | 2.5274 | (13, 14) | −1.1726 |
| (2, 8) | −1.6031 | (14, 14) | 3.0534 |
| (3, 8) | −1.0029 |
| Parameters Name | Value |
|---|---|
| Heat power of Source 1 (MW) | 1.055355 |
| Electrical power of Source 1 (MW) | 0.811811 |
| Heat power of Source 2 (MW) | 0.810157 |
| Electrical power of Source 2 (MW) | 0.499981 |
| Electricity losses (MW) | 0.011792 |
| Heat losses (MW) | 0.081259 |
Appendix B
| Node No. of EN | Electrical Load (MW) |
|---|---|
| e1 | 0.2 |
| e2 | 0 |
| e3 | 0.5 |
| e4 | 0.5 |
| e5 | Electrical source node |
| e6 | 0.2 |
| e7 | 0.2 |
| e8 | Electrical source node |
| e9 | Electrical source node |
| Node No. of DHN | Heating Load (MW) | Node No. of DHN | Heating Load (MW) |
|---|---|---|---|
| h1 | 0.107 | h17 | 0.0805 |
| h2 | 0 | h18 | 0.0805 |
| h3 | 0.107 | h19 | 0 |
| h4 | 0.107 | h20 | 0.0805 |
| h5 | 0 | h21 | 0.0805 |
| h6 | 0.107 | h22 | 0 |
| h7 | 0.107 | h23 | 0.107 |
| h8 | 0.107 | h24 | 0.107 |
| h9 | 0.107 | h25 | 0 |
| h10 | 0.107 | h26 | 0.107 |
| h11 | 0.145 | h27 | 0.107 |
| h12 | 0.107 | h28 | 0 |
| h13 | 0 | h29 | 0.107 |
| h14 | 0.0805 | h30 | Heat source node |
| h15 | 0 | h31 | Heat source node |
| h16 | 0.0805 | h32 | Heat source node |
References
- Jin, H. A new principle of synthetic cascade utilization of chemical energy and physical energy. Sci. China Ser. E 2005, 48, 163–179. [Google Scholar] [CrossRef]
- Huang, A.Q.; Crow, M.L.; Heydt, G.T.; Zheng, J.P.; Dale, S.J. The Future Renewable Electric Energy Delivery and Management (FREEDM) System: The Energy Internet. Proc. IEEE 2011, 99, 133–148. [Google Scholar] [CrossRef]
- Li, G.; Zhang, R.; Jiang, T.; Chen, H.; Bai, L.; Li, X. Security-constrained bi-level economic dispatch model for integrated natural gas and electricity systems considering wind power and power-to-gas process. Appl. Energy 2017, 194, 696–704. [Google Scholar] [CrossRef]
- Chang, M.; Lund, H.; Thellufsen, J.Z.; Østergaard, P.A. Perspectives on purpose-driven coupling of energy system models. Energy 2023, 265, 126335. [Google Scholar] [CrossRef]
- Dong, H.; Fang, Z.; Ibrahim, A.-W.; Cai, J. Optimized Operation of Integrated Energy Microgrid with Energy Storage Based on Short-Term Load Forecasting. Electronics 2022, 11, 22. [Google Scholar] [CrossRef]
- Gao, F.; Gao, J.; Huang, N.; Wu, H. Optimal Configuration and Scheduling Model of a Multi-Park Integrated Energy System Based on Sustainable Development. Electronics 2023, 12, 1204. [Google Scholar] [CrossRef]
- Tahir, M.F.; Chen, H.; Javed, M.S.; Jameel, I.; Khan, A.; Adnan, S. Integration of Different Individual Heating Scenarios and Energy Storages into Hybrid Energy System Model of China for 2030. Energies 2019, 12, 2083. [Google Scholar] [CrossRef]
- Pan, Z.; Guo, Q.; Sun, H. Interactions of district electricity and heating systems considering time-scale characteristics based on quasi-steady multi-energy flow. Appl. Energy 2016, 167, 230–243. [Google Scholar] [CrossRef]
- Yin, X.; Ye, C.; Ding, Y.; Song, Y. Exploiting Internet Data Centers as Energy Prosumers in Integrated Electricity-Heat System. IEEE Trans. Smart Grid 2023, 14, 167–182. [Google Scholar] [CrossRef]
- Guo, S.; Ji, W.; Wang, C.; Song, T.; Wang, J. Hydraulic-thermal coupling dynamic models based on mechanism and data-driven methods of the heating networks in integrated energy systems. Energy Convers. Manag. 2023, 292, 117353. [Google Scholar] [CrossRef]
- Chong, Z.; Yang, L.; Jiang, Y. Hybrid-timescale dispatch of heat and electricity integrated system considering dynamic heat flow. Electr. Power Syst. Res. 2023, 224, 109713. [Google Scholar] [CrossRef]
- Guan, A.; Zhou, S.; Gu, W.; Zhang, K.; Ding, L.; Lv, H. An optimal step-size simulation framework for large-scale heat-electric integrated energy system considering fault states. Electr. Power Syst. Res. 2023, 223, 109617. [Google Scholar] [CrossRef]
- Liu, X.; Wu, J.; Jenkins, N.; Bagdanavicius, A. Combined analysis of electricity and heat networks. Appl. Energy 2016, 162, 1238–1250. [Google Scholar] [CrossRef]
- Liu, X. Combined Analysis of Electricity and Heat Networks. Ph.D. Thesis, Cardiff University, Cardiff, Wales, 2013. [Google Scholar]
- Hassine, I.B.; Eicker, U. Impact of load structure variation and solar thermal energy integration on an existing district heating network. Appl. Therm. Eng. 2013, 50, 1437–1446. [Google Scholar] [CrossRef]
- Li, G.; Zhang, R.; Jiang, T.; Chen, H.; Bai, L.; Cui, H.; Li, X. Optimal dispatch strategy for integrated energy systems with CCHP and wind power. Appl. Energy 2017, 192, 408–419. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. An Integrated Steady-State Operation Assessment of Electrical, Natural Gas, and District Heating Networks. IEEE Trans. Power Syst. 2016, 31, 3636–3647. [Google Scholar] [CrossRef]
- Wang, J.; Qi, X.; Ren, F.; Zhang, G.; Wang, J. Optimal design of hybrid combined cooling, heating and power systems considering the uncertainties of load demands and renewable energy sources. J. Clean. Prod. 2021, 281, 125357. [Google Scholar] [CrossRef]
- Biswas, R.S.; Pal, A.; Werho, T.; Vittal, V. A Graph Theoretic Approach to Power System Vulnerability Identification. IEEE Trans. Power Syst. 2021, 36, 923–935. [Google Scholar] [CrossRef]
- Huang, W.; Du, E.; Capuder, T.; Zhang, X.; Zhang, N.; Strbac, G.; Kang, C. Reliability and Vulnerability Assessment of Multi-Energy Systems: An Energy Hub Based Method. IEEE Trans. Power Syst. 2021, 36, 3948–3959. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, B.; Ma, H.; Wang, H. Evaluating the vulnerability of integrated electricity-heat-gas systems based on the high-dimensional random matrix theory. CSEE J. Power Energy Syst. 2020, 6, 878–889. [Google Scholar] [CrossRef]
- Oh, U.; Lee, Y.; Choi, J.; Karki, R. Reliability evaluation of power system considering wind generators coordinated with multi-energy storage systems. IET Gener. Transm. Distrib. 2020, 14, 786–796. [Google Scholar] [CrossRef]
- Mu, Y.; Wang, C.; Kang, G.; Wang, Z.; Jiang, T.; Li, J.; Dou, W. Research on sensitivity analysis of wind power consumption capability of integrated energy system based on unified optimal power flow model. J. Eng. 2019, 2019, 8471–8476. [Google Scholar] [CrossRef]
- Liu, T.; Jiao, W.; Tian, X. A framework for uncertainty and sensitivity analysis of district energy systems considering different parameter types. Energy Rep. 2021, 7, 6908–6920. [Google Scholar] [CrossRef]
- Ji, L.; Liang, X.; Xie, Y.; Huang, G.; Wang, B. Optimal design and sensitivity analysis of the stand-alone hybrid energy system with PV and biomass-CHP for remote villages. Energy 2021, 225, 120323. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Liang, X.; Huang, B. Event-Triggered-Based Distributed Cooperative Energy Management for Multienergy Systems. IEEE Trans. Ind. Inform. 2019, 15, 2008–2022. [Google Scholar] [CrossRef]
- Dancker, J.; Wolter, M. Power-Transfer-Distribution-Factor-based Sensitivity Factors for Integrated Energy Systems. IEEE Trans. Sustain. Energy 2023, 1–13. [Google Scholar] [CrossRef]
- Ruiz-Tipán, F.; Barrera-Singaña, C.; Valenzuela, A. Reactive power compensation using power flow sensitivity analysis and QV curves. In Proceedings of the 2020 IEEE ANDESCON, Quito, Ecuador, 13–16 October 2020; pp. 1–6. [Google Scholar]
- Zhao, B.; Luo, B.; Zhou, J.; Meng, X.; Li, Z. Static sensitivity analysis method of integrated energy system based on power flow model. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–9. [Google Scholar]
- Li, Z.; Wu, L.; Xu, Y. Risk-Averse Coordinated Operation of a Multi-Energy Microgrid Considering Voltage/Var Control and Thermal Flow: An Adaptive Stochastic Approach. IEEE Trans. Smart Grid 2021, 12, 3914–3927. [Google Scholar] [CrossRef]
- Wang, H.; Gu, C.; Zhang, X.; Li, F. Optimal CHP Planning in Integrated Energy Systems Considering Network Charges. IEEE Syst. J. 2020, 14, 2684–2693. [Google Scholar] [CrossRef]
- Hongfu, W.; Xianghong, T.; Zhiqiang, Z.; Chong, G.; Hao, Y.; Shixia, M. An improved DC power flow algorithm with consideration of network loss. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 455–460. [Google Scholar]
- Hu, W.; Wu, Y.; Jing, J.; Jiang, X.; Li, X.; Wang, C. Multi-Energy Flow Calculation Model and Solution Method for Regional Integrated Energy System. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2021; pp. 238–241. [Google Scholar]
- Chen, Y.; Zhao, J.; Ma, J. Fast Decoupled Multi-energy Flow Calculation for Integrated Energy System. J. Mod. Power Syst. Clean Energy 2020, 8, 951–960. [Google Scholar] [CrossRef]
- Zhu, M.; Xu, C.; Dong, S.; Tang, K.; Gu, C. An integrated multi-energy flow calculation method for electricity-gas-thermal integrated energy systems. Prot. Control Mod. Power Syst. 2021, 6, 5. [Google Scholar] [CrossRef]
- Fu, X.; Sun, H.; Guo, Q.; Pan, Z.; Xiong, W.; Wang, L. Uncertainty analysis of an integrated energy system based on information theory. Energy 2017, 122, 649–662. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, W.; Zhao, Q.; Du, Y.; Chen, J.; Zhao, J. Distributed Real-time State Estimation for Combined Heat and Power Systems. J. Mod. Power Syst. Clean Energy 2021, 9, 316–327. [Google Scholar] [CrossRef]



| Node Number | Voltage Amplitude (pu.) | Voltage Phase Angle (rad) |
|---|---|---|
| 1 | 1.0488 | −0.6306 |
| 2 | 1.0488 | −0.6288 |
| 3 | 1.0490 | −0.6633 |
| 4 | 1.0493 | −0.7060 |
| 5 | 1.0500 | −0.7599 |
| 6 | 1.0500 | −0.7500 |
| 7 | 1.0499 | −0.7409 |
| 8 | 1.0500 | −0.7245 |
| 9 | 1.0200 | 0.0000 |
| Pipe Number | Mass Flow Rate (kg/s) | Supply Temperature (°C) | Return Temperature (°C) |
|---|---|---|---|
| 1 | 4.7989 | 69.4452 | 30.0000 |
| 2 | 0.6510 | 69.7533 | 29.7125 |
| 3 | 0.8760 | 69.3056 | 30.0000 |
| 4 | 3.2719 | 69.5789 | 30.0000 |
| 5 | 0.6664 | 69.4764 | 29.6517 |
| 6 | −0.8795 | 68.3922 | 30.0000 |
| 7 | 0.6585 | 69.6565 | 29.6881 |
| 8 | 0.6529 | 68.8553 | 30.0000 |
| 9 | 0.6637 | 69.1867 | 30.0000 |
| 10 | 3.4850 | 68.5489 | 30.0000 |
| 11 | 0.6593 | 69.3903 | 29.7259 |
| 12 | 4.1926 | 68.8091 | 30.0000 |
| 13 | 4.1926 | 69.1845 | 29.7243 |
| 14 | 1.0062 | 69.0566 | 29.7669 |
| 15 | 0.5024 | 68.9282 | 29.7738 |
| 16 | 0.5038 | 68.3122 | 30.0000 |
| 17 | 0.5021 | 68.2114 | 30.0000 |
| 18 | 2.1914 | 68.3359 | 30.0000 |
| 19 | 0.5031 | 68.9761 | 29.7605 |
| 20 | 0.5030 | 68.2579 | 30.0000 |
| 21 | 1.1853 | 68.2697 | 30.0000 |
| 22 | 0.6699 | 68.8312 | 29.8015 |
| 23 | 0.6680 | 68.1952 | 30.0000 |
| 24 | −0.1526 | 68.2995 | 30.0000 |
| 25 | 0.6528 | 69.7547 | 29.7795 |
| 26 | 0.6519 | 69.1947 | 30.0000 |
| 27 | −1.4573 | 69.2461 | 30.0000 |
| 28 | 0.6480 | 69.8821 | 29.7956 |
| 29 | 0.6486 | 69.4858 | 30.0000 |
| 30 | 2.7539 | 70.0000 | 29.6552 |
| 31 | 3.4997 | 70.0000 | 29.5907 |
| 32 | 2.2471 | 70.0000 | 29.6314 |
| Method | Time (s) |
|---|---|
| Power flow calculation (Total time for 6 sessions) | 0.275367 |
| Sensitivity calculation | 0.037139 |
| Heat-to-Electric Ratio of CHP1 | Heat-to-Electric Ratio of CHP2 | |
|---|---|---|
| scenario 1 | (gas turbines) | (condensing steam turbine with extraction) |
| scenario 2 | (gas turbines) | (gas turbines) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Nie, Y.; Yang, L. Vulnerable Area Identification of Islanded Combined Electrical and Heat Networks Based on Static Sensitivity Analysis. Electronics 2023, 12, 3936. https://doi.org/10.3390/electronics12183936
Song Z, Nie Y, Yang L. Vulnerable Area Identification of Islanded Combined Electrical and Heat Networks Based on Static Sensitivity Analysis. Electronics. 2023; 12(18):3936. https://doi.org/10.3390/electronics12183936
Chicago/Turabian StyleSong, Zhifan, Yu Nie, and Liulin Yang. 2023. "Vulnerable Area Identification of Islanded Combined Electrical and Heat Networks Based on Static Sensitivity Analysis" Electronics 12, no. 18: 3936. https://doi.org/10.3390/electronics12183936
APA StyleSong, Z., Nie, Y., & Yang, L. (2023). Vulnerable Area Identification of Islanded Combined Electrical and Heat Networks Based on Static Sensitivity Analysis. Electronics, 12(18), 3936. https://doi.org/10.3390/electronics12183936





