An Objective Holographic Feedback Linearization Based on a Sliding Mode Control for a Buck Converter with a Constant Power Load

Abstract

As a typical load, the constant power load (CPL) has negative impedance characteristics. The stability of the buck converter system with a mixed load of CPL and resistive load is affected by the size of the CPL. When the resistive load is larger than the CPL, the buck converter with the output voltage as an output function is a non-minimum phase nonlinear system, because its linear approximation has a right-half-plane pole. The non-minimum phase characteristic limits the application of many control techniques, but the objective holographic feedback linearization control (OHFLC) method is a good control strategy that can bypass the non-minimum phase system and make the system stable. However, the traditional OHFLC method, in designing the controller, generally uses a linear optimal quadratic design method to obtain a linear feedback control law. It requires a state quantity component with a one-order relative degree to the system. But it is not easy to find such a suitable state quantity with a one-order relative degree to the system. In this paper, an improved OHFLC method is proposed for Buck converters with a mixed loads of CPL and resistive loads, using the sliding mode control (SMC) theory to design the controller, so that the output state quantity components with different relative degrees to the system can be used in the holographic feedback linearization method. Finally, the simulation and experimental results also demonstrate that this method has the same, or even better, dynamic response performance and robustness than the traditional OHFLC method.

1. Introduction

A DC–DC converter, as a device to convert DC power, has been widely used and can be seen in DC microgrids, electric vehicles (EVs), portable electronic devices, and other fields or products. In DC microgrids, in order to manage the power flow between different parts of the DC microgrids, the DC–DC converter becomes the hub to connect various DC sources and buses, and buses to different buses, and is responsible for the safe, stable, and efficient operation of the DC microgrid system while meeting the power demand of each part [1]. In EVs, DC–DC converters play a pivotal role in EV charging, power steering systems, and composite power systems as their essential components [2,3]. And, at a time of rapid development of portable electronic devices, linear regulators and switched capacitors (also known as charge pumps), which are part of the practical application of DC–DC converters in portable electronic devices, have likewise been developed rapidly [4].

Power electronic systems using cascaded distributed DC–DC converters are being used in a wide range of scenarios, including smart microgrids, spacecraft, telecommunications, automotive power systems, ships, ground-based computer systems, and medical electronics [5,6,7]. In a cascaded system of DC–DC converters, the later stage’s DC converter with a closed-loop control can be considered as a CPL for the previous stage’s DC converter. The CPL has a positive transient impedance, but a negative incremental impedance (in terms of small signals), which tends to produce an instability effect. This instability effect causes the closed-loop system to enter a positive feedback state, showing oscillations and becoming unstable at the output. In addition, the CPL affects the power quality and system reliability. Therefore, the voltage regulation control method must ensure large signal stability [7,8].

There are many ways to solve the instability problems caused by CPL. One of the common approaches is to add passive damping to the circuit. In [9], the system’s instability is avoided by adding a passive damping circuit to change the system damping, effectively canceling out the negative impedance characteristics of the CPL. This approach can also be seen as a design for filters. However, adding passive damping elements increases the size of the converter, reduces the compatibility of the damping elements with the circuit, reduces the system efficiency, and increases the total cost.

An alternative approach to solve the CPL problem is through an active damping technique. In [10], the authors propose an active damping control technique by creating a virtual resistor at the source-side converter of a DC microgrid. This approach does not degrade the performance of the CPL, but it requires a more demanding LC input filter design. In [11], the authors propose an active Loop-Cancellation technique for compensating any number of CPLs and adjusting the damping of the system, which can configure the poles of the system to the right position and suppress the poles of the right half-plane generated by the system through feedback, solving the instability effect caused by the CPL. In [12], a controlled DC–DC power converter in parallel with the load is added at the midpoint of the circuit network to expand the web so that the system can be input–output linearized, and then a nonlinear control law based on an adaptive observer is proposed to make the system stable. It can also be considered as an active damping technique.

There are also nonlinear control methods, such as sliding mode control and model predictive control. SMC, as an inverse control technique, requires stability of the internal dynamics. In [13], a multi-state process variables-feedback SMC method of a bidirectional DC/DC converter is proposed, which defines a multivariable weight combination-based sliding-mode surface, then effectively improve the stability of the DC bus voltage, despite dynamic power disturbances. In [14], an adaptive backstepping sliding mode control technique is proposed to design the control law. However, the problems of jitter and variable switching frequency arising in sliding mode control force us to apply higher filtering requirements to the converter [15]. An improved version based on direct model predictive control is implemented in [16], and is able to maintain system stability under different CPL requirements and system failures.

Feedback linearization is a nonlinear control method, which can also be classified as an active damping method, used to compensate for CPL effects in a system. We can eliminate the nonlinearity due to the presence of a CPL by selecting nonlinear feedback. Theoretically, feedback linearization can compensate for any amount of CPL and stabilize the system in a large signal sense [17]. Feedback linearization is usually based on finding nonlinear feedback, and the application can eliminate nonlinear characteristics. Therefore, we can use linear control tools to design controllers. The main drawback of this approach compared to techniques that directly deal with nonlinearities, such as sliding mode control and cooperative control, is the noise sensitivity due to the presence of differentiators and slower transient response [18,19]. In [20], A multi-objective feedback linearization control method is proposed, which linearizes a nonlinear system into a combination of linear subsystems and nonlinear subsystems. The linear part adopts the linear optimal control theory to design the controller, while the nonlinear part ensures the stability of the original nonlinear system by adjusting the coefficients of the output function. The exact feedback linearization (EFL) theory has been exploited in [21] to convert the reduced-order multilevel boost converter model to Brunovsky’s canonical form, and to develop an adaptive backstepping controller by using the estimation of nonlinear disturbance observer. It can strictly guarantee the stability of the microgrid bus voltage under large signals.

The objective holographic feedback linearization method is a nonlinear control method that bypasses the nonminimum-phase system by selecting the state variables of interest so that the system is stable and each state quantity can effectively track its reference value. In [8], the authors use the OHFLC method to design a controller for a non-minimum phase system, a boost converter with CPL, by incorporating the target state variables into the linear space and then using the linear optimal quadratic form of the linear control method. This method does not require complex mathematical analysis, and by changing the control parameters, the system poles can be adjusted for the purpose of stabilizing the system and tracking control [22]. However, in the traditional OHFLC method, because an optimal linear quadratic is used in the design of the controller, a state variable with a one-order degree relative to the system must exist to solve the original nonlinear control rate when selecting the output vector to be incorporated into the linear space [23,24]. However, there exist cases where the original nonlinear control law of the system derived by solving using a state variable with a one-order relative degree does not make the system stable. For example, in a boost converter with constant resistance load, its inductor current and capacitor voltage both have a one-order relative degree to the system, but when using the OHFLC strategy, only the state variable of the inductor current can be used to design and solve the control law of the system, because if using the capacitor voltage to design and solve, it cannot make the one-order linearized approximation of the system stable.

In this paper, we propose an objective holographic feedback control strategy based on a sliding mode control to design a controller for a buck converter with CPL. By designing different sliding mode surfaces, state variables with different relative degrees to the system can solve the initial nonlinear control law instead of being limited to the traditional requirement of state variables with one order of relative degree. In addition, the tracking performance and stability of the states under this method are analytically demonstrated. The latter part of the article performs simulation experiments and physical experiments to verify this control method.

2. Modeling of Buck Converter System and Construction of Brunovsky’s Canonical Form

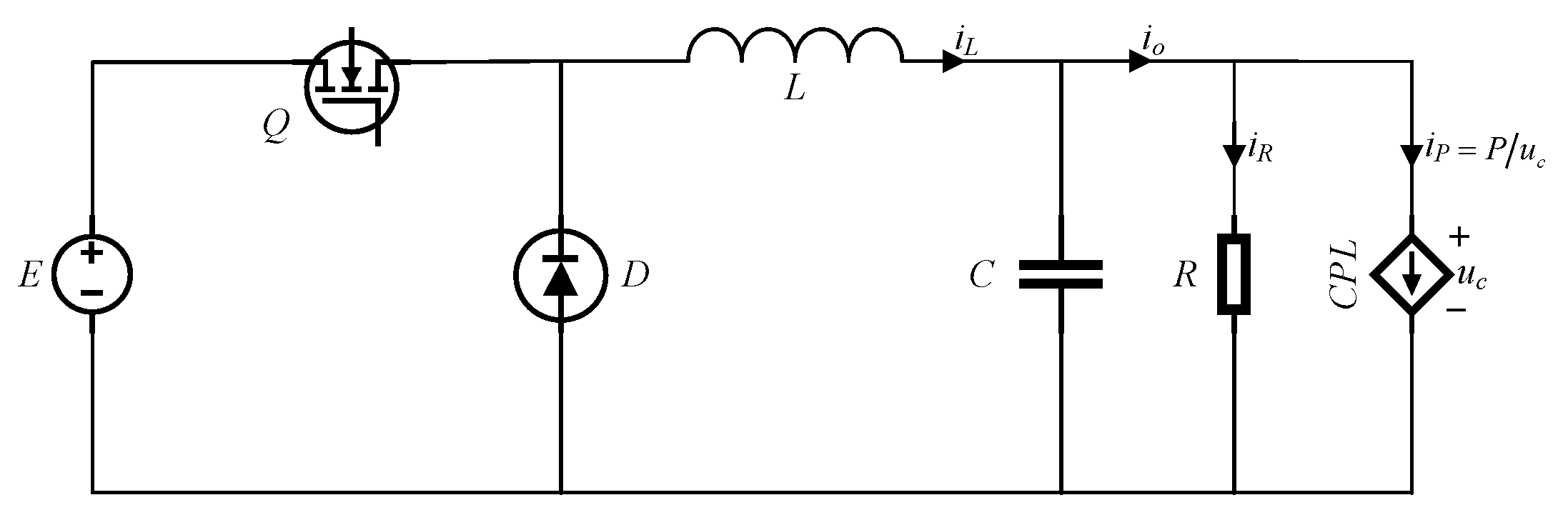
For the convenience of analysis, the values of equivalent series resistance of output capacitance and equivalent series resistance of filter inductance are ignored. The system structure of the simplified buck converter is shown in Figure 1. The CPL is connected to the output of the converter in parallel with the resistive load, the output voltage can be regarded as the DC bus voltage, and the converter needs to provide a stable voltage output under load fluctuation. E is the input voltage, Q is the switching device, D is the diode, L is the filter inductor, C is the filter capacitor, R is the resistive load, P is the constant, u_c is the capacitor voltage, i_L is the filter inductor current, i_o is the instantaneous load current, i_R is the instantaneous current on the resistive load, and i_P = P/u_c is the instantaneous current on CPL.

Let the duty cycle d be the input quantity, and use the state space averaging method to obtain the state equation of Buck converter under continuous conduction mode (CCM):

$$\{\begin{array}{l}L\frac{d{i}_L}{dt}=-u_c+E·d\hfill \\ C\frac{d{u}_c}{dt}=i_L-\frac{u_c}{R}-\frac{P}{u_c}\hfill \end{array}$$

(1)

Considering the state vector $x={\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]}^T={\left[\begin{array}{cc}{i}_L& u_c\end{array}\right]}^T$, and their reference $x_{ref}={\left[\begin{array}{cc}{x}_{1ref}& x_{2ref}\end{array}\right]}^T={\left[\begin{array}{cc}{i}_{Lref}& u_{cref}\end{array}\right]}^T$, Equation (1) can be described with the following affine nonlinear model:

$$\dot{x}=f(x)+g(x)d,$$

(2)

where $f(x)={\left[\begin{array}{cc}-\frac{x_2}{L}& \frac{x_1}{C}-\frac{x_2}{RC}-\frac{P}{C{x}_2}\end{array}\right]}^T$, $g(x)={\left[\begin{array}{cc}\frac{E}{L}& 0\end{array}\right]}^T$.

The system’s output vector is chosen as $y={\left[\begin{array}{cc}{y}_1& y_2\end{array}\right]}^T={\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]}^T$. According to the definition of the Lie derivative in [25], the relative degree of each output state variable to the system can be determined by finding the Lie derivative under that state variable in the following manner:

$$L_g{L}_f^0{y}_1(x)=\frac{\partial y_1}{\partial x}g=\frac{E}{L}\ne 0,\{\begin{array}{l}{L}_g{L}_f^0{y}_2(x)=\frac{\partial y_2}{\partial x}g=0\hfill \\ L_g{L}_f^1{y}_2(x)=\frac{\partial L_f{y}_2}{\partial x}g=\frac{E}{LC}\ne 0\hfill \end{array}.$$

The relative degree of the output functions y₁ and y₂ to the system can be found to be r₁ = 1 and r₂ = 2.

Let the deviation of the state $e={[x_1-x_{1ref},x_2-x_{2ref}]}^T$, and the final control goal is to make $\underset{t\to \infty }{\lim }\left|e\right|=0$. According to the traditional design of OHFLC methods, Brunovsky’s canonical form needs to be actively constructed using the deviations of the states and making the derivative of one of the deviations of the states with a one-order relative degree to the system equal to the linear control law under the standard type. The method mentioned in this paper does not require a harsh relative degree. Since there are two relative degrees of the above two output functions to the system, the following is a theoretical analysis and comparison of the two different situations by constructing Brunovsky’s canonical form.

Situation ①: choose the state variable of output voltage with a two-order relative degree to the system for the design, and let ${\dot{e}}_2={\dot{x}}_2-{\dot{x}}_{2ref}$ equal to the linear control law v. The actively constructed Brunovsky’s canonical form is:

$$\left[\begin{array}{c}{\dot{e}}_1\\ {\dot{e}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{e}_1\\ e_2\end{array}\right]+\left[\begin{array}{c}0\\ 1\end{array}\right]v.$$

(3)

Situation ②: choose the state variable of inductance current with a one-order relative degree to the system for the design, and let ${\dot{e}}_1={\dot{x}}_1-{\dot{x}}_{1ref}$ equal to the linear control law v, the actively constructed Brunovsky’s canonical form is:

$$\left[\begin{array}{c}{\dot{e}}_2\\ {\dot{e}}_1\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{e}_2\\ e_1\end{array}\right]+\left[\begin{array}{c}0\\ 1\end{array}\right]v.$$

(4)

3. Application of Sliding Mode Control

Different measures are needed to solve the control law of the system for the above two cases. For situation ①, based on Equation (3), the following can be obtained:

$${\dot{e}}_2={\dot{x}}_2-{\dot{x}}_{2ref}=v.$$

(5)

Further derivatives of both sides of Equation (5) are:

$${\ddot{e}}_2={\ddot{x}}_2-{\ddot{x}}_{2ref}=\dot{v}.$$

(6)

Since x₂ (or e₂) has a two-order relative degree to the system, the following Equation holds:

$$\begin{array}{l}{\ddot{x}}_2=L_f^2{x}_2+L_g{L}_f{x}_2·d\\ =-\frac{x_1}{R{C}^2}+(\frac{1}{R^2{C}^2}-\frac{1}{LC})x_2+\frac{P{x}_1}{C^2{x}_2^2}-\frac{P^2}{C^2{x}_2^3}+\frac{E}{LC}d.\end{array}$$

(7)

Combined Equation (6) with Equation (7), the control law of the original nonlinear system can be obtained as:

$$d=[\dot{v}+\frac{x_1}{R{C}^2}-(\frac{1}{R^2{C}^2}-\frac{1}{LC})x_2-\frac{P{x}_1}{C^2{x}_2^2}+\frac{P^2}{C^2{x}_2^3}]\frac{LC}{E}.$$

(8)

From (8), It is known that to find the original nonlinear control law d, we must first solve $\dot{v}$, and the following is the solution using sliding mode control theory.

Choosing the Lyapunov function:

$$V=\frac{1}{2}{s}^2,$$

(9)

where s is the sliding mode surface function to be found with respect to time t.

If the sliding mode approach law is used, then:

$$\dot{s}=-\epsilon sgn(s)-ks \epsilon >0,k>0.$$

(10)

In order to weaken the jitter existing in the sliding mode, replacing the symbolic function sgn(s) with the saturated continuous function sat(s). By such a continuous process, using the normal switching control outside the boundary layer can make the system converge to the sliding mode quickly, and the feedback control is used inside the boundary layer can reduce the jitter generated by the sliding mode during the fast switching [26].

$$sat(s)=\{\begin{array}{c}1s>\mu \\ \frac{s}{\mu }\left|s\right|<\mu \\ -1s<-\mu \end{array}\mu >0,$$

where μ is the thickness of the boundary layer, and the value is related to the control effect of the controller. Figure 2 shows the sliding process and the graphical representation of the sliding surface and boundary layer.

Then, the sliding mode approach law changes to:

$$\dot{s}=-\epsilon sat(s)-ks \epsilon >0,k>0.$$

(11)

So

$$\dot{V}=s\dot{s}=s(-\epsilon sat(s)-ks)\le -\epsilon \left|s\right|-k{s}^2\le -\frac{k}{2}V.$$

(12)

The solution is:

$$V(t)\le e^{-\frac{k}{2}(t-t_0)}V(t_0).$$

(13)

It can be seen that the V(t) exponent converges to 0 and the convergence rate is related to k. Therefore, according to Equation (9), $\underset{t\to \infty }{\lim }s=0$ holds. That is, the system designed with this convergence rate will eventually stabilize on the sliding mode surface.

The next step is to consider how to construct the sliding mode function s. For the system to stabilize on the sliding mode surface and the state quantities converge to their reference values, the following sliding mode surface is used to derive $\dot{v}$, such that:

$$s={\dot{e}}_2+c_1{e}_1+c_2{e}_2,$$

(14)

where c₁, c₂ are parameters. Combining Equations (2), (3), (6) and (14) we obtain the relationship between $\dot{s}$ and $\dot{v}$ as follows:

$$\begin{array}{l}\dot{s}={\ddot{e}}_2+c_1{\dot{e}}_1+c_2{\dot{e}}_2\\ =\dot{v}+c_1{e}_2+c_2{\dot{x}}_2\\ =\dot{v}+c_1{e}_2+c_2(\frac{x_1}{C}-\frac{x_2}{RC}-\frac{P}{C{x}_2}).\end{array}$$

(15)

Reconnecting Equations (11) and (15) the expression for $\dot{v}$ can be found:

$$\dot{v}=-\epsilon sat(s)-ks-c_1{e}_2-c_2(\frac{x_1}{C}-\frac{x_2}{RC}-\frac{P}{C{x}_2}).$$

(16)

Finally, substituting Equation (16) into Equation (8) to obtain the final desired control law of the initial nonlinear system:

$$\begin{array}{c}d=[-\epsilon sat(s)-ks-c_1{e}_2-c_2(\frac{x_1}{C}-\frac{x_2}{RC}-\frac{P}{C{x}_2})\\ +\frac{x_1}{R{C}^2}-(\frac{1}{R^2{C}^2}-\frac{1}{LC})x_2-\frac{P{x}_1}{C^2{x}_2^2}+\frac{P^2}{C^2{x}_2^3}]\frac{LC}{E}.\end{array}$$

(17)

The following is an analysis of the tracking performance of system (3), which is a controllable system and, under the control law control of Equation (17), if system (3) can be stabilized, then there is:

$${\dot{e}}_1={\dot{e}}_2=0.$$

(18)

Thus, according to Equation (3) there is:

$${\dot{e}}_1=e_2=0.$$

(19)

According to the principle of approaching law-based sliding mode control, the system will eventually stabilize at the sliding mode surface, i.e.,

$$s={\dot{e}}_2+c_1{e}_1+c_2{e}_2=0,$$

(20)

thus, there is $e_1=0$.

In summary, there are:

$$\{\begin{array}{c}{e}_1=e_2=0\\ {\dot{e}}_1={\dot{e}}_2=0\end{array}$$

(21)

This ensures both static and dynamic performance of system (3), and each state variable keeps track of its own target value.

For situation ②, according to Equation (4), we can obtain:

$${\dot{e}}_1={\dot{x}}_1-{\dot{x}}_{1ref}={\dot{x}}_1=v.$$

(22)

Since x₁ (or e₁) has a one-order relative order to the system, the following equation holds:

$${\dot{x}}_1=-\frac{x_2}{L}+\frac{E}{L}d.$$

(23)

Thus

$$d=\frac{(Lv+x_2)}{E}.$$

(24)

To find the original nonlinear control law d, we must first solve for v. Similarly to situation ①, using sliding mode control design method, let the sliding mode function

$$s=e_1+c_2{e}_2+c_1{\displaystyle {\int }_0^t{e}_2}d\tau .$$

(25)

Combining Equations (4) and (25), we have:

$$\dot{s}={\dot{e}}_1+c_2{\dot{e}}_2+c_1{e}_2=v+c_2{e}_1+c_1{e}_2.$$

(26)

In this case, if we use the same exponential approximation law with saturation function as Equation (11), then Equations (11) and (26) are combined to obtain:

$$v=-\epsilon sat(s)-ks-c_2{e}_1-c_1{e}_2.$$

(27)

In Equation (25) of the sliding mode surface, the introduction of the traditional integral term is beneficial to the intuitive analysis of the principle, but it may lead to the deterioration of the transient performance of the system in the experiment because of the large initial error, so a nonlinear integral sliding mode surface can also be introduced in the real experiment, and the traditional integral term in the original sliding mode surface is replaced by the nonlinear integral term. Using this method can eliminate the steady-state error without generating large overshoot, and has good spreading performance [27,28], The form of this sliding mode surface containing nonlinear integral term is as follows:

$$\{\begin{array}{l}s=e_1+c_2{e}_2+c_1\sigma \hfill \\ \dot{\sigma }=g(e_2)\hfill \end{array}$$

(28)

where g(e₂) is a smooth nonlinear saturation function with “small error amplification and large error saturation”, which is obtained by deriving the potential energy function for e₂ as follows:

$$G(e_2)=\{\begin{array}{l}\frac{2{\beta }^2}{\pi }\left(1-\cos \left(\frac{\pi }{2\beta }{e}_2\right)\right),\left|e_2\right|<\beta \\ \beta e_2-\frac{\pi -2}{\pi }{\beta }^2,e_2\ge \beta \\ -\beta e_2-\frac{\pi -2}{\pi }{\beta }^2,e_2\le -\beta \end{array}$$

(29)

where $\beta >0$ is the design parameter. The derivative of the above equation with respect to e₂ yields a nonlinear function g(e₂), as shown below:

$$g(e_2)=\{\begin{array}{l}\beta \sin \left(\frac{\pi e_2}{2\beta }\right),\left|e_2\right|<\beta \\ \begin{array}{l}\beta ,e_2\ge \beta \\ -\beta ,e_2\le -\beta \end{array}\end{array}$$

(30)

For the functions G(e₂) and g(e₂) it is not difficult to derive the following properties:

Property (1): G(e₂) is continuous quadratic differentiable.

Property (2): If $e_2\ne 0$, then $G(e_2)>0$; If $e_2=0$, then $G(e_2)=g(e_2)=0$.

Combine Equations (4), (11) and (28), then the expression for v obtained by using the modified integral sliding mode surface is:

$$v=-\epsilon sat(s)-ks-c_2{e}_1-c_{1}g(e_2).$$

(31)

According to Equations (24) and (31), the initial nonlinear control rate of the system is obtained:

$$d=\frac{L(-\epsilon sat(s)-ks-c_2{e}_1-c_{1}g(e_2))+x_2}{E}$$

(32)

Regarding the tracking performance of the system, in the stable case system (4), we have $e_1={\dot{e}}_2={\dot{e}}_1=0$, since $s=e_1+c_2{e}_2+c_1\sigma =0$ and $\dot{s}$ are consistently continuous when $t\to \infty$, it follows from Barbalat’s lemma that when $t\to \infty$, there is:

$$\dot{s}={\dot{e}}_1+c_2{\dot{e}}_2+c_{1}g(e_2)=0.$$

(33)

We can obtain $\underset{t\to \infty }{\lim }{e}_2=0$, and in summary, when $t\to \infty$, the system is stabilized on this nonlinear integral sliding mode surface and also has $e_1=e_2={\dot{e}}_1={\dot{e}}_2=0$.

4. Stability Analysis

This section shows how we make the system stable by choosing the values of the parameters c₁ and c₂ under the control method proposed in this paper. Only the case where the equilibrium point of the nonlinear system $x_e={[x_{1e},x_{2e}]}^T$ is hyperbolic is discussed in this article. According to the Hartman–Grobman theorem, the dynamical system orbit of a nonlinear system near the hyperbolic equilibrium point structure is topologically equivalent to the orbital structure of a linearized dynamical system, so that the nonlinear system is also stable if the first-order approximate linear system of the original nonlinear system is stable in the neighborhood Ω of the eligible equilibrium point. The equation of the state of the original system is now expanded by the Taylor series at the equilibrium point x_e and, after neglecting the higher-order terms, we have:

$$\{\begin{array}{l}{\dot{x}}_{1o}=-\frac{x_{2o}}{L}+\frac{E}{L}{d}_o\hfill \\ {\dot{x}}_{2o}=\frac{x_{1o}}{C}+\left(\frac{P}{C{x}_{2e}^2}-\frac{1}{RC}\right)x_{2o}\hfill \end{array}$$

(34)

Let Ω be a neighborhood of the equilibrium point x_e that satisfies the conditions of the Hartman–Grobman theorem, and $x_o={\left[x_{1o},x_{2o}\right]}^T$ be the dynamic trajectory of the system state variables in this neighborhood. Assuming that $x_{or}={\left[x_{1or},x_{2or}\right]}^T$ is the reference trajectory, its trajectory must also satisfy Equation (34), so that we have:

$$\{\begin{array}{l}{\dot{x}}_{1or}=-\frac{x_{2or}}{L}+\frac{E}{L}{d}_{or}\hfill \\ {\dot{x}}_{2or}=\frac{x_{1or}}{C}+\left(\frac{P}{C{x}_{2e}^2}-\frac{1}{RC}\right)x_{2or}\hfill \end{array}$$

(35)

Let e_s = x_o − x_or, then the equation of state of the error system is:

$${\dot{e}}_s=\left[\begin{array}{cc}0& -\frac{1}{L}\\ \frac{1}{C}& \frac{P}{C{x}_{2e}^2}-\frac{1}{RC}\end{array}\right]e_s+\left[\begin{array}{c}\frac{E}{L}\\ 0\end{array}\right](d_o-d_{or}).$$

(36)

The following will be the ideal case where the system is stabilized at the sliding mode surface, i.e., s = 0 for situations ① and ② is analyzed:

Situation ①:

$${\dot{v}}_o=-\epsilon sat(s)-ks-c_1{e}_{2s}-c_2{\dot{e}}_{2s}=-c_1{e}_{2s}-c_2{\dot{e}}_{2s}.$$

(37)

Since x_2o has a one-order relative degree to the system,

$${\ddot{x}}_{2o}=-\frac{x_{1o}}{R{C}^2}+\frac{P{x}_{1o}}{C^2{x}_{2e}^2}+(\frac{1}{R^2{C}^2}-\frac{1}{LC})x_{2o}+\frac{3P^2{x}_{2o}}{C^2{x}_{2e}^4}-\frac{2P{x}_{1e}{x}_{2o}}{C^2{x}_{2e}^3}+\frac{E}{LC}{d}_o.$$

(38)

Then the reference trajectory x_2or also satisfies

$${\ddot{x}}_{2or}=-\frac{x_{1or}}{R{C}^2}+\frac{P{x}_{1or}}{C^2{x}_{2e}^2}+(\frac{1}{R^2{C}^2}-\frac{1}{LC})x_{2or}+\frac{3P^2{x}_{2or}}{C^2{x}_{2e}^4}-\frac{2P{x}_{1e}{x}_{2or}}{C^2{x}_{2e}^3}+\frac{E}{LC}{d}_{or}.$$

(39)

According to the principle of linearization of objective holographic feedbacks and linearization based on sliding mode control described earlier, the control law of the system (36) is designed as follows:

$$\begin{array}{l}{d}_o=\frac{LC}{E}({\dot{v}}_o+{\ddot{x}}_{2or}+\frac{x_{1o}}{R{C}^2}-\frac{P{x}_{1o}}{C^2{x}_{2e}^2}-(\frac{1}{R^2{C}^2}-\frac{1}{LC})x_{2o}-\frac{3P^2{x}_{2o}}{C^2{x}_{2e}^4}+\frac{2P{x}_{1e}{x}_{2o}}{C^2{x}_{2e}^3})\\ =\frac{LC}{E}(-c_1{e}_{2s}-c_2{\dot{e}}_{2s}+\frac{e_{1s}}{R{C}^2}-\frac{P{e}_{1s}}{C^2{x}_{2e}^2}-(\frac{1}{R^2{C}^2}-\frac{1}{LC})e_{2s}\\ -\frac{3P^2{e}_{2s}}{C^2{x}_{2e}^4}+\frac{2P{x}_{1e}{e}_{2s}}{C^2{x}_{2e}^3}+\frac{E}{LC}{d}_{or}).\end{array}$$

(40)

Bringing Equation (40) into Equation (36) yields:

$$\{\begin{array}{l}\begin{array}{c}{\dot{e}}_{1s}=(\frac{1}{RC}-\frac{P}{C{x}_{2e}^2})e_{1s}+(\frac{2P{x}_{1e}}{C{x}_{2e}^3}-\frac{3P^2}{C{x}_{2e}^4}\\ -\frac{1}{R^{2}C}-C{c}_1)e_{2s}-C{c}_2{\dot{e}}_{2s}\end{array}\hfill \\ {\dot{e}}_{2s}=\frac{e_{1s}}{C}+\left(\frac{P}{C{x}_{2e}^2}-\frac{1}{RC}\right)e_{2s}\hfill \end{array}$$

(41)

So

$$\{\begin{array}{l}\begin{array}{c}{\dot{e}}_{1s}=(\frac{1}{RC}-\frac{P}{C{x}_{2e}^2}-c_2)e_{1s}+(\frac{2P{x}_{1e}}{C{x}_{2e}^3}\\ -\frac{c_{2}P}{x_{2e}^2}-\frac{3P^2}{C{x}_{2e}^4}-\frac{1}{R^{2}C}-C{c}_1+\frac{c_2}{R})e_{2s}\end{array}\hfill \\ {\dot{e}}_{2s}=\frac{e_{1s}}{C}+\left(\frac{P}{C{x}_{2e}^2}-\frac{1}{RC}\right)e_{2s}\hfill \end{array}$$

(42)

The system matrix of this autonomous system is:

$$A=\left[\begin{array}{ll}\frac{1}{RC}-\frac{P}{C{x}_{2e}^2}-c_2\hfill & \frac{2P{x}_{1e}}{C{x}_{2e}^3}-\frac{c_{2}P}{x_{2e}^2}-\frac{3P^2}{C{x}_{2e}^4}-\frac{1}{R^{2}C}-C{c}_1+\frac{c_2}{R}\hfill \\ \frac{1}{C}\hfill & \frac{P}{C{x}_{2e}^2}-\frac{1}{RC}\hfill \end{array}\right]$$

(43)

Putting Equation (43) into $\left|\lambda E-A\right|$ to obtain the characteristic polynomial gives:

$${\lambda }^2+c_2\lambda +c_1+\frac{2P}{R{C}^2{x}_{2e}^2}+\frac{3P^2}{C^2{x}_{2e}^4}-\frac{P^2}{C^2{x}_{2e}^4}-\frac{2P{x}_{1e}}{C^2{x}_{2e}^3}.$$

(44)

From Equation (44), for the two-order system characteristic equation, according to the Hurwitz criterion, the system (36) can be stabilized only by choosing the values of the parameters c₁, c₂, so that

$$\{\begin{array}{c}{c}_2>0\\ c_1+\frac{2P}{R{C}^2{x}_{2e}^2}+\frac{3P^2}{C^2{x}_{2e}^4}-\frac{P^2}{C^2{x}_{2e}^4}-\frac{2P{x}_{1e}}{C^2{x}_{2e}^3}>0\end{array}$$

(45)

Situation ②, the analysis method is similar to situation ①; if the conventional integral sliding mode surface is used, then when s = 0

$$v_o=-\epsilon sat(s)-ks-c_2{e}_{1s}-c_1{e}_{2s}=-c_2{e}_{1s}-c_1{e}_{2s}.$$

(46)

Since x_1o has a one-order relative degree to the system,

$${\dot{x}}_{1o}=-\frac{x_{2o}}{L}+\frac{E}{L}{d}_o.$$

(47)

Then the reference trajectory x_1or also satisfies,

$${\dot{x}}_{1or}=-\frac{x_{2or}}{L}+\frac{E}{L}{d}_{or}.$$

(48)

Let the system (36) of the control law be as follows:

$$\begin{array}{l}{d}_o=\frac{L}{E}(v_o+{\dot{x}}_{1or}+\frac{x_{2o}}{L})\\ =\frac{L}{E}(-c_2{e}_{1s}-c_1{e}_{2s}-\frac{x_{2or}}{L}+\frac{E}{L}{d}_{or}+\frac{x_{2o}}{L})\\ =\frac{L}{E}(-c_2{e}_{1s}-c_1{e}_{2s}+\frac{e_{2s}}{L}+\frac{E}{L}{d}_{or}).\end{array}$$

(49)

Bringing Equation (49) into Equation (36) yields:

$$\{\begin{array}{l}{\dot{e}}_{1s}=-c_2{e}_{1s}-c_1{e}_{2s}\hfill \\ {\dot{e}}_{2s}=\frac{e_{1s}}{C}+(\frac{P}{C{x}_{2e}^2}-\frac{1}{RC})e_{2s}\hfill \end{array}$$

(50)

Let

$$A=\left[\begin{array}{cc}-c_2& -c_1\\ \frac{1}{C}& (\frac{P}{C{x}_{2e}^2}-\frac{1}{RC})\end{array}\right].$$

(51)

Putting Equation (51) into $\left|\lambda E-A\right|$ to obtain the characteristic polynomial:

$${\lambda }^2+(c_2+\frac{1}{RC}-\frac{P}{C{x}_{2e}^2})\lambda +\frac{c_2}{RC}+\frac{c_1}{C}-\frac{c_{2}P}{C{x}_{2e}^2},$$

(52)

also, based on the Hurwitz criterion, choosing the values of the parameters c₁ and c₂, so that

$$\{\begin{array}{c}{c}_2+\frac{1}{RC}-\frac{P}{C{x}_{2e}^2}>0\\ \frac{c_2}{RC}+\frac{c_1}{C}-\frac{c_{2}P}{C{x}_{2e}^2}>0\end{array}$$

(53)

System (36) can be stable.

If using a modified nonlinear integral sliding mode surface, we can obtain $\underset{t\to \infty }{\lim }\dot{s}=0$ from Equation (33), then combined with the deviated system equation of state (4) with $t\to \infty$, when

$$\dot{s}={\dot{e}}_1+c_2{\dot{e}}_2+c_{1}g(e_2)={\ddot{e}}_2+c_2{\dot{e}}_2+c_{1}g(e_2)=0.$$

(54)

The alternative Lyapunov function is:

$$V_1=\frac{1}{2}{\dot{e}}_2^2+c_{1}G(e_2).$$

(55)

Notice that $G(e_2)$ is a radially unbounded function, and from property 2 of $G(e_2)$, we know that $G(0)=0$, $e_2\ne 0$ when $G(e_2)>0$, so when $c_1>0$, Equation (55) is also a radially unbounded and positive definite function. Calculating the derivative function of Equation (55) along Equation (54) and letting $c_2>0$ yields:

$$\begin{array}{l}{\dot{V}}_1={\dot{e}}_2{\ddot{e}}_2+c_{1}g(e_2){\dot{e}}_2\\ ={\dot{e}}_2(-c_2{\dot{e}}_2-c_{1}g(e_2))+c_{1}g(e_2){\dot{e}}_2\\ =-c_2{\dot{e}}_2^2\le 0.\end{array}$$

(56)

Let ${\dot{V}}_1\equiv 0$ then ${\dot{e}}_2\equiv 0$, so ${\ddot{e}}_2=0$; bringing this into Equation (54), we obtain $e_2=0$, and then combined with Equation (4), we have $e_1={\dot{e}}_2\equiv 0$, and we can obtain ${\dot{e}}_1=0$. So, in summary, by solving ${\dot{V}}_1\equiv 0$, we can obtain ${\dot{e}}_1={\dot{e}}_2=e_1=e_2=0$.

This solution is exactly the steady-state solution of system (4). Therefore, it is known from LaSalle’s invariance principle that the system with this nonlinear integral sliding mode surface for sliding mode control is asymptotically stable at $c_1>0,c_2>0$, and the state quantities converge to the reference value at $t\to \infty$.

5. Simulation and Experimental Results

A buck converter with a mixed-load simulation model was implemented on the MATLAB/Simulink simulation platform to evaluate the performance of the proposed nonlinear control strategy, as shown in Figure 3.

Compare conventional OHFLC method with the proposed control strategy using the circuit parameters of the buck converter with L = 0.56 mH, C = 470 μF, and fs = 20 kHz. In the conventional OHFLC method, the scale factors selected in the simple optimal quadratic control law are, respectively, k₁ = 1.2 × 10⁴ and k₂ = 1 × 10⁵. The parameters selected for the proposed control strategy in situation ① are c₁ = 2 × 10³, c₂ = 4 × 10⁵, ε = 5 × 10³, k = 4 × 10², μ = 0.1. In situation ②, c₁ = 2 × 10⁴, c₂ = 4 × 10⁴, ε = 5 × 10³, k = 10, μ = 0.1, β = 0.2.

In Figure 4, v₁, v₂, and v₁₂ represent the output voltages in the CPL leap experiment under the control law of situation ①, the control law of situation ②, and the control law of the conventional OHFLC method, respectively. i₁, i₂, and i₁₂ represent the inductor currents at the above three control laws in the CPL leap experiment, respectively. As shown in Figure 4, the CPL suddenly jumps from 5 W to 15 W at 0.04 s and then drops from 15 W to 5 W at 0.06 s. It can be observed that both control methods stabilize the output voltage at a reference value of 12 V. The overshoot of the proposed control strategy at 0.04 s and 0.06 s is 0.13 V and 0.12 V in situation ①, and 0.07 V and 0.07 V in situation ②, respectively. In contrast, the overshoot of the output voltage at 0.04 s and 0.06 s is 0.11 V and 0.14 V in the conventional OHFLC method. This indicates that, compared to the conventional OHFLC method, the proposed method can obtain a similar or even smaller overshoot than the conventional OHFLC method when changing the CPL. In terms of response time, both methods can complete the dynamic response process in a similar and very short time.

In Figure 5, v₃, v₄, and v₃₄ represent the output voltages in load R leap experiment under the control law of situation ①, the control law of situation ②, and the control law of the conventional OHFLC method, respectively. i₃, i₄, and i₃₄ represent the inductor currents at the above three control laws in the load R leap experiment, respectively. As shown in Figure 5, the load R suddenly drops from 20 Ω to 10 Ω at 0.04 s and then rises from 10 Ω to 20 Ω at 0.06 s. It can be observed that both control methods can stabilize the output voltage at the reference value of 12 V. The overshoot of the proposed control strategy at 0.04 s and 0.06 s is 0.03 V and 0.02 V in situation ① and 0.02 V and 0.03 V in situation ②, respectively, while the overshoot of the output voltage at 0.04 s and 0.06 s is 0.07 V and 0.05 V, respectively, under the conventional OHFLC method. It indicates that, compared to the conventional OHFLC method, the proposed method can obtain a smaller overshoot when changing the resistive load. In terms of response time, both methods can complete the dynamic response process in a similar and very short time.

Therefore, it can be seen from the simulation results that the proposed holographic feedback linearization method based on sliding mode control in this paper is comparable to or even better than the traditional OHFLC method using linear optimal quadratic control in terms of response speed and overshoot.

To further verify the effectiveness of the proposed control strategy, an experimental platform of a buck converter with a mixed load was constructed (see Figure 6), which consists of an ITECH IT8812 DC electronic load, an ITECH IT6952A Auto Range DC power supply as the input, a detection module with two voltage and two current detection circuits integrated. In addition, there are buck converters, load resistors, a digital signal processor (TMS320F28335), and a Tektronix TDS 2024C four-channel digital storage oscilloscope.

The circuit parameters of the buck converter are selected as follows:

• L = 0.56 mH;
• C = 470 μF;
• Power MOSFET (International Rectifier IRF3710);
• The gate drive circuit (International Rectifier IR2109);
• The input voltage E = 24 V;
• The switching frequency fs = 20 kHz.

The detection module used consists of a CHB-25NP Hall current sensor, a CHV-25P Hall voltage sensor followed by a hold circuit, and a proportional circuit to sample the inductor current, the load current, and the output voltage, respectively. The voltage and current collected by the detection circuit and held by a voltage follower, and then the voltage signal outputs after being stepped down by the proportional circuit. Since the load current is directly connected to the oscilloscope in the form of a voltage signal after passing through the detection module, the relationship between the output signal OUT and the input load current is $OUT=0.591i_o$. To ensure the sampling accuracy, the DSP collects the voltage and current data several times, filters them in the program, and takes the average value as the input quantity of the control algorithm.

Figure 7a shows the waveform of experimental prototype with a constant resistance of 20 Ω in situation ①, when P jumps from 5 W to 15 W. The observed phenomenon is a slight drop of about 0.2 V in the output voltage (colored in yellow) at the instant of the CPL change. However, after about 3 ms of adjustment time, it returns to the reference voltage of 12 V. For the same CPL change, the waveform observed in situation ② is shown in Figure 7b, where there is almost no change in output voltage at the instant of load change, and the output voltage always stays near 12 V.

Figure 8a and Figure 8b show the waveforms in situation ① and situation ②, respectively, when the R is constant at 20 Ω, and P jumps from 15 W to 5 W. This process is opposite to the previous CPL change, where the output voltage observed in situation ① rises about 0.2 V at the instant of the CPL jump and returns to the 12 V reference value after about 7 ms. In situation ②, the output voltage remains without significant change and is always stable around 12 V. Experiment results have demonstrated the robustness of the proposed control strategy to CPL variations in mixed loads.

Figure 9a shows the waveform of the experimental prototype with a CPL of 10 W in situation ①, when R jumps from 20 Ω to 10 Ω. The observed phenomenon is a slight drop of about 0.1 V in the output voltage (colored in yellow) at the moment of resistive load R change. However, it returns to the reference voltage of 12 V after about 5 ms of adjustment time. For the same R change, the waveform observed in situation ② is shown in Figure 9b, where there is almost no change in the output voltage at the instant of load change, and the output voltage stays at 12 V.

Figure 10a and Figure 10b show the waveforms in situation ① and situation ②, respectively, when the CPL is constant at 10 W and R jumps from 10 Ω to 20 Ω. The output voltage observed in situation ① rises about 0.1 V at the instant of load R jump and returns to the 12 V reference value after about 3 ms. In situation ②, the output voltage remains without significant change and is always stable around 12 V. Experiment results have demonstrated the robustness of the proposed control strategy to resistive load R variations in mixed loads.

Since the experimental load currents are converted into voltage quantities using Hall element measurements and appropriately reduced to 0.591 times the original by a proportional circuit, and then connected to an oscilloscope for observation, the following table (see

Table 1. Current in different experiments with the ideal conditions.

$R\equiv 20\Omega$	P(W)	iR(A)	iP(A)	io(A) = iR + iP	0.591 io(A)
	5	0.6	0.417	1.017	0.601
	15	0.6	1.25	1.85	1.093
$P\equiv 10\mathrm{W}$	R(Ω)	iR(A)	iP(A)	io(A) = iR + iP	0.591 io(A)
	10	1.2	0.833	2.033	1.202
	20	0.6	0.833	1.433	0.847

) lists the corresponding current on resistor R i_R, current on CPL i_P, the actual load circuit io, and the observed load current 0.591i_o values for different experiments under ideal conditions. We can compare the actual conditions of the current in the experiment with the ideal conditions.

In general, the experimental results are similar to the simulation results. The reason for the error between them can be attributed to the fact that the physical object has various parasitic parameters and more losses than the ideal simulation components, and the electronic load also takes some time to change, which may lead to a slight difference between the experimental and simulation waveforms. Therefore, it can be said that the experimental results are consistent with the simulation results, which proves the correctness and effectiveness of the proposed control strategy.

6. Conclusions

In this paper, a nonlinear control technique based on objective holographic feedback linearization with a sliding mode control is designed for a buck converter by combining CPL with resistive loads. Also, it demonstrates that the proposed control strategy can stabilize the system by adjusting the control parameters, and that each state quantity can track its own reference value. Depending on the relative degree of the state variables incorporated in the output vector, the described method allows for the design of different sliding mode surfaces, and different Brunovsky’s canonical form state space equations formed by error functions for solving the nonlinear control rate of the original system. Unlike the traditional OHFLC method, it does not impose the use of state variables with a one-order relative degree to solve the control law. It broadens the applicability of the OHFLC method. Future work can extend the method to multiple-input multiple-output systems, or higher-order systems.