Design of Efficient Concurrent Dual-Frequency Doherty Power Amplifier Based on Step Impedance Low-Pass Filter
Abstract
:1. Introduction
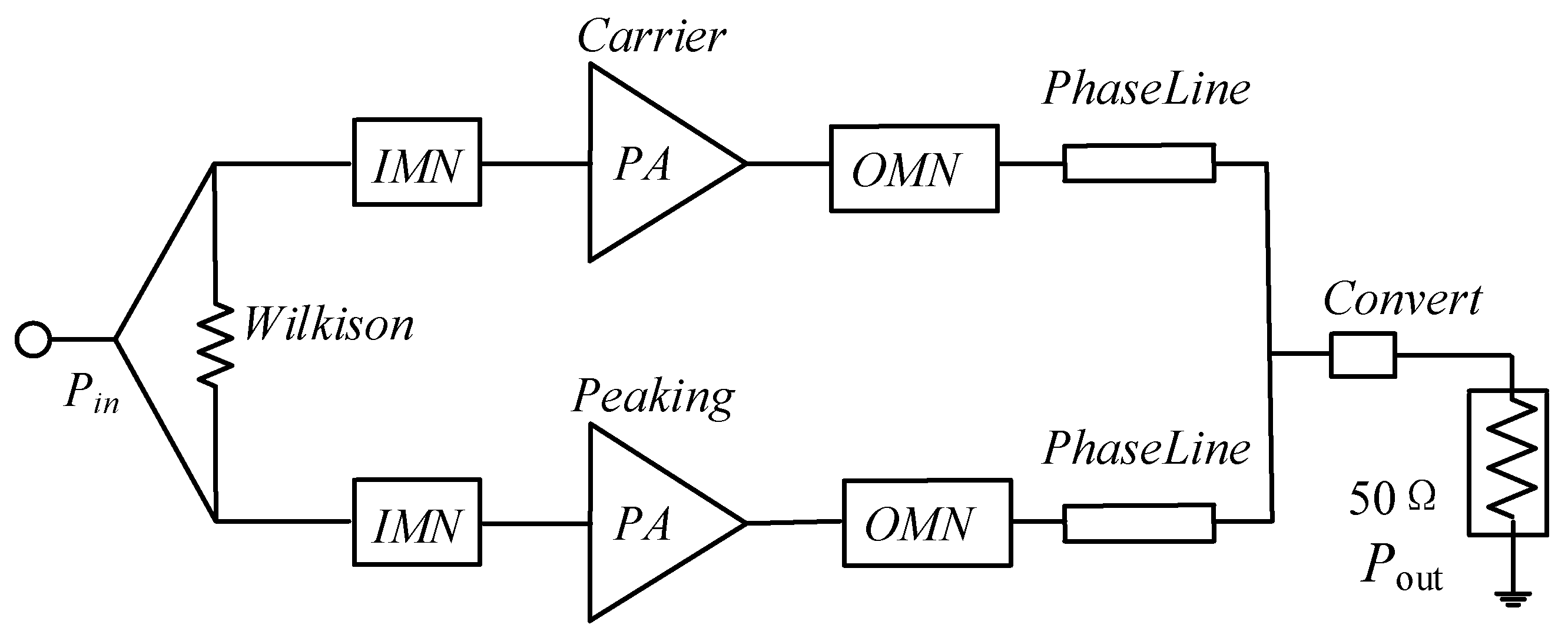
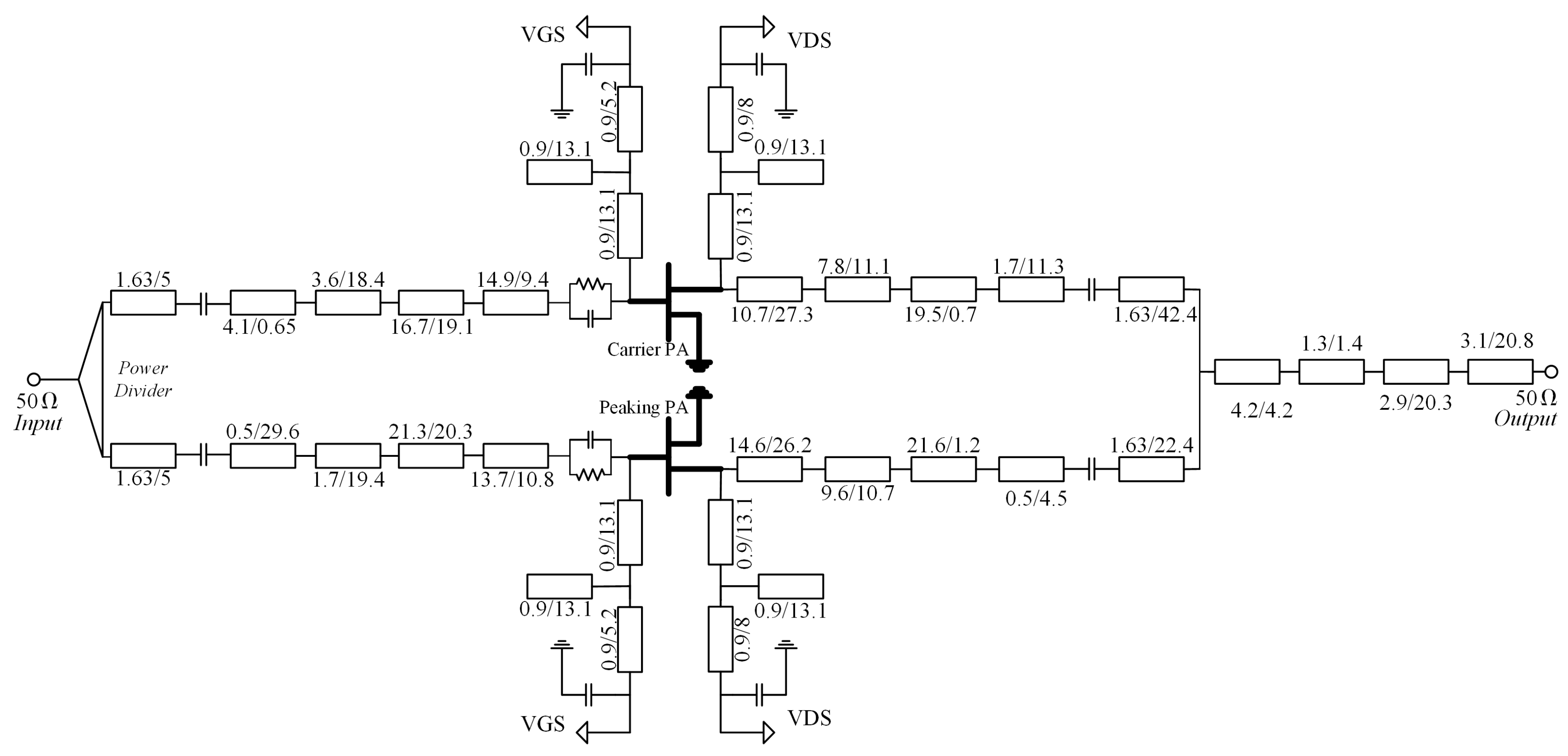
2. Design of Concurrent Dual-Band Doherty Power Amplifier
2.1. Design of Carrier Power Amplifier
2.2. Design of Peak Power Amplifier
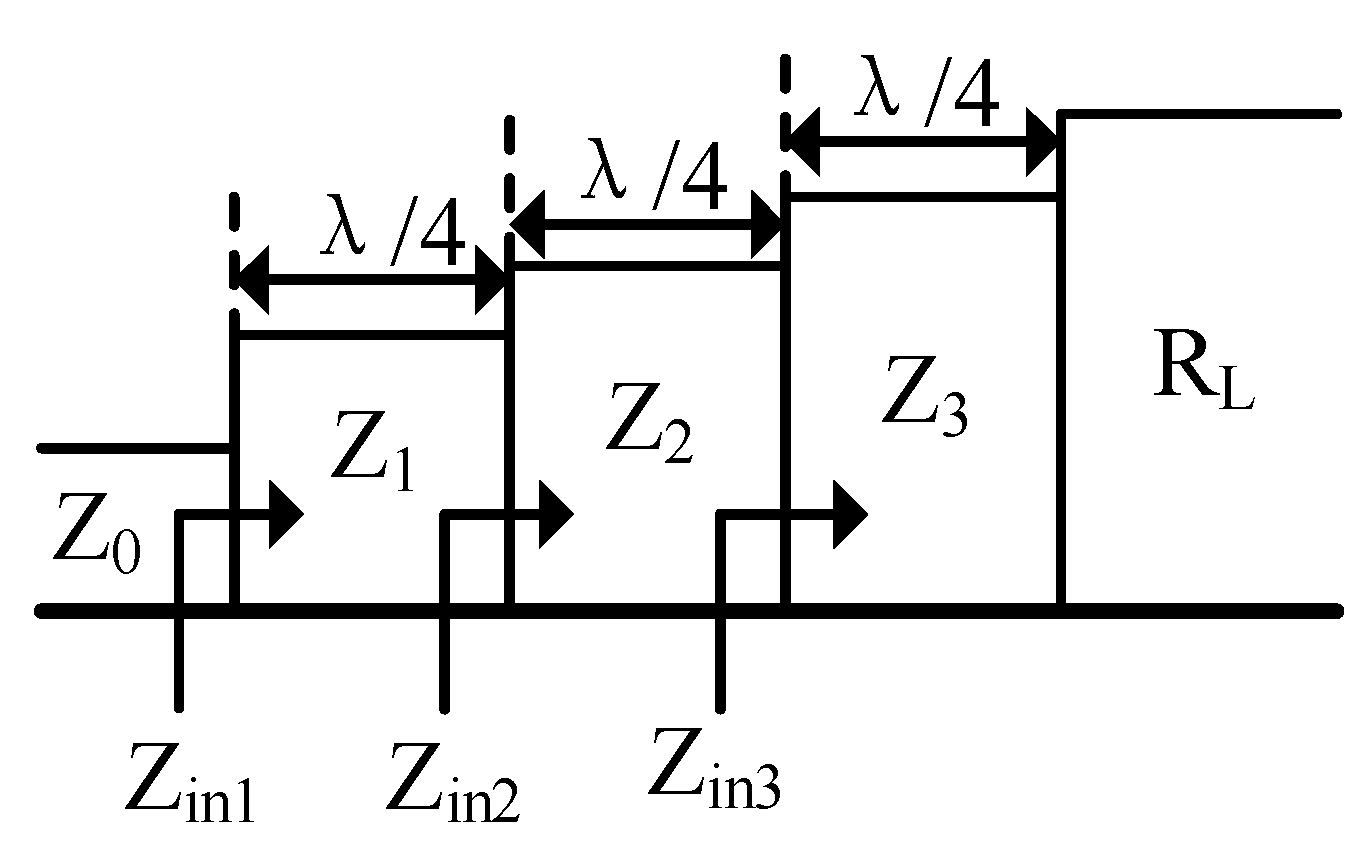
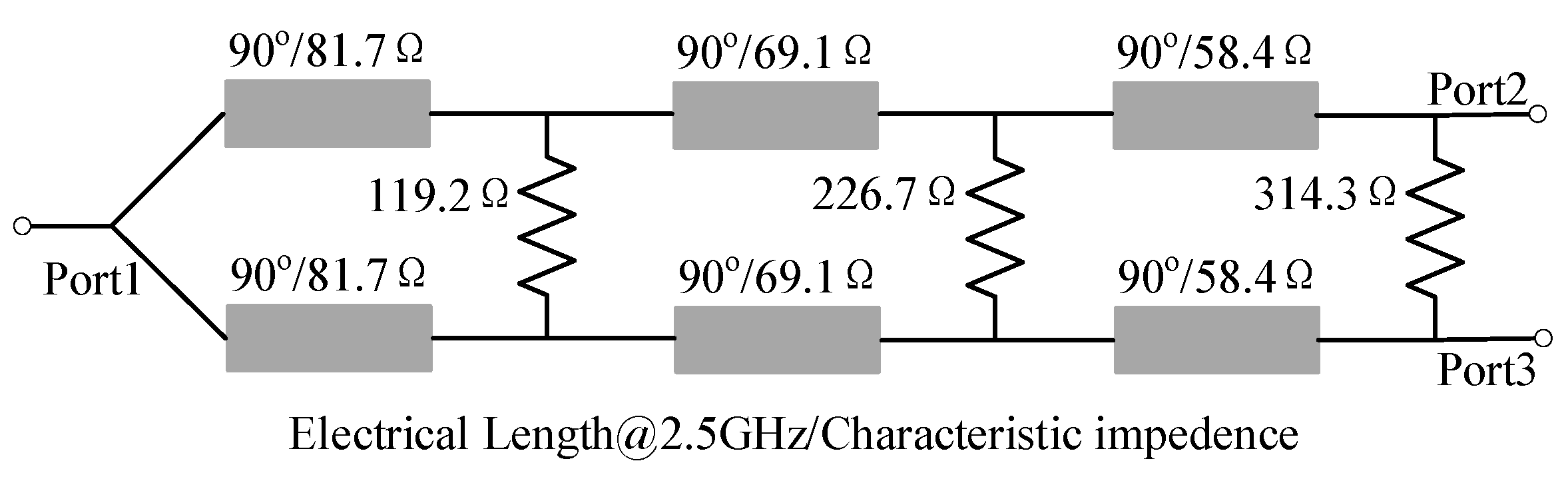
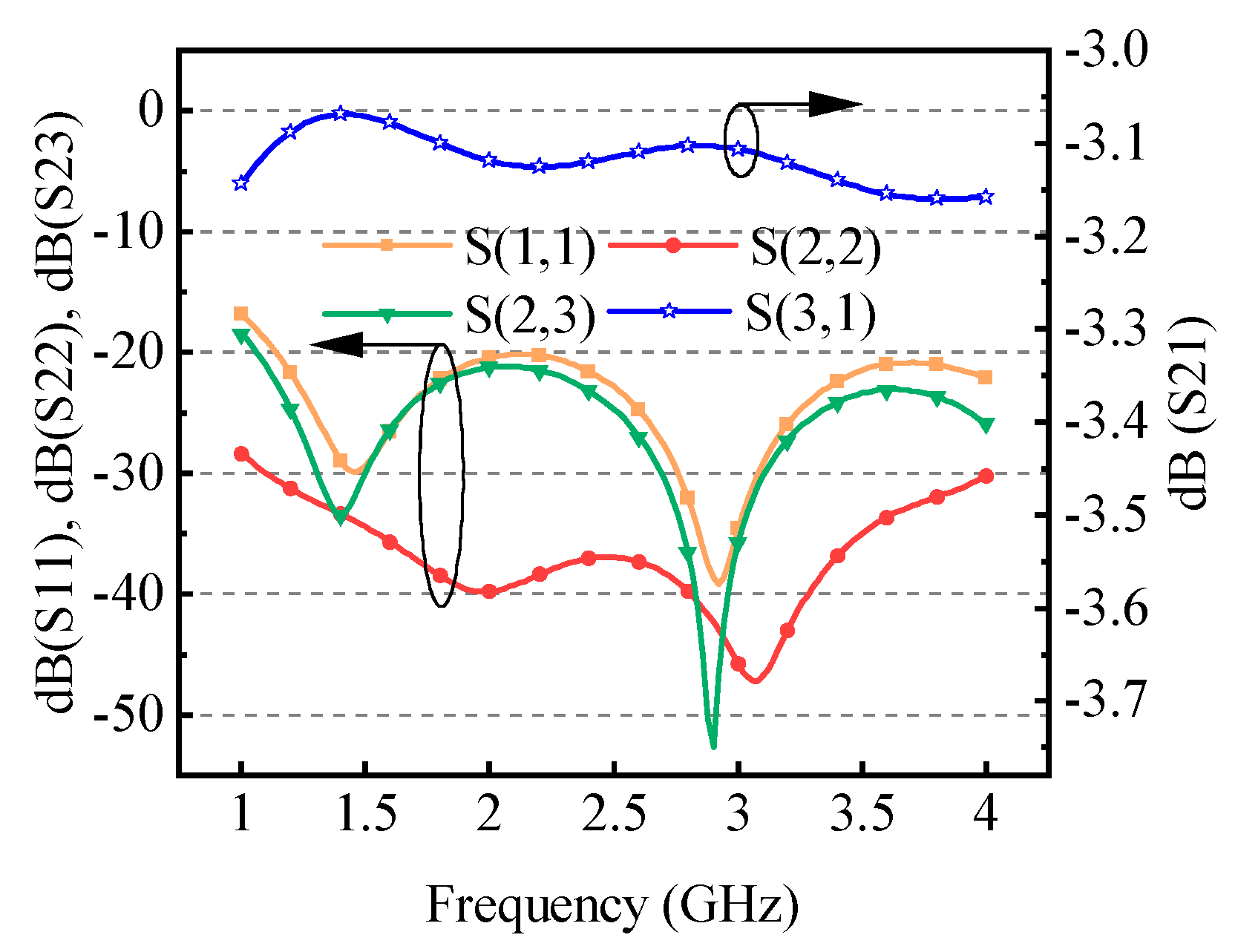
3. Broadband Wilkinson Power Divider
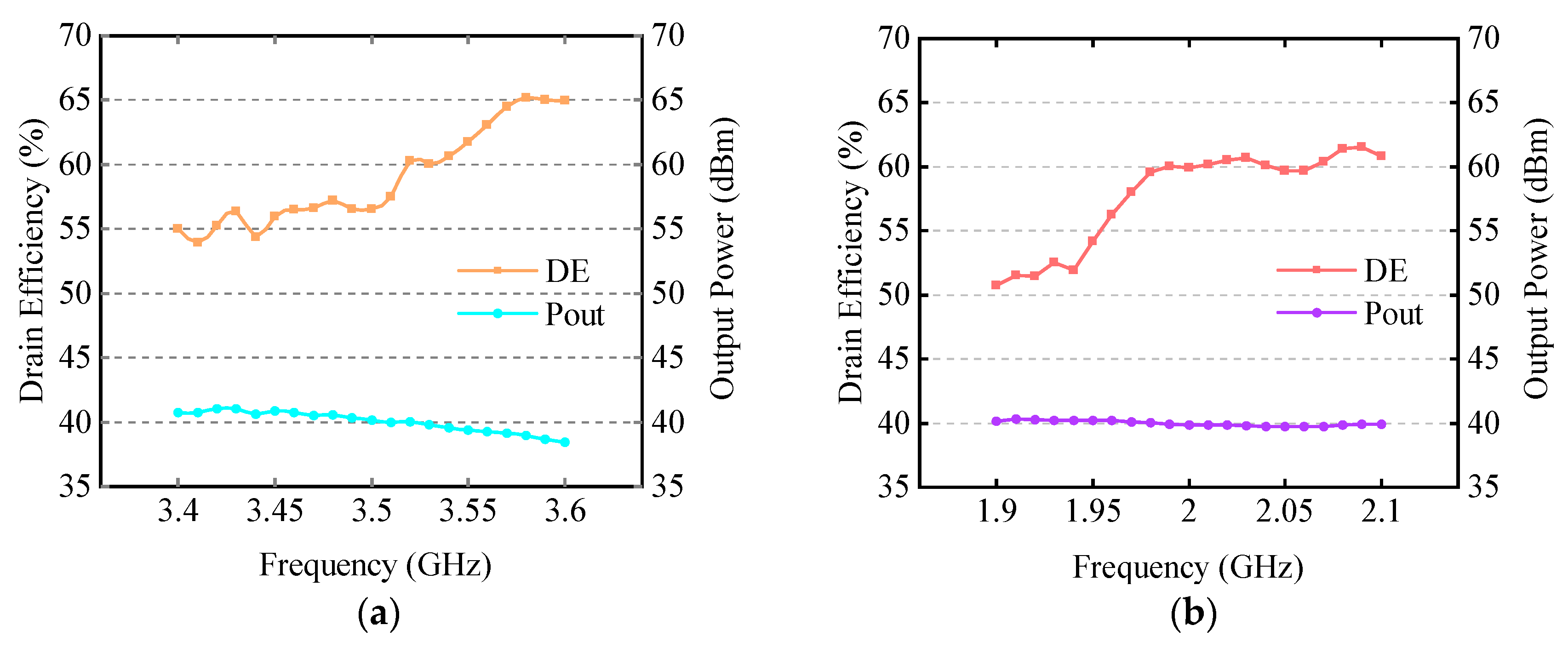
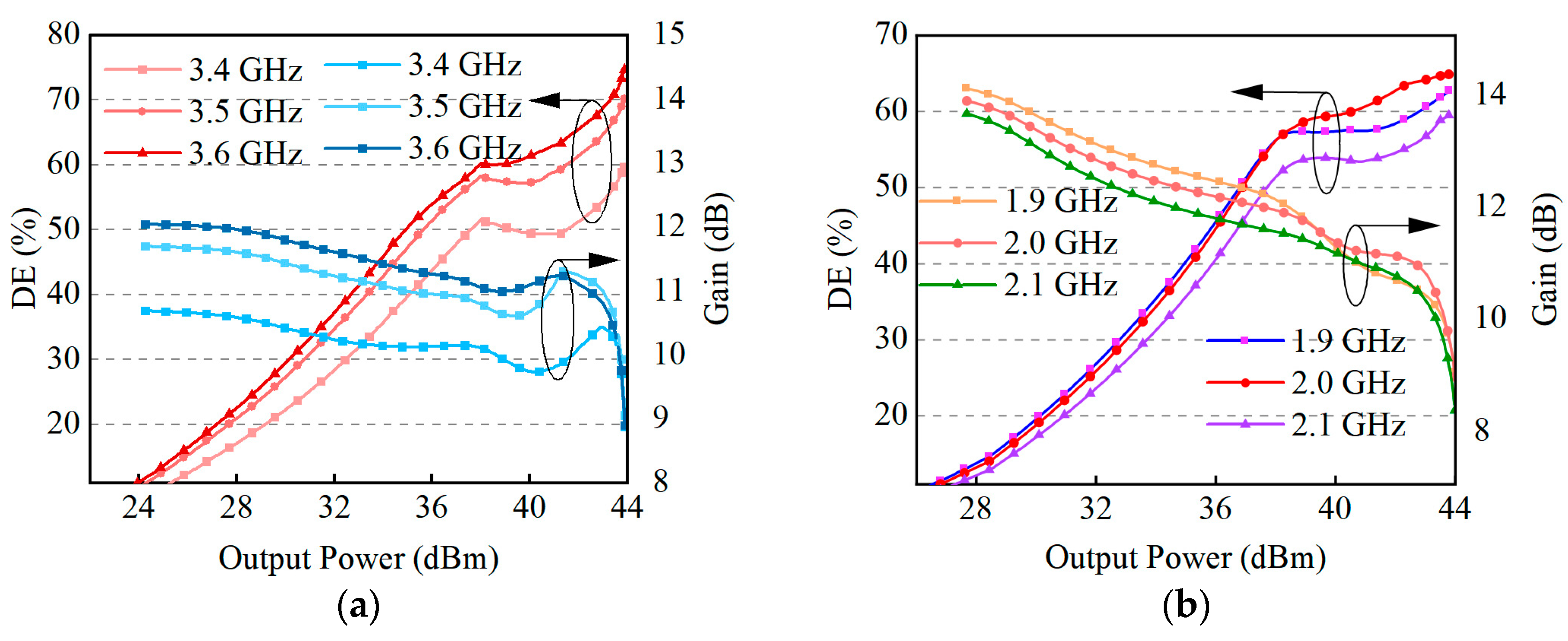
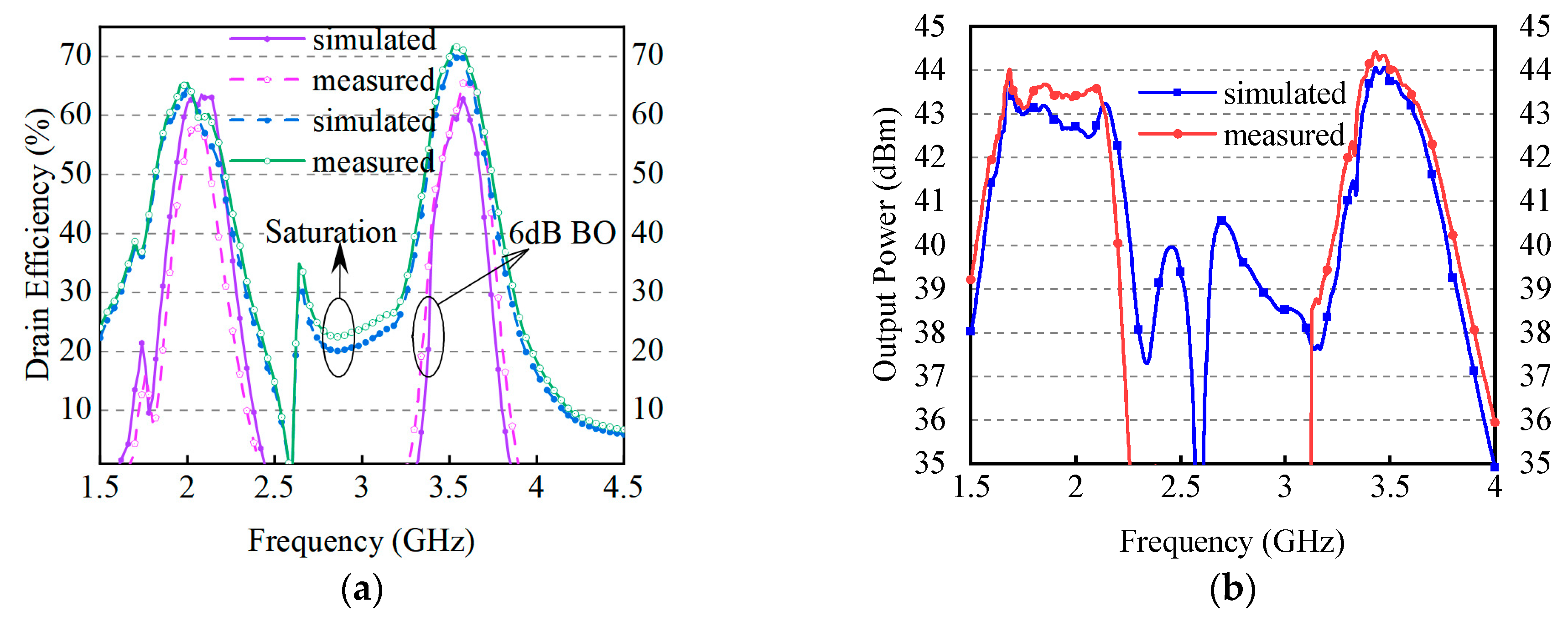
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Li, C.; Xia, X.; Quan, X.; Liu, D.; Xu, Q.; Pan, W.; Tang, Y. Multiband User Equipment Prototype Hardware Design for 5G Communications in Sub-6-GHz Band. IEEE Trans. Microw. Theory Tech. 2019, 67, 2916–2927. [Google Scholar] [CrossRef]
- Lim, J.; Kang, W.; Ku, H. Compensation of path imbalance in LINC transmitters using EVM and ACPR look up tables. In Proceedings of the 2010 Asia-Pacific Microwave Conference, Yokohama, Japan, 7–10 December 2010; pp. 1296–1299. [Google Scholar]
- Su, Z.; Yu, C.; Tang, B. A Concurrent Dual-band Doherty Power Amplifier with Performance Enhancement Using a Novel Impendence Invert Network. In Proceedings of the 2019 IEEE MTT-S International Wireless Symposium (IWS), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar]
- Li, X.; Chen, W.; Zhang, Z.; Feng, Z.; Tang, X.; Mouthaan, K. A concurrent dual-band doherty power amplifier. In Proceedings of the 2010 Asia-Pacific Microwave Conference, Yokohama, Japan, 7–10 December 2010; pp. 654–657. [Google Scholar]
- Yang, F.; Yu, H.; Li, J.; Guo, C.; Yan, S.; Chen, X.; Zhang, A.; Jin, Z. A Class-F Based Power Amplifier with Optimized Efficiency in Triple-Band. Electronics 2022, 11, 310. [Google Scholar] [CrossRef]
- Abdulkhaleq, A.M.; Yahya, M.A.; McEwan, N.; Rayit, A.; Abd-Alhameed, R.A.; Ojaroudi Parchin, N.; Al-Yasir, Y.I.A.; Noras, J. Recent Developments of Dual-Band Doherty Power Amplifiers for Upcoming Mobile Communications Systems. Electronics 2019, 8, 638. [Google Scholar] [CrossRef]
- Rawat, K.; Ghannouchi, F.M. Design Methodology for Dual-Band Doherty Power Amplifier with Performance Enhancement Using Dual-Band Offset Lines. IEEE Trans. Ind. Electron. 2012, 59, 4831–4842. [Google Scholar] [CrossRef]
- Saad, P.; Colantonio, P.; Piazzon, L.; Giannini, F.; Andersson, K.; Fager, C. Design of a Concurrent Dual-Band 1.8–2.4-GHz GaN-HEMT Doherty Power Amplifier. IEEE Trans Microw Theory Tech. 2012, 60, 1840–1849. [Google Scholar] [CrossRef]
- Pang, J.; He, S.; Dai, Z.; Huang, C.; Peng, J.; You, F. Novel design of highly-efficient concurrent dual-band GaN Doherty power amplifier using direct-matching impedance transformers. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar]
- Yildiz, S.; Aksen, A.; Yarman, S.B. Dual band matching network design via real frequency technique by mapping from a band pass prototype. In Proceedings of the 2016 16th Mediterranean Microwave Symposium, Abu Dhabi, United Arab Emirates, 14–16 November 2016; pp. 1–4. [Google Scholar]
- Liu, M.; Golestaneh, H.; Boumaiza, S. A concurrent 2.15/3.4 GHz dual-band Doherty power amplifier with extended fractional bandwidth. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium, San Francisco, CA, USA, 22–27 May 2016; pp. 1–3. [Google Scholar]
- Cidronali, A.; Maddio, S.; Giovannelli, N.; Collodi, G. Frequency analysis and multiline implementation of compensated impedance inverter for wideband Doherty high-power amplifier design. IEEE Trans. Microw. Theory Tech. 2016, 64, 1359–1372. [Google Scholar] [CrossRef]
- Pang, J.; Dai, Z.; Li, Y.; Li, M.; Zhu, A. Multiband dual-mode Doherty power amplifier employing phase periodic matching network and reciprocal gate bias for 5G applications. IEEE Trans. Microw. Theory Tech. 2020, 68, 2382–2397. [Google Scholar] [CrossRef]
- Li, M.; Pang, J.; Li, Y.; Zhu, A. Ultra-wideband dual-mode Doherty power amplifier using reciprocal gate bias for 5G applications. IEEE Trans. Microw. Theory Tech. 2019, 67, 4246–4259. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Lee, M.-W.; Kam, S.-H.; Jeong, Y.-H. A New Wideband Distributed Doherty Amplifier for WCDMA Repeater Applications. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 668–670. [Google Scholar]
- Rubio, J.M.; Fang, J.; Camarchia, V.; Quaglia, R.; Pirola, M.; Ghione, G. 3–3.6-GHz Wideband GaN Doherty Power Amplifier Exploiting Output Compensation Stages. IEEE Trans. Microw. Theory Tech. 2012, 60, 2543–2548. [Google Scholar] [CrossRef]
- Kim, I.; Cha, J.; Hong, S.; Kim, J.; Woo, Y.Y.; Park, C.S.; Kim, B. Highly linear three-way Doherty amplifier with uneven power drive for repeater system. IEEE Microw. Wirel. Compon. Lett. 2006, 16, 176–178. [Google Scholar] [CrossRef]
- Kim, J.; Fehri, B.; Boumaiza, S.; Wood, J. Power efficiency and linearity enhancement using optimized asymmetrical Doherty power amplifiers. IEEE Trans. Microw. Theory Tech. 2011, 59, 425–434. [Google Scholar] [CrossRef]
- Pang, J.; He, S.; Dai, Z.; Huang, C.; Peng, J.; You, F. Design of a post-matching asymmetric Doherty power amplifier for broadband applications. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 52–54. [Google Scholar] [CrossRef]
- Luo, Y.; Xuan, D.; Wang, Z.; Gao, W.; Yang, W.; Yuan, S. A concurrent 2.6/3.5GHz dual-band Doherty power amplifier with matching network based on composite right/left-handed unit cell. IEICE Electron. Express 2022, 19, 20210470. [Google Scholar] [CrossRef]
- Chen, H.; Xu, J.-X.; Chen, W.; Zhang, X.Y. High-Efficiency Dual-Band Filtering Doherty Power Amplifier Based on Multi-Function Circuit. IEEE Trans. Microw. Theory Tech. 2022, 70, 2697–2709. [Google Scholar] [CrossRef]
- Xuan, A.N.; Negra, R. Design of concurrent multiband biasing networks for multiband RF power amplifiers. In Proceedings of the 2012 42nd European Microwave Conference, Amsterdam, The Netherlands, 29 October–1 November 2012; pp. 1–4. [Google Scholar]
- Nasri, A.; Estebsari, M.; Toofan, S.; Piacibello, A.; Pirola, M.; Camarchia, V.; Ramella, C. Design of a Wideband Doherty Power Amplifier with High Efficiency for 5G Application. Electronics 2021, 10, 873. [Google Scholar] [CrossRef]









| Ref. | Frequency/GHz | DE@Sat/DE@OBO/% | Output Power@Sat/@OBO/dBm |
|---|---|---|---|
| [3] | 1.42/2.4 | 69.8/61 and 65.8/52.8 | 43.5/37.5 and 43.6/37.6 |
| [7] | 1.8/2.4 | 64/60 and 54/44 | 43/37 and 43/37 |
| [8] | 0.85/2.33 | 47.5/45 and 41/35 | 44/38 and 42.5/36.5 |
| [10] | 1.96/3.5 | 59.5/50.8 and 49.6/42.9 | 39.2/33.1 and 29.1/24.8 |
| [11] | 1.42/2.24 | 69/61 and 65.8/52.8 | 43.5/37.5 and 43.6/37.6 |
| [20] | 2.6/3.5 | 55.8/49.6 and 55.2/49.3 | 43.3/38.5 and 43.6/38.5 |
| [21] | 2.14/2.6 | 64.4/50 and 69/57 | 43.25/37.25 and 43.3/37.3 |
| This work | 2.0/3.5 | 66/55 and 71/62 | 44.2/38.2 and 43.8/37.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Xu, W.; Nan, J.; Gao, M. Design of Efficient Concurrent Dual-Frequency Doherty Power Amplifier Based on Step Impedance Low-Pass Filter. Electronics 2023, 12, 4092. https://doi.org/10.3390/electronics12194092
Li G, Xu W, Nan J, Gao M. Design of Efficient Concurrent Dual-Frequency Doherty Power Amplifier Based on Step Impedance Low-Pass Filter. Electronics. 2023; 12(19):4092. https://doi.org/10.3390/electronics12194092
Chicago/Turabian StyleLi, Guojin, Wenyuan Xu, Jingchang Nan, and Mingming Gao. 2023. "Design of Efficient Concurrent Dual-Frequency Doherty Power Amplifier Based on Step Impedance Low-Pass Filter" Electronics 12, no. 19: 4092. https://doi.org/10.3390/electronics12194092
APA StyleLi, G., Xu, W., Nan, J., & Gao, M. (2023). Design of Efficient Concurrent Dual-Frequency Doherty Power Amplifier Based on Step Impedance Low-Pass Filter. Electronics, 12(19), 4092. https://doi.org/10.3390/electronics12194092





