Minimally Persistent Graph Generation and Formation Control for Multi-Robot Systems under Sensing Constraints
Abstract
:1. Introduction
2. Preliminaries and Problem Statement
2.1. Rigid and Persistent Graph
2.2. Control Barrier Function
2.3. The Pebble Game Algorithm
2.4. Problem Formulation
3. Main Results
3.1. Definitions
3.2. The FOV Pebble Game
| Algorithm 1 FOV pebble game |
|
| Algorithm 2 |
|
| Algorithm 3 |
|
- 1.
- ,
- 2.
- .
3.3. Distributed Control of Persistent Formation
4. Simulation and Experimental Results
4.1. Simulation Results
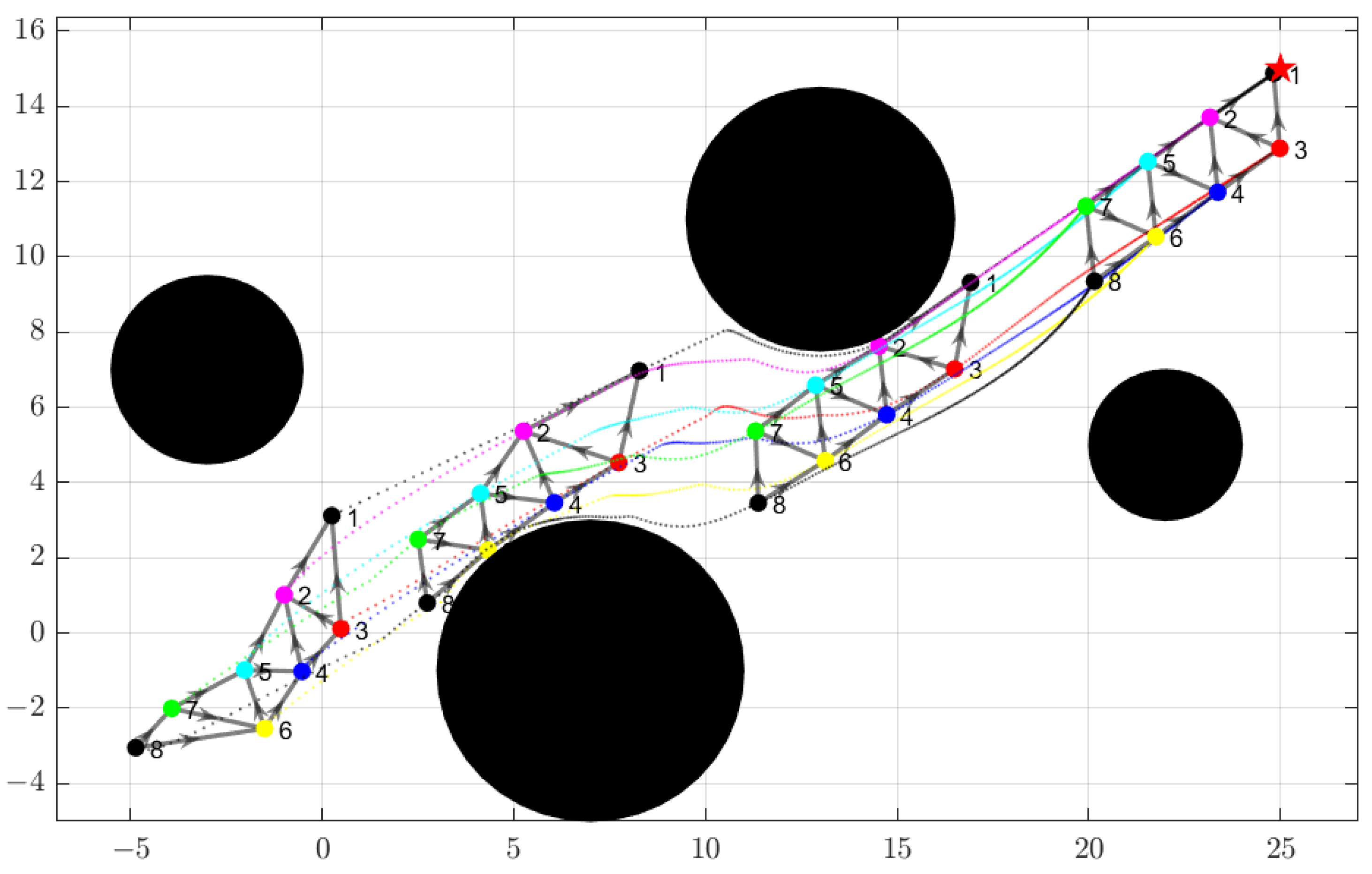
4.1.1. Minimally FOV Persistent Graph
4.1.2. Formation Control
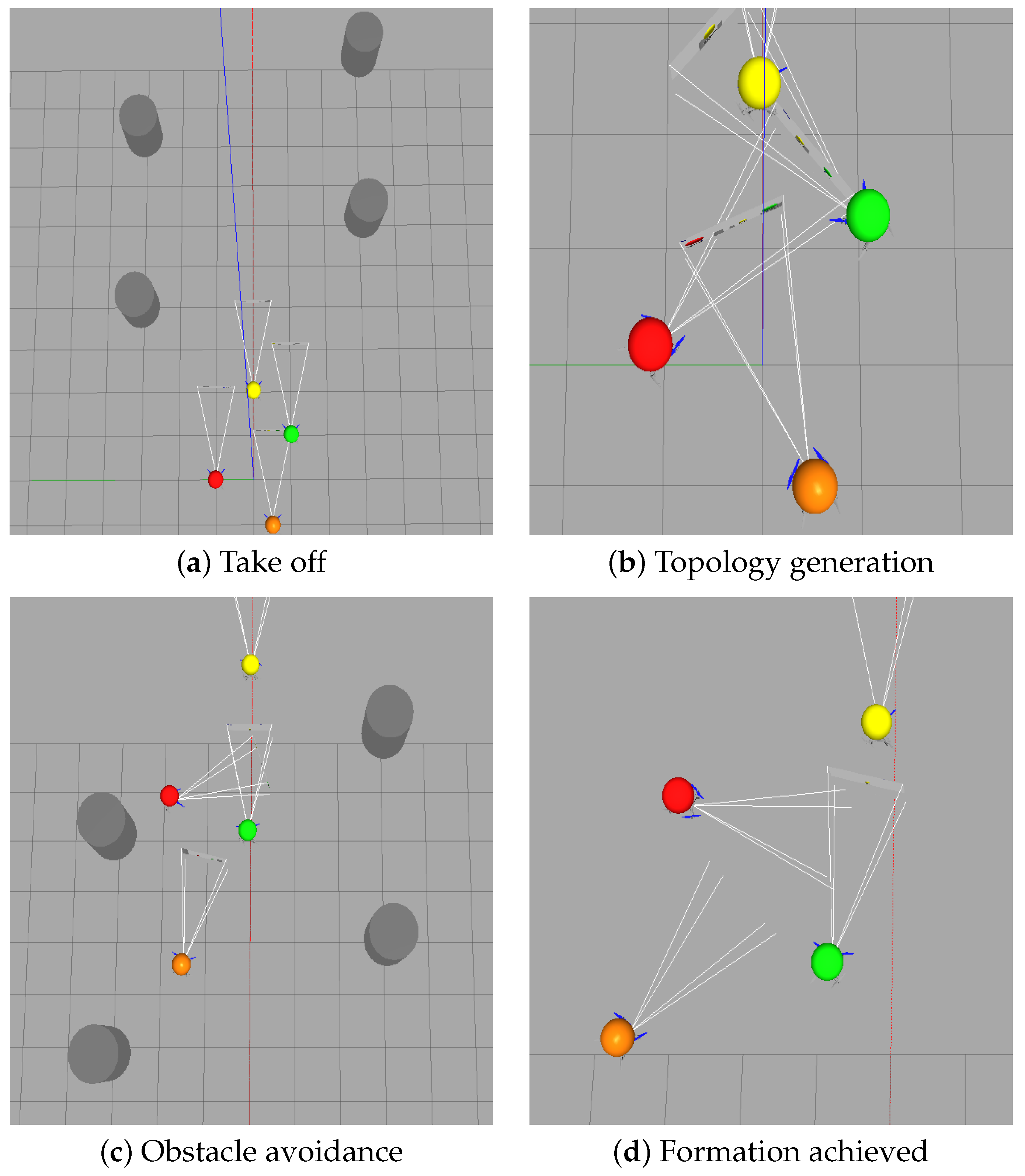
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Ding, X.; Wang, C.; Liang, L.; Hu, H. Affine formation control for multi-agent systems with prescribed convergence time. J. Frankl. Inst. 2021, 358, 7055–7072. [Google Scholar] [CrossRef]
- Li, Q.; Hua, Y.; Dong, X.; Yu, J.; Ren, Z. Time-Varying Formation Tracking Control for Unmanned Aerial Vehicles with the Leader’s Unknown Input and Obstacle Avoidance: Theories and Applications. Electronics 2022, 11, 2334. [Google Scholar] [CrossRef]
- Wen, J.; Yang, J.; Li, Y.; He, J.; Li, Z.; Song, H. Behavior-Based Formation Control Digital Twin for Multi-AUG in Edge Computing. IEEE Trans. Netw. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Fu, H.; Wang, S.; Ji, Y.; Wang, Y. Formation Control of Unmanned Vessels with Saturation Constraint and Extended State Observation. J. Mar. Sci. Eng. 2021, 9, 772. [Google Scholar] [CrossRef]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, A.; Lai, C.; Li, H. Velocity-Free Formation Control and Collision Avoidance for UUVs via RBF: A High-Gain Approach. Electronics 2022, 11, 1170. [Google Scholar] [CrossRef]
- Yang, Q.; Fang, H.; Cao, M.; Chen, J. Planar Affine Formation Stabilization via Parameter Estimations. IEEE Trans. Cybern. 2022, 52, 5322–5332. [Google Scholar] [CrossRef]
- Xiao, F.; Yang, Q.; Zhao, X.; Fang, H. A Framework for Optimized Topology Design and Leader Selection in Affine Formation Control. IEEE Robot. Autom. Lett. 2022, 7, 8627–8634. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, G.; Li, Y.; Dong, W. Agile Formation Control of Drone Flocking Enhanced With Active Vision-Based Relative Localization. IEEE Robot. Autom. Lett. 2022, 7, 6359–6366. [Google Scholar] [CrossRef]
- Kabore, K.M.; Güler, S. Distributed Formation Control of Drones With Onboard Perception. IEEE/ASME Trans. Mechatron. 2022, 27, 3121–3131. [Google Scholar] [CrossRef]
- Wang, Y.; Shan, M.; Yue, Y.; Wang, D. Vision-Based Flexible Leader–Follower Formation Tracking of Multiple Nonholonomic Mobile Robots in Unknown Obstacle Environments. IEEE Trans. Control Syst. Technol. 2020, 28, 1025–1033. [Google Scholar] [CrossRef]
- Li, X.; Tan, Y.; Mareels, I.; Chen, X. Compatible Formation Set for UAVs with Visual Sensing Constraint. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 2497–2502. [Google Scholar] [CrossRef]
- Liu, X.; Ge, S.S.; Goh, C.H. Vision-Based Leader–Follower Formation Control of Multiagents With Visibility Constraints. IEEE Trans. Control Syst. Technol. 2019, 27, 1326–1333. [Google Scholar] [CrossRef]
- Miao, Z.; Zhong, H.; Lin, J.; Wang, Y.; Chen, Y.; Fierro, R. Vision-Based Formation Control of Mobile Robots With FOV Constraints and Unknown Feature Depth. IEEE Trans. Control Syst. Technol. 2021, 29, 2231–2238. [Google Scholar] [CrossRef]
- Mukherjee, P.; Santilli, M.; Gasparri, A.; Williams, R.K. Distributed Adaptive and Resilient Control of Multi-Robot Systems With Limited Field of View Interactions. IEEE Robot. Autom. Lett. 2022, 7, 5318–5325. [Google Scholar] [CrossRef]
- Dai, S.L.; Lu, K.; Jin, X. Fixed-Time Formation Control of Unicycle-Type Mobile Robots with Visibility and Performance Constraints. IEEE Trans. Ind. Electron. 2021, 68, 12615–12625. [Google Scholar] [CrossRef]
- Yang, Q.; Cao, M.; Fang, H.; Chen, J. Constructing Universally Rigid Tensegrity Frameworks With Application in Multiagent Formation Control. IEEE Trans. Autom. Control 2019, 64, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, D.J.; Hendrickson, B. An Algorithm for Two-Dimensional Rigidity Percolation: The Pebble Game. J. Comput. Phys. 1997, 137, 346–365. [Google Scholar] [CrossRef]
- Hendrickx, J.M.; Anderson, B.D.O.; Delvenne, J.C.; Blondel, V.D. Directed graphs for the analysis of rigidity and persistence in autonomous agent systems. Int. J. Robust Nonlinear Control 2007, 17, 960–981. [Google Scholar] [CrossRef]
- Hendrickx, J.; Fidan, B.; Yu, C.; Anderson, B.; Blondel, V. Elementary Operations for the Reorganization of Minimally Persistent Formations. In Proceedings of the International Symposium on Mathematical Theory of Networks and Systems (MTNS 2006), Kyoto, Japan, 24–28 July 2006; pp. 859–873. [Google Scholar]
- Yu, D.; Chen, C.L.P. Automatic Leader–Follower Persistent Formation Generation With Minimum Agent-Movement in Various Switching Topologies. IEEE Trans. Cybern. 2020, 50, 1569–1581. [Google Scholar] [CrossRef]
- Luo, X.-Y.; Li, S.-B.; Guan, X.-P. Automatic generation of min-weighted persistent formations. Chin. Phys. B 2009, 18, 3104. [Google Scholar] [CrossRef]
- Smith, B.S.; Egerstedt, M.; Howard, A. Automatic Generation of Persistent Formations for Multi-Agent Networks Under Range Constraints. Mob. Netw. Appl. 2009, 14, 322–335. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Li, S.; Guan, X. Automatic generation of minimally persistent formations using rigidity matrix. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 1198–1203. [Google Scholar] [CrossRef]
- Wang, H.; Guo, Y. Minimal persistence control on dynamic directed graphs for multi-robot formation. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1557–1563. [Google Scholar] [CrossRef] [Green Version]
- Borrmann, U.; Wang, L.; Ames, A.D.; Egerstedt, M. Control Barrier Certificates for Safe Swarm Behavior. IFAC-PapersOnLine 2015, 48, 68–73, Analysis and Design of Hybrid Systems ADHS. [Google Scholar] [CrossRef]
- Son, T.D.; Nguyen, Q. Safety-Critical Control for Non-affine Nonlinear Systems with Application on Autonomous Vehicle. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 7623–7628. [Google Scholar] [CrossRef]
- Zheng, D.; Wang, H.; Wang, J.; Zhang, X.; Chen, W. Toward Visibility Guaranteed Visual Servoing Control of Quadrotor UAVs. IEEE/ASME Trans. Mechatron. 2019, 24, 1087–1095. [Google Scholar] [CrossRef]
- Laman, G. On graphs and rigidity of plane skeletal structures. J. Eng. Math. 1970, 4, 331–340. [Google Scholar] [CrossRef]
- Hendrickx, J.M.; Fidan, B.; Yu, C.; Anderson, B.D.O.; Blondel, V.D. Primitive operations for the construction and reorganization of minimally persistent formations. arXiv 2006, arXiv:cs/0609041. [Google Scholar]
- Wieland, P.; Allgöwer, F. Constructive safety using control barrier functions. IFAC Proc. Vol. 2007, 40, 462–467. [Google Scholar] [CrossRef]
- Ames, A.D.; Grizzle, J.W.; Tabuada, P. Control barrier function based quadratic programs with application to adaptive cruise control. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 6271–6278. [Google Scholar] [CrossRef]
- Ames, A.D.; Xu, X.; Grizzle, J.W.; Tabuada, P. Control Barrier Function Based Quadratic Programs for Safety Critical Systems. IEEE Trans. Autom. Control 2017, 62, 3861–3876. [Google Scholar] [CrossRef]
- Ames, A.D.; Coogan, S.; Egerstedt, M.; Notomista, G.; Sreenath, K.; Tabuada, P. Control Barrier Functions: Theory and Applications. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 3420–3431. [Google Scholar] [CrossRef] [Green Version]
- Summers, T.H.; Yu, C.; Dasgupta, S.; Anderson, B.D.O. Control of Minimally Persistent Leader-Remote-Follower and Coleader Formations in the Plane. IEEE Trans. Autom. Control 2011, 56, 2778–2792. [Google Scholar] [CrossRef]
- Wang, L.; Ames, A.; Egerstedt, M. Safety barrier certificates for heterogeneous multi-robot systems. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 5213–5218. [Google Scholar] [CrossRef] [Green Version]
- Fu, J.; Lv, Y.; Wen, G.; Yu, X. Local Measurement Based Formation Navigation of Nonholonomic Robots With Globally Bounded Inputs and Collision Avoidance. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2342–2354. [Google Scholar] [CrossRef]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.; Marín-Jiménez, M. Automatic generation and detection of highly reliable fiducial markers under occlusion. Pattern Recognit. 2014, 47, 2280–2292. [Google Scholar] [CrossRef]
- Amovlab. Prometheus Autonomous UAV Opensource Project. Available online: https://github.com/amov-lab/Prometheus (accessed on 1 October 2021).
- Ferreau, J.; Kirches, C.; Potschka, A.; Bock, H.; Diehl, M. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Programm. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Yang, Q.; Liu, Q.; Yin, Y.; Wei, Y.; Fang, H. Minimally Persistent Graph Generation and Formation Control for Multi-Robot Systems under Sensing Constraints. Electronics 2023, 12, 317. https://doi.org/10.3390/electronics12020317
Zhao X, Yang Q, Liu Q, Yin Y, Wei Y, Fang H. Minimally Persistent Graph Generation and Formation Control for Multi-Robot Systems under Sensing Constraints. Electronics. 2023; 12(2):317. https://doi.org/10.3390/electronics12020317
Chicago/Turabian StyleZhao, Xinyue, Qingkai Yang, Qi Liu, Yuhan Yin, Yue Wei, and Hao Fang. 2023. "Minimally Persistent Graph Generation and Formation Control for Multi-Robot Systems under Sensing Constraints" Electronics 12, no. 2: 317. https://doi.org/10.3390/electronics12020317
APA StyleZhao, X., Yang, Q., Liu, Q., Yin, Y., Wei, Y., & Fang, H. (2023). Minimally Persistent Graph Generation and Formation Control for Multi-Robot Systems under Sensing Constraints. Electronics, 12(2), 317. https://doi.org/10.3390/electronics12020317





