Phase Diffusion in Low-EJ Josephson Junctions at Milli-Kelvin Temperatures
Abstract
:1. Introduction
2. Phase Diffusion in Underdamped Junctions
3. Experimental Techniques
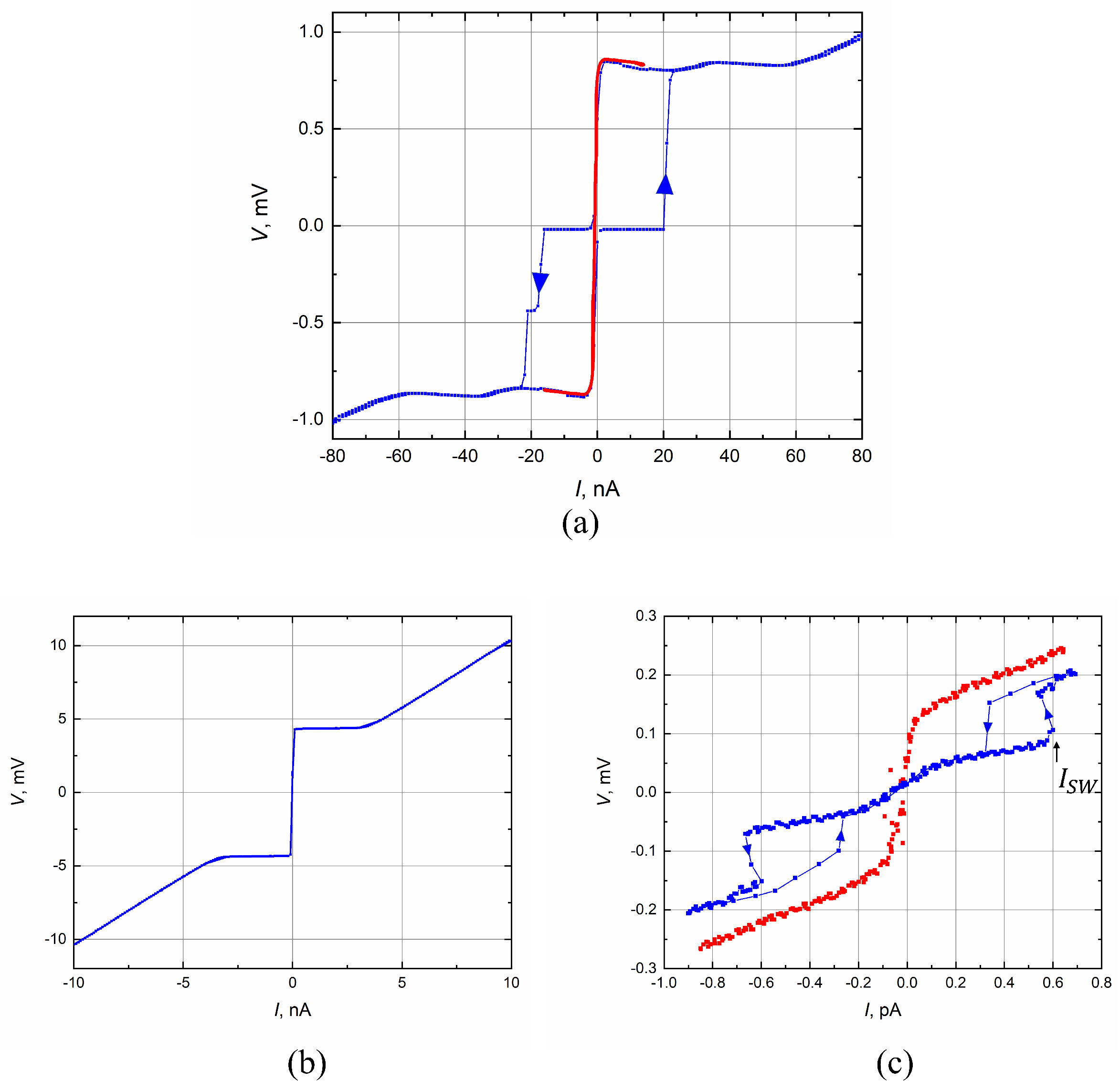
4. Current-Voltage Characteristics of Low- Junctions
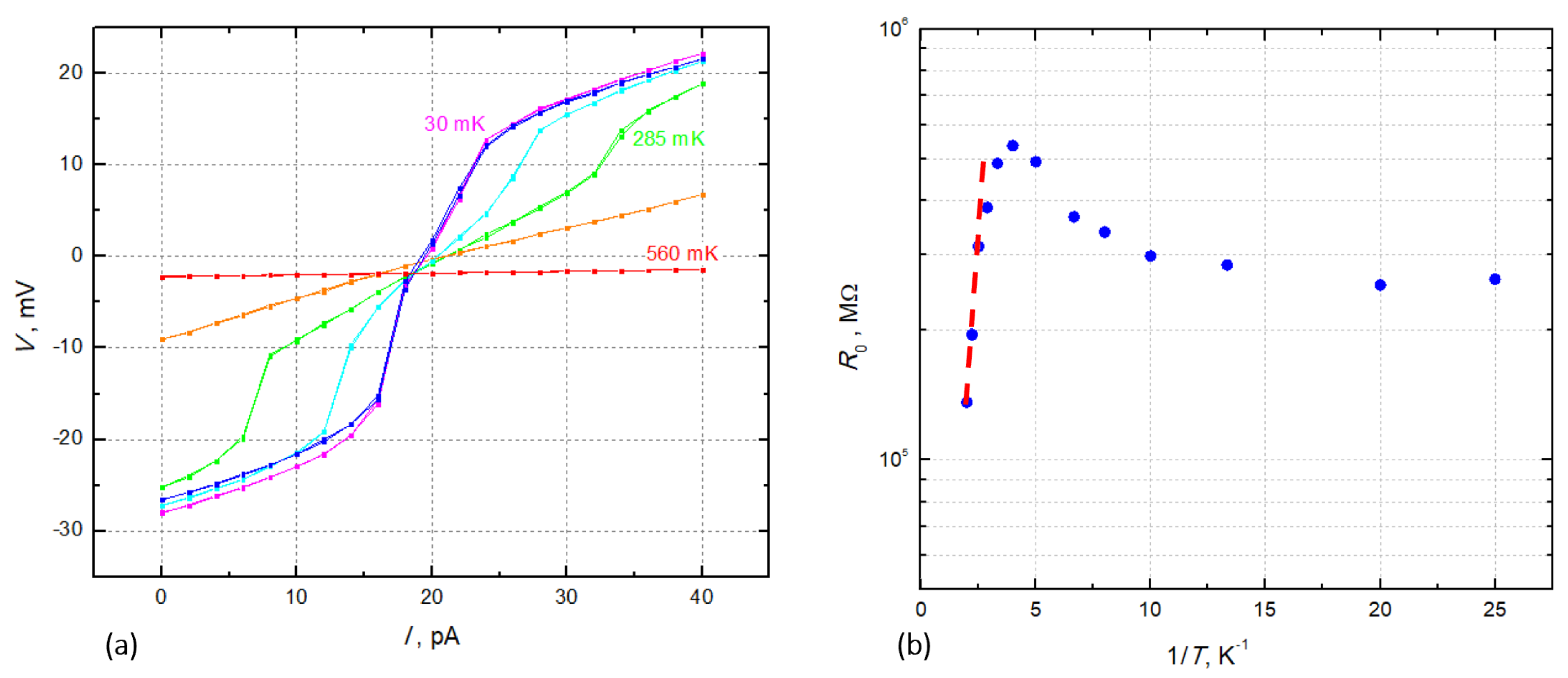
4.1. The Switching Current and the Zero-Bias Resistance
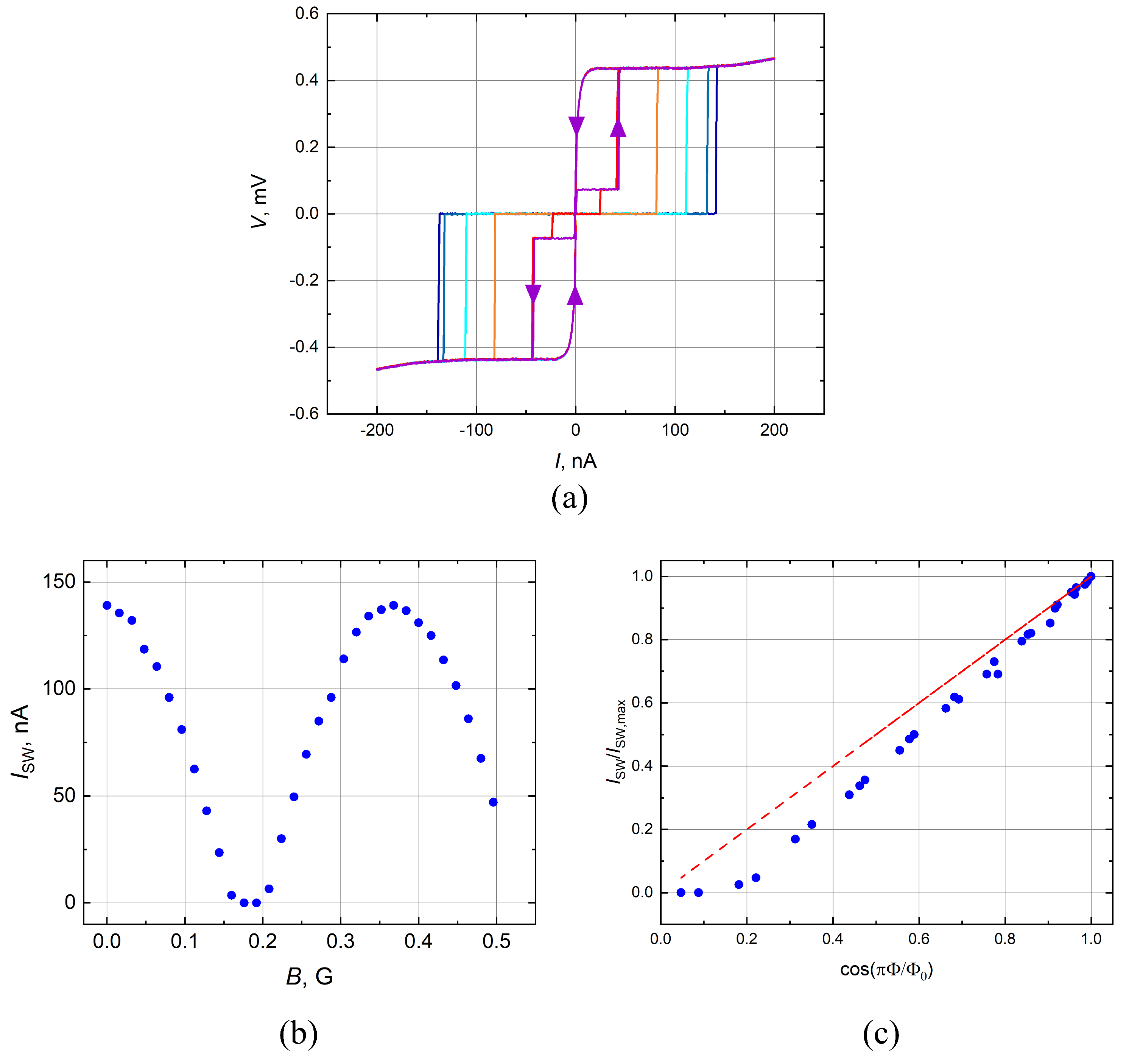
4.2. The IVC Hysteresis
4.3. The Dependences
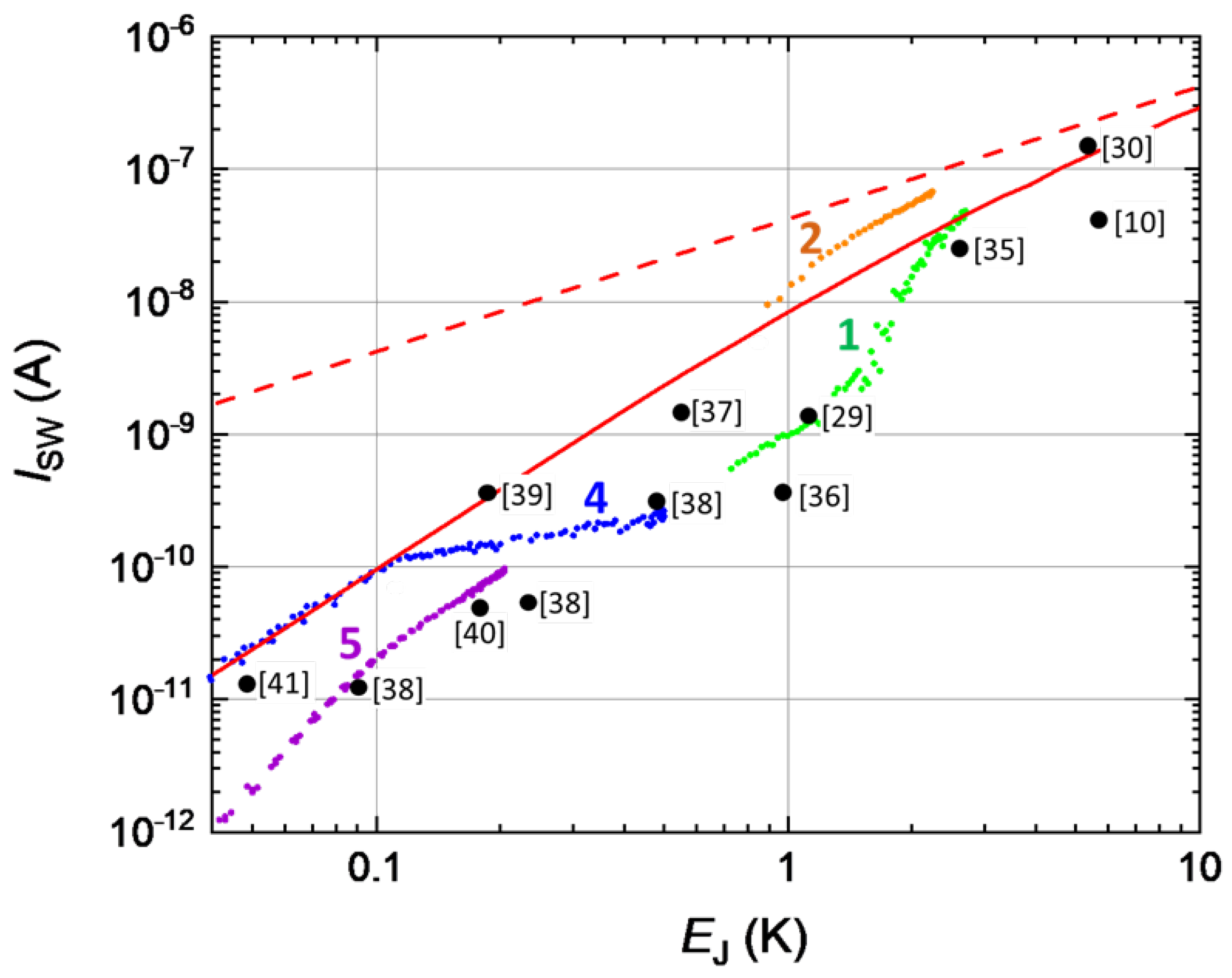
5. Discussion
5.1. The Switching Currents
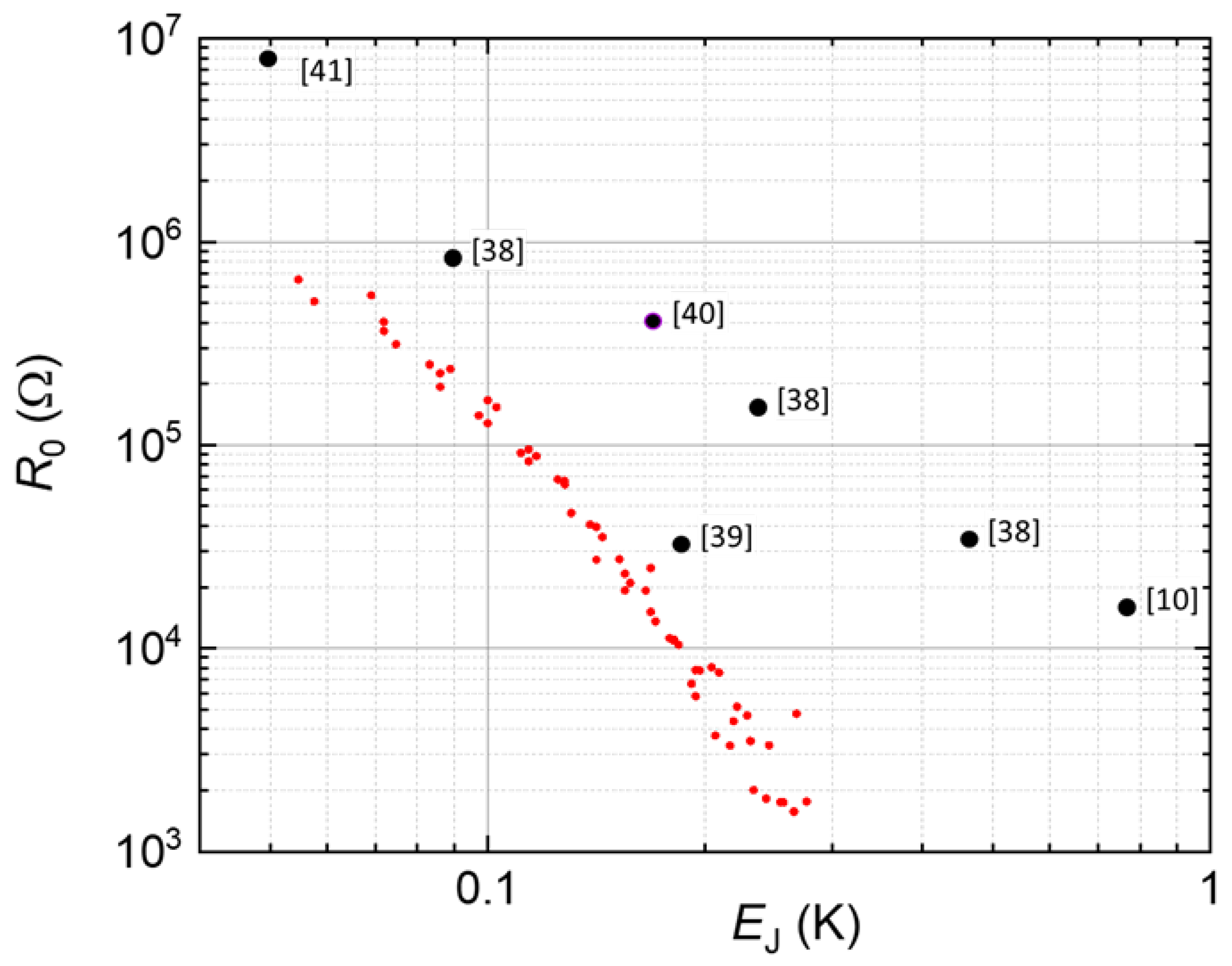
5.2. The Zero-Bias Resistance
| Reference | (K) | (nA) | (nA) | (k) | |
|---|---|---|---|---|---|
| Watanabe 2003 [10] sample C | 5.7 | 8 | 240 | 40 | 0.6 |
| Kivioja 2005 [30] | 5.2 | 500 | 220 | 145 | |
| Schmidlin 2013 [33], Figure 5.2 | 2.5 | 50 | 106 | 25 | 0.13 |
| Shimada 2016 [29], SQUID at | 1.1 | 14 | 47 | 1.2 | 0.11 |
| Weissl 2015 [36], SQUID at | 0.95 | 10 | 38 | 0.35 | 0.14 |
| Watanabe 2003 [10] sample G | 0.76 | 1 | 32 | 14 | |
| Jäck 2015 [38] Figure 4.6 | 0.54 | 1.5 | 13 | ||
| Senkpiel 2020 [37] | 0.47 | 0.3 | 33 | ||
| Senkpiel 2020 [37] | 0.23 | 0.07 | 143 | ||
| Yeh 2012 [39] | 0.18 | 1.3 | 6.5 | 0.35 | 31 |
| Jäck 2017 [40] | 0.17 | 7..5 | 0.05 | 400 | |
| Murani 2020 [14] | 0.12 | 5 | 0.07 | ||
| Senkpiel 2020 [37] | 0.09 | 0.012 | 830 | ||
| Kuzmin 1991 [41] | 0.05 | 0.014 | 8000 |
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| JJs | Josephson Junctions |
| IPS | Incoherent Phase Slips |
| QPS | Quantum Phase Slip |
| IVC | Current-Voltage Characteristics |
| IZ | Ivanchenko and Zilberman |
| SQUIDs | Superconducting Quantum Interference Devices |
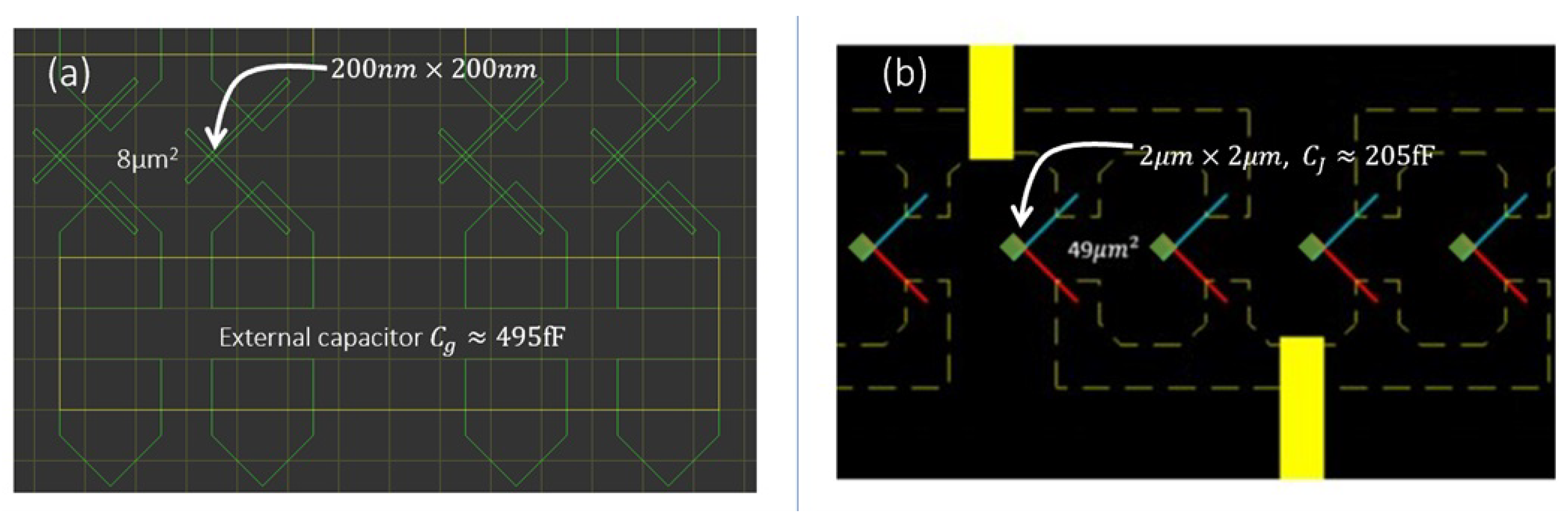
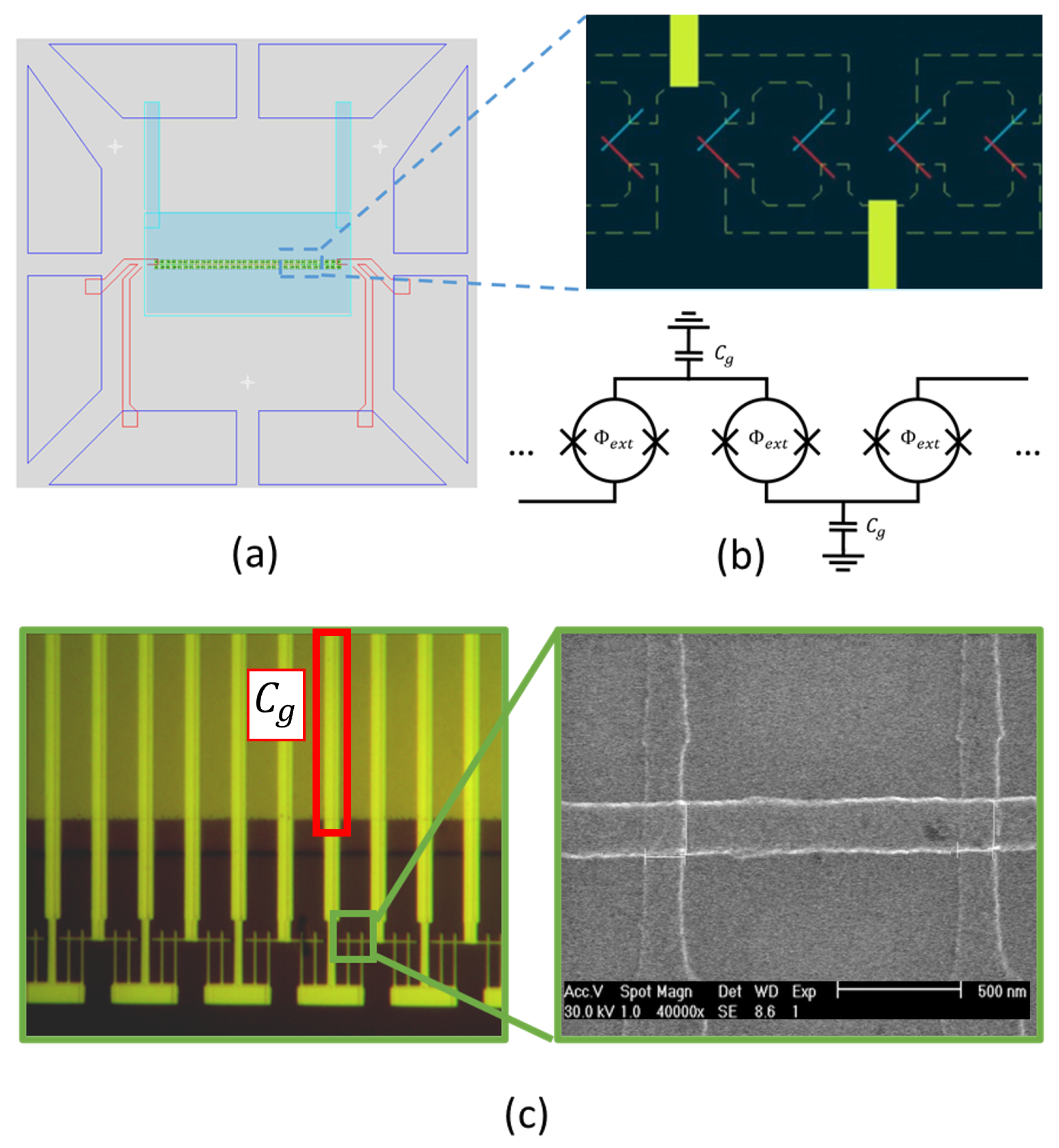
Appendix A. Device Design and Fabrication
Appendix B. Measurement Setup

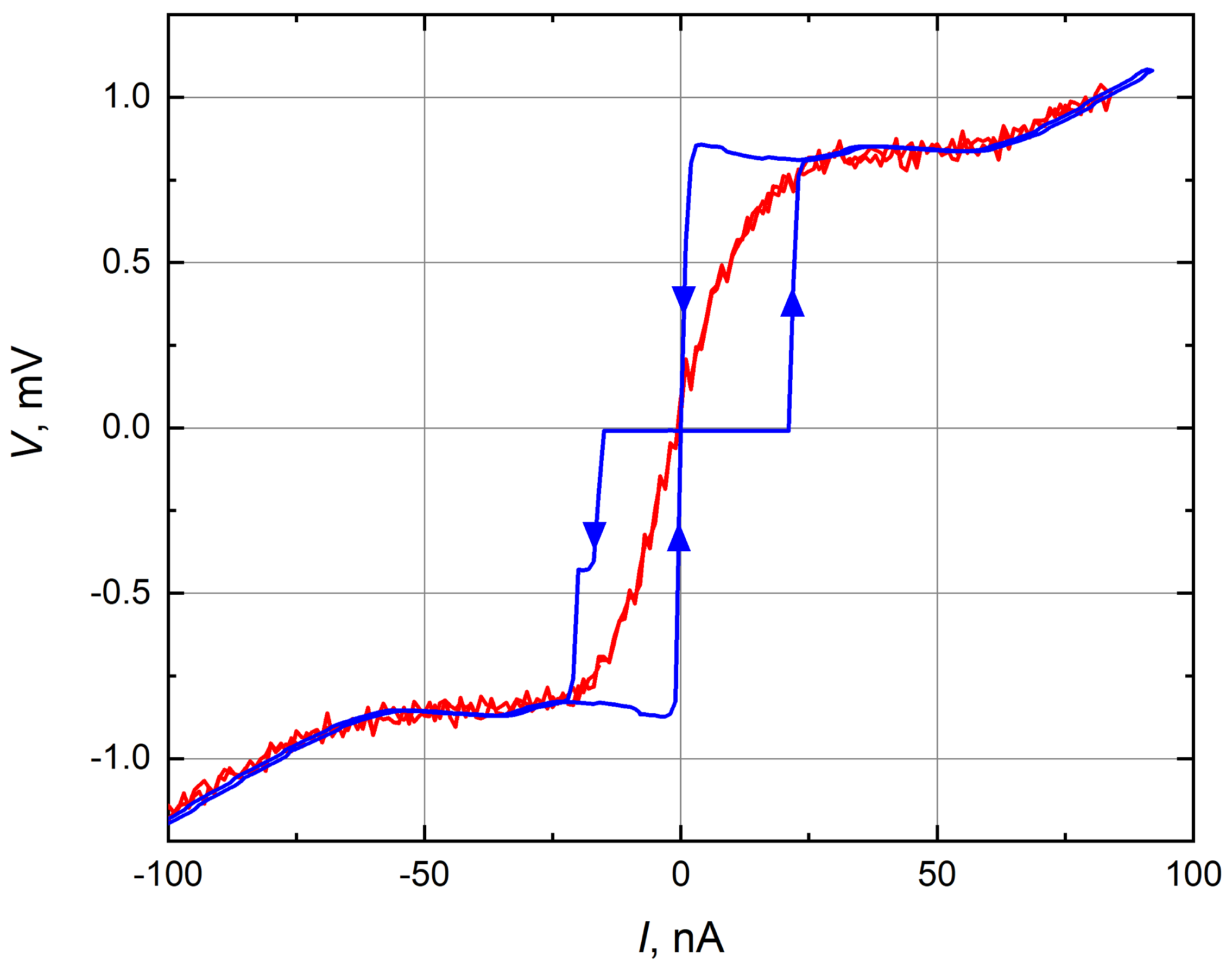
Appendix C. The Effect of Noise on the Current-Voltage Characteristics
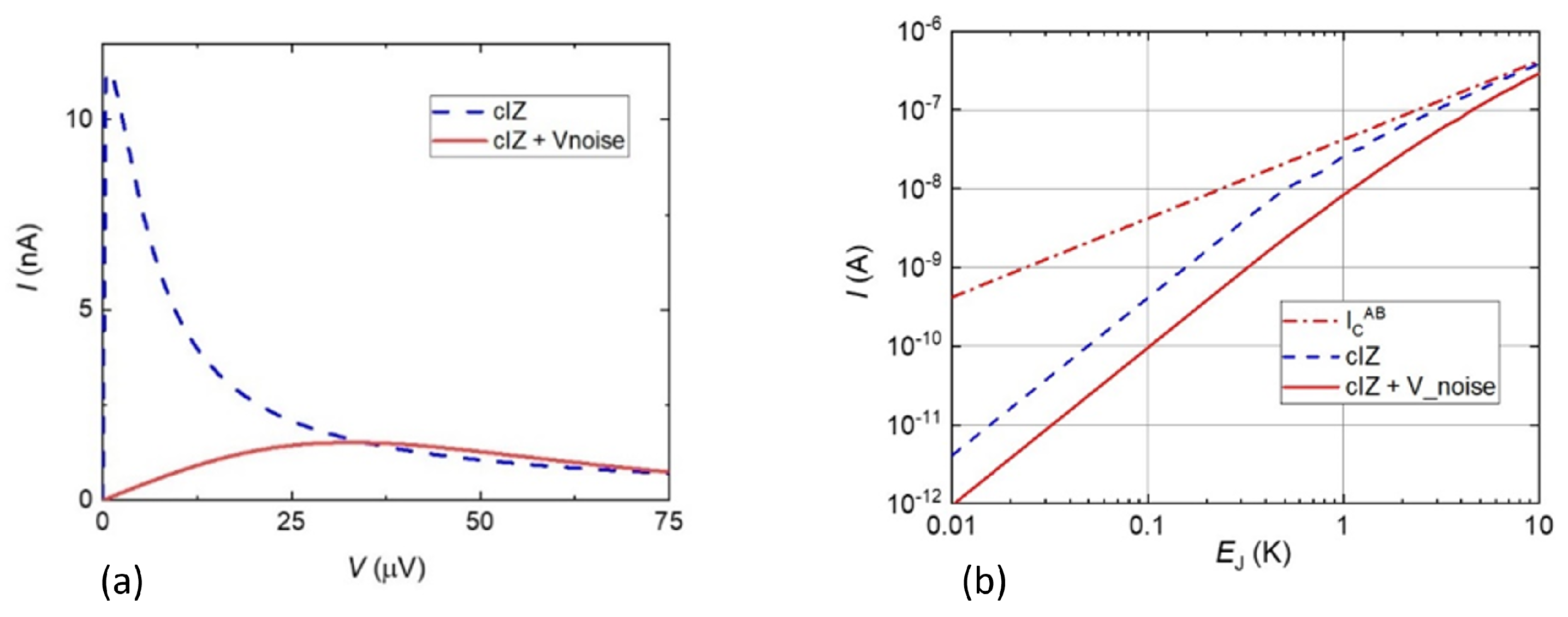
Appendix D. Modeling the Effect of Thermal Noise
References
- Nguyen, L.B.; Lin, Y.-H.; Somoroff, A.; Mencia, R.; Grabon, N.; Manucharyan, V.E. High-Coherence fluxonium qubit. Phys. Rev. X 2019, 9, 041041. [Google Scholar] [CrossRef] [Green Version]
- Gyenis, A.; Mundada, P.S.; Paolo, A.D.; Hazard, T.M.; You, X.; Schuster, D.I.; Koch, J.; Blais, A.; Houck, A.A. Experimental realization of a protected superconducting circuit derived from the 0–π qubit. PRX Quantum 2021, 2, 010339. [Google Scholar] [CrossRef]
- Zhang, H.; Chakram, S.; Roy, T.; Earnest, N.; Lu, Y.; Huang, Z.; Weiss, D.K.; Koch, J.; Schuster, D.I. Universal fast-flux control of 387 a coherent, low-frequency qubit. Phys. Rev. X 2021, 11, 011010. [Google Scholar]
- Peruzzo, M.; Trioni, A.; Hassani, F.; Zemlicka, M.; Fink, J.M. Surpassing the resistance quantum with a geometric superinductor. Phys. Rev. Appl. 2020, 14, 044055. [Google Scholar] [CrossRef]
- Somoroff, A.; Ficheux, Q.; Mencia, R.A.; Xiong, H.; Kuzmin, R.V.; Manucharyan, V.E. Millisecond coherence in a superconducting qubit. arXiv 2021, arXiv:2103.08. [Google Scholar]
- Tinkham, M. Introduction to Superconductivity; Dover Publications: Mineola, NY, USA, 1996. [Google Scholar]
- Martinis, J.M.; Kautz, R.L. Classical phase diffusion in small hysteretic Josephson junctions. Phys. Rev. Lett. 1989, 63, 1507–1510. [Google Scholar] [CrossRef]
- Kautz, R.L.; Martinis, J.M. Noise-affected i-v curves in small hysteretic Josephson junctions. Phys. Rev. B 1990, 42, 9903. [Google Scholar] [CrossRef]
- Eiles, T.M.; Martinis, J.M. Combined Josephson and charging behavior of the supercurrent in the superconducting singleelectron transistor. Phys. Rev. B 1994, 50, 627–630. [Google Scholar] [CrossRef]
- Watanabe, M.; Haviland, D.B. Quantum effects in small-capacitance single Josephson junctions. Phys. Rev. B 2003, 67, 094505. [Google Scholar] [CrossRef] [Green Version]
- Fazio, R.; van der Zan, H. Quantum phase transitions and vortex dynamics in superconducting networks. Phys. Rep. 2001, 355, 235–334. [Google Scholar] [CrossRef] [Green Version]
- Bard, M.; Protopopov, I.V.; Gornyi, I.V.; Shnirman, A.; Mirlin, A.D. Superconductor-insulator transition in disordered Josephson-junction chains. Phys. Rev. B 2017, 96, 064514. [Google Scholar] [CrossRef] [Green Version]
- Ast, C.R.; Jäck, B.; Senkpiel, J.; Eltschka, M.; Etzkorn, M.; Ankerhold, J.; Kern, K. Sensing the quantum limit in scanning tunnelling spectroscopy. Nat. Commun. 2016, 7, 13009. [Google Scholar] [CrossRef] [PubMed]
- Murani, A.; Bourlet, N.; Sueur, H.; Portier, F.; Altimiras, C.; Esteve, D.; Grabert, H.; Stockburger, J.; Ankerhold, J.; Joyez, P. Absence of a dissipative quantum phase transition in Josephson junctions. Phys. Rev. X 2020, 10, 021003. [Google Scholar] [CrossRef] [Green Version]
- Matveev, K.A.; Larkin, A.I.; Glazman, L.I. Persistent Current in Superconducting Nanorings. Phys. Rev. Lett. 2002, 89, 096802. [Google Scholar] [CrossRef] [Green Version]
- Manucharyan, V.E.; Masluk, N.A.; Kamal, A.; Koch, J.; Glazman, L.I.; Devoret, M.H. Evidence for coherent quantum phase slips across a Josephson junction array. Phys. Rev. B 2012, 85, 024521. [Google Scholar] [CrossRef] [Green Version]
- Koch, J.; Yu, T.M.; Gambetta, J.; Houck, A.A.; Schuster, D.I.; Majer, J.; Blais, A.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 2007, 76, 042319. [Google Scholar] [CrossRef] [Green Version]
- Gyenis, A.; Paolo, A.D.; Koch, J.; Blais, A.; Houck, A.A.; Schuster, D.I. Moving beyond the transmon: Noise-Protected superconducting quantum circuits. PRX Quantum 2021, 2, 030101. [Google Scholar] [CrossRef]
- Earnest, N.; Chakram, S.; Lu, Y.; Irons, N.; Naik, R.K.; Leung, N.; Ocola, L.; Czaplewski, D.A.; Baker, B.; Lawrence, J.; et al. Realization of a Λ system with metastable states of a capacitively shunted fluxonium. Phys. Rev. Lett. 2018, 120, 150504. [Google Scholar] [CrossRef] [Green Version]
- Mooij, J.E.; Nazarov, Y.V. Superconducting nanowires as quantum phase-slip junctions. Nat. Phys. 2006, 2, 169–172. [Google Scholar] [CrossRef]
- Astafiev, O.V.; Ioffe, L.B.; Kafanov, S.; Pashkin, Y.A.; Arutyunov, K.Y.; Shahar, D.; Cohen, O.; Tsai, J.S. Coherent quantum phase slip. Nature 2012, 484, 355. [Google Scholar] [CrossRef] [Green Version]
- Svetogorov, A.E.; Taguchi, M.; Tokura, Y.; Basko, D.M.; Hekking, F.W.J. Theory of coherent quantum phase slips in Josephson junction chains with periodic spatial modulations. Phys. Rev. B 2018, 97, 104514. [Google Scholar] [CrossRef] [Green Version]
- Arutyunov, K.Y.; Golubev, D.S.; Zaikin, A.D. Superconductivity in one dimension. Phys. Rep. 2008, 464, 1–70. [Google Scholar] [CrossRef]
- Semenov, A.G.; Zaikin, A.D. Quantum phase slip noise. Phys. Rev. B 2016, 94, 014512. [Google Scholar] [CrossRef] [Green Version]
- Schön, G.; Zaikin, A.D. Quantum coherent effects, phase transitions, and the dissipative dynamics of ultra small tunnel junctions. Phys. Rep. 1990, 198, 237–412. [Google Scholar] [CrossRef]
- Vion, D.; Götz, M.; Joyez, P.; Esteve, D.; Devoret, M.H. Thermal activation above a dissipation barrier: Switching of a small Josephson junction. Phys. Rev. Lett. 1996, 77, 3435–3438. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fistul, M.V. Josephson phase diffusion in small josephson junctions: A strongly nonlinear regime. In No-Nonsense Physicist; Polini, M., Vignale, G., Pellegrini, V., Jain, J.K., Eds.; Publications of the Scuola Normale Superiore; Edizioni della Normale: Pisa, Italy, 2016; Volume 2, pp. 73–80. [Google Scholar]
- Ivanchenko, Y.M.; Zil’berman, L.A. The Josephson effect in small tunnel contacts. Sov. Phys. JETP 1969, 28, 1272. [Google Scholar]
- Shimada, H.; Katori, S.; Gandrothula, S.; Deguchi, T.; Mizugaki, Y. Bloch oscillation in a one-dimensional array of small Josephson junctions. J. Phys. Soc. Jpn. 2016, 85, 074706. [Google Scholar] [CrossRef]
- Kivioja, J.M.; Nieminen, T.E.; Claudon, J.; Buisson, O.; Hekking, F.W.J.; Pekola, J.P. Observation of transition from escape dynamics to underdamped phase diffusion in a Josephson junction. Phys. Rev. Lett. 2005, 94, 247002. [Google Scholar] [CrossRef] [Green Version]
- Lu, W.-S. Josephson Circuits for Protected Quantum Bits. Ph.D. Thesis, Rutgers University, New Brunswick, NJ, USA, 2021. [Google Scholar]
- McCumber, D.E. Effect of ac impedance on dc Voltage-Current characteristics of superconductor Weak-Link junctions. J. Appl. Phys. 1968, 39, 3113–3118. [Google Scholar] [CrossRef]
- Schmidlin, S. Physics and Technology of Small Josephson Junctions. Ph.D. Thesis, Royal Holloway, University of London, Egham, UK, 2013. [Google Scholar]
- Coon, D.D.; Fiske, M.D. Josephson ac and step structure in the supercurrent tunneling characteristic. Phys. Rev. 1965, 138, A744–A746. [Google Scholar] [CrossRef]
- Wilen, C.D.; Abdullah, S.; Kurinsky, N.A.; Stanford, C.; Cardani, L.; D’Imperio, G.; Tomei, C.; Faoro, L.; Ioffe, L.B.; Liu, C.H.; et al. Correlated charge noise and relaxation errors in superconducting qubits. Nature 2021, 594, 369–373. [Google Scholar] [CrossRef] [PubMed]
- Weißl, T.; Rastelli, G.; Matei, I.; Pop, I.M.; Buisson, O.; Hekking, F.W.J.; Guichard, W. Bloch band dynamics of a Josephson junction in an inductive environment. Phys. Rev. B 2015, 91, 014507. [Google Scholar] [CrossRef] [Green Version]
- Senkpiel, J.; Dambach, S.; Etzkorn, M.; Drost, R.; Padurariu, C.; Kubala, B.; Belzig, W.; Yeyati, A.L.; Cuevas, J.C.; Ankerhold, J.; et al. Single channel Josephson effect in a high transmission atomic contact. Commun. Phys. 2020, 3, 1–6. [Google Scholar] [CrossRef]
- Jäck, B. Josephson Tunneling at the Atomic Scale. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2015. [Google Scholar]
- Yeh, S.-S.; Chen, K.-W.; Chung, T.-H.; Wu, D.-Y.; Lin, M.-C.; Wang, J.-Y.; Ho, I.-L.; Wu, C.-S.; Kuo, W.; Chen, C. A method for determining the specific capacitance value of mesoscopic Josephson junctions. Appl. Phys. Lett. 2012, 101, 232602. [Google Scholar] [CrossRef]
- Jäck, B.; Senkpiel, J.; Etzkorn, M.; Ankerhold, J.; Ast, C.R.; Kern, K. Quantum brownian motion at strong dissipation probed by superconducting tunnel junctions. Phys. Rev. Lett. 2017, 119, 147702. [Google Scholar] [CrossRef] [Green Version]
- Kuzmin, L.S.; Nazarov, Y.V.; Haviland, D.B.; Delsing, P.; Claeson, T. Coulomb blockade and incoherent tunneling of cooper pairs in ultrasmall junctions affected by strong quantum fluctuations. Phys. Rev. Lett. 1991, 67, 1161–1164. [Google Scholar] [CrossRef] [PubMed]
- Manucharyan, V. Private Communication, 2020.
- Bell, M.T.; Sadovskyy, I.A.; Ioffe, L.B.; Kitaev, A.Y.; Gershenson, M.E. Quantum superinductor with tunable nonlinearity. Phys. Rev. Lett. 2012, 109, 137003. [Google Scholar] [CrossRef] [Green Version]
- Martinis, J.M.; Devoret, M.H.; Clarke, J. Experimental tests for the quantum behavior of a macroscopic degree of freedom: The phase difference across a Josephson junction. Phys. Rev. B 1987, 35, 4682–4698. [Google Scholar] [CrossRef]
| Sample | (k) | (K) | (m) | (nA) | |
|---|---|---|---|---|---|
| 1 | 2.4 | 2.9 | 1.9 | 130 | 48 |
| 2 | 2.9 | 2.4 | 3.74 | 107 | 68 |
| 3 | 9.4 | 0.76 | 0.04 | 33 | 9 |
| 4 | 15.8 | 0.45 | 0.04 | 20 | 0.3 |
| 5 | 16.6 | 0.43 | 0.04 | 19 | 0.1 |
| 6 | 175 | 0.04 | 0.04 | 1.8 | 0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.-S.; Kalashnikov, K.; Kamenov, P.; DiNapoli, T.J.; Gershenson, M.E. Phase Diffusion in Low-EJ Josephson Junctions at Milli-Kelvin Temperatures. Electronics 2023, 12, 416. https://doi.org/10.3390/electronics12020416
Lu W-S, Kalashnikov K, Kamenov P, DiNapoli TJ, Gershenson ME. Phase Diffusion in Low-EJ Josephson Junctions at Milli-Kelvin Temperatures. Electronics. 2023; 12(2):416. https://doi.org/10.3390/electronics12020416
Chicago/Turabian StyleLu, Wen-Sen, Konstantin Kalashnikov, Plamen Kamenov, Thomas J. DiNapoli, and Michael E. Gershenson. 2023. "Phase Diffusion in Low-EJ Josephson Junctions at Milli-Kelvin Temperatures" Electronics 12, no. 2: 416. https://doi.org/10.3390/electronics12020416
APA StyleLu, W.-S., Kalashnikov, K., Kamenov, P., DiNapoli, T. J., & Gershenson, M. E. (2023). Phase Diffusion in Low-EJ Josephson Junctions at Milli-Kelvin Temperatures. Electronics, 12(2), 416. https://doi.org/10.3390/electronics12020416






