The Analysis of Permanent Magnet Vernier Synchronous Machine Vibration and Noise
Abstract
:1. Introduction
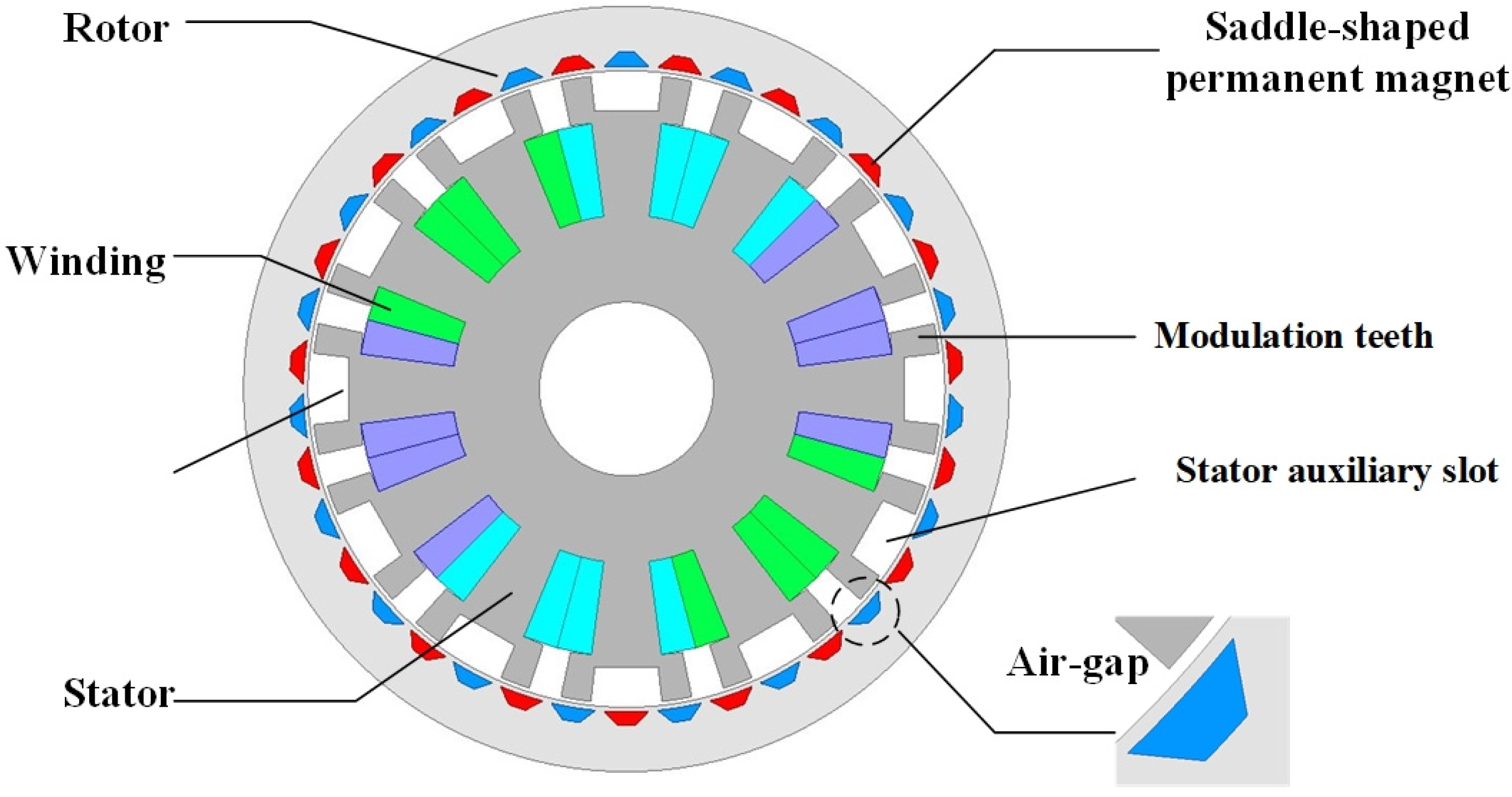
2. The Structure of the PMVSM
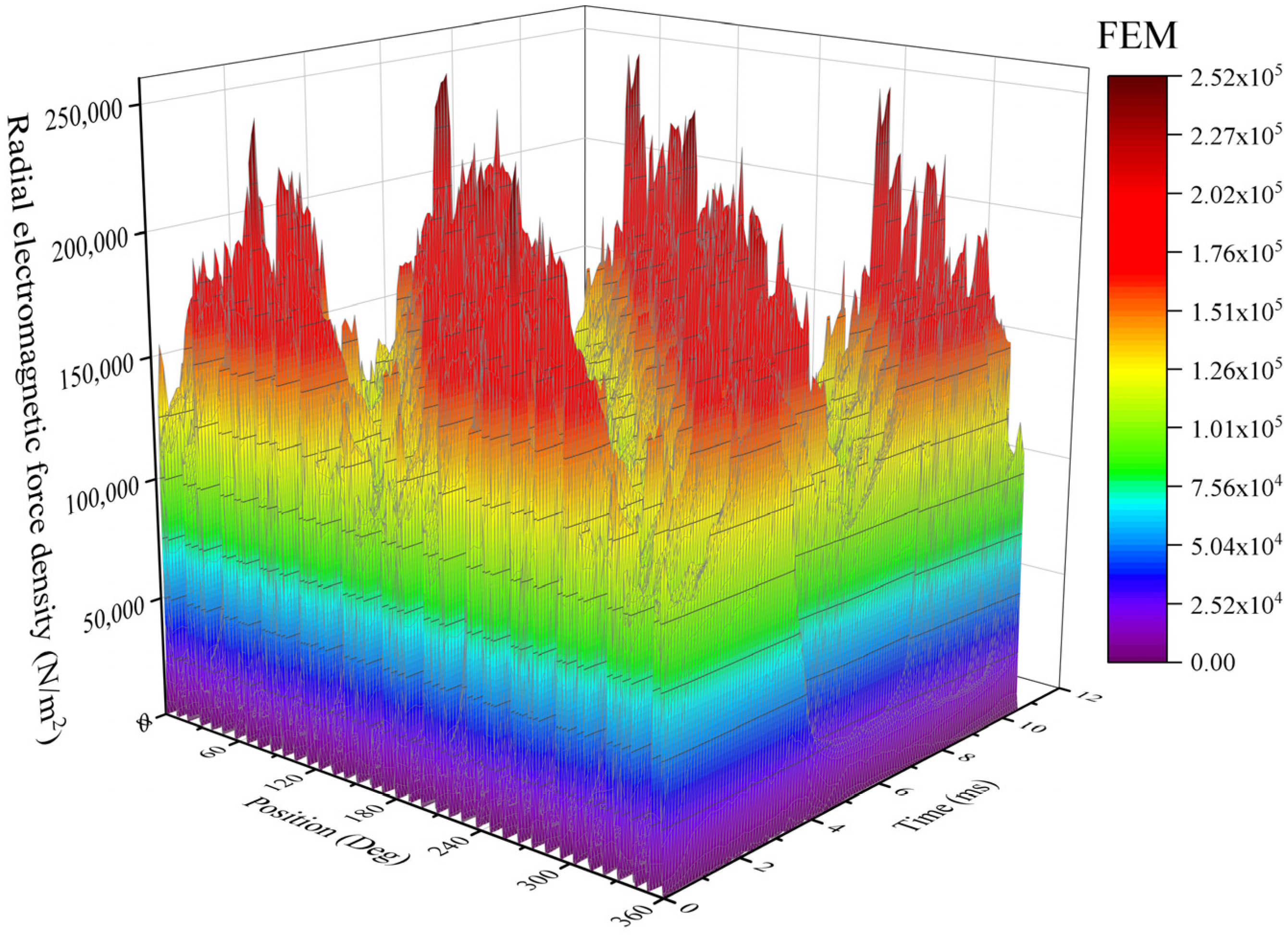
3. The Calculation of Radial Electromagnetic Force
4. The Vibration and Noise of the PMVSM
4.1. The Radial Electromagnetic Force of the PMVSM
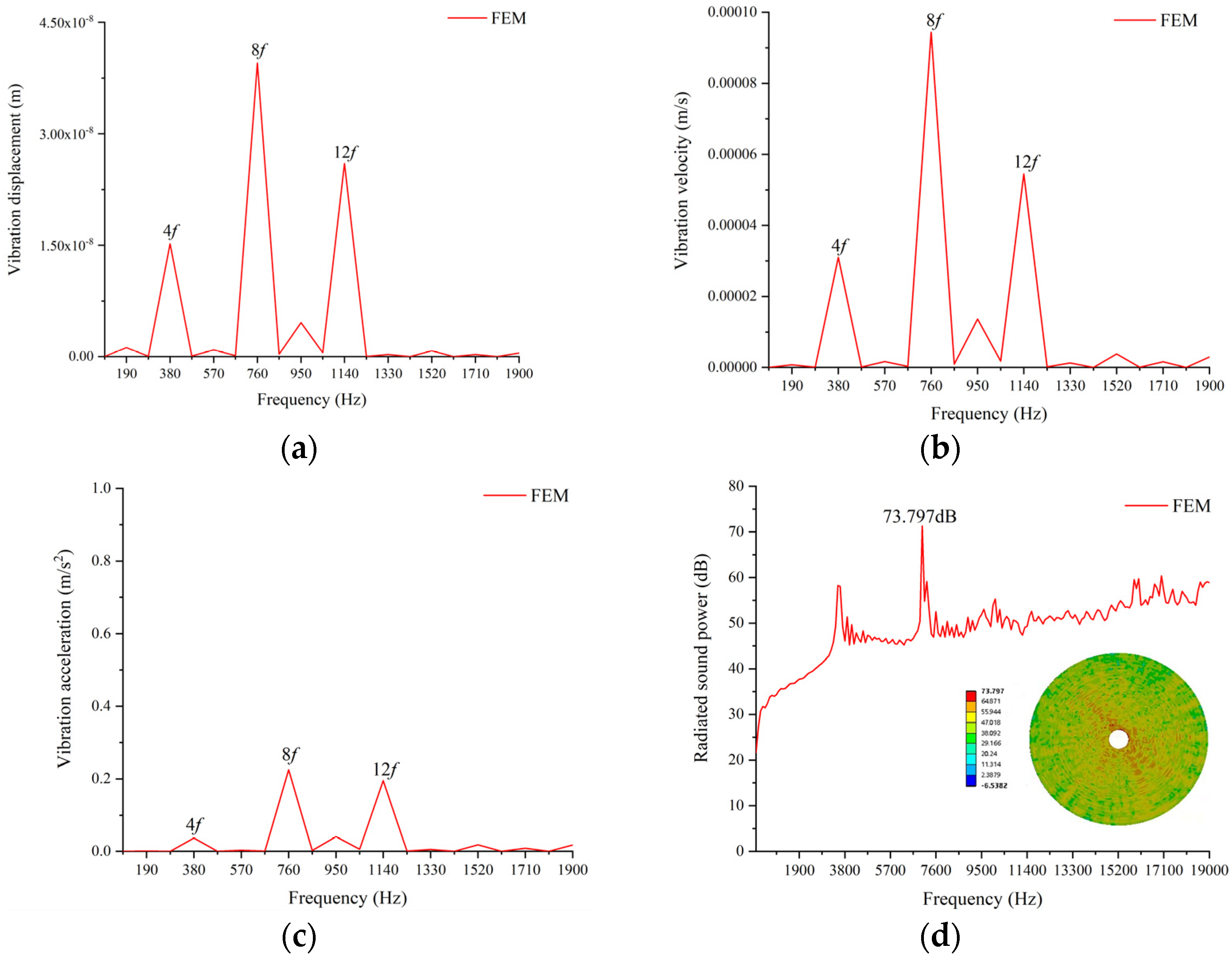
4.2. The Modal Analysis and Vibration and Noise of the PMVSM
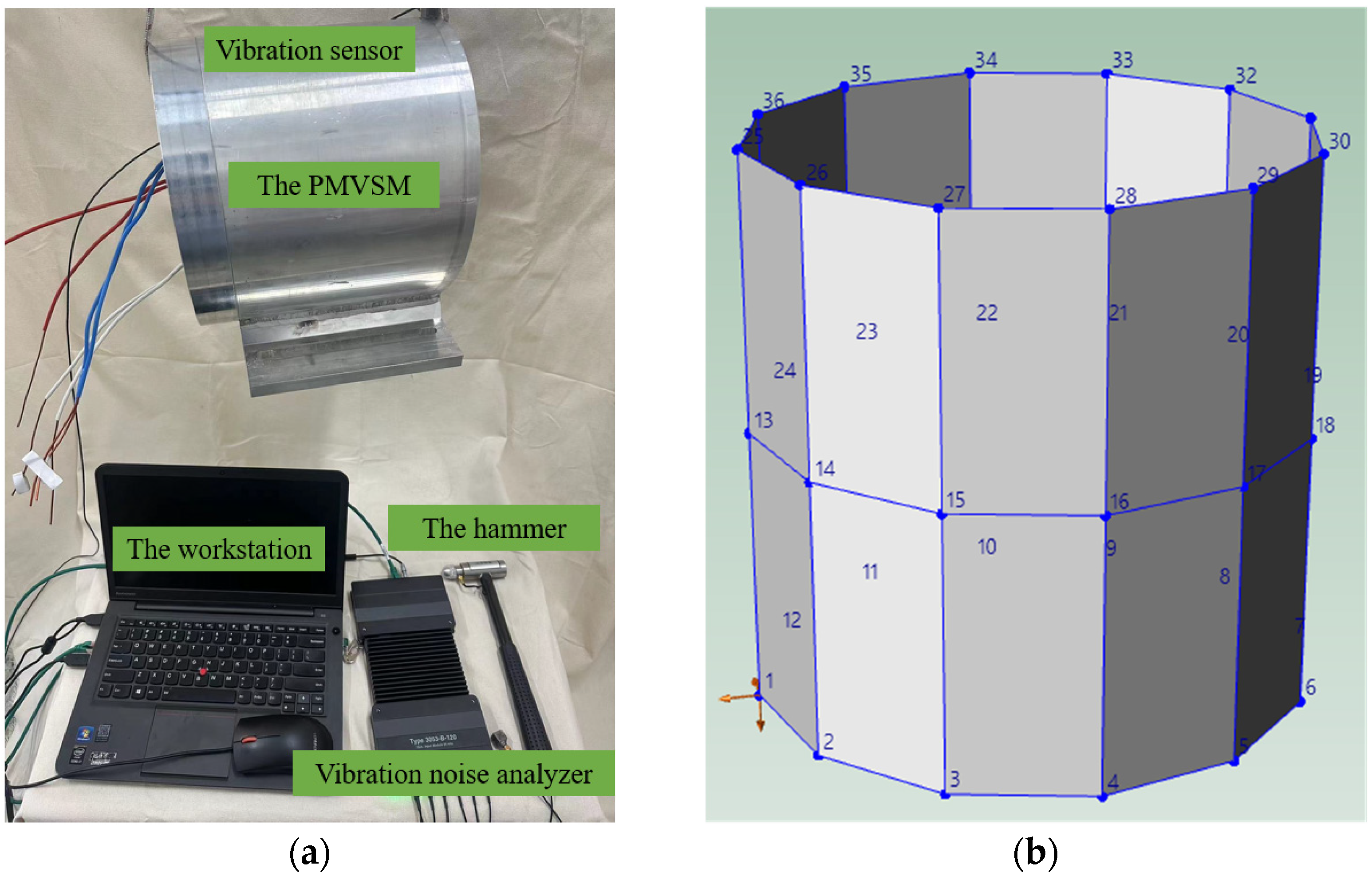
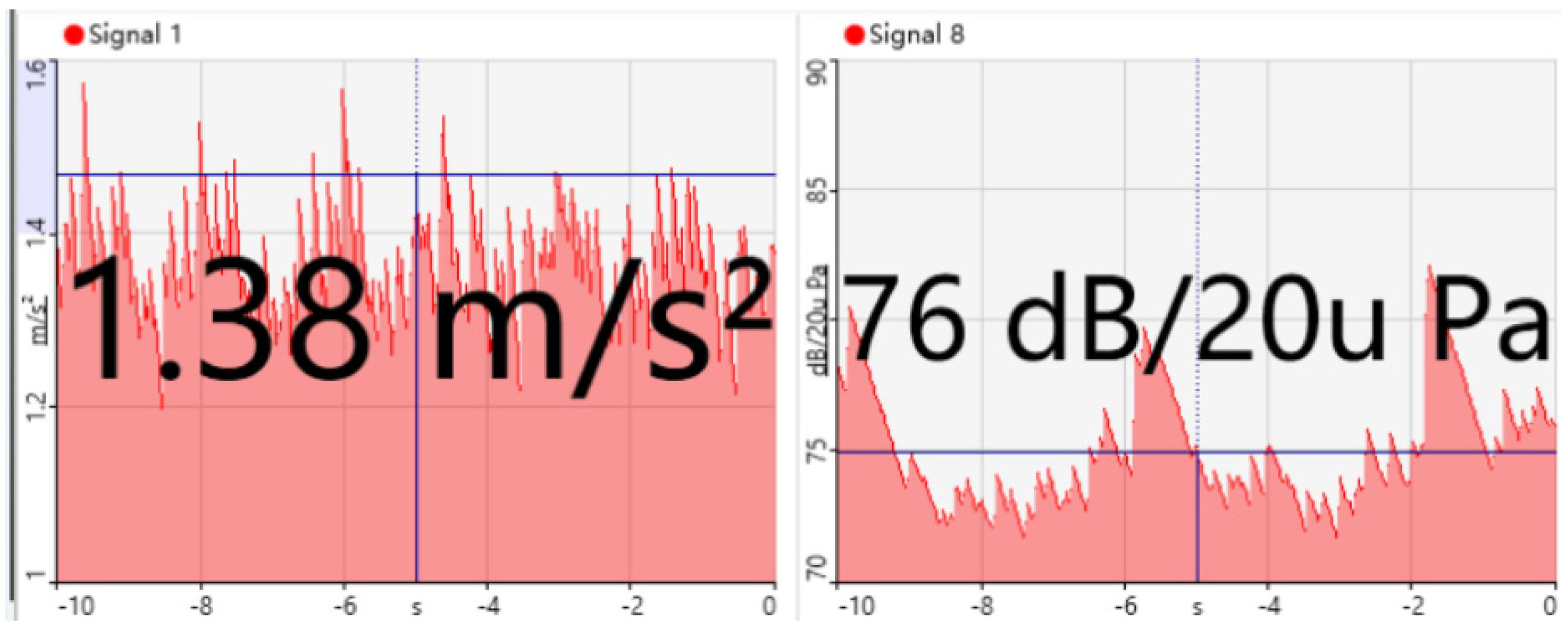
5. PMVSM Modal and Noise Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Spatiotemporal Distribution | The Main Source of Radial Electromagnetic Force Density |
|---|---|
| (−2, 2f) | Mainly generated by (1) the fundamental and the 13th stator magnetic field and the 11th tooth harmonic; (2) the fundamental and the 11th stator magnetic field and the 8th tooth harmonic; (3) the fundamental and the 13th stator magnetic field and the 8th tooth harmonic; (4) the fundamental rotor magnetic field and the 13th stator magnetic field and the 11th tooth harmonic. |
| (10, 2f) | Mainly generated by (1) the fundamental rotor magnetic field and the second tooth harmonic; (2) the fundamental rotor magnetic field and the first tooth harmonic; (3) the fundamental stator magnetic field and the first tooth harmonic; (4) the fundamental stator magnetic field and the second tooth harmonic; (5) the fundamental rotor magnetic field and the fundamental stator magnetic field and the second tooth harmonic. |
| (−4, 4f) | Mainly generated by (1) the fundamental and third rotor magnetic field and the third tooth harmonic; (2) the fundamental stator magnetic field and the third tooth harmonic; (3) the third rotor magnetic field and the fundamental stator magnetic field and third tooth harmonic; (4) the fifth rotor magnetic field and the fundamental stator magnetic field and third tooth harmonic; (5) the fundamental rotor magnetic field and the fundamental stator magnetic field and the third tooth harmonic. |
| (8, 4f) | Mainly generated by (1) the fundamental and 3rd stator magnetic field and the 13th tooth harmonic; (2) the fundamental and 5th stator magnetic field and the 10th tooth harmonic; (3) the fundamental rotor magnetic field and 13th stator magnetic field and 13th tooth harmonic. |
| (6, 6f) | Mainly generated by (1) the fundamental and fifth rotor magnetic field and the fifth tooth harmonic; (2) the fundamental stator magnetic field and the fifth tooth harmonic; (3) the fundamental rotor magnetic field and the fundamental stator magnetic field and fifth tooth harmonic. |
| (−8, 8f) | Mainly generated by (1) the third and fifth rotor magnetic field and the sixth tooth harmonic; (2) the fundamental and seventh rotor magnetic field and the sixth tooth harmonic; (3) the fundamental rotor magnetic field and sixth tooth harmonic; (4) the fundamental stator magnetic field and the sixth tooth harmonic; (5) the seventh rotor magnetic field and fundamental stator magnetic field and the sixth tooth harmonic; (6) the fundamental rotor magnetic field and fundamental stator magnetic field and sixth tooth harmonic. |
| (−12, 12f) | Mainly generated by (1) the fundamental and 11th rotor magnetic field and the 9th tooth harmonic; (2) the 5th and 7th rotor magnetic field and the 9th tooth harmonic; (3) the 3rd and 5th rotor magnetic field and 9th tooth harmonic; (4) the fundamental and 7th rotor magnetic field and 9th tooth harmonic; (5) the fundamental stator magnetic field and the 9th tooth harmonic; (6) the 11th rotor magnetic field and fundamental stator magnetic field and 9th tooth harmonic; (7) the 5th rotor magnetic field and fundamental stator magnetic field and 9th tooth harmonic; (8) the 7th rotor magnetic field and fundamental stator magnetic field and 9th tooth harmonic. |
References
- Zou, T.; Li, D.; Chen, C.; Qu, R.; Jiang, D. A Multiple Working Harmonic PM Vernier Machine with Enhanced Flux-Modulation Effect. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Niu, S.; Ho, S.L.; Fu, W.N.; Wang, L.L. Quantitative Comparison of Novel Vernier Permanent Magnet Machines. IEEE Trans. Magn. 2010, 46, 2032–2035. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Zhu, Z.Q. Comparative Study of Air-Gap Field Modulation in Flux Reversal and Vernier Permanent Magnet Machines. IEEE Trans. Magn. 2018, 54, 1–6. [Google Scholar] [CrossRef]
- Li, D.; Qu, R.; Lipo, T.A. High-Power-Factor Vernier Permanent-Magnet Machines. IEEE Trans. Ind. Appl. 2014, 50, 3664–3674. [Google Scholar] [CrossRef]
- Yu, S.; Tang, R. Electromagnetic and mechanical characterizations of noise and vibration in permanent magnet synchronous machines. IEEE Trans. Magn. 2006, 42, 1335–1338. [Google Scholar]
- Wang, X.; Sun, X.; Gao, P. A Study on the Effects of Rotor Step Skewing on the Vibration and Noise of a PMSM for Electric Vehicles. IET Electr. Power Appl. 2020, 14, 131–138. [Google Scholar] [CrossRef]
- Tsoumas, I.P.; Tischmacher, H. Influence of the inverter’s modulation technique on the audible noise of electric motors. IEEE Trans. Ind. Appl. 2014, 50, 269–278. [Google Scholar] [CrossRef]
- Jiao, G.; Rahn, C.D. Field weakening for radial force reduction in brushless permanent-magnet dc motors. IEEE Trans. Magn. 2004, 40, 3286–3292. [Google Scholar] [CrossRef]
- Qiu, Z.; Chen, Y.; Liu, X.; Kang, Y.; Liu, H. Analysis of the sideband current harmonics and vibro-acoustics in the PMSM with SVPWM. IET Power Electron. 2020, 13, 1033–1040. [Google Scholar] [CrossRef]
- Lin, C.; Wang, S.; Moallem, M.; Fahimi, B.; Tschida, C. Analysis of vibration in permanent magnet synchronous machines due to variable speed drives. IEEE Trans. Energy Conver. 2017, 32, 582–590. [Google Scholar] [CrossRef]
- Liang, W.; Wang, J.; Patrick, C.K.; Luk, W.; Fei, W. The analytical study of stator tooth modulation on electromagnetic radial force in permanent magnet synchronous machines. IEEE Trans. Ind. Electron. 2021, 68, 11731–11739. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, T.; Zhang, H.; Zhang, Z.; Cao, Y. Simulation Analysis on Electromagnetic Vibration and Noise of Novel Mechatronic-Electro-Hydraulic Coupler. Machines 2022, 10, 762. [Google Scholar] [CrossRef]
- Ge, H.; Guo, B.; Qiu, X.; Yang, J.; Feng, C.; Bai, C.; Jin, Z.; Zhang, Y. Optimising the flux barriers of interior permanent magnet machine for noise reduction under certain load conditions. IET Electr. Power Appl. 2021, 15, 1512–1528. [Google Scholar] [CrossRef]
- Xing, Z.; Wang, X.; Zhao, W. Research on weakening measure of radial electromagnetic force waves in permanent magnet synchronous motors by inserting auxiliary slots. IET Electr. Power Appl. 2020, 14, 1381–1395. [Google Scholar] [CrossRef]
- Xing, Z.; Zhao, W.; Wang, X.; Sun, Y. Reduction of radial electromagnetic force waves based on PM segmentation in SPMSMs. IEEE Trans. Magn. 2020, 56, 7507107. [Google Scholar] [CrossRef]
- Teng, X.; Li, Y.; Zhang, B.; Feng, G.; Liu, Z. Analysis and weakening of radial electromagnetic forces in highspeed permanent magnet motors with external rotors based on shape functions. IET Electr. Power Appl. 2023, 1–14. [Google Scholar] [CrossRef]
- Chai, F.; Li, Y.; Pei, Y.; Yu, Y. Analysis of Radial Vibration Caused by Magnetic Force and Torque Pulsation in Interior Permanent Magnet Synchronous Motors Considering Air-gap Deformations. IEEE Trans. Ind. Electron. 2019, 66, 6703–6714. [Google Scholar] [CrossRef]
- Pindoriya, R.M.; Gautam, G.; Rajpurohit, B.S. A Novel Application of Pseudorandom based Technique for Acoustic Noise and Vibration Reduction of PMSM Drive. IEEE Trans. Ind. Appl. 2020, 56, 5511–5522. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, S.; Hong, J.; Liu, C. Vibration Reduction by Segmented Continuous Variable Width Pole for Rotating Armature Permanent Magnet Motors. IEEE Trans. Ind. Appl. 2021, 57, 4657–4664. [Google Scholar] [CrossRef]
- Lin, F.; Zuo, S.; Deng, W.; Wu, S. Modeling and Analysis of Electromagnetic Force, Vibration and Noise in Permanent Magnet Synchronous Motor Considering Current Harmonics. IEEE Trans. Ind. Electron. 2016, 63, 7455–7466. [Google Scholar] [CrossRef]
- Zuo, S.; Lin, F.; Wu, X. Noise Analysis, Calculation and Reduction of External Rotor Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2015, 62, 6204–6212. [Google Scholar] [CrossRef]





| Item | Value | Unit |
|---|---|---|
| Diameter of rotor | 220 | mm |
| Diameter of stator | 180.8 | mm |
| Inner diameter of rotor | 183 | mm |
| Inner diameter of stator | 50 | mm |
| Diameter of stator auxiliary slot bottom | 160.4 | mm |
| Air gap length | 1.1 | mm |
| Core length | 100 | mm |
| The depth of SPM | 10 | mm |
| Angle of short side of SPM | 4 | ° |
| Angle of long side of SPM | 8 | ° |
| Length of VPM | 13.1 | mm |
| Width of VPM | 3 | mm |
| Modes | Modal Shapes and Natural Frequencies | |
|---|---|---|
| (2, 0) |  | 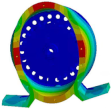 |
| 822.4 Hz | 838.3 Hz | |
| (2, 1) |  |  |
| 1298.7 Hz | 1331.5 Hz | |
| (3, 0) | 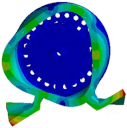 |  |
| 2097.8 Hz | 2156.6 Hz | |
| (3, 1) | 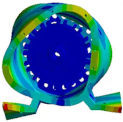 | 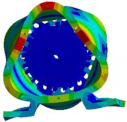 |
| 2404.4 Hz | 2491.6 Hz | |
| (4, 0) | 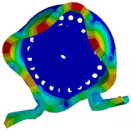 | 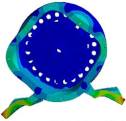 |
| 3936.1 Hz | 3988.3 Hz | |
| (4, 1) | 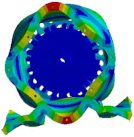 | 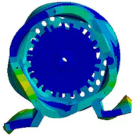 |
| 4253.5 Hz | 4310.5 Hz | |
| Modes | Modal Shapes and Natural Frequencies | |
|---|---|---|
| (2, 0) and (2, 1) |  |  |
| 831 Hz | 1303.4 Hz | |
| (3, 0) and (3, 1) |  |  |
| 2120.2 Hz | 2477.1 Hz | |
| (4, 0) and (4, 1) | 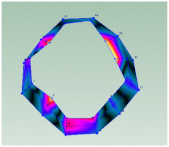 |  |
| 3950.3 Hz | 4278.3 Hz | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Li, D.; Zhang, Y.; Wang, L.; Ye, B.; Zhang, F. The Analysis of Permanent Magnet Vernier Synchronous Machine Vibration and Noise. Electronics 2023, 12, 4341. https://doi.org/10.3390/electronics12204341
Yang F, Li D, Zhang Y, Wang L, Ye B, Zhang F. The Analysis of Permanent Magnet Vernier Synchronous Machine Vibration and Noise. Electronics. 2023; 12(20):4341. https://doi.org/10.3390/electronics12204341
Chicago/Turabian StyleYang, Fan, Daolu Li, Yi Zhang, Lijing Wang, Bitian Ye, and Fang Zhang. 2023. "The Analysis of Permanent Magnet Vernier Synchronous Machine Vibration and Noise" Electronics 12, no. 20: 4341. https://doi.org/10.3390/electronics12204341
APA StyleYang, F., Li, D., Zhang, Y., Wang, L., Ye, B., & Zhang, F. (2023). The Analysis of Permanent Magnet Vernier Synchronous Machine Vibration and Noise. Electronics, 12(20), 4341. https://doi.org/10.3390/electronics12204341










