Robust Position Control for an Electrical Automatic Transmission under Gear-Shifting Link Friction

Abstract

The automotive industry is evolving, with software becoming a vital part of vehicles. Conventional automakers are shifting to software-centric entities, embracing over-the-air (OTA) updates and service-centric models. To move software-driven vehicles, the vehicle must also be electrified. Several automobile manufacturers are electrifying vehicle parts, and recently, a gear shift selector for automatic transmissions was adapted from mechanical to electronic. However, as conventional mechanical systems are modified to electrical systems, problems such as shift delay and accuracy emerge. This study addresses these problems that emerge in the electronic system type of automatic transmission, including a gear shift selector developed to electrify automobiles. Accordingly, we first analyze the structure of automatic transmission systems, then define the operation sequence. Next, a novel position control algorithm based on a disturbance observer is proposed to reduce shift delay and increase accuracy. The proposed algorithm operates harmoniously with the vehicle control unit (VCU). To verify the proposed algorithm, a hardware-in-the-loop simulation (HILS) was developed to experiment with vehicle shifting using a commercial electronic gear shift selector. Moreover, the proposed control algorithm for gear shifting in an automatic transmission was analyzed using experimental results obtained by assuming a specific driving situation in the HILS.

1. Introduction

In the last century, the automotive industry predominantly outsourced software development, concentrating its efforts on the mechanical aspects of vehicle design. However, the landscape is rapidly shifting, with software technology emerging as a decisive factor in automotive distinctiveness. Software has emerged as the most significant driver of revenue growth for automotive manufacturers. Consequently, conventional automakers are evolving from their conventional identities, becoming tech-centric entities specializing in automotive software. This transformation can be tangibly observed in numerous automotive manufacturers that have adopted software updates in their vehicles, triggering seismic shifts within the automotive OTA software market. As vehicular hardware evolves to facilitate software updates, the revenue model is experiencing a tectonic shift from an asset-centric to a service-centric paradigm.

Simultaneously, worldwide digital companies such as Amazon Web Services (AWS), Google, Alibaba, and Tencent are poised to expand their footprint in the automotive technology arena. These software-driven enterprises are aggressively embedding vehicles into their ecosystems and are ready to deliver novel vehicle-connected services. The efficacy and functionality of these diverse services depend on the underlying software, similar to the dependence of a smartphone’s capabilities on its operating system. Such vehicles are referred to as software-defined vehicles (SDVs) [1].

Several automotive components should be electrified to enhance the performance and functionality centered around software [2]. Successfully commercialized electrified components include parts that interact with the driver, such as steering, transmission, pedal, and other features. These electrified components all adhere to the X-by-wire paradigm, undergoing a transformation from conventional mechanical operations to an electrical signal-based module [3]. Notably, automotive automatic transmission systems exemplify this transition.

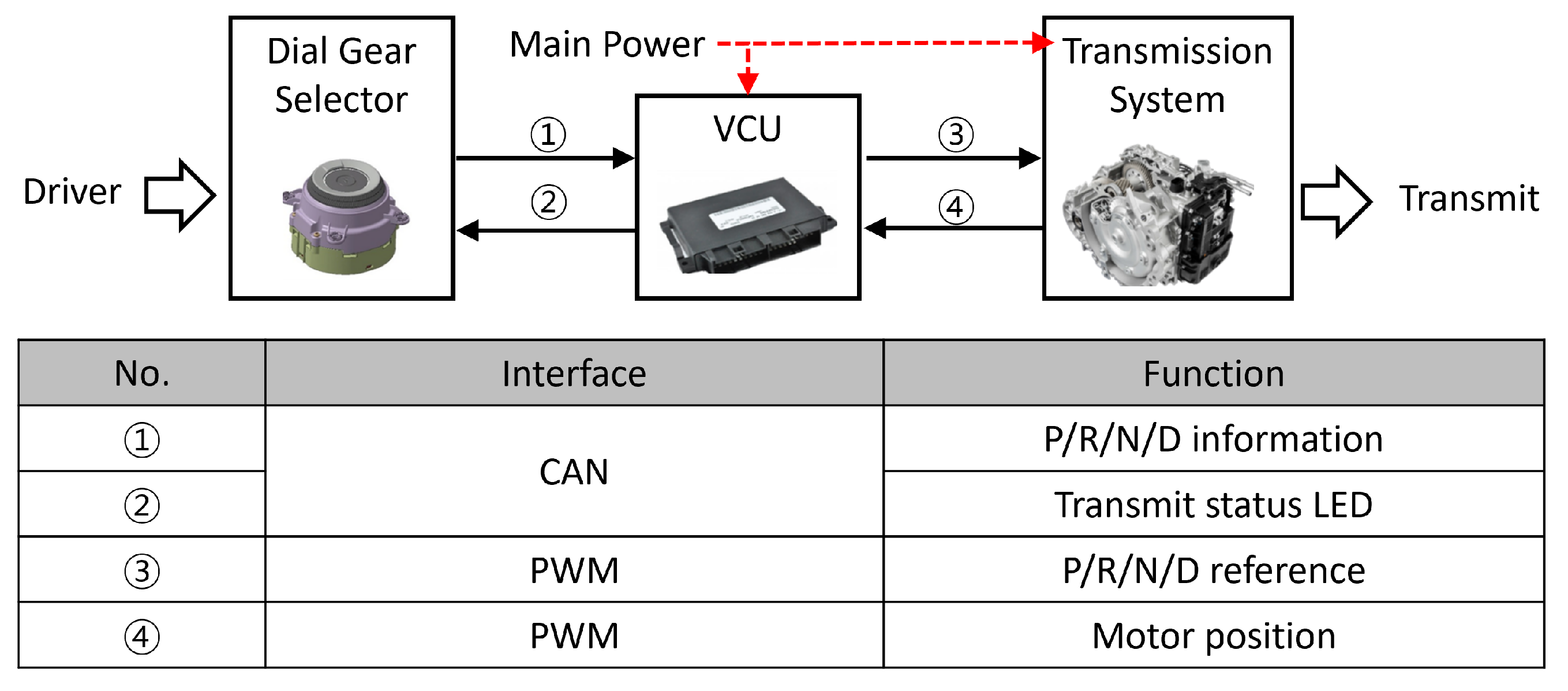
In particular, automatic transmission systems are being altered from mechanical gear shift selectors to electronic systems such as button-, rotary-, and dial-type systems. In automatic transmission systems based on mechanical gear shift selectors, the driver’s manipulation of the selector mechanically alters the automatic transmission’s gears via cables. However, developing fully electrified automatic transmission systems eliminates mechanical cables and physical selectors. Mechanical gear shift selectors have been supplanted by buttons, rotary controls, and dials, transmuting the driver’s input into electrical signals conveyed via a VCU to the automatic transmission.

Applying fully electrified automatic transmission systems engenders several benefits, including heightened vehicle interior design flexibility. Electronic gear shift selectors based on buttons or dials, which replace conventional mechanical gear shift selectors typically adorning the center console, function as design elements and enable the versatile utilization of surrounding spaces. Moreover, these electronic controls facilitate the implementation of driving convenience features such as remote smart parking assistance systems and smart valet parking [4], tasks hitherto impossible without the driver’s input in conventional mechanical gear lever systems.

A fully electrified automatic transmission system has several advantages, including new functionalities, design adaptability, enhanced user experience, alignment with prevailing trends, and cost-effectiveness for both manufacturers and consumers. However, several considerations should be addressed [5,6], most importantly the nominal time delay between the driver manipulating buttons or controls and the execution of the corresponding gear selection within the vehicle. This temporal lag emanates from the time required for the VCU to interpret, process, and transmit the signal of the gear shift selector to the actuator inside the automatic transmission. The time delay in fully electrified automatic transmission systems is typically well under 1 second [7]. In scenarios necessitating precise vehicle movements within confined spaces, this delay may cause discomfort to the driver. Secondly, the position control performance of the automatic transmission should be guaranteed. Given that the force acting upon the automatic transmission varies depending on the selected gear, the actuator should surmount these forces while maintaining precise positional control [8]. These issues are unique to fully electrified automatic transmission systems and absent in conventional automatic transmission systems.

The merits of conventional automatic transmission systems lie in their intuitiveness and unwavering reliability. The gear sequence (P–R–N–D) is a universal standard across all automotive models worldwide [9]. Furthermore, each gear is mechanically linked via cables, ensuring palpable tactile feedback for the driver and real-time recognition of gear changes. Significantly, the position of the gear lever is mechanically determined, ensuring consistent transmission to the transmission and precise gear selection.

Therefore, the electrification of transmission systems necessitates addressing the challenges of minimizing time delays and preserving gear selection accuracy—attributes inherently embedded in conventional transmission systems. Several research groups have developed algorithms for fully electrified automatic transmission systems, including gear shift selectors [7,10,11]. However, these studies focused on the performance improvement inside the automatic transmission system, such as gear shift timing.

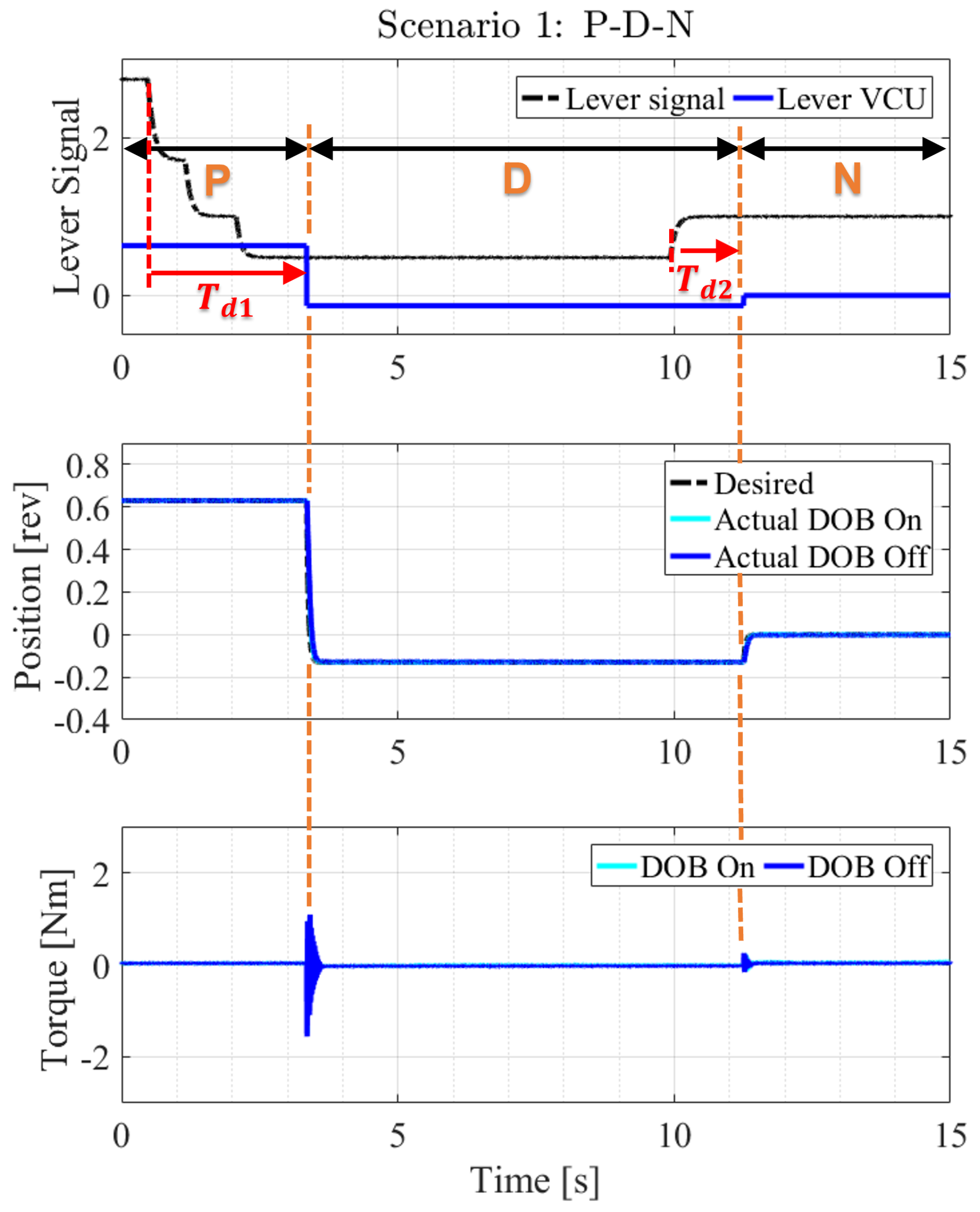
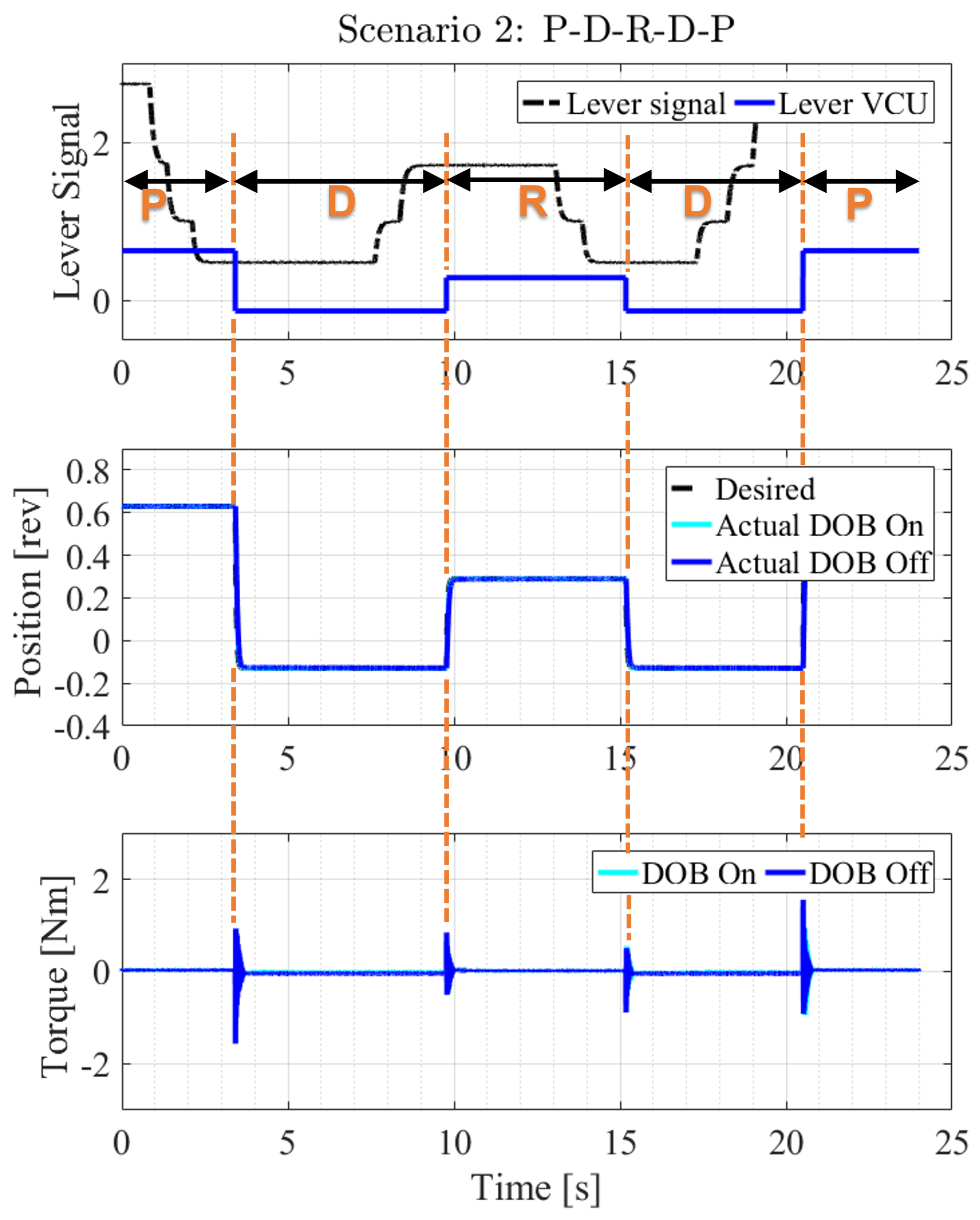
This study attempts to augment the responsiveness of the automatic transmission actuator in response to driver-initiated gear selections while concurrently enhancing positional accuracy in the presence of external perturbations. Accordingly, the characteristics of the electric gear shift selector (E-shifter)–VCU–actuator are first analyzed, which are components of the gear shift system, and a shift operation algorithm is designed considering the interface between components to minimize the overall shift time delay. In addition, to improve the position control performance of the automatic transmission actuator, a position control algorithm robust to disturbances generated in the automatic transmission is proposed. Control stability analysis was also performed to prevent malfunctions of the proposed actuator’s position control algorithm. A hardware-in-the-loop simulation (HILS) system was developed using an actual mass-produced dial-type gear shift selector to verify the operation algorithm of the electronic shifting system proposed in this study. The proposed electronic shifting operation algorithm was verified via various driving scenarios based on the HILS.

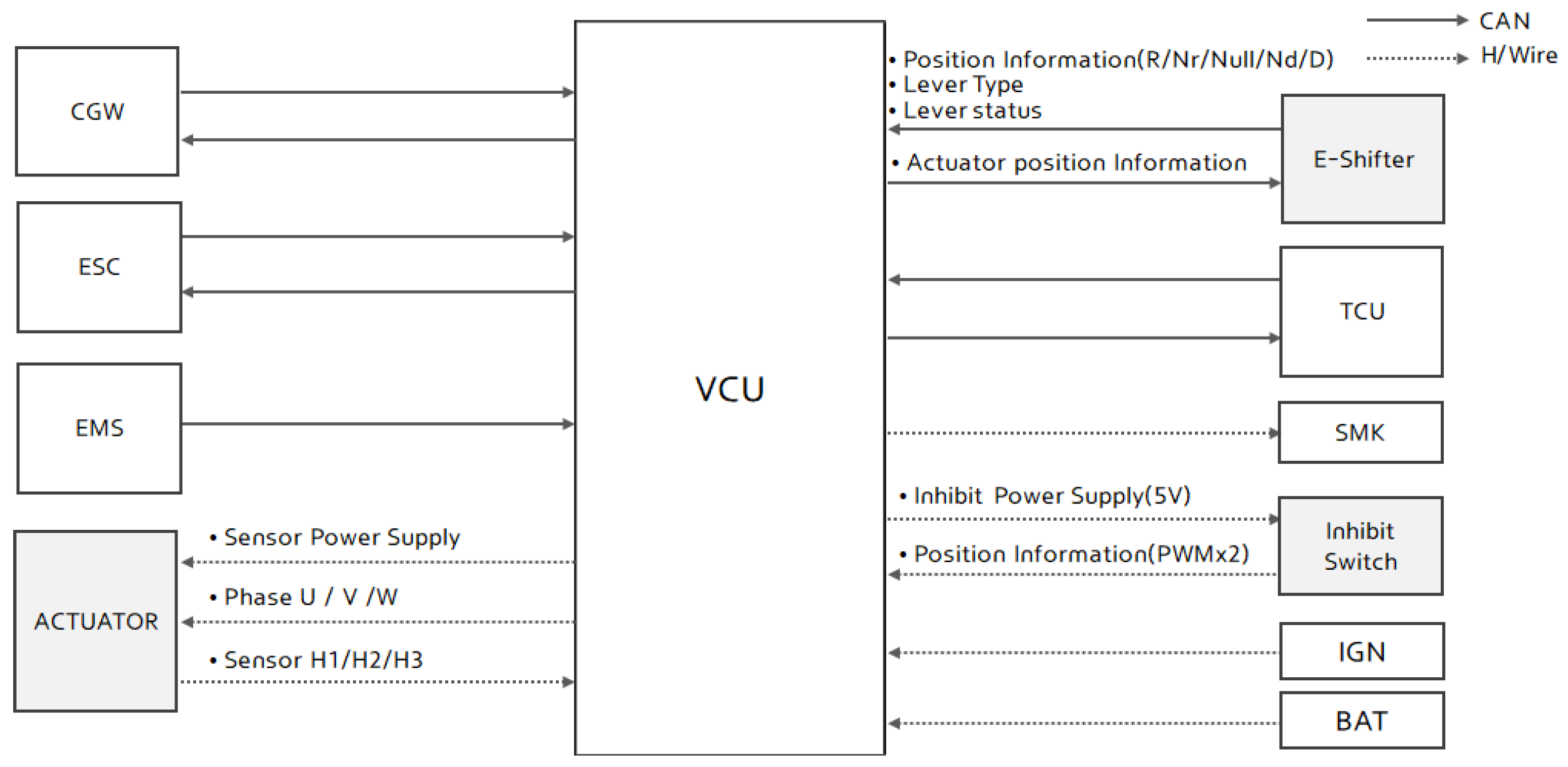
The remainder of this paper is organized as follows. Section 2 comprehensively describes the configuration and electrical interfaces of the automatic transmission systems. In Section 3, we develop the operational sequence of the actuator for automatic transmission, design a robust position control algorithm that handles external automatic transmission forces, and conduct a control stability analysis. In Section 4, we verify the proposed algorithm via an experimental setup and present the results for several driving scenarios. Section 5 concludes this paper.

2. System Overview

In this section, an exploration of the intricate workings of the E-shift system is presented. The gear status of the automatic transmission is determined through a meticulous process that involves the comprehensive collection and analysis of various pieces of state information from the vehicle. This includes the examination of factors such as the current state of the dial switch, the vehicle’s speed at any given moment, and the precise location of the shift motor. To simplify the evaluation and analysis of the control algorithm governing the automatic transmission system, a deliberate decision was made to streamline the selection of the appropriate shift stage. This simplified approach mirrors the operation of the E-shifter–VCU–actuator, as meticulously illustrated in Figure 1. This decision, while seemingly straightforward, allows for a more focused and in-depth exploration of this advanced electronic shift system in the context of our research.

2.1. Configuration of the E-Shift System

Figure 1 illustrates the overall hardware structure of the E-sift system. First, there is a dial-type selector that the user manipulates for shifting. A dial-type selector does not necessarily have to be utilized in a shift-by-wire vehicle; a button- or bar-type selector can also be adopted. With the dial-type selector utilized in this study, the shift intention of a driver can be input into the vehicle. As illustrated in Figure 2a, the operation method is structured such that when the user turns the dial to the desired gear shift selector, the selector is caught in the groove to fit into that position. Subsequently, the dial returns to its original position, provided the driver releases their hand. When the user rotates the dial to a specific position among P/R/N/D, this positional information is transmitted to the VCU via pulse-width modulation (PWM) (➀ in Figure 1).

Subsequently, the VCU determines the final E-shift position of the vehicle and transmits one of the P/R/N/D signals to the transmission motor via controller area network (CAN) communication (➂ in Figure 1).

To determine the final gear position, the VCU collects several pieces of vehicle information. This process is comprehensively presented in Section 3.1. The transmission motor moves to the received shift position, where a physical shift occurs. At this point, the transmission motor rotates to the determined shift position and transmits the current position to the VCU (➃ in Figure 1). Then, the VCU receives the position of the transmission motor and determines whether or not to shift. To inspect whether the transmission is complete, the VCU utilizes the PWM signal from the inhibit switch. If the transmission is completed successfully, the PWM duty sum should be within 100 ± 2%. Then, the VCU transmits the final gear position to the dial-type selector again as a PWM signal (➁ in Figure 1). Finally, the LED display of the dial-type selector indicates the current shift status, as shown in Figure 2b.

2.2. Description of the Electrical Interface

The VCU is a critical component of the E-shift system in determining the current shifting state and controlling the shift motor position.

Figure 3 comprehensively illustrates the process of transferring the gear shift intention of the driver to the shifting motor and recognizing the current shifting state from the VCU.

In addition to the parts mentioned in Figure 1, vehicle information is collected from various elements in the vehicle to transfer the gear shift intention to the transmission. First, the CGW module checks the driver’s readiness to drive by identifying the states of the door and seat. Then, the brake light switch (BLS) module checks the braking pedal response. Most gear shifts, except between N and D, are executed when the driver works the braking pedal. Next, the VCU also checks the accelerator pedal from the EMS module to switch the gear from P to R, N, or D. Finally, the VCU measures the vehicle speed, using ESC to change the gear from D to R. As the vehicle speed approaches zero, these gears can be switched.

Therefore, the E-shift system executes gear shifting by comprehensively considering various pieces of information about vehicle status.

3. Control Algorithm for Gear Position in an Automatic Transmission System

In this Section, a comprehensive analysis is presented, elucidating the intricate shifting sequence from the dial selector all the way to the shifting actuator within the automatic transmission. This meticulous examination takes us through the step-by-step process, dissecting the multifaceted mechanics that underlie the gear shifting mechanism. Subsequently, we delve into the development and proposal of a sophisticated control algorithm meticulously designed for the shifting actuator. This algorithm, while seemingly straightforward in theory, stands the test of real-world challenges with resilience, particularly when confronted with issues like inherent friction within the system. The intricate analysis undertaken in this section delves deep into the complexities of overcoming these practical challenges, offering valuable insights into the optimization of the shifting actuator’s performance.

3.1. Gear Shift Process in the Automatic Transmission Using a Dial-Type Gear Selector

For the shifting actuator to move at a predetermined shift angle as intended by the driver, there must be a shift angle corresponding to the rotation angle of the dial-type selector. For example, as shown in Figure 2a, if the driver rotates the dial to ${\theta }_{Dial}$ for the P gear input, the shifting motor should be turned to ${\theta }_{Motor}$, as defined by Equation (1).

$$\begin{array}{c}\hfill {\theta }_{Motor}=K_{\mathrm{Dial}2\mathrm{Motor}}^{\mathrm{P}/\mathrm{R}/\mathrm{N}/\mathrm{D}}{\theta }_{Dial},\end{array}$$

(1)

where $K_{\mathrm{Dial}2\mathrm{Motor}}^{\mathrm{P}/\mathrm{R}/\mathrm{N}/\mathrm{D}}$ represents a proportional factor for ${\theta }_{Dial}$, as indicated in

Table 1. Ratio between the dial-type selector and shift motor angle in (1).

Parameter	Value
$K_{\mathrm{Dial}2\mathrm{Motor}}^{\mathrm{P}}$	1.2
$K_{\mathrm{Dial}2\mathrm{Motor}}^{\mathrm{R}}$	0.9
$K_{\mathrm{Dial}2\mathrm{Motor}}^{\mathrm{N}}$	1.3
$K_{\mathrm{Dial}2\mathrm{Motor}}^{\mathrm{D}}$	1.5

.

In addition, because the dial-type selector cannot independently input the desired gear shift, unlike the button type or bar type, the VCU should determine the driver’s intention by observing the staying time on the corresponding gears on the dial-type selector.

Consequently, the VCU measures the time the dial-type selector stays in a specific range ($T_{Dial}$), as expressed in Equation (2), to determine the driver’s final shift intention.

3.2. Robust Position Control Based on a Transmission-Disturbance Observer

When the shifting position is determined from the dial, the actuator in the automatic transmission moves to the predefined gear position. The automatic transmission mechanism has a link that presses it with a spring such that the angle is not altered at the preset position. Therefore, the actuator overcomes this spring force and moves over the groove to shift; hence, a robust position control algorithm is required for this actuator.

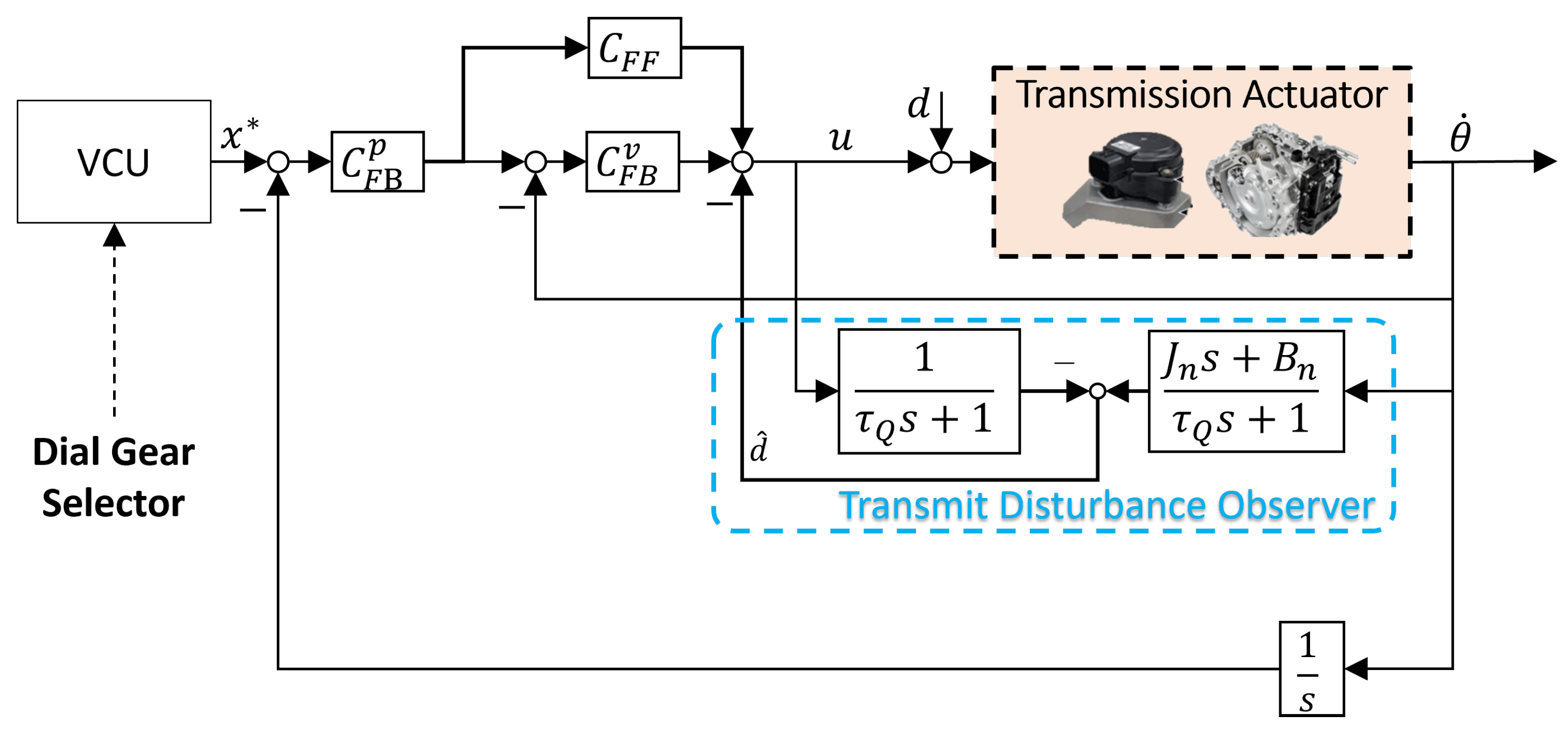
Therefore, we propose a robust position control algorithm for the gearbox, as illustrated in Figure 4. In the proposed algorithm, all external forces, including the spring force acting on the gearbox during shifting, are assumed to be lumped transmission disturbances.

A disturbance observer (DOB) [12] is the most effective technique for estimating the disturbance and can also be adopted to suppress the gear transmission disturbance.

In particular, the DOB observes the disturbance acting on the system by utilizing the nominal model of the system and Q filter. The nominal model in this automatic transmission system includes a transmission actuator and a transmit link. Figure 5 presents the dynamic characteristics of the transmission actuator system using the frequency response from motor torque to the speed. The speed of the actuator can be calculated from the encoder attached to the motor shaft. Considering the dynamic characteristics, the nominal model of the system is assumed to be a first-order dynamic system in the frequency domain and expressed as

$$\begin{array}{c}\hfill P_n\left(s\right)=\frac{1}{J_{n}s+B_n},\end{array}$$

(2)

where the plant model parameters are assumed to be $J_n=37\times {10}^{-7}$ and $B_n=16\times {10}^{-6}$. Therefore, the estimated lumped disturbance can be calculated using the nominal model ($P_n\left(s\right)$) and expressed as

$$\begin{array}{c}\hfill {\widehat{d}}_T=Q\left(s\right)(P_n^{-1}-u),\end{array}$$

(3)

where $Q\left(s\right)$, which mostly influences the robustness of the DOB system, is designed as a first-order low-pass filter to satisfy the causality in a first-order dynamic system. The cutoff frequency of the filter ($Q\left(s\right)$) is set as 13 $\mathrm{Hz}$. Notably, the sensor measurement noise and model uncertainty are not considered in Equation (3). Hence, the closed-loop transfer function of the automatic transmission system from motor torque to speed is determined as

$$\begin{array}{c}\hfill T_{u\to y}\left(s\right)=\frac{1}{1-Q+Q{P}_n^{-1}P}\left(s\right).\end{array}$$

(4)

Therefore, the closed-loop transfer function of the position controller, including the transmission disturbance observer (T-DOB), is derived as

$$\begin{array}{cc}\hfill & T_{p\to y_p}\left(s\right)=\hfill \\ \hfill & \frac{P{C}_{FB}^p\left(C_{FF}+C_{FB}^v\right)}{1-Q+Q{P}_n^{-1}P+P\left(C_{FB}^v+C_{FB}^p\left(C_{FF}+C_{FB}^v\right)\right)}\left(s\right),\hfill \end{array}$$

(5)

where $T_{•\to \circ }$ denotes the transfer function from • to ∘; $C_{FB}^p$ represents the feedback controller of the position control loop, with a transfer function defined as $C_{FB}^p\left(s\right)=k_p^p+k_D^{p}s$; $C_{FB}^v$ represents the feedback controller of the speed control loop, with a transfer function defined as $C_{FB}^v\left(s\right)=k_p^v+k_d^{v}s$; and $C_{FF}$ represents the feed-forward controller of the speed control loop, with a transfer function defined as $C_{FF}\left(s\right)=Q\left(s\right)P_n^{-1}$. Because the spring presses the groove to fix the gear link, the frictional force acts differently when the motor moves. Accordingly, the stability of the controller should be satisfied even when the dynamic characteristics of the system are subject to change. The dynamic characteristics that change in the nominal model are expressed as $\Delta \left(s\right)$ in Figure 6a. Then, the actual plant model can be expressed as

$$\begin{array}{c}\hfill P\left(s\right)=P_n\left(s\right)(1+\Delta \left(s\right))).\end{array}$$

(6)

The parameter to be changed can be regarded as a $B_n$ term in (2) and is assumed to have the following range ($B_{n,\min }$ < $B_n$ < $B_{n,\max }$). By applying this range, the model variation ($\Delta \left(s\right)$) is derived as

$$\begin{array}{c}\hfill \Delta \left(j\omega \right)\left(s\right)=\frac{P\left(s\right)-P_n\left(s\right)}{P_n\left(s\right)}.\end{array}$$

(7)

To ensure stability, the small-gain theorem [13] is adopted. According to this theorem, the infinity norm should be less than 1 to guarantee closed-loop stability, expressed as

$$\begin{array}{c}\hfill {\left|\Delta \left(j\omega \right)T\left(j\omega \right)\right|}_{\infty }<1\mathrm{for}\mathrm{all}\omega \in \Re .\end{array}$$

(8)

where $T\left(j\omega \right)$ represents the complementary sensitivity function calculated from the block diagram in Figure 6a and derived as

$$T\left(j\omega \right)=\frac{C_A\left(j\omega \right)P_n\left(j\omega \right)+Q\left(j\omega \right)}{1+C_A\left(j\omega \right)P_n\left(j\omega \right)},$$

(9)

where $C_A\left(j\omega \right)=C_{FB}^v\left(j\omega \right)C_{FB}^p\left(j\omega \right)C_1\left(j\omega \right)+C_{FB}^v\left(j\omega \right)+C_{FB}^p\left(j\omega \right)C_{FF}\left(j\omega \right)C_{FF}\left(j\omega \right)$, and $C_1\left(j\omega \right)$ represents the integral operator ($\frac{1}{s}$) required to obtain the motor angle from the speed.

Figure 6b demonstrates that $T\left(j\omega \right)$ is the inverse of $\Delta \left(j\omega \right)$ and that the stability of the closed-loop system is guaranteed in the overall frequency. Model parameter $B_n$ varies within the range of $18\times {10}^{-6}\le B_n\le 18\times {10}^{-5}$. The parameters of each controller are set as follows: $K_p^p=1.2$, $K_d^p=2\times {10}^{-3}$, $K_p^v=74\times {10}^{-8}$, and $K_d^v=24\times {10}^{-8}$.

4. Experimental Results

This section provides a comprehensive overview of the experimental findings, highlighting the effectiveness of the position control algorithm in the proposed automatic transmission system. The summary begins with a detailed exploration of the experimental setup, as outlined in Section 4.1. This section encompasses the meticulous design of the test bench and the integration of advanced technologies such as Matlab/Simulink and real-time DAQ equipment from Quanser [14]. This setup serves as the robust foundation for the subsequent analyses, allowing for the precise application of the control algorithm to the physical plant and facilitating the collection of real-time sensor data. Following the discussion of the experimental setup, Section 4.2 takes us through the operating scenarios and the wealth of data collected during these scenarios. The focus is on the simulation of both vehicle driving and parking modes, with a detailed examination of the driver’s dial selector movements and the VCU’s role in recognizing the intended gear shifts. The analyses cover recognition times, steady-state errors, and the impact of the proposed T-DOB approach on the control of the final shift position. These analyses span both no-load and load conditions, providing comprehensive insights into the algorithm’s performance under varying levels of friction. Overall, this section offers valuable insights into the algorithm’s robustness and performance in a real-world context, positioning it as a promising solution for practical applications in the field of automatic transmission systems.

4.1. Experimental Setup

A test bench was fabricated to verify the position control algorithm of the proposed automatic transmission system, as illustrated in Figure 7. The control algorithm and process of the VCU were implemented in Matlab/Simulink, and a DAQ instrument from Quanser [14], which guarantees real-time control [15], was utilized. Using this equipment, the control value, which was calculated using Simulink, was input to the actual plant, and external sensor data were collected. Moreover, regarding the dials, prototypes used in actual vehicles were utilized. Regarding the shifting actuator, comprises a servo motor similar to that found in an actual vehicle environment. In contrast, because the shift link is part of the automatic transmission system of the vehicle, the separated shift link is manufactured to reproduce the only friction effect of the shift link, as illustrated in Figure 7.

4.2. Operating Scenario and Experimental Results

Two experimental scenarios are presented: vehicle driving and parking. First, when the vehicle is in the driving scenario, the driver moves the position of the dial-type selector in the order of P, R, N, and D. At this point, it is assumed that the VCU recognizes the driver’s intention for the gear shift. Therefore, the VCU sends the target position information—not of all positions the selector has passed (R and N) but the final selector position (D)—to the shift motor. The recognition time is indicated as $T_d$ in Figure 8 and varies with the final dial shift position. Next, it is assumed that the dial-type selector is changed to P, D, R, D, and P to reproduce the parking mode. At this point, the VCU sends the target position information to the shift motor in the order of P, D, R, D, and P by recognizing the driver’s intention.

Regarding experimental results, Figure 8, Figure 9, Figure 10 and Figure 11 present the position control performance and torque in the driving scenario. Figure 8 and Figure 9 represent the results under the no-load condition for the gear shift to verify the proposed control algorithm. In these cases, it is assumed that there is no disturbance in the shift link to switch the gear. Although the control performance seems similar between the two approaches (DOB on and off), the performance is improved, as shown in

Table 2. Position control performance metrics by load condition and gear shift scenario.

Load Condition	Gear Shift Scenario	RMSE in DOB Off	RMSE in DOB On	Improvement
No load	P-D-N	0.0159	0.0136	14.2%
	P-D-R-D-P	0.0198	0.0171	13.5%
Load	P-D-N	0.0192	0.0157	18.0%
	P-D-R-D-P	0.0236	0.0199	15.8%

.

In contrast, Figure 10 and Figure 11 represent the experimental results under the load condition in the gear shift to reproduce the actual gear shift condition.

Figure 10 presents the results for the driving scenario. First, considering the graph when T-DOB is not utilized (blue solid line), it is inferred that a steady-state error occurs. This is because the control algorithm does not sufficiently compensate for the friction generated in the gearbox. In contrast, in the case where T-DOB is applied (a cyan solid line), it can be observed that the steady-state error of the final shift position is significantly minimized. Figure 11 presents the experimental results for the parking scenario. The experiment results show that a position error occurs at each shift position. In the parking mode of the vehicle, shift timing and the number of types of shifts are greater than those in the driving mode; thus, a positional error (blue solid line) of the transmission gear may trigger a severe problem in the automatic transmission. However, in the case of applying T-DOB (a cyan solid line), despite the several types of shifting present, the shift link exhibits robust performance at a given shift position. In other words, the proposed position control algorithm exhibits robust position control performance, even with varying friction depending on the shift link position. The performance metric of position control under various conditions is shown in Table 2.

5. Conclusions

This study presents a novel position control algorithm based on a dynamic model of the gear shift actuator in an automatic transmission system. The primary focus was on suppressing friction in the automatic transmission link by employing a lumped disturbance model through T-DOB, eliminating the need for a separate experiment to measure friction and any substantial control algorithm modifications. The key objective of this research was to verify the effectiveness of the proposed control algorithm in managing the dynamic characteristics of the shift link, accommodating diverse shift timings and various types of shifting tests. The parking- and driving-mode experiments yielded insightful results, demonstrating the algorithm’s capability to adapt to real-world gear shift scenarios. The findings emphasize the position control algorithm’s practicality and efficacy in electric shift-by-wire systems. The algorithm’s robustness and potential for implementation in automotive transmission systems have been showcased by successfully overcoming the challenges associated with varying shift dynamics. This research contributes to the growing knowledge of transmission control and electric shift-by-wire technology through comprehensive experimentation and analysis. The proposed algorithm represents a valuable advancement in improving the performance and reliability of gear shifting in modern vehicles. As this technology continues to evolve, this work underscores the importance of innovative control algorithms in enhancing the overall driving experience and safety provided by the automotive industry.