A Review for the Euler Number Computing Problem
Abstract
:1. Introduction
- (1)
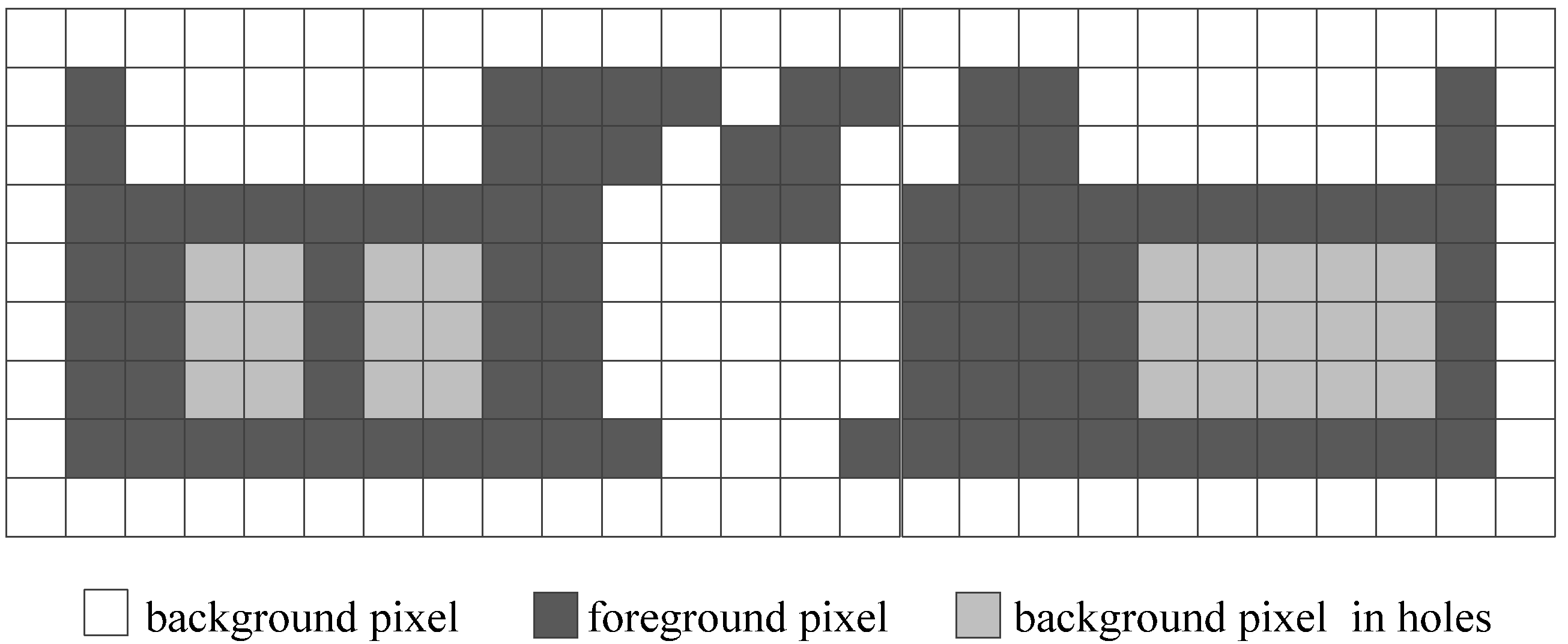
- Algorithms that compute the Euler number by the definition in [9,10]. As described above, for a given image, the definition of the Euler number is the disparity between the numbers of connected components and holes. Thus, to compute the Euler number, these algorithms need to obtain the number of holes and the number of connected components in the given image. Accordingly, to achieve this goal, complicated labeling operations need to be conducted to distinguish every connected component and every hole in the image. Once the number of holes and connected components is acquired, we can obtain the Euler number easily.
- (2)
- Algorithms that compute the Euler number by utilizing the intrinsic features of the image [11,12,13,14,15,16]. In these algorithms, different features of an image are used to calculate the Euler number. For example, taking advantages of the skeleton, the perimeter/contact perimeter and the special contour pixels of the image, we can compute the Euler number in different ways.
- (3)
- Algorithms that compute the Euler number by counting specific blocks/patterns in the image [17,18,19,20,21,22,23,24,25]. In these algorithms, specific patterns with 2 × 2 pixels and consecutive foreground pixel blocks in the same row in the image, called runs, can be employed for calculating the Euler number. Moreover, using a raster scan, these algorithms can be easily implemented in practice.
- (4)
- Algorithms that compute the Euler number with a special data structure [26,27,28,29,30,31,32,33]. Trees and graphs are special data structures for representing an image. By representing an image as a tree or a graph, these algorithms can compute the Euler number through the theorems or conclusions in the data structure of the tree or graph.
- (5)
- Algorithms that compute the Euler number using machine learning methods [34,35,36]. In the past decade, machine learning/deep learning methods have been widely adopted for image classification and image recognition tasks. Then, some researchers have adopted these methods for Euler number computation. Experimental results have verified the accuracy of these methods in Euler number computation. However, these methods need to collect a lot of samples and take a long time to train the samples. Therefore, for only obtaining the Euler number, these methods may not be so efficient.
- (6)
- Algorithms that compute the Euler number using special structure computers [37,38,39,40,41,42]. As mentioned in Class (3), the Euler number can be determined by identifying specific patterns within the raster scan and counting them. Then, VLSI (very large-scale integration), co-processor, and pipeline architecture can be employed for counting these patterns within different regions of a given image simultaneously to improve the conventional algorithms.
- (a)
- Algorithm that computes the Euler number with the definition proposed in Ref. [9];
- (b)
- Algorithm that computes the Euler number with the skeleton of a given image, as proposed in Ref. [11];
- (c)
- Algorithm that computes the Euler number via the perimeter of connected components in a given image, as proposed in Ref. [12];
- (d)
- Algorithm that computes the Euler number via corner codification of foreground pixels in a given image, as proposed in Ref. [16];
- (e)
- Algorithm that computes the Euler number via specific 2 × 2 bit-quad patterns in a given image, as proposed in Ref. [17];
- (f)
- Algorithm that computes the Euler number via runs in a given image, as proposed in Ref. [23];
- (g)
- Algorithm that computes the Euler number by representing a given image as a graph, as proposed in Ref. [27];
- (h)
- Algorithm that computes the Euler number by representing a given image as a tree, as proposed in Ref. [31];
- (i)
- Algorithm that computes the Euler number via graph representation of specific runs in a given image, as proposed in Ref. [33].
2. Reviews of State-of-the-Art Euler Number Computing Algorithms
2.1. Algorithms That Compute the Euler Number through the Definition
2.2. Algorithms That Compute the Euler Number by Utilizing Intrinsic Features
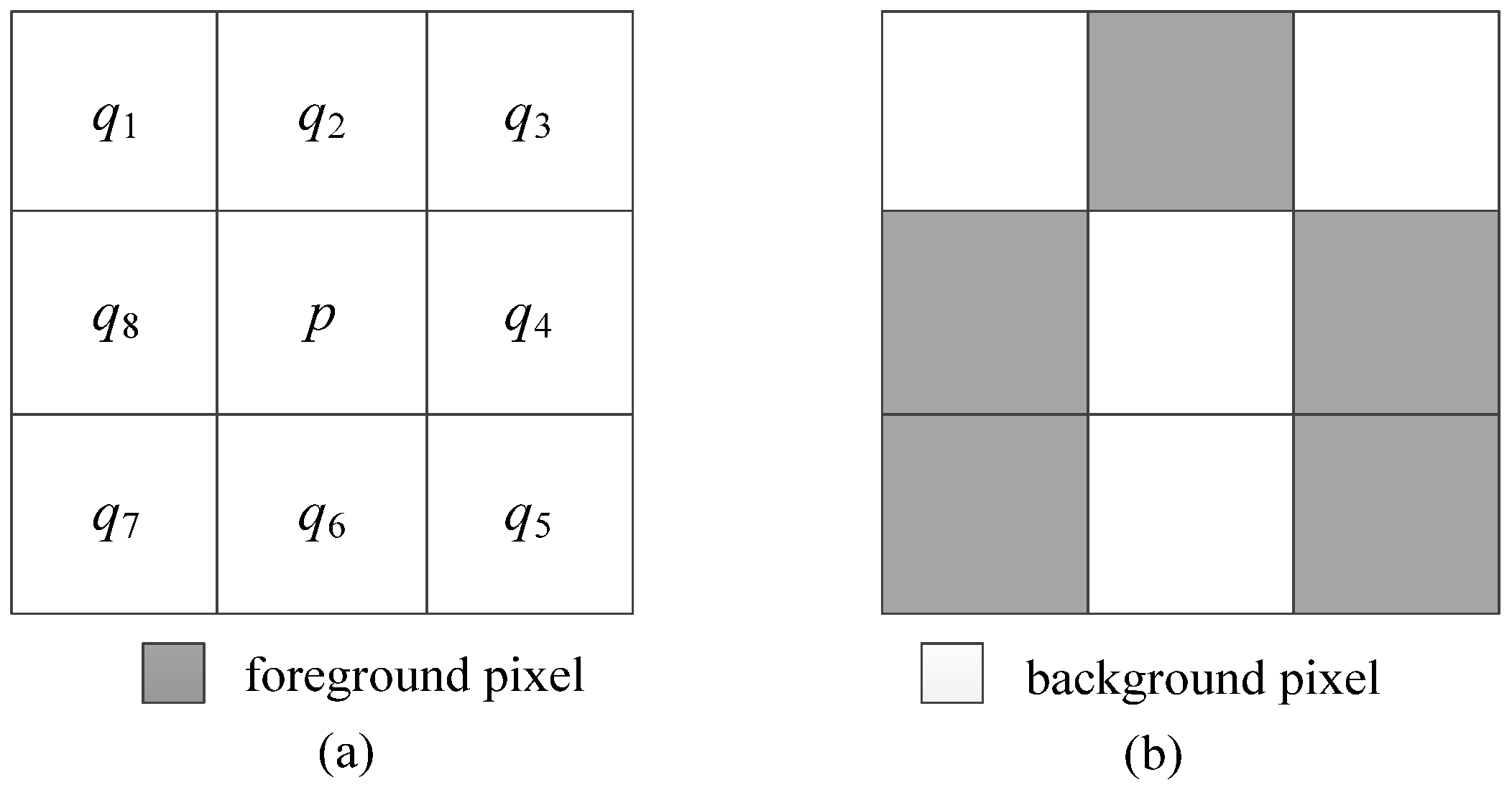
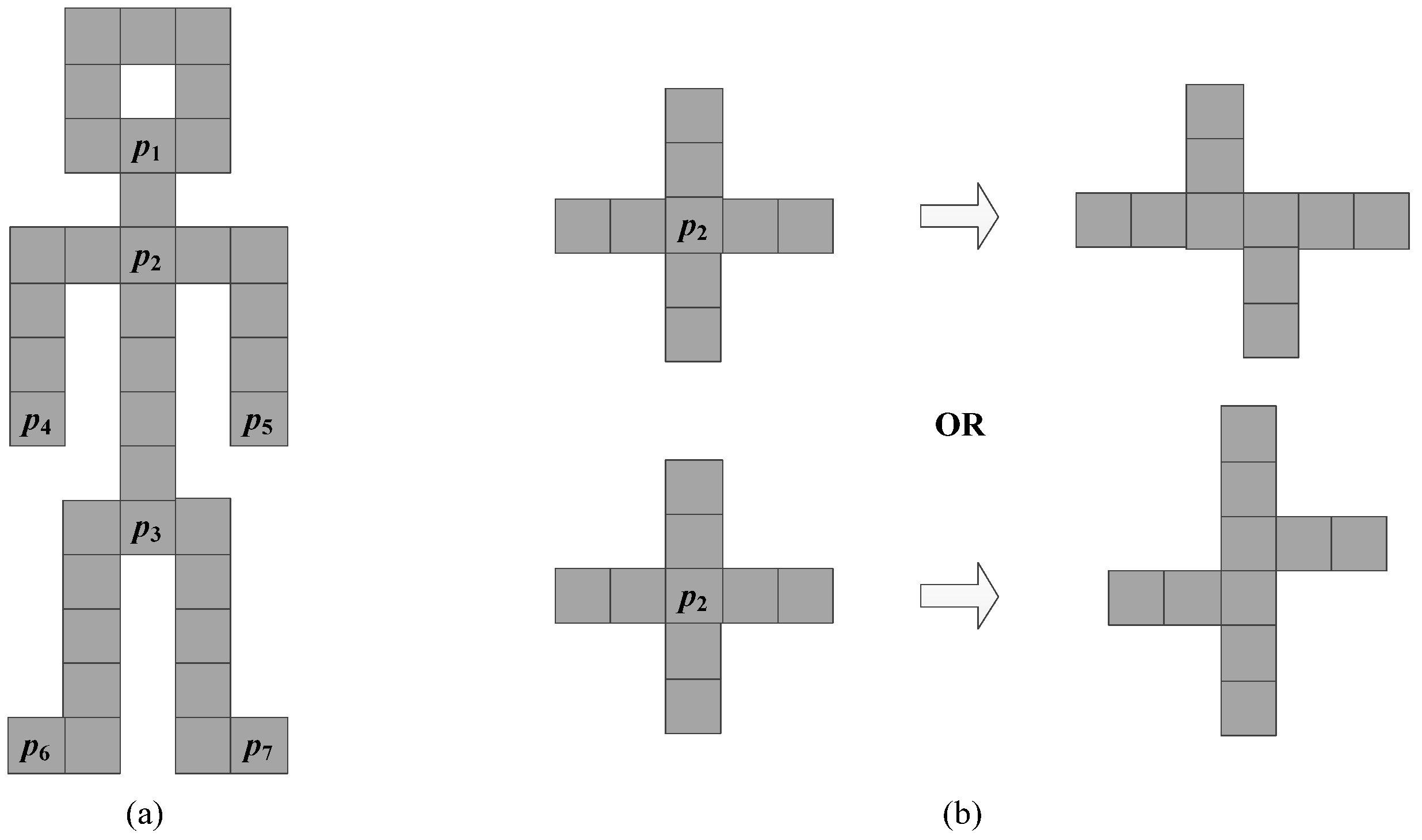
2.2.1. Skeleton-Based Euler Number Computing Algorithm
- (1)
- If Nc(p) = 1, pixel p is called a terminal pixel (Tp);
- (2)
- If Nc(p) = 2, pixel p is called an internal pixel;
- (3)
- If Nc(p) = 3, pixel p is called a three-edge pixel (TEp);
- (4)
- If Nc(p) > 3, pixel p is called a crossing pixel.
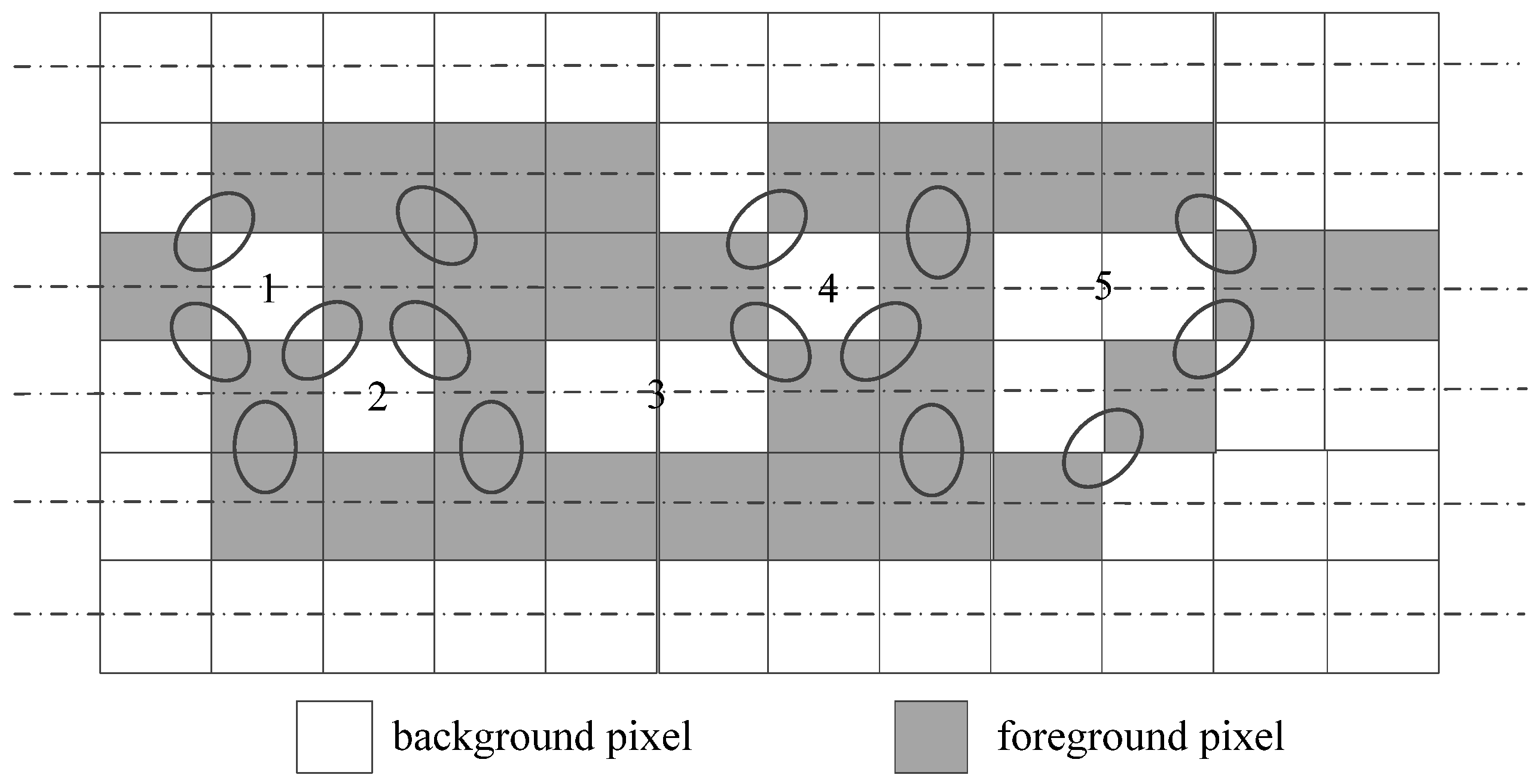
2.2.2. Perimeter-Based Euler Number Computing Algorithm
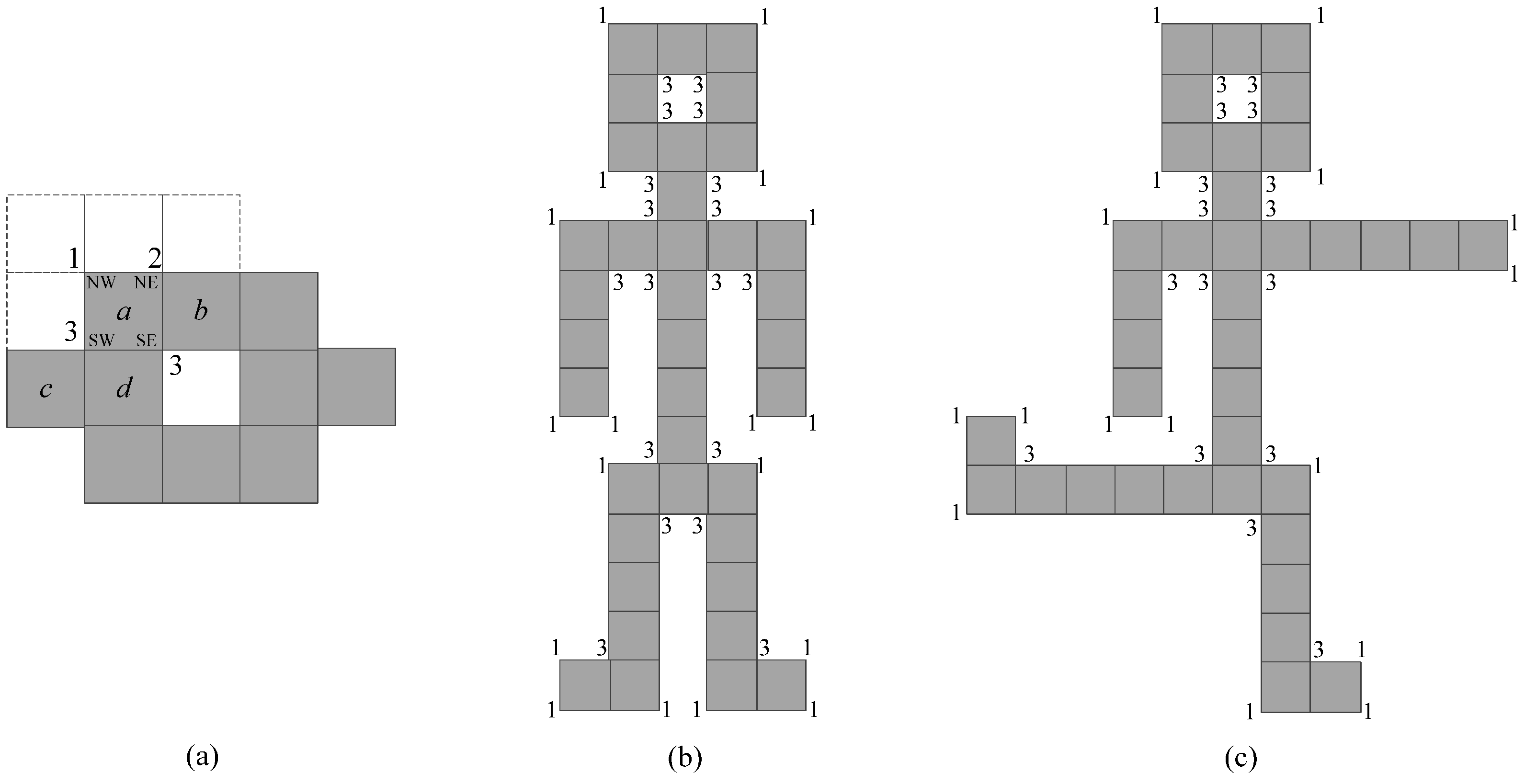
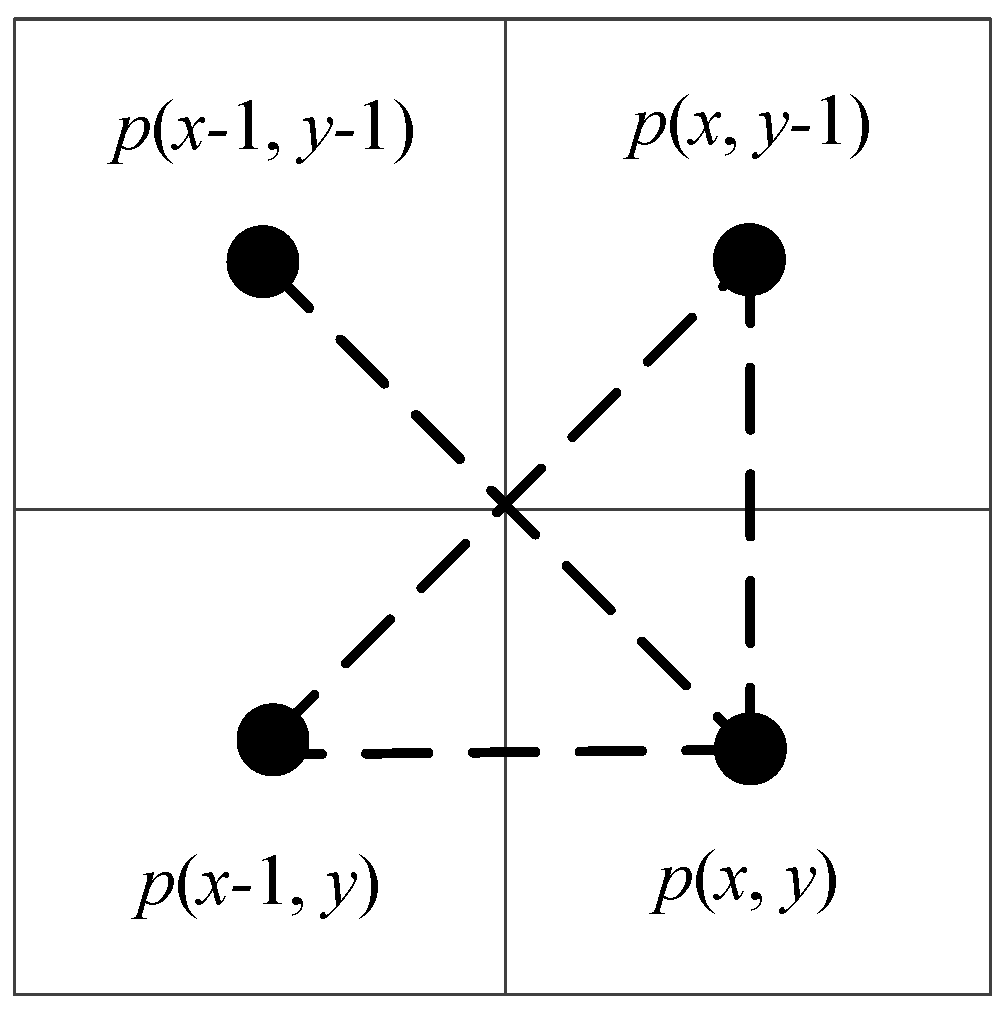
2.2.3. Corner Codification-Based Euler Number Computing Algorithm
- (1)
- The NW corner touches one foreground pixel, i.e., pixel a; thus, the codification of this corner is 1.
- (2)
- The NE corner touches two foreground pixels, i.e., pixel a and pixel b; thus, the codification of this corner is 2.
- (3)
- The SW corner touches three foreground pixels, i.e., pixel a, pixel c, and pixel d; thus, the codification of this corner is 3.
- (4)
- The SE corner touches three foreground pixels, i.e., pixel a, pixel b, and pixel d; thus, the codification of this corner is 3.
2.3. Algorithms That Compute the Euler Number by Counting Specific Blocks/Patterns in the Image
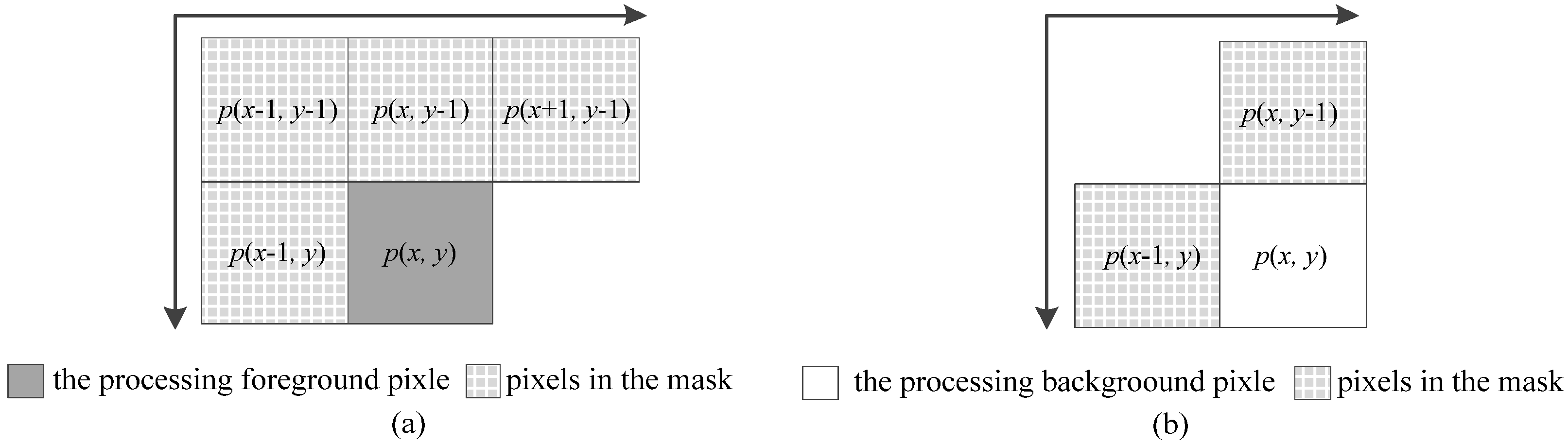
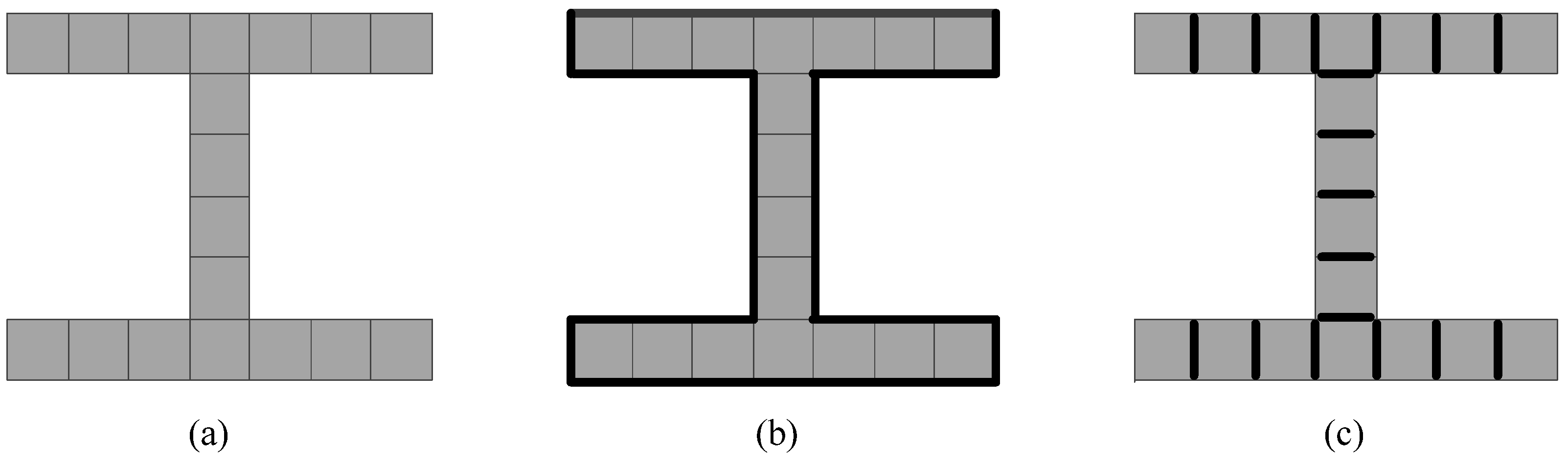
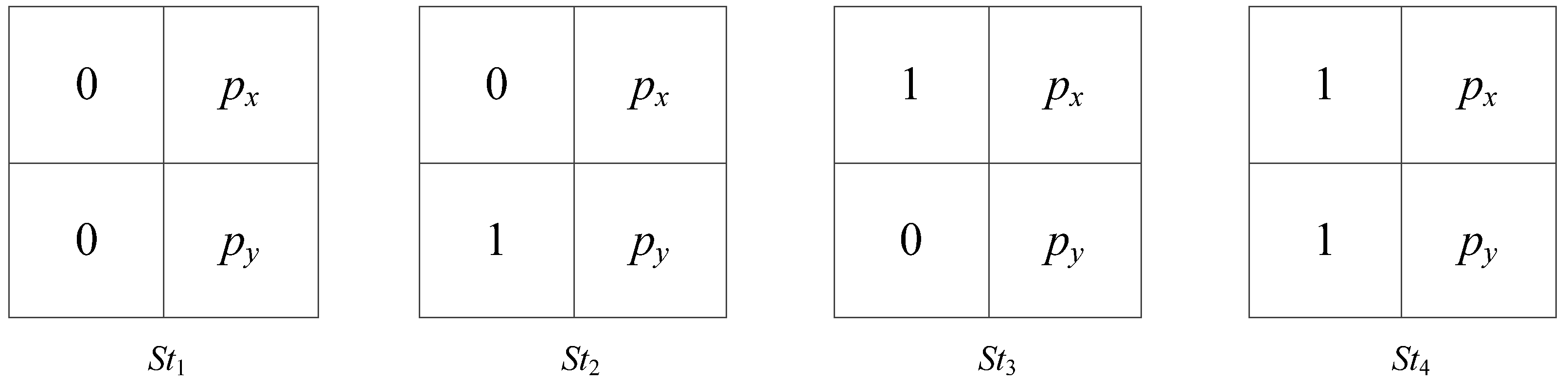
2.3.1. Bit-Quad-Based Euler Number Computing Algorithm
- Strategy of state transition
- 2.
- Strategy of multi-row scanning
2.3.2. Run-Based Euler Number Computing Algorithm
2.4. Algorithms That Compute the Euler Number by Special Data Structure
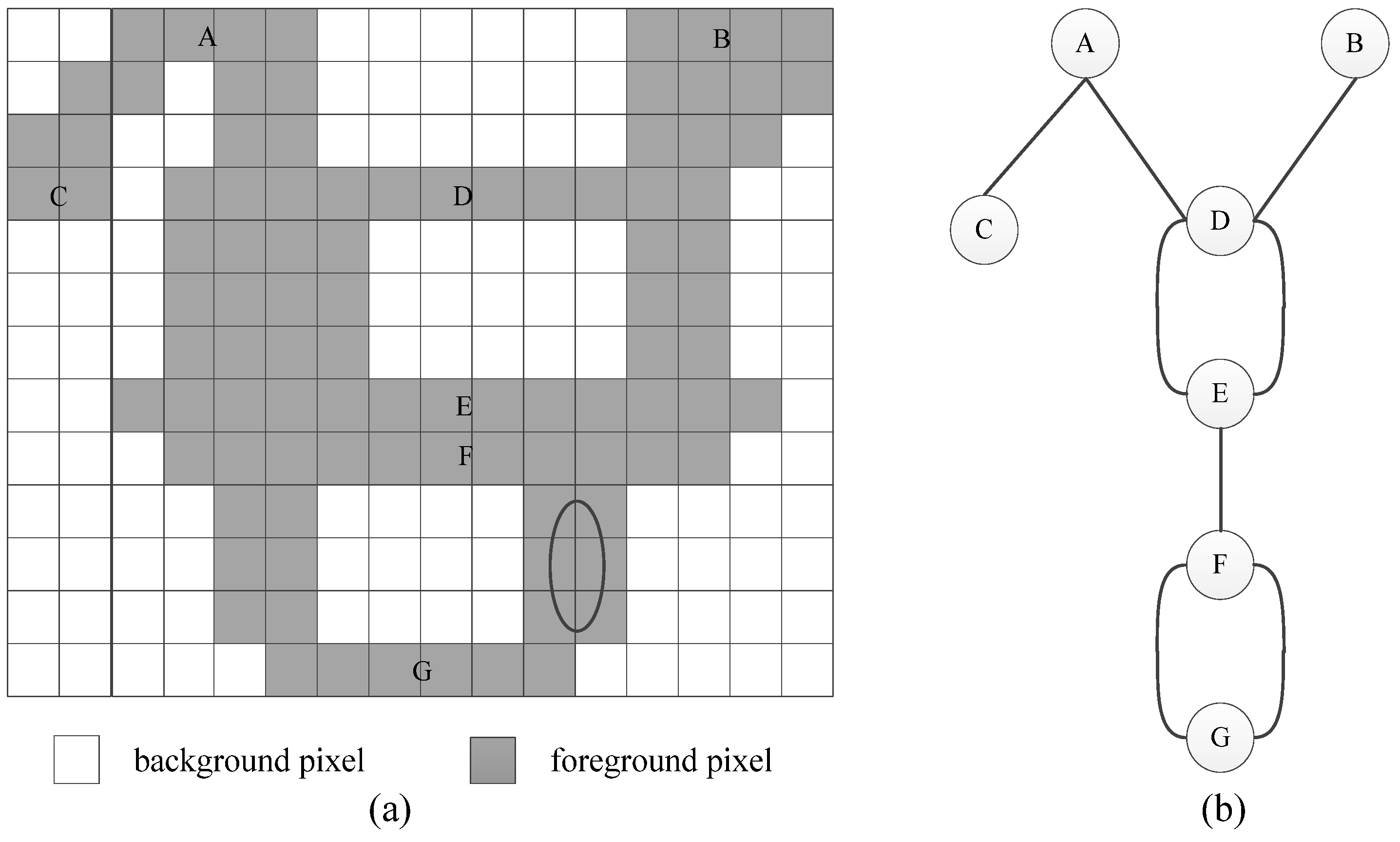
2.4.1. Graph-Representing-Based Euler Number Computing Algorithm
2.4.2. Tree-Representing-Based Euler Number Computing Algorithm
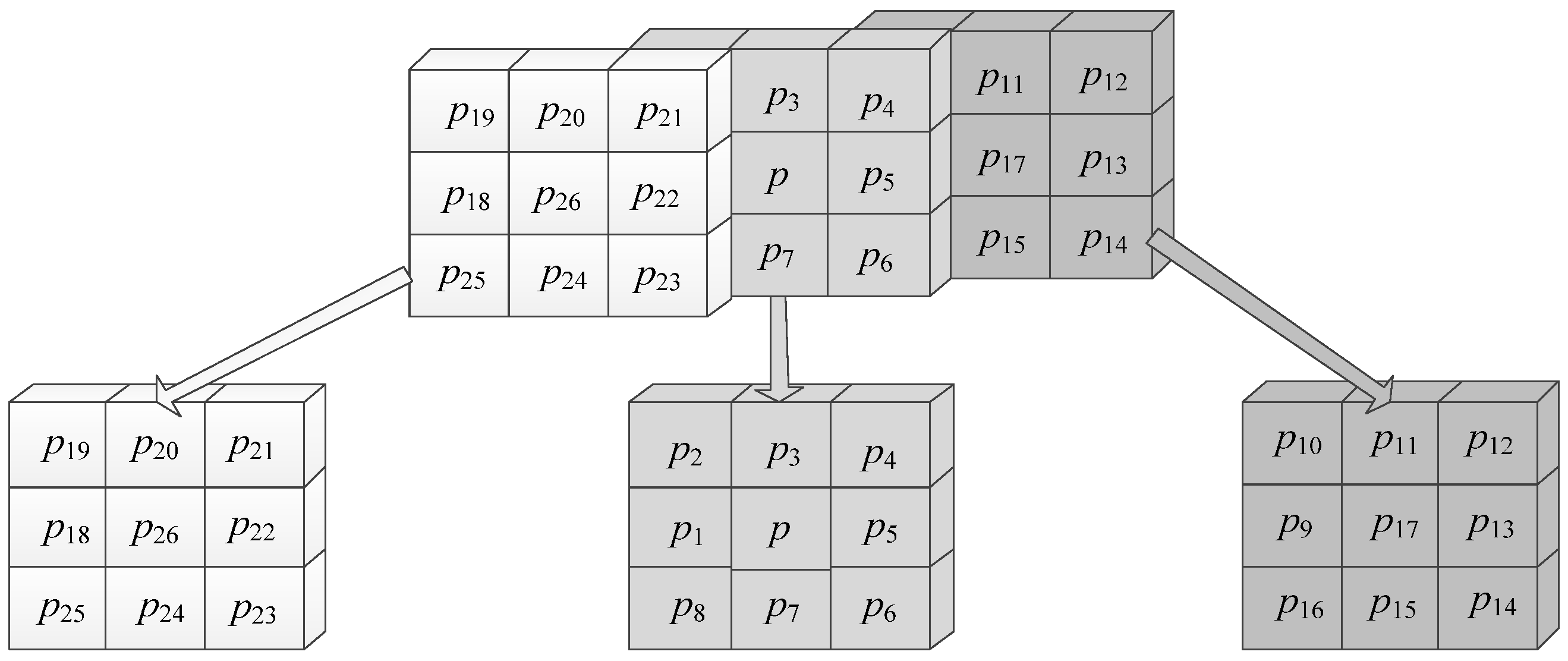
2.4.3. Graph Run-Representing-Based Euler Number Computing Algorithm
2.5. Algorithms That Compute the Euler Number via Machine Learning
3. Experimental Results
3.1. Experimental Results of Noise Images
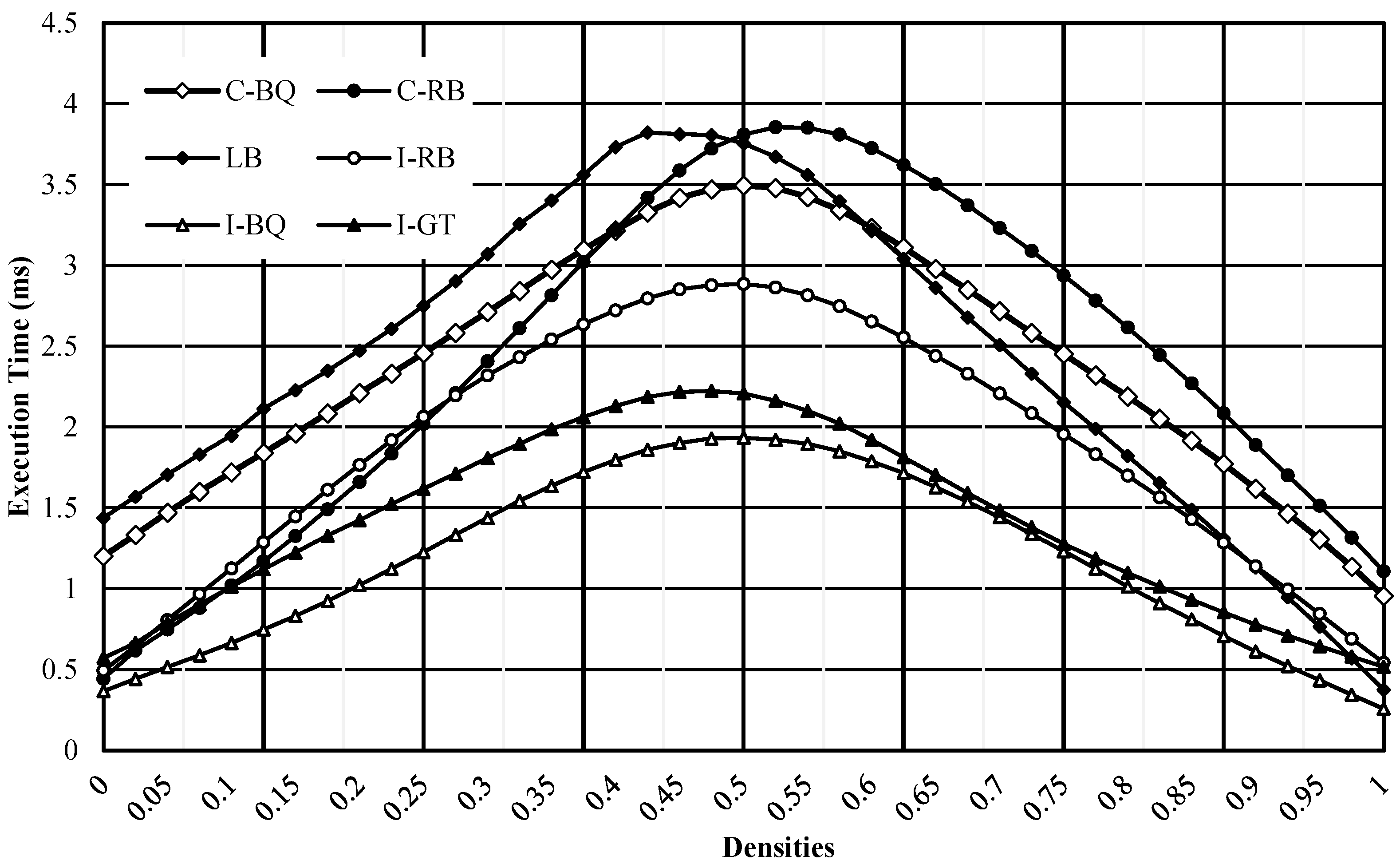
3.1.1. Execution Time versus Density of Noise Images
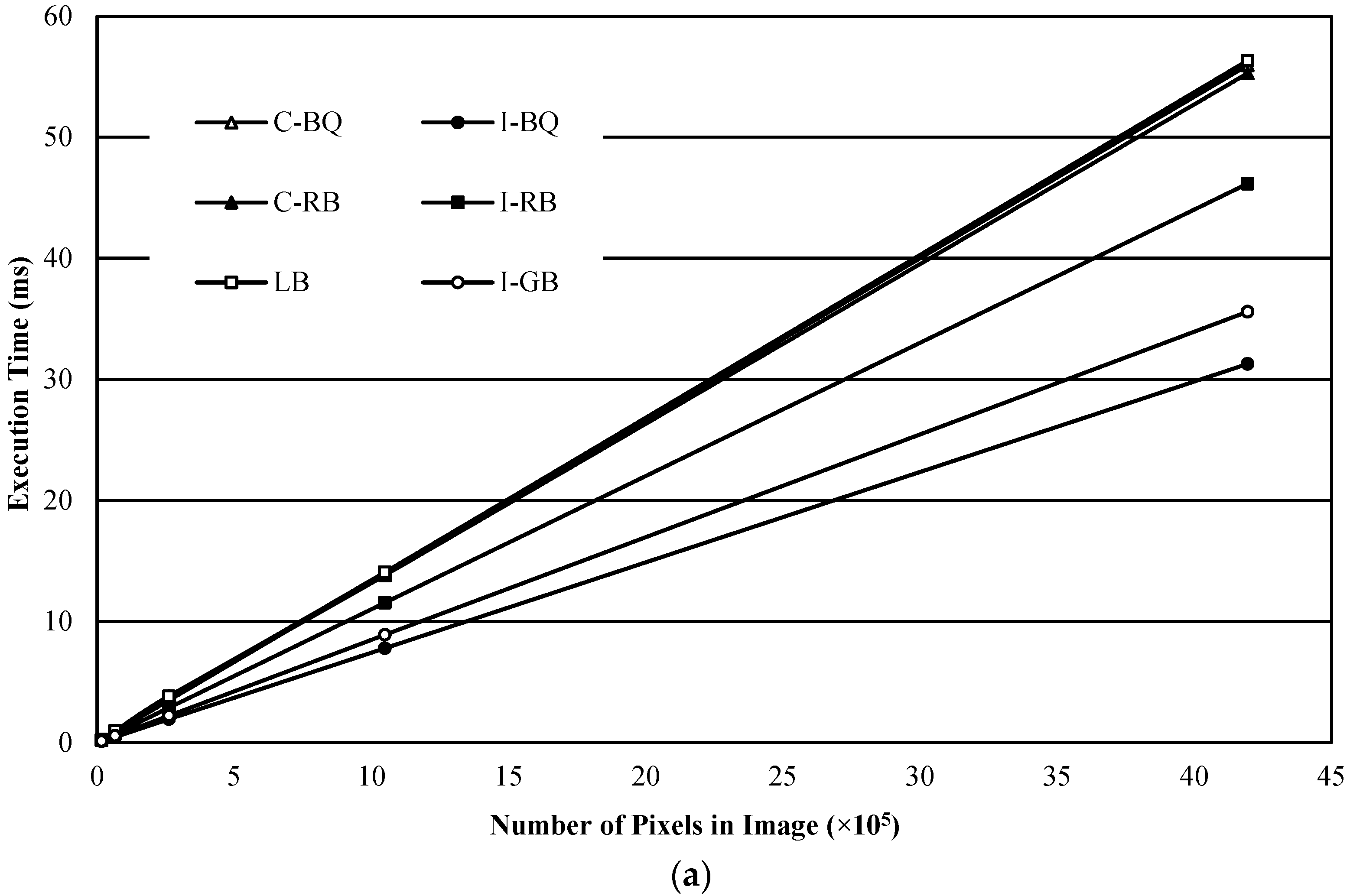
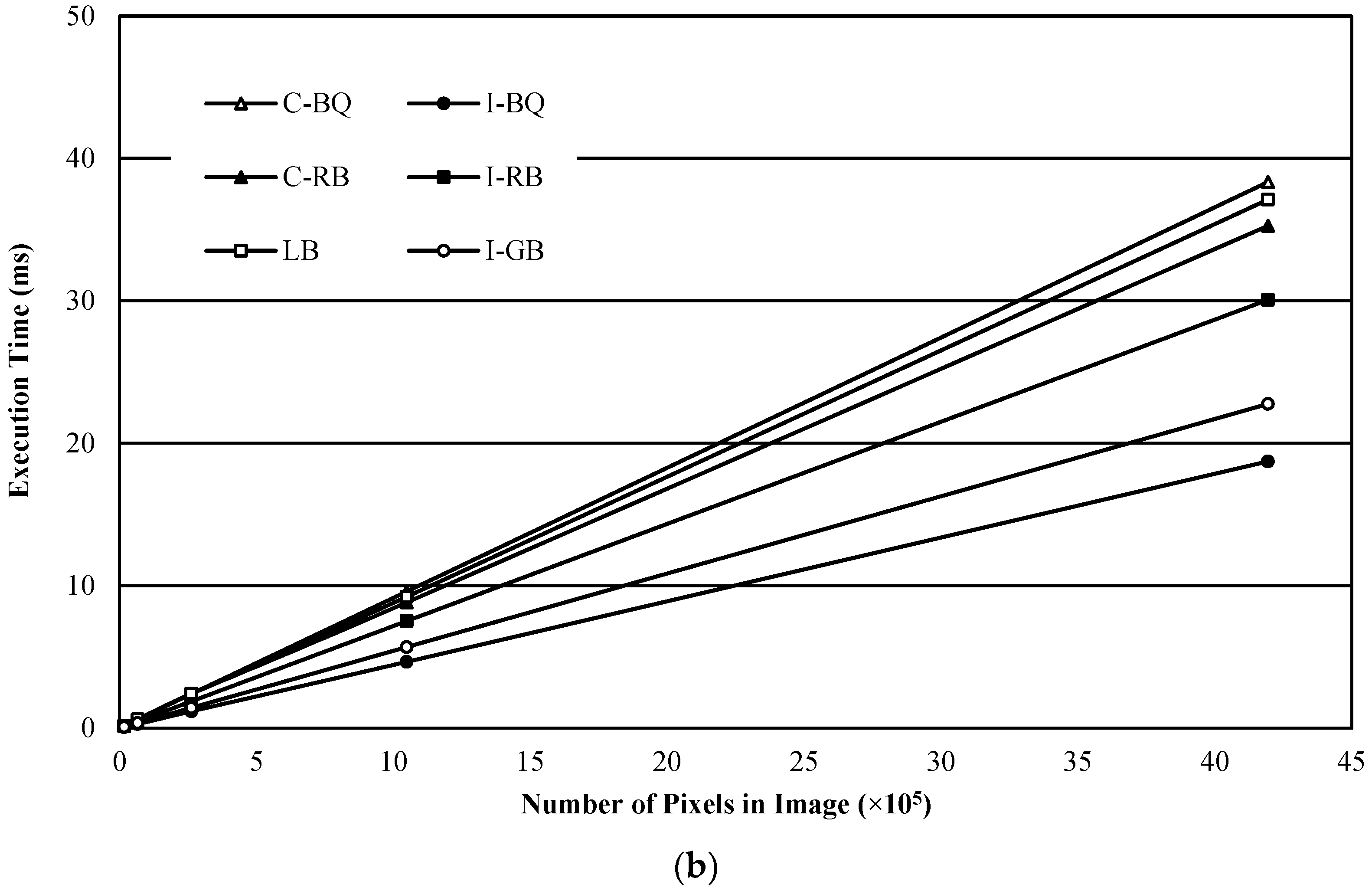
3.1.2. Execution Time versus Resolution of Images
3.2. Experimental Results of Authentic Images
4. Relevant Issues
4.1. Parallel Implementation of Euler Number Computing Algorithms
4.2. Euler Number Computation of 3D Images
5. Concluding Remarks
- (1)
- To further improve the efficiency of Euler number computing for embedded image-processing systems, it would be worthwhile to explore hardware implementation and parallel implementation of the bit-quad-based and run-based algorithms on multiple FPGAs (field programmable gate arrays).
- (2)
- Efficient hardware and parallel implementations of the latest Euler number computing algorithms for 3D and higher-dimensional images could be pursued to improve the processing efficiency for such complex image data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, H.; Sengupta, S. Intelligent shape recognition for complex industrial tasks. IEEE Control Syst. Mag. 1988, 8, 23–30. [Google Scholar] [CrossRef]
- Hashizume, A.; Suzuki, R.; Yokouchi, H.; Horiuchi, H.; Yamamoto, S. An algorithm of automated RBC classification and its evaluation. Bio Med. Eng. 1990, 28, 25–32. [Google Scholar]
- Nayar, S.; Bolle, R. Reflectance-based object recognition. Int. J. Comput. Vis. 1996, 17, 219–240. [Google Scholar] [CrossRef]
- Rosin, P.; Ellis, T. Image difference threshold strategies and shadow detection. In Proceedings of the British Machine Vision Conference, Birmingham, UK, 10–13 September 1995; pp. 347–356. [Google Scholar]
- Moraru, L.; Cotoi, O.; Szendrei, F. Euler number: A method for statistical analysis of ancient pottery porosity. Eur. J. Sci. Theol. 2011, 7, 99–108. [Google Scholar]
- Qin, X.; Xia, Y.; Wu, J.; Sun, C.; Zeng, J.; Xu, K.; Cai, J. Influence of pore morphology on permeability through digital rock modeling: New insights from the Euler number and shape factor. Energy Fuels 2022, 36, 7519–7530. [Google Scholar] [CrossRef]
- Gonzalez, R.; Woods, R. Digital Image Processing, 3rd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2008; pp. 642–647. [Google Scholar]
- Bovik, A.C. The Essential Guide to Image Processing, 2nd ed.; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2009; pp. 70–75. [Google Scholar]
- He, L.; Chao, Y. A very fast algorithm for simultaneously performing connected-component labeling and Euler number computing. IEEE Trans. Image Process. 2015, 24, 2725–2735. [Google Scholar]
- He, L.; Chao, Y.; Suzuki, K. An algorithm for connected-component labeling, hole labeling and Euler number computing. J. Comput. Sci. Technol. 2013, 28, 468–478. [Google Scholar] [CrossRef]
- Juan, L.; Sossa, J. On the computation of the Euler number of a binary object. Pattern Recognit. 1996, 29, 471–476. [Google Scholar]
- Bribiesca, E. Computation of the Euler number using the contact perimeter. Comput. Math. Appl. 2010, 60, 1364–1373. [Google Scholar] [CrossRef]
- Bribiesca, E. Measuring 2D shape compactness using the contact perimeter. Comput. Math. Appl. 1997, 33, 1–9. [Google Scholar] [CrossRef]
- Sossa, J.; Cuevas, E.; Zaldivar, D. Alternative way to compute the Euler number of a binary image. J. Appl. Res. Technol. 2011, 9, 335–341. [Google Scholar]
- Sossa, J.; Espino, E.; Santiago, R.; López, A.; Ayala, A.; Jimenez, E. Alternative formulations to compute the binary shape Euler number. IET Comput. Vis. 2014, 8, 171–181. [Google Scholar]
- Sossa, J.; Santiago, R.; Pérez, M.; Espino, E. Computing the Euler number of a binary image based on a vertex codification. J. Appl. Res. Technol. 2013, 11, 360–370. [Google Scholar] [CrossRef]
- Gray, S.B. Local properties of binary images in two dimensions. IEEE Trans. Comput. 1971, C–20, 551–561. [Google Scholar] [CrossRef]
- Thompson, C.; Shure, L. Image Processing Toolbox; The Math Works Inc.: Natick, MA, USA, 2017. [Google Scholar]
- Yao, B.; Wu, H.; Yang, Y.; Chao, Y.; Ohta, A.; Kawanaka, H.; He, L. An efficient strategy for bit-quad-based Euler number computing algorithm. IEICE Trans. Inf. Syst. 2014, E97–D, 1374–1378. [Google Scholar] [CrossRef]
- Yao, B.; He, L.; Kang, S.; Zhao, X.; Chao, Y. Bit-quad-based Euler number computing. IEICE Trans. Inf. Syst. 2017, E100–D, 2197–2204. [Google Scholar] [CrossRef]
- Gomez, W.; Sossa, J.; Arce, F. Finding the optimal bit-quad patterns for computing the Euler number of 2D binary image using simulated annealing. In Proceedings of the 13th Mexican Conference on Pattern Recognition, Mexico City, Mexico, 23–26 June 2021; pp. 240–250. [Google Scholar]
- Sossa, J.; Carreón, Á.; Santiago, R.; Bribiesca, E.; Petrilli-Barceló, A. Efficient computation of the Euler number of a 2-D binary image. In Proceedings of the 15th Mexican International Conference on Artificial Intelligence, Cancún, Mexico, 23–28 October 2016; pp. 401–413. [Google Scholar]
- Bishnu, A.; Bhattacharya, B.; Kundu, M.; Murthy, C.; Acharya, T. A pipeline architecture for computing the Euler number of a binary image. J. Syst. Archit. 2005, 51, 470–487. [Google Scholar] [CrossRef]
- Lin, X.; Sha, Y.; Ji, J.; Wang, Y. A proof of image Euler number formula. Sci. China Ser. F Inf. Sci. 2006, 49, 364–371. [Google Scholar] [CrossRef]
- Yao, B.; He, L.; Kang, S.; Zhao, X.; Chao, Y. A new run-based algorithm for Euler number computing. Pattern Anal. Appl. 2017, 20, 49–58. [Google Scholar] [CrossRef]
- Chen, M.; Yan, P. A fast algorithm to calculate the Euler number for binary images. Pattern Recognit. Lett. 1988, 8, 295–297. [Google Scholar] [CrossRef]
- Yao, B.; He, L.; Kang, S.; Chao, Y.; Zhao, X. A novel bit-quad-based Euler number computing algorithm. Springerplus 2015, 4, 1–16. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Yao, B.; Zhao, X.; Yang, Y.; Shi, Z.; Kasuya, H.; Chao, Y. A fast algorithm for integrating connected-component labeling and Euler number computation. J. Real-Time Image Process. 2018, 15, 709–723. [Google Scholar] [CrossRef]
- Bieri, H.; Nef, W. Algorithms for the Euler Characteristic and related additive functionals of digital objects. Comput. Vis. Graph. Image Process. 1984, 28, 166–175. [Google Scholar] [CrossRef]
- Bieri, H. Computing the Euler characteristic and related additive functionals of digital objects from their bintree representation. Comput. Vis. Graph. Image Process. 1987, 28, 115–126. [Google Scholar] [CrossRef]
- Dyer, C. Computing the Euler number of an image from its quadtree. Comput. Graph. Image Process. 1981, 13, 270–276. [Google Scholar] [CrossRef]
- Samet, H.; Tamminen, M. Computing geometric properties of images represented by linear quadtrees. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 229–240. [Google Scholar] [CrossRef]
- Di Zenzo, S.; Cinque, L.; Levialdi, S. Run-based algorithms for binary image analysis and processing. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 83–89. [Google Scholar] [CrossRef]
- Sossa, J.; Carreón, Á.; Santiago, R.; Petrilli, A. Support vector machines applied to 2-D binary image Euler number computation. In Proceedings of the International Conference on Mechatronics, Electronics and Automotive Engineering, Cuernavaca, Mexico, 22–25 November 2016; pp. 3–8. [Google Scholar]
- Santiago, R. Training a multilayered perceptron to compute the Euler number of a 2-D binary image. In Proceedings of the Mexican Conference on Pattern Recognition, Guanajuato, Mexico, 22–25 June 2016; pp. 44–53. [Google Scholar]
- Sossa, J.; Carreón, Á.; Guevara, E.; Santiago, R. Computing the 2-D image Euler number by an artificial neural network. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 June 2016; pp. 1609–1616. [Google Scholar]
- Dey, S.; Bhattacharya, B.; Kundu, M.; Acharya, T. A fast algorithm for computing the Euler number of an image and its VLSI implementation. In Proceedings of the International Conference on VLSI Design, Science City, India, 3–7 January 2000; pp. 330–335. [Google Scholar]
- Dey, S.; Bhattacharya, B.; Kundu, M.; Bishnu, A.; Acharya, T. A co-processor for computing Euler number of a binary image using divide and conquer strategy. Fundam. Inform. 2007, 76, 75–89. [Google Scholar]
- Chiavetta, F.; Di Gesù, V. Parallel computation of the Euler number via connectivity graph. Pattern Recognit. Lett. 1993, 14, 849–859. [Google Scholar] [CrossRef]
- Bishnu, A.; Bhattacharya, B.; Kundu, M.; Murthy, C.; Acharya, T. On-chip computation of Euler number of a binary image for efficient database search. In Proceedings of the International Conference on Image Processing, Thessaloniki, Greece, 7–10 October 2001; pp. 310–313. [Google Scholar]
- Abbasi, N.; Athow, J.; Amer, A. Real-time FPGA architecture of modified Stable Euler-number algorithm for image binarization. In Proceedings of the International Conference on Image Processing, Cairo, Egypt, 7–10 November 2009; pp. 3253–3256. [Google Scholar]
- Pradeep, K.; Veeraiah, N. VLSI implementation of Euler number computation and stereo vision concept for CORDIC based image registration. In Proceedings of the International Conference on Communication Systems and Network Technologies, Bhopal, India, 18–19 June 2021; pp. 269–272. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Akira, N.; Aizawa, K. On the recognition of properties of three-dimensional pictures. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 708–713. [Google Scholar]
- Velichko, A.; Holzapfel, C.; Siefers, A.; Schladitz, K.; Mücklich, F. Unambiguous classification of complex microstructures by their three-dimensional parameters applied to graphite in cast iron. Acta Mater. 2008, 56, 1981–1990. [Google Scholar] [CrossRef]
- Vogel, H.J.; Roth, K. Quantitative morphology and network representation of soil pore structure. Adv. Water Resour. 2001, 24, 233–242. [Google Scholar] [CrossRef]
- Park, C.; Rosenfeld, A. Connectivity and Genus in Three Dimensions; Computer Science Center, University of Maryland: College Park, MD, USA, 1971; Technical Report TR-156. [Google Scholar]
- Toriwaki, J.; Yonekura, T. Euler number and connectivity indexes of a three dimensional digital picture. Forma 2002, 17, 183–209. [Google Scholar]
- Lin, X.; Xiang, S.; Gu, Y. A new approach to compute the Euler number of 3D image. In Proceedings of the IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008; pp. 1543–1546. [Google Scholar]
- Lin, X.; Ji, J.; Huang, S.; Yang, J. A proof of new formula for 3D images Euler number. Pattern Recognit. Artif. Intell. 2010, 23, 52–58. [Google Scholar]
- Sossa, J.; Rubío, E.; Ponce, V.; Sánchez, H. Vertex codification applied to 3-D binary image Euler number computation. Adv. Soft Comput. 2019, 11835, 701–713. [Google Scholar]
- Lee, C.; Poston, T. Winding and Euler numbers for 2D and 3D digital images. Graph. Models Image Process. 1991, 53, 522–537. [Google Scholar] [CrossRef]
- Sánchez, H.; Sossa, J.; Braumann, U.-D.; Bribiesca, E. The Euler-Poincaré formula through contact surfaces of voxelized objects. J. Appl. Res. Technol. 2013, 11, 65–78. [Google Scholar] [CrossRef]
- Čomića, L.; Magillo, P. Surface-based computation of the Euler characteristic in the cubical grid. Graph. Models 2020, 112, 101093. [Google Scholar] [CrossRef]
- Morgenthaler, D. Three-Dimensional Digital Image Processing; University of Maryland: College Park, MD, USA, 1981. [Google Scholar]
- Yao, B.; He, H.; Kang, S.; Chao, Y.; He, L. Efficient strategies for computing Euler number of a 3d binary image. Electronics 2023, 12, 1726. [Google Scholar] [CrossRef]











| Pattern Names | Bit-Quad Patterns | Δn | Δe | Δf | ΔE = Δn − Δe + Δf |
|---|---|---|---|---|---|
| P1 |  | 0 | 0 | 0 | 0 |
| P2 |  | 1 | 0 | 0 | 1 |
| P3 |  | 0 | 0 | 0 | 0 |
| P4 |  | 1 | 1 | 0 | 0 |
| P5 |  | 0 | 0 | 0 | 0 |
| P6 |  | 1 | 1 | 0 | 0 |
| P7 |  | 0 | 1 | 0 | −1 |
| P8 |  | 1 | 3 | 1 | −1 |
| P9 |  | 0 | 0 | 0 | 0 |
| P10 |  | 1 | 1 | 0 | 0 |
| P11 |  | 0 | 0 | 0 | 0 |
| P12 |  | 1 | 2 | 1 | 0 |
| P13 |  | 0 | 0 | 0 | 0 |
| P14 |  | 1 | 2 | 1 | 0 |
| P15 |  | 0 | 1 | 1 | 0 |
| P16 |  | 1 | 3 | 2 | 0 |
| Pattern Names | Bit-Quad Patterns | Vectors | ΔE | y1 | y2 |
|---|---|---|---|---|---|
| P1 |  | [0 0 0 0]T | 0 | −1 | |
| P2 |  | [0 0 0 1]T | 1 | 1 | 1 |
| P3 |  | [0 0 1 0]T | 0 | −1 | |
| P4 |  | [0 0 1 1]T | 0 | −1 | |
| P5 |  | [0 1 0 0]T | 0 | −1 | |
| P6 |  | [0 1 0 1]T | 0 | −1 | |
| P7 |  | [0 1 1 0]T | −1 | 1 | −1 |
| P8 |  | [0 1 1 1]T | −1 | 1 | −1 |
| P9 |  | [1 0 0 0]T | 0 | −1 | |
| P10 |  | [1 0 0 1]T | 0 | −1 | |
| P11 |  | [1 0 1 0]T | 0 | −1 | |
| P12 |  | [1 0 1 1]T | 0 | −1 | |
| P13 |  | [1 1 0 0]T | 0 | −1 | |
| P14 |  | [1 1 0 1]T | 0 | −1 | |
| P15 |  | [1 1 1 0]T | 0 | −1 | |
| P16 |  | [1 1 1 1]T | 0 | −1 |
| Name | Version |
|---|---|
| Processor | Intel Core i5-3470 |
| Frequency | 3.20 GHz |
| Memory | 4 GB |
| Operating system | Ubuntu Linux 16.10 |
| GCC compiler | 4.2.3 |
| Density | C-BQ | C-RB | LB | I-RB | I-BQ | I-GT |
|---|---|---|---|---|---|---|
| 0.000 | 1.202 | 0.444 | 1.438 | 0.494 | 0.366 | 0.572 |
| 0.025 | 1.334 | 0.618 | 1.570 | 0.644 | 0.442 | 0.664 |
| 0.050 | 1.472 | 0.748 | 1.706 | 0.806 | 0.516 | 0.788 |
| 0.075 | 1.600 | 0.882 | 1.830 | 0.966 | 0.588 | 0.902 |
| 0.100 | 1.720 | 1.020 | 1.948 | 1.126 | 0.664 | 1.012 |
| 0.125 | 1.840 | 1.168 | 2.114 | 1.288 | 0.748 | 1.120 |
| 0.150 | 1.962 | 1.326 | 2.228 | 1.448 | 0.832 | 1.224 |
| 0.175 | 2.086 | 1.492 | 2.348 | 1.612 | 0.924 | 1.328 |
| 0.200 | 2.210 | 1.660 | 2.474 | 1.766 | 1.022 | 1.424 |
| 0.225 | 2.332 | 1.836 | 2.608 | 1.918 | 1.122 | 1.524 |
| 0.250 | 2.456 | 2.020 | 2.750 | 2.064 | 1.226 | 1.618 |
| 0.275 | 2.584 | 2.210 | 2.902 | 2.196 | 1.334 | 1.712 |
| 0.300 | 2.712 | 2.408 | 3.070 | 2.320 | 1.438 | 1.808 |
| 0.325 | 2.842 | 2.612 | 3.256 | 2.432 | 1.544 | 1.896 |
| 0.350 | 2.974 | 2.816 | 3.402 | 2.542 | 1.636 | 1.986 |
| 0.375 | 3.098 | 3.022 | 3.560 | 2.636 | 1.722 | 2.062 |
| 0.400 | 3.218 | 3.222 | 3.732 | 2.722 | 1.796 | 2.130 |
| 0.425 | 3.328 | 3.418 | 3.822 | 2.796 | 1.860 | 2.186 |
| 0.450 | 3.418 | 3.588 | 3.812 | 2.852 | 1.902 | 2.218 |
| 0.475 | 3.472 | 3.724 | 3.806 | 2.878 | 1.930 | 2.224 |
| 0.500 | 3.496 | 3.810 | 3.754 | 2.886 | 1.934 | 2.208 |
| 0.525 | 3.480 | 3.856 | 3.672 | 2.864 | 1.922 | 2.162 |
| 0.550 | 3.424 | 3.852 | 3.560 | 2.816 | 1.896 | 2.100 |
| 0.575 | 3.342 | 3.810 | 3.396 | 2.748 | 1.850 | 2.022 |
| 0.600 | 3.232 | 3.726 | 3.222 | 2.654 | 1.788 | 1.920 |
| 0.625 | 3.112 | 3.622 | 3.042 | 2.554 | 1.716 | 1.814 |
| 0.650 | 2.980 | 3.504 | 2.862 | 2.440 | 1.628 | 1.704 |
| 0.675 | 2.850 | 3.372 | 2.678 | 2.330 | 1.538 | 1.592 |
| 0.700 | 2.718 | 3.232 | 2.508 | 2.208 | 1.442 | 1.484 |
| 0.725 | 2.584 | 3.090 | 2.330 | 2.086 | 1.338 | 1.380 |
| 0.750 | 2.452 | 2.938 | 2.154 | 1.956 | 1.232 | 1.278 |
| 0.775 | 2.320 | 2.782 | 1.990 | 1.832 | 1.124 | 1.186 |
| 0.800 | 2.190 | 2.616 | 1.822 | 1.700 | 1.014 | 1.098 |
| 0.825 | 2.052 | 2.446 | 1.654 | 1.566 | 0.910 | 1.014 |
| 0.850 | 1.916 | 2.270 | 1.488 | 1.430 | 0.810 | 0.932 |
| 0.875 | 1.772 | 2.086 | 1.310 | 1.286 | 0.708 | 0.854 |
| 0.900 | 1.620 | 1.890 | 1.132 | 1.138 | 0.612 | 0.778 |
| 0.925 | 1.466 | 1.702 | 0.948 | 0.996 | 0.522 | 0.710 |
| 0.950 | 1.306 | 1.514 | 0.766 | 0.844 | 0.434 | 0.644 |
| 0.975 | 1.136 | 1.316 | 0.570 | 0.690 | 0.344 | 0.580 |
| 1.000 | 0.956 | 1.108 | 0.374 | 0.542 | 0.258 | 0.518 |
| Densities | C-BQ | C-RB | LB | I-RB | I-BQ | I-GT | |
|---|---|---|---|---|---|---|---|
| Natural | Min. | 1.10 | 0.61 | 0.87 | 0.53 | 0.31 | 0.49 |
| Average | 1.42 | 1.07 | 1.40 | 0.82 | 0.50 | 0.71 | |
| Max. | 1.86 | 1.69 | 1.97 | 1.29 | 0.82 | 1.02 | |
| Medical | Min. | 1.17 | 0.75 | 0.91 | 0.62 | 0.36 | 0.54 |
| Average | 1.29 | 0.92 | 1.25 | 0.68 | 0.42 | 0.62 | |
| Max. | 1.47 | 1.07 | 1.50 | 0.84 | 0.52 | 0.73 | |
| Textural | Min. | 1.00 | 1.04 | 0.51 | 0.54 | 0.28 | 0.51 |
| Average | 1.38 | 1.35 | 1.10 | 0.87 | 0.48 | 0.68 | |
| Max. | 1.73 | 1.66 | 1.60 | 1.19 | 0.71 | 0.92 | |
| Artificial | Min. | 0.28 | 0.24 | 0.32 | 0.17 | 0.08 | 0.11 |
| Average | 0.70 | 0.67 | 0.70 | 0.48 | 0.21 | 0.28 | |
| Max. | 1.11 | 1.03 | 1.35 | 0.92 | 0.32 | 0.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, B.; He, H.; Kang, S.; Chao, Y.; He, L. A Review for the Euler Number Computing Problem. Electronics 2023, 12, 4406. https://doi.org/10.3390/electronics12214406
Yao B, He H, Kang S, Chao Y, He L. A Review for the Euler Number Computing Problem. Electronics. 2023; 12(21):4406. https://doi.org/10.3390/electronics12214406
Chicago/Turabian StyleYao, Bin, Haochen He, Shiying Kang, Yuyan Chao, and Lifeng He. 2023. "A Review for the Euler Number Computing Problem" Electronics 12, no. 21: 4406. https://doi.org/10.3390/electronics12214406
APA StyleYao, B., He, H., Kang, S., Chao, Y., & He, L. (2023). A Review for the Euler Number Computing Problem. Electronics, 12(21), 4406. https://doi.org/10.3390/electronics12214406







