An Application Study of Improved Iris Image Localization Based on an Evolutionary Algorithm

Abstract

This study aims to enhance the localization of the inner and outer circles of the iris while addressing issues of excessive invalid computations and inaccuracies. To achieve this objective, diverse methods are employed to improve the process to varying extents. Initially, the image undergoes pre-processing operations, including grayscale conversion, mathematical morphological transformation, noise reduction, and image enhancement. Subsequently, the accurate localization of the inner and outer edges is achieved by applying algorithms such as Canny edge detection and the Hough transform, allowing for the determination of their corresponding center and radius values within the iris image. Lastly, an improvement is made to the particle swarm optimization algorithm by combining various algorithms, namely LinWPSO, RandWPSO, contraction factor, LnCPSO, and AsyLnCPSO, employing mechanisms such as simulated annealing and the ant colony algorithm. Through dual validation on the CASIA-Iris-Syn dataset and a self-built CASIA dataset, this approach significantly enhances the precision of iris localization and reduces the required iteration count.

1. Introduction

Iris recognition is a highly regarded research area in the field of biometrics. By analyzing and identifying the unique characteristics of the human iris, iris recognition technology provides a highly reliable solution for personal identity recognition, authentication, and security protection in various domains. In recent years, there has been a shift toward integrating iris recognition with other biometric modalities, such as facial recognition or fingerprint recognition, in multimodal biometric systems. This integration aims to enhance the security and accuracy of biometric systems by combining multiple sources of information. The iris, as a part of the human eye, contains rich biometric information that is distinct from an individual’s genetic makeup. The iris patterns of each person are unique, making iris recognition research of significant theoretical and practical value.

Over the years, computer vision techniques and heuristic algorithms have made great strides in enabling the analysis and understanding of visual content, including tasks such as object recognition, image segmentation, and image classification. The iris localization discussed in this paper refers to the process of detecting and locating the iris region in images or videos. Iris localization is critical for various applications, including biometric identity verification systems, access control, and surveillance systems. By exploring the similarities and differences between iris features in depth, we can establish an efficient and accurate iris localization and recognition algorithm system and framework, providing reliable identity verification technology for various application scenarios. The development of iris recognition technology holds tremendous potential and opportunities for personal privacy protection, electronic payments, and border security. Therefore, iris recognition technology occupies an important position in current and future research endeavors.

In the past few decades, iris localization techniques have been widely researched and applied. Early iris localization methods primarily relied on manual operations and simple image processing algorithms. For instance, the renowned scholar Daugman [1] initially defined the iris segmentation method by combining the iris with a circular shape and segmenting images using circular detection matchers. Further advancements were made by applying Daugman’s J integral and Wildes’ R algorithms [2]. However, these methods were subject to several limitations, including variations in lighting conditions, resolution, and pose changes [3]. These limitations manifested as computational complexity, excessive perimeter for iris localization, and large volumes of Hough transformed data. Despite exhibiting good robustness and resilience in iris localization, these methods suffered from a long computation time. With the rapid development of computer science and image processing technologies, iris localization methods based on computer vision and pattern recognition have constantly emerged, resulting in remarkable achievements [4].

In recent years, there have been further advancements in the research of iris localization algorithms. Seung-Jin Baek et al. [5] proposed using a spherical model of the human eye and estimating the radius of the iris from frontal- and forward-looking images of the eye. Ning Wang [6] proposed a recognition performance method for noisy iris images by filling the reflection points using a restoration method based on the Navier–Stokes equation and detecting the pupil edges using a probabilistic boundary edge detection operator to obtain accurate circular parameters. Abduljalil Radman et al. [7] proposed a method to find the approximate location of the pupil center using a circular Gabor filter. Secondly, considering that the true centers of the iris and pupil are located in a small region around the rough location of the pupil center, the IDO was used to locate the iris and pupil circularly. Lu Wang et al. [8] proposed a fast iris localization algorithm based on an improved Hough transform based on geometric and grayscale features of human eye images. This is many-to-one mapping, thus avoiding the huge computational effort of the standard Hough transform one-to-many mapping. In order to reduce the memory requirement, it can be implemented using a dynamic linked list structure. Rabih Nachar et al. [9] proposed a method for iris recognition using the fuzzy logic system, which has a high recognition accuracy but suffers from poor noise immunity and is prone to local extremes. Radu Gabriel Bozomitu et al. [10] proposed an iris localization algorithm that combines edge detection with the Hough transform to combine with the Hough transform for an iris localization algorithm, where the grayscale map is processed with a binary edge. The grayscale map is processed by binary edge processing, and then the Hough transform is used to vote the edge point parameters to obtain the inner and outer circle boundary parameters. The iris region is then segmented by voting the edge point parameters with the Hough transform, and the iris region is finally segmented. This algorithm has a poor localization effect on blocked, incomplete, or poorly lit images. This algorithm has a poor localization effect on some obscured, incomplete, or poorly lit images. Mountain Sambit Bakshi et al. [11] proposed a method to localize the inner and outer circular boundaries of the iris based on morphological operations and Hough transform. This method is faster but less robust and unstable. Vineet Kumar et al. [12] used a modified Daugman IDO to detect the outer border of the iris and proposed a technique based on thresholding and morphological operations to reduce the number of pixels to which IDO is applied to detect the pupil. While the localization time is fast, the accuracy of the localization still needs improvement. Young Won Lee et al. [13] proposed an efficient method to determine the center of the iris in low-resolution images in the visible spectrum. Jose Luis Gil Rodriguez et al. [14] first segmented the pupil using the clustering method, coarsely located the pupil based on geometric features, then calculated the pupil’s center and radius, and finally located the iris using the pupil circumference parameter and a priori knowledge. Sardan et al. [15] proposed a new soft computational method for iris segmentation based on rough directionality and localization using circular sector analysis to minimize uncertainty. Wang Bao Qiang et al. [16] used a rectangular frame to estimate the pupil, eliminated non-horizontal edge points by a horizontal edge point selection rule, and finally used the Hough transform and the obtained parameters to locate the iris. Bodade M. Rajesh et al. [17] took advantage of the coupling between the inner and outer boundaries of the iris in order to reduce the search scope in the boundary parameter space and adopted the methods of “sampling first and then transforming” and “from coarse to fine”. Zuraini Othman et al. [18] proposed an iris localization method for ideal and non-ideal iris images. In this study, the algorithm determines all regions of interest (ROI) classifications using a support vector machine (SVM) and a histogram using gray levels as descriptors in all display growers. Aniu et al. [19] proposed a CGA-based circle detection algorithm to detect iris edges and pupil boundaries for accurate and fast iris localization.

Although a large number of research works have achieved many results, the traditional iris localization algorithms process a large amount of data and do not have high localization accuracy, so they still need further research and improvement. Firstly, the process of acquiring iris images requires high-quality imaging equipment and standardized operating procedures, which pose certain difficulties in establishing and applying large-scale iris datasets [20]. Secondly, the accuracy and robustness of iris recognition need further improvement under complex environmental conditions, such as low lighting, eye fatigue, and occlusion [21]. Furthermore, with the expansion of iris recognition application scenarios, there is an increasing demand for real-time performance and efficiency, hence requiring more efficient iris localization algorithms and system architectures.

This paper introduces the iris image pre-processing process in Section 2, analyses and simulates the iris localization algorithm using the Hough transform and particle swarm algorithm in Section 3, improves the particle swarm optimization algorithm in Section 4, introduces a simulated annealing mechanism and an ant colony algorithm to the particle swarm optimization algorithm in Section 5, and finally concludes the paper in Section 6.

2. Iris Image Pre-Processing

In this study, iris images obtained from the CASIA-Iris-Syn dataset were utilized along with a specialized infrared 850 nm narrowband KS2A17 model 3.9 mm camera. The human eye is an independent organ of the human body, consisting of various structures and tissues, mainly including the iris, pupil, ciliary body, lens, vitreous body, and other parts. The iris is a part of the human eye, located in front of the pupil, showing a mottled pattern of various colors. Iris feature extraction is a biometric technique that identifies and verifies the identity of an individual by analyzing and comparing feature points and texture details in an iris image. However, iris images are susceptible to interference caused by eye hair, eyelashes, facial hair, as well as subjective factors related to the photographer’s skill level and objective factors such as uneven lighting, lens distance, and other potential sources of disruption [22]. Consequently, these factors can hinder the accurate extraction of iris feature data. To address this issue and simplify the subsequent feature texture extraction process, a pre-processing step was performed on the iris images in this research. Specifically, a weighted average method was employed to merge the red, green, and blue channels into a composite image (R = G = B). Additionally, grayscale processing was applied to obtain a grayscale image [23], as illustrated by Equation (1).

$$\mathrm{G}\mathrm{r}\mathrm{a}\mathrm{y}(\mathrm{x},\mathrm{y})=0.299\mathrm{R}\mathrm{e}\mathrm{d}(\mathrm{x},\mathrm{y})+0.587\ast \mathrm{G}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}(\mathrm{x},\mathrm{y})+0.114\ast \mathrm{B}\mathrm{l}\mathrm{u}\mathrm{e}(\mathrm{x},\mathrm{y})$$

(1)

In grayscale mathematical morphology, the operational objects are image functions. Let f(x, y) represent the input image and b(x, y) represent the structuring element [24]. The dilation and erosion operations on the input image y using the structuring element b are defined as Equations (2) and (3), respectively.

$$(\mathrm{f}\oplus \mathrm{b})(\mathrm{s},\mathrm{t})=\mathrm{m}\mathrm{a}\mathrm{x}\left\{\mathrm{f}\right(\mathrm{s}-\mathrm{x},\mathrm{t}-\mathrm{y})+\mathrm{b}(\mathrm{x},\mathrm{y}\left)\right|(\mathrm{s}-\mathrm{x},\mathrm{t}-\mathrm{y})\in {\mathrm{D}}_{\mathrm{f}},(\mathrm{x},\mathrm{y})\in {\mathrm{D}}_{\mathrm{b}}$$

(2)

$$(\mathrm{f}\odot \mathrm{b})(\mathrm{s},\mathrm{t})=\mathrm{m}\mathrm{i}\mathrm{n}\left\{\mathrm{f}\right(\mathrm{s}+\mathrm{x},\mathrm{t}+\mathrm{y})+\mathrm{b}(\mathrm{x},\mathrm{y}\left)\right|(\mathrm{s}+\mathrm{x},\mathrm{t}+\mathrm{y})\in {\mathrm{D}}_{\mathrm{f}},(\mathrm{x},\mathrm{y})\in {\mathrm{D}}_{\mathrm{b}}$$

(3)

The grayscale iris image in Figure 1a is subjected to morphological processing, corrosion, and then expansion of the open operation for the purpose of denoising to achieve Figure 1b, then binarization based on the grayscale histogram to achieve Figure 1c, Canny operator edge detection to achieve Figure 1d, and then closed operation of first expansion and then corrosion for the filling of the image, and enhancement to achieve Figure 1e, which completes the pre-processing of the iris image.

3. Analysis and Simulation of Iris Localization Algorithm with Hough Transform and Particle Swarm Algorithm

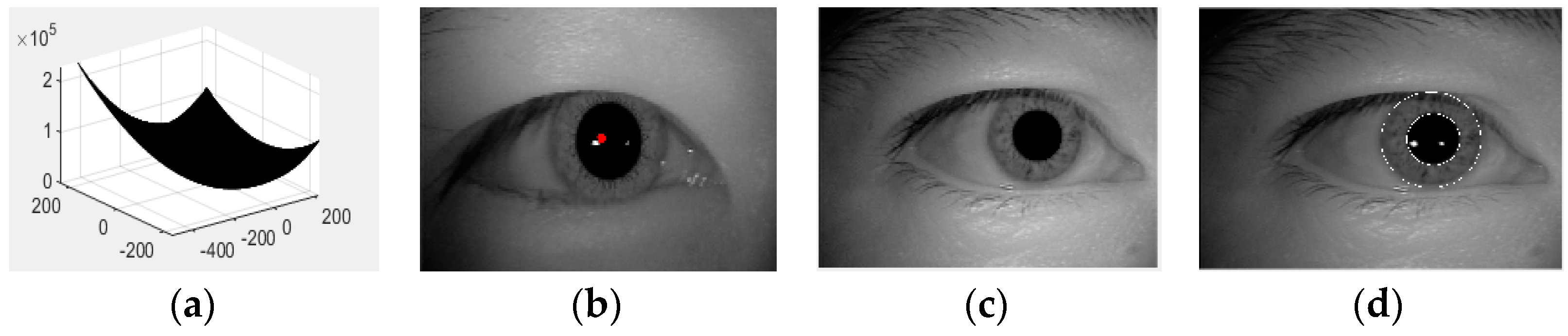
3.1. Hough Transform Fitting the Inner and Outer Circles of the Iris

The basic principle of the Hough transform method is to convert specific features in the image space into the parameter space and then identify the features with the highest number of votes in the parameter space using a voting mechanism, which represents the target shape present in the image [25]. A major advantage of the Hough transform method is its ability to detect geometric shapes that are unaffected by appearance, noise, or image transformations. It is widely employed in various aspects of computer vision, including edge detection, shape analysis, and object detection, and holds significant value in the field of image processing and computer vision [26]. Initially developed for detecting simple shapes like circles and lines, the Hough transform method has been extended through mathematical research to facilitate the detection of any type of shape, including parameter-based ones. Firstly, the image is processed using Hough transform to identify accumulators and their corresponding ρ, θ parameters that exceed the threshold, enabling the localization of the centers of the inner and outer circles, as shown in Figure 2a,b. Secondly, mathematical morphological opening and closing operations are performed on the iris image to eliminate glare, resulting in Figure 2c. Finally, the localization of the inner and outer circles is achieved, as illustrated in Figure 2d. However, the Hough transform suffers from a large number of ineffective samples and accumulations when localizing the inner and outer circles of the iris [27]. Although it offers high accuracy, the localization process is time-consuming. Hence, in this study, the particle swarm optimization (PSO) algorithm is employed for the fitting and localization of the inner and outer circles.

3.2. Particle Swarm Algorithm to Locate Inner and Outer Iris Circles Analysis and Simulation

Particle swarm optimization (PSO) is an optimization algorithm based on the theory of swarm intelligence, initially proposed by Eberhart and Kennedy in 1995 [28]. The PSO algorithm starts by randomly initializing a swarm of particles in both the feasible solution search space and velocity space, determining the particles’ initial positions and velocities. It utilizes cooperation among particles and information sharing to search for the optimal solution, without relying on the gradient information of the problem. It is suitable for continuous optimization problems and nonlinear problems. However, a common issue with PSO is that it can easily become trapped in local optima during the iteration process, leading to inaccurate localization. This problem can be avoided by employing proper swarm coordination and information exchange to escape local optima. In summary, PSO possesses a global search capability and fast convergence speed, making it suitable for solving various problems [29]. However, for different problems and application scenarios, it is crucial to select parameters and fine-tune the algorithm appropriately. The specific formulas of the PSO algorithm and the fitness function to be optimized in this paper are presented below.

The dth dimensional velocity update formula for particle i is given in Equation (4).

$${\mathrm{V}}_{\mathrm{i}\mathrm{d}}^{\mathrm{k}}={\mathrm{w}\mathrm{v}}_{\mathrm{i}\mathrm{d}}^{\mathrm{k}-1}+{\mathrm{c}}_1{\mathrm{r}}_1({\mathrm{p}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}\mathrm{d}}-{\mathrm{x}}_{\mathrm{i}\mathrm{d}}^{\mathrm{k}-1})+{\mathrm{c}}_2{\mathrm{r}}_2({\mathrm{g}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}\mathrm{d}}-{\mathrm{x}}_{\mathrm{i}\mathrm{d}}^{\mathrm{k}-1})$$

(4)

The dth dimensional position update formula for particle i is given in Equation (5).

$${\mathrm{X}}_{\mathrm{i}\mathrm{d}}^{\mathrm{k}}={\mathrm{X}}_{\mathrm{i}\mathrm{d}}^{\mathrm{k}-1}+{\mathrm{V}}_{\mathrm{i}\mathrm{d}}^{\mathrm{k}-1}$$

(5)

${\mathrm{X}}_{\mathrm{i}\mathrm{d}}^{\mathrm{k}}$ is the dth dimensional component of the position vector of particle i at the kth iteration, and V denotes the dth dimensional component of the flight velocity vector of particle i at the kth iteration. w is the inertia weight of 1, ${\mathrm{c}}_1$ is the learning factor of 0.5, ${\mathrm{c}}_2$ is the learning factor of 1.25, number of iterations of 200, Xbest is the optimal position, p represents the current optimal position, and g represents the global optimal position. Finding 12 points in the external contour of the pupil, where the distance between two points is equal, the particle swarm algorithm determines the center of the circle O(x,y) and the radius r of the inner boundary of the iris, where the formula for the best fit of the function to fit the circle to the inner and outer edges of the iris is Equation (6). The theoretical test results are shown in Figure 3, and the fitting results are shown in Figure 4. The simulation of the algorithm and fitting of the effect plots were done using matlab version 202b.

$$\mathrm{f}{=}_{\mathrm{x},\mathrm{y},\mathrm{r}}^{\mathrm{m}\mathrm{i}\mathrm{n}}{\sum }_{\mathrm{i}=1}^{12}|{(\mathrm{x}-{\mathrm{x}}_{\mathrm{i}})}^2+{(\mathrm{y}-{\mathrm{y}}_{\mathrm{i}})}^2-{\mathrm{r}}^2|$$

(6)

3.3. Conclusion of the Experiment

Through the experimental research data analysis in

Table 1. Comparison table of experimental effects.

Use of Algorithms (Image Selection)	Average Time for Internal Circle Positioning	Average Time for Cylindrical Positioning	Success Rate
Hough transform (CASIA-Iris-Syn)	0.088 s	2.302 s	89%
Hough transform (KS2A17)	0.150 s	5.581 s	87%
Particle swarm algorithm (CASIA-Iris-Syn)	0.047 s	0.738 s	46%
Particle swarm algorithm (KS2A17)	0.050 s	0.579 s	53%

, it is easy to observe that when facing the high-quality CASIA-Iris-Syn iris database from the Chinese Academy of Sciences (CAS), the improved Hough transform method exhibits a significant enhancement in recognition speed and accuracy despite suffering from a substantial number of ineffective sampling and accumulation issues, resulting in increased processing time. On the other hand, although the particle swarm optimization (PSO) algorithm has been improved to focus on the optimal positions of individual particles, it still suffers from poor accuracy. When using the infrared 850 nm narrowband KS2A17 camera with a 3.9 mm lens to capture photos, the Hough transform method still encounters a large number of ineffective sampling and accumulation issues, leading to a twofold increase in processing time. Moreover, its time complexity and space complexity are higher. Although the particle swarm optimization algorithm slightly improves both time and accuracy when dealing with images with significant differences in quality, the overall performance is still unsatisfactory. Therefore, further improvements should be made to enhance the recognition accuracy of the algorithm. Currently, most particle swarm optimization algorithms focus on improving convergence speed and escaping local optima [30]. In this study, we propose the LinWPSO, RandWPSO, contraction factor method, LnCPSO, and AsyLnCPSO algorithms to improve the particle swarm optimization algorithm, resulting in significant improvements in performance.

4. Particle Swarm Optimization Algorithm Improvement

4.1. LinWPSO

The linear decreasing weight method (LinWPSO), $\mathsf{\omega }$, represents the inertia weight; the $\mathsf{\omega }$ value is small, easy to fall into the local optimal, and $\mathsf{\omega }$ is bigger when there is more focus on global search. ${\mathsf{\Omega }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ means that $\mathsf{\omega }$ pulls the full maximum value; ${\mathsf{\omega }}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ means that $\mathsf{\omega }$ takes the smallest value; s represents the number of iterations; ${\mathrm{s}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ means that s pulls the full maximum value so that ${\mathsf{\omega }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ linearly decreases to ${\mathsf{\omega }}_{\mathrm{m}\mathrm{i}\mathrm{n}}$, which is the first focus in the global search and then later tends to the gradual local search. In order to achieve the purpose of finding the optimal solution, the specific formula is shown in Equation (7).

$$\mathsf{\omega }={\mathsf{\omega }}_{\mathrm{m}\mathrm{a}\mathrm{x}}-\frac{\mathrm{t}({\mathsf{\omega }}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathsf{\omega }}_{\mathrm{m}\mathrm{i}\mathrm{n}})}{{\mathrm{s}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}$$

(7)

4.2. RandWPSO

The stochastic weighting method (RandWPSO) is used in order to solve the shortcomings brought about by the linear diminishing change process. One, LinWPSO produces too small a value initially, which can lead to the convergence rate then accelerating, and two, LinWPSO cannot find the best point initially, and it cannot find it in the end. But RandWPSO can solve this problem well, where $\mathcal{N}$ is (0,1) the normally distributed random number, ${\mathcal{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the o stretched to the maximum value, ${\mathcal{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is the o reduced to the minimum value, and $\mathsf{\sigma }$ represents the weight variance (of stochastic nature), and its improvement formula is (8) and (9).

$$\mathsf{\omega }=\mathcal{R}+\mathsf{\sigma }·\mathcal{N}(0,1)$$

(8)

$$\mathcal{R}={\mathcal{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}+({\mathcal{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathcal{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}})·\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}(0,1)$$

(9)

4.3. SAPSO

The adaptive weighting method (SAPSO), which balances global and local search, has been accompanying the particle swarm algorithm all the time. $\mathsf{\Omega }$ denotes the value of inertia weights, ${\mathsf{\omega }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ represents the maximum value pulling full, and ${\mathsf{\omega }}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ represents the decrease to the minimum value. The current fitness of the function is denoted by f, ${\mathrm{f}}_{\mathrm{a}\mathrm{v}\mathrm{g}}$ averages its positional fitness, and ${\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ represents the decreasing to the minimum fitness. The value of $\mathsf{\omega }$ will be presented with the fitness formula of the function changes, and its target improvement formula is (10).

$$\mathsf{\omega }=\left\{\begin{array}{c}{\mathsf{\omega }}_{\mathrm{m}\mathrm{i}\mathrm{n}}\frac{({\mathsf{\omega }}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathsf{\omega }}_{\mathrm{m}\mathrm{i}\mathrm{n}})}{{\mathrm{f}}_{\mathrm{a}\mathrm{v}\mathrm{g}}-{\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}\\ {\mathsf{\omega }}_{\mathrm{m}\mathrm{a}\mathrm{x}},\mathrm{f}>{\mathrm{f}}_{\mathrm{a}\mathrm{v}\mathrm{g}}\end{array}\right.,\mathrm{f}\le {\mathrm{f}}_{\mathrm{a}\mathrm{v}\mathrm{g}}$$

(10)

4.4. LnCPSO

The learning factor synchronously changing particle swarm algorithm (LnCPSO) IPSO algorithm is suitable for global search in the early stage and focuses on local search in the later stage, which is the best state. The learning factor plays a vital role in the global search capability, and the same is true for the local search. ${\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ represents the learning factor stretched to the maximum value, ${\mathrm{c}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ represents the learning factor reduced to the minimum value, and the number of iterations is denoted by t. The synchronously varying learning factor particle swarm algorithm (LnCPSo) has learning factors ${\mathrm{c}}_1$ and ${\mathrm{c}}_2$, both of which vary linearly from ${\mathrm{c}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ to ${\mathrm{c}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ progressively, and the learning factor formulae are (11):

$${\mathrm{C}}_1={\mathrm{C}}_2={\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-\frac{{\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{C}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}·\mathrm{t}.$$

(11)

4.5. AsyLCPSO

In the asynchronous transformation learning factor particle swarm algorithm (AsyLCPSO), ${\mathrm{C}}_{1,\mathrm{i}\mathrm{n}\mathrm{i}}$ and ${\mathrm{C}}_{2,\mathrm{i}\mathrm{n}\mathrm{i}}$ represent the default values of the learning factors ${\mathrm{C}}_1$ and ${\mathrm{C}}_2$ in the initial state.${\mathrm{C}}_{1,\mathrm{f}\mathrm{i}\mathrm{n}}$ and ${\mathrm{C}}_{2,\mathrm{f}\mathrm{i}\mathrm{n}}$ represent the final values of the learning factors ${\mathrm{C}}_1$ and ${\mathrm{C}}_2$, iteratively. After a large amount of data, it is shown that in most cases, ${\mathrm{C}}_{1,\mathrm{i}\mathrm{n}\mathrm{i}}$ = 2.5, ${\mathrm{C}}_{1,\mathrm{f}\mathrm{i}\mathrm{n}}$ = 0.5, ${\mathrm{C}}_{1,\mathrm{i}\mathrm{n}\mathrm{i}}$ = 0.5, and ${\mathrm{C}}_{2,\mathrm{f}\mathrm{i}\mathrm{n}}$ = 2.5 situation is optimal with the following learning factor Formulas (12) and (13):

$${\mathrm{C}}_1={\mathrm{C}}_{1,\mathrm{i}\mathrm{n}\mathrm{i}}+\frac{{\mathrm{C}}_{1,\mathrm{f}\mathrm{i}\mathrm{n}}-{\mathrm{C}}_{1,\mathrm{i}\mathrm{n}\mathrm{i}}}{{\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}·\mathrm{t}$$

(12)

$${\mathrm{C}}_2={\mathrm{C}}_{2,\mathrm{i}\mathrm{n}\mathrm{i}}+\frac{{\mathrm{C}}_{2,\mathrm{f}\mathrm{i}\mathrm{n}}-{\mathrm{C}}_{2,\mathrm{i}\mathrm{n}\mathrm{i}}}{{\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}·\mathrm{t}$$

(13)

4.6. Shrinkage Factor Method

In order to ensure that the algorithm focuses on local convergence at a later stage, we investigated the solution of the shrinkage factor method by restricting the inertia weights with ${\mathsf{\phi }}_1$, ${\mathsf{\phi }}_2$, which is represented by the model K, Equation (14). The model parameters ${\mathsf{\phi }}_1$, ${\mathsf{\phi }}_2$ are pre-set default value parameters. The update formula is (15).

$${\mathrm{V}}_{\mathrm{i}\mathrm{d}}=\mathrm{K}[{\mathrm{V}}_{\mathrm{i}\mathrm{d}}+{\mathsf{\phi }}_1{\mathrm{r}}_1({\mathrm{p}\mathrm{b}\mathrm{e}\mathrm{s}}_1-{\mathrm{X}}_{\mathrm{i}\mathrm{d}})+{\mathsf{\phi }}_2{\mathrm{r}}_2(\mathrm{g}\mathrm{b}\mathrm{e}\mathrm{s}{\mathrm{t}}_{\mathrm{d}}-{\mathrm{x}}_{\begin{array}{c}\mathrm{i}\mathrm{d}\\ \end{array}}\left)\right]$$

(14)

$$\mathrm{K}=\frac{2}{|2-\mathsf{\phi }-\mathsf{\phi }-\sqrt{{\mathsf{\phi }}^2-4\mathsf{\phi }}|},\mathsf{\phi }={\mathsf{\phi }}_1+{\mathsf{\phi }}_2,\mathsf{\phi }>4$$

(15)

4.7. Conclusion of the Experiment

The theoretical part of different PSO algorithm improvement measures has been introduced above. Here in this paper, several typical methods are selected and simulation tests are carried out to achieve the average positioning time, success rate, and improvement percentage of their inner and outer circles, and the specific experimental data are shown in

Table 2. Comparison of the lifting effect of different algorithms.

Use of Algorithms (Image Selection)	Average Time for Internal Circle Positioning	Average Time for Cylindrical Positioning	Success Rate	Scale Up
LinWPSO	0.064 s	0.777 s	60.5%	14.4%
Shrinkage factor method 2	0.0544 s	0.5489 s	53.4%	7.3%
LnCPSO	0.0540 s	0.6235 s	52.7%	6.6%
AsyLnCPSO	0.0614 s	0.5394 s	56.3%	10.2%
RandWPSO	0.0513 s	0.6533 s	52.4%	5.2%
SAPSO	0.0716 s	0.5474 s	51.6%	4.7%

.

5. Introduction of Simulated Annealing Mechanism and Ant Colony Algorithm

5.1. Particle Swarm Algorithm Combined with Ant Colony Algorithm

The ant colony algorithm (ACO) is a process of many ants searching for food; they always find the shortest path to carry the food, and it achieves efficient problem solving through the interaction of pheromone and heuristic functions [30]. It has achieved more satisfactory results in solving the TSP (Traveler Problem), and here we use it to solve the inner and outer circle localization problem. In the problem of inner and outer circle localization of iris, the particle swarm algorithm has an advantage in speed, but there is a problem in robustness, such as in Figure 5a, where there is a phenomenon of inner and outer circle localization offset; in Figure 5b, where there is a problem of inaccurate localization; and in Figure 5c, where there is a phenomenon of poor robustness and localization offset. Here, our particle swarm algorithm initializes the population and parameters, which are the initial pheromone distribution, and transforms the better solution obtained by the particle swarm algorithm into the ACO algorithm. The block diagram of its ACO algorithm flow is shown in Figure 6, and the core formula of transfer probability (16) and the final effect are experimentally ideal, as shown in Figure 7a–c. The iris image processing and inner and outer circle localization are both improved to different degrees.

$${\mathrm{P}}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}\left(\mathrm{t}\right)=\left\{\begin{array}{c}\frac{{\left[{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}\right(\mathrm{t}\left)\right]}^{\mathsf{\alpha }}{\left[{\mathrm{n}}_{\mathrm{i}\mathrm{j}}\right(\mathrm{t}\left)\right]}^{\mathsf{\beta }}}{\sum _{\mathrm{s}\mathsf{ϵ}{\mathrm{J}}_{\mathrm{k}}\left(\mathrm{i}\right)}{\left[{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}\right(\mathrm{t}\left)\right]}^{\mathsf{\alpha }}{\left[{\mathrm{n}}_{\mathrm{i}\mathrm{j}}\right(\mathrm{t}\left)\right]}^{\mathsf{\beta }}},\mathrm{j}\mathsf{ϵ}{\mathrm{J}}_{\mathrm{k}}\left(\mathrm{i}\right)\\ 0,\mathrm{j}\notin {\mathrm{J}}_{\mathrm{k}}\left(\mathrm{i}\right)\end{array}\right.$$

(16)

where ${\mathrm{P}}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}\left(\mathrm{t}\right)$ is the tth generation of ants and the k ants choose to break into the east or go to the west of the probability; that is, the probability of ants k choosing to go from i~j, $\mathsf{\alpha }$ on behalf of the degree of importance of the heuristic factor, β for the relative degree of importance of the heuristic factor, and ${\mathrm{n}}_{\mathrm{i}\mathrm{j}}$ on behalf of the heuristic audience factor. ${\mathrm{J}}_{\mathrm{k}}\left(\mathrm{i}\right)$ here represents the pupil of the iris outside of the 12 points at equal distances (note: each point can only be walked once).

When all the ants have finished one iteration, the road, the pheromone of the path passed through, must be changed [31], and it is necessary to update the pheromone in time. ${\mathsf{{\rm T}}}_{\mathrm{i}\mathrm{j}}$ denotes the pheromone on the i~j path at the tth moment (the tth generation of ants), and its formula is as follows:

$${\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}(\mathrm{t}+1)=(1-\mathrm{p}){\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}\left(\mathrm{t}\right)+∆{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}$$

(17)

$∆{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}$ represents the sum of pheromone left by m ant pairs on the path i~j, $∆{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}$ represents the pheromone of the kth ant on the path it I ~ j traveled (Q represents the pheromone that an ant possesses in its lifetime), $\mathrm{K}$ represents the number of ants, $\mathrm{m}$ means the number of ants, and $\mathsf{\rho }$ denotes the degree of pheromone dilution (the ratio of the pheromone decreasing over time [32]). The formula in (18) will finally achieve the optimal solution of the fitness function and output the optimal path.

$$\left\{\begin{array}{c}∆{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}={\sum }_{\mathrm{i}=1}^{\mathrm{m}}∆{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}\\ ∆{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}=\frac{\mathrm{Q}}{{\mathrm{L}}_{\mathrm{k}}}\end{array}\right.$$

(18)

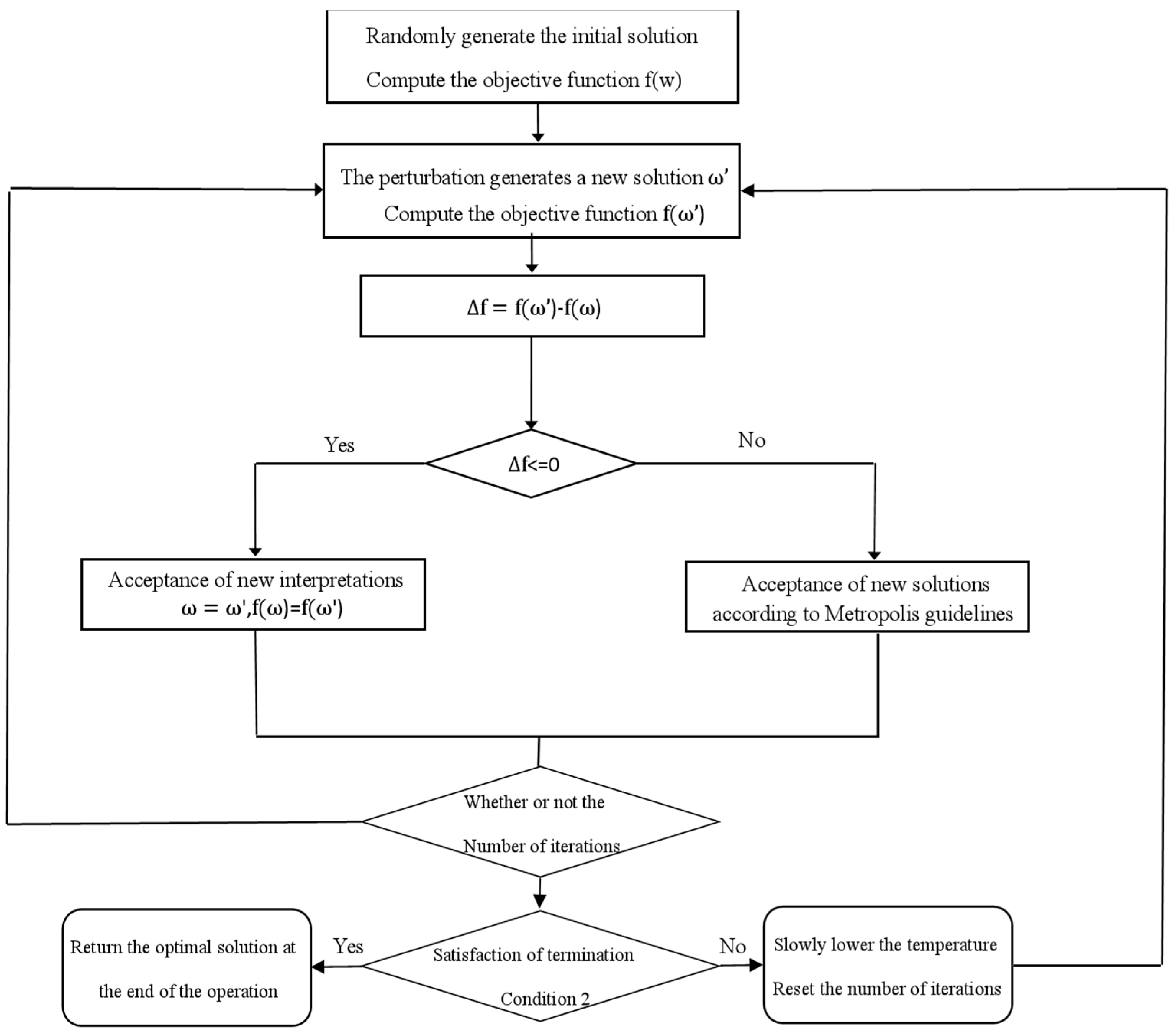
5.2. Introduction of a Simulated Annealing Mechanism

The block diagram of the process is shown in Figure 8. The particle is initialized with velocity and position; the initial solution $\mathsf{\omega }$ is generated randomly; and the optimal solution is generated with perturbation to obtain $∆\mathrm{f}$. The PSO algorithm combines the annealing mechanism for updating the velocity and position and accepts the global optimal solution through the Metropolis principle [33].

Assuming that x(n) is the previous target state, the system, according to the gradient descent, uses the energy of the previous section to obtain the current state of the x(n + 1) target, and the system target energy evolves from the corresponding E(n) to (n + 1), which evolves the probability of receiving the acceptance P in Equation (19).

$$\mathrm{P}=\left\{\begin{array}{c}1,\mathrm{E}(\mathrm{n}+1)<\mathrm{E}\left(\mathrm{n}\right)\\ {\mathrm{e}}^{-\frac{\mathrm{E}(\mathrm{n}+1)-\mathrm{E}\left(\mathrm{n}\right)}{\mathrm{T}}},\mathrm{E}(\mathrm{n}+1)\ge \mathrm{E}\left(\mathrm{n}\right)\end{array}\right.$$

(19)

As can be seen from the formula, the size of the energy takes the value, and the global optimal solution presents a linear connection; T carries out the size of the probability formula, and P is closely related to the amount of change in the P target energy, so this optimal solution of the objective function adaptation is dynamic [34]. The solution of the heuristic algorithm and the initial state solution default value parameter setting and the initial trial state are independent; the simulated annealing algorithm (SA) has gradual convergence [35].

The combination of the simulated annealing mechanism and the ant colony algorithm both improve the PSO algorithm, to a certain extent, to avoid falling into the local optimum, which leads to inaccurate positioning of the inner and outer iris circles. The success rate is increased by more than 10%, while the operation speed is almost unchanged. Based on the above two algorithms, we constructed a more efficient iris positioning algorithm system, such as Figure 9a, which improved particle swarm algorithm optimization of the inner circle; Figure 9b, the results of the inner circle positioning; Figure 9c, the improved particle swarm algorithm for outer circle localization; Figure 9d, the success of the outer circle positioning; and ultimately, as shown in Figure 9e, to complete the completion of our highly efficient iris positioning algorithm system.

6. Discussion

This study addresses the crucial task of iris image localization, which plays a fundamental role in various biometric authentication systems. Our research focuses on proposing and evaluating an innovative approach that combines multiple methods to achieve improved accuracy and efficiency in iris image localization.

The motivation for this research stems from the growing demand for accurate and reliable biometric identification techniques in fields such as security, access control, and forensics. Iris recognition has gained significant attention due to its distinct advantages, including uniqueness, stability, and resistance to various environmental conditions. However, accurate iris localization remains a challenging task due to factors such as occlusions, iris deformation, and low image quality.

To overcome these challenges, our research employs a novel multi-method improvement framework that integrates the advantages of different iris image localization algorithms. We propose a hybrid technique combining edge detection, Hough transform, and evolutionary learning methods to improve accuracy and robustness. Through extensive experiments on the CASIA-Iris-Syn dataset and the self-constructed CASIA dataset, we demonstrate the effectiveness of our approach, and its performance leads to more favorable results.

The contributions of our work can be summarized as follows:

• A novel multi-method improvement framework is proposed for iris image localization.
• Avoiding falling into local optimality is a difficult problem that heuristic algorithms need to address. Although there are various improved particle swarm optimization (PSO) algorithms, they are only used for function-specific test experiments and fail to find optimal solutions for all test functions. This study further advances the theoretical study of the algorithm by applying it to the localization of iris inner and outer circle fitting in practical engineering.
• We tried various methods, including the Hough transform, particle swarm optimization algorithm, and combinations of LinWPSO, RandWPSO, shrinkage factor, LnCPSO, and AsyLnCPSO. In addition, by applying the simulated annealing algorithm and the ant colony algorithm, we improved the particle swarm optimization algorithm to different degrees. Finally, based on the theoretical support, we successfully solved the inaccuracy problem of the particle swarm optimization algorithm in inner and outer iris circle localization, and constructed a more efficient iris localization algorithm and system architecture.
• Comprehensive experiments are conducted to evaluate and verify the effectiveness and superiority of our method.
• Demonstrate the improved accuracy and robustness of iris image localization for real-world application scenarios.

The findings of this study have practical implications for improving the accuracy and efficiency of biometric authentication systems that rely on iris recognition. Through extensive experiments on both public datasets and our self-built dataset, we demonstrate the effectiveness of our method, which achieves superior performance compared to existing methods.