Abstract
Aiming at the problem of the excessive error of direction of arrival (DOA) estimation caused by the position disturbance of a UAV swarm during flight, a robust polarization-DOA estimation method based on sparse Bayesian learning (SBL) is proposed. First, the algorithm decomposes the covariance matrix of the received data of the UAV swarm vector array and then constructs the determination matrix of the UAV position coordinates by exploiting the orthogonality of the eigenvalues and eigenvectors. Then, the optimal solution of the semi-positive definite programming (SDP) problem is solved using the constrained global least square method, and the exact self-positioning coordinates of UAVs are obtained. Second, we construct a spatially discrete grid to model the received data of the UAV group vector array. The SBL theory is then applied to obtain the posterior probability distribution of the sparse signal matrix. The sparsity of the signal matrix is controlled with a hyperparameter, and the estimation of the DOA is conducted using a fixed-point iteration to obtain the maximum posterior estimate of the signal matrix. Finally, according to the estimated DOA, the polarization parameter is obtained from the constructed objective function of the polarization parameter estimation. The simulation results show that the proposed algorithm achieves higher accuracy and robustness than the traditional 2D DOA estimation algorithm in the direction-finding system for UAV swarm vector arrays.
1. Introduction
In recent years, due to the low cost and miniaturization of unmanned aerial vehicles (UAVs), the UAV swarm has become an important part of UAV cooperation and has gained more and more attention in the military and civilian in recent years [1,2,3,4,5]. A UAV swarm consists of a large number of smaller UAVs equipped with a small number of antennas in a certain arrangement [6,7,8,9,10,11]. Compared with the traditional array, a swarm of UAVs can form a massive antenna array, which can improve spatial resolution, spectral efficiency, and energy efficiency [12,13]. Based on the above merits, the direction of arrival (DOA) estimation using the UAV swarm array has been widely studied in fields such as reconnaissance, sensor detection, automotive radar, geodesy, and emergency rescue.
In the pursuit of swift direction finding (DF) for transmitters aboard UAVs in future wireless networks, researchers have delved into developing innovative solutions. One such approach, outlined in [14], presents a streamlined DOA estimation architecture tailored for massive multiple-input multiple-output (MIMO) receiver arrays. In parallel, ref. [15] proposed a novel beam space DOA estimation matrix algorithm rooted in UAV group dynamics. This method establishes rotation invariance between beam clusters, effectively addressing random phase differences and enabling multi-source DOA estimation. Another noteworthy contribution, detailed in [16], proposed a UAV-based DOA frequency domain estimation algorithm. This technique transforms received signals into the frequency domain, constructs covariance matrices based on Toeplitz matrix features, and employs the low-complexity root-MUSIC algorithm to achieve precise DOA estimation. Additionally, ref. [17] tackled the challenge posed by mutual coupling among UAVs in DOA estimation. This study devises an advanced signal model incorporating the mutual coupling matrix, enhancing the MUSIC algorithm’s capability to estimate DOA in the presence of mutual coupling.
Recently, electromagnetic vector antennas have been favored by many researchers due to their ability to simultaneously obtain both airspace information and polarization information of information sources, as well as their enhanced anti-jamming capability, higher resolution capability, more robust detection capability, and polarization multiple access capability [18,19,20]. Thus, placing electromagnetic vector antennas on multiple UAVs can constitute a new type of UAV swarm vector array. Several attempts, such as the application of ℓp-norm (0 ≤ p ≤ 1) methods [21,22,23,24,25], orthogonal matching pursuit (OMP) methods [26,27], and the sparse Bayesian learning (SBL) methods [28,29,30,31], have aroused a lot of attention in DOA estimation. The essential idea of these algorithms is that the directions of incident sources are substantially sparse in the spatial domain, which is intrinsically different from the subspace-based algorithms. Related methods have been shown to gain a much-enhanced performance over the subspace-based methods in the condition of low SNR and limited snapshots. In [32], a joint DOA, power, and polarization estimation method using the concentered orthogonal loop and dipole array is proposed by utilizing the signal reconstruction method. By exploiting the sparsity of the incident signals in the spatial domain, ref. [33] proposed a novel method to estimate the DOA and polarization parameters by using the SBL method. In [34], a novel off-grid hierarchical block-sparse Bayesian method for DOA and polarization parameters estimation was presented to improve the estimation accuracy [35].
However, the DOA estimation methods mentioned above have a common assumption: precise knowledge of the array’s position. In practical UAV swarm scenarios, UAVs experience continuous shaking during flight, leading to constant shifts in antenna positions. Despite the availability of Global Positioning System (GPS) data for UAV location tracking, the inherent GPS accuracy, typically at the meter level, falls short due to the minimal scale of UAV position jitter, often less than 1 m [36,37]. Consequently, the existing GPS accuracy fails to meet the stringent requirements of UAV localization amid these subtle positional fluctuations. Hence, how to achieve robust and high-precision polarization DOA estimation is a critical issue for UAV array signal processing in an environment where the array is moving in real-time, and the precise UAV position information is unknown. In a recent study [38], a novel framework was introduced, offering computational efficiency while enabling the positioning of unidentified UAVs. Previous research efforts, documented in [39,40], focused on UAV self-positioning algorithms. However, these studies lacked a suitable direction of arrival (DOA) estimation method, merely providing rudimentary channel state information estimations. Complicating matters further, UAV swarms contend with substantial interference during flight. Consequently, enhancing the performance of robust DOA estimation algorithms within UAV swarm arrays, all while achieving high-precision self-positioning has emerged as a focal point in contemporary array signal processing research.
Based on the aforementioned analyses, one can find that (i) the accurate position of the element is very important for the DOA estimation method, so it is necessary to realize the accurate self-positioning of the element, and (ii) the SBL technique is able to enhance the resolution of DOA estimation. Thus, in this paper, we study the self-positioning problem of the UAV swarm and propose a novel joint polarization-DOA estimation algorithm based on SBL of UAV swarm vector array (U-SBL). The main contributions of this paper are summarized as follows.
- In order to accurately estimate the array position during the flight of the UAVs, the orthogonality of the eigenvalues and eigenvectors is used to construct a termination matrix for the UAV’s position coordinates. Then, the exact self-positioning coordinates of UAVs are obtained by solving the optimal solution of the semi-positive definite programming (SDP) problem with the constrained global least square method. This provides a guarantee for the subsequent implementation of accurate DOA estimation.
- By using the 2D joint sparsity signals of the incident, A 2D sparse received signal model based on the vector array of the UAV swarm is constructed. Then, the SBL algorithm is utilized to obtain the maximum posterior probability density of the target parameters. After iterative convergence, the DOA estimate of the target is obtained from the maximum value of the power spectrum.
- Additionally, the polarization parameter is solved by building an objective function for polarization parameter estimation based on the estimated DOA parameter. To avoid 2D spectrum peak searching, the minimum eigenvector method (MEM) is adopted to realize the polarization parameter estimation.
- The simulation results demonstrate the superior performance of the proposed algorithm. The algorithm can solve the problem of accurate self-positioning of UAVs and provide high-precision polarization-DOA estimation jointly under low signal-to-noise ratio (SNR) and small snapshot conditions.
The rest of this paper is organized as follows. In Section 1, we describe the UAV swarm vector array model for self-positioning and DOA estimation. In Section 2, we describe the novel U-SBL algorithm, as the proposed DOA and self-positioning estimation method with sparse Bayesian learning is presented in this Section. In Section 3, we derive the CRB of the novel U-SBL algorithm. In Section 4, we summarize the complexity of the proposed method. The simulation results and conclusion follow in Section 5 and Section 6, respectively.
The symbols related to this paper are shown in Notations.
2. System Model
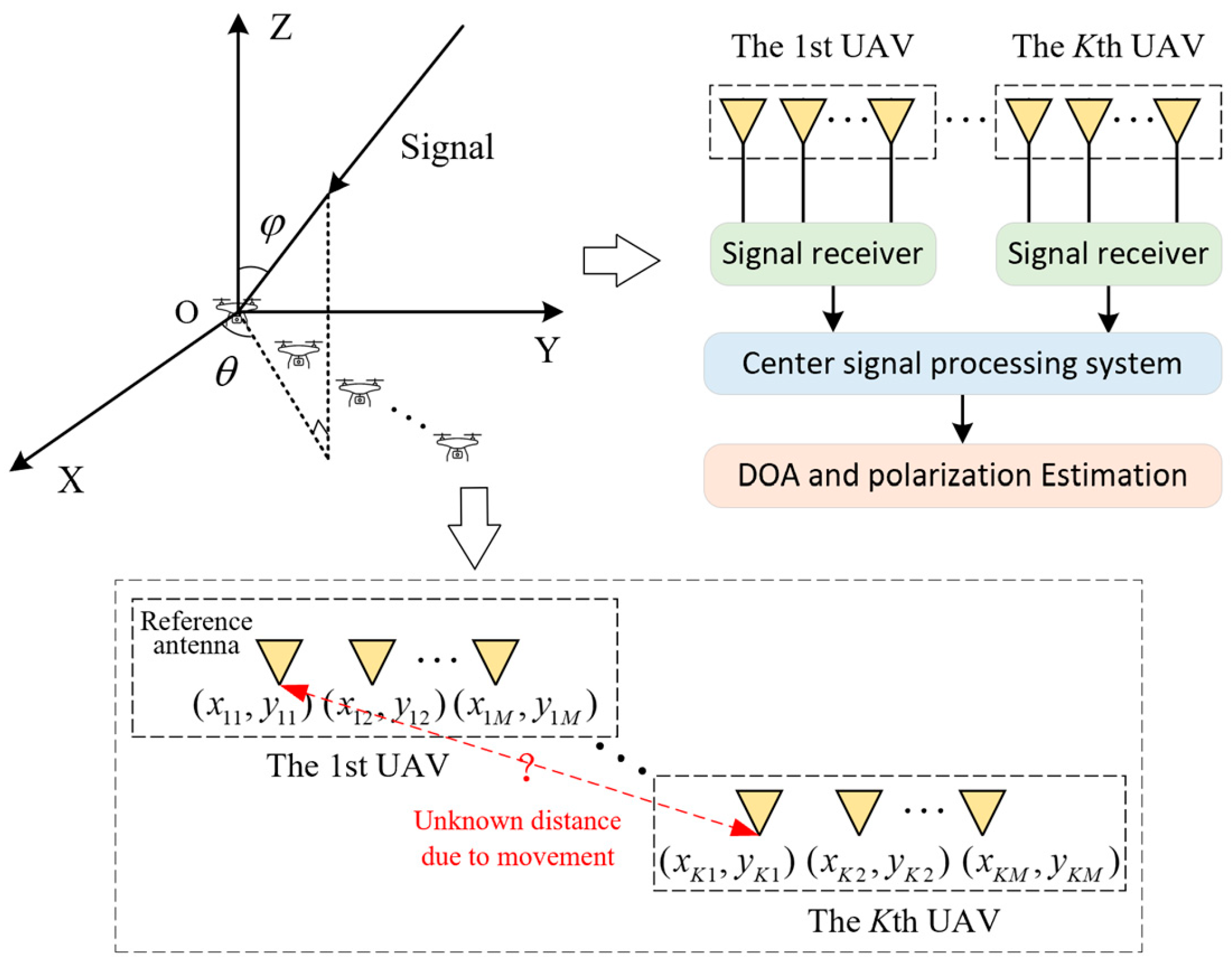
Consider a UAV swarm that includes arbitrary non-overlapping UAVs. Each UAV is installed with electromagnetic vector antennas. Each electromagnetic vector antenna contains three electric dipoles and three magnetic rings. Number of array elements is . The spacing between the array elements on the same UAV is ( denotes the signal wavelength). A model of the UAV swarm array system and signal flowchart diagram is shown in Figure 1.
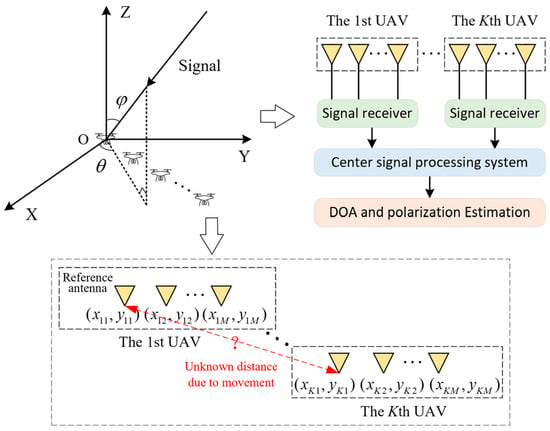
Figure 1.
UAV swarm vector array system and signal flowchart diagram.
For simplicity, assume all the UAVs fly in the same plane, the z-axis coordinates of the UAV could be 0. The coordinates of each antenna element on the kth UAV are expressed as , where k = 1, 2, …, K and m = 1, 2, …, M. Considering that the independent far-field narrow-band fully polarized incident signals impinged on this array, the DOA and polarization parameters of the lth incident signal are denoted as , where the , , , and are defined as azimuth angle, elevation angle, polarization auxiliary angle, and polarized phase angle, respectively. The array spatial polarization steering vector of the lth signal is defined as
where denotes the spatial steering vector, denotes the spatial-polarization vector, and their expressions are formulated as follows:
where and represent the spatial and polarization information of the incident signal, respectively. and are the three electric and three magnetic field components of the output of each vector antenna, respectively. Hence, the data received by the whole UAV swarm vector array at time t for L signals can be expressed as
where is the array steering matrix, is the signal vector, and is noise vector, which denotes is the additive white Gaussian noise with zero mean and variance .
3. The Novel U-SBL Algorithm
3.1. High-Precision Self-Positioning Algorithm
As analyzed above, the accurate position of array elements is one of the important preconditions for accurate DOA estimation. However, in the UAV swarm scenario, the location of the array elements is unknown because the aircraft is constantly moving. However, in the UAV swarm scenario, the location of the array elements is unknown because the aircraft is constantly moving. Since the relative positions of the antennas on each UAV are fixed and known, the coordinates of all antenna arrays can be obtained simply by obtaining the position of the first antenna on each UAV.
Now, we assume that and denote the relative position of the mth antenna in the kth UAV to the 1st antenna in the same UAV in x-axis and y-axis, respectively. It is seen that the coordinates are a priori, but is what we need to find. As a result, (2) can be rewritten as
where
where is the steering vector of the kth UAV, and . is the steering vector of the 1st antenna of each UAV. It is seen that by finding the matrix P exactly, the precise position of each antenna of the UAV array can be obtained. As we all know, the covariance matrix of (5) is
where denotes the signal subspace eigenvector; the diagonal matrix contains eigenvalues, and denotes the noise subspace eigenvector. By utilizing the orthogonality of the steering matrix and noise subspace, we have
Substituting (1) and (6) into (10), we have
where is defined as the determination matrix.
The next step is to solve the precise position information, which is comprised in . Observing from (11), the is included in the null space of the determination matrix . Due to the orthogonality of and , , the determination matrix has unique null-space eigenvectors collinear with position vectors for every [24]. Assuming the null-space eigenvector is denoted as , and the estimated result of is
where is the first element of the , and the first element of is always 1. By (7) and Formula (12), we have
where is the kth phase of . is phase delay, is integer. is the maximum diameter of the area where the UAV is located. Then, (13) can be rewritten as
It can be further written as
where
Based on the above analysis, the combined constrained population least squares method can be used to transform the above problem of solving UAV coordinates into an SDP optimization problem to obtain position estimation. The constrained optimization criterion is formulated as follows:
where is reversible, and is the diameter of the area where the UAV swarm is located. Through to satisfy the convergence condition and , is threshold. Solving for K functions of (13) yields the positions of K UAVs. It is worth noting that the same array positions of the UAV are all fixed-calibrated. Depending on the position of the K UAVs, the position of the matrix can be obtained. The position of the mth matrix of the kth UAV is . Then, the steering matrix can be obtained by returning from (2) of the matrix positions based on the new coordinates.
3.2. The Polarization-DOA Estimation Algorithm
In order to utilize the spatial sparsity of the signal sources and apply the SBL theorem, the visible angular range is discretized to the set of Q directions , . The true directions are contained in with moderately small quantization errors. For simplicity, the sparsity of the polarization information is not considered. Thus, the estimation problem turns out to be that of recovering the sparse signal vector in correspondence with the user-defined Q-sampling of the angular range [37,38]. Therefore, the observation matrix X can be presented as
where is the over-complete array steering matrix, and is the sparse direction weights; it has non-zero value only at the true source directions.
Assume that the elements of the signal are independent of each other and that the columns obey a Gaussian distribution with mean 0 and variance of .
where is the variance matrix of the source signal amplitude. Hyperparameter represents the source signal spatial power, and controls the sparsity of ’s rows. The conditional probability density function of the amplitude is given via
where represents the Frobenius norm of the observation matrix. According to the Bayesian probability theorem, the posterior probability density function of the source signal with respect to the data received by the array is
where the posterior mean and posterior covariance matrix of the signal is, respectively, given as
The likelihood function for about is
where , and its minimum value is . According to (22), the objective function of the incident signal on is
According to the fixed-point iteration method, minimizing Equation (27) yields , and its iteration can be expressed as
where is , and are calculated by (23) and (24), respectively. denotes the -th line of , denotes the elements of row- and column-. Iterate until the convergence condition is satisfied, or the maximum number of iterations is reached.
The mean and variance of can be output in . The powers from different directions are obtained by substituting the estimated into the power function, where the power of the -th impinging signal is expressed as
By searching the spectrum peak of (28), the corresponding can be estimated.
Next, we are going to estimate the polarization parameters. According to (1), (4), and (10), we have
It can be seen that and only contain the polarization information but not DOA information. Then, we can define
Then, the polarization parameters will be estimated using the minimum eigenvalue method (MEM). Substitute the L estimated DOAs into (30), and L is obtained. Let , where indicates the value corresponding to the l-DOA. is the eigenvector corresponding to the minimum eigenvalue, which can be obtained via the generalized eigenvalue decomposition. Then, the polarization parameter is given as follows
where denotes the ith element in the eigenvector.
Based on the above analysis, it becomes evident that while traditional sparse classification algorithms can resolve the 2D DOA estimation challenge, they prove to be unsuitable for UAV swarm arrays due to their continuous shifting dynamics. In contrast, the proposed algorithm excels in achieving high-precision auto-positioning and 2-D DOA estimation even with limited snapshots. It is important to note that this approach is not restricted to UAV swarm vector arrays alone. It seamlessly adapts to a variety of arbitrary UAV swarm array structures. To summarize, the overall workflow of the algorithm is outlined as Algorithm 1.
| Algorithm 1: U-SBL Algorithm Steps |
| Input: Array receives data , Maximum diameter of the UAV area , Threshold and , Iterations , Grid point set ; |
| 1 According to Formulas (16) and (17) obtain and ; 2 Self-positioning coordinates are obtained according to Formula (18); 3 After the sparse signal model is obtained from Formula (19), The posterior probability density function is obtained according to Equation (22); 4 The iteration begins, updated and according to Equations (23) and (24); 5 Update the hyperparameters according to Equation (27); 6 If and , it will return to step 4; 7 The end of the iteration. Output the DOA estimation results and ; 8 The polarization parameter estimation result and are calculated from Equations (31) and (32); Output: Parameters of all incident signals |
Remark 1.
The self-positioning algorithm functions independently and is not related to the sparse Bayesian learning algorithm used for DOA estimation. In the algorithm sequence, self-positioning occurs first, followed by DOA estimation, with both processes complementing each other. This process is also applicable to other DOA estimation algorithms.
Remark 2.
The proposed algorithm is applicable to any UAV formation as long as there is no occlusion between UAVs, which also provides ideas for our future research on sparse arrays and UAV-based 3D arrays.
Remark 3.
According to empirical, the initial threshold is initialized to 0.01, which can ensure high-precision self-positioning. and represent the termination threshold and maximum iterative number, respectively.
4. Cramer–Rao Bound
The observations are assumed to satisfy the following deterministic model
The coordinate position uses the vector between the different UAVs to represents as
where , , angle , signal , and noise variance are all taken as unknown parameters. The closed form expression for Cramer–Rao Bound (CRB) is given below. Self-localized Cramer–Rao Bound and DOA estimates of the Cramer–Rao Bound are derived from the following equation.
where the specific derivation process can be referred to the following equation from [41].
Note that the above formula is a vector containing only the dimension of element 1, the first column of matrix is deleted, each non-zero element is replaced with 1, and the resulting matrix is in the above formula.
5. The Computational Cost Analysis
The computational complexity of the RARE [39], MUSIC [42], OMP [43], and U-SBL algorithm is given in Table 1. denotes the number of snapshots. Therefore, the complexity of the proposed U-SBL algorithm mainly consists of two parts: the self-positioning part and the parameter estimation part. The computational complexity of self-positioning is , while the computational complexity of polarization-DOA estimation algorithm, which is mainly determined by calculating the posterior probability density, as shown in Equations (27) and (28), is . So, the total computational cost is . In general, , to obtain a better sparsity, the sparsity degree of the U-SBL algorithm takes a higher value. As a result, the complexity of the proposed U-SBL algorithm is higher than other algorithms. Hence, how to reduce the complexity of the U-SBL algorithm is another main direction in future research.

Table 1.
Algorithm complexity analysis.
6. Simulation Results
In this section, we have organized a group of 5 UAVs within a 2D setting, the configuration is shown as Figure 1. It is worth mentioning that all the UAVs should be flying in the same XOY plane; thus, the position coordinates of the UAVs are defined as , , , , and , respectively. Each UAV is equipped with a three-element linear array with array elements that are spaced by . Suppose that there are three independent signal sources in space, with incidence angles are , , and , respectively. Other main simulation parameters are shown in Table 2. In all examples, the signal frequency is assumed as 1 GHz. The simulation results were obtained on a personal computer with MATLAB R2021b, Intel Core i5 @3.0 GHz processor, and 16 GB LPDDR3 @ 6000 MHz.

Table 2.
Main simulation parameters.
In the subsequent simulations, the efficacy of the proposed algorithm is validated by comparing with RARE, MUSIC, and OMP algorithms. The performance of the algorithm is measured from two perspectives: estimation accuracy and resolution. The accuracy of the algorithm estimation is evaluated using the Root Mean Square Error (RMSE) and the resolution is evaluated via the probability of successful detection. The RMSE for self-position estimation and angle estimation as (37) and (38), respectively. It is necessary to mention that the RMSE formula is the same for each estimated parameter. Thus, and are defined as the set of antenna coordinates and the set of angels, respectively. It is noteworthy that all these four algorithms are built upon the self-positioning algorithm proposed in this paper.
where is the number of Monte Carlo simulations. and are the set of estimated value and true value of antenna coordinates, respectively. and are the set of estimated values and true values of angel parameter, respectively. I is set to 200 in the following simulations.
Additionally, the resolution is evaluated via the probability of the successful detection, and “a successful detection” is recognized if the absolute error of all the estimated angles is smaller than a fixed value. The probability of successful detection is the ratio of the number of successful detections to the total number of trials.
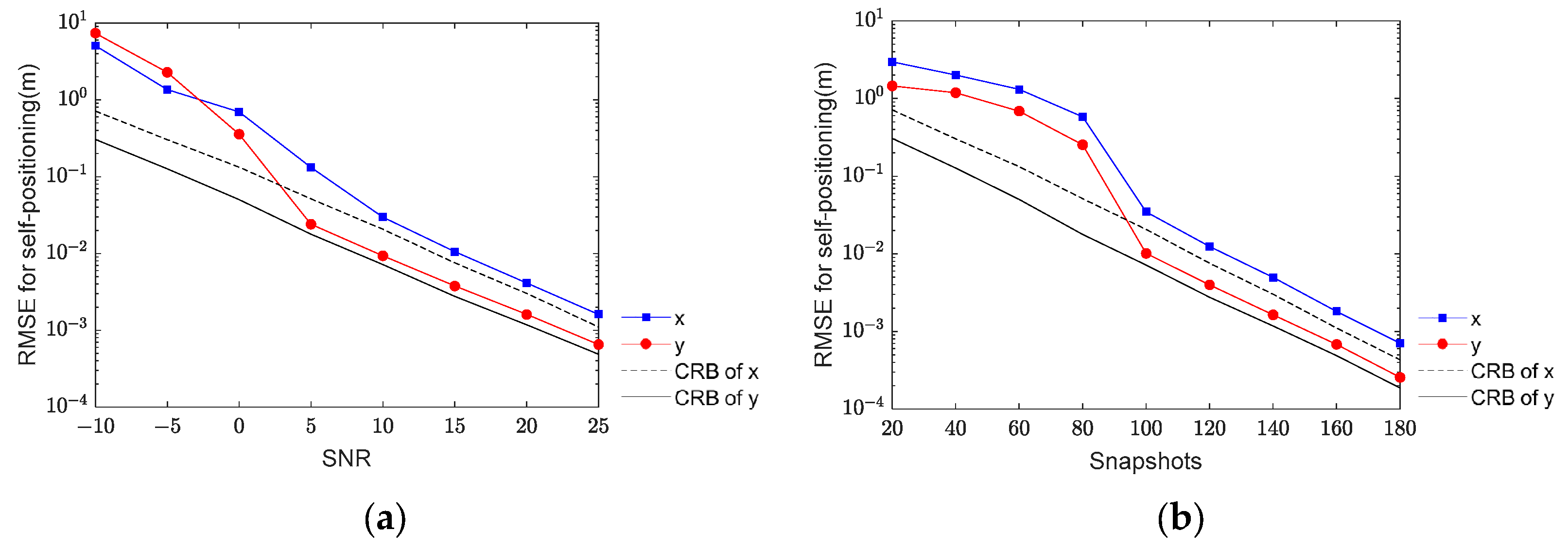
In this simulation, the accuracy of self-positioning is examined concerning SNR and the number of snapshots, as illustrated in Figure 2. With a fixed number of snapshots at 100, Figure 2a displays the RMSE of self-positioning concerning SNR ranging from −10 dB to 25 dB, while Figure 2b demonstrates the RMSE concerning snapshots varying from 20 to 180 at a constant SNR of 5 dB. As depicted in Figure 2, the algorithm’s self-localization accuracy improves with increasing SNR and snapshots. This trend confirms the effectiveness of the self-localization algorithm. Enhanced SNR leads to improved accuracy in the determination matrix, which subsequently lifts the accuracy of the derived position vectors. As the position vector critically influences UAV self-positioning accuracy, higher SNR levels result in accuracy approaching the CRB. Similarly, an increase in the number of snapshots augments the volume of data within the determination matrix, which subsequently improves the accuracy of the position vector. Subsequently, the accuracy of UAV self-positioning increases with a higher number of snapshots and SNR.
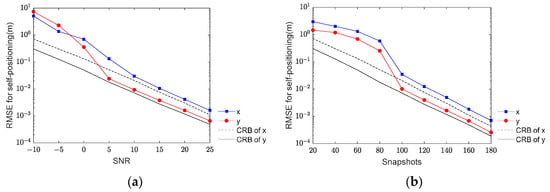
Figure 2.
The RMSE of self-positioning algorithm versus SNR and snapshots: (a) the RMSE of self-positioning algorithm versus SNR; (b) the RMSE of self-positioning algorithm versus snapshots.
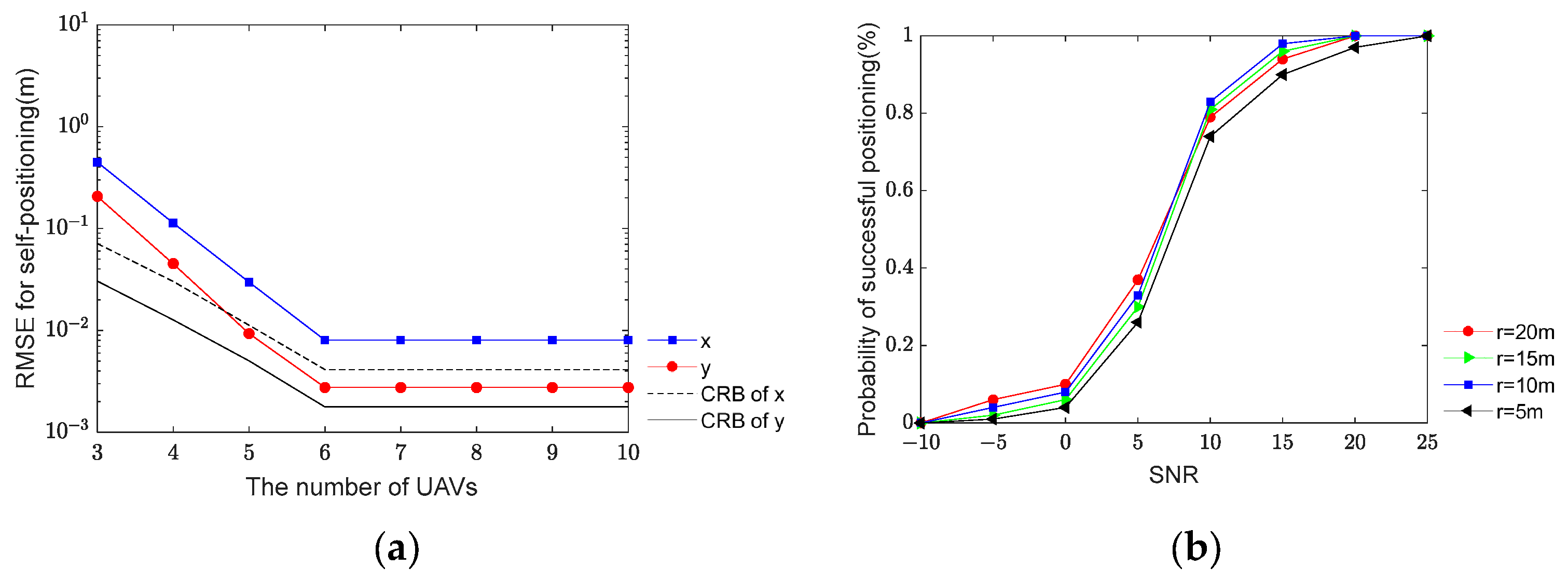
In the subsequent simulation, the accuracy of self-positioning concerning the number of UAVs and the probability of successful positioning relative to the maximum diameter r is presented in Figure 3a and Figure 3b, respectively. The SNR is set at 5 dB, and there are 100 snapshots for each scenario. Figure 3a illustrates the RMSE of the self-positioning algorithm while varying the number of UAVs from 3 to 10 uniformly. In Figure 3b, the number of UAVs is fixed at 5, SNR is set at 5 dB, and there are 100 snapshots. Define that “one successful positioning” is when both and are satisfied. Varying the SNR from −10 dB to 25 dB, the probability of successful positioning versus different diameters r is shown in Figure 3b. The probability of successful positioning can be defined as , where C is the number of “one successful positioning”.
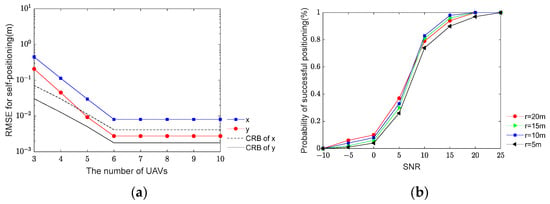
Figure 3.
Self-positioning accuracy and probability of successful positioning versus different parameters: (a) Self-positioning accuracy of algorithm versus numbers of UAVs. (b) probability of successful positioning versus diameters r.
As illustrated in Figure 3a, the self-positioning accuracy of the algorithm improves with the increasing number of UAVs. However, once the number of UAVs exceeds six, the accuracy levels closely approach the Cramér–Rao bound (CRB). This phenomenon occurs because the position vector derived from the determination matrix, which is crucial in UAV self-positioning, initially gains dimensionality as the number of UAVs increases. As the number of UAVs increases, although more data will be accumulated, the number of positional parameters to be estimated will also increase. Thus, after a certain threshold, the accuracy reflected by this vector is already exceptionally high, approaching the CRB. Consequently, further increasing the number of UAVs does not significantly enhance the localization accuracy. In Figure 3b, the probability of successful positioning under different diameters r is improved with the SNR increasing. The larger the r, the greater the probability of successful positioning. However, the r should not be chosen too large because the larger r will bring a higher number of iterations during the localization search, and this will cause a larger computational complexity of the algorithm. Therefore, the diameter should be chosen relatively appropriately. Experimentally, it can be seen that diameter r = 10 m is the best. In the following simulation, we select r as 10 m.
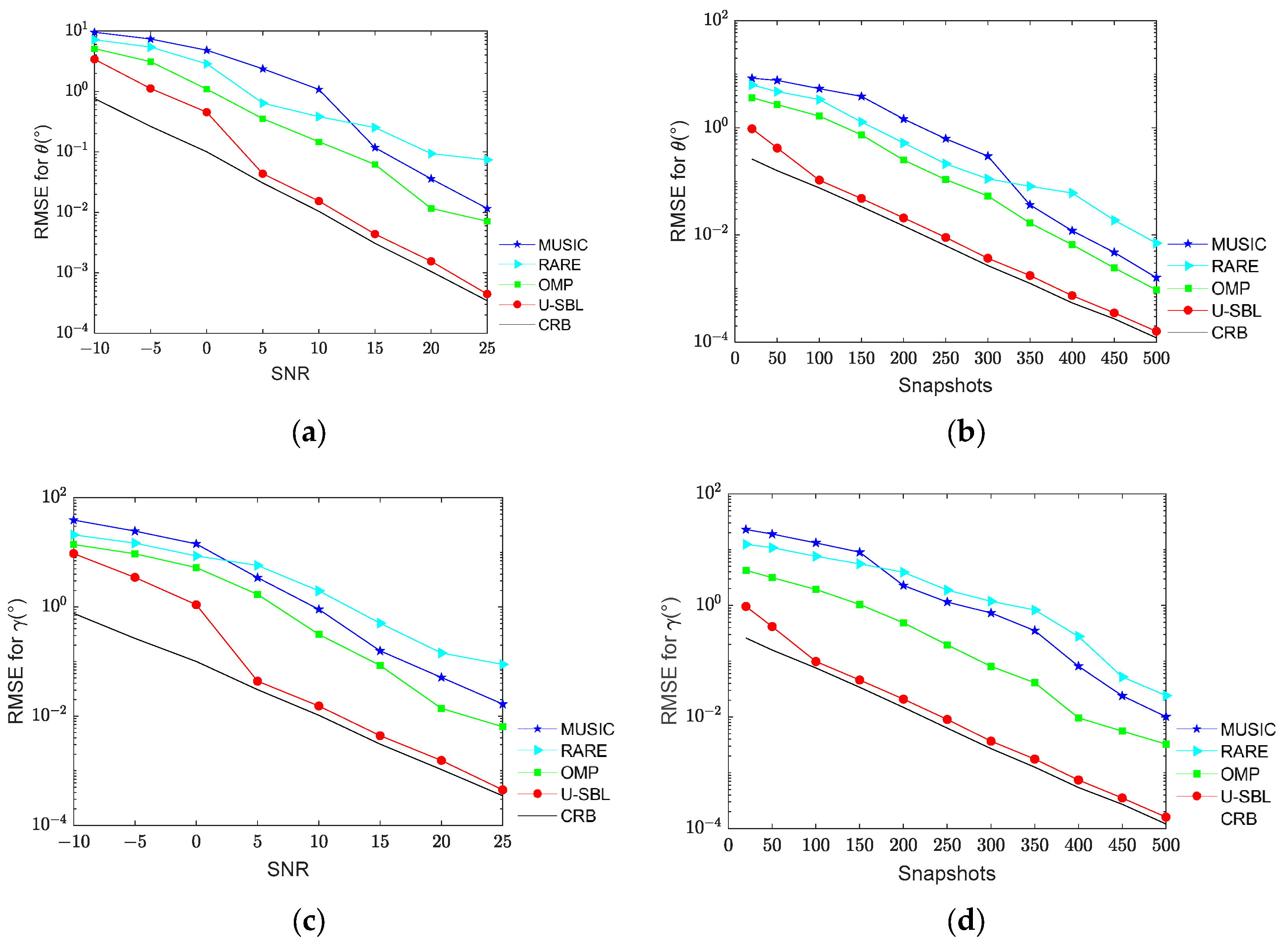
In this simulation, the accuracy of DOA and polarization estimation versus SNR and snapshots are shown in Figure 4. The snapshots are set to 100, and the SNR varies uniformly from −10 dB to 25 dB with a step size of 5 dB. The RMSE of DOA and polarization estimation versus SNR are shown in Figure 4a and Figure 4c, respectively. The SNR is set to 5 dB, and the snapshots vary from 20 to 500. The RMSE of DOA and polarization estimation versus snapshots are shown in Figure 4b and Figure 4d, respectively. Because the RMSE curve character of and are consistent, only the RMSE curve of is drawn in Figure 4a,b. Similarly, only the RMSE curve of the polarization auxiliary angle is plotted in Figure 4c,d.
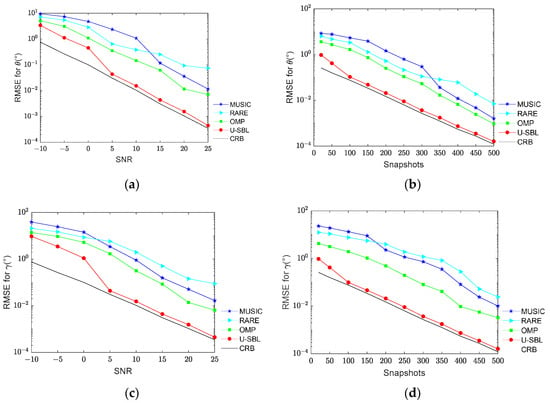
Figure 4.
The RMSE of DOA and polarization versus SNR and snapshots. (a) The RMSE of DOA estimation versus SNR. (b) The RMSE of DOA estimation versus snapshots. (c) The RMSE of polarization estimation versus SNR. (d) The RMSE of polarization estimation versus snapshots.
As seen in Figure 4a,c, the four algorithms’ RMSE of DOA and polarization estimation are improved with the increase in SNR. However, the RARE algorithm is not able to achieve global optimization, resulting in limited accuracy and the lowest estimation accuracy at high SNR. Although the MUSIC algorithm has higher estimation accuracy at higher SNRs, it lacks accuracy at lower SNRs. The OPM algorithm deals with a sparse signal matrix, and although the signal components are reconstructed, the UAV group vector array is subject to strong interference, resulting in limited estimation accuracy. In contrast, the proposed U-SBL algorithm has the highest estimation accuracy, which is close to CRB, and the algorithm is robust. As seen in Figure 4b,d, when the snapshots increase, the estimation accuracy of the four algorithms is improved. The MUSIC and OMP algorithms can achieve better results when the number of snapshots is large, but accuracy is not guaranteed when the number of snapshots is smaller. Moreover, the estimation accuracy can be closer to the CRB when the SNR is higher, and the number of snapshots is larger.
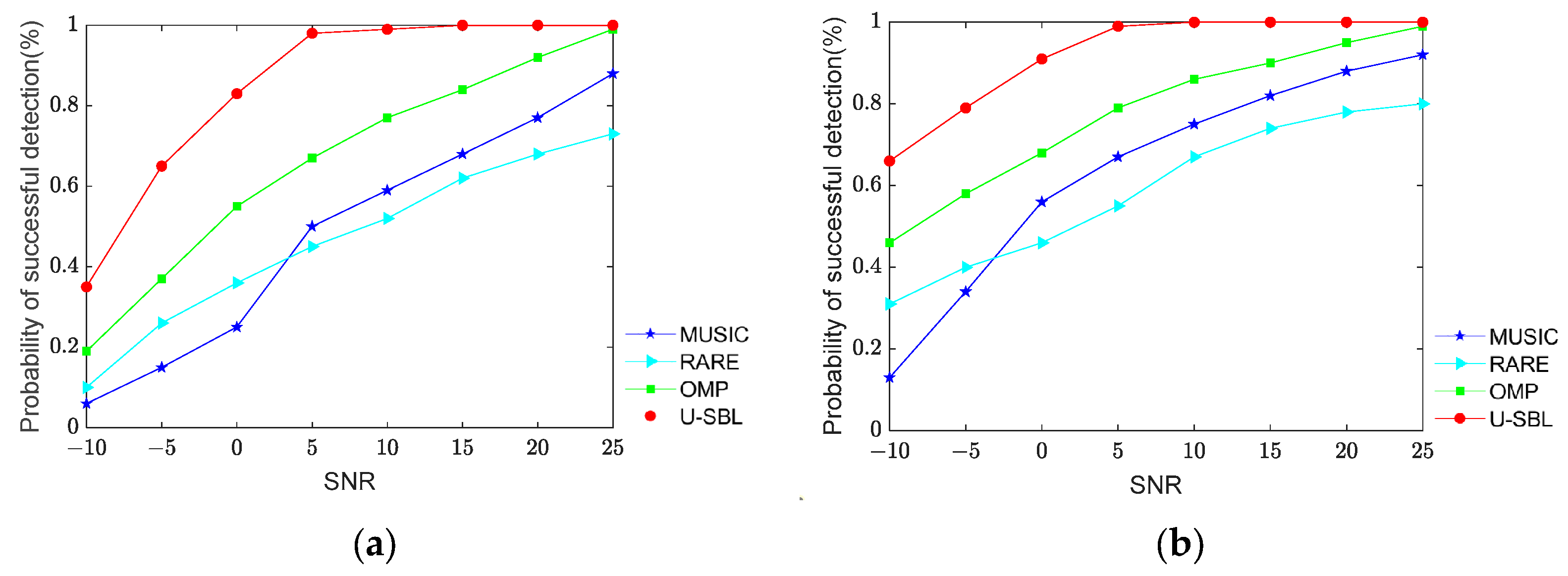
In Figure 5, the resolution of the proposed algorithm is evaluated using the probability of successful detection. In this simulation, the “successful detection” is defined as the error between the estimated value and the true value of each parameter being less than 1°. The number of snapshots is set to be fixed to 100, and the SNR varies from −10 dB to 25 dB with a step size of 5 dB. The four algorithms’ probability of the successful detection of DOA estimation are shown in Figure 5a, and the four algorithms’ probability of the successful detection of polarization estimation are shown in Figure 5b. As seen in Figure 5, the resolution of the four algorithms improves with increasing SNR, but the proposed U-SBL algorithm achieves better resolution than the other three algorithms. Moreover, the proposed method still performs relatively higher resolution even at lower SNR, which further validates the effectiveness of the proposed algorithm.
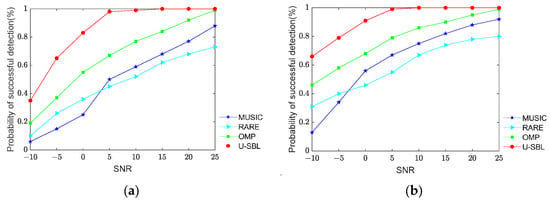
Figure 5.
The resolution of DOA and polarization estimation versus SNR. (a) The resolution of DOA estimation versus SNR. (b) The resolution of polarization estimation versus SNR.
7. Conclusions
In this research paper, we introduce a novel polarization-DOA estimation algorithm tailored for vector arrays within UAV swarms. This algorithm effectively addresses the challenge of robust polarization-DOA parameter estimation in UAV swarm vector arrays, achieving high-precision UAV self-positioning and DOA estimation. The proposed method first acquires the precise coordinate positions of the UAVs via a self-positioning algorithm and then reconstructs the sparse signal using the SBL method. The underlying principle of the algorithm is clear, and the system demonstrates robustness against interference. The simulation results show that the proposed algorithm has a higher probability of successful self-positioning and estimation accuracy, better robustness, and can accurately estimate polarization and DOA parameters compared to other algorithms based on UAV swarm antenna arrays. Massive simulation results have verified that the proposed method can accurately perform DOA and self-positioning estimation. For future works, it is an exciting direction to consider the DOA estimation methods with lower computational complexity. In addition, we will focus on the theoretical analysis of the hyperparameter selection. We will further improve the performance of the proposed method and implement it into a hardware system to apply it to real-world scenarios.
Author Contributions
Conceptualization, X.L. and K.W.; methodology, X.L. and K.W.; software simulation and parameter optimization, X.L. and K.W.; validation, E.W. and Y.T.; writing—original draft preparation, X.L. and K.W.; writing—review and editing, M.D.; supervision, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 61801308; Aeronautical Science Foundation of China, grant number 2020Z017054001; the National Natural Science Foundation of China, grant number 62173237; Xingliao Talent Program Project of Liaoning Province, grant number XLYC1907195; Liaoning Provincial Education Department Facial Project, grant number LJKMZ20220535; Songshan Laboratory Pre-Research Project, grant number YYJC062022017. The Open Fund of the State Key Laboratory of Dynamic Measurement Technology, North University of China
Data Availability Statement
The MATLAB code is available from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Notations
| Notations | Definitions |
| lowercase bold italic letters | vectors |
| capital bold italic letters | matrices |
| inverse operation | |
| transpose operation | |
| conjugate-transpose operation | |
| diagonalization operation | |
| extract the phase angle | |
| trace of the matrix | |
| Hadamard product | |
| Khatri-Rao product | |
| Kronecker product | |
| complex matrix set | |
| the nearest integer to | |
| 2-norm | |
| The minimum eigenvector of a matrix |
References
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Gupta, L.; Jain, R.; Vaszkun, G. Survey of important issues in UAV communication networks. IEEE Commun. Surv. Tutor. 2015, 18, 1123–1152. [Google Scholar]
- Jiang, H.; Zhang, Z.C.; Gui, G. Three-dimensional non-stationary wideband geometry-based UAV channel model for A2G communication environments. IEEE Access 2019, 7, 26116–26122. [Google Scholar] [CrossRef]
- Wang, X.R.; Zhai, W.; Zhang, X.; Wang, X.H.; Amin, M.G. Enhanced Automotive Sensing Assisted by Joint Communication and Cognitive Sparse MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4782–4799. [Google Scholar]
- Huang, H.; Liu, Q.; So, H.C. Low-Rank and Row-Sparse Decomposition for Joint DOA Estimation and Distorted Sensor Detection. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4763–4773. [Google Scholar]
- Xiao, Z.Y.; Xia, P.F.; Xia, X.G. Enabling UAV cellular with millimeter wave communication: Potentials and approaches. IEEE Commun. Mag. 2016, 54, 66–73. [Google Scholar] [CrossRef]
- Lin, X.P.; Zhang, X.F.; He, L. Multiple emitters localization by UAV with nested linear array: System scheme and 2D-DOA estimation algorithm. China Commun. 2020, 17, 117–130. [Google Scholar]
- Shi, B.; Ma, X.; Zhang, W. Complex-valued convolutional neural networks design and its application on UAV DOA estimation in urban environments. J. Commun. Inf. Netw. 2020, 5, 130–137. [Google Scholar] [CrossRef]
- Wang, L.; Huang, Y. UAV-Based Estimation of Direction of Arrival: An Approach Based on Image Processing. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; pp. 1165–1169. [Google Scholar]
- Yang, T.Y.; Maio, A.D.; Zheng, J.B. An adaptive DOA estimation strategy for UAVs detection. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021. [Google Scholar] [CrossRef]
- Murata, S.; Matsuda, T.; Nishimori, K.; Mitsui, T. Performance Evaluation of Wave Source Localization Method Using UAVs Based on the Maximum Likelihood Estimation. In Proceedings of the 2020 International Symposium on Antennas and Propagation (ISAP), Osaka, Japan, 25–28 January 2021; pp. 135–136. [Google Scholar]
- Marzetta, T.L. Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Boccardi, F.; Heath, R.W.; Lozano, A. Five disruptive technology directions for 5G. IEEE Commun. Mag. 2014, 52, 74–80. [Google Scholar]
- Chen, Y.W.; Jie, Q.J.; Zhang, Y.Q.; Shu, F.; Zhan, X.C.; Yan, S.H.; Cai, W.L. Two Rapid Power Iterative DOA Estimators for UAV Emitter Using Massive/Ultra-Massive Receive Array. Drones 2023, 7, 361. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, W.; Hong, X.; Wang, Y. A Beamspace Multi-sources DOA Estimation Method for UAV Cluster Systems. In Proceedings of the 2022 16th IEEE International Conference on Signal Processing (ICSP), Beijing, China, 21–24 October 2022; pp. 27–31. [Google Scholar]
- Zhu, B.; Hayashi, K.; Li, B.; Li, J.; Zhang, X. A Frequency Domain Direction of Arrival Estimation Algorithm for UAV Remote-control Signal. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–5. [Google Scholar]
- Kim, J. Performance analysis of DOA estimation in the presence of mutual coupling for UAV. In Proceedings of the 2016 IEEE International Conference on Network Infrastructure and Digital Content (IC-NIDC), Beijing, China, 23–25 September 2016; pp. 254–256. [Google Scholar]
- Nehorai, A.; Paldi, E. Vector-sensor array processing for electromagnetic source localization. IEEE Trans. Signal Process. 1994, 42, 376–398. [Google Scholar] [CrossRef]
- Donelli, M.; Viani, F.; Rocca, P. An innovative multiresolution approach for DOA estimation based on a support vector classification. IEEE Trans. Antennas Propag. 2009, 57, 2279–2292. [Google Scholar] [CrossRef]
- Wen, F.Q.; Gui, G.; Gacanin, H. Compressive sampling framework for 2D-DOA and polarization estimation in mmWave polarized massive MIMO systems. IEEE Trans. Wirel. Commun. 2023, 22, 3071–3083. [Google Scholar] [CrossRef]
- Bohra, P.; Unser, M. Continuous-Domain Signal Reconstruction Using Lp-Norm Regularization. IEEE Trans. Signal Process. 2020, 68, 4543–4554. [Google Scholar]
- Zuo, M.; Xie, S.; Zhang, X.; Yang, M. DOA estimation based on weighted l1-norm sparse representation for low SNR scenarios. Sensors 2021, 21, 4614. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, W.P.; Yan, J. A High-Resolution DOA Estimation Method With a Family of Nonconvex Penalties. IEEE Trans. Veh. Technol. 2018, 67, 4925–4938. [Google Scholar] [CrossRef]
- Yin, J.; Chen, T. Direction-of-arrival estimation using a sparse representation of array covariance vectors. IEEE Trans. Signal Process. 2011, 59, 4489–4493. [Google Scholar] [CrossRef]
- Bai, H.; Darte, M.F.; Janaswamy, R. Direction of arrival estimation for complex sources through ℓ1-norm sparse Bayesian learning. IEEE Signal Process. Lett. 2019, 26, 765–769. [Google Scholar] [CrossRef]
- Leite, W.S.; de Lamare, R.C. List-based OMP and an enhanced model for DOA estimation with nonuniform arrays. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4457–4464. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Yuan, Y.; Jiang, T. Low-Complexity DOA Estimation via OMP and Majorization-Minimization. In Proceedings of the 2018 IEEE Asia-Pacific Conference on Antennas and Propagation (APCAP), Auckland, New Zealand, 5–8 August 2018; pp. 18–19. [Google Scholar]
- Fu, M.; Zheng, Z.; Wang, W. 2-D DOA estimation for nested conformal arrays via sparse reconstruction. IEEE Commun. Lett. 2020, 25, 980–984. [Google Scholar] [CrossRef]
- Uemura, S.; Nishimori, K.; Taniguchi, R.; Inomata, M.; Kitao, K.; Imai, T.; Suyama, S.; Ishikawa, H.; Oda, Y. Direction-of-arrival estimation with circular array using compressed sensing in 20 GHz band. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 703–707. [Google Scholar] [CrossRef]
- Chen, P.; Cao, Z.; Chen, Z.; Wang, X. Off-grid DOA estimation using sparse Bayesian learning in MIMO radar with unknown mutual coupling. IEEE Trans. Signal Process. 2018, 67, 208–220. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction of arrival estimation using sparse Bayesian inference. IEEE Trans. Signal Process. 2012, 61, 38–43. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, H. DOA, power and polarization angle estimation using sparse signal reconstruction with a COLD array. AEU-Int. J. Electron. Commun. 2015, 69, 1606–1612. [Google Scholar] [CrossRef]
- Liu, Z. DOA and polarization estimation via signal reconstruction with linear polarization-sensitive arrays. Chin. J. Aeronaut. 2015, 28, 1718–1724. [Google Scholar] [CrossRef]
- Zhao, P.; Hu, G.; Zhou, H. An Off-grid block-sparse Bayesian method for direction of arrival and polarization estimation. Circuits Syst. Signal Process. 2020, 39, 4378–4398. [Google Scholar] [CrossRef]
- Li, B.; Bai, W.; Zheng, G.; He, X.; Xue, B.; Zhang, M. BSBL-based DOA and polarization estimation with linear spatially separated polarization sensitive array. Wirel. Pers. Commun. 2019, 109, 2051–2065. [Google Scholar] [CrossRef]
- Parkinson, B.; Spilker, J. Global Positioning System: Theory Application; American Institute of Astronautics and Aeronautics: Reston, VA, USA, 1996. [Google Scholar]
- Drawil, N.M.; Amar, H.M.; Basir, O.A. GPS localization accuracy classification: A context-based approach. IEEE Trans. Intell. Transp. Syst. 2012, 14, 262–273. [Google Scholar] [CrossRef]
- Wen, F.Q.; Shi, J.P.; Gui, G. 3-D positioning method for anonymous UAV based on bistatic polarized MIMO radar. IEEE Internet Things J. 2023, 10, 815–827. [Google Scholar] [CrossRef]
- Fan, D.; Gao, F.F.; Ai, B. Channel estimation and self-positioning for UAV swarm. IEEE Trans. Commun. 2019, 67, 7994–8007. [Google Scholar] [CrossRef]
- Freddy, Y.P.; Feng; Rihan, M.; Huang, L. Positional Perturbations Analysis for Micro-UAV Array With Relative Position-Based Formation. IEEE Commun. Lett. 2021, 25, 2918–2922. [Google Scholar]
- See, C.M.S.; Gershman, A.B. Direction-of-arrival estimation in partly calibrated subarray-based sensor arrays. IEEE Trans. Signal Process. 2004, 52, 329–338. [Google Scholar] [CrossRef]
- Hua, Y.B. A pencil-MUSIC algorithm for finding two-dimensional angles and polarizations using crossed dipoles. IEEE Trans. Antennas Propag. 1993, 41, 370–376. [Google Scholar] [CrossRef]
- Elbir, A.M.; Chatzinotas, S. BSA-OMP: Beam-Split-Aware Orthogonal Matching Pursuit for THz Channel Estimation. IEEE Wirel. Commun. Lett. 2023, 12, 738–742. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).