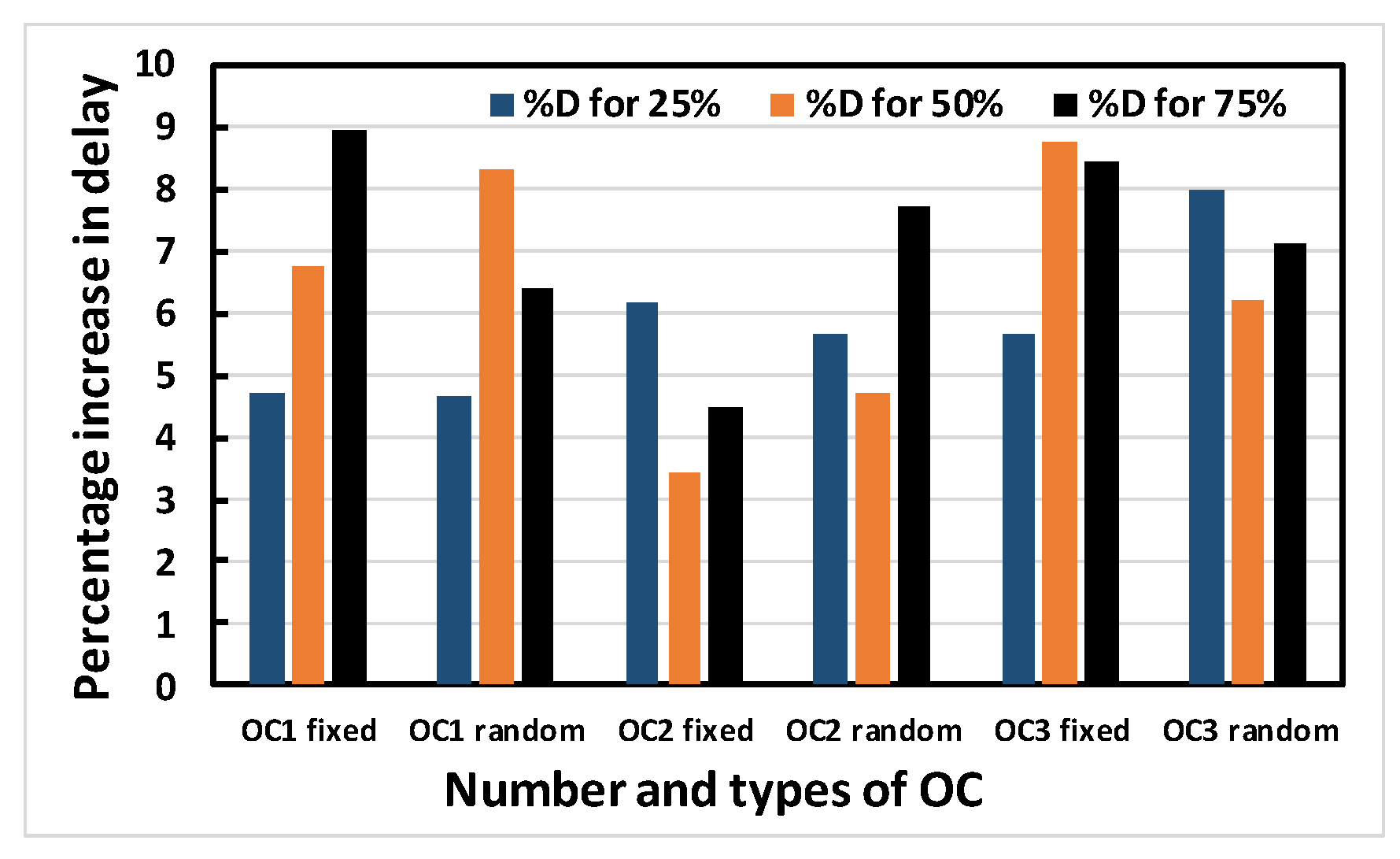Abstract
This paper proposes a new framework for post-synthesis obfuscation of digital circuits using a mixture of cells combined with an Anti-SAT block. Furthermore, a novel integrated framework has been established wherein obfuscation, along with Anti-SAT and validation of the benchmarks, progress through MATLAB®, Python, Cadence RTL Encounter® and Cadence LEC® to implement the proposed methodology. Area, delay, leakage power and total power are adopted as elements of the evaluation matrix. These parameters are compared between the original circuit, the circuit after obfuscation, the circuit after integration with Anti-SAT and the circuit after implementation of the proposed method of multiple-cell obfuscation with Anti-SAT. The probability of breaking a circuit is taken as the security criterion. It is mathematically proven that as the number of types of obfuscated cells used increases, then the probability of breaking the circuit decreases. The results obtained accord with the mathematical proof. The framework minimizes the delay by inserting obfuscation cells (OCs) in the non-critical paths, strengthens the security by using several types of OCs and allows the user to select a design based on justified area, leakage power and total power. However, against a Boolean SATisfiability (SAT) attack, obfuscation with multiple cells is not a sufficient defense. An Anti-SAT block performs better than obfuscation but has its own limitations. Thus, use of an Anti-SAT block in combination with multiple-cell obfuscation is proposed and implemented, giving better results against an efficient SAT attack. The number of iterations, as well as runtime to obtain the correct keys, increase significantly for the Anti-SAT block combined with multiple-cell obfuscation compared to the Anti-SAT or obfuscation block alone.
1. Introduction
Modern Integrated Circuit (IC) technology faces threats from overbuilding, IC and Intellectual Property (IP) piracy and reverse engineering as part of an effort to reduce cost in advanced technology nodes by shifting to a fabless business model [1] and transferring the final assembly to an offshore merchant fabrication house. The cost of such fabless production exceeds $5 billion [2,3]. As the technology becomes more sophisticated, the system becomes larger and detecting hidden hardware Trojans become more difficult [4,5,6,7]. As reported in [8,9], the cost of counterfeiting and piracy for G20 nations might have recently exceeded US $1.7 trillion, causing elimination of 2.5 million jobs. The estimated loss due to IP infringement in the semiconductor industry is $4 billion annually [10,11]. Therefore, a topic of great interest in contemporary academic research and industrial production is the development of a low-cost technique that will enable IC designers to shield their integrated IC and IP from rogue systems on integrators (SoC) and fabrication houses [12]. However, very few countries, among them USA and Japan, follow standard protocols to prevent IC and IP piracy [13,14,15,16,17].
One technique to prevent counterfeiting in digital circuits is to functionally encrypt the circuit using key-based logic obfuscation [8,11,12,13,14,18,19,20,21,22,23,24]. However, corrupt SoC vendors and manufacturers continue to find new ways to determine the keys of an obfuscated circuit. Thus, IC designers face challenges in making obfuscation hard for their adversaries to decode. R. S. Chakraborty and S. Bhunia [25] implemented Finite State Machine (FSM)- and XOR-based obfuscation, wherein the nodes having larger fan-in and fan-out cones are identified first, and these nodes are then altered. The problem with this technique is that critical paths may also be modified, worsening the delay. The security strength of circuits using FSM to create invalid states and obscure the correct outputs was not measured by comparing the corrupt and correct outputs.
J. Zhang [8] proposed obfuscation based on inverter, mux and Physical Unclonable Function (PUF). Although PUF provides unique keys for the chip at low cost, it is prone to damage from changes in surrounding and functional conditions, such as temperature, aging and humidity, necessitating adoption of a robust error-correction scheme [26,27].
Combinational logic encryption by placing XOR/XNOR key gates randomly in the circuit design was proposed by Roy et al. in [20]. Some other authors used XOR- and XNOR-based obfuscation and replaced XOR with XNOR and inverters and XNOR with XOR and inverters to impede identification of the type of the gates and deduction of the keys. However, researchers concluded that randomly inserting XOR/XNOR cannot achieve 50% Hamming distance (HD), leaving the design still exposed to possible attacks [28]. Moreover, functional behavior might be correct in these circuits even when the wrong key is provided [28]. Such randomly placed gates cannot fully prevent attacks on obfuscation. The random keys may be placed on nets where they are easily recognizable or can be placed in a critical data path, thus causing more exposure to information leakage [29].
Fault impact analysis [14] is a development in random placement that can fulfill the requirement of 50% HD but cannot ensure performance around 50% HD for any design, especially for those circuits with large numbers of gates and output bits. If the IC chip has a large number of gates, then the algorithm needs several months to achieve around 50% HD, which is practically impossible, and the performance overhead might be very large. Additionally, integration of the hardware implementation of Rivest-Shamir-Adleman (RSA) with this technique is very expensive and can consume the area of the VIRTEX5–XC5VLX50T device needed to implement such cryptography with a key size of only 32 bits. If PUF is used with this type of obfuscation, then it comes along with the shortcomings already mentioned for PUFs.
Although MUX Insertion Based on Half Output Bits [7] is efficient against various threats, such as IP piracy and counterfeiting, it might be vulnerable to an attacker who can determine the functionality of an IC based on exposed output bits. To ward off experienced attackers, the full MUX insertion technique [7] was proposed. Although inserting MUX at each output bit will obviously maximize the protection of the design and obfuscate points of attack, the power and area overheads will increase significantly. Both half and full MUX insertion approaches are vulnerable to Linear Feedback Shift Register tracking attacks.
In all the above work, only one type of key is used. One contemporary attack technique is Boolean SAT attack. To counter this attack, Anti-SAT block was introduced. One weakness of Anti-SAT block is that if keys are assigned “all 0” or “all 1”, then the guess acts as a successful keyword. Thus, if the attacker starts with a guess of all keys “0” or all “1”, then he has a tremendous advantage and acquires the correct keys in two cycles of iteration.
To address this problem, mixing of XOR and XNOR gates in the inputs of only Anti-SAT block has been proposed in the literature [30]. This approach ensures that the two key vectors in the Anti-SAT block are unequal. However, removal attack can still be employed against the Anti-SAT block.
Although the use of an Anti-SAT block integrated with only one type of obfuscation based on XOR or XNOR gates has been reported in the literature, it has certain limitations. For Anti-SAT with XOR based obfuscation, “all 0” key is a valid key, whereas for XNOR, “all 1” is a valid key. The technique proposed in this paper eliminates the possibility of the attacker trying “all 0” or “all 1” as an initial guess and thus succeeding in breaking the Anti-SAT block with only two tries, as using a mixture of obfuscation cells ensures that a combination including both “0 s” and “1 s” is required to obtain the correct key. Moreover, the Anti-SAT block cannot be easily identified and isolated to facilitate SAT attack on the remaining circuit due to the presence of obfuscation cells combined with Anti-SAT.
In this paper, a design framework is proposed wherein a mix of 1 to 3 types of cells can be used for obfuscation from a suite of 6 cells (AND, OR, XOR, XNOR, NAND and NOR gates-based keys) or more. This paper proposes a method wherein the type of the keys can be 1, 2 or 3, chosen randomly, until the obfuscation cells are completely different. In that case, they are termed “random OCs”. If instead they are chosen from the minimum, average and maximum number of gates, they are termed “fixed Ocs”. The framework also has a provision by which to increase the number of types of cells. Additionally, when the obfuscation cell is not chosen randomly, then the cell may be any one of the maximum, minimum or average cell types used in the circuit under consideration. However, this obfuscation technique is susceptible to SAT attack. As a result, the Anti-SAT technique was developed. This approach has the limitation of being vulnerable to cracking with “all 0” or “all 1” as a valid key word. For this reason, this paper proposes combining this multiple-cell obfuscation technique with Anti-SAT such that “all 0” or “all 1” does not act as valid key. The proposed method has better security performance compared to Anti-SAT with XOR/XNOR base obfuscation (i.e., one type of OC) or obfuscation alone. The security of three techniques—obfuscation, existing Anti-SAT and multiple-cell obfuscation combined with Anti-SAT—are compared in the paper based on the results of simulated key-breaking. The performance overhead of the three schemes is also reported in this paper.
The contributions of the paper are listed below.
- The paper proposes a new framework for post-synthesis obfuscation using a mixture of cells with Anti-SAT block.
- Area, delay, leakage power and total power are compared between the original circuit, the circuit after obfuscation, the circuit after integration of Anti-SAT and the circuit constructed according to the proposed method.
- It is mathematically proven that as the number of types of obfuscated cells used increases, the probability of breaking the circuit decreases.
- The number of iterations and runtime needed to obtain the correct keys increase significantly with the proposed technique.
- The inherent drawback of integrating Anti-SAT with one type of obfuscation cell is also eliminated by combining multiple-cell obfuscation and Anti-SAT block because the trivial solution of an “all 0” or “all 1” key is not viable.
- In this scheme, isolation of the Anti-SAT block is also not possible due to the interconnection of the Anti-SAT block and the obfuscation cells.
The remainder of the paper is organized as follows. Section 2 discusses different threat models for logic locking and the defense scheme adopted in this paper. Section 3 describes the methodology followed in this paper. Section 4 explains the SAT attack simulation. Section 5 presents the results and discussion. Section 6 contains an analysis of security issues. Finally, the Conclusions are given in Section 7.
2. Threat Models and Defense Strategy
In the recent literature [31], there are three threat models for logic locking. Each model assumes different capabilities on the part of the attacker. Therefore, the defence objectives for different threat models also vary.
Threat model 1 assumes that the attacker has only oracle access, i.e., a working chip. Therefore, the attacker can vary inputs and infer the possible values of keys from input-output relationships. The attacker can be the test facility or end user.
Threat model 2 assumes that the attacker attacker has access to the locked netlist but no oracle access. He can try either to isolate the locking circuit or to guess the key values from the structure. He can simulate the netlist and also try all the key values using brute force and choose the most likely key values from the input-output relationship of the simulated netlist. The attacker can be an untrusted fab who has access to GDSII files and can use reverse engineering to obtain the locked netlist. Alternatively, he can be an end user who can reverse-engineer an IC to obtain the locked netlist. This model is of practical importance in the cases in which the chip is used by few clients and the IC is not available in the market [32].
Threat model 3 assumes that the attacker has both oracle access and a locked netlist. In that case, he can apply different inputs and then compare the outputs with those of a simulated netlist to eliminate incorrect key values and obtain the correct key. He can use a SAT-based oracle-guided attack to remove multiple keys in a single run and enhance the effectiveness of the attack.
It is assumed that the keys are stored in tamper-proof memory and that the attacker has no access to the memory. It is also assumed that optical probing is not available or that the available package-level defence thwarts it or that anti-tamper provisions erase the keys in the event that optical probing is used [32].
In this paper, it is assumed that threat model 3 is active. The proposed defense, a combination of multiple-cell obfuscation and Anti-SAT block, works against this model, supposing that the attacker uses a SAT algorithm. The defense effectively protects the IC from an SoC integrator, foundry, test facility and end users whoever can obtain the locked netlist together with a working chip. This approach will protect the IC from reverse engineering, overproduction, cloning and Trojan insertion.
3. Methodology
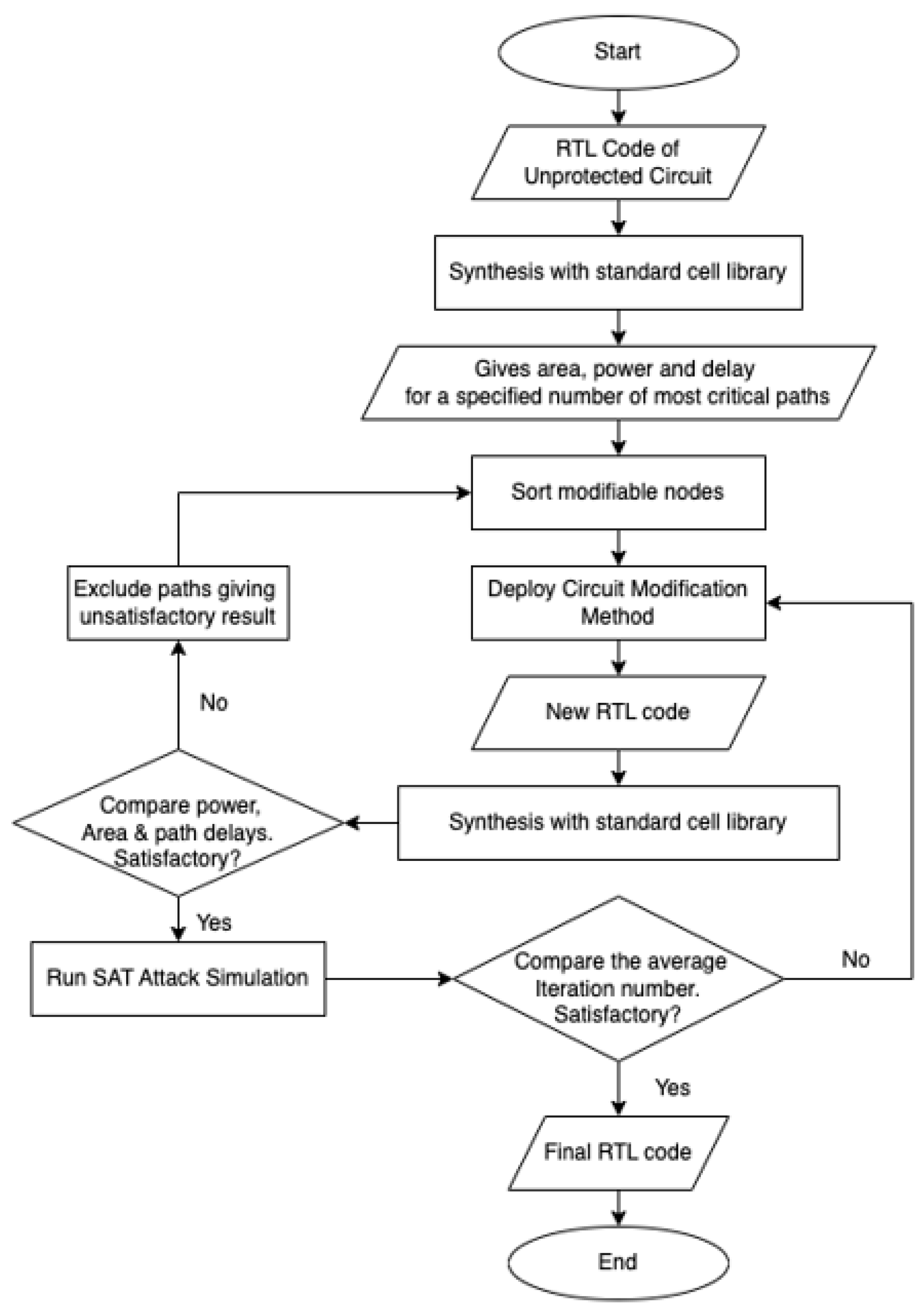
The methodology shown in Figure 1 starts by taking Register Transfer Level (RTL) code of the design as input and synthesizing it with a standard cell library. In this paper, ISCAS 89 [33] original benchmark circuits are taken as examples of input circuits. Then, a tcl script is run to calculate the area and power and generate a timing report for a specified number of the most critical paths of the synthesized circuit. The synthesized netlist and the timing report are pre-processed to find the modifiable nodes. To avoid the pitfalls of random insertion, the modifiable nodes are selected from the nodes that are not (a) input pins or (b) output pins and (c) do not fall in worst critical paths so that performance is not compromised further. The number of inputs and outputs is usually small. Thus, if OCs are placed at the input and output nodes, they are easily recognized by an attacker. Additionally, they often fall in the critical paths, so they are excluded from the list of modifiable nodes as well. OCs can be inserted at the modifiable nodes. The types of gates to be used as OCs (randomly or in a fixed way) are determined, if necessary, from the count of the cells used in the circuit. For this reason, a MATLAB® script was written to count the number of gates in the synthesized netlist using Cadence RTL Encounter® in a 45 nm Nangate typical cell library. Those gates (except DFF, MUX, AOI22 and INV) were then used as the key gates, depending on the count in the case of fixed OC. For random OC, the count of gates is not necessary and the OC is chosen randomly. Obfuscation of different ISCAS 89 benchmark circuits is accomplished using one obfuscation cell (either chosen from average of the cells and henceforth termed OC1 fixed, or randomly chosen and henceforth termed OC1 random), two obfuscation cells (either chosen from the maximum and minimum of the cells and henceforth termed OC2 fixed, or randomly chosen and henceforth termed OC2 random) or three obfuscation cells (chosen from maximum, minimum and average of the cells and henceforth termed OC3 fixed, or randomly chosen and henceforth termed OC3 random).
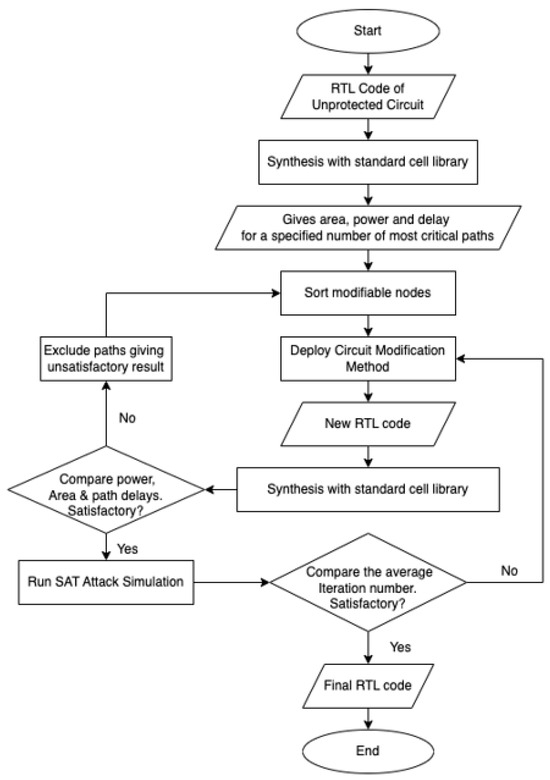
Figure 1.
Flowchart of the proposed framework for protecting hardware intellectual property.
The OCs are inserted at a certain percentage of the modifiable nodes. Care is taken to ensure that the delay is minimally affected because the most critical paths are not affected. The obfuscation cells were inserted in noncritical paths which so that delays were not exacerbated. The output pins of the newly inserted gates are connected to the inputs of the next gate in the path, and a new netlist is created. The keys are stored according to the OC type Cadence LEC® is used within the framework to verify that the new netlist and the original golden circuit are identified as equivalent when correct keys are provided and non-equivalent when incorrect keys are given. The obfuscation cells were inserted in the circuits, and then validation was performed with correct keys using Cadence LEC®. Initially, this method was tried with small circuits. It was then extended successfully to medium-to-large circuits without any issues. Hence, the proposed methodology is scalable to large circuits.
The present work considered only keys based on AND, OR, XOR, XNOR, NAND and NOR gates. With reverse engineering (RE) by image processing, the keys can be inferred from the types of the obfuscation cells. To block this approach, XOR can be replaced by XNOR followed by inverters and XNOR can be replaced by XOR followed by inverters. However, this method incurs high area and power penalties owing to the logic redesign according to De Morgan’s law.
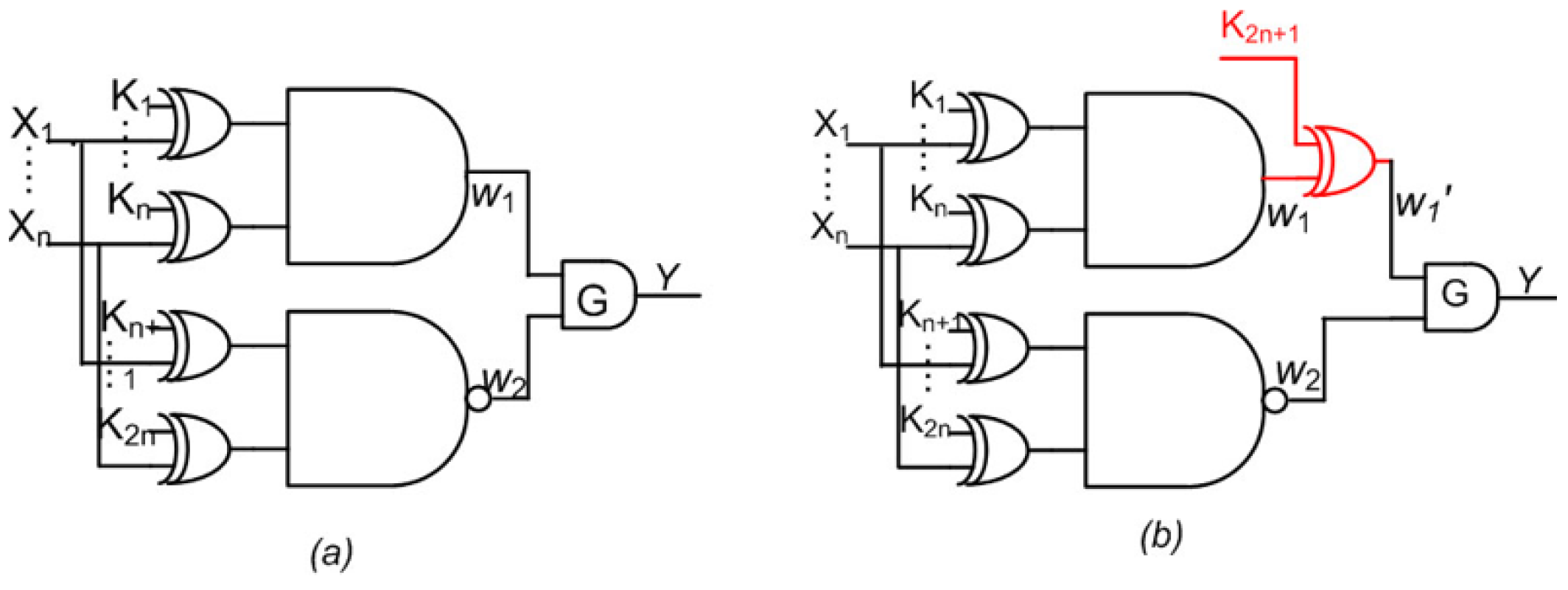
SAT attack can identify the secret keys of the obfuscation cell with minimal effort and iterations. To make it difficult to obtain the keys via SAT attack, an Anti-SAT block is introduced. The anti-SAT block, however, has a serious flaw. For an anti-SAT block, there are (2k) correct keys where the total number of keys is (22k) [19]. The correct key is obtained when the two subsets of keys fed into the Anti-SAT block are the same. Among these correct keys, there are 2 keys which contain either “1” in all bits or “0” in all bits. To overcome this shortcoming, a small number of key bits of the anti-SAT block are selected normally and applied to the obfuscation block. Thus, these bits of anti-SAT block are fixed at either “1” or “0”, which essentially reduces the number of correct key bits by small amount. In this system, an attacker cannot try “all 1” or “all 0” as a key. A SAT attack is usually able to eliminate a large number of incorrect keys with one input combination when obfuscation is used alone. However, when obfuscation with multiple cells is integrated with Anti-SAT block, the security of the circuit improves by a large margin. Figure 2a illustrates the method incorporating Anti-SAT block, whereas Figure 2b shows this block combined with only one type of OC (i.e., XOR in this case).
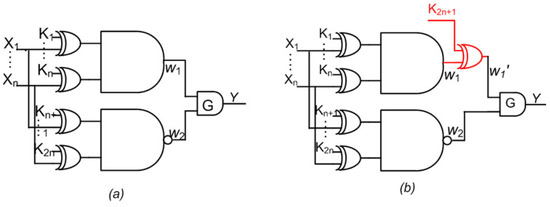
Figure 2.
(a). Anti-SAT and (b). Existing Anti-SAT + Obfuscation with only one type of key gate.
The final netlists are re-synthesized in an RTL compiler to further obfuscate the logic and to calculate area, power and timing overheads. Security indices are calculated using MATLAB®. It is mathematically proven that security increases when a variety of OCs are used in the same circuit. Python code is run to experimentally obtain the number of iterations and the simulation time required to break the secret key. It is observed that both the number of iterations and the simulation time to find the secret keys increase when Anti-SAT block is used in combination with multiple-cell obfuscation compared to Anti-SAT block or obfuscation alone. Moreover, as mentioned earlier, the “all 0” or “all 1” key does not work for this combination, in contrast to Anti-SAT block with only one type of obfuscation cell. Because the obfuscation cells are intermingled with Anti-SAT, the Anti-SAT block cannot be isolated either. The user can deploy the framework and obtain sets of circuits as solutions, each having different values for area, delay, leakage power, power and security. The user can choose to optimize one of these options. For example, if security is to be enhanced, then area, delay, leakage power and power have to be compromised. The user can choose the best option for their requirements and specifications. The algorithm ends by choosing the most suitable option from the design framework. Additionally, functional and structural obfuscation may be added to protect the circuit from removal and SPS attacks.
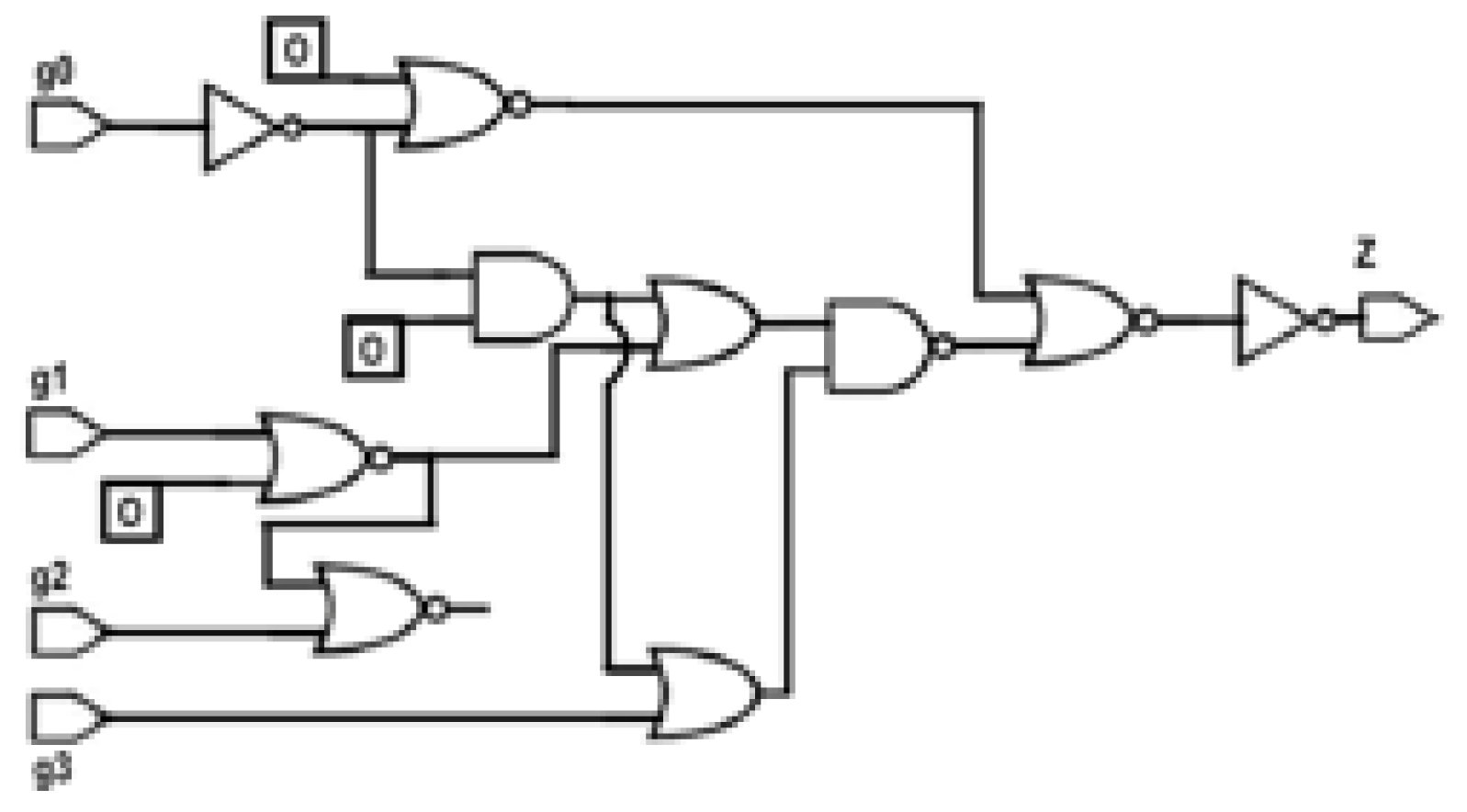
Converting a sequential circuit to a combinational circuit: The proposed algorithm is applicable to a combinational circuit only. Thus, to ensure that this algorithm can be applied to sequential circuit, the sequential circuits are converted to combinational circuits. This conversion involves removing the flip-flops and setting the output nodes of the flip-flops to a 0 or a 1, assuming similar initial values. Similarly, if there is any feedback, the feedback path can be broken and an initial value of 0 or 1 can be inserted at the input node of the feedback. In this paper, all such initial values are forced to 0. This approach is illustrated in Figure 3 and Figure 4 for an s27 circuit. Figure 3 shows the original s27 circuit, which is a sequential circuit. In Figure 4, the original s27 circuit is converted to a combinational circuit wherein all of the feedback paths, including the flip-flops, are deleted. The initial values of the input nodes of the feedback are forced to 0, as shown by the numbers in the boxes in Figure 4.
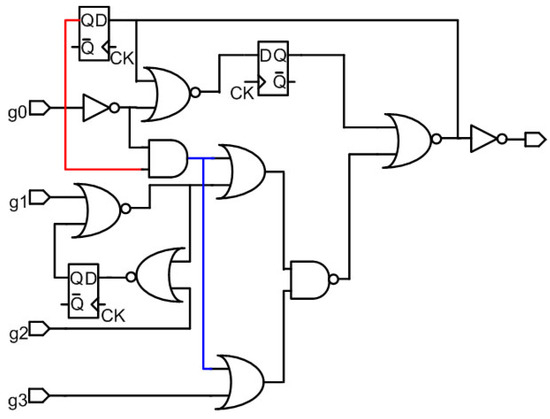
Figure 3.
Original s27 circuit.
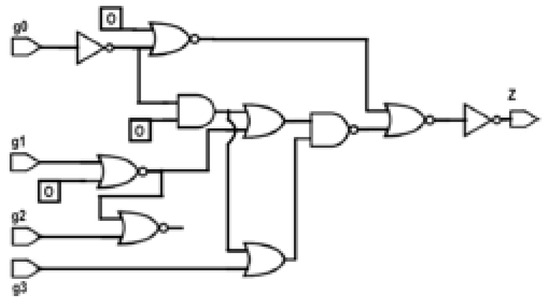
Figure 4.
s27 circuit converted to a combinational circuit.
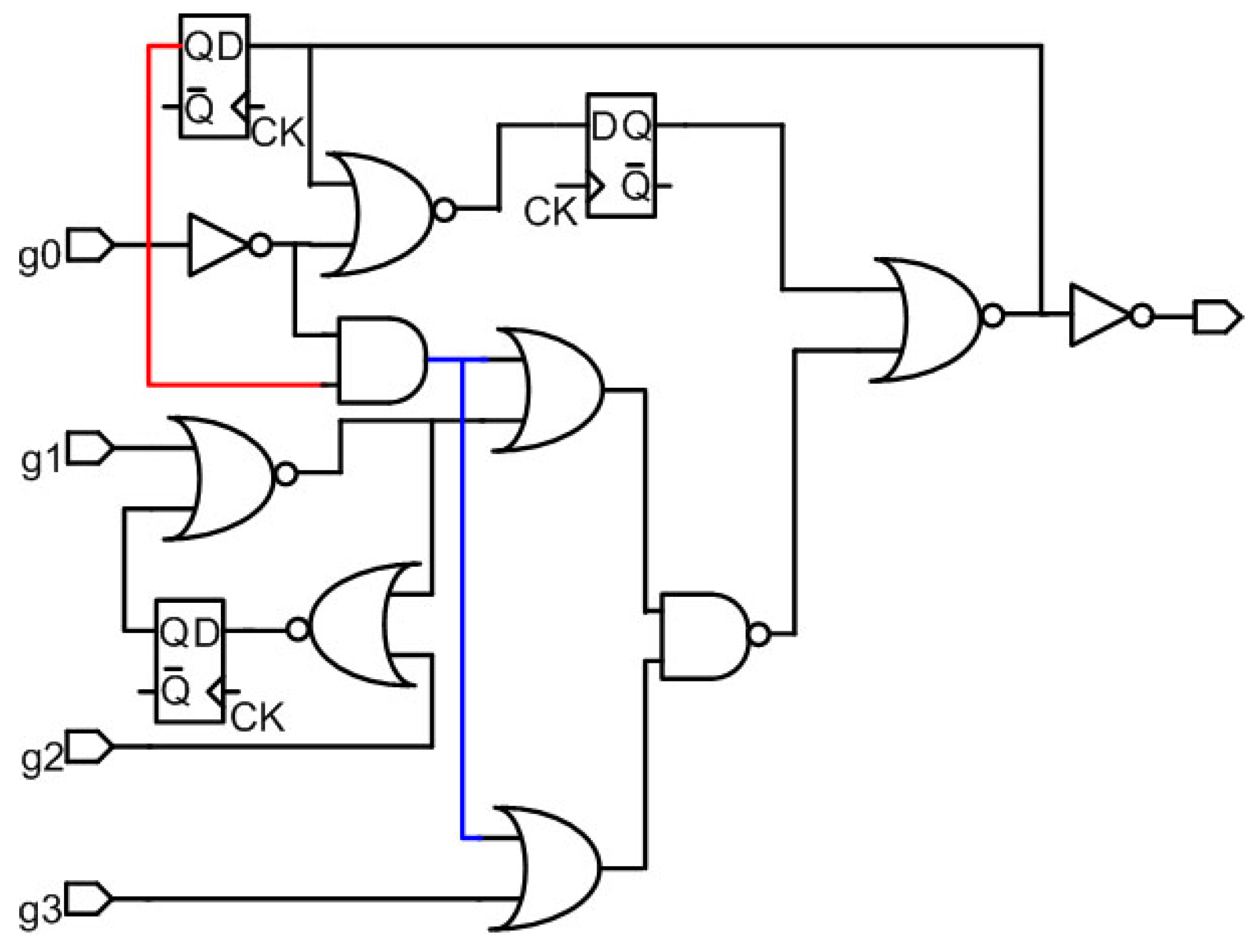
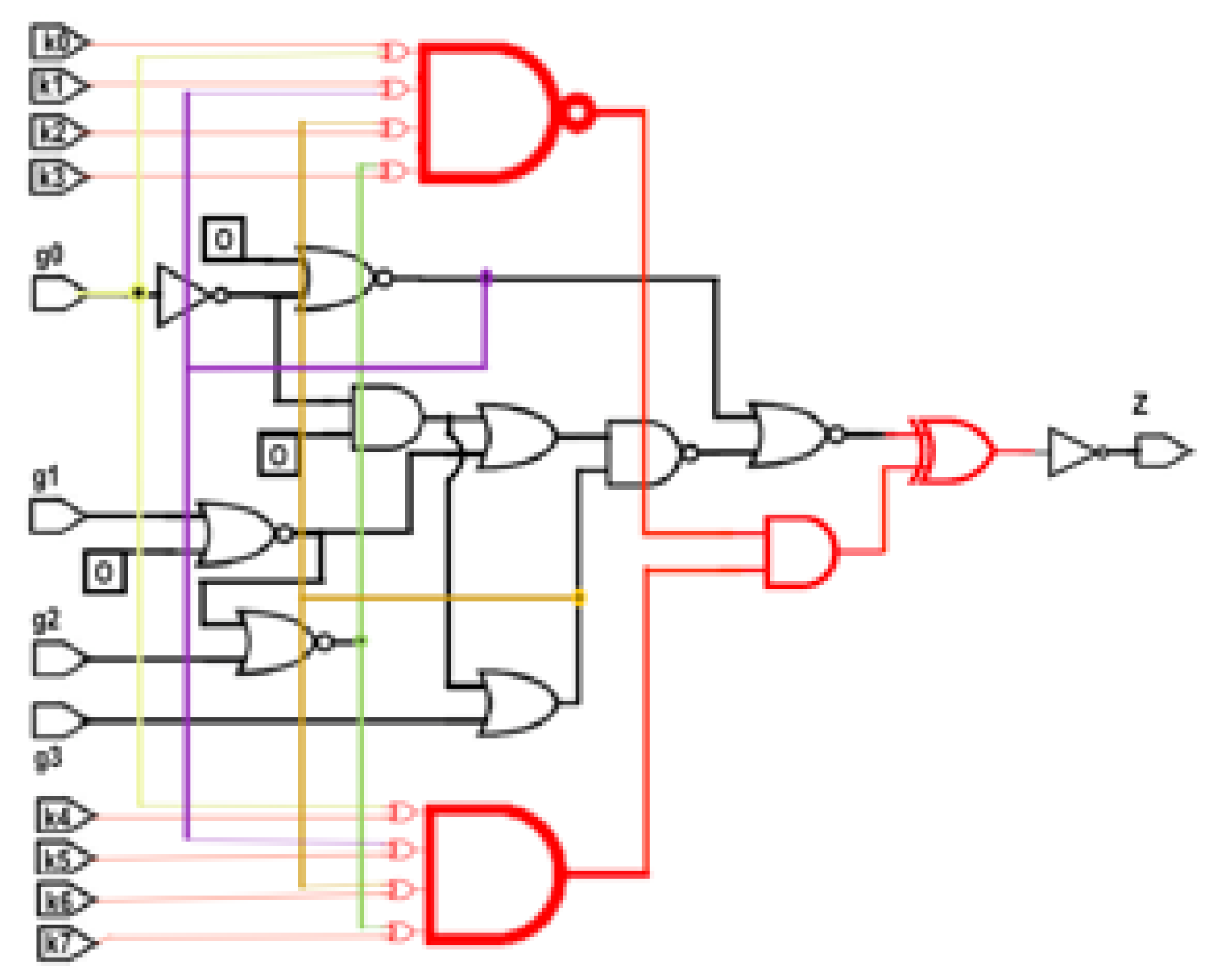
Anti-SAT block implemented in s27 benchmark circuit: Figure 2a shows an anti-SAT block and Figure 5 shows this block integrated with s27 circuit. One of the main shortcomings of the Anti-SAT block shown in Figure 5 is that it can be isolated and removed from the circuit by identifying the complementary signals. Another disadvantage is that if k0k1k2k3 = k4k5k6k7, then it is a correct key vector. Thus, [k0k1k2k3k4k5k6k7] = [00000000] or [11111111] are both correct keywords. This problem can be solved by randomly changing some of the XOR gates into XNOR gates, as reported in [30]. However, the Anti-SAT block can still be identified and isolated easily.
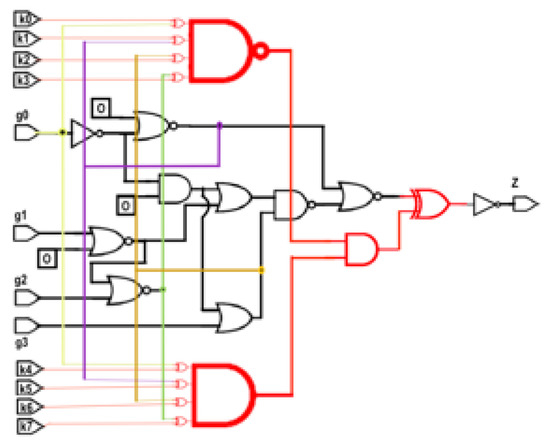
Figure 5.
Anti-SAT implemented in an s27 circuit.
Existing System of Anti-SAT + Obfuscation with only one type of key gate: Figure 2b shows an existing system of Anti-SAT integrated with Obfuscation using XOR gates only fed by K2n+1. This type of Anti-SAT together with only one type of Obfuscation with XOR gates was implemented in [19]. The functional obfuscation hinders the identification of complementary gates and easy isolation of the Anti-SAT block. However, the other disadvantage of Anti-SAT block still exists. Thus, [K1K2 …KnKn+1Kn+2… K2nK2n+1 K2n+2…] = [00…000…000…] i.e., “all 0”, is a valid key vector. Similarly, if the functional obfuscation is done using only XNOR gates, then [K1K2 …KnKn+1Kn+2… K2nK2n+1 K2n+2…] = [11…111…111…] i.e., “all 1”, becomes a valid key vector. Thus, if the attacker tries an “all 0” or “all 1” key vector in this type of system (i.e., Anti-SAT and obfuscation with only one type of key gate), then he succeeds with only two trials. This possibility gives him a tremendous advantage.
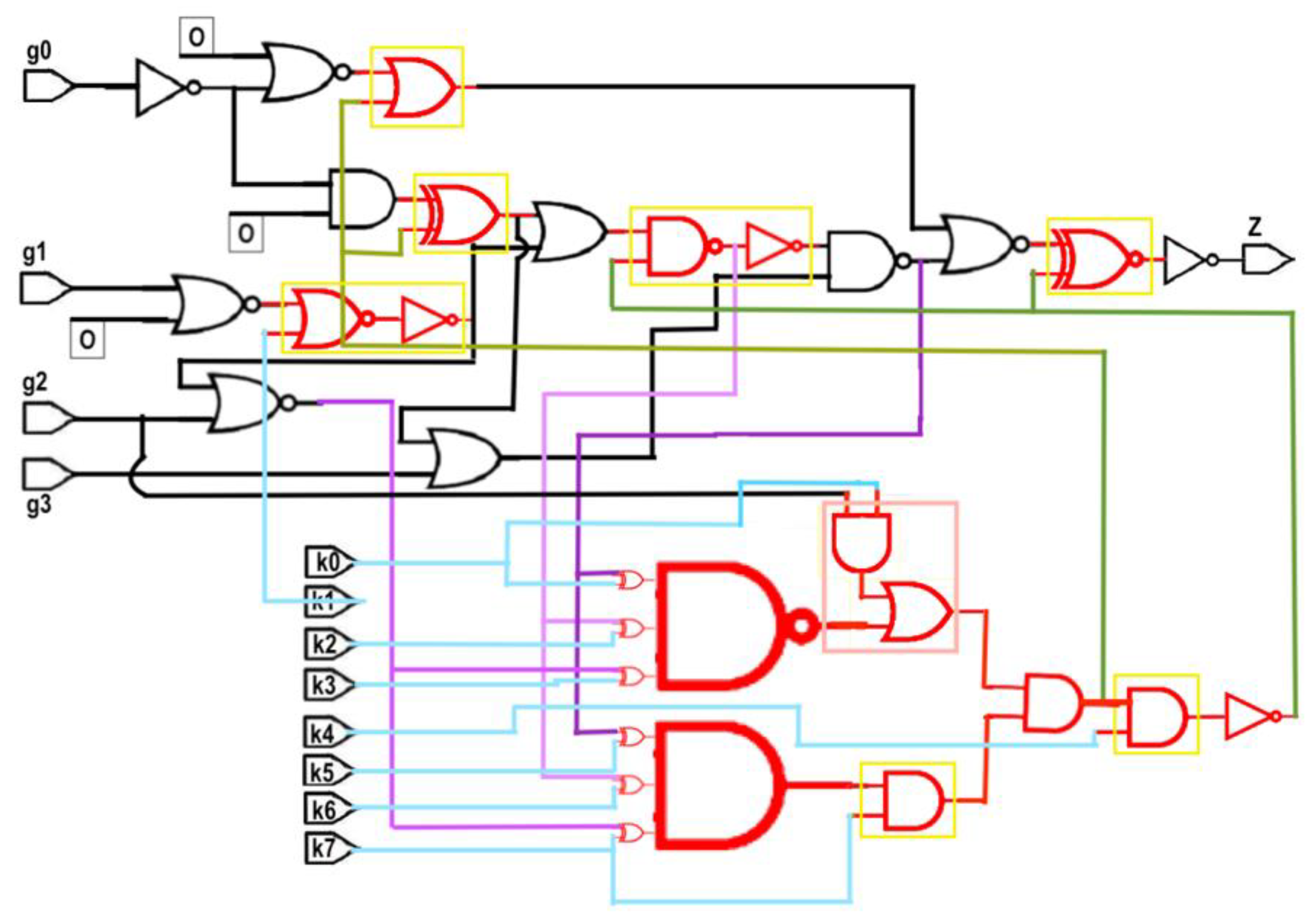
Proposed System of Anti-SAT + Obfuscation with multiple types of key gates: Figure 6 shows the proposed system: Anti-SAT integrated with Obfuscation with multiple types of key gates, implemented in an s27 benchmark circuit converted to a combinational circuit, as described above. The parts shown in red only are the components of the Anti-SAT block, and the red parts in yellow boxes are the portions of the proposed obfuscation cells. The black lines are the input and output lines in the original benchmark circuit whereas the light blue and magenta lines are the inputs to the Anti-SAT block. In this system, [k0k1k2k3k4k5k6k7] = [00k2k31k5k61] with [k0k2k3] = [k5k6k7] as per the requirement of the Anti-SAT block, i.e., k3 = k7 = 1, k5 = k0 = 0, k2 = k6. Thus, [k0k1k2k3k4k5k6k7] = [00k2110k61] with k2 = k6 is a valid keyword.
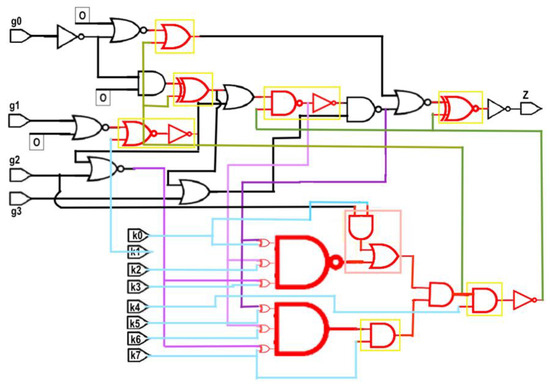
Figure 6.
Proposed system of Anti-SAT + Obfuscation with multiple types of key gates, implemented in an s27 circuit.
Therefore, [k0k1k2k3k4k5k6k7] = [00011001] or [00111011] are the two correct key words. It can be seen that “all 0” or “all 1” keyword does not work as a guess due to the multiple types of obfuscation cell. Moreover, due to the sharing of key bits between the Anti-SAT block and obfuscation cells, some keys of the Anti-SAT block contain both “0” and “1”. The sharing ensures that the Anti-SAT block cannot be isolated from the main circuit, while the existence of both “0” and “1” key bits eliminate the possibility of succeeding with a trial key vector of “all 0” or “all 1”.
4. SAT Attack Simulator
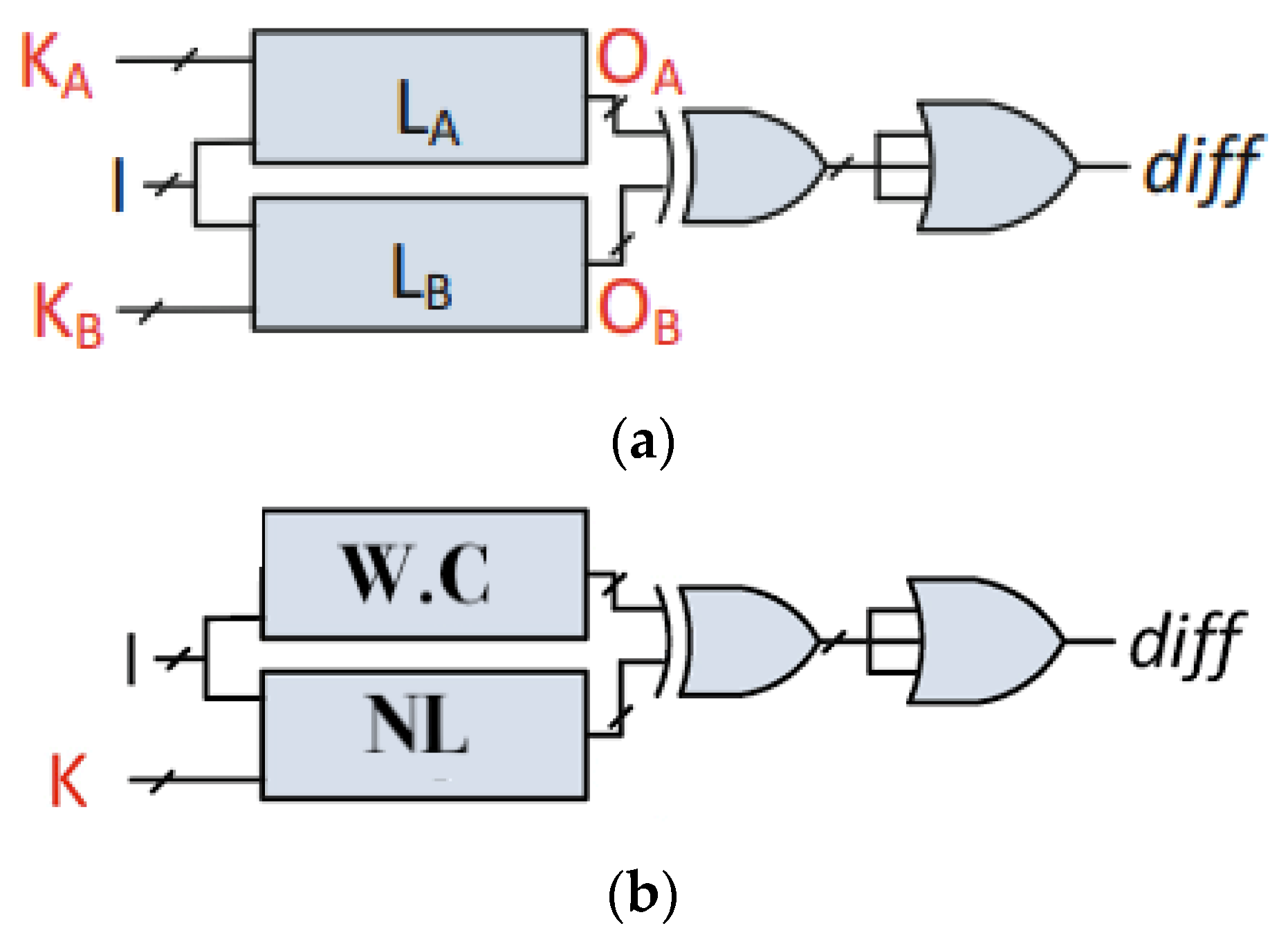
A Boolean satisfiability attack or SAT attack requires a working chip and the netlist [34]. An SAT attack is constructed on the conjunctive normal form (CNF) clauses stored in the SAT solver [35]. This construction uses a miter-like circuit having two copies of the locked netlist. As shown in Figure 7a, the corresponding outputs of the two circuits are XORed and then Ored, which produces the diff signal. With diff = 1, the outputs OA and OB for the two copies are different for the two key values KA and KB and an input pattern I.
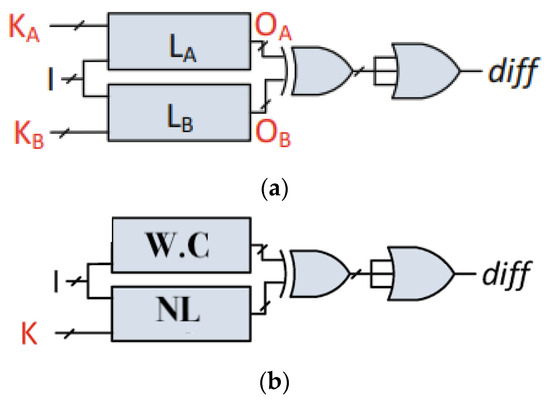
Figure 7.
(a). SAT Attack Circuit Diagram. (b). SAT Attack Circuit Diagram [34].
As shown in Figure 7b, if I is applied to the working chip (W. C) and the netlist (NL) and then KA produces diff = 0 as in Figure 7b, then KB is discarded and KA is kept as a probable key vector. The process is repeated with a new I, as in Figure 7a, until no more key vectors can be discarded.
This method provides certainty of getting the correct key by the end of the simulation. In the paper, the SAT Attack Simulator is implemented in Python. Here, this simulation has an extra step. If no elimination occurs for any input, then it checks the first keyword of the keyword vector. If the first keyword satisfies the Boolean setup for all input combinations, then it is a correct keyword. This step reduces the number of iterations and stops the iteration effectively if there are multiple correct keys, which is a feature of the Anti-SAT block [19].
To illustrate the whole process, a circuit with the Anti-SAT block with 3 bits in input and 4 bits in the key is chosen. In Table 1, the result of the SAT attack is shown on a circuit that is protected by the Anti-SAT block only.

Table 1.
Illustration of the output diff in Figure 7b as SAT attack simulation proceeds on a 3-input and 4-keybit circuit, as done in this paper.
Before the simulation starts, the synthesized Verilog code is converted to a graph in Python, which is used in the simulation. At the beginning of the simulation, an input combination “101” is chosen randomly from the input combination vector. The input combination is removed from the input vector after the simulation using that input. During the simulation, the key that returns “1” in the “diff” in Figure 7b is removed from the key vector. In this case, K4, K6 and K7 are removed, so these keys will not be checked again. Then, the next input combination is also chosen randomly. To show the extra step of this simulation, here, “100” is considered, and there is no elimination of the key. Thus, the program calls the key satisfiability step to check whether the first key is the correct key or not. If the result for all diff as “0”, then it is the correct key. In this case, it is the correct key, and the program stops and returns the first key (“000”) as a correct key. Thus, the total number of iterations required by the proposed SAT attack is (16 + 13 + 6) or 35. If the attack attempted to eliminate all the incorrect keys, it would need a minimum of (16 + 13 + 10 + 7) or 46 iterations. Clearly, the simulation algorithm implemented in the paper is thus more efficient than the conventional SAT attack for this type of data. The pseudo-algorithm of the SAT simulator is provided below in Algorithm 1.
| Algorithm 1 Pseudo-algorithm of the SAT simulator |
| Input vector: input combinations Key vector: key combinations While input vector is not empty do Input: randomly chosen element from Input vector set Input to the input pin of both circuit graphs Initialize elimination: = 0 For all Key in the Key vector do set Key to the key pin of NL circuit graph diff: (W.C Output bit1 ^ NL Output bit1) | (W.C Output bit2 ^ NL Output bit2) ………. If diff = = 1 then remove Key from Key vector elimination++ end remove Input from Input vector If elimination= = 0 then //Key satisfiability step Key: Key vector [0] set Key to the key pin of NL circuit graph For all Input in the Input vector do set Input to the input pin of both circuit graph diff: (W.C Output bit1 ^ NL Output bit1) | (W.C Output bit2 ^ NL Output bit2) ………. If diff = = 1 then remove Key from Key vector elimination++ break end If elimination == 0 then return Key end return Key vector [0] |
5. Result and Discussion
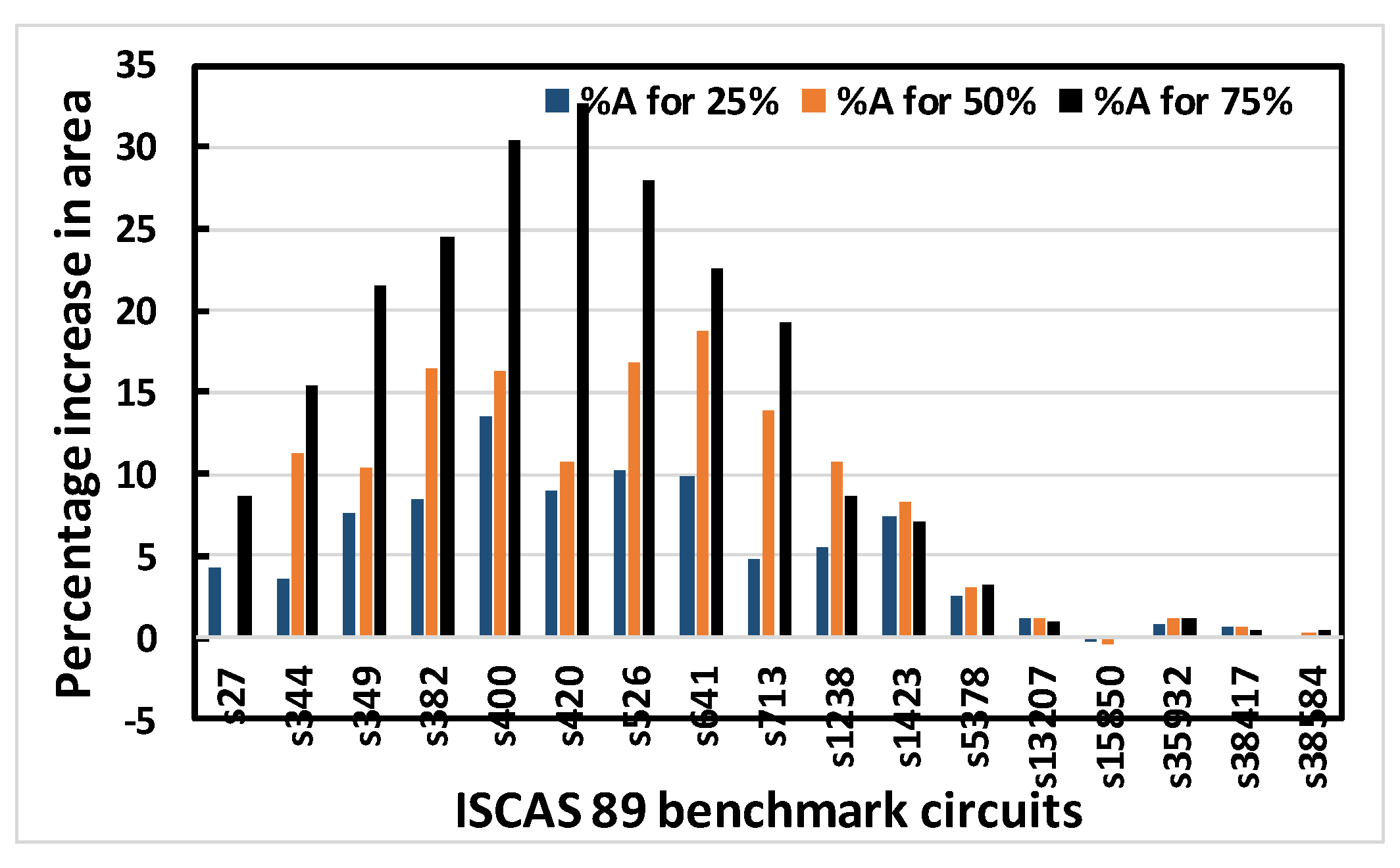
Simulations are extensively performed on the ISCAS 89 benchmark circuits shown in Table 2, ranging from small, to medium, to moderately large circuits. The percentage increase in area, delay, leakage power and total power for obfuscating different ISCAS 89 benchmark circuits using OC1, OC2 or OC3 (either random or fixed) are recorded. It is desirable that the cost for fabricating or operating a chip be minimized. To reduce the cost of fabrication, the area must be minimized, while the reduction of power ensures a reduced operating cost. On the other hand, the performance of a chip also depends on its speed, which is determined by the delay. Thus, these characteristics were chosen as the components of the performance matrix. Obfuscation was done for 25%, 50% and 75% of the modifiable nodes, respectively. However, a limit of 80 key bits is set as an upper bound. In the recent literature, it has been reported that an upper limit of 80 key bits is sufficient for security purposes. Above that number, circuit overhead becomes excessive. This limit is chosen for that reason. For larger circuits, this upper bound is more likely to be reached earlier than the 25%, 50% or 75% obfuscation level. Thus, the percentage increase in area, leakage power and total power are reduced in the larger circuits compared to the smaller ones. In Figure 8, Figure 9, Figure 10 and Figure 11, the larger circuits are shown in the right side of the x-axis, and the graphs show that the percentage increase in area, leakage power and total power increase up to some point along x-axis and decrease afterwards, as expected and explained above for the larger circuits. Similar trends are observed for OC1, OC2 and OC3. As an example, the following graphs (Figure 8, Figure 9, Figure 10 and Figure 11) show the percentage increase in area, delay, leakage power and total power for obfuscating different ISCAS 89 benchmark circuits using 3 different OCs randomly chosen to obfuscate 25%, 50% and 75% of the modifiable nodes, respectively.

Table 2.
Description containing number of cells of the ISCAS 89 benchmark circuits.
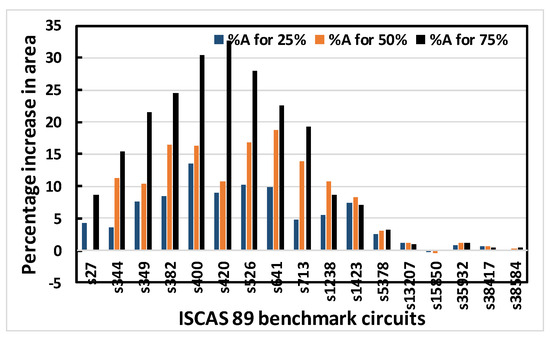
Figure 8.
Percentage increase in area for 25%, 50% and 75% obfuscation levels of ISCAS 89 benchmark circuits using OC3 random.
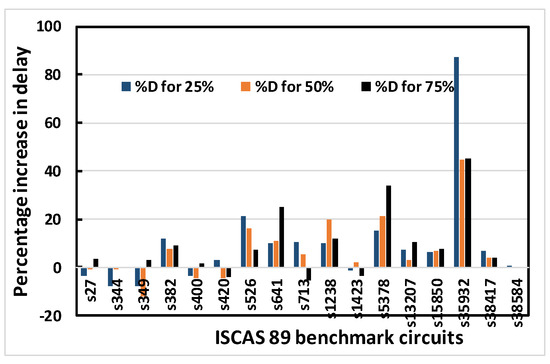
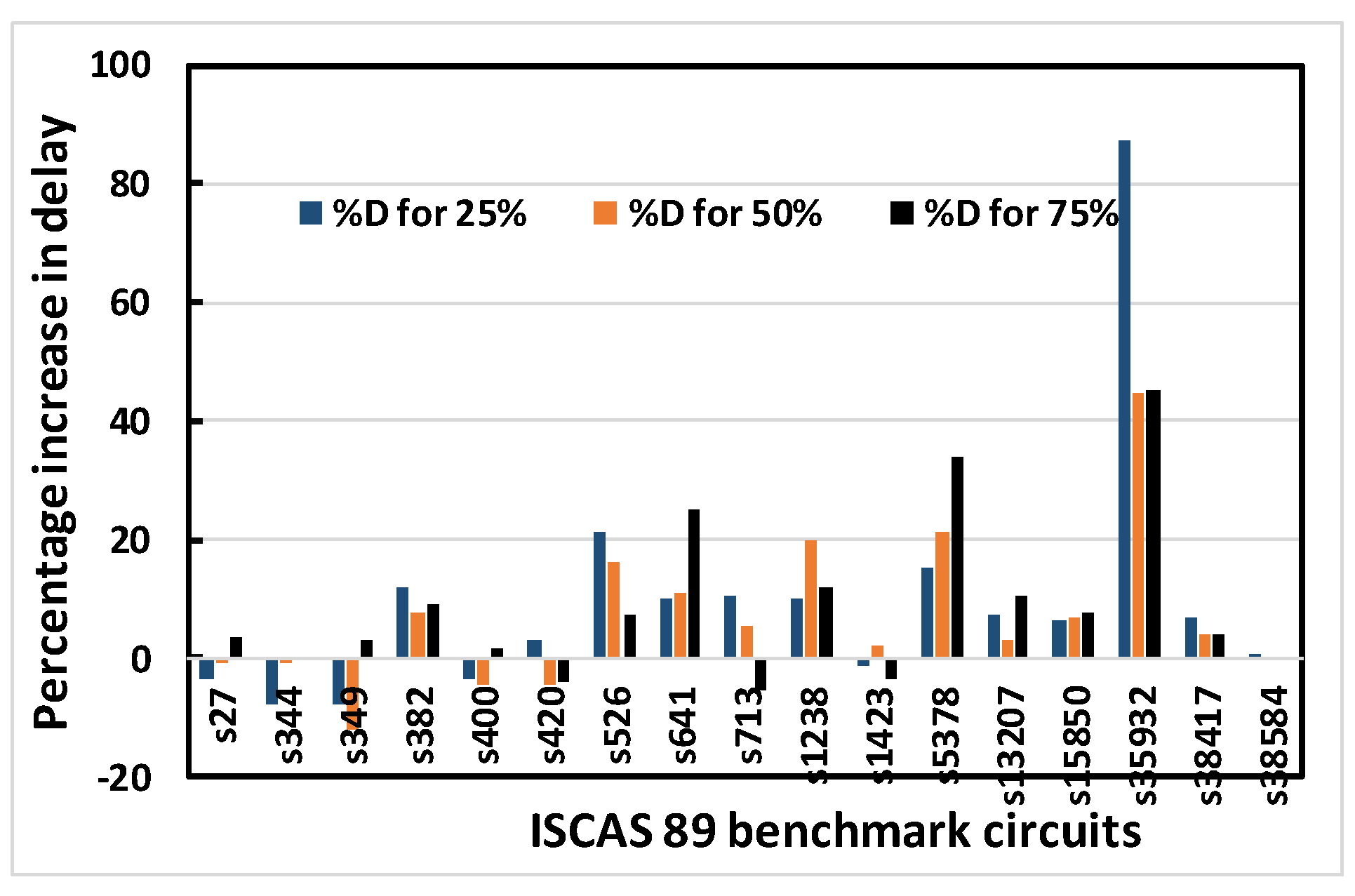
Figure 9.
Percentage increase in delay for 25%, 50% and 75% obfuscation levels of ISCAS 89 benchmark circuits using OC3 random.
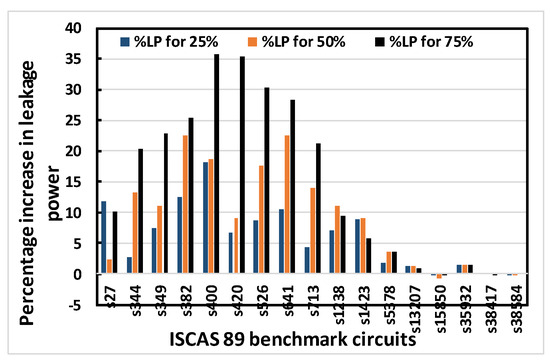
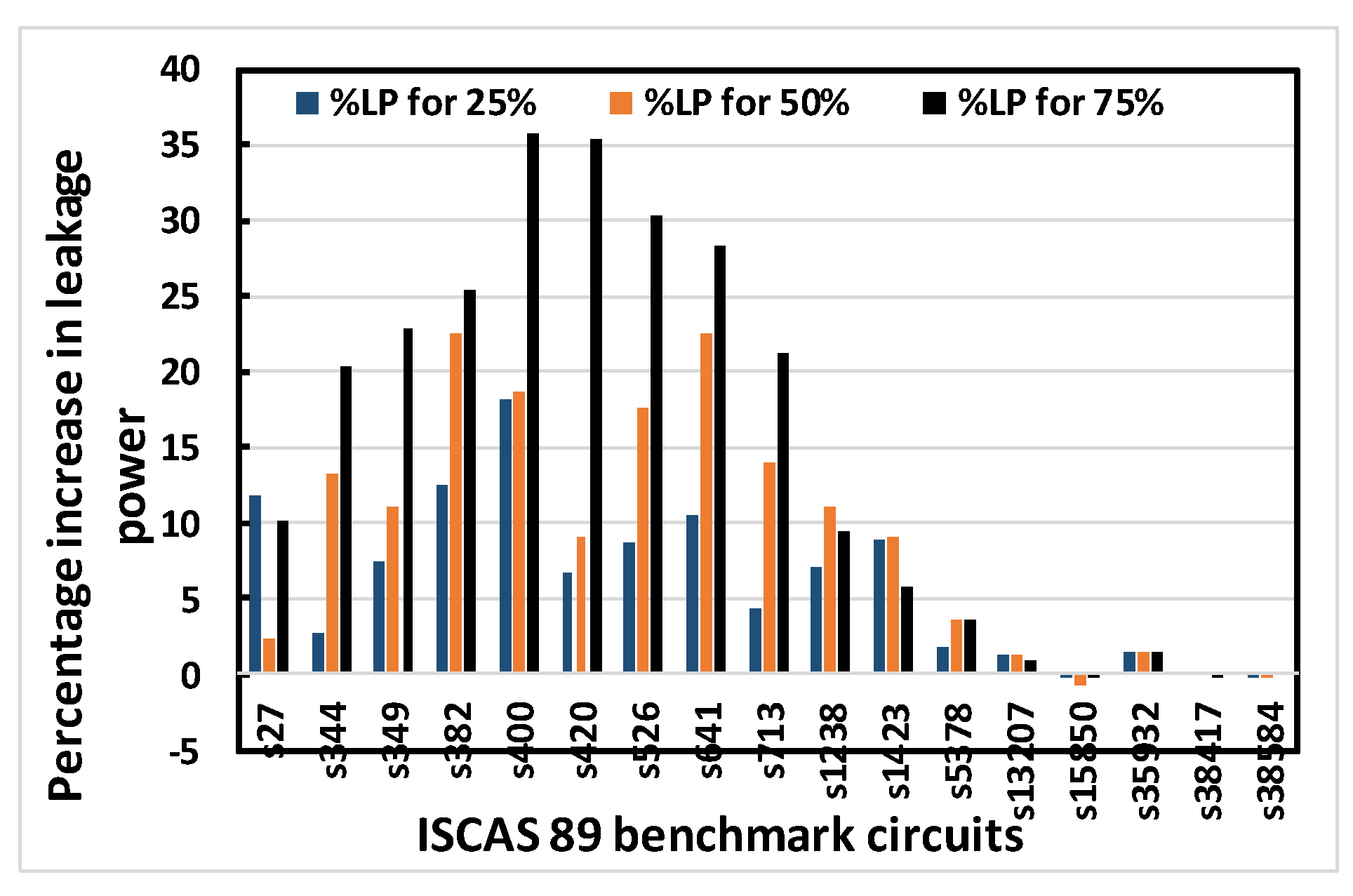
Figure 10.
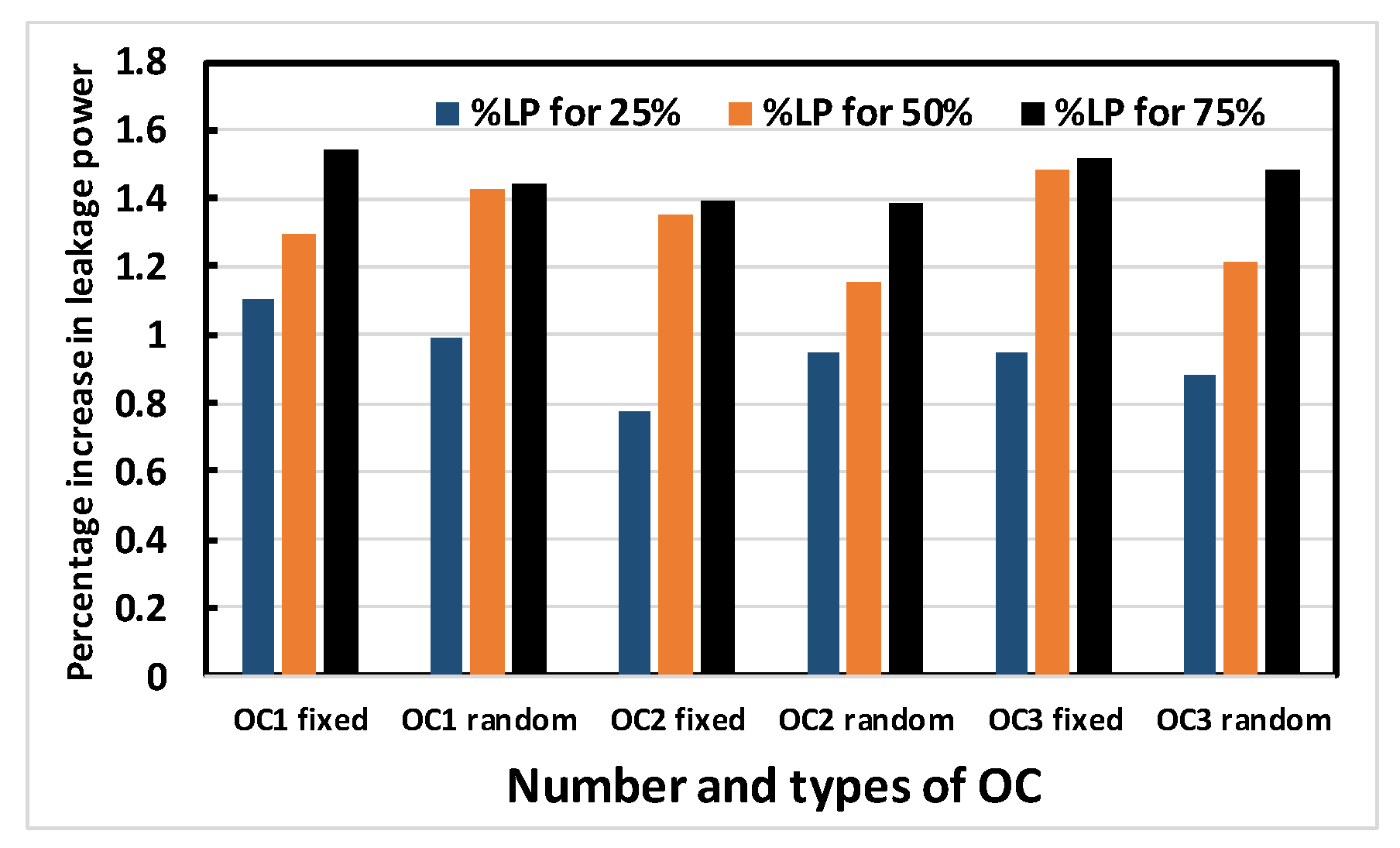
Percentage increase in leakage power for 25%, 50% and 75% obfuscation levels of ISCAS 89 benchmark circuits using OC3 random.
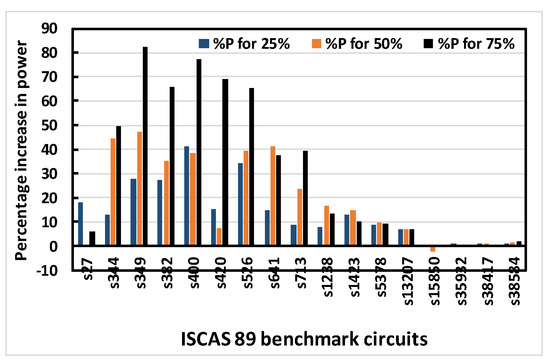
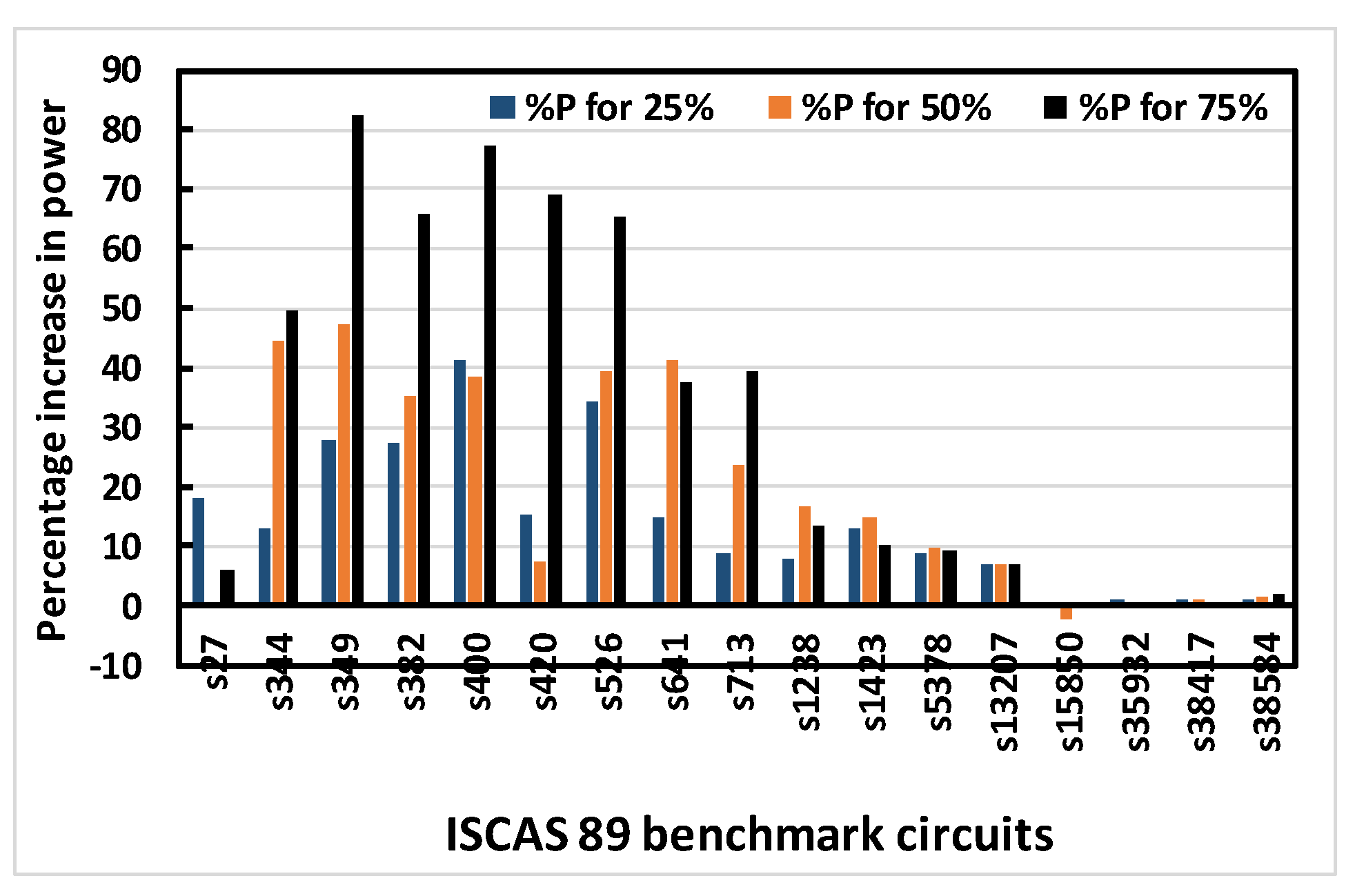
Figure 11.
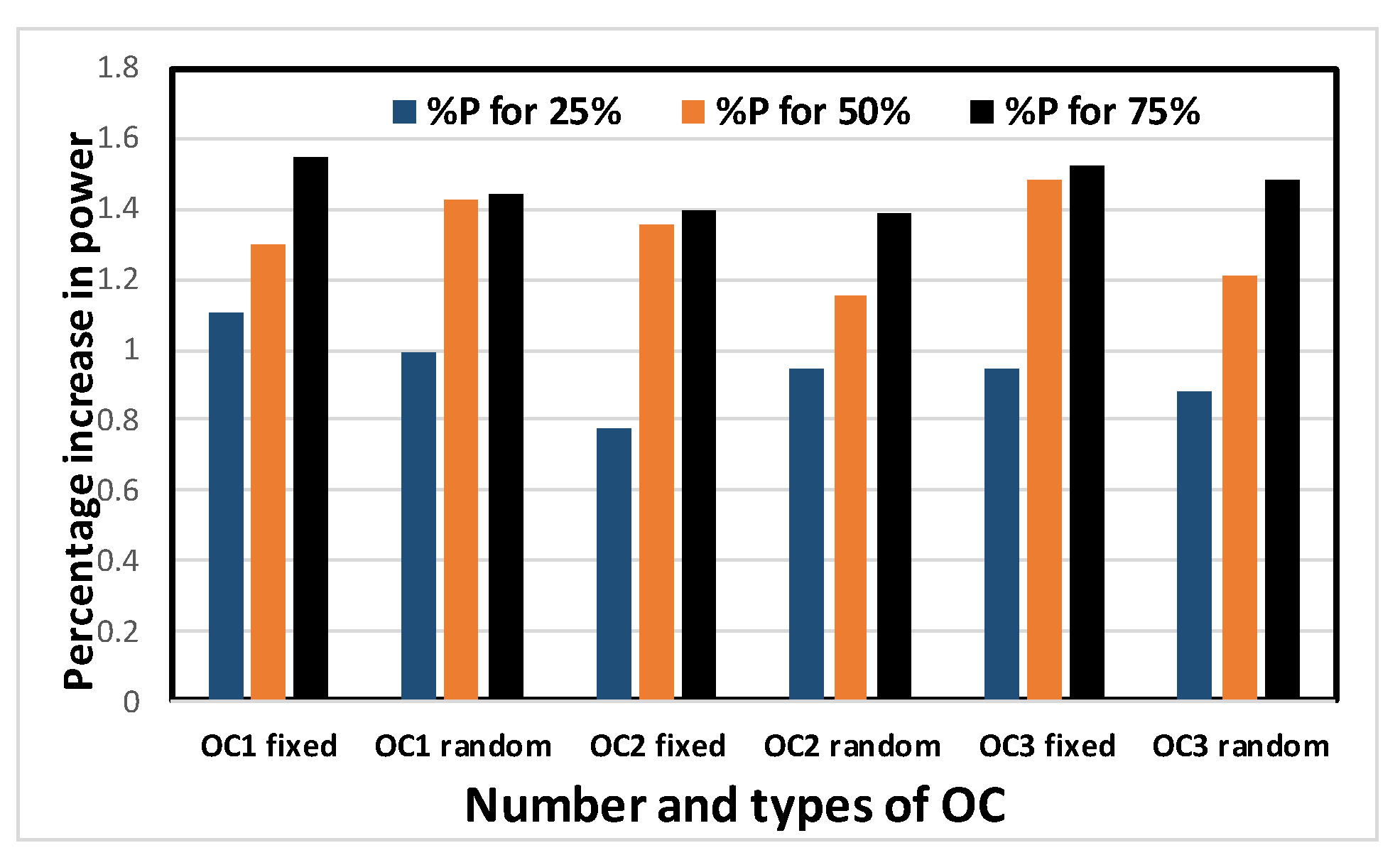
Percentage increase in total power for 25%, 50% and 75% obfuscation levels of ISCAS 89 benchmark circuits using OC3 random.
Figure 8, Figure 9, Figure 10 and Figure 11 show that area, delay, leakage power and total power, respectively, increase with increasing obfuscation levels up to some benchmark circuits with some minor exceptions in between. For example, Figure 8 shows that area increases for increasing obfuscation levels up to the s713 circuit, although s27 is an exception. After that, the upper bound of 80 key bits is reached and there is therefore no correlation between area and obfuscation level, with area depending solely on the OC chosen. Similar trends are observed for delay, leakage power and total power. The decreases in area, delay, leakage power and total power in some benchmark circuits with increasing obfuscation levels are due to the upper bound of 80 key bits, randomness of the chosen OC and its area, the contribution of delay towards the worst-case scenario, leakage power and total power requirements. Delay is an exception because the old critical path is not touched when OCs are inserted. Therefore, after synthesis, delay may even decrease, as seen from Figure 9.
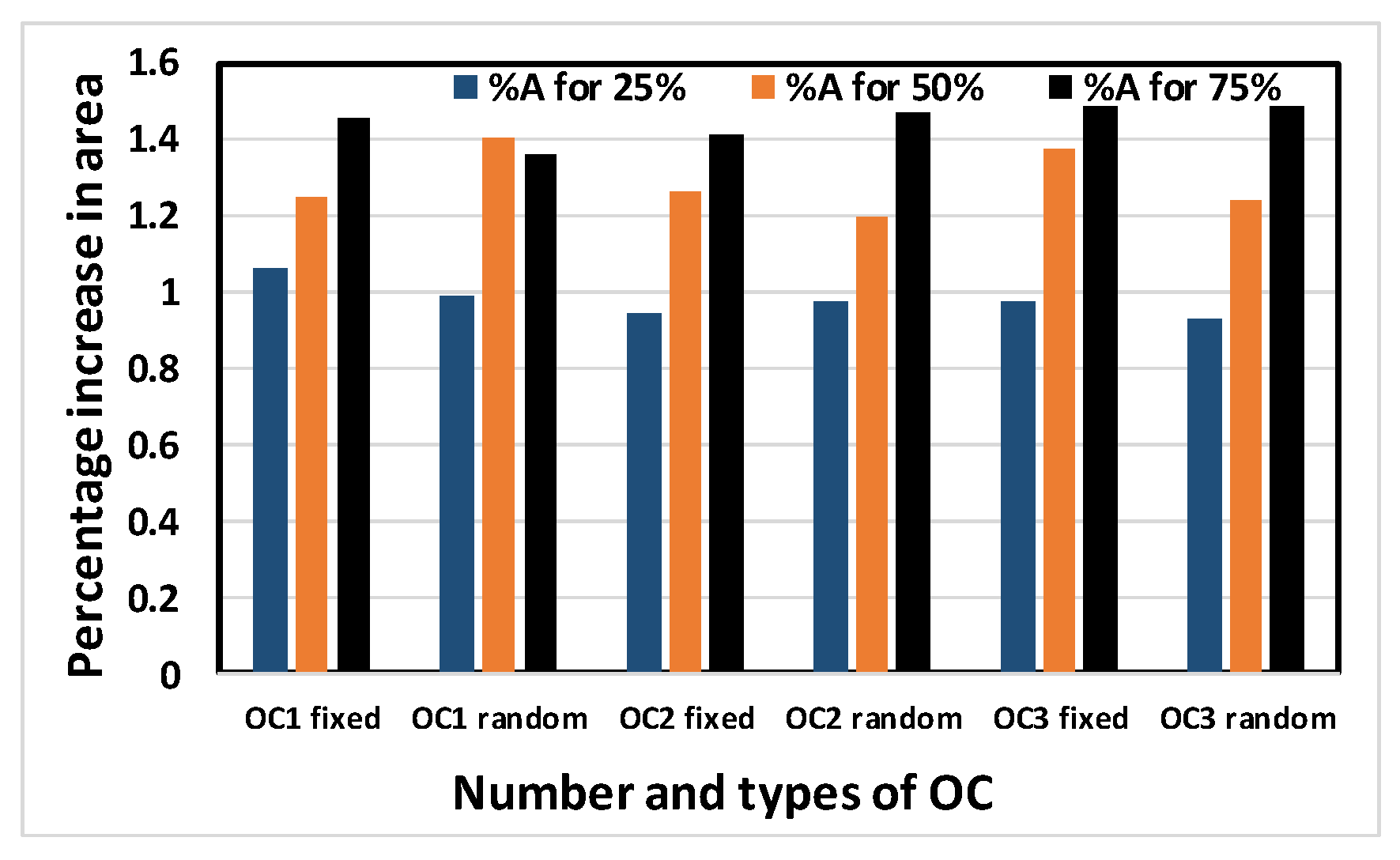
Figure 12, Figure 13, Figure 14 and Figure 15 show the average percentage increases of area, delay, leakage power and total power, respectively, as calculated for all simulated benchmark circuits. The results show that the average percentage increase of area, leakage power and total power occur at almost constant rates with increasing obfuscation levels, with some minor intermediate deviations. These deviations are predictable, as the same OC is not used when the obfuscation level is increased causing different area, leakage power and total power requirements per OC. If the same cells were chosen with increasing obfuscation levels, area, leakage power and total power would also increase if the number of key bits were not constrained by the upper limit of 80. The only exception is the delay. The reason average percentage delay does not increase at a constant rate is that the inserted OCs do not touch the old critical path, as mentioned in the algorithm; rather, they burden the non-critical paths. As a result, the delay determined by the critical path may not increase linearly with obfuscation levels and may even decrease.
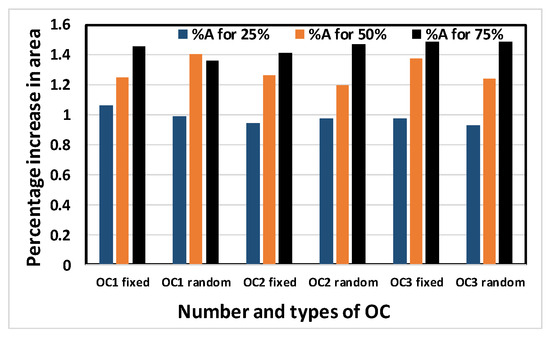
Figure 12.
Average percentage increase in area of the benchmark circuits with different numbers and types of OC.
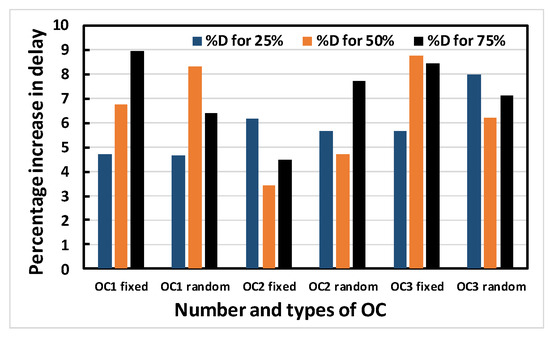
Figure 13.
Average percentage increase in delay of the benchmark circuits with different numbers and types of OC.
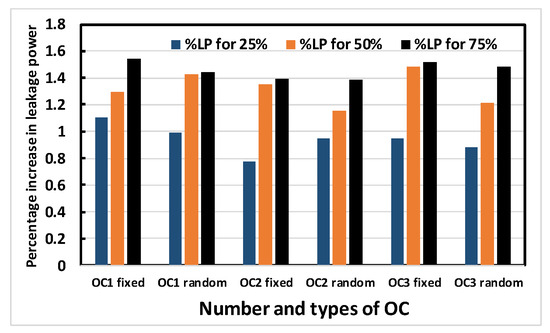
Figure 14.
Average percentage increase in leakage power of the benchmark circuits with different numbers and types of OC.
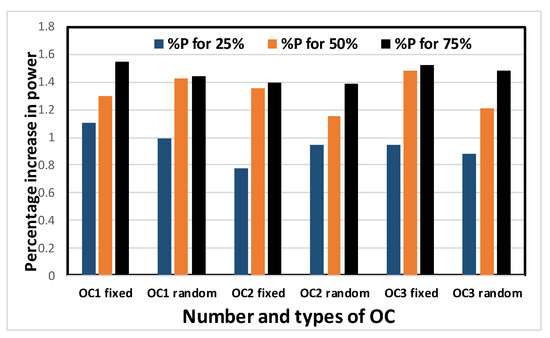
Figure 15.
Average percentage increase in total power of the benchmark circuits with different numbers and types of OC.
Table 3 summarizes the comparison of performance of the proposed technique with other techniques. When the number of key gates inserted is 5% of the number of gates in the original ISCAS-85 combinational benchmarks, the area overhead and the power-delay product overhead for random insertion yields average overheads of about 26% and 25%, respectively [36], whereas for the proposed method, the area overhead is around 1.44%, delay overhead is 7.18%, leakage power overhead is 1.46% and power overhead is 3.05% for 75% obfuscation of the modifiable nodes. This value is significantly lower. For 25% or 50% obfuscation, the results are even better. Note also that the level of obfuscation is 75% of the modifiable nodes for the case presented in this paper, which is a number that is likely to constitute more than 5% of the total number of nodes. J. Zhang [8] used the PUF response to unlock the function of the chip. The designer often computes the error correcting code (ECC) to adjust for any bit flips to the PUF output (response) because the absolutely stability in the PUF output is hard to maintain due to noise or other sources of physical uncertainty. Notably, he did not report the overhead of implementing PUFs and ECC methods in his brief [8]. If he had, his area, delay and power overhead would be much higher than 0.63%, 0% and 2.6% [8], as he would need memory block, which would occupy a large area. R. S. Chakraborty and S. Bhunia [25] reported area, delay and power overhead of 4% (8.89%), −1% (−1%) and 7% (13%), respectively, under 5% (and 10%) area constraint for under 13% obfuscation of the total number of nodes in all cases. Thus, the results obtained with the proposed method are still far better than those previously reported.

Table 3.
Comparison of performance of the proposed technique with those of other techniques.
- Why the performance overhead improved so drastically for the proposed method:
A comparison of the performance of the proposed technique with those of other techniques is shown in Table 3. As can be seen from the table, significant improvements in performance in area, delay, power and leakage power and delay power have been obtained. In some cases, the improvement is drastic, which can be explained by the discussion below.
It is assumed in this paper that all the chips are fabricated from the same wafer. The larger circuits contributed to a very small percentage increase in the area, power and leakage power, as the upper bound of 80 key gates is reached before 25%, 50% or 75% obfuscation. Earlier papers reported the average of the area, delay, power and leakage power overhead. However, in this paper, these figures were calculated from the total increase in the area, power and leakage power of all the circuits. Due to the smaller contribution of overhead by the larger circuits when ratioed by a larger total denominator to determine the percentage overhead, the corresponding figures show much better results in this paper compared to the results in previous papers, in which the average yielded higher values due to a higher contribution from smaller circuits. It is logical that the percentage overhead should be calculated from the total increase of area, leakage power or power as a percentage of the total of these parameters for all circuits considered.
However, it is to be noted that the overhead of tamperproof memory is not included in any of our calculations. If it were included, results would be less impressive. Tamperproof memory was not included in the design analyzed in this paper. Thus, it was not included in the overhead calculation.
6. Security Analysis
Recent studies have assessed the strictness of security of an obfuscation scheme by any one of three methods: (1) Hamming distance between the simulated and the original output, (2) verification failure between the original circuit and an obfuscated circuit by software and (3) the probability of breaking the secret keys and placing the obfuscation cells in the correct position.
A Hamming distance of 0% means success in breaking the key. A 100% Hamming distance means a complete failure; in such a case, the attacker simply has to flip all the bits of his outputs by adding inverters. Thus, a 50% Hamming distance between the actual outputs and the simulated outputs generated from the keys guessed by rogue attacker is the most desirable. Hamming distance is suitable for determining the strength of a code. However, to an attacker, it is important not only to find the correct keys, but to place the correct obfuscation cells at the accurate positions. This second step is critical, especially when generating the pirated version of the original circuit from the truth table of the input-output relationship [37] is his main objective. If the attacker calculates and compares the Hamming distance recursively and adjusts the guess key at each iteration in an attempt to break the key, the code may be broken; however, the type and position of the obfuscated cells in the circuit will still not be obtained.
Verification tools try to mitigate this vulnerability to finding the keys using Hamming distance. Here, to simulate the circumstances of the attack, it is assumed that the attacker can buy a golden circuit from the market and that he also has access to an obfuscated circuit. The verification engineer, like the attacker, changes keys and the netlist of the obfuscated circuit and verifies whether the golden circuit is equivalent to the obfuscated circuit. The more times verification fails, the tighter the encryption becomes. Assessing security through verification failure requires expensive cutting-edge software tools, a cost that is usually comparable with the predicted cost of verification failure. The computation time required by the verification tool is enormous compared to the time required for prediction. Additionally, the average prediction error is only about 5% [25], rendering the simulation unnecessary.
On the other hand, if the probability of breaking a circuit with correct keys is taken as the security index, then the minimum value of that probability indicates the security of that circuit. The probability can be calculated very easily with minimum computational time and effort. Considering all these factors, the probability of breaking a circuit with correct keys is taken as the security index in this paper.
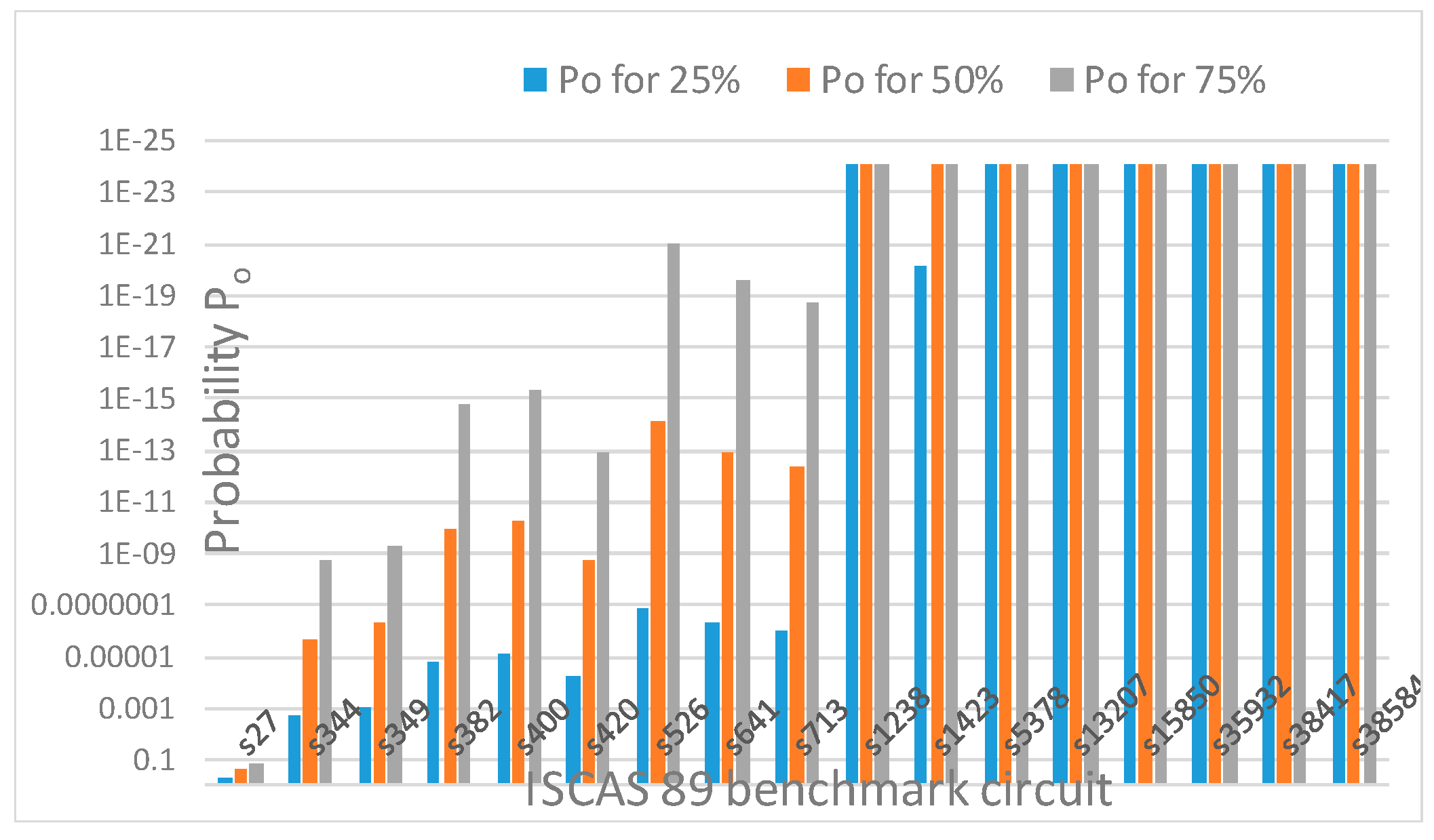
Table 4 shows that the no. of keys, k, increases with increasing obfuscation levels up to 80 keys, which is the upper limit. The probability of detecting correct output,
therefore decreases for increasing obfuscation levels until the upper limit of keys is reached, as is evident from Table 4 and Figure 16. Once the limit is reached, Po becomes constant and there is therefore no reason to select a circuit with a higher obfuscation level unless the delay improves. In Figure 16, probability Po is plotted on a log scale in reverse order against ISCAS 89 benchmark circuits.

Table 4.
Probability of detecting correct output for different obfuscation levels.
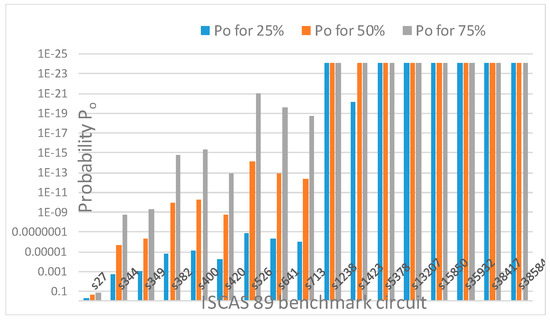
Figure 16.
Probability of detecting correct output for 25%, 50% and 75% obfuscation levels in ISCAS 89 benchmark circuits.
Table 5 shows that as k increases up to 80 keys, the probability of detecting the correct OCs and placement in the correct key position once the keys are accurately determined, pc, does not vary with obfuscation levels for OC1. The reason is that
for OC1, where m = No. of available types of OCs and r = No. of types of OCs used. For the case studied in this paper, m = 6 (AND, OR, NAND, NOR, XOR and XNOR) and r = 1 for OC1. Therefore,
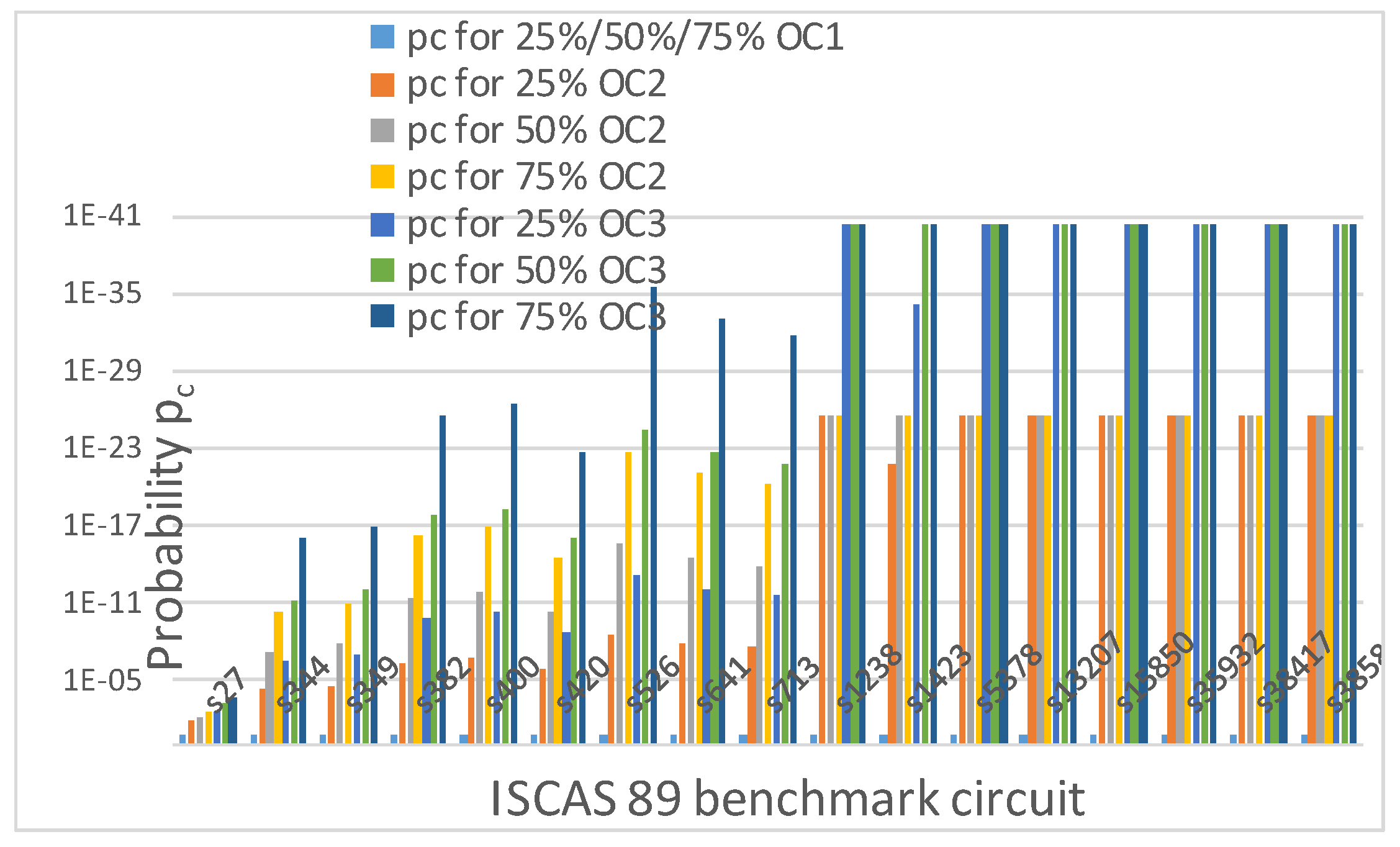
remains constant for OC1. It is observed in Figure 17 that probability, pc, for OC1 is the same for the 25%, 50% and 75% obfuscation levels.

Table 5.
Probability of correctly determining the obfuscation circuit for different obfuscation schemes.
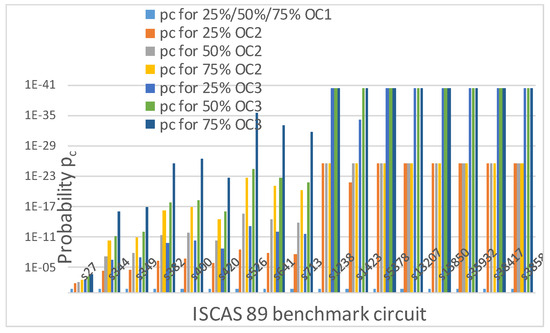
Figure 17.
Probability of detecting the correct OC at the correct location for 25%, 50% and 75% obfuscation levels with different numbers of OCs in ISCAS 89 benchmark circuits.
Figure 17 also shows that probability, pc, decreases if the obfuscation level is increased continuously from 25% to 75% unless the upper bound of 80 keys is reached or the number of OC is increased from 2 to 3 (OC2 to OC3). As the upper bound of 80 keys is reached, pc remains constant and does not vary with obfuscation level if r is not varied. As already explained, for OC1, pc does not change with obfuscation level.
For OC2 and OC3, r = 2 and 3, respectively. The corresponding expressions are
and
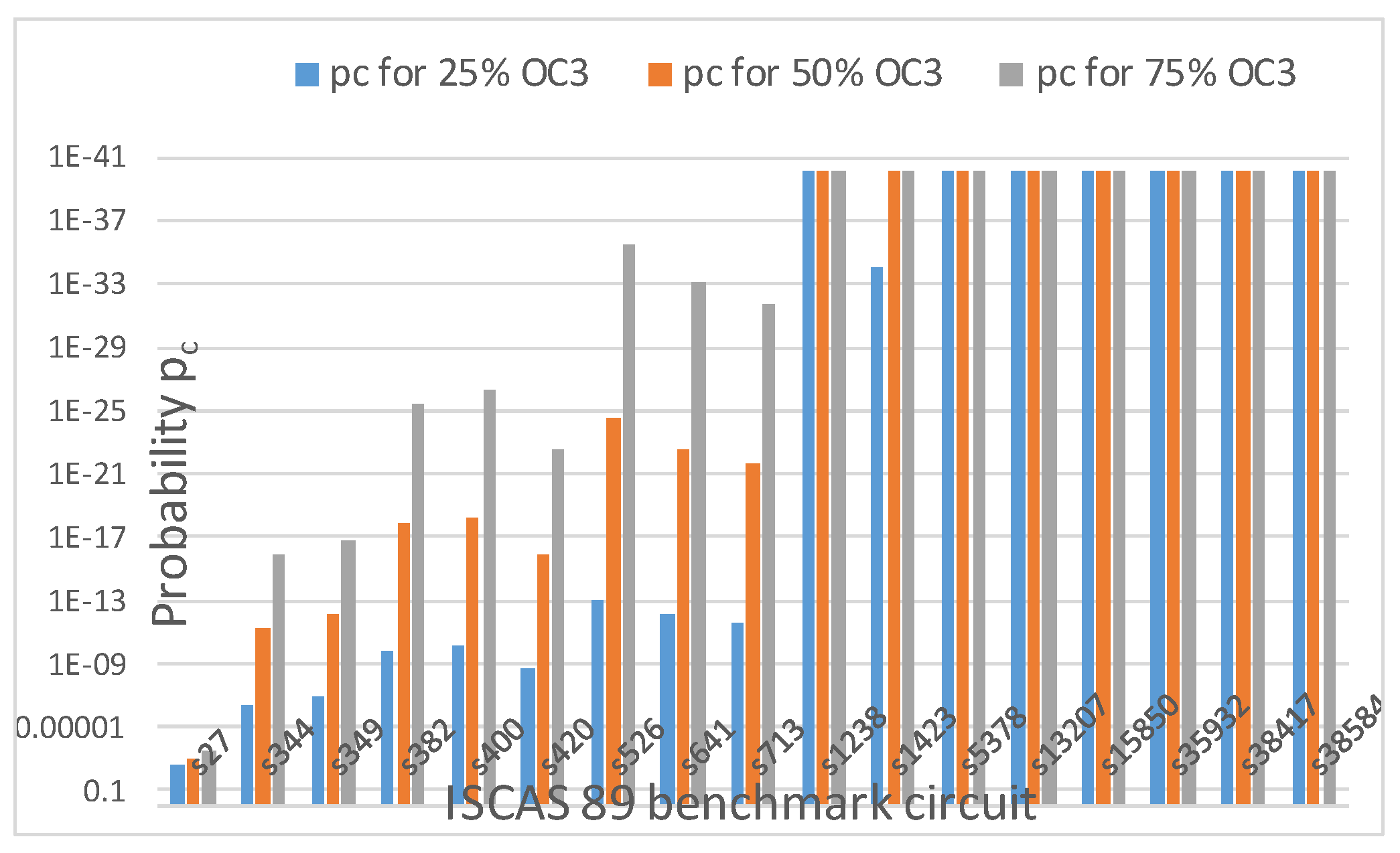
for OC2 and OC3, respectively. Thus, as k increases with increasing obfuscation levels (up to 80 keys), pc decreases for a fixed r. Figure 18 shows this pattern for OC3. As seen from Figure 18, as obfuscation level increases from 25% to 50% and 75% for OC3, pc decreases unless k reaches the upper bound of 80. Similar results are obtained for OC2. As explained earlier, OC1 is an exceptional case and does not follow this trend.
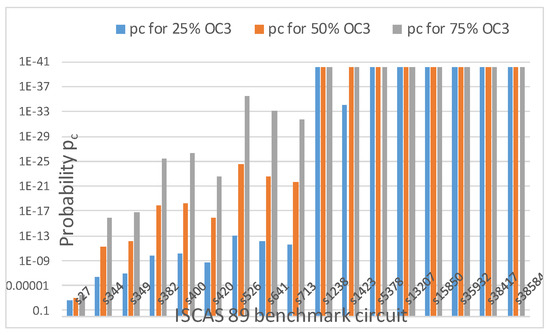
Figure 18.
Probability of detecting correct OC at precise location for 25%, 50% and 75% obfuscation levels with OC3 for ISCAS 89 benchmark circuits.
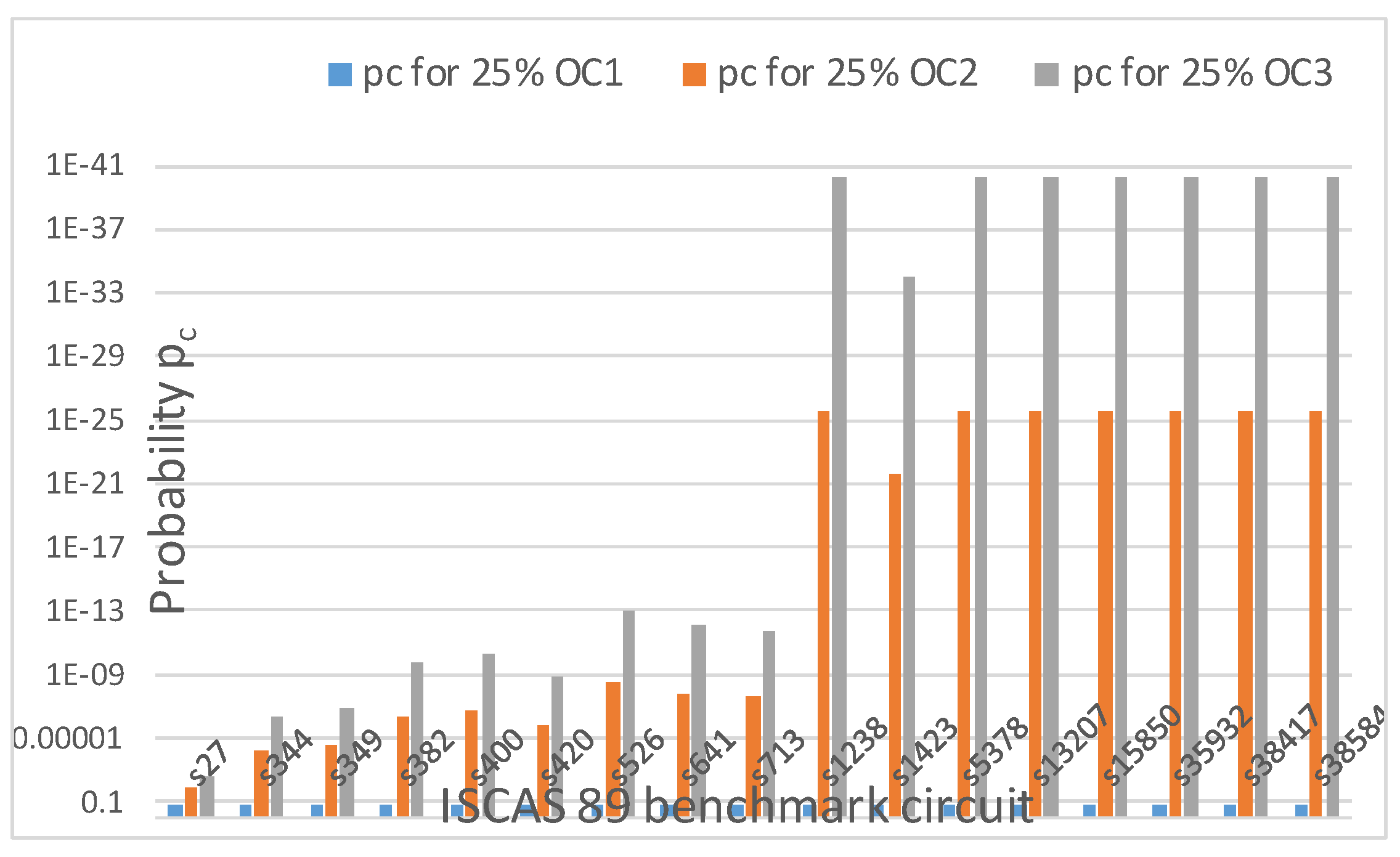
Most importantly, as shown in Figure 19, even if k remains the same for the same obfuscation level of 25%, r may increase as the types of OCs increase (i.e., OC1, OC2, OC3 etc.). As a result, pc decreases even though k remains constant, but r increases. Therefore, when an attacker tries to find the keys in a circuit using brute force (attempting all the possible combinations one by one), he is stymied more as r increases, as shown in Figure 19, Table 5 and Equations (2)–(5). This result suggests that the incorporation of mix of OCs will improve the security index, SI. Similar results are obtained for 50% and 75% obfuscation.
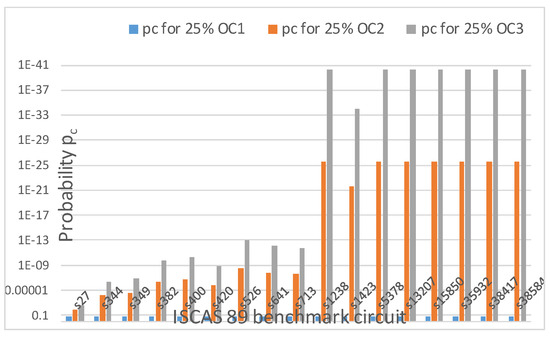
Figure 19.
Probability of detecting the correct OC at the correct location for 25% obfuscation levels with different numbers of OCs for ISCAS 89 benchmark circuits.
From Table 4 and Table 5 and Figure 16, Figure 17, Figure 18 and Figure 19, it is observed that probability Po and pc do not depend on obfuscation types, i.e., on whether random or fixed obfuscations are used. They instead depend on the number of types of obfuscation cells and obfuscation levels, as long as the upper limit of 80 keys is not reached.
6.1. Mathematical Evaluation of Security Index, SI, for Multiple Obfuscation
If N = Total no. of nodes in the circuit, then the attacker must also find the precise location of the k key bits. Therefore, to determine the probability of detecting the correct OCs and correct placement, PC,
and
SI is minimized when the denominator is maximized.
For the minimum value of SI,
and
As r must be an integer, for large values of k,
Thus, the circuit becomes more secure if the number of types of obfuscated cells used, r, approaches the number of available types of OCs, m.
6.2. Evaluation of Security by Simulation
To evaluate the security of different schemes, s344 and s38417 circuits were chosen. Three different security measures were taken—obfuscation, Anti-SAT and Anti-SAT in combination with multiple-cell obfuscation. A SAT attack was performed on all three schemes. The key size was kept within 20 bits to match with the physical limitations. The simulation was performed on a server with a configuration of 2 × 14 CPU (Total 56 virtual cores), 150 GB HDD, 512 GB RAM and a Windows server 2019 (Shared) Operating System. The program was written to utilize multiple cores and eventually used all, 56 virtual cores.
The results are presented in Table 6, which shows clearly that the number of iterations and simulation time required to obtain the correct keys are increased in the case of multiple-cell obfuscation combined with Anti-SAT compared to multiple-cell obfuscation or Anti-SAT alone. In some cases, the proposed scheme even reaches the time-out limit of two days.

Table 6.
Comparison of different schemes of defense against SAT attack.
Table 7 shows the performance overhead of multiple-cell obfuscation, Anti-SAT and Anti-SAT combined with multiple-cell obfuscation using 20 keys in an s38417 circuit. From Table 7, it is clear that the overhead of the proposed scheme is very small. The overhead of tamperproof memory is not included in any calculation.

Table 7.
Comparison of performance overhead of different defense schemes using 20 keys in an s38417 circuit.
7. Conclusions
In this paper, a simple methodology is proposed for obfuscation of the netlist of a digital circuit with a mixture of multiple cells integrated with an Anti-SAT block. Obfuscating the circuit is done in such a way that delay is minimally affected, while security is maximized. A mathematical analysis is given showing that the security index increases with multiple-cell obfuscation. Graphical results from the simulation support the mathematical proof. A SAT attack algorithm is implemented, and it is shown that the attack requires fewer iterations for a specific case. To address the implemented SAT attack, an Anti-SAT block is incorporated with multiple-cell obfuscation, providing better security in terms of iteration and simulation time compared to the Anti-SAT or obfuscation alone, as seen from the results of the simulation. The inherent drawback of using an Anti-SAT integrated with one type of obfuscation cell is also eliminated in the combined multiple-cell obfuscation and Anti-SAT block, as the trivial solution of an “all 0” or “all 1” key does not work. Additionally, in this scheme, isolation of the Anti-SAT block is not possible due to the interconnection of the Anti-SAT block and the obfuscation. The inclusion of multiple-cell obfuscation thus improves the performance of the Anti-SAT block multifold when the two work in conjunction. The framework designed here allows the user to choose a scheme that suits his area, delay, leakage power, total power and safety requirements.
Author Contributions
Conceptualization, A.B.M.H.-u.R.; Data curation, H.R.; Formal analysis, H.R.; Investigation, H.R.; Methodology, H.R.; Validation, H.R.; Writing—original draft preparation, H.R. and M.H.; Resources, A.B.M.H.-u.R.; Supervision, A.B.M.H.-u.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank Uday Kamal and Anupam Golder of Georgia Institute of Technology, North Avenue, Atlanta, GA 30332, USA for their valuable suggestions for writing this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Amir, S.; Shakya, B.; Xu, X.; Jin, Y.; Bhunia, S.; Tehranipoor, M.; Forte, D. Development and Evaluation of Hardware Obfuscation Benchmarks. J. Hardw. Syst. Secur. 2018, 2, 142–161. [Google Scholar] [CrossRef]
- Karmakar, R.; Prasad, N.; Chattopadhyay, S.; Kapur, R.; Sengupta, I. A New Logic Encryption Strategy Ensuring Key Interdependency. In Proceedings of the International Conference on VLSI Design and International Conference on Embedded Systems (VLSID), Hyderabad, India, 7–11 January 2017; pp. 429–434. [Google Scholar] [CrossRef]
- Trends in the Global IC Design Service Market. DIGITIMES Research. Available online: http://www.digitimes.com/news/a20120313RS400.html?chid=2 (accessed on 20 November 2021).
- Hu, S.; Jin, Y.; Heffner, K.; Tehranipoor, M. Hardware/Software Cross-Layer Technologies for Trustworthy and Secure Computing. IEEE Trans. Multi-Scale Comput. Syst. 2016, 2, 144–145. [Google Scholar] [CrossRef]
- Goertzel, K.M.; Hamilton, B.A. Integrated Circuit Security Threats and Hardware Assurance Countermeasures. CrossTalk 2013, 26, 33–38. [Google Scholar]
- Tehranipoor, M.; Koushanfar, F. A Survey of Hardware Trojan Taxonomy and Detection. IEEE Des. Test Comput. 2010, 27, 10–25. [Google Scholar] [CrossRef]
- Alasad, Q.; Bi, Y.; Yuan, J. E2LEMI: Energy-Efficient Logic Encryption Using Multiplexer Insertion. Electronics 2017, 6, 16. [Google Scholar] [CrossRef]
- Zhang, J. A Practical Logic Obfuscation Technique for Hardware Security. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2016, 24, 1193–1197. [Google Scholar] [CrossRef]
- Chen, M.; Moghaddam, E.; Mukherjee, N.; Rajski, J.; Tyszer, J.; Zawada, J. Hardware Protection via Logic Locking Test Points. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 3020–3030. [Google Scholar] [CrossRef]
- Innovation Is at Risk: Losses of up to $4 Billion Annually due to IP Infringement. Available online: http://www.semi.org/en/Issues/IntellectualProperty/ssLINK/P043785 (accessed on 20 November 2021).
- Chen, X.; Liu, Q.; Wang, Y.; Xu, Q.; Yang, H. Low-overhead implementation of logic encryption using gate replacement techniques. In Proceedings of the 18th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 14–15 March 2017; pp. 257–263. [Google Scholar] [CrossRef]
- Plaza, S.M.; Markov, I.L. Solving the Third-Shift Problem in IC Piracy with Test-Aware Logic Locking. IEEE Trans. Comput.-Aided des. Integr. Circuits Syst. 2015, 34, 961–971. [Google Scholar] [CrossRef]
- Yasin, M.; Rajendran, J.; Sinanoglu, O.; Karri, R. On Improving the Security of Logic Locking. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2016, 35, 1411–1424. [Google Scholar] [CrossRef]
- Rajendran, J.; Zhang, H.; Zhang, C.; Rose, G.; Pino, Y.; Sinanoglu, O.; Karri, R. Fault Analysis-Based Logic Encryption. IEEE Trans. Comput. 2015, 64, 410–424. [Google Scholar] [CrossRef]
- Bi, Y.; Shamsi, K.; Yuan, J.; Gaillardon, P.; Micheli, G.; Yin, X.; Hu, X.; Niemier, M.; Jin, Y. Emerging Technology-Based Design of Primitives for Hardware Security. J. Emerg. Technol. Comput. Syst. 2016, 13, 1–19. [Google Scholar] [CrossRef]
- Bi, Y.; Shamsi, K.; Yuan, J.; Jin, Y.; Niemier, M.; Hu, X. Tunnel FET Current Mode Logic for DPA-Resilient Circuit Designs. IEEE Trans. Emerg. Top. Comput. 2017, 5, 340–352. [Google Scholar] [CrossRef]
- Bi, Y.; Shamsi, K.; Yuan, J.; Standaert, F.; Jin, Y. Leverage Emerging Technologies For DPA-Resilient Block Cipher Design. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 14–18 March 2016; pp. 1538–1543. [Google Scholar]
- Yasin, M.; Mazumdar, B.; Rajendran, J.; Sinanoglu, O. SARLock: SAT attack resistant logic locking. In Proceedings of the IEEE International Symposium on Hardware Oriented Security and Trust (HOST), McLean, VA, USA, 3–5 May 2016; pp. 236–241. [Google Scholar] [CrossRef]
- Xie, Y.; Srivastava, A. Mitigating SAT Attack on Logic Locking. In Proceedings of the International Conference on Cryptographic Hardware and Embedded Systems (CHES), Santa Barbara, CA, USA, 17–19 August 2016; pp. 127–146. [Google Scholar] [CrossRef]
- Roy, J.A.; Koushanfar, F.; Markov, I.L. EPIC: Ending Piracy of Integrated Circuits. In Proceedings of the Design, Automation and Test in Europe (DATE), Munich, Germany, 10–14 March 2008; pp. 1069–1074. [Google Scholar] [CrossRef]
- Baumgarten, A.; Tyagi, A.; Zambreno, J. Preventing IC Piracy Using Reconfigurable Logic Barriers. IEEE Des. Test Comput. 2010, 27, 66–75. [Google Scholar] [CrossRef]
- Wendt, J.B.; Potkonjak, M. Hardware Obfuscation Using PUF-based Logic. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 2–6 November 2014; pp. 270–271. [Google Scholar] [CrossRef]
- Lee, Y.W.; Touba, N.A. Improving logic obfuscation via logic cone analysis. In Proceedings of the 16th Latin-American Test Symposium (LATS), Puerto Vallarta, Mexico, 25–27 March 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Plaza, S.M.; Markov, I.L. Protecting Integrated Circuits from Piracy with Test-aware Logic Locking. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 2–6 November 2014; pp. 262–269. [Google Scholar] [CrossRef]
- Chakraborty, R.S.; Bhunia, S. Hardware protection and authentication through netlist level obfuscation. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 10–13 November 2008; pp. 674–677. [Google Scholar] [CrossRef]
- Holcomb, D.E.; Burleson, W.P.; Fu, K. Power-Up SRAM State as an Identifying Fingerprint and Source of True Random Numbers. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2009, 58, 1198–1210. [Google Scholar] [CrossRef]
- Mustapa, M.; Niamat, M. Temperature, Voltage, and Aging Effects in Ring Oscillator Physical Unclonable Function. In Proceedings of the IEEE 17th International Conference on High Performance Computing and Communications, IEEE 7th International Symposium on Cyberspace Safety and Security, and IEEE 12th International Conference on Embedded Software and Systems, New York, NY, USA, 24–26 August 2015; pp. 1699–1702. [Google Scholar] [CrossRef]
- Rajendran, J.; Pino, Y.; Sinanoglu, O.; Karri, R. Logic encryption: A fault analysis perspective. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 12–16 March 2012; pp. 953–958. [Google Scholar] [CrossRef]
- Contreras, G.K.; Nahiyan, A.; Bhunia, S.; Forte, D.; Tehranipoor, M. Security vulnerability analysis of design-for-test exploits for asset protection in SoCs. In Proceedings of the 22nd Asia and South Pacific Design Automation Conference (ASP-DAC), Chiba, Japan, 16–19 January 2017; pp. 617–622. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X. Generalized SAT-Attack-Resistant Logic Locking. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2581–2592. [Google Scholar] [CrossRef]
- Sengupta, A.; Nabeel, M.; Limaye, N.; Ashraf, M.; Sinanoglu, O. Truly Stripping Functionality for Logic Locking: A Fault-based Perspective. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 4439–4452. [Google Scholar] [CrossRef]
- Chakraborty, A.; Jayasankaran, N.G.; Liu, Y.; Rajendran, J.; Sinanoglu, O.; Srivastava, A.; Xie, Y.; Yasin, M.; Zuzak, M. Keynote: A Disquisition on Logic Locking. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 1952–1972. [Google Scholar] [CrossRef]
- Available online: http://www.pld.ttu.ee/~maksim/benchmarks/iscas89/verilog/ (accessed on 20 November 2021).
- Yasin, M.; Rajendran, J.J.; Sinanoglu, O. The SAT Attack. In Trustworthy Hardware Design: Combinational Logic Locking Techniques; Analog Circuits and Signal Processing; Springer: Cham, Switzerland, 2019; pp. 47–56. [Google Scholar] [CrossRef]
- Zhong, Y.; Guin, U. Complexity Analysis of the SAT Attack on Logic Locking. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 3143–3156. [Google Scholar] [CrossRef]
- Rajendran, J.; Pino, Y.; Sinanoglu, O.; Karri, R. Security analysis of logic obfuscation. In Proceedings of the 49th Annual Design Automation Conference, San Francisco, CA, USA, 3–7 June 2012; pp. 83–89. [Google Scholar] [CrossRef]
- Available online: https://www.coursera.org/learn/hardware-security/lecture/qL9Ri/physical-attacks-andcountermeasures;timestamp (accessed on 20 November 2021).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).