Dynamical Analysis of a Memristive Chua’s Oscillator Circuit
Abstract
:1. Introduction
2. The Memristive Chua’s Oscillator
2.1. The Memristor’s Emulator
2.2. The Proposed Circuit
3. Theoretical Analysis
3.1. Dissipativity Analysis
3.2. Equilibrium Points
3.3. Stability
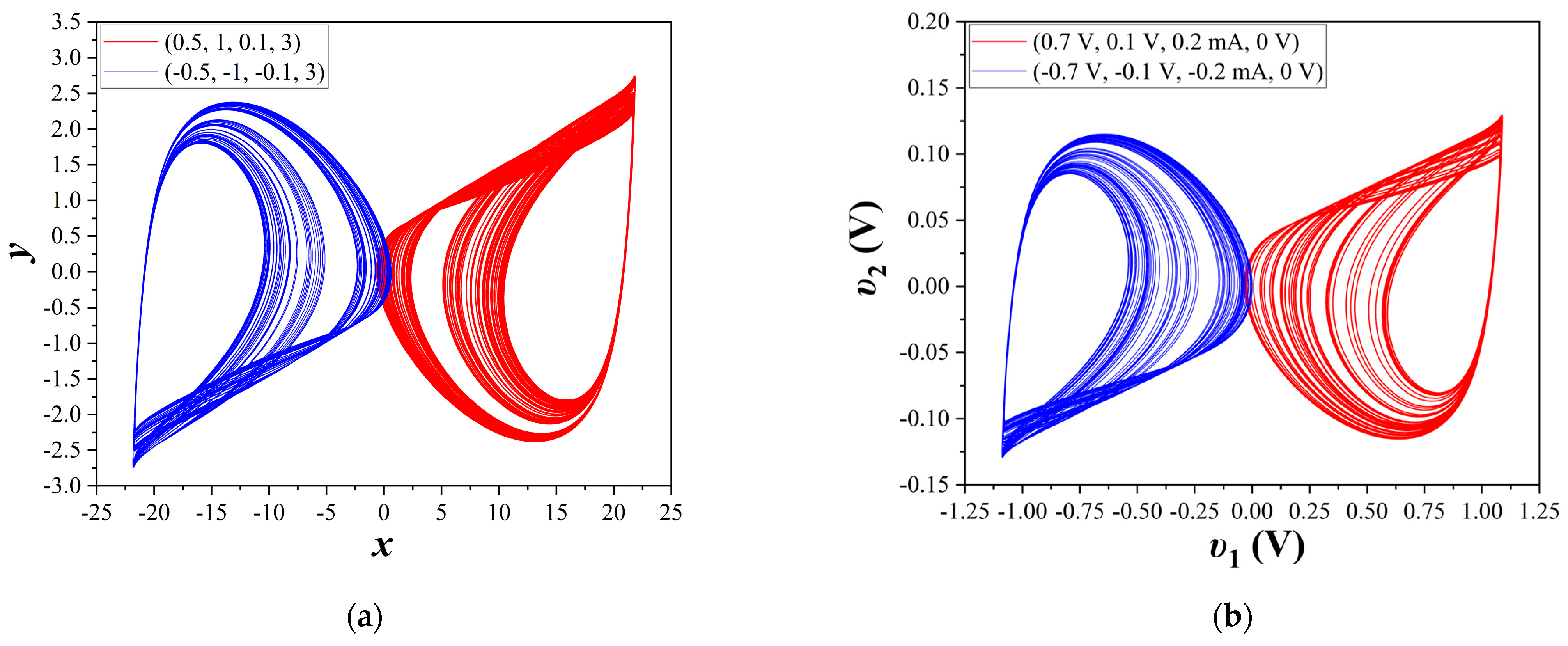
3.4. Symmetry
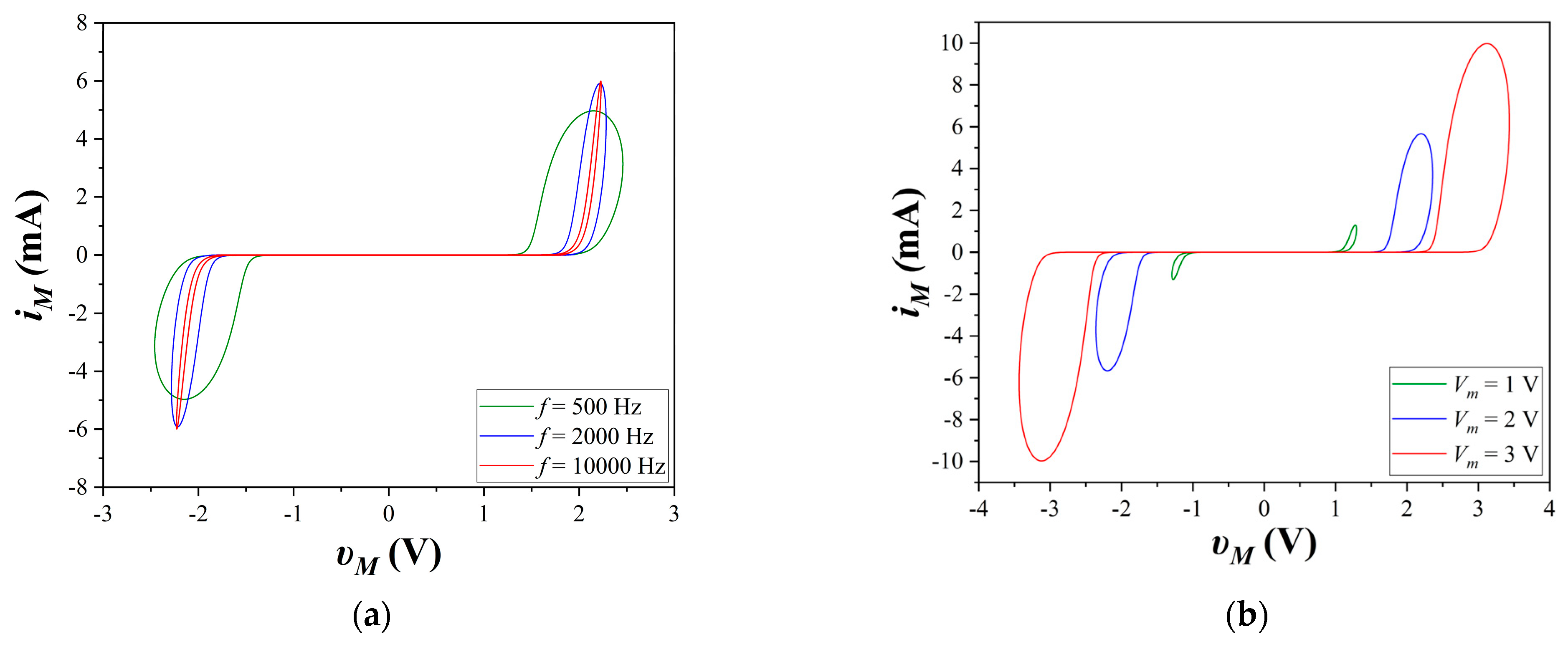
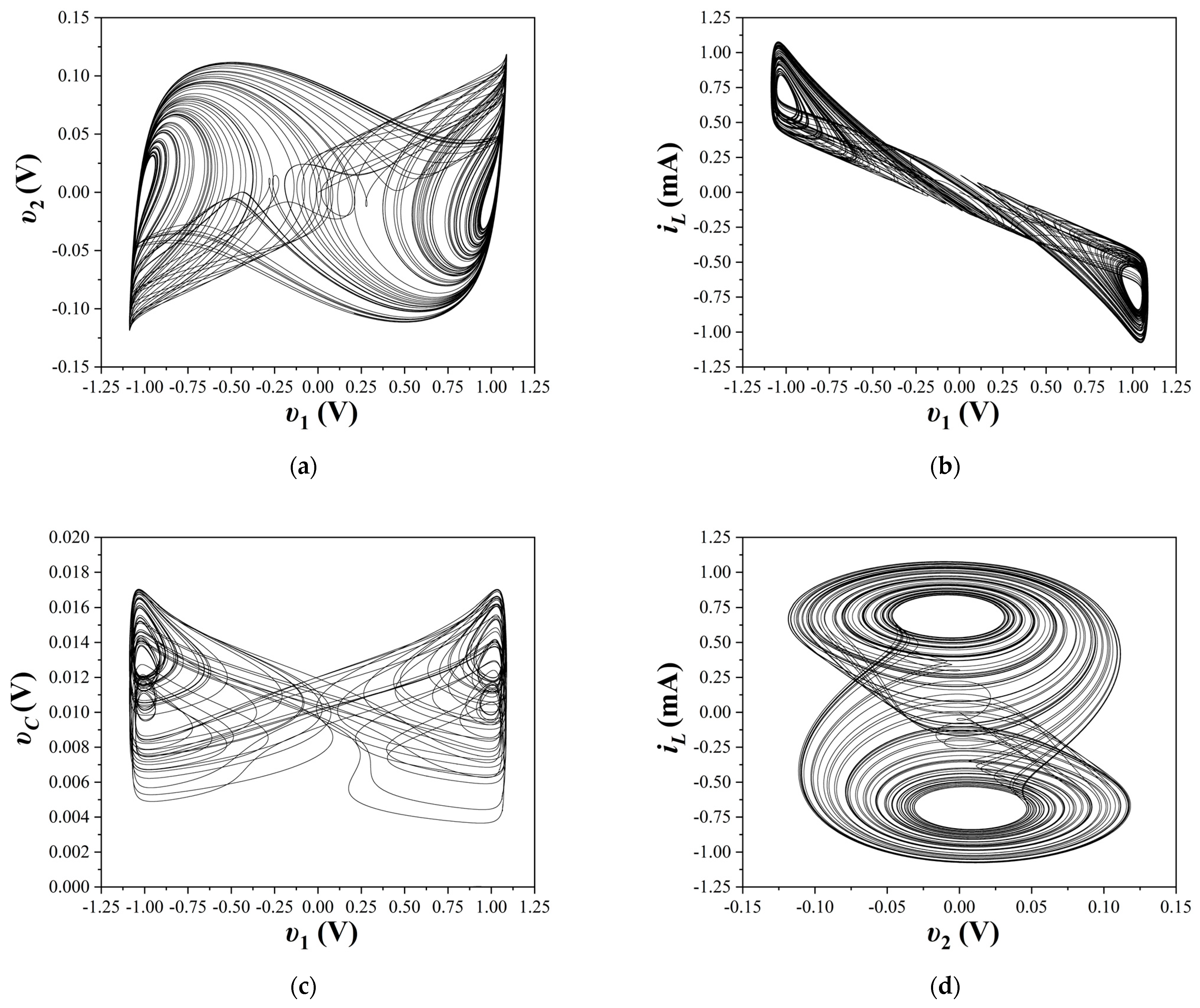
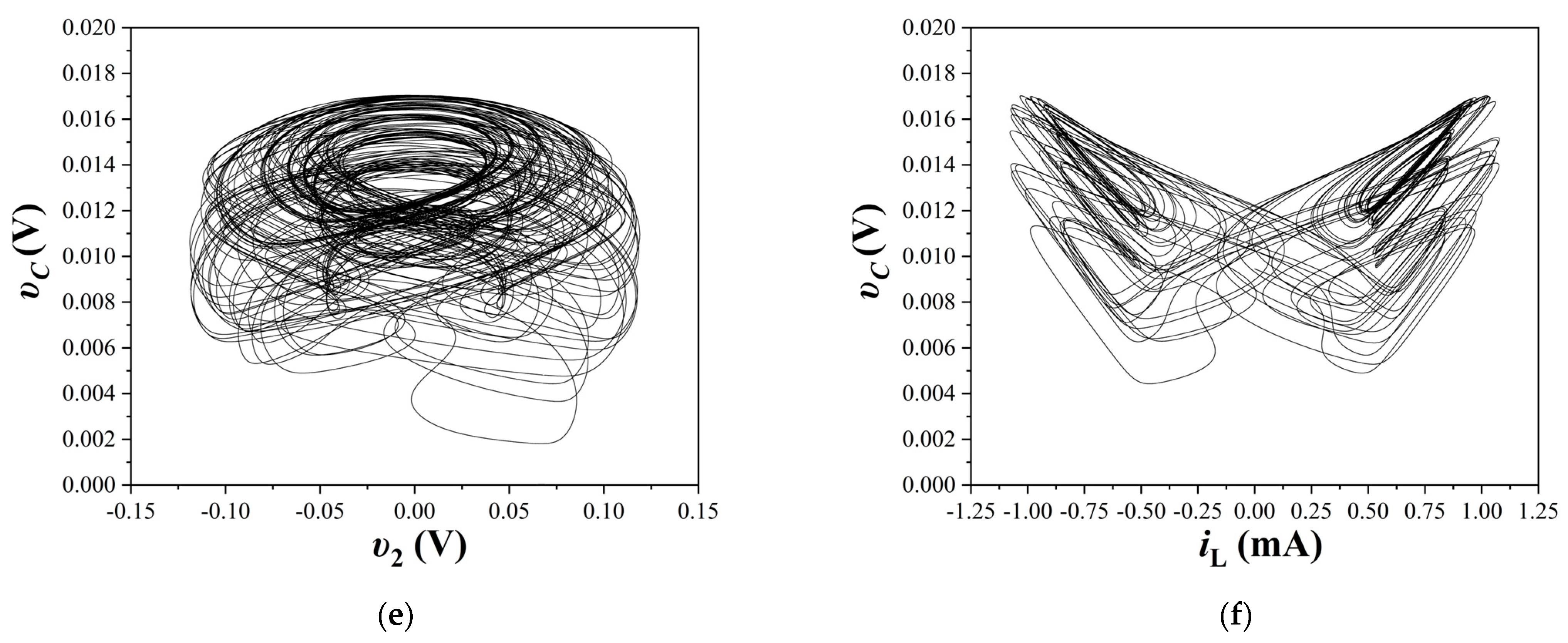
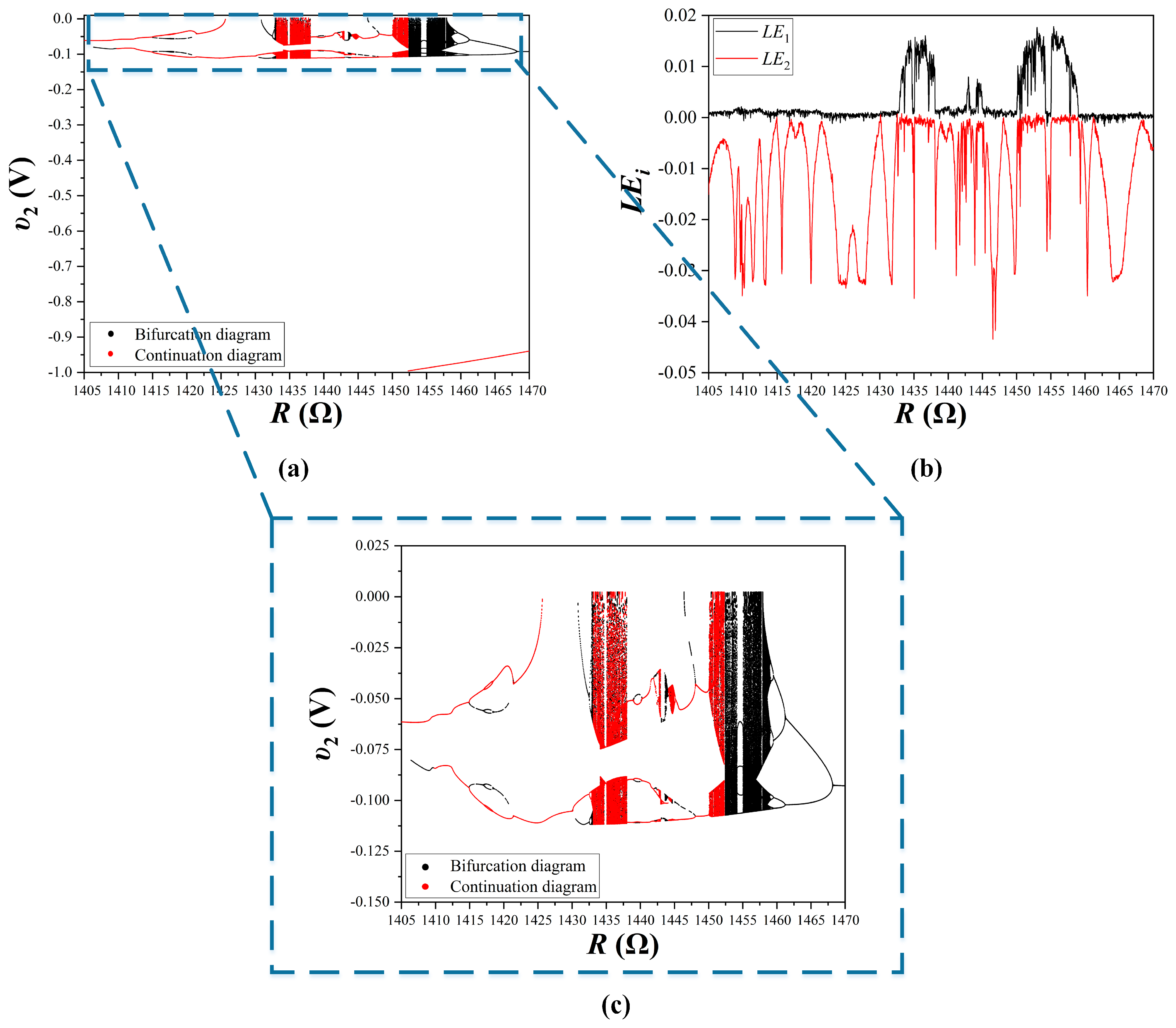
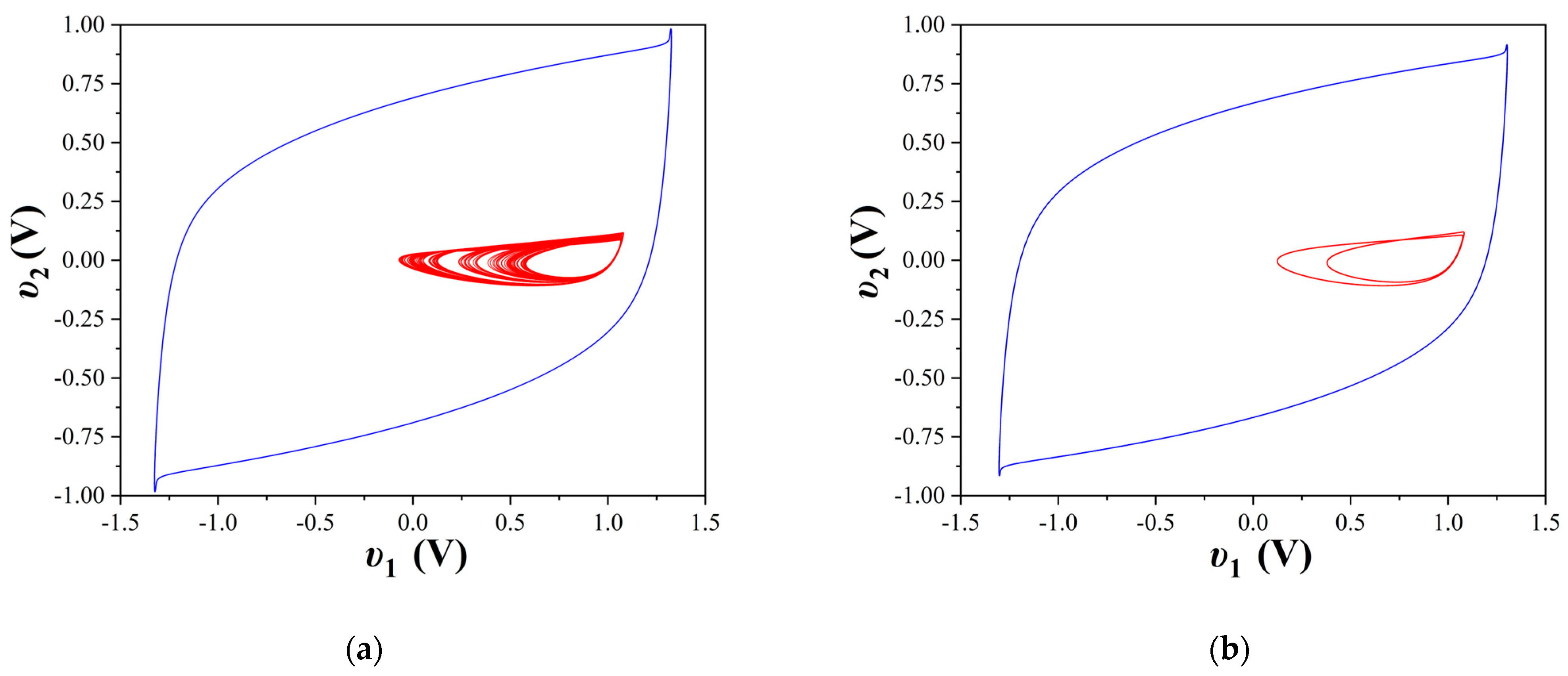
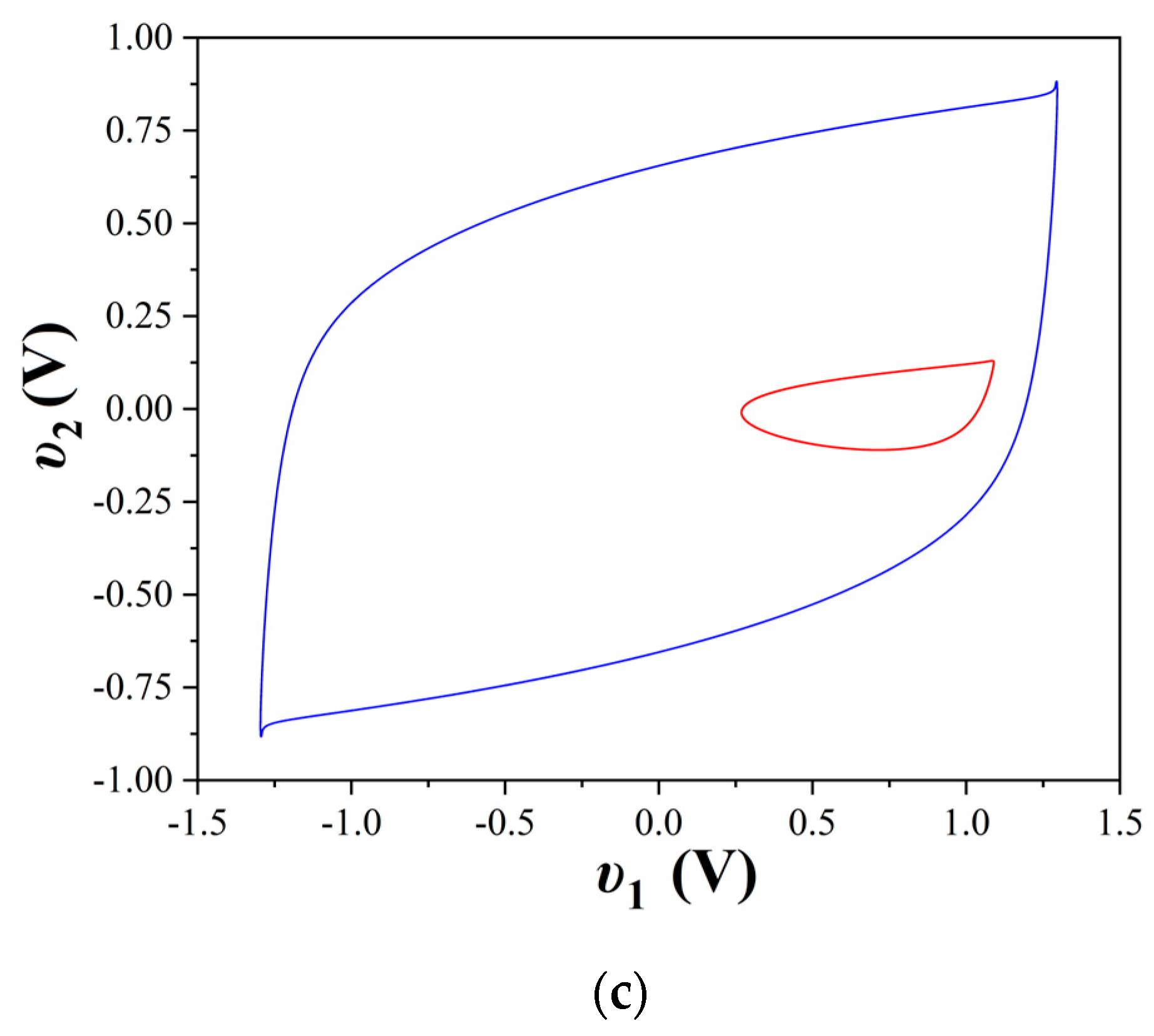
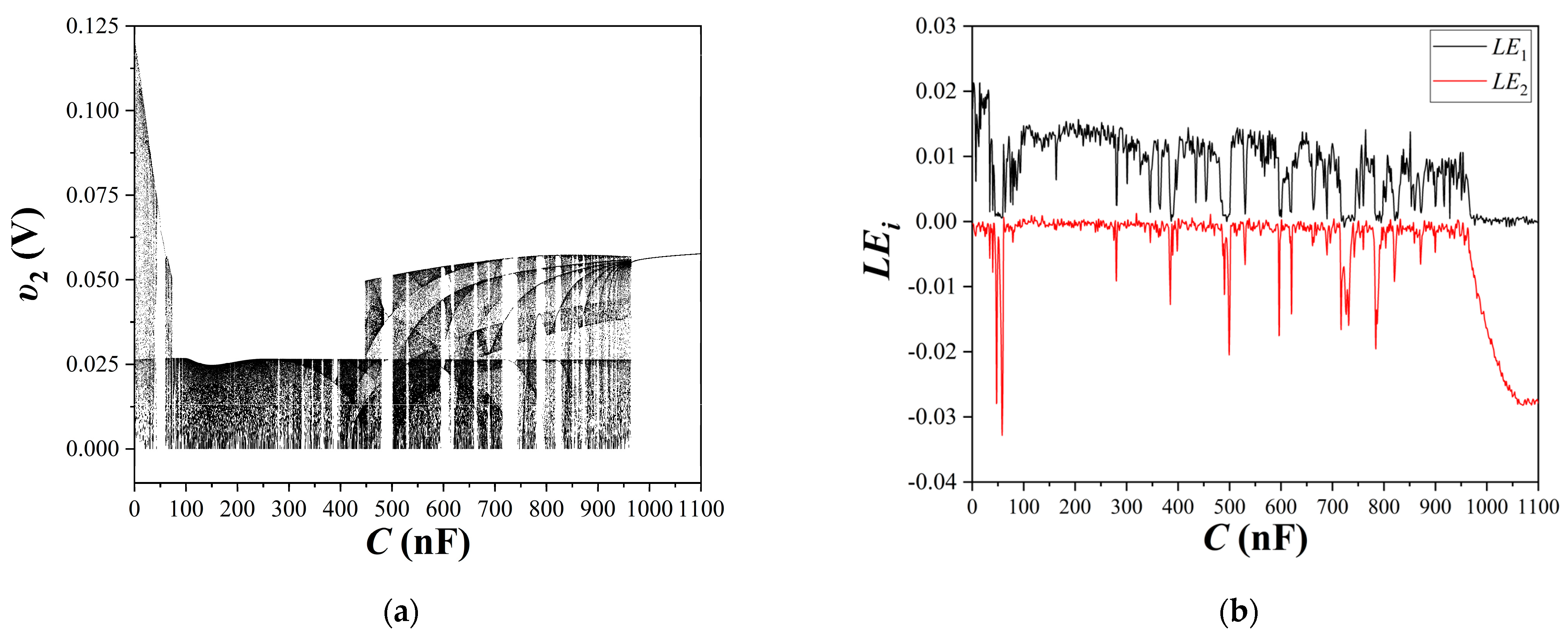
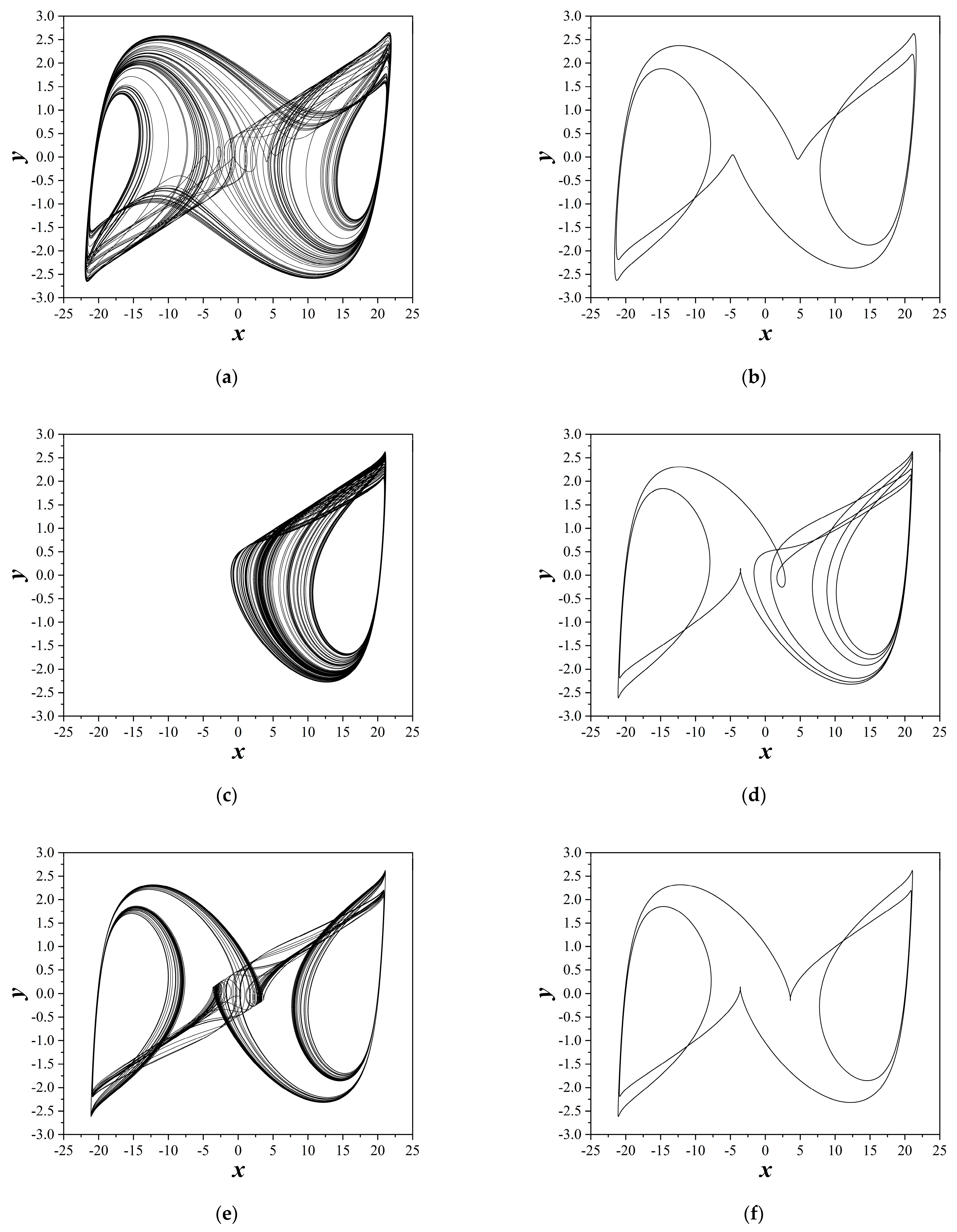
4. Simulation Results
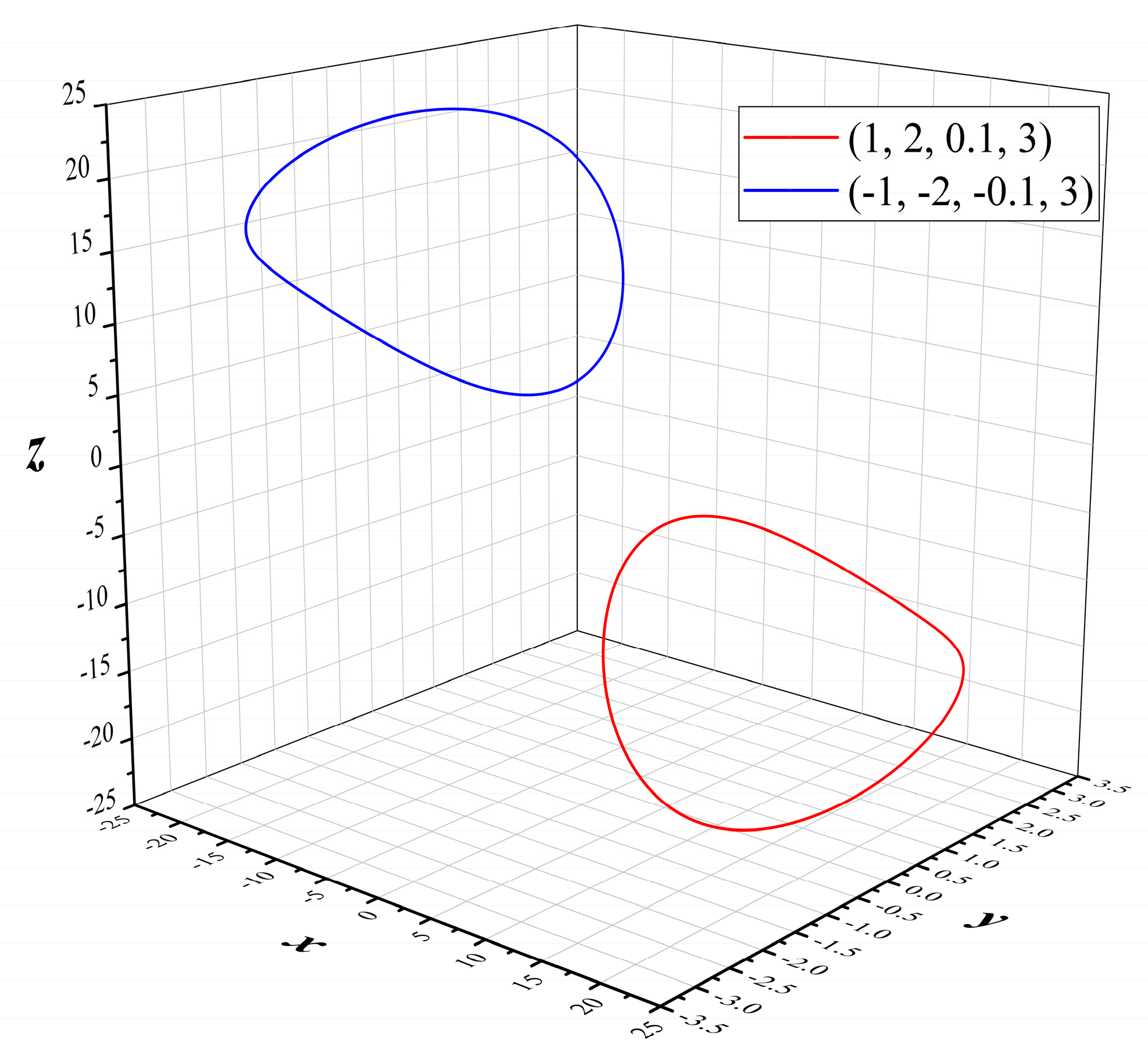
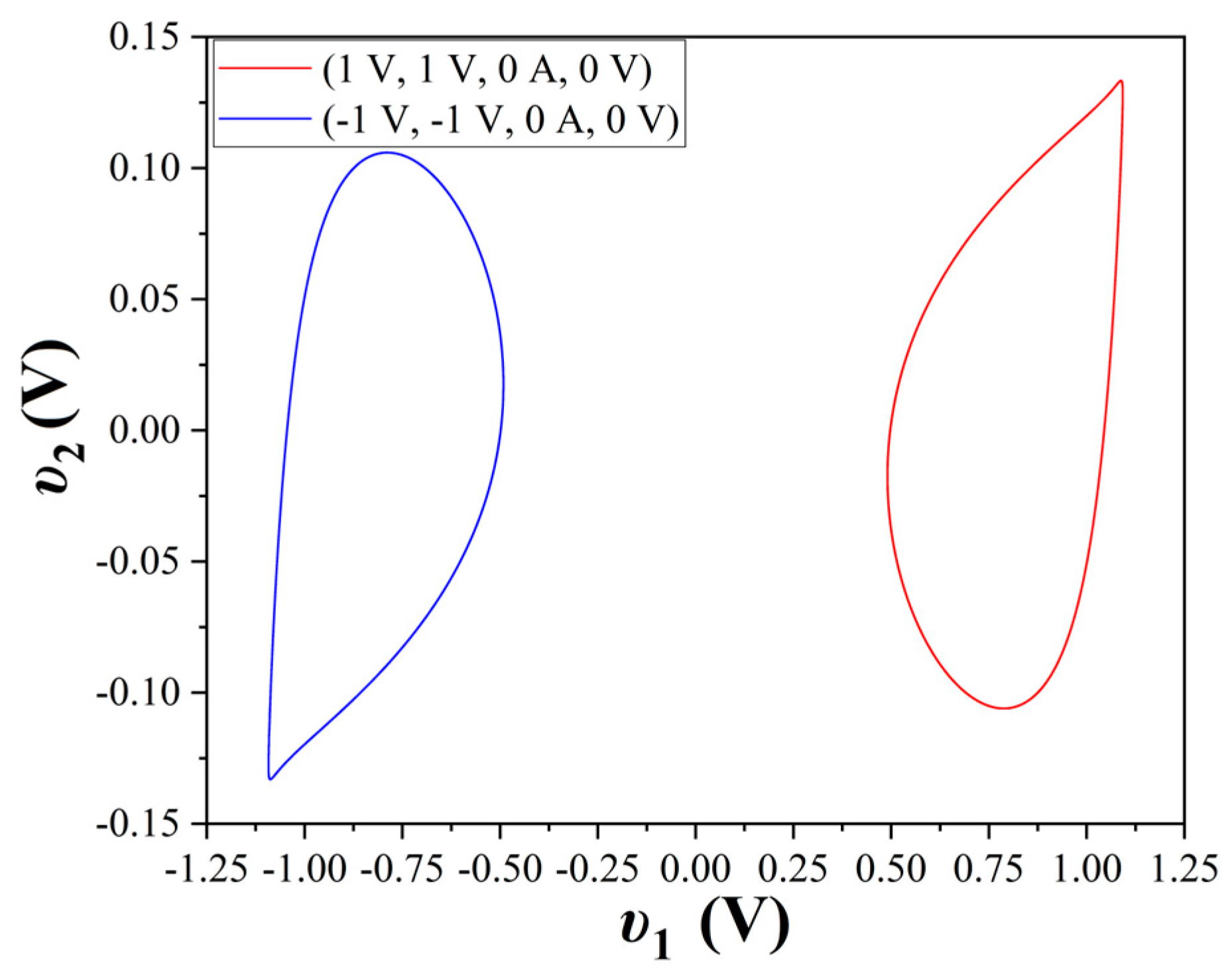
4.1. First Case of the Study
4.2. Second Case of the Study
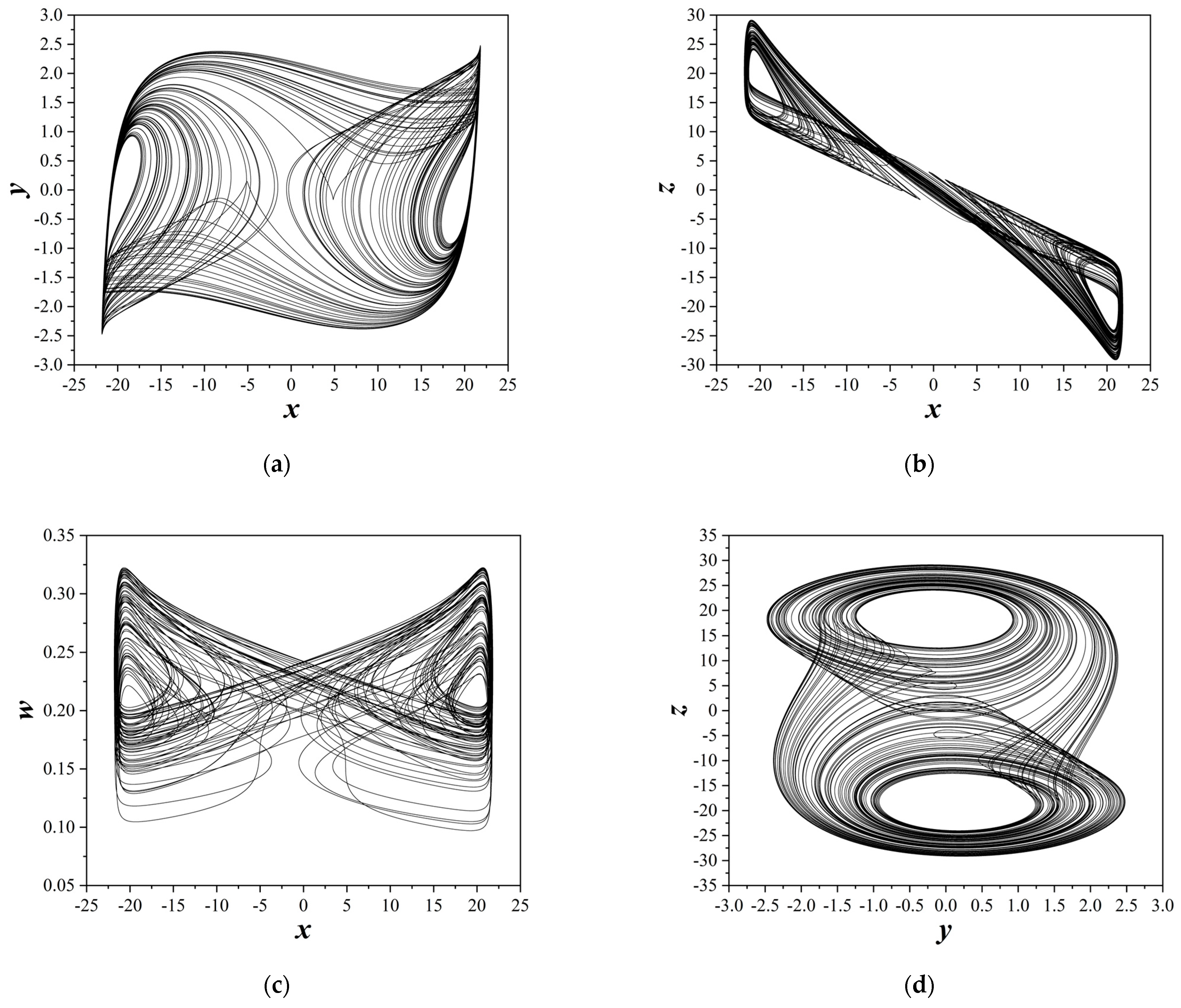
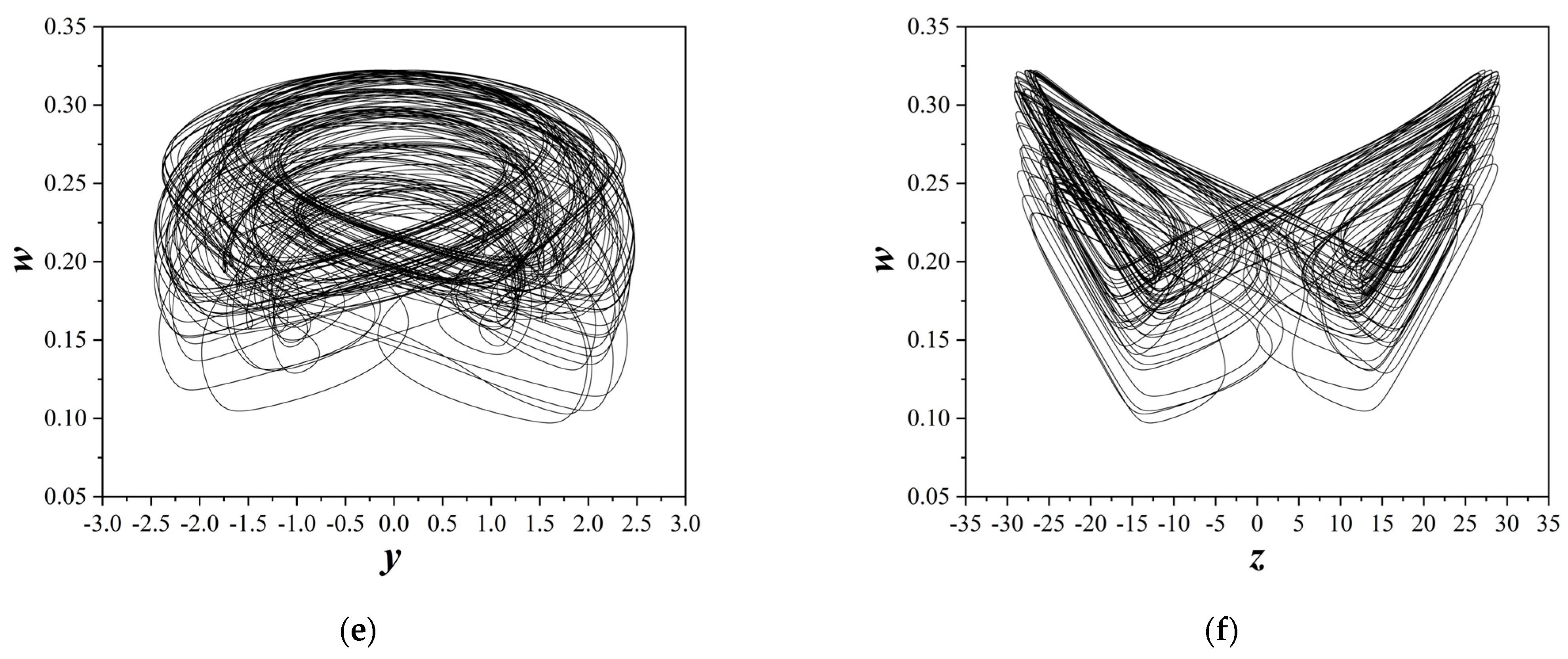
4.3. Third Case of the Study
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poincaré, J.H. Sur le problème des trois corps et les équations de la dynamique. Acta Math. 1890, 13, A3–A270. [Google Scholar]
- Lorenz, E.N. Deterministic non-periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman Company: New York, NY, USA, 1977. [Google Scholar]
- Field, R.J.; Györgyi, L. Chaos in Chemistry and Biochemistry; World Scientific Publishing: Singapore, 1993. [Google Scholar]
- Grebogi, C.; Yorke, J. The Impact of Chaos on Science and Society; United Nations University Press: Tokyo, Japan, 1997. [Google Scholar]
- Kyrtsou, C.; Vorlow, C. Complex dynamics in macroeconomics: A novel approach. In New Trends in Macroeconomics; Diebolt, C., Kyrtsou, C., Eds.; Springer: Berlin, Germany, 2005; pp. 223–245. [Google Scholar]
- May, R.M. Theoretical Ecology: Principles and Applications; W.B. Saunders Company: Philadelphia, PA, USA, 1976. [Google Scholar]
- Moon, F.C. Chaotic Vibrations: An Introduction for Applied Scientists and Engineers; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Hasselblatt, B.; Katok, A. A First Course in Dynamics: With a Panorama of Recent Developments; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Chua, L.O. Chua’s circuit 10 year later. Int. J. Bifurcat. Chaos 1994, 22, 279–305. [Google Scholar] [CrossRef]
- Chua, L.O.; Wu, C.W.; Huang, A.; Zhong, G.Q. A universal circuit for studying and generating chaos—Part I: Routes to chaos. IEEE Trans. Circuits Syst. I 1993, 40, 732–744. [Google Scholar] [CrossRef]
- Chua, L.O.; Wu, C.W.; Huang, A.; Zhong, G.Q. A universal circuit for studying and generating chaos—Part II: Strange attractors. IEEE Trans. Circuits Syst. I 1993, 40, 745–761. [Google Scholar] [CrossRef]
- Fortuna, L.; Frasca, M.; Xibilia, M.G. Chua’s Circuit Implementations: Yesterday, Today and Tomorrow; World Scientific: Singapore, 2009. [Google Scholar]
- Hull, A.W. The dynatron: A vacuum tube possessing negative electric resistance. Proc. Inst. Radio. Eng. 1918, 6, 5–35. [Google Scholar] [CrossRef]
- Brunetti, C. The transitron oscillator. Proc. IRE 1939, 27, 88–94. [Google Scholar] [CrossRef]
- Turner, L.B. The Kallirotron. An aperiodic negative-resitance triode combination. Radio. Rev. 1920, 1, 317–329. [Google Scholar]
- Arns, R.G. The other transistor: Early history of the metal-oxide semiconductor field-effect transistor. Eng. Sci. Educ. J. 1998, 7, 233–240. [Google Scholar] [CrossRef]
- Esaki, L. New phenomenon in narrow germanium p-n junctions. Phys. Rev. 1958, 109, 603. [Google Scholar] [CrossRef]
- Voelcker, J. The Gunn effect. IEEE Spectr. 1989, 26, 24. [Google Scholar] [CrossRef]
- Kennedy, M.P. Robust op amp realization of Chua’s circuit. Frequenz 1992, 46, 66–80. [Google Scholar] [CrossRef]
- Zhong, G.Q.; Ayron, F. Experimental confirmation of chaos from Chua’s circuit. Int. J. Circuit Theory Appl. 1985, 13, 93–98. [Google Scholar] [CrossRef]
- Matsumoto, T. A chaotic attractor from Chua’s circuit. IEEE Trans. Circuits Syst. 1984, 31, 1055–1058. [Google Scholar] [CrossRef]
- Matsumoto, T.; Chua, L.O.; Tokumasu, K. Double scroll via a two-transistor circuit. IEEE Trans. Circuits Syst. 1986, 33, 828–835. [Google Scholar] [CrossRef]
- Cruz, J.M.; Chua, L.O. A CMOS IC Nonlinear Resistor for Chua’s Circuit. IEEE Trans. Circuits Syst. I 1992, 39, 985–995. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor Found. Nature 2008, 453, 80. [Google Scholar] [CrossRef]
- Chua, L.O. Memristor-The missing circuit element. IEEE Trans. Circuits Syst. I 1971, 18, 507. [Google Scholar] [CrossRef]
- Driscoll, T.; Quinn, J.; Klein, S.; Kim, H.T.; Kim, B.J.; Pershin, Y.V.; Di Ventra, M.; Basov, D.N. Memristive adaptive filters. Appl. Phys. Lett. 2010, 97, 093502. [Google Scholar] [CrossRef]
- Yang, J.J.; Strukov, D.B.; Stewart, D.R. Memristive devices for computing. Nat. Nanotechnol. 2013, 8, 13. [Google Scholar] [CrossRef]
- Adhikari, S.P.; Yang, C.; Kim, H.; Chua, L.O. Memristor Bridge Synapse-Based Neural Network and Its Learning. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1426. [Google Scholar] [CrossRef] [PubMed]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. The memristor as an electric synapse—Synchronization phenomena. In Proceedings of the 2011 17th International Conference on Digital Signal Processing (DSP), Corfu, Greece, 6–8 July 2011; pp. 1–6. [Google Scholar]
- Pershin, Y.V.; Di Ventra, M. Experimental demonstration of associative memory with memristive neural networks. Neural Netw. 2010, 23, 881. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhang, C.; Chen, L.; Lai, J.; Tong, J. A novel memristor-based rSRAM structure for multiple-bit upsets immunity. IEICE Electron. Expr. 2012, 9, 861. [Google Scholar] [CrossRef]
- Shang, Y.; Fei, W.; Yu, H. Analysis and modeling of internal state variables for dynamic effects of nonvolatile memory devices. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 1906. [Google Scholar] [CrossRef]
- Shin, S.; Kim, K.; Kang, S.M. Memristor applications for programmable analog ICs. IEEE Trans. Nanotechnol. 2011, 10, 266. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Memristor oscillators. Int. J. Bifurcat Chaos 2008, 18, 3183. [Google Scholar] [CrossRef]
- Iu, H.H.C.; Fitch, A.L. Development of Memristor Based Circuits; World Scientific: Singapore, 2013. [Google Scholar]
- Muthuswamy, B. Implementing Memristor based chaotic circuits. Int. J. Bifurcat Chaos 2010, 20, 1335. [Google Scholar] [CrossRef]
- Bao, B.C.; Xu, J.P.; Zhou, G.H.; Ma, Z.H.; Zou, L. Chaotic memristive circuit: Equivalent circuit realization and dynamical Analysis. Chin. Phys. B 2011, 20, 1. [Google Scholar] [CrossRef]
- Li, Y.; Huang, X.; Guo, M. The generation, analysis and circuit implementation of a new memristor based chaotic system. Math. Probl. Eng. 2013, 2013, 398306. [Google Scholar] [CrossRef]
- Buscarino, A.; Fortuna, L.; Frasca, M.; Gambuzza, L.V. A chaotic circuit based on Hewlett-Packard memristor. Chaos 2012, 22, 023136. [Google Scholar] [CrossRef]
- Bao, B.; Yu, J.; Hu, F.; Liu, Z. Generalized memristor consisting of diode bridge with first order parallel RC filter. Int. J. Bifurcat Chaos 2014, 24, 1450143. [Google Scholar] [CrossRef]
- Stork, M. Simple chaotic oscillators with diode bridges. In Proceedings of the 7th IEEE Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 10–14 June 2018; pp. 1–4. [Google Scholar]
- Kengne, J.; Negou, A.N.; Tchiotsop, D. Antimonotonicity, chaos and multiple attractors in a novel autonomous memristor-based jerk circuit. Nonlinear Dyn. 2017, 88, 2589–2608. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Fotsin, H.B.; Negou, A.N.; Tchiotsop, D. Coexistence of multiple attractors and crisis route to chaos in a novel memristive diode bidge-based Jerk circuit. Chaos Solit Fractals 2016, 91, 180–197. [Google Scholar] [CrossRef]
- Fonzin, T.F.; Srinivasan, K.; Kengne, J.; Pelap, F.B. Coexisting bifurcations in a memristive hyperchaotic oscillator. AEU-Int. J. Electron. Commun. 2018, 90, 110–122. [Google Scholar] [CrossRef]
- Kengne, L.K.; Pone, J.R.M.; Fotsin, H.B. On the dynamics of chaotic circuits based on memristive diode-bridge with variable symmetry: A case study. Chaos Solit. Fractals 2021, 145, 110795. [Google Scholar] [CrossRef]
- Xu, Q.; Cheng, S.; Ju, Z.; Chen, M.; Wu, H. Asymmetric coexisting bifurcations and multi-stability in an asymmetric memristive diode-bridge-based jerk circuit. Chin. J. Phys. 2021, 70, 69–81. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, J.; Chen, M.; Xu, Q.; Bao, B. DC-offset induced asymmetry in memristive diode-bridge-based Shinriki oscillator. Chaos Solit. Fractals 2022, 154, 111624. [Google Scholar] [CrossRef]
- Ramadoss, J.; Kengne, J.; Telem, A.N.K.; Rajagopal, K. Broken symmetry and dynamics of a memristive diodes bridge-based Shinriki oscillator. Phys. A Stat. Mech. Appl. 2022, 588, 126562. [Google Scholar] [CrossRef]
- Chen, M.; Yu, J.; Yu, Q.; Li, C.; Bao, B. A memristive diode bridge-based canonical Chua’s circuit. Entropy 2014, 16, 6464–6476. [Google Scholar] [CrossRef]
- Basha, T.; Mohamed, I.R.; Chithra, A. Design and Study of Memristor based Non-autonomous Chua’s circuit. In Proceedings of the 4th IEEE International Conference on Devices, Circuits and Systems (ICDCS), Coimbatore, India, 16–17 March 2018; pp. 203–206. [Google Scholar]
- Chen, M.; Li, M.; Yu, Q.; Bao, B.; Xu, Q.; Wang, J. Dynamics of self-excited attractors and hidden attractors in generalized memristor-based Chua’s circuit. Nonlinear Dyn. 2015, 81, 215–226. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, N.; Bao, B.; Chen, M.; Li, C. A feasible memristive Chua’s circuit via bridging a generalized memristor. J. Appl. Anal. Comput. 2016, 6, 1152–1163. [Google Scholar]
- Chua, L. Everything you wish to know about memristors but are afraid to ask. In Handbook of Memristor Networks; Springer: Berlin, Germany, 2019; pp. 89–157. [Google Scholar]
- Sprott, J.C.; Wang, X.; Chen, G.R. Coexistence of point, periodic and strange attractors. Int. J. Bifurcat Chaos 2013, 23, 1350093. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Dawson, S.P.; Grebogi, C.; Yorke, J.A.; Kan, I.; Koçak, H. Antimonotonicity: Inevitable reversals of period-doubling cascades. Phys. Lett. A 1992, 162, 249–254. [Google Scholar] [CrossRef]
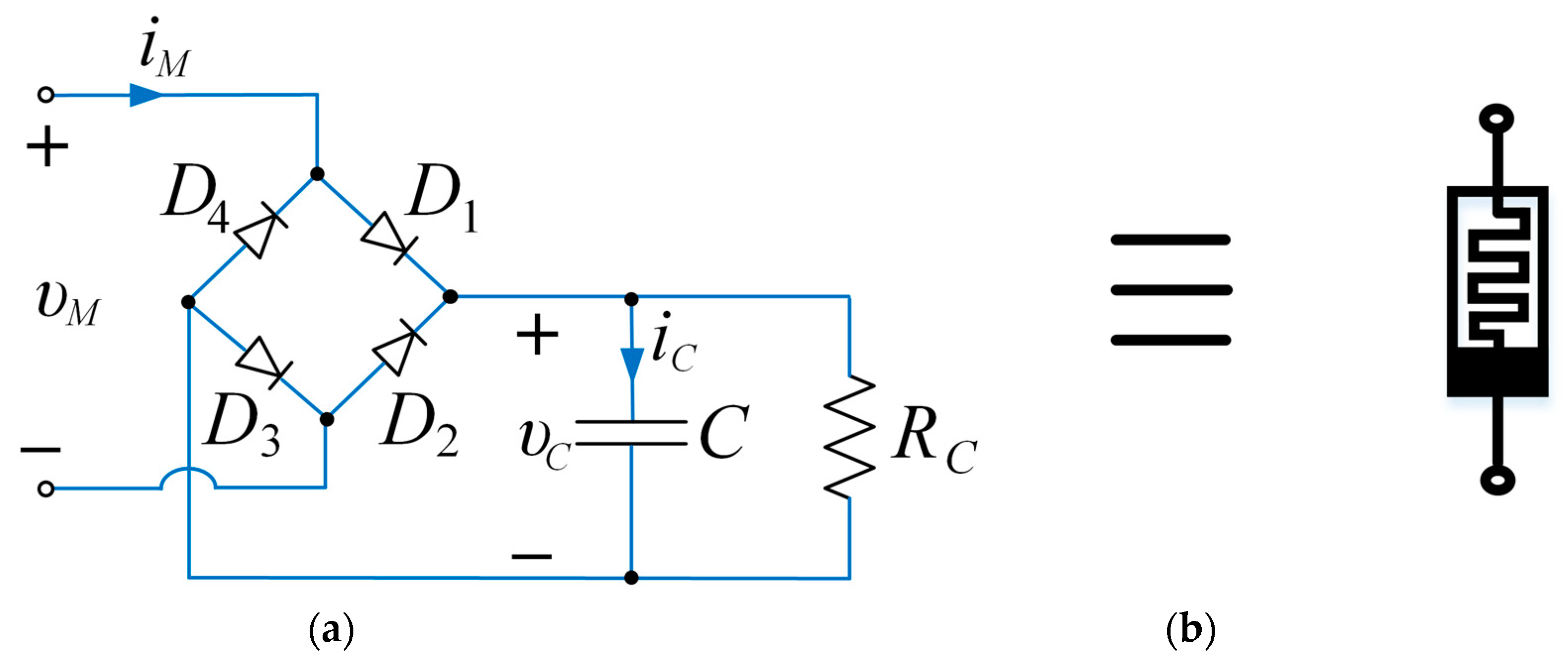
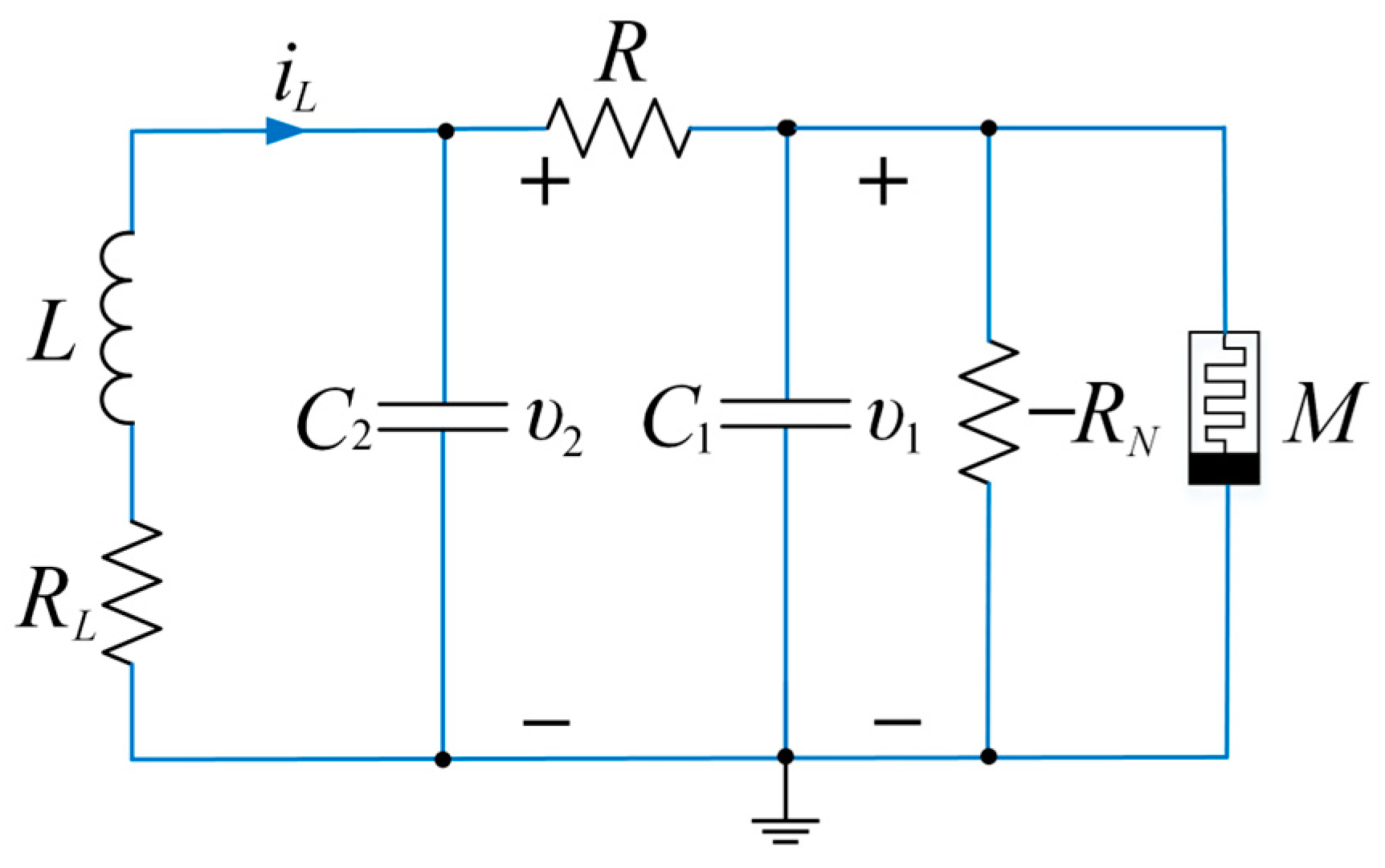
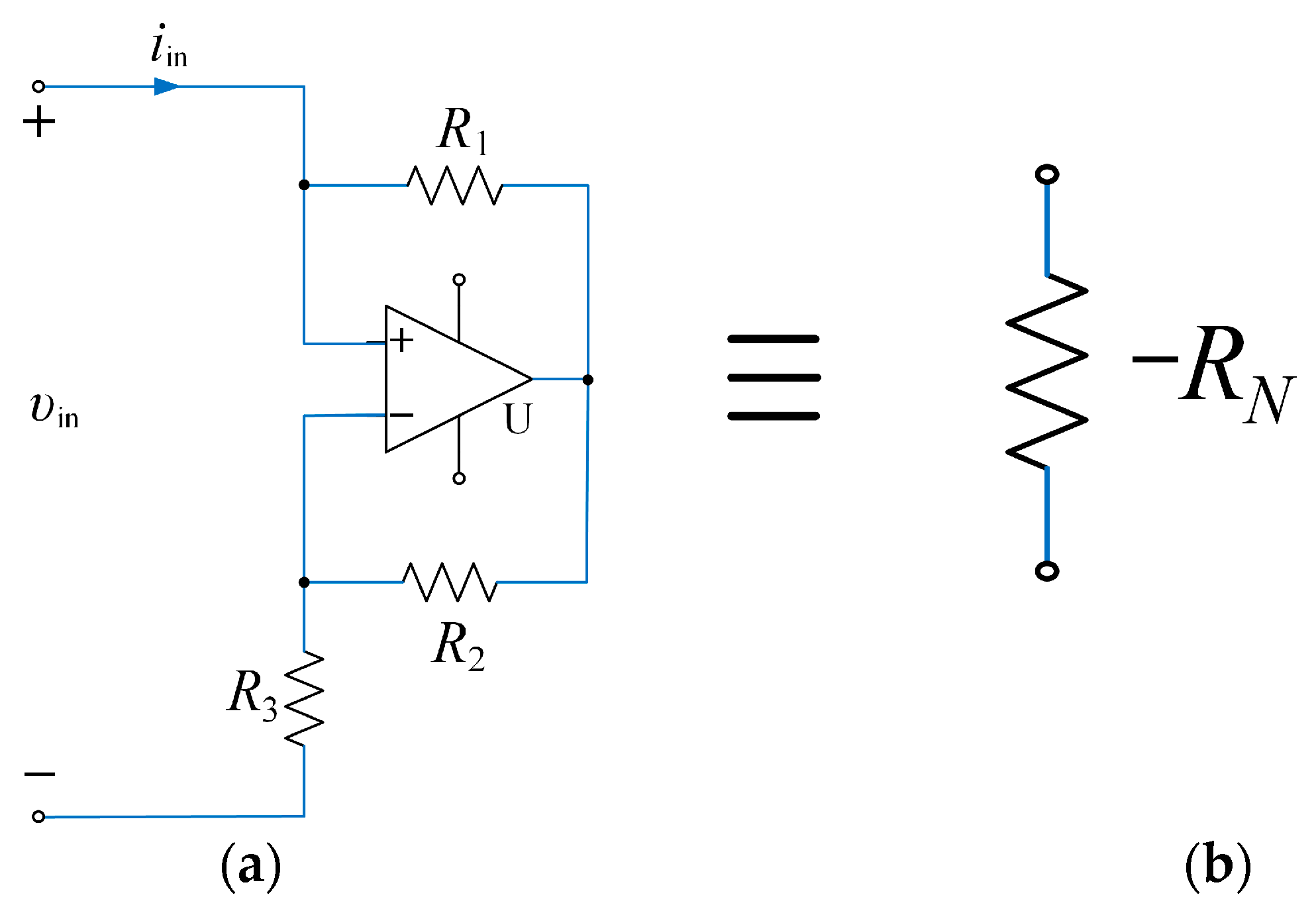



| Parameters | Significations | Values |
|---|---|---|
| Saturation current of 1N4149 diode | 0.1 pA | |
| Thermal voltage of 1N4149 diode | 27 mV | |
| n | Emission coefficient of 1N4149 diode | 1 |
| C | Capacitance | 1 μF |
| RC | Resistance | 500 Ω |
| Parameters | Significations | Values |
|---|---|---|
| Inductance | 15 mH | |
| Capacitance | 8 nF | |
| Capacitance | Variable | |
| R | Resistance | Variable |
| Resistance | 10 Ω | |
| = | Linear resistance of the NIC | 1400 Ω |
| = | Other resistances of the NIC | 1000 Ω |
| VS | Voltage Supply | ±15 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volos, C. Dynamical Analysis of a Memristive Chua’s Oscillator Circuit. Electronics 2023, 12, 4734. https://doi.org/10.3390/electronics12234734
Volos C. Dynamical Analysis of a Memristive Chua’s Oscillator Circuit. Electronics. 2023; 12(23):4734. https://doi.org/10.3390/electronics12234734
Chicago/Turabian StyleVolos, Christos. 2023. "Dynamical Analysis of a Memristive Chua’s Oscillator Circuit" Electronics 12, no. 23: 4734. https://doi.org/10.3390/electronics12234734
APA StyleVolos, C. (2023). Dynamical Analysis of a Memristive Chua’s Oscillator Circuit. Electronics, 12(23), 4734. https://doi.org/10.3390/electronics12234734






