Real-Time Telemetry-Based Recognition and Prediction of Satellite State Using TS-GCN Network
Abstract
:1. Introduction
- This study proposes a new satellite wheel motion state, the unloading and subsequent maneuver process, which addresses the issue of insufficient use of on-orbit telemetry data for evaluating the operating state of satellite attitude control systems in past satellite wheel designs. By analyzing the telemetry data of a certain model of an on-orbit satellite’s attitude system, this study fills the gap in using on-orbit telemetry data for analyzing the satellite attitude control system and fully utilizes on-orbit telemetry data for evaluating the operating state of the satellite attitude control system, which has important reference value;
- We propose an advanced recognition and prediction model based on a two-stage graph neural network model for the research gap in the state recognition and prediction of the satellite attitude control system. This paradigm aims to optimize the model’s feature extraction capability by aggregating different data features, thus achieving a significant improvement in the accuracy and robustness of recognition and prediction tasks and providing a baseline for this problem.
2. Problem Description
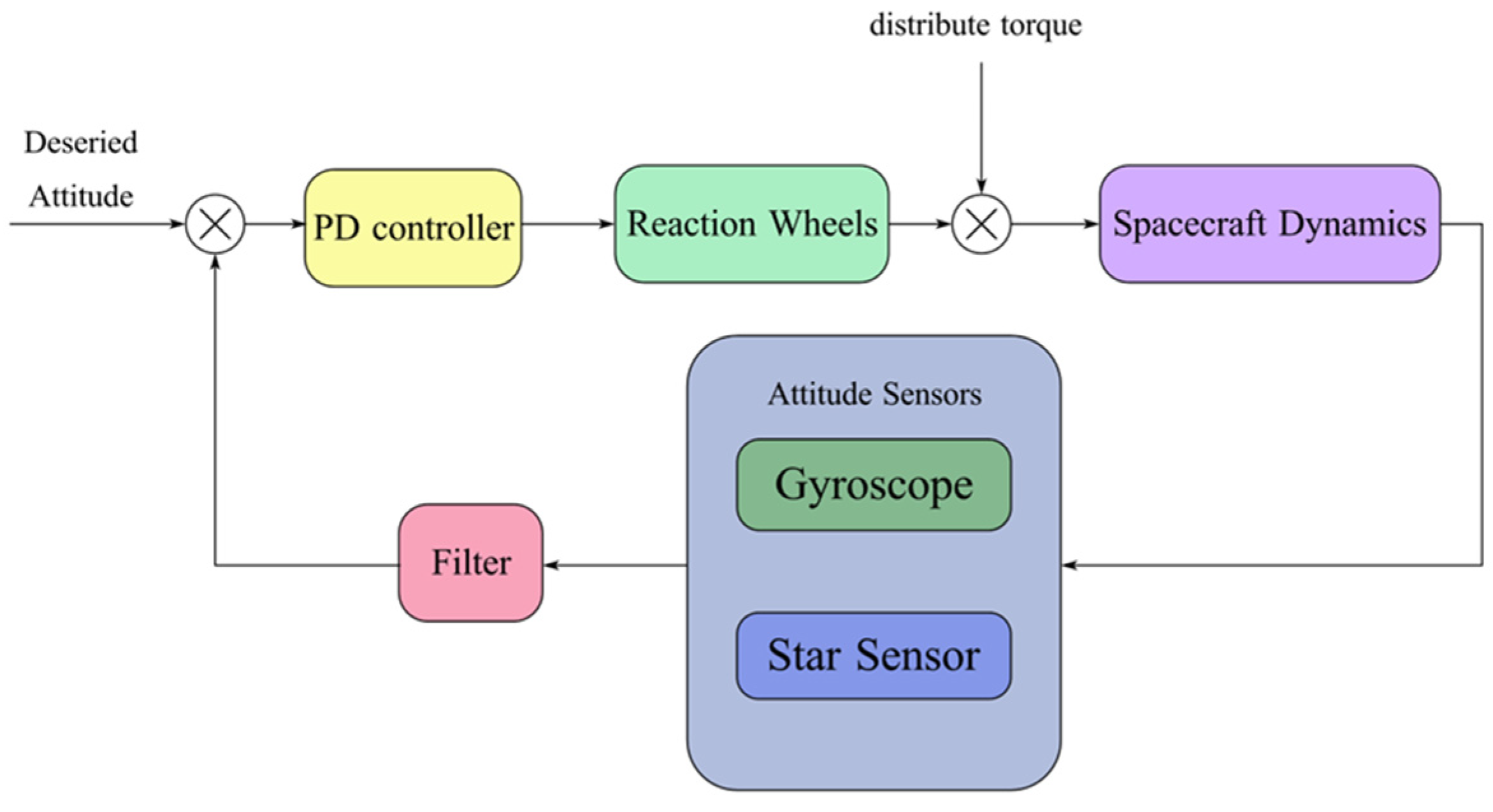
2.1. Satellite Attitude Control System and Its Telemetry
2.2. Model-Based Working States of Satellite Reaction Wheels
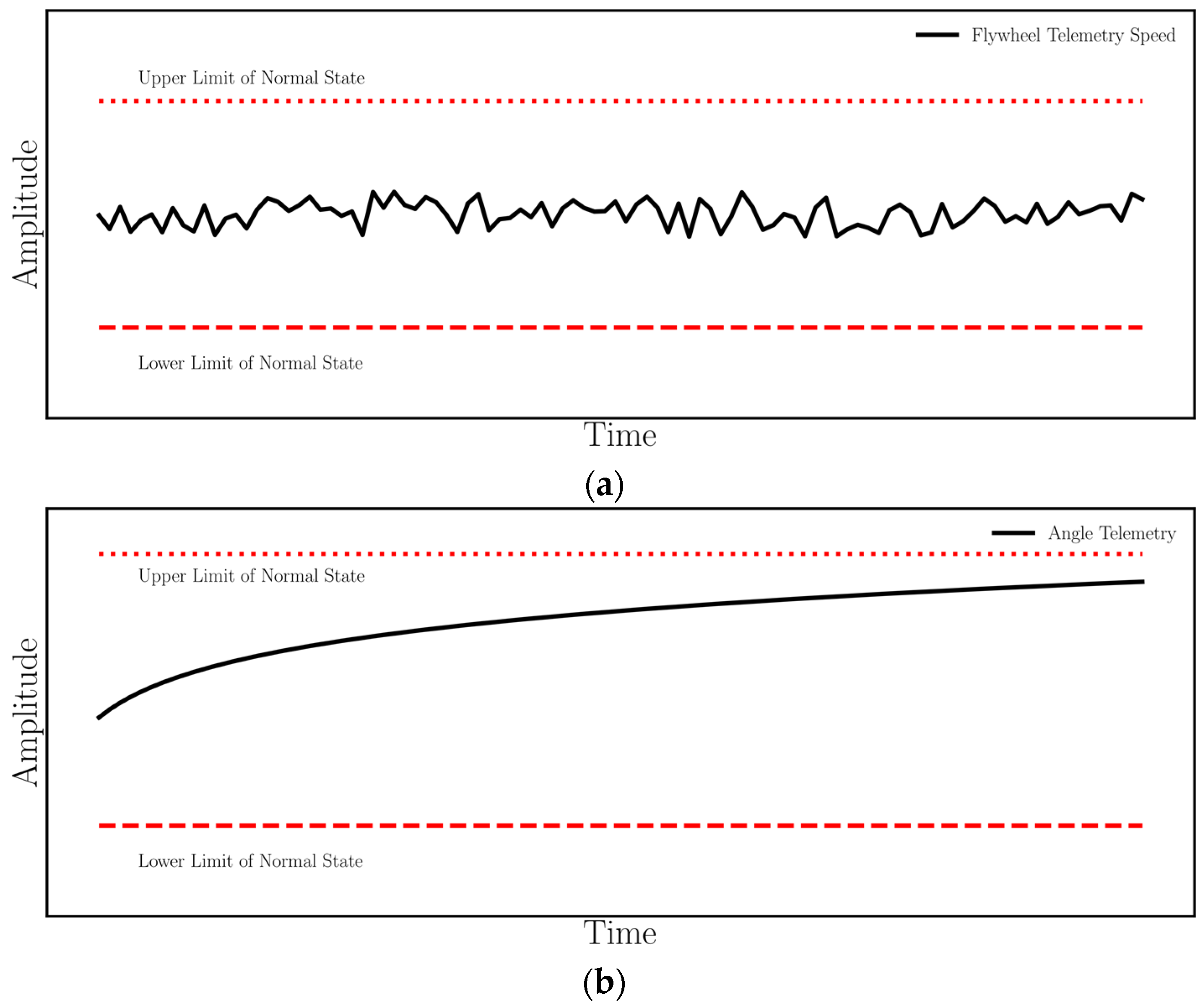
- Normal State:
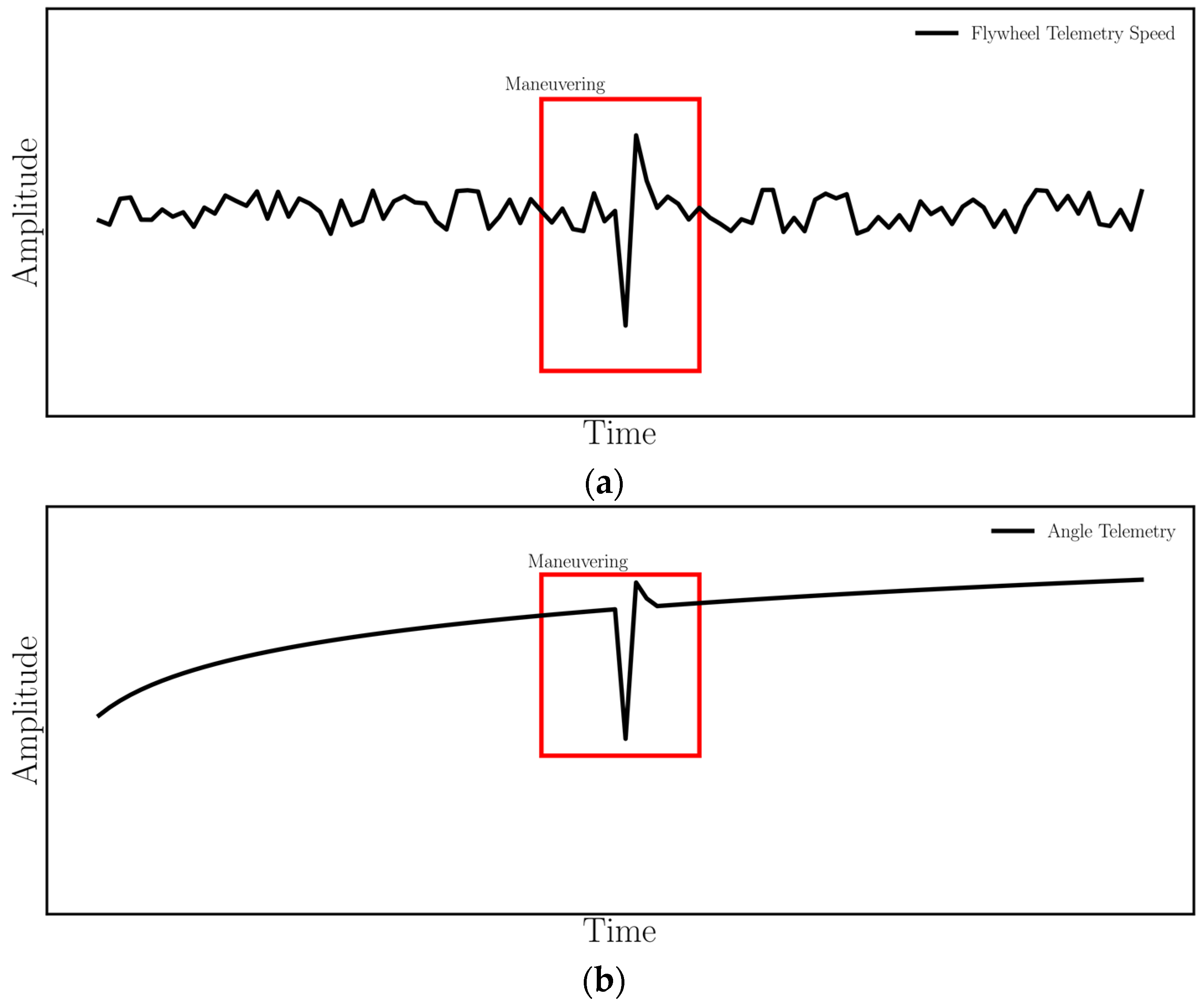
- Maneuvering:
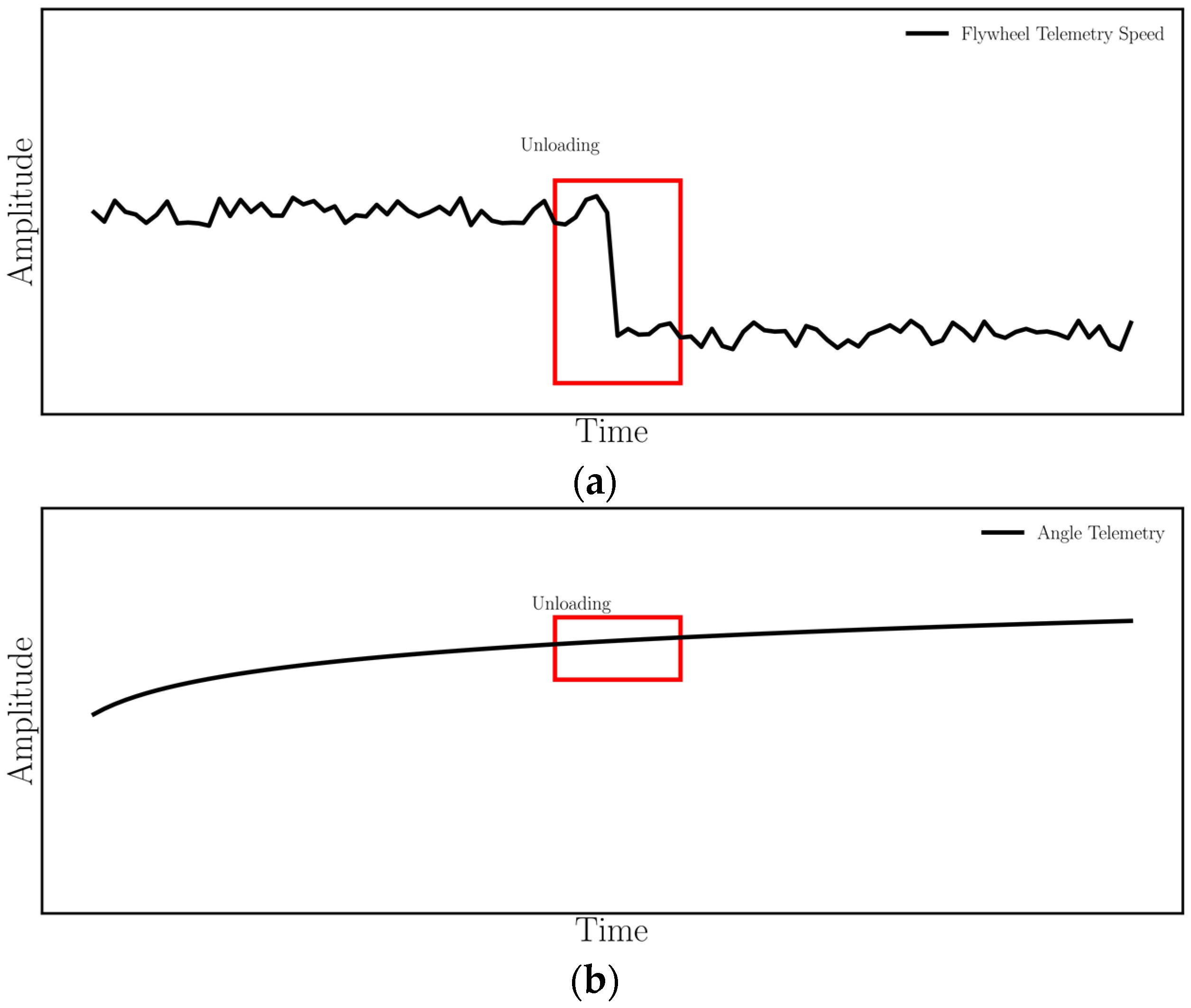
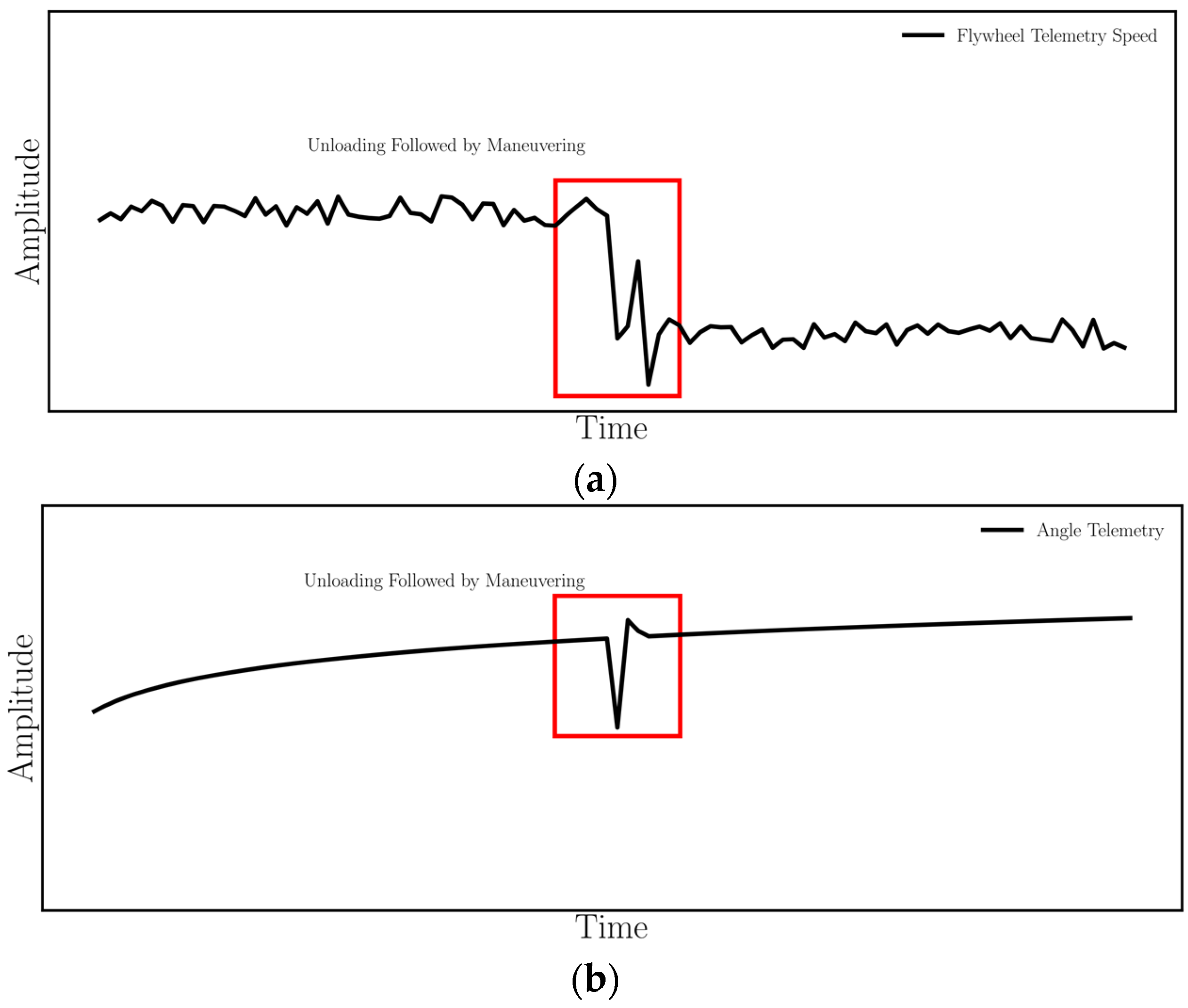
- Unloading:
2.3. Telemetry-Based Working State of Satellite Reaction Wheels
2.4. Problem of Recognition and Prediction of Working State of Satellite Reaction Wheels
3. Methodology
3.1. Satellite Telemetry Data to Graph Data
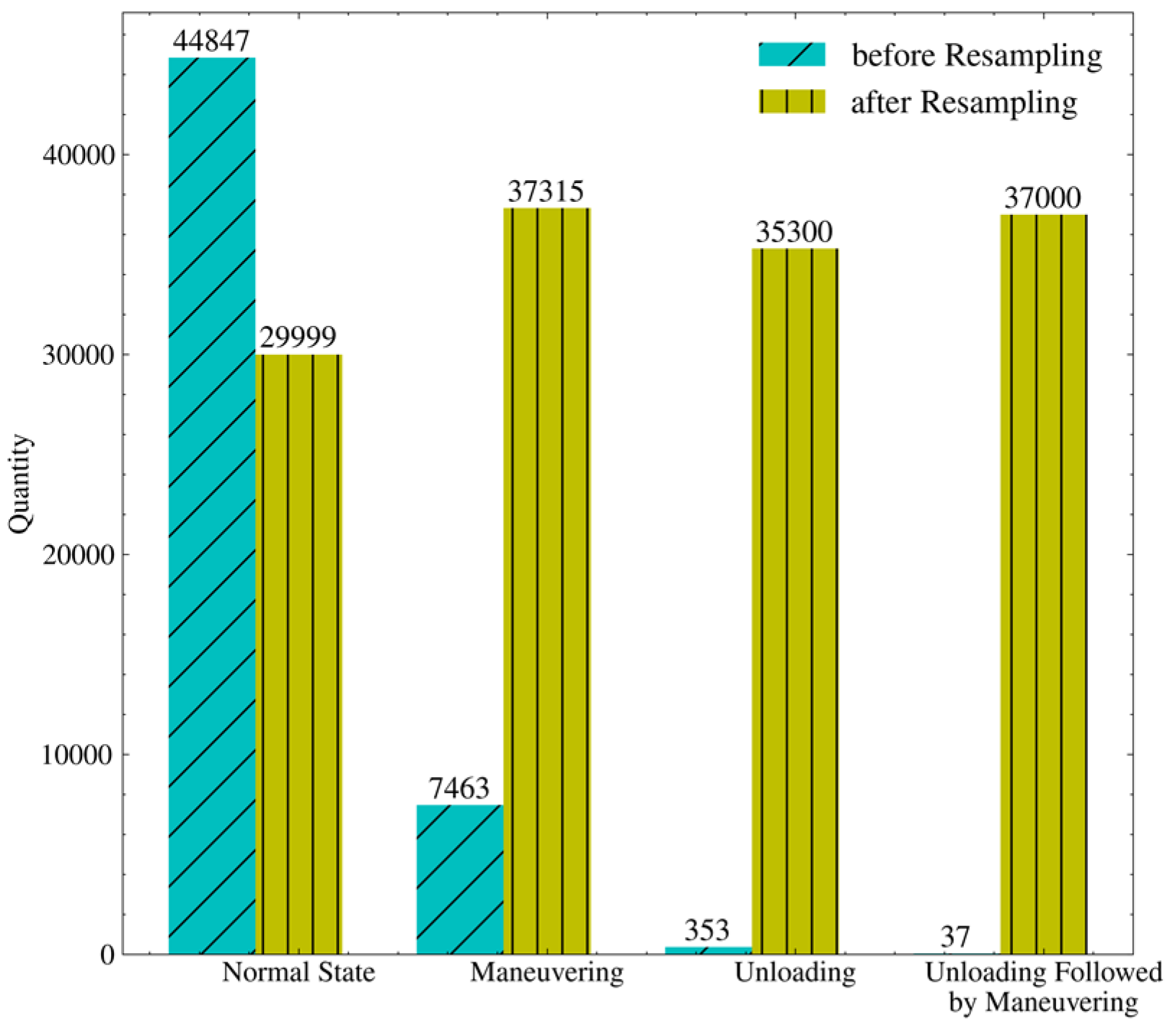
3.2. Data Resampling
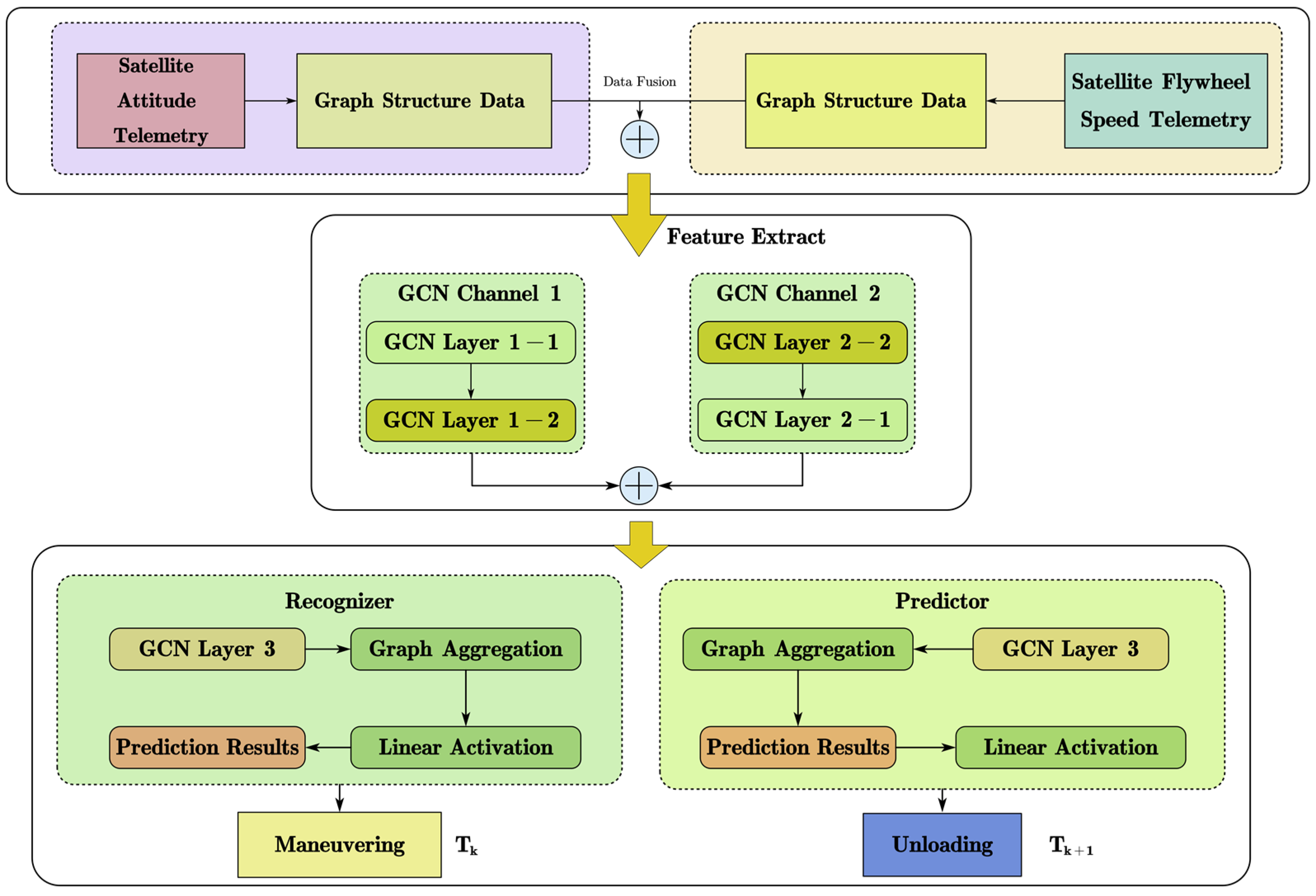
3.3. Two-Step Graph Neural Network
3.4. Process of State Recognition and Prediction
- Telemetry data to graph structure data conversion. Firstly, the telemetry data from the satellite attitude control system are reconstructed into a graph structure through normalization and resampling. Subsequently, the training graph set and the verification graph set for state recognition are generated;
- Recognition model training. The training graph set is input into the dual-channel graph convolutional network state recognition module, and feature extraction and feature fusion are performed in turn through dual-channel graph convolutional layers. The corresponding classification results, loss, and accuracy are output through the graph information aggregation layer and classification activation layer;
- Prediction model training. The training graph set is fed into the graph convolutional network fusion prediction module. Through the graph convolutional layers and a linear predictor, the module generates categorical predictions for the operating state of the satellite attitude control system at the next moment, along with the corresponding loss value with the cross-entropy loss function;
- Model validation. The test set is fed into the previously trained TS-GCN model. The model performs data recognition, classifies the data, and predicts the operating state of the satellite attitude control system for the next moment.
4. Experiments and Results
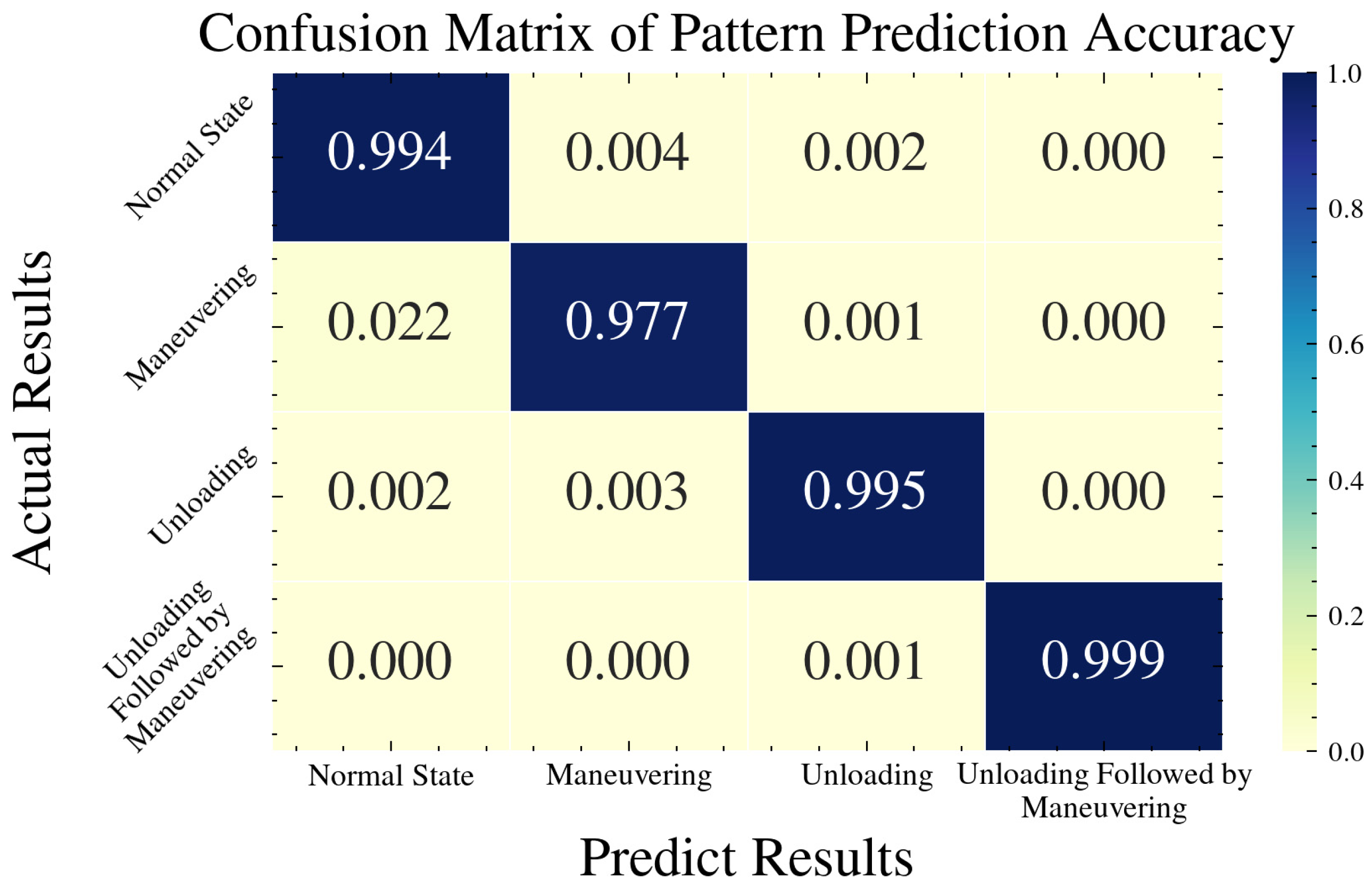
4.1. Result of State Recognition
4.2. Result of State Prediction
5. Conclusions
- This study introduces a novel operational state for the reaction wheel compared to the conventional state, incorporating an analysis of its performance using historical telemetry data. Building upon this framework, the problems of recognizing and predicting the operational modes of the satellite attitude control system are proposed;
- To address the problems of recognizing and predicting the operational states of the satellite attitude control system, this study proposes a two-step graph convolutional neural network (GCN) model. The model is designed based on the GCN framework and aims to achieve intelligent satellite management and control (ISMC) by providing a deep learning-based solution. In the first step, the proposed graph convolutional state recognition module utilizes satellite telemetry data for the task of recognizing the system’s operational states. Compared to traditional neural network models such as Standard CCN and ResNet-18, this module achieves an accuracy of 98.93% and has a smaller number of network parameters. In the second step, the model achieves an accuracy of 99.13% for the state prediction task. This research fills a research gap in the field of recognizing and predicting the operational states of satellite attitude control systems based on satellite telemetry data. Compared to traditional single-channel networks, multi-channel networks can reduce feature loss and have better performance. The model performs data recognition, classifies the data, and predicts the operating state of the satellite attitude control system for the next moment. This process enables high-precision state recognition, classification, and prediction of satellite attitude control system telemetry data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Furano, G.; Meoni, G.; Dunne, A.; Moloney, D.; Ferlet-Cavrois, V.; Tavoularis, A.; Byrne, J.; Buckley, L.; Psarakis, M.; Voss, K.-O.; et al. Towards the use of artificial intelligence on the edge in space systems: Challenges and opportunities. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 44–56. [Google Scholar] [CrossRef]
- Tian, M.; Huang, P.; Ma, G.; Li, W.; Li, X. Intelligent Management of Satellite Ground System. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 4045–4050. [Google Scholar]
- Plis, S.M.; Ferguson, D.C.; Plis, E.A. Application of Machine Learning to Investigation of Arcing on Geosynchronous Satellites. J. Astronaut. Sci. 2022, 69, 570–580. [Google Scholar] [CrossRef]
- Oche, P.A.; Ewa, G.A.; Ibekwe, N. Applications and challenges of artificial intelligence in space missions. IEEE Access 2021, 1. [Google Scholar] [CrossRef]
- Yang, C.; Lu, W.; Xia, Y. Uncertain optimal attitude control for space power satellite based on interval Riccati equation with non-probabilistic time-dependent reliability. Aerosp. Sci. Technol. 2023, 139, 108406. [Google Scholar] [CrossRef]
- Ibrahim, S.K.; Ahmed, A.; Zeidan, M.A.E.; Ziedan, I.E. Machine Learning Methods for Spacecraft Telemetry Mining. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1816–1827. [Google Scholar] [CrossRef]
- Yang, J.; Du, C.; Liu, W.; Wang, T.; Yan, L.; Gao, Y.; Cheng, X.; Zuo, P.; Ma, Y.; Yin, G.; et al. State-of-health estimation for satellite batteries based on the actual operating parameters--Health indicator extraction from the discharge curves and state estimation. J. Energy Storage 2020, 31, 101490. [Google Scholar] [CrossRef]
- Sebestyen, G.; Fujikawa, S.; Galassi, N.; Chuchra, A. Low Earth Orbit Satellite Design; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Hassanien, A.E.; Darwish, A.; Abdelghafar, S. Machine learning in telemetry data mining of space mission: Basics, challenging and future directions. Artif. Intell. Rev. 2020, 53, 3201–3230. [Google Scholar] [CrossRef]
- Xue, Z.; Liu, J.; Wu, C.; Tong, Y. Review of in-space assembly technologies. Chin. J. Aeronaut. 2021, 34, 21–47. [Google Scholar] [CrossRef]
- Abdelghafar, S.; Darwish, A.; Hassanien, A.E. Intelligent health monitoring systems for space missions based on data mining techniques. In Machine Learning and Data Mining in Aerospace Technology; Springer: Berlin/Heidelberg, Germany, 2020; pp. 65–78. [Google Scholar]
- Pang, J.; Liu, D.; Peng, Y.; Peng, X. Intelligent pattern analysis and anomaly detection of satellite telemetry series with improved time series representation. J. Intell. Fuzzy Syst. 2018, 34, 3785–3798. [Google Scholar] [CrossRef]
- Chen, J.; Pi, D.; Wu, Z.; Zhao, X.; Pan, Y.; Zhang, Q. Imbalanced satellite telemetry data anomaly detection model based on Bayesian LSTM. Acta Astronaut. 2021, 180, 232–242. [Google Scholar] [CrossRef]
- Wang, X.; Pi, D.; Zhang, X.; Liu, H.; Guo, C. Variational transformer-based anomaly detection approach for multivariate time series. Measurement 2022, 191, 110791. [Google Scholar] [CrossRef]
- Yang, L.; Ma, Y.; Zeng, F.; Peng, X.; Liu, D. Improved deep learning based telemetry data anomaly detection to enhance spacecraft operation reliability. Microelectron. Reliab. 2021, 126, 114311. [Google Scholar] [CrossRef]
- Pan, D.; Song, Z.; Nie, L.; Wang, B. Satellite telemetry data anomaly detection using bi-lstm prediction based model. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 1–6. [Google Scholar]
- Zilong, Z.; Wei, Q. Intelligent fault diagnosis of rolling bearing using one-dimensional multi-scale deep convolutional neural network based health state classification. In Proceedings of the 2018 IEEE 15th International Conference on Networking, Sensing and Control (ICNSC), Zhuhai, China, 27–29 March 2018; pp. 1–6. [Google Scholar]
- Xie, L.; Pi, D.; Zhang, X.; Chen, J.; Luo, Y.; Yu, W. Graph neural network approach for anomaly detection. Measurement 2021, 180, 109546. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Z.; Sun, C.; Yan, R.; Chen, X. Multireceptive field graph convolutional networks for machine fault diagnosis. IEEE Trans. Ind. Electron. 2020, 68, 12739–12749. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, J.; Peng, T.; Yang, C. Graph Convolutional Network-Based Method for Fault Diagnosis Using a Hybrid of Measurement and Prior Knowledge. IEEE Trans. Cybern. 2022, 52, 9157–9169. [Google Scholar] [CrossRef]
- Li, T.; Zhou, Z.; Li, S.; Sun, C.; Yan, R.; Chen, X. The emerging graph neural networks for intelligent fault diagnostics and prognostics: A guideline and a benchmark study. Mech. Syst. Signal Process. 2022, 168, 108653. [Google Scholar] [CrossRef]
- Welling, M.; Kipf, T.N. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations (ICLR 2017), Toulon, France, 24–26 April 2017. [Google Scholar]
- Yang, C.Y.; Zhou, K.B.; Liu, J. SuperGraph: Spatial-Temporal Graph-Based Feature Extraction for Rotating Machinery Diagnosis. IEEE Trans. Ind. Electron. 2022, 69, 4167–4176. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.M.; Zhan, Z.H.; Wu, Q.Q.; Zhang, H.D. Multiscale Graph-Guided Convolutional Network with Node Attention for Intelligent Health State Diagnosis of a 3-PRR Planar Parallel Manipulator. IEEE Trans. Ind. Electron. 2022, 69, 11733–11743. [Google Scholar] [CrossRef]
- Zhou, K.B.; Yang, C.Y.; Liu, J.; Xu, Q. Deep graph feature learning-based diagnosis approach for rotating machinery using multi-sensor data. J. Intell. Manuf. 2023, 34, 1965–1974. [Google Scholar] [CrossRef]
- Qing-Dao-Er-Ji, R.; Ying, Q.; Tiancheng, L. Application of Convolution Neural Network Based on Transfer Learning in Sandstorm Prediction in Inner Mongolia. In Proceedings of the 2020 5th International Conference on Computer and Communication Systems (ICCCS), Shanghai, China, 15–18 May 2020; pp. 120–124. [Google Scholar]
- Ranasinghe, K.; Sabatini, R.; Gardi, A.; Bijjahalli, S.; Kapoor, R.; Fahey, T.; Thangavel, K. Advances in Integrated System Health Management for mission-essential and safety-critical aerospace applications. Prog. Aerosp. Sci. 2022, 128, 100758. [Google Scholar] [CrossRef]
- Hu, C.; Liu, M.; Li, H.; Hu, X. Sliding Mode Observer-Based Stuck Fault and Partial Loss-of-Effectiveness (PLOE) Fault Detection of Hypersonic Flight Vehicle. Electronics 2022, 11, 3059. [Google Scholar] [CrossRef]
- Villegas-Ch, W.; García-Ortiz, J. A Long Short-Term Memory-Based Prototype Model for Drought Prediction. Electronics 2023, 12, 3956. [Google Scholar] [CrossRef]
- Xu, D.; Wu, Y. An Efficient Detector with Auxiliary Network for Remote Sensing Object Detection. Electronics 2023, 12, 4448. [Google Scholar] [CrossRef]
- Yang, C.; Ouyang, H. A novel load-dependent sensor placement method for model updating based on time-dependent reliability optimization considering multi-source uncertainties. Mech. Syst. Signal Process. 2022, 165, 108386. [Google Scholar] [CrossRef]
- Sun, Z.; Simo, J.; Gong, S. Satellite Attitude Identification and Prediction Based on Neural Network Compensation. Space Sci. Technol. 2023, 3, 0009. [Google Scholar] [CrossRef]
- Zhu, W.; Mu, J.; Shao, C.; Hu, J.; Wang, B.; Wen, Z.; Han, F.; Li, S. System Design for Pose Determination of Spacecraft Using Time-of-Flight Sensors. Space Sci. Technol. 2022, 2022, 98. [Google Scholar] [CrossRef]
- Ovchinnikov, M.Y.; Roldugin, D.S. A survey on active magnetic attitude control algorithms for small satellites. Prog. Aerosp. Sci. 2019, 109, 100546. [Google Scholar] [CrossRef]
- Babuska, V.; Beatty, S.M.; Deblonk, B.J.; Fausz, J.L. A review of technology developments in flywheel attitude control and energy transmission systems. In Proceedings of the 2004 IEEE Aerospace Conference Proceedings (IEEE Cat. No. 04TH8720), Big Sky, MT, USA, 6–13 March 2004; Volume 4, pp. 2784–2800. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, X.; Wang, S. Graphsmote: Imbalanced node classification on graphs with graph neural networks. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual Event. Jerusalem, Israel, 8–12 March 2021. [Google Scholar]



| Network Module | Layers | Input Size | Output Size |
|---|---|---|---|
| GCN Layer 1-1 | |||
| GCN Layer 1-1 | |||
| Dual-channel | GCN Layer 1-2 | ||
| Feature Extraction | GCN Layer 2-1 | ||
| Module State Recognition Module State Prediction Module | GCN Layer 2-2 GCN Layer 3 Classifier GCN Layer 4 Predictor |
| Hyperparameters | Value |
|---|---|
| Learning rate | 0.0001 |
| Training epochs | 100 |
| Batchsize | 128 |
| Dropout probability | 0.4 |
| Methods | Average Accuracy | Maximum Accuracy | Minimum Accuracy | Parameters | Time |
|---|---|---|---|---|---|
| Standard CNN | 23.28% | 26.72% | 21.46% | 18 s | |
| Standard GCN | 60.44% | 65.01% | 58.28% | 20 s | |
| ResNet-18 | 61.56% | 71.63% | 60.69% | 24 s | |
| Manually (one person) | 100% | 100% | 100% | \ | 22 h |
| TS-GCN | 98.93% | 99.18% | 98.58% | 16 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Qiu, S.; Li, H.; Liu, M. Real-Time Telemetry-Based Recognition and Prediction of Satellite State Using TS-GCN Network. Electronics 2023, 12, 4824. https://doi.org/10.3390/electronics12234824
Liu S, Qiu S, Li H, Liu M. Real-Time Telemetry-Based Recognition and Prediction of Satellite State Using TS-GCN Network. Electronics. 2023; 12(23):4824. https://doi.org/10.3390/electronics12234824
Chicago/Turabian StyleLiu, Shuo, Shi Qiu, Huayi Li, and Ming Liu. 2023. "Real-Time Telemetry-Based Recognition and Prediction of Satellite State Using TS-GCN Network" Electronics 12, no. 23: 4824. https://doi.org/10.3390/electronics12234824
APA StyleLiu, S., Qiu, S., Li, H., & Liu, M. (2023). Real-Time Telemetry-Based Recognition and Prediction of Satellite State Using TS-GCN Network. Electronics, 12(23), 4824. https://doi.org/10.3390/electronics12234824





