Market and Sharing Alternatives for the Provision of Massive Machine-Type and Ultra-Reliable Low-Latency Communications Services over a 5G Network
Abstract
:1. Introduction
- Two business models are proposed to provide URLLC and mMTC services over the same 5G network. Additionally, two network models are proposed to investigate the sharing of network resources between URLLC and mMTC services.
- Game theory is employed to examine the strategic interactions between operators and users within each business/network model; the equilibrium of each model is studied in relation to the most significant parameters, including service priority, delay sensitivity, and pay-per-user price.
- Our results suggest that implementing network slicing over a 5G network for sharing network resources between URLLC and mMTC services is an economically viable strategy, allowing for the coexistence of operators and services.
- This work establishes the essential requirements for business models to be viable.
Related Works
2. Model Description
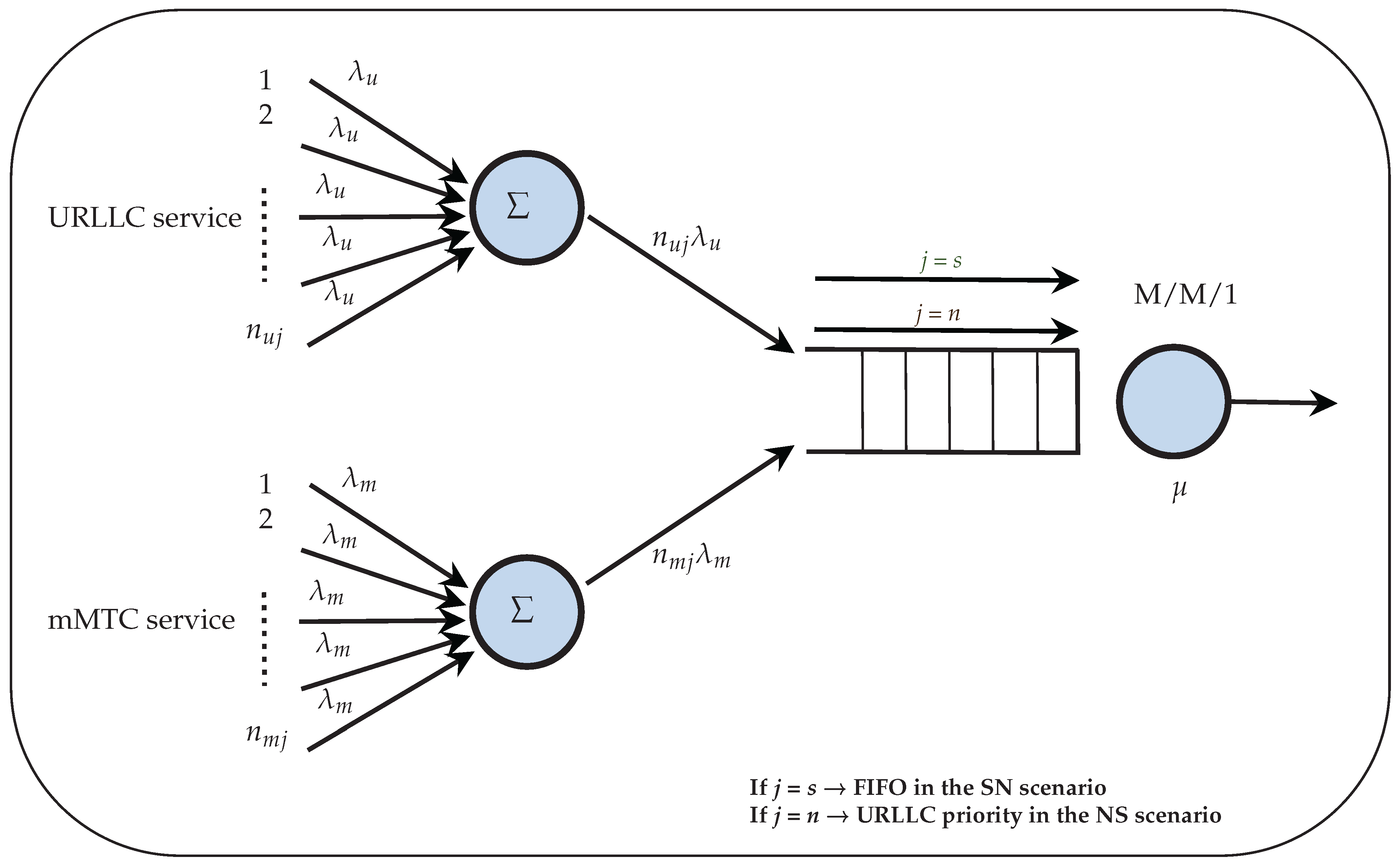
- A plain 5G network (modeled as a queue without service priority), where network resources are shared between the two services without service priority.
- A 5G network with network slicing (modeled as a queue with service priority), where network resources are shared between the two services but assigned a higher priority to the URLLC service.
2.1. System Model
2.2. Economic Model
2.2.1. SN Scenario
2.2.2. NS Scenario
2.2.3. Monopoly
2.2.4. Duopoly
2.3. Game
- Monopoly
- 1.
- URLLC and mMTC users’ subscription decisions are influenced by the monopoly operator’s pricing decisions.
- 2.
- The subscription decisions of URLLC users depend on the subscription decisions of mMTC users through . In turn, the subscription decisions of mMTC users depend on the subscription decisions of URLLC users through .
- 3.
- The monopoly operator’s profit depends on the subscription decisions of both types of users for the corresponding service.
- Duopoly
- 1.
- The subscription decisions of Op-U and Op-m users are influenced by the respective pricing decisions of each operator.
- 2.
- There is a strategic interaction between the subscription decisions of Op-U and Op-m users, as the subscription decisions of URLLC users depend on the subscription decisions of mMTC users through , and vice versa through .
- 3.
- Op-U’s profit depends on the subscription decisions of its users, whereas Op-m’s profit depends on the decisions of its users.
- 4.
- The profit of Op-m is indirectly influenced by Op-U’s pricing decisions through the subscription decisions of Op-U users.
- Monopoly: Stage I involves a single player (monopoly operator), setting both and .
- Duopoly: Stage I involves two players, Op-U and Op-m, each determining the price of their respective services.
2.3.1. Stage II—User Subscription
- Case a:
- Case b:
- Case c:
- Case d:where the functions and are expressed in terms of and , as explained in the section that analyzes the models. In addition, we apply the constraint to guarantee the stability of the network.
2.3.2. Stage I: Operator Pricing
2.4. Social Optimum Model
3. Analysis
3.1. Analysis of Stage II
3.1.1. SN Scenario
3.1.2. NS Scenario
3.2. Analysis of Stage I
3.2.1. Monopoly Model in the SN and NS Scenarios
3.2.2. Duopoly Model in the SN Scenario
3.2.3. Duopoly Model in the NS Scenario
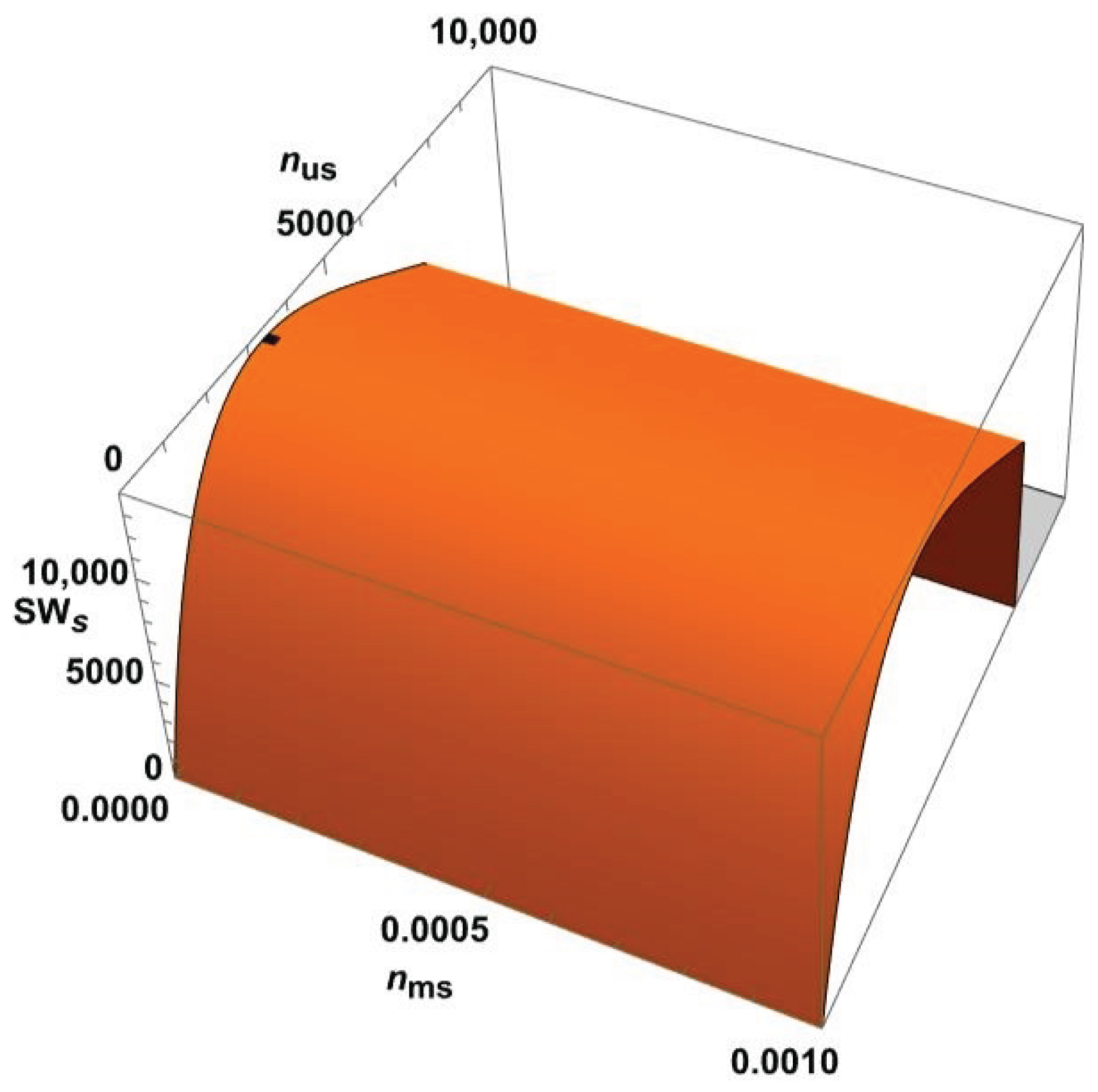
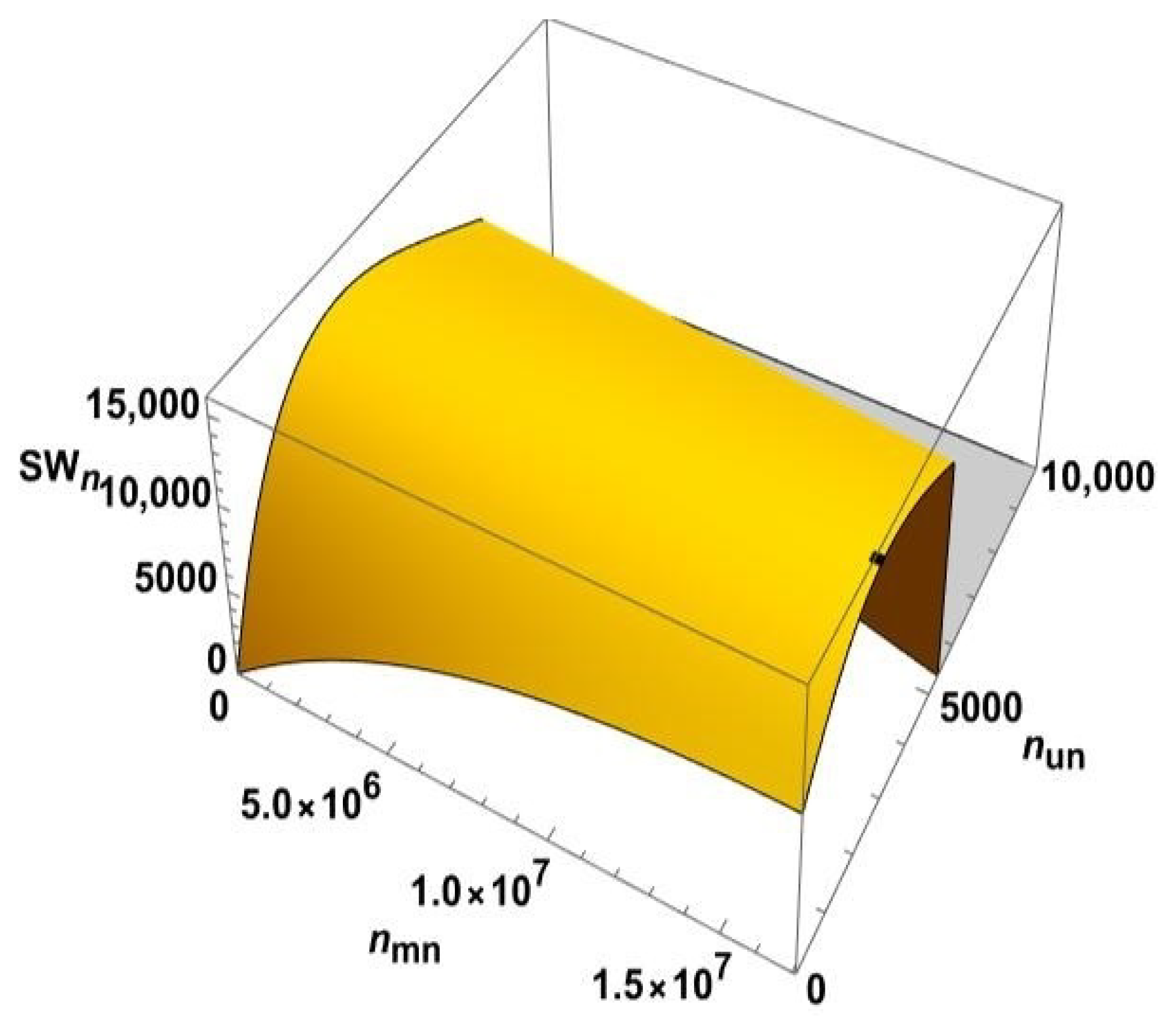
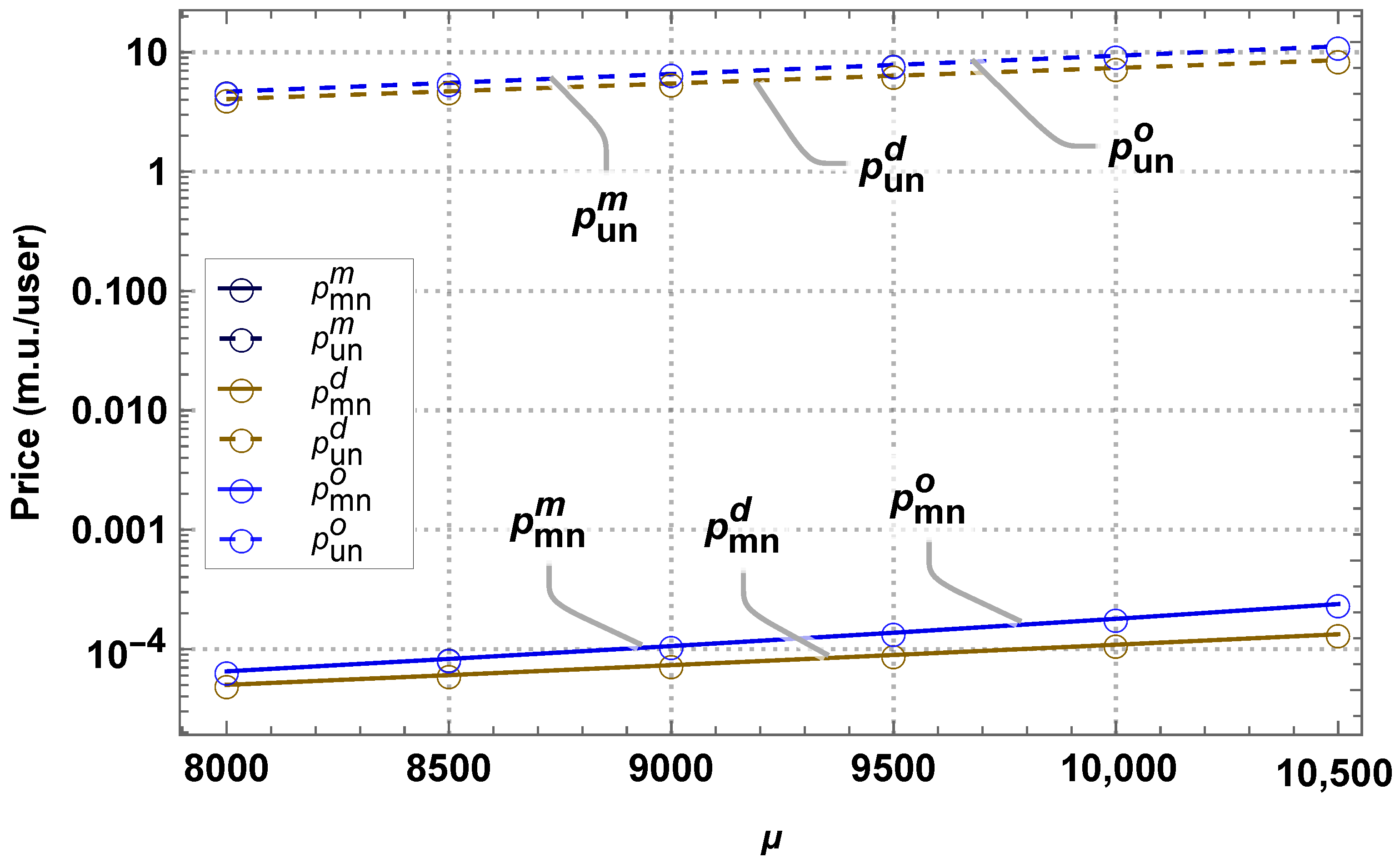
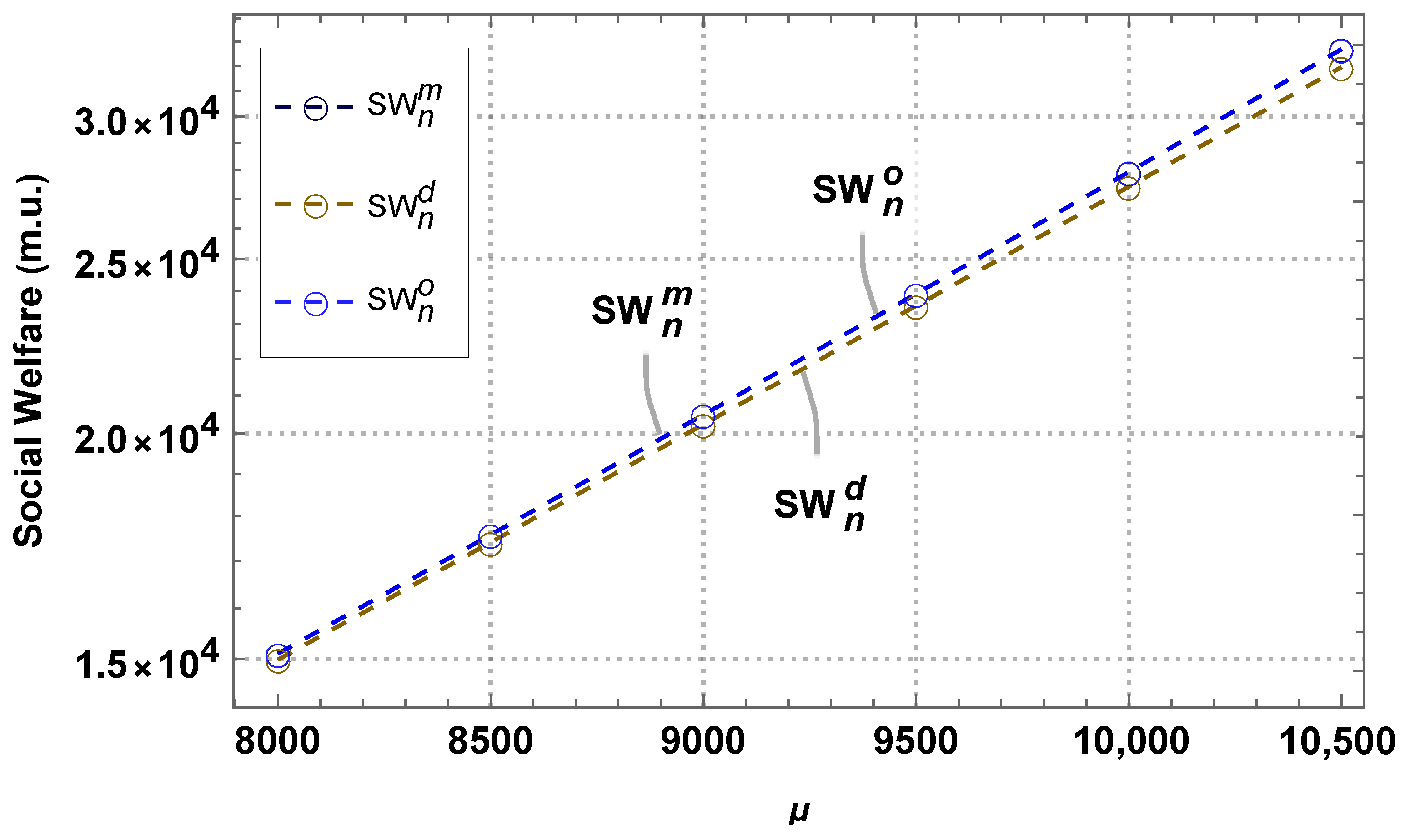
4. Results and Discussion
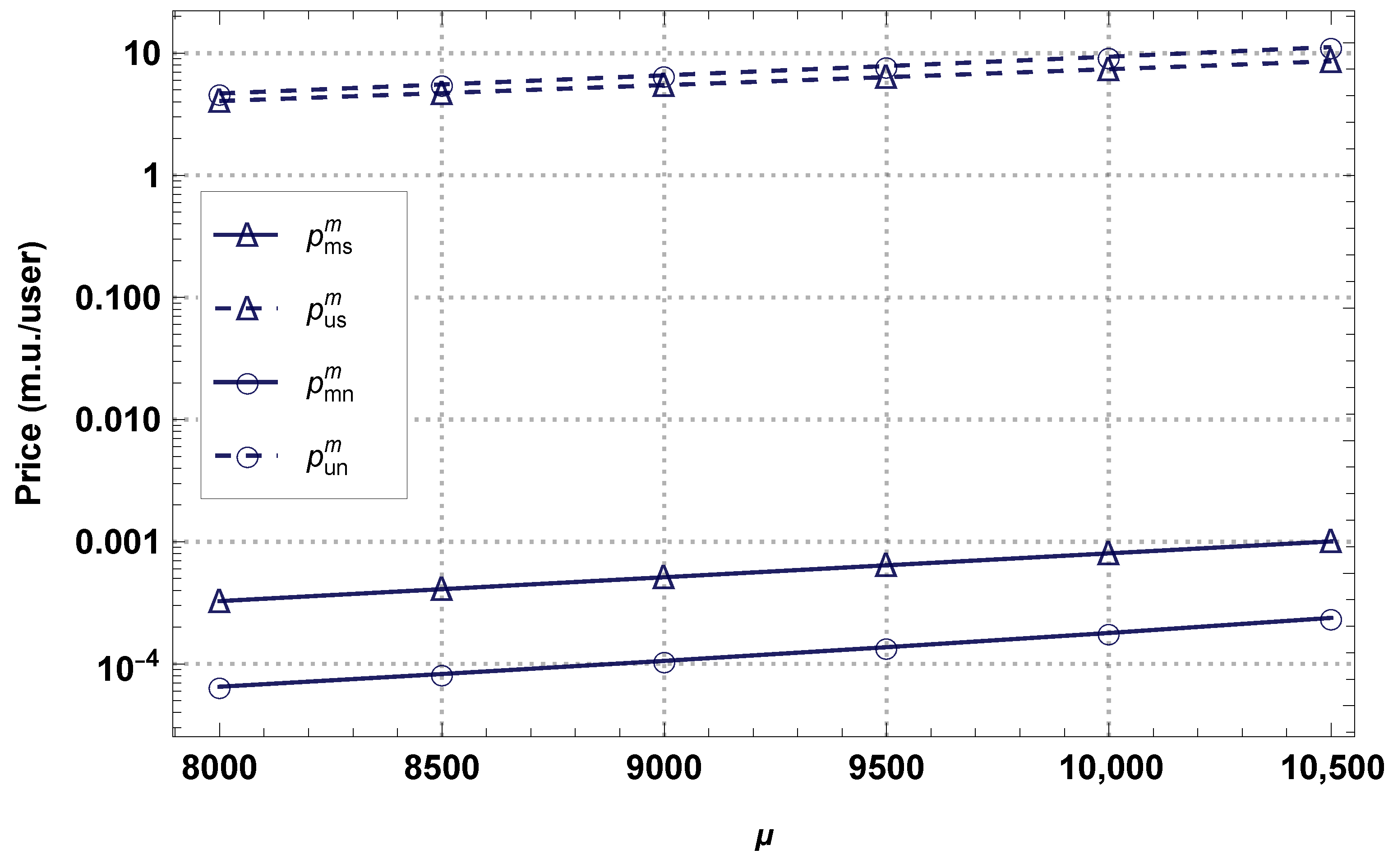
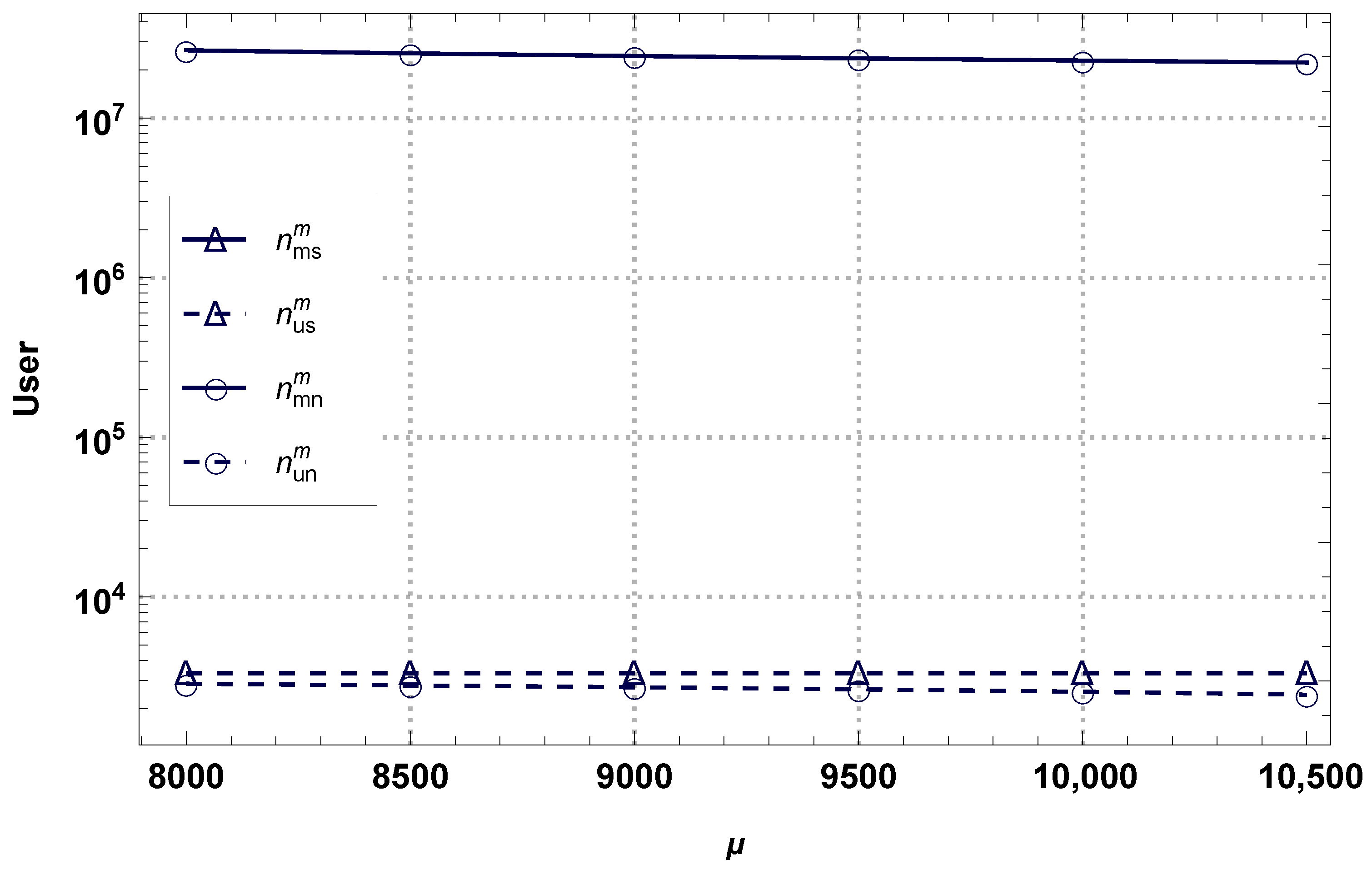
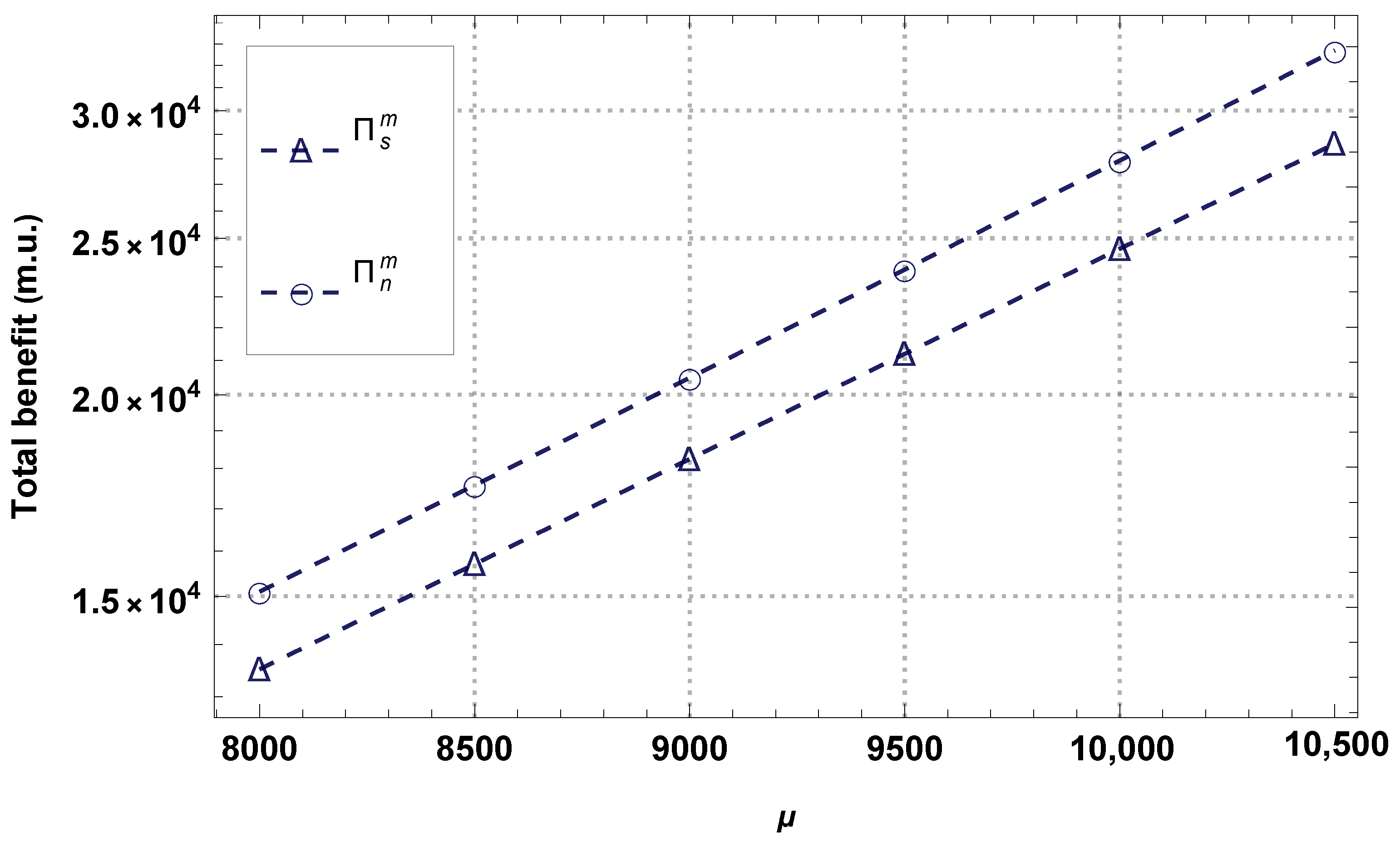
4.1. Monopoly Business Model
4.2. Duopoly Business Model
4.3. Comparison of Models in the NS Scenario
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Banda, L.; Mzyece, M.; Mekuria, F. 5G Business Models for Mobile Network Operators—A Survey. IEEE Access 2022, 10, 94851–94886. [Google Scholar] [CrossRef]
- Yang, W.; Li, C.P.; Fakoorian, A.; Hosseini, K.; Chen, W. Dynamic URLLC and eMBB multiplexing design in 5G new radio. In Proceedings of the 2020 IEEE 17th Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 10–13 January 2020; pp. 1–5. [Google Scholar]
- Aranda, J.; Sacoto Cabrera, E.J.; Haro Mendoza, D.; Astudillo Salinas, F. 5G networks: A review from the perspectives of architecture, business models, cybersecurity, and research developments. Novasinergia 2021, 4, 6–49. [Google Scholar]
- Miladić-Tešić, S.; Marković, G.; Peraković, D.; Cvitić, I. A review of optical networking technologies supporting 5G communication infrastructure. Wirel. Netw. 2022, 28, 459–467. [Google Scholar] [CrossRef]
- Popovski, P.; Trillingsgaard, K.F.; Simeone, O.; Durisi, G. 5G wireless network slicing for eMBB, URLLC, and mMTC: A communication-theoretic view. IEEE Access 2018, 6, 55765–55779. [Google Scholar] [CrossRef]
- Xiang, W.; Zheng, K.; Shen, X.S. 5G Mobile Communications; Springer: London, UK, 2016. [Google Scholar]
- Chen, W.E.; Fan, X.Y.; Chen, L.X. A CNN-based Packet Classification of eMBB, mMTC and URLLC Applications for 5G. In Proceedings of the 2019 International Conference on Intelligent Computing and Its Emerging Applications (ICEA), Tainan, Taiwan, 30 August–1 September 2019; pp. 140–145. [Google Scholar]
- Pokhrel, S.R.; Ding, J.; Park, J.; Park, O.S.; Choi, J. Towards enabling critical mMTC: A review of URLLC within mMTC. IEEE Access 2020, 8, 131796–131813. [Google Scholar] [CrossRef]
- Le, T.K.; Salim, U.; Kaltenberger, F. An overview of physical layer design for Ultra-Reliable Low-Latency Communications in 3GPP Releases 15, 16, and 17. IEEE Access 2020, 9, 433–444. [Google Scholar] [CrossRef]
- Li, Z.; Uusitalo, M.A.; Shariatmadari, H.; Singh, B. 5G URLLC: Design challenges and system concepts. In Proceedings of the 2018 15th International Symposium on Wireless Communication Systems (ISWCS), Lisbon, Portugal, 28–31 August 2018; pp. 1–6. [Google Scholar]
- Nwakanma, C.I.; Anantha, A.P.; Islam, F.B.; Lee, J.M.; Kim, D.S. 3GPP release-16 for industrial Internet of Things and mission critical communications. In Proceedings of the 2020 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 21–23 October 2020; pp. 403–406. [Google Scholar]
- Nwadiugwu, W.P.; Nwakanma, C.I.; Lee, J.M.; Kim, D.S. Achieving reliable URLLC-based network in industrial and military embedded systems. In Proceedings of the 2019 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 16–18 October 2019; pp. 642–645. [Google Scholar]
- Foukas, X.; Patounas, G.; Elmokashfi, A.; Marina, M.K. Network slicing in 5G: Survey and challenges. IEEE Commun. Mag. 2017, 55, 94–100. [Google Scholar] [CrossRef]
- Osborne, M.J. An Introduction to Game Theory; Oxford University Press: New York, NY, USA, 2004; Volume 3. [Google Scholar]
- Antoniou, J. Game Theory, the Internet of Things and 5G Networks; Springer: London, UK, 2020. [Google Scholar]
- Guijarro, L.; Pla, V.; Vidal, J.R.; Naldi, M. Competition in data-based service provision: Nash equilibrium characterization. Future Gener. Comput. Syst. 2019, 96, 35–50. [Google Scholar] [CrossRef]
- Dhanare, R.; Nagwanshi, K.K.; Varma, S. A Study to Enhance the Route Optimization Algorithm for the Internet of Vehicle. Wirel. Commun. Mob. Comput. 2022, 2022, 1453187. [Google Scholar] [CrossRef]
- Yan, X.; Huang, C.; Gan, J.; Wu, X. Game Theory-Based Energy-Efficient Clustering Algorithm for Wireless Sensor Networks. Sensors 2022, 22, 478. [Google Scholar] [CrossRef]
- Sadreddini, Z.; Masek, P.; Cavdar, T.; Ometov, A.; Hosek, J.; Gudkova, I.; Andreev, S. Dynamic resource sharing in 5G with LSA: Criteria-based management framework. Wirel. Commun. Mob. Comput. 2018, 2018, 7302025. [Google Scholar] [CrossRef]
- Khan, L.U.; Yaqoob, I.; Tran, N.H.; Han, Z.; Hong, C.S. Network slicing: Recent advances, taxonomy, requirements, and open research challenges. IEEE Access 2020, 8, 36009–36028. [Google Scholar] [CrossRef]
- Wong, S.; Han, B.; Schotten, H.D. 5G Network Slice Isolation. Network 2022, 2, 153–167. [Google Scholar] [CrossRef]
- Alliance, N. 5G Mobile Network Sharing Security 2022. Available online: https://www.ngmn.org/wp-content/uploads/221026-NGMN-5G-Mobile-Network-Sharing-Security-v1.02-2.pdf (accessed on 1 May 2023).
- Samdanis, K.; Costa-Perez, X.; Sciancalepore, V. From network sharing to multi-tenancy: The 5G network slice broker. IEEE Commun. Mag. 2016, 54, 32–39. [Google Scholar] [CrossRef]
- Allon, G.; Federgruen, A. Service competition with general queueing facilities. Oper. Res. 2008, 56, 827–849. [Google Scholar] [CrossRef]
- Smail, G.; Weijia, J. Techno-economic analysis and prediction for the deployment of 5G mobile network. In Proceedings of the 2017 20th Conference on Innovations in Clouds, Internet and Networks (ICIN), Paris, France, 7–9 March 2017; pp. 9–16. [Google Scholar]
- Stojanović, M. Monetization and pricing of the 5G-enabled smart residential services. E-Bus. Technol. Conf. Proc. 2022, 2, 70–73. [Google Scholar]
- Li, X.; Samaka, M.; Chan, H.A.; Bhamare, D.; Gupta, L.; Guo, C.; Jain, R. Network slicing for 5G: Challenges and opportunities. IEEE Internet Comput. 2017, 21, 20–27. [Google Scholar] [CrossRef]
- Mendelson, H. Pricing computer services: Queueing effects. Commun. ACM 1985, 28, 312–321. [Google Scholar] [CrossRef]
- Hayel, Y.; Ros, D.; Tuffin, B. Less-than-best-effort services: Pricing and scheduling. In Proceedings of the IEEE INFOCOM 2004, Hong Kong, China, 7–11 March 2004; Volume 1. [Google Scholar]
- Sacoto Cabrera, E.J.; Guijarro, L.; Maillé, P. Game Theoretical Analysis of a Multi-MNO MVNO Business Model in 5G Networks. Electronics 2020, 9, 933. [Google Scholar] [CrossRef]
- Guijarro, L.; Pla, V.; Tuffin, B. Entry game under opportunistic access in cognitive radio networks: A priority queue model. In Proceedings of the 2013 IFIP Wireless Days (WD), Valencia, Spain, 13–15 November 2013; pp. 1–6. [Google Scholar]
- Han, B.; Tayade, S.; Schotten, H.D. Modeling profit of sliced 5G networks for advanced network resource management and slice implementation. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 576–581. [Google Scholar]
- Han, B.; Feng, D.; Ji, L.; Schotten, H.D. A profit-maximizing strategy of network resource management for 5G tenant slices. arXiv 2017, arXiv:1709.09229. [Google Scholar]
- Sacoto-Cabrera, E.J.; Sanchis-Cano, A.; Guijarro, L.; Vidal, J.R.; Pla, V. Strategic interaction between operators in the context of spectrum sharing for 5G networks. Wirel. Commun. Mob. Comput. 2018, 2018, 4308913. [Google Scholar] [CrossRef]
- Sanchis-Cano, A.; Guijarro, L.; Pla, V.; Vidal, J.R. Economic viability of HTC and MTC service provision on a common network infrastructure. In Proceedings of the 2017 14th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 8–11 January 2017; pp. 1044–1050. [Google Scholar]
- Sacoto-Cabrera, E.J.; Guijarro, L.; Vidal, J.R.; Pla, V. Economic feasibility of virtual operators in 5G via network slicing. Future Gener. Comput. Syst. 2020, 109, 172–187. [Google Scholar] [CrossRef]
- Cohen, M.F. An Introduction to Logic and Scientific Method; Read Books Ltd.: Redditch, UK, 2011. [Google Scholar]
- Afolabi, I.; Taleb, T.; Samdanis, K.; Ksentini, A.; Flinck, H. Network slicing and softwarization: A survey on principles, enabling technologies, and solutions. IEEE Commun. Surv. Tutor. 2018, 20, 2429–2453. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Rassias, T.M.; Khan, A.A. Nonlinear Analysis and Variational Problems; Springer: New York, NY, USA, 2010. [Google Scholar]
- Hassin, R.; Haviv, M. To Queue or Not to Queue: Equilibrium Behavior in Queueing Systems; Springer: Luxembourg, 2003; Volume 59. [Google Scholar]
- Maillé, P.; Tuffin, B. Telecommunication Network Economics: From Theory to Applications; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Papoulis, A.; Unnikrishna Pillai, S. Probability, Random Variables and Stochastic Processes; McGraw-Hill: Boston, MA, USA, 2002. [Google Scholar]
- Maschler, M.; Zamir, S.; Solan, E. Game Theory; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Anand, A.; De Veciana, G.; Shakkottai, S. Joint scheduling of URLLC and eMBB traffic in 5G wireless networks. IEEE/ACM Trans. Netw. 2020, 28, 477–490. [Google Scholar] [CrossRef]







| Description | Notation | Equation |
|---|---|---|
| URLLC user utility in scenario j | (5) | |
| mMTC user utility in scenario j | (6) | |
| URLLC QoS over scenario j | (1), (3) | |
| mMTC QoS over scenario j | (2), (4) | |
| Delay threshold for URLLC service | (1) | |
| Delay threshold for mMTC service | (2) | |
| Number of URLLC users in scenario j for business model i | - | |
| Number of mMTC users in scenario j for business model i | - | |
| Conversion factor for URLLC service | (1) | |
| Conversion factor for mMTC service | (2) | |
| Mean service rate | (1) | |
| Network capacity utilization factor | (10) | |
| Individual arrival rate of URLLC packets in the system | (1) | |
| Individual arrival rate of mMTC packets in the system | (2) | |
| Price of URLLC service in scenario j for business model i | - | |
| Price of mMTC service in scenario j for business model i | - | |
| Best response from the URLLC operator | (15) | |
| Best response from the mMTC operator | (16) | |
| Profit obtained by URLLC service in scenario j | (8) | |
| Profit obtained by mMTC service in scenario j | (9) | |
| Total benefit of business model i in scenario j | (7) | |
| Social welfare in scenario j for business model i | (21) |
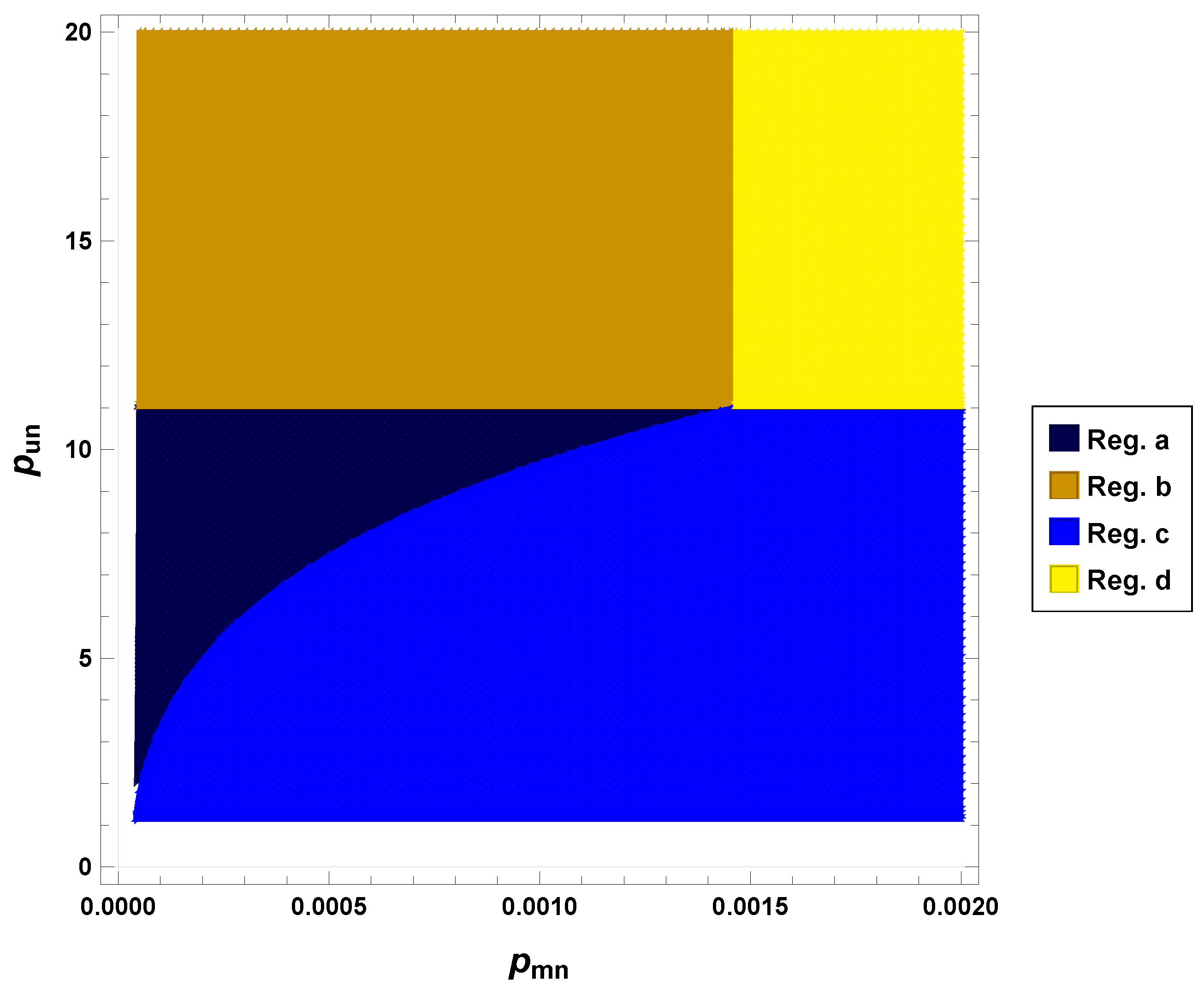
| Reg. | ||||
|---|---|---|---|---|
| a | (46), (48) | (47), (49) | ||
| b | 0 | |||
| c | 0 | |||
| d | 0 | 0 |
| Reg. | ||||
|---|---|---|---|---|
| a | (65) | |||
| b | 0 | |||
| c | 0 | |||
| d | 0 | 0 |
| Parameter | Value |
|---|---|
| 1 | |
| 0.00004 | |
| 8000 packets/s | |
| 0.95 | |
| 0.00030 s | |
| 0.00045 s | |
| 1 packets/s | |
| 0.00013 packets/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno-Cardenas, E.; Guijarro, L. Market and Sharing Alternatives for the Provision of Massive Machine-Type and Ultra-Reliable Low-Latency Communications Services over a 5G Network. Electronics 2023, 12, 4994. https://doi.org/10.3390/electronics12244994
Moreno-Cardenas E, Guijarro L. Market and Sharing Alternatives for the Provision of Massive Machine-Type and Ultra-Reliable Low-Latency Communications Services over a 5G Network. Electronics. 2023; 12(24):4994. https://doi.org/10.3390/electronics12244994
Chicago/Turabian StyleMoreno-Cardenas, Edison, and Luis Guijarro. 2023. "Market and Sharing Alternatives for the Provision of Massive Machine-Type and Ultra-Reliable Low-Latency Communications Services over a 5G Network" Electronics 12, no. 24: 4994. https://doi.org/10.3390/electronics12244994
APA StyleMoreno-Cardenas, E., & Guijarro, L. (2023). Market and Sharing Alternatives for the Provision of Massive Machine-Type and Ultra-Reliable Low-Latency Communications Services over a 5G Network. Electronics, 12(24), 4994. https://doi.org/10.3390/electronics12244994







