Trajectory Tracking Control of Fast Parallel SCARA Robots with Fuzzy Adaptive Iterative Learning Control for Repetitive Pick-and-Place Operations

Abstract

Aiming at enhanced suppression of external disturbances and high-precision trajectory tracking of parallel SCARA robot dedicating to fast pick-and-place operations, this work presents the integrated control design of iterative learning algorithm, adaptive control and fuzzy rules, namely, fuzzy adaptive iterative learning control, for such type of robots. A step-design approach is adopted to ensure the adaptability of the designed control law, which is reflected in two aspects: ① the feedback gain of the controller is adjusted by the fuzzy rules; ② the adaptive unknown parameters are obtained by means of iterative learning estimation to suppress the uncertainties and external disturbances. The stability of the designed controller is analyzed and proved by the Lyapunov theory, and the effectiveness is verified by observing the tracking errors in joint space along with the testing pick path, in comparison with different iterative learning based algorithms. After the first-iteration learning, the motion errors of the four actuated joints can be reduced by $56.5\%$, $45.8\%$, $46.4\%$ and $39.8\%$, respectively, and after 15 iterations of learning control, the final angular errors by the designed control law converge to $0.7\times {10}^{-4}$ degree maximally. The varying maximum, root-mean-squared and mean angular displacement errors of the actuation joints can converge to zero values with the increasing iterations rapidly, which shows the robustness, effectiveness and advantages of the designed control law. The designed control law can be generalized to high-speed parallel pick-and-place robot to ensure high-precision trajectory tracking for high-quality material handling tasks.

1. Introduction

Lightweight parallel robots featuring SCARA motion (the term “SACRA” means Selective Compliance Assembly Robot Arm, a.k.a., Schönflies motion, namely, three independent translations and one rotation around an axis of fixed direction) have been extensively deployed in production lines for material handling [1], which usually carry out repetitive tasks. Considering the continuous execution of identical trajectory tracking, this results in the accumulated motion errors in the motion process. If the previous problem cannot be handled effectively in time, the robot will eventually deviate from the expected trajectory, leading to the reduced work quality. Besides, the presence of uncertainties in the working environment will also decrease the control quality of the robot [2]. In this light, the key issue to improve the tracking accuracy lies in the avoidance of error accumulation and improved robustness of the system. The focus of this work is the control design for this type of robot.

The trajectory tracking control of a robot means that it is essential to design a reasonable control law for robotic joints with a determined trajectory, which makes the real end-effector position, velocity and accelerations consistent with the expected motion parameters [3]. The PID control has been commonly adopted for various robots since it was proposed, thanks to the simple control scheme and eased parameter tuning. On the other hand, the uncertainties cannot be readily handled in the use of this type of control law, and therefore, the PID control is usually designed in combination with other control algorithms to improve the tracking accuracy [4,5,6,7,8,9,10], e.g., feedforward [11], adaptive [12,13], robust [14], fuzzy control [15], etc. Besides, a number of different control algorithms have been proposed and applied to the parallel pick-and-place (PnP) robots, such as computed-torque control (CTC) [16] and sliding mode control (SMC) [17,18], but these heavily depends on the accurate dynamic model of the robots, which is a challenging task due to the highly nonlinear coupled system. Other robust control, such as $H_2$ [19] and $H_{\infty }$ [20] controls, are suitable for noise signals with known power spectral density or for the condition of satisfying energy boundedness without enough information about the noise signal [21]. In light of the repetitive tasks of the family of parallel SCARA robots, an algorithm of iterative learning control (ILC) is well adapted with the repetitive characteristics, compared to the commonly used control laws.

The concept of iterative learning originated from the experienced learning knowledge and was proposed by Uchiyama in 1978 [22], which is free of feedback control to overcome the presence of disturbance and uncertainties in the control. Modifications and improvements to ILC algorithm have been made to enhance the trajectory tracking performance for the robots. As an open-loop control algorithm, ILC algorithms can be designed combining P, D and PD units of PID control, of which the architecture of the integrated control laws can be classified into open-, closed- and open-closed-loops. In Ref. [23], an open-loop PD-ILC is designed for Delta robots, which requires multiple iterations for convergence of tracking errors, leading to increased computational burden. Aiming at suppression of the longitudinal slippage disturbance, an open-closed-loop P-ILC algorithm is designed and applicable to a mobile robot [24]. It is difficult for the previous control law to be compatible with learning stability and feedback convergence, since the single proportion gain is simultaneously in charge of the feedback task of the control system and learning gain. In addition, optimization algorithm, such as the artificial bee colony algorithm, can also be adopted to optimize the initial parameters of the iterations, which can produce a better performance compared to the ILC with a constant gain [25]. To improve the control performance of nonlinear systems, a discrete high-order PID-ILC is proposed, which is complicated in the real control due to that it requires the numerous information of foregoing iterations rather than the current iteration [26]. Aiming to suppress aperiodic external disturbance, an ILC algorithm with forgetting factor (i.e., working as a filter) is proposed, which can effectively reduce the accumulated disturbance varying with the iterations and can make the tracking error converge to a certain range [27,28]. The fuzzy rules can be integrated to ILC algorithm for real-time tuning of control parameter to resist external disturbances in fewer iterations, compared to the classic PD-ILC [29]. Combining neural network, a high-order ILC is designed, consisting of two aspects, namely, neural network feedforward item and high-order P-type iterative feedback item, which corresponds to the suppression of periodic disturbance and the control stability [30]. In view of the present ICL-based control laws, an integrated fuzzy adaptive ILC algorithm is to be designed to discard the shortcomings of a single control law, for the enhancement of the trajectory tracking accuracy.

In this work, the adaptability of the combined ILC control law is reflected in two aspects: ① the feedback gain of the controller is adjusted by the fuzzy rule; ② the adaptive unknown parameters are obtained by means of iterative learning estimation to suppress the uncertainties and external disturbances caused by the unknown parameters to improve the trajectory tracking performance of the system. The stability of the controller is proved with the Lyapunov theory. The proposed algorithm was verified in comparison with the different ILC-based algorithms, of which the results show the robustness and effectiveness of the proposed algorithm, resulting in high tracking accuracy of the robot.

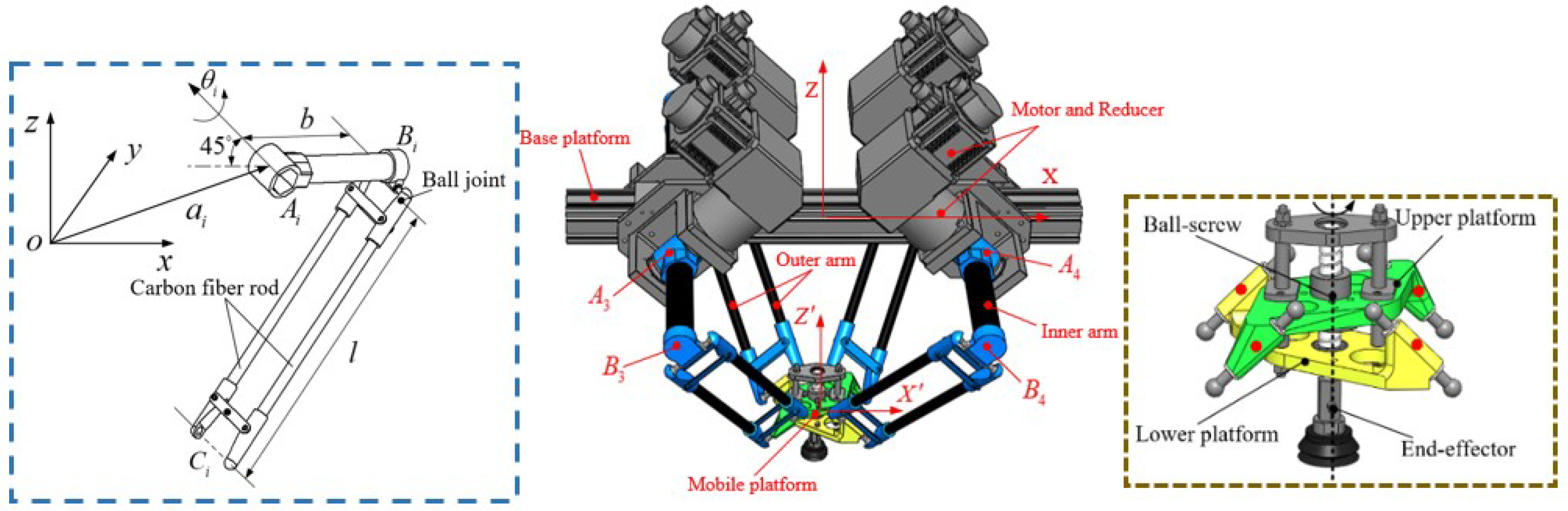
2. Pick-and-Place Robot and Dynamic Model

Figure 1 shows a parallel SCARA robot, which is composed of four identical revolute-revolute-parallelogram-revolute (i.e., RR$\mathsf{\Pi }$R) linkages and a screw pair-based mobile platform. In each limb, the driving link is to provide the power to the parallelogram structure from the actuation unit of servo motor and reducer. The parallelogram, a.k.a., $\mathsf{\Pi }$ joint, is made up of carbon fiber, for a lightweight design as well as increased rigidity and stability of the robot structure. The corresponding parameterized CAD model is depicted in Figure 2.

Prior to the control design of the robot, the dynamic model is to be derived, which can be expressed as:

$$\mathit{\tau }=\mathbf{M}(\mathbf{q})\ddot{\mathbf{q}}+\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}+\mathbf{G}(\mathbf{q})+\mathit{\omega }(\mathbf{q},\dot{\mathbf{q}},t)$$

(1)

where $\mathit{\tau }\in {\mathbb{R}}^4$ represents a vector of the driving torque, $\mathbf{q}={\left[\begin{array}{cccc}{\theta }_1& {\theta }_2& {\theta }_3& {\theta }_4\end{array}\right]}^T$ represents the generalized coordinates, and $\dot{\mathbf{q}}$, $\ddot{\mathbf{q}}$ denote the corresponding joint angular velocities and accelerations, respectively. The term $\mathit{\omega }(\mathbf{q},\dot{\mathbf{q}},t)$ represents the modeling error due to parameter uncertainties and external disturbance by changed environment. Moreover, $\mathbf{M}(\mathbf{q})$, $\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})$ and $\mathbf{G}(\mathbf{q})$ stand for the inertia matrix, Coriolis and centrifugal term and gravity term, respectively, expressed as:

$$\begin{array}{cc}\hfill & \mathbf{M}(\mathbf{q})={\mathbf{J}}_1^T{\mathbf{M}}_1{\mathbf{J}}_1+{\mathbf{J}}_2^T{\mathbf{M}}_2{\mathbf{J}}_2+{\mathbf{I}}_b\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill & \mathbf{C}(\mathbf{q},\dot{\mathbf{q}})={\mathbf{J}}_1^T{\mathbf{M}}_1{\dot{\mathbf{J}}}_1+{\mathbf{J}}_2^T{\mathbf{M}}_2{\dot{\mathbf{J}}}_2\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill & \mathbf{G}(\mathbf{q})=-\left({\mathbf{J}}_1^T{\mathbf{M}}_2+{\mathbf{J}}_2^T{\mathbf{M}}_2+{\mathbf{M}}_b\right)\mathbf{g}\hfill \end{array}$$

(2c)

with:

$$\begin{array}{cc}\hfill & {\mathbf{M}}_{1/2}=(m_{1/2}+2m_l)\mathrm{diag}\left[\begin{array}{cccc}1& 1& 1& 0\end{array}\right]\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill & {\mathbf{I}}_b=\left(\frac{1}{3}{m}_b+m_l\right)b^2{\mathbf{I}}_4\hfill \end{array}$$

(3b)

$$\begin{array}{cc}\hfill & {\mathbf{M}}_b=\left(\frac{1}{2}{m}_b+m_l\right)\mathrm{diag}\left[\begin{array}{cccc}cos{\theta }_1& cos{\theta }_2& cos{\theta }_3& cos{\theta }_4\end{array}\right]\hfill \end{array}$$

(3c)

$$\begin{array}{cc}\hfill & {\mathbf{J}}_1=\left[\begin{array}{cc}{({\mathbf{c}}_i-{\mathbf{b}}_i)}^T& -\mathrm{mod}(i+1,2)\frac{h}{2\pi }{({\mathbf{c}}_i-{\mathbf{b}}_i)}^T\mathbf{k}\end{array}\right]\hfill \end{array}$$

(3d)

$$\begin{array}{cc}\hfill & {\mathbf{J}}_2=\left[\begin{array}{cc}{({\mathbf{c}}_i-{\mathbf{b}}_i)}^T& -\mathrm{mod}(i,2)\frac{h}{2\pi }{({\mathbf{c}}_i-{\mathbf{b}}_i)}^T\mathbf{k}\end{array}\right]\hfill \end{array}$$

(3e)

$$\begin{array}{cc}\hfill & \mathbf{g}={\left[\begin{array}{cccc}0& 0& -1& 0\end{array}\right]}^T\hfill \end{array}$$

(3f)

where ${\mathbf{J}}_1$ and ${\mathbf{J}}_2$ represent the Jacobian matrices mapping the velocities between the active joints and the upper/lower sub-platforms, respectively, ${\mathbf{b}}_i$ and ${\mathbf{c}}_i$ represent the Cartesian coordinates of points $B_i$ and $C_i$ in the reference frame and k denotes the unit vector of z-axis. Moreover, ${\mathbf{I}}_4$ is a four-dimensional identity matrix. Skipping the details, the kinematic and dynamic models have been well documented in the previous works [2,31], together with the link dimensions and mass properties listed in

Table 1. Geometric and mass parameters of the parallel robot.

Parameters	Meaning	Value	Unit
$(a_x,a_y)$	x-/y-coordinates of joint position	$(286,132)$	$\mathrm{mm}$
$b/l$	lengths of proximal/distal links	$300/600$	$\mathrm{mm}$
r	radius of moving platform	100	$\mathrm{mm}$
h	pitch of lead screw	10	$\mathrm{mm}$
$m_b/m_l$	masses of proximal/distal links	$0.5101/0.2670$	$\mathrm{kg}$
$m_1/m_2$	masses of upper/lower sub-platforms	$0.9789/0.8914$	$\mathrm{kg}$

.

3. Fuzzy Adaptive Iterative Learning Control Design

In this section, the controller design for the robot under study is accomplished by the integrated design of ILC and adaptive control law as well as fuzzy rules.

3.1. Design of the Iterative Learning Control Law

Considering the nonlinear time-varying robotic system with repetitive work over a finite interval time $t\in [0,T]$, the following reasonable assumptions can be made:

Assumption 1.

The robotic system can meet the boundary condition, i.e., ${\mathbf{q}}_k(0)={\mathbf{q}}_d(0)$, ${\dot{\mathbf{q}}}_k(0)={\dot{\mathbf{q}}}_d(0)$, where ${\mathbf{q}}_k$ and ${\mathbf{q}}_d(0)$ stand for the real and expected trajectories, respectively, and k depicts the iteration number in the control law.

Assumption 2.

The external disturbance $\mathit{\tau }(\mathbf{q},\dot{\mathbf{q}},t)$ of the robot is bounded, which can meet an inequality $\sup \parallel \mathit{\tau }(\mathbf{q},\dot{\mathbf{q}},t)\parallel \le l$, with l being a positive constant.

For a general robotic manipulator, the dynamic system can have the following three properties:

Property 1.

For the bounded and positive-definite inertia matrix $\mathbf{M}({\mathbf{q}}_k,t)$ of a robot, there exists the constants δ and ζ to meet the inequality:

$$0<\delta <\parallel \mathbf{M}({\mathbf{q}}_k,t)\parallel <\zeta ,0<\delta <\zeta$$

(4)

Property 2.

Since the inertia matrix can meet the global Lipschitz condition [33], there is a positive constant L to hold the following inequality:

$$\parallel \mathbf{M}({\mathbf{q}}_k,t)-\mathbf{M}({\mathbf{q}}_{k-1},t)\parallel \le L\parallel {\mathbf{q}}_k(t)-{\mathbf{q}}_{k-1}(t)\parallel$$

(5)

Property 3.

The Coriolis, centrifugal and gravitational terms of the dynamic equation can meet the condition of $\mathbf{C}({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k){\dot{\mathbf{q}}}_d+\mathbf{G}({\mathbf{q}}_k)=\mathbf{\Phi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k){\mathit{\gamma }}_k(t)$, where $\mathbf{\Phi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k)\in {\mathbf{R}}^{n\times m}$ represents the regression matrix to depict the motions of robotic joints and ${\mathit{\gamma }}_k(t)\in {\mathbf{R}}^{m\times 1}$ is a vector of unknown parameters with regard to the robot.

With the aforementioned conditions and constraints, an iterative learning algorithm is able to be designed to make full use of the effective information stored in the system for learning, which can ensure that the output variables converge to the bounded threshold of desired values, expressed as [34]:

$${\mathit{\tau }}_{k+1}(t)={\mathit{\tau }}_k(t)+{\mathit{\tau }}_{fore}+{\mathit{\tau }}_{back}$$

(6)

where $\mathit{\tau }$ represents the input torque and ${\mathit{\tau }}_{fore}$, ${\mathit{\tau }}_{back}$ stand for the feedforward and feedback compensation torques, respectively, which take the following form:

$$\begin{array}{cc}\hfill & {\mathit{\tau }}_{fore}={\mathbf{K}}_p{\mathbf{e}}_k(t)+{\mathbf{K}}_d{\dot{\mathbf{e}}}_k(t)\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill & {\mathit{\tau }}_{back}=(1-\alpha ){\mathbf{K}}_p{\mathbf{e}}_{k+1}(t)+(1-\beta ){\mathbf{K}}_d{\dot{\mathbf{e}}}_{k+1}(t)\hfill \end{array}$$

(7b)

where ${\mathbf{K}}_p$ and ${\mathbf{K}}_d$ are, respectively, diagonal positive gain matrices for proportion and differential PD parameters in the feedforward control, ${\mathbf{e}}_k(t)$ and ${\dot{\mathbf{e}}}_k(t)$ represent the joint errors in terms of angular displacements and velocities, respectively, in the kth iteration and $\alpha$ and $\beta$ stand for the gain coefficients.

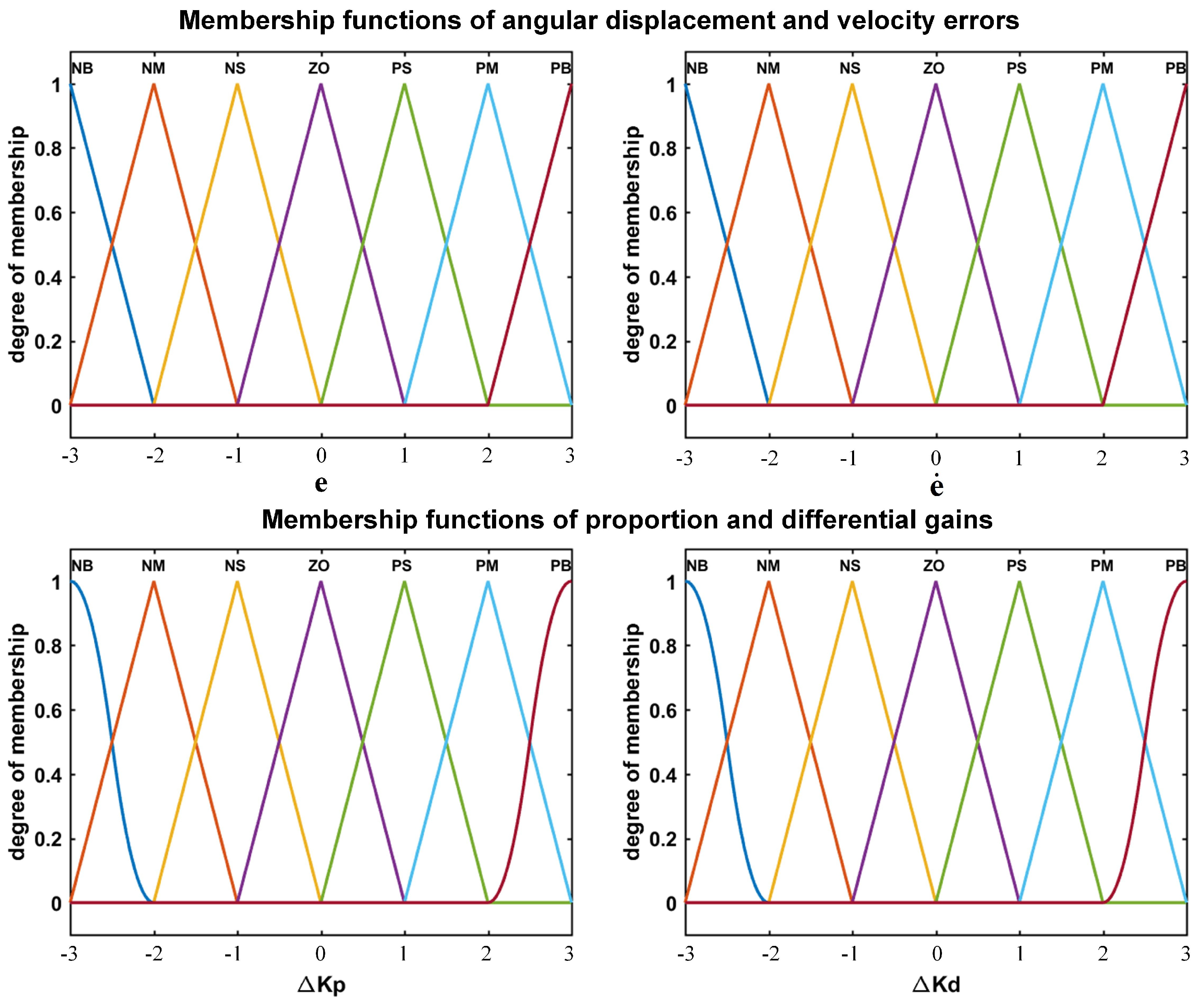
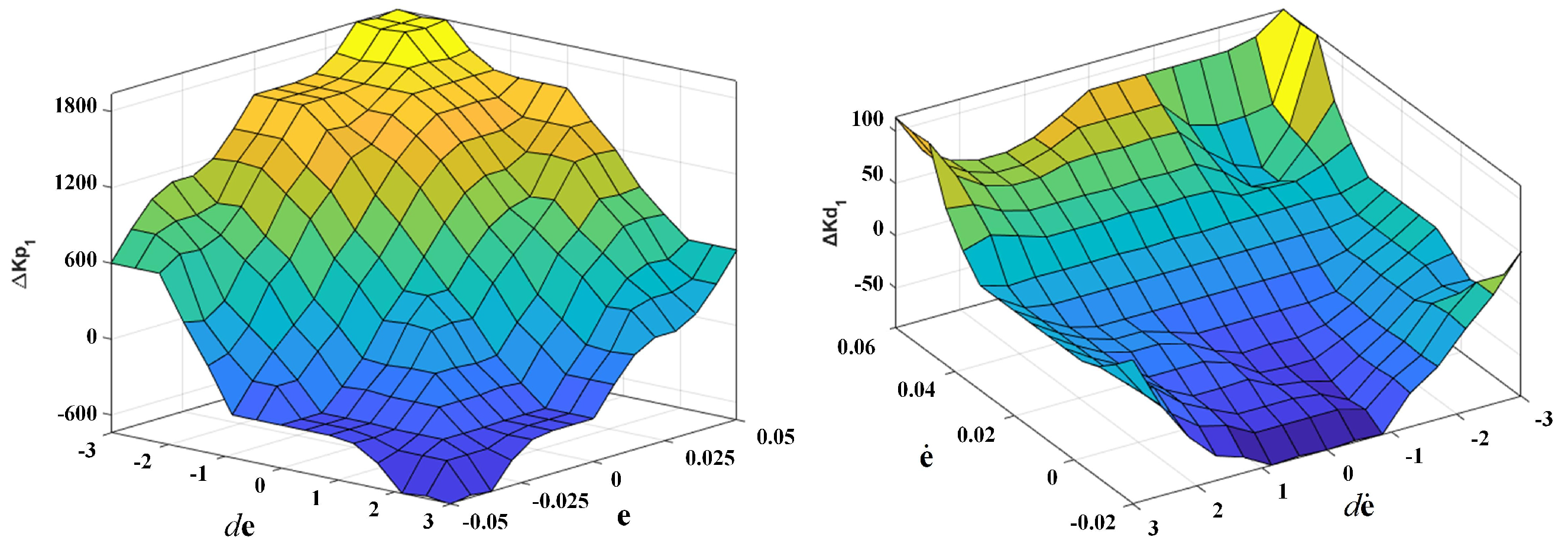
3.2. Fuzzy Controller Design

In the control design, the fuzzy rule is adopted to adaptively adjust the gain of the controller for the improved suppression of the disturbance of the system. A particular control algorithm is formulated as:

$$\begin{array}{cc}\hfill & {\mathbf{K}}_p={\mathbf{K}}_{p0}+\Delta {\mathbf{K}}_p\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill & {\mathbf{K}}_d={\mathbf{K}}_{d0}+\Delta {\mathbf{K}}_d\hfill \end{array}$$

(8b)

where ${\mathbf{K}}_{p0}$ and ${\mathbf{K}}_{d0}$ represent the initial values of the gain and $\Delta {\mathbf{K}}_p$, $\Delta {\mathbf{K}}_d$ are the corresponding compensation values of the fuzzy control output.

Let us define a fuzzy set with seven fuzzy subsets, i.e., $\{NB,NM,NS,ZO,PS,PM,PB\}$, which, respectively, stand for Negative Big, Negative Medium, Negative Small, Zero, Positive Small, Positive Medium and Positive Big in the fuzzy control language [35]. Taking the motion errors of angular displacement $\mathbf{e}$ and velocity $\dot{\mathbf{e}}$ of the actuated joints as the input variables of the controller, the physical domains of angular displacement $\mathbf{e}$ and velocity $\dot{\mathbf{e}}$ errors of joints 1 and 3 are, respectively, set to $\{-0.05,0.05\}$ and $\{-0.01,0.05\}$, while the physical domains of motion errors $\mathbf{e}$ and $\dot{\mathbf{e}}$ for joints 2 and 4 are, respectively, set to $\{-0.01,0.01\}$ and $\{-0.01,0.05\}$, in accordance with the parameter tuning determined in previous research [32]. On the other hand, the controller gain compensations $\Delta {\mathbf{K}}_p$ and $\Delta {\mathbf{K}}_d$ are used as output variables, of which the ranges are set to $\{-500,2000\}$ and $\{-80,120\}$, respectively. The fuzzy domains are defined in its generalized form, for which the values are set to $\{-3,3\}$. Moreover, the physical and fuzzy domains are mapped by means of scaling factors. To this end, the membership functions for the input and output variables of the controller are depicted in Figure 3. Here, the triangular membership function is adopted to ease the control algorithm for fast computation, while Z/S-shaped membership functions are used at the boundaries of the output parameters to realize the parameter regulation for enhanced adaptability of the controller.

When the robot moves with angular displacement and velocity errors, which offsets from the expected trajectory, the fuzzy subset of gain compensations can be obtained from the fuzzy rule table. Based upon the analysis of the influence of proportional and differential gains onto the performance of the controller, the fuzzy strategies are summarized in

Table 2. Fuzzy rule table of proportional gain tuning.

$\mathbf{\Delta }{\mathit{K}}_{\mathit{p}}$				$\mathit{d}\mathit{e}$
$\mathbf{e}$	$NB$	$NM$	$NS$	$ZO$	$PS$	$PM$	$PB$
$NB$	$PB$	$PB$	$PM$	$PM$	$PS$	$PS$	$ZO$
$NM$	$PB$	$PB$	$PM$	$PM$	$PS$	$ZO$	$ZO$
$NS$	$PM$	$PM$	$PM$	$PS$	$ZO$	$NS$	$NM$
$ZO$	$PM$	$PS$	$PS$	$ZO$	$NS$	$NM$	$NM$
$PS$	$PS$	$PS$	$ZO$	$NS$	$NS$	$NM$	$NM$
$PM$	$ZO$	$ZO$	$NS$	$NM$	$NM$	$NM$	$NB$
$PB$	$ZO$	$NS$	$NS$	$NM$	$NM$	$NB$	$NB$

and

Table 3. Fuzzy rule table of differential gain tuning.

$\mathbf{\Delta }{\mathit{K}}_{\mathit{D}}$				$\mathit{d}\dot{\mathbf{E}}$
$\dot{\mathbf{e}}$	$NB$	$NM$	$NS$	$ZO$	$PS$	$PM$	$PB$
$NB$	$NB$	$NB$	$NM$	$NM$	$NS$	$ZO$	$ZO$
$NM$	$NB$	$NB$	$NM$	$NM$	$NS$	$ZO$	$ZO$
$NS$	$NM$	$NM$	$NM$	$NS$	$ZO$	$PS$	$PM$
$ZO$	$NM$	$NS$	$NS$	$ZO$	$PS$	$PM$	$PM$
$PS$	$NS$	$NS$	$ZO$	$PS$	$PS$	$PM$	$PM$
$PM$	$ZO$	$ZO$	$PS$	$PM$	$PM$	$PM$	$PB$
$PB$	$ZO$	$ZO$	$PS$	$PM$	$PM$	$PB$	$PB$

, respectively. After the operation of defuzzification, the surfaces of varying proportional and differential gains of fuzzy algorithm for joint 1 is plotted in Figure 4, and the surfaces of the remaining joints have the similar distributions over different physical domains as previously mentioned.

3.3. Adaptive Iterative Learning Law

The use of the ILC algorithm is to learn the useful information from previous movements to correct the current state, which can effectively suppress the repetitive uncertain disturbances. On the other hand, there exists some non-repetitive external disturbances in a real situation. In order to make the robot adaptive to the external environment and to improve the trajectory tracking precision, an adaptive [36] ILC law is designed below:

$${\mathit{\tau }}_k(t)={\mathbf{K}}_p{\mathbf{e}}_k(t)+{\mathbf{K}}_d{\dot{\mathbf{e}}}_k(t)+\mathit{\xi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\mathit{\gamma }}_k(t)+{\mathit{\omega }}_k(t)+\mathbf{D}sat({\mathbf{y}}_k(t))$$

(9)

with:

$${\mathit{\gamma }}_k(t)={\mathit{\gamma }}_{k-1}(t)+\alpha {\mathit{\xi }}^T({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\mathbf{y}}_k(t)$$

(10)

where $\{{\mathbf{K}}_p,{\mathbf{K}}_d\}\in {\mathbb{R}}^n$ are the gain matrices corresponding to the proportion and differential parts in PD control and ${\mathbf{e}}_k(t)={\mathbf{q}}_d(t)-{\mathbf{q}}_k(t)$, ${\dot{\mathbf{e}}}_k(t)={\dot{\mathbf{q}}}_d(t)-{\dot{\mathbf{q}}}_k(t)$ represent the motion errors of the actuated joints in terms of angular displacement and velocity, respectively. For the vector of unknown parameters of the robot ${\mathit{\gamma }}_k(t)$, ${\mathit{\gamma }}_{k-1}(t)=\mathbf{0}$ exists. The generalized error is expressed as ${\mathbf{y}}_k(t)={\dot{\mathbf{e}}}_k(t)+\mathsf{\Lambda }{\mathbf{e}}_k(t)$, $\mathsf{\Lambda }$ being a positive constant. The expression $\parallel {\mathit{\omega }}_{k+1}^{(l)}(t)-{\mathit{\omega }}_k^{(l)}(t)\parallel \le \mathbf{D}$ exists, where ${\mathit{\omega }}^{(l)}$ depicts the repetitive external disturbance. Let us define ${\mathit{\xi }}^T({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k)=\left[\begin{array}{cc}\varphi ({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k)& sat({\mathbf{y}}_k)\end{array}\right]$, with $sat({\mathbf{y}}_k)$ being the saturation form of the generalized error, which can decrease the influence of discontinuous torques caused by the switching function, to ensure the controller have continuous output.

3.4. Integration of Fuzzy Adaptive ILC

On the basis of previously designed control laws, the integrated control scheme is designed as depicted in Figure 5, which consists of three major control laws, i.e., adaptive control of parameter tuning, adaptive feedback control of gains and compensation robust control of external disturbances. The adaptive parameters are updated in the time and iterative domains simultaneously, where the parameter correction term includes a partially linearized dynamic model of the robot and a saturated generalized error. The design of the generalized error as a saturated function is able to learn from the displacement and velocity errors, to reduce the joint buffetings in the function switching. Moreover, the fuzzy controller for the adaptive feedback of gain can work to adjust PD gains in real time, which can ensure the stability of the closed-loop system. The robust control item can help to suppress periodic disturbances.

3.5. Controller Stability Analysis Using the Lyapunov Theory

The dynamic system of a robotic manipulator can meet the following two conditions, namely:

• The inertia matrix $\mathbf{M}({\mathbf{q}}_k)$ is a positive-definite and bounded matrix, and thus, there exists $\parallel \mathbf{M}({\mathbf{q}}_k){\ddot{\mathbf{q}}}_d-{\mathbf{d}}_k\parallel \le \mathsf{\Gamma }$ with $\forall t\in [0,T]$, $\mathsf{\Gamma }\in \mathbb{R}$
• Matrix $\dot{\mathbf{M}}({\mathbf{q}}_k)-2\mathbf{C}({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k)$ is a skew-symmetric matrix, which meets ${\mathbf{q}}_k^T[\dot{\mathbf{M}}({\mathbf{q}}_k)-2\mathbf{C}({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k)]{\mathbf{q}}_k=0$, $\forall {\mathbf{q}}_k\in \mathbb{R}$. This existing skew asymmetry can be helpful in the control law design for robots.

Let us define $\zeta (t)=\left[\begin{array}{cc}{\mathbf{q}}^T& \mathsf{\Gamma }\end{array}\right]$, and ${\tilde{\zeta }}_k=\zeta -{\widehat{\zeta }}_k$, the Lyapunov function [37] can be built below:

$$W_k({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{e}}_k,{\dot{\mathbf{e}}}_k)=V_k({\mathbf{q}}_k,{\mathbf{e}}_k,{\dot{\mathbf{e}}}_k)+\frac{1}{2\alpha }{\int }_0^t{\tilde{\zeta }}_k(\mathit{\tau }){\widehat{\zeta }}_k(\mathit{\tau })\mathrm{d}\tau$$

(11)

with:

$$V_k({\mathbf{q}}_k,{\mathbf{e}}_k,{\dot{\mathbf{e}}}_k)=\frac{1}{2}{\dot{\mathbf{e}}}_k^T\mathbf{M}({\mathbf{q}}_k){\dot{\mathbf{e}}}_k+\frac{1}{2}{\mathbf{e}}_k^T{\mathbf{K}}_p{\mathbf{e}}_k$$

(12)

As a consequence, the following equation is obtained:

$$\begin{array}{cc}\Delta W_k\hfill & =W_k-W_{k-1}\hfill \\ \hfill & =V_k-V_{k-1}+\frac{1}{2\alpha }{\int }_0^t\left({\tilde{\zeta }}_k^T\tilde{\zeta }-{\tilde{\zeta }}_{k-1}^T{\tilde{\zeta }}_{k-1}\right)\mathrm{d}\tau \hfill \\ \hfill & =V_k-V_{k-1}-\frac{1}{2\alpha }{\int }_0^t\left({\overline{\zeta }}_k^T\overline{\zeta }+2{\overline{\zeta }}_{k-1}^T{\overline{\zeta }}_{k-1}\right)\mathrm{d}\tau \hfill \end{array}$$

(13)

where ${\overline{\zeta }}_k={\widehat{\zeta }}_k-{\widehat{\zeta }}_{k-1}$, and $V_k({\mathbf{q}}_k,{\mathbf{e}}_k,{\dot{\mathbf{e}}}_k)$ can be written as:

$$V_k({\mathbf{q}}_k,{\mathbf{e}}_k,{\dot{\mathbf{e}}}_k)=V_k({\mathbf{q}}_k(0),{\mathbf{e}}_k(0),{\dot{\mathbf{e}}}_k(0))+{\int }_0^t\left({\ddot{\mathbf{e}}}_k^T\mathbf{M}({\mathbf{q}}_k){\ddot{\mathbf{e}}}_k+\frac{1}{2}{\dot{\mathbf{e}}}_k^T\dot{\mathbf{M}}({\mathbf{q}}_k){\dot{\mathbf{e}}}_k+{\mathbf{e}}_k^T{\mathbf{K}}_p{\mathbf{e}}_k\right)\mathrm{d}\tau$$

(14)

(1)

Proof of the compound energy function $W_k$ being a non-incremental function

Let $V_k(0)=V_k({\mathbf{q}}_k(0),{\mathbf{e}}_k(0),{\dot{\mathbf{e}}}_k(0))$, in accordance with the control law in Equation (9) and the two foregoing conditions; thus, one obtains:

$$\begin{array}{cc}{V}_k({\mathbf{q}}_k,{\mathbf{e}}_k,{\dot{\mathbf{e}}}_k)\hfill & =V_k(0)+{\int }_0^t{\dot{\mathbf{e}}}_k^T\left[\mathbf{M}({\mathbf{q}}_k)({\ddot{\mathbf{q}}}_d-{\ddot{\mathbf{q}}}_k)+{\dot{\mathbf{e}}}_k^T\mathbf{C}({\mathbf{q}}_k){\dot{\mathbf{e}}}_k+{\mathbf{e}}_k^T{\mathbf{K}}_p{\mathbf{e}}_k\right]\mathrm{d}\tau \hfill \\ \hfill & \le V_k(0)+{\int }_0^t{\dot{\mathbf{e}}}_k^T\left[\mathbf{M}({\mathbf{q}}_k){\ddot{\mathbf{q}}}_d-{\mathbf{d}}_k+\mathbf{C}({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k){\mathbf{q}}_d+\mathbf{G}({\mathbf{q}}_k)\right.\hfill \\ \hfill & \left.-\mathit{\xi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\widehat{\mathbf{q}}}_k(t)-{\mathbf{K}}_d{\dot{\mathbf{e}}}_k-\mathbf{D}sat({\mathbf{y}}_k)\right]\mathrm{d}\tau \hfill \\ \hfill & \le V_k(0)+{\int }_0^t{\dot{\mathbf{e}}}_k^T\left[\mathit{\varphi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k)\mathit{\zeta }+\mathsf{\Gamma }sat({\mathbf{y}}_k)-\mathit{\xi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\widehat{\mathbf{q}}}_k(t)\right.\hfill \\ \hfill & \left.-{\mathbf{K}}_d{\dot{\mathbf{e}}}_k-\mathbf{D}sat({\mathbf{y}}_k)\right]\mathrm{d}\tau \hfill \\ \hfill & \le V_k(0)+{\int }_0^t\left[{\dot{\mathbf{e}}}_k^T\mathit{\xi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\tilde{\mathbf{q}}}_k(t)-{\dot{\mathbf{e}}}_k^T{\mathbf{K}}_d{\dot{\mathbf{e}}}_k\right]\mathrm{d}\tau \hfill \end{array}$$

(15)

It is known that $V_k({\mathbf{q}}_k(0),{\mathbf{e}}_k(0),{\dot{\mathbf{e}}}_k(0))=0$, and thus:

$$\begin{array}{cc}\Delta W_k\hfill & =V_k-V_{k-1}-\frac{1}{2\alpha }{\int }_0^t\left({\overline{\zeta }}_k^T\overline{\zeta }+2{\overline{\zeta }}_{k-1}^T{\overline{\zeta }}_{k-1}\right)\mathrm{d}\tau \hfill \\ \hfill & \le -V_{k-1}+{\int }_0^t\left[{\dot{\mathbf{e}}}_k^T\mathit{\xi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\tilde{\mathbf{q}}}_k(t)-{\dot{\mathbf{e}}}_k^T{\mathbf{K}}_d{\dot{\mathbf{e}}}_k\right]\mathrm{d}\tau \hfill \\ \hfill & -\frac{\alpha }{2}{\int }_0^t\left[{\mathbf{y}}_k^T(t)\mathit{\xi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\mathit{\xi }}^T({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\mathbf{y}}_k(t)\right]\mathrm{d}\tau \hfill \\ \hfill & -{\int }_0^t\left[{\mathbf{y}}_k^T(t)\mathit{\xi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\tilde{\mathbf{q}}}_k(t)\right]\mathrm{d}\tau \hfill \end{array}$$

(16)

Substituting the generalized errors ${\mathbf{y}}_k(t)={\dot{\mathbf{e}}}_k(t)+\mathsf{\Lambda }{\mathbf{e}}_k(t)$ into the previous equation leads to:

$$\begin{array}{cc}\Delta W_k\hfill & \le -V_{k-1}-\frac{\alpha }{2}{\int }_0^t\left[{\mathbf{y}}_k^T(t)\mathit{\xi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\mathit{\xi }}^T({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\mathbf{y}}_k(t)\right]\mathrm{d}\tau \hfill \\ \hfill & -{\int }_0^t{\dot{\mathbf{e}}}_k^T{\mathbf{K}}_d{\dot{\mathbf{e}}}_k\mathrm{d}\tau -{\int }_0^t\left[\mathsf{\Lambda }{\mathbf{e}}_k^T\mathit{\xi }({\mathbf{q}}_k,{\dot{\mathbf{q}}}_k,{\mathbf{y}}_k){\tilde{\mathbf{q}}}_k(t)\right]\mathrm{d}\tau \le 0\hfill \end{array}$$

(17)

from which it turns out that the energy increment $\Delta W_k$ is a non-positive value with the increasing iterations, and thus, $W_k$ with the increasing iteration constitute a decreasing sequence, namely, a non-incremental function.

(2)

Proof of boundedness and convergence of motion errors

The next step is to prove that $W_0$ is bounded, and considering $k=0$, the differentiation of Equation (11) results in:

$${\dot{W}}_0={\dot{V}}_k(0)({\mathbf{q}}_k(0),{\mathbf{e}}_k(0),{\dot{\mathbf{e}}}_k(0))+\frac{1}{2\alpha }{\tilde{\mathit{\zeta }}}_k(\mathit{\tau })\tilde{\mathit{\zeta }}(\mathit{\tau })$$

(18)

Combining Equation (15) with the foregoing expression yields:

$$\begin{array}{cc}{\dot{W}}_0\hfill & \le {\dot{\mathbf{e}}}_0^T\left[\mathit{\xi }({\mathbf{q}}_0,{\dot{\mathbf{q}}}_0,{\mathbf{y}}_0){\tilde{\mathbf{q}}}_0-{\mathbf{K}}_d{\dot{\mathbf{e}}}_0-\mathbf{D}sat({\mathbf{y}}_0)\right]+\frac{1}{2\alpha }{\tilde{\mathit{\zeta }}}_0^T{\tilde{\mathit{\zeta }}}_0\hfill \\ \hfill & \le {\dot{\mathbf{e}}}_0^T\left[\mathit{\xi }({\mathbf{q}}_0,{\dot{\mathbf{q}}}_0,{\mathbf{y}}_0){\tilde{\mathbf{q}}}_0-{\mathbf{K}}_d{\dot{\mathbf{e}}}_0\right]+\frac{1}{2\alpha }{\tilde{\mathit{\zeta }}}_0^T{\tilde{\mathit{\zeta }}}_0\hfill \end{array}$$

(19)

Due to the presence of ${\widehat{\mathbf{q}}}_{-1}(t)=0$, in accordance with Equation (10), the following equation exists:

$${\mathit{\gamma }}_0(t)=\alpha \mathit{\xi }({\mathbf{q}}_0,{\dot{\mathbf{q}}}_0,{\mathbf{y}}_0){\mathbf{y}}_0(t)$$

(20)

which can be substituted into Equation (21):

$${\dot{W}}_0\le -{\dot{\mathbf{e}}}_0^T{\mathbf{K}}_d{\dot{\mathbf{e}}}_0+\frac{1}{\alpha }{\mathit{\gamma }}_0^T{\tilde{\mathit{\zeta }}}_0+\frac{1}{2\alpha }{\tilde{\mathit{\zeta }}}_0^T{\tilde{\mathit{\zeta }}}_0\le -{\dot{\mathbf{e}}}_0^T{\mathbf{K}}_d{\dot{\mathbf{e}}}_0-\frac{1}{2}{\tilde{\mathit{\zeta }}}_0^T{\alpha }^{-1}{\tilde{\mathit{\zeta }}}_0+{\mathit{\zeta }}^T{\alpha }^{-1}{\tilde{\mathit{\zeta }}}_0$$

(21)

Based upon Young inequality [38], the following can be obtained:

$${\mathit{\zeta }}^T{\alpha }^{-1}{\tilde{\mathit{\zeta }}}_0\le \eta \parallel {\alpha }^{-1}{\tilde{\mathit{\zeta }}}_0\parallel +\frac{1}{4\eta }{\parallel \mathit{\zeta }\parallel }^2$$

(22)

Consequently, the following inequality can be deduced:

$${\dot{W}}_0\le -\left[\frac{1}{2}{\lambda }_{min}({\alpha }^{-1})-\eta {\lambda }_{max}({\alpha }^{-1})\right]\parallel {\tilde{\mathit{\zeta }}}_0{\parallel }^2-{\lambda }_{min}({\mathbf{K}}_d)\parallel {\dot{\mathbf{e}}}_0{\parallel }^2+\frac{1}{4\eta }{\parallel \mathit{\zeta }\parallel }^2$$

(23)

with:

$$\eta \le \frac{{\lambda }_{min}({\alpha }^{-1})}{2\eta {\lambda }_{max}^2({\alpha }^{-1})}$$

(24)

where ${\lambda }_{min}(·)$ and ${\lambda }_{max}(·)$ stand for the minimum and maximum eigenvalues of $(·)$, respectively. Since $\parallel {\dot{\mathbf{e}}}_0\parallel$, $\parallel {\tilde{\mathit{\zeta }}}_0\parallel$ and $\parallel \mathit{\zeta }\parallel$ are bounded in the time domain $[0,T]$, $W_0$ is bounded, from which the following condition can be derived:

$$\underset{k\to \infty }{lim}{e}_k(t)=0\&\underset{k\to \infty }{lim}{\dot{e}}_k(t)=0,\forall t\in [0,T]$$

(25)

The foregoing equation implies that the motion errors have the characteristics of iterative convergence, and when the expected errors do not vary with the iterations, the errors converge to null.

To this end, the stability of the designed controller is analyzed and proved.

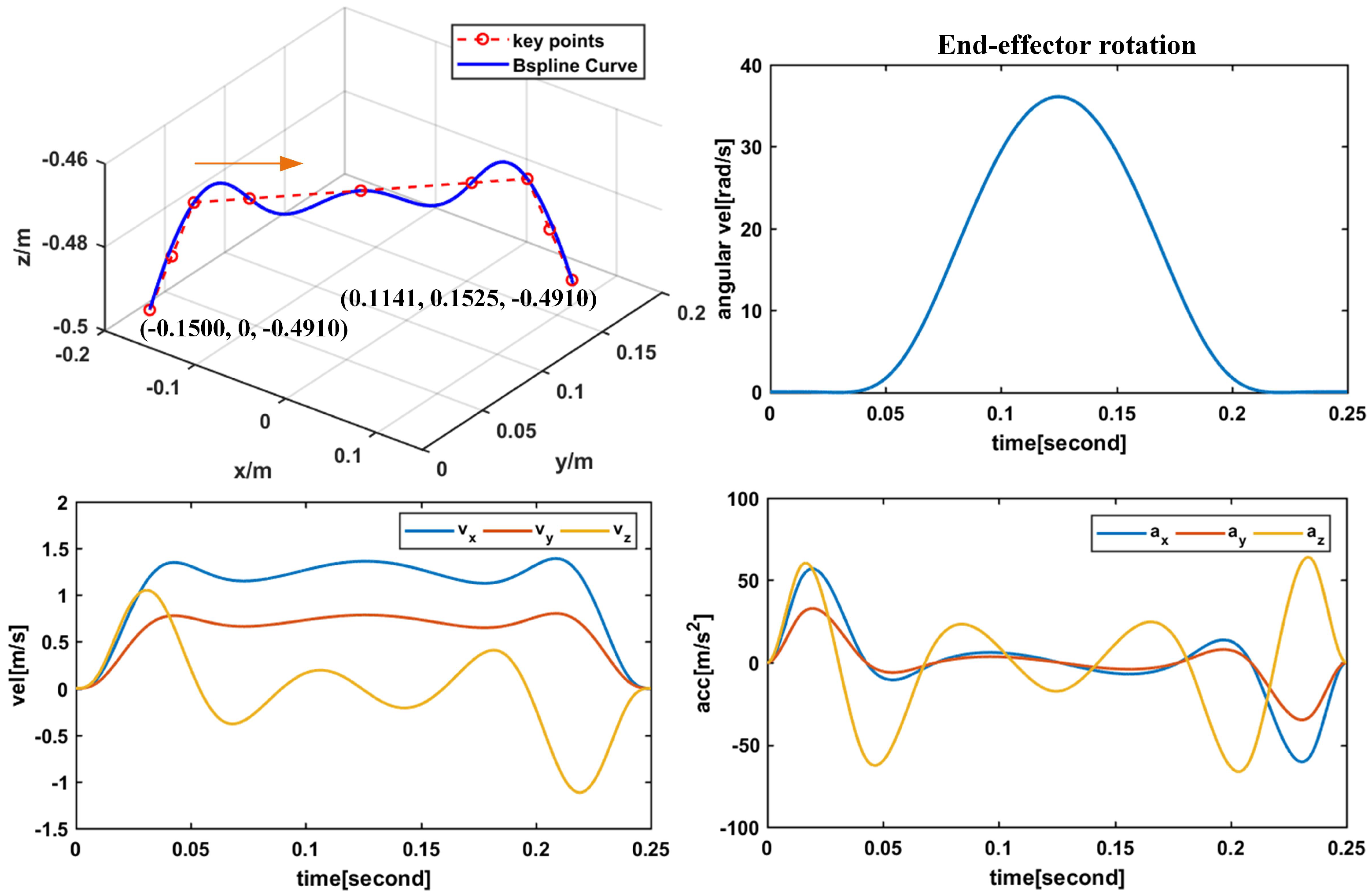
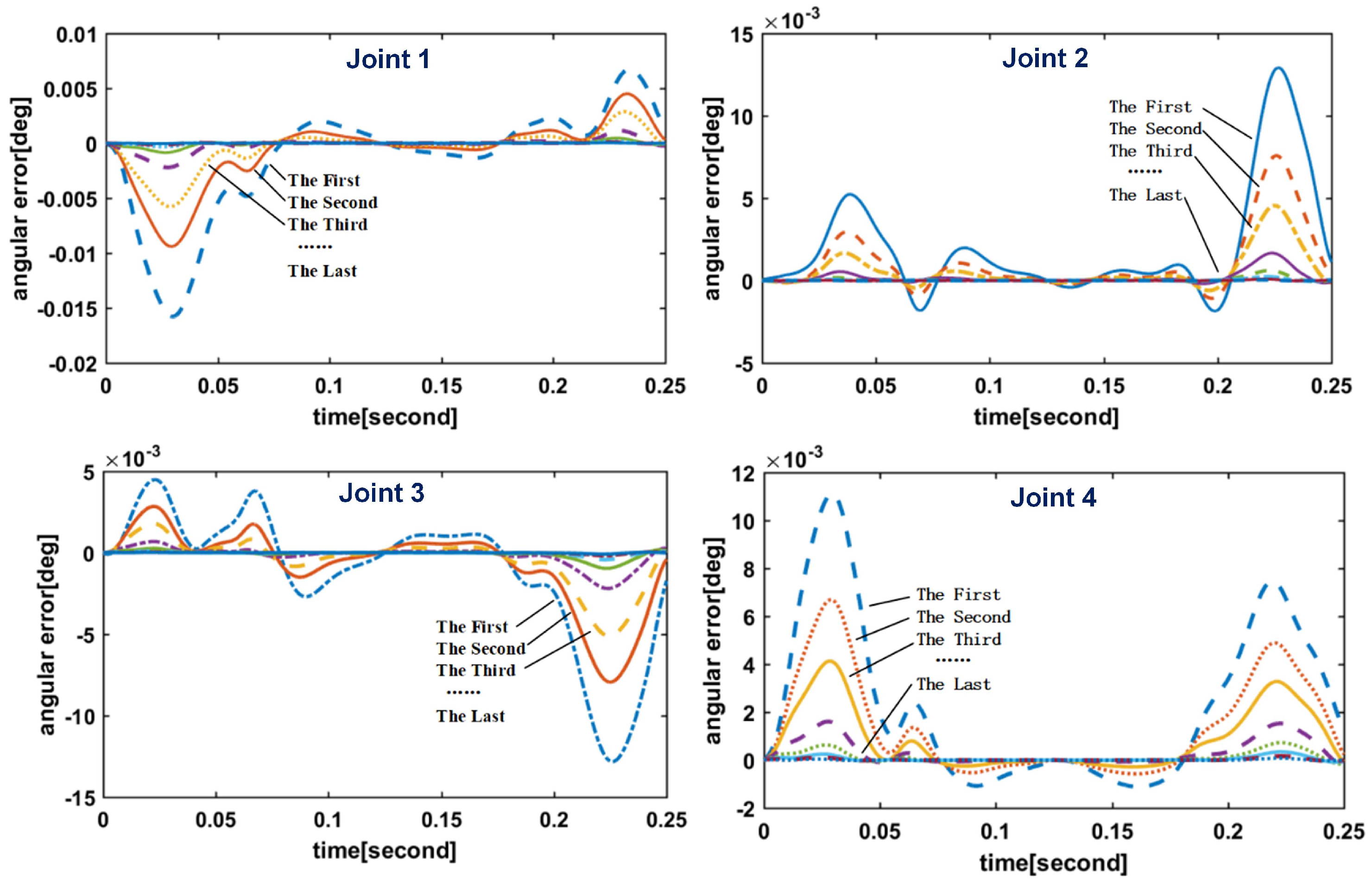
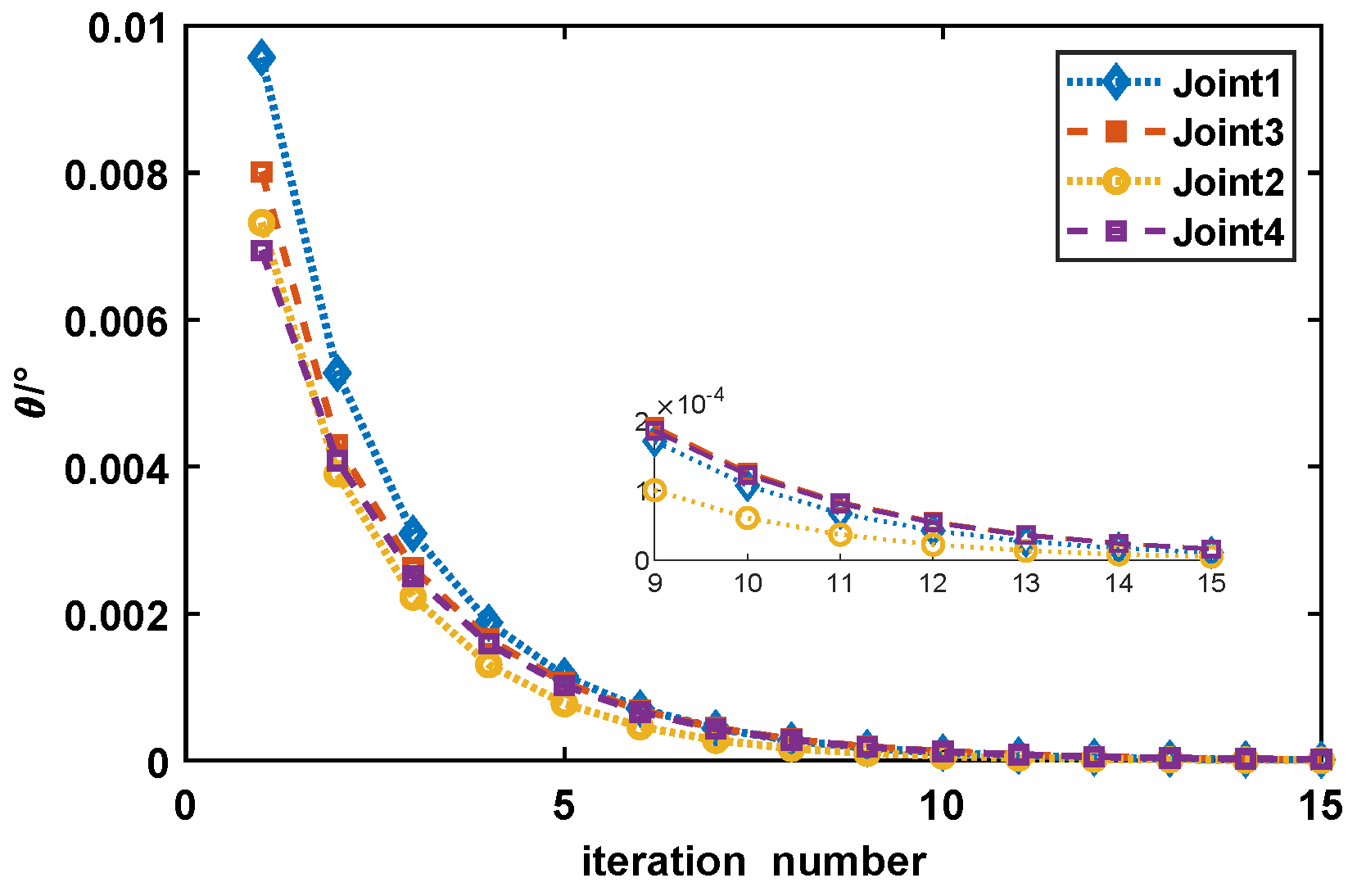
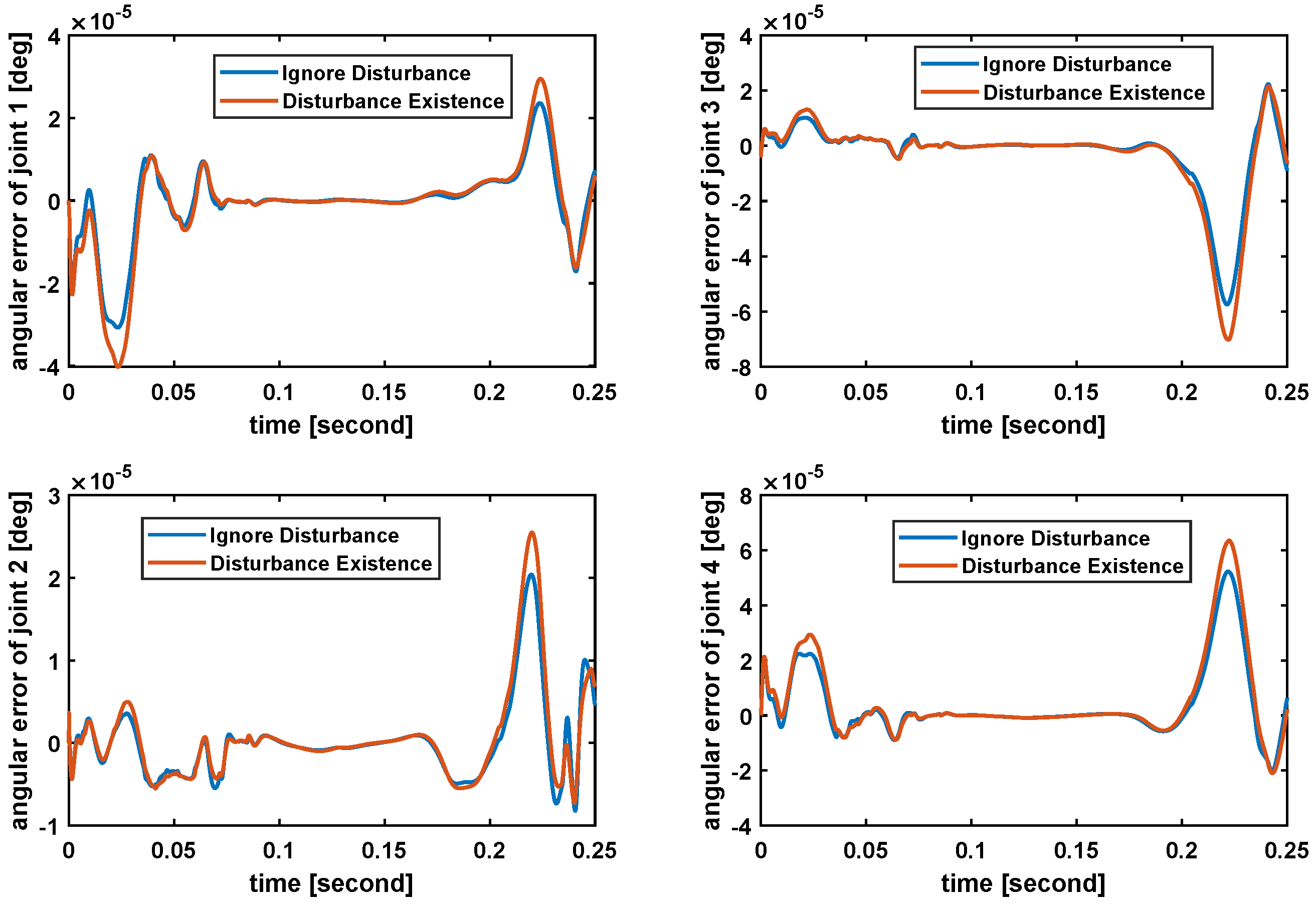
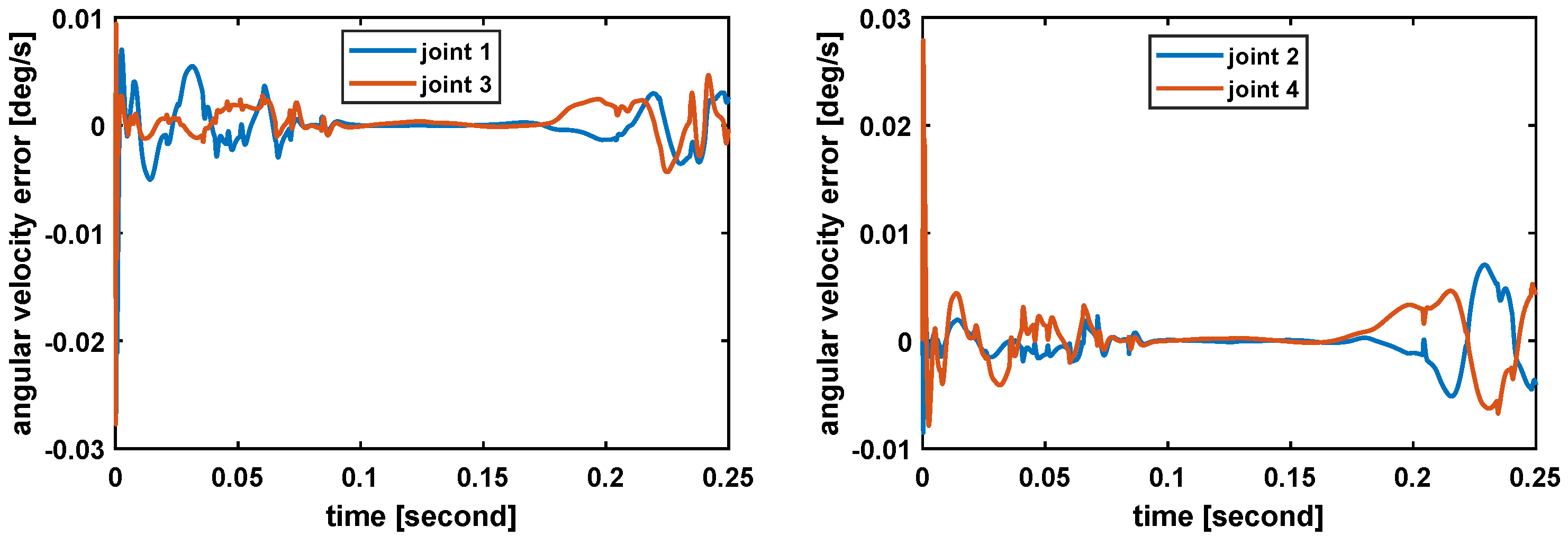
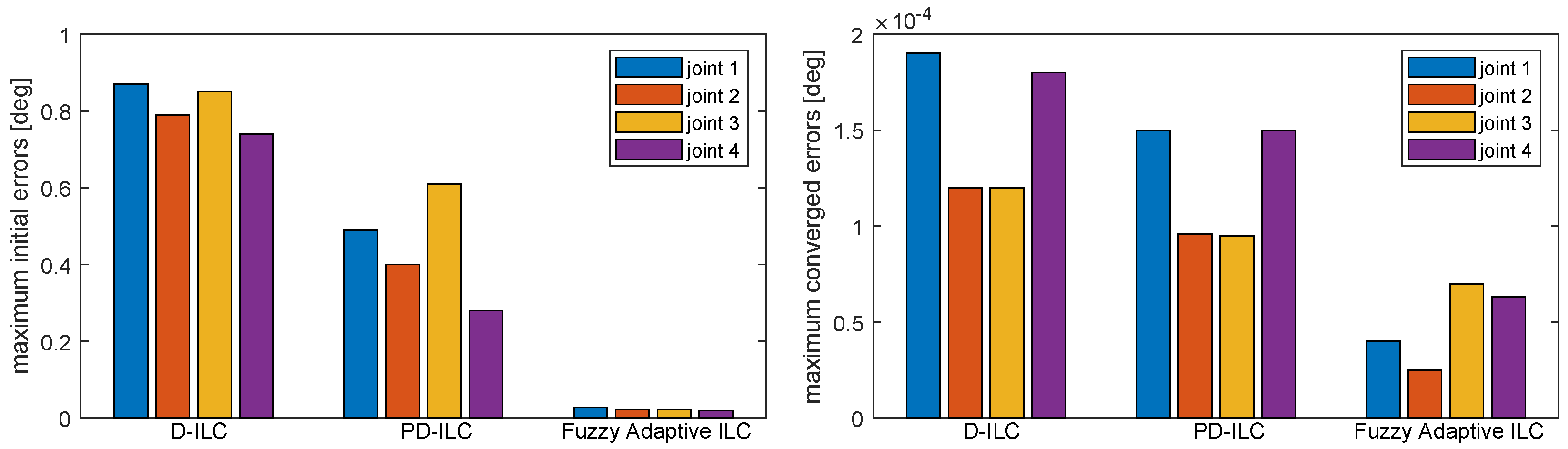
4. Results and Discussions of the Control Design

In order to verify the effectiveness of the designed control algorithm, the SCARA parallel robot (see Figure 2) is tested along with a PnP trajectory with the dimension of $25\times 305\times 25$ $\mathrm{mm}$, which is written as a B-spline curve [39] for trajectory smoothing. Figure 6 shows the testing trajectory as well as the motion profiles of the end-effector, and the traveling time is $0.25\mathrm{s}$, which means that the working frequency is 120 CPM (i.e., cycles per minute [40]).

To simulate the designed control algorithm, a control platform is built with the Matlab/Simscape of version 2020a, which consists of five modules in terms of trajectory planning, control law of fuzzy AIL, external disturbance, robot system and sensor measurement, as depicted in Figure 7. The input motion parameters in the module of “trajectory generation” are calculated from the inverse kinematics according to the tracked trajectory, as displayed in Figure 6. The designed control algorithm depicted in Figure 5 is embodied in the “fuzzy-AIL control” block, and the external disturbance is managed with “Flag_Ft” function as the Switch to be included in the simulation or not. The multi-body system in the “Parallel Robot” module is generated and imported from Solidworks^TM 2016 through the Matlab-Solidworks interface addon “Simscape Multibody Link” for mechanics simulation, and the torque feedforward control is adopted as the close-loop control law based on the dynamic model, as depicted in Figure 8. The “measurement” module outputs the sensor data attached to the joints in the Simscape package.

In the previous work [2], torque feedforward control was designed and the PD parameters were optimized by minimizing the trajectory tracking errors. Comparing the tracking accuracy with different local optimums of the control parameters, the control parameters of the gains are selected as:

$${\mathbf{K}}_p=diag\left[\begin{array}{cccc}2.4& 2.4& 2.4& 2.4\end{array}\right]\times {10}^4,{\mathbf{K}}_d=diag\left[\begin{array}{cccc}1.2& 1.2& 1.2& 1.2\end{array}\right]\times {10}^2$$

(26)

and the adaptive parameters are set to:

$$\mathit{\alpha }=diag\left[\begin{array}{ccccc}82& 82& 82& 82& 82\end{array}\right],\mathsf{\Lambda }=340$$

(27)

When the robot tracks the planned path in Figure 6, the sampling time and the number of iterations are set to $1\mathrm{ms}$ and 15, respectively. Here, three indices, the maximum ($E_{max}$), mean ($E_{ave}$) and root-mean-squared ($E_{rms}$) angular errors of the joints, are defined for the evaluation of the tracking accuracy. Figure 9 depicts the varying angular errors of the joints with respect to the times from the first to final iterations, from which it can be seen that the angular errors of all the joints in the initial iteration are large and converge to very small values in the last iteration. The varying motion errors verify the convergence of the designed control law with the increasing iterations.

Moreover, the convergence curves of the angular errors $E_{rms}$ for all joints varying with the iterations are given in Figure 10. It can be observed that in the first iteration without controller learning to store the previously information, the errors of angular displacements are relatively large. After the learning of first iteration, the errors of each joint can be reduced by $56.5\%$, $45.8\%$, $46.4\%$ and $39.8\%$, respectively. With the iterations increasing, all the angular errors of joints gradually become smaller; particularly, the errors significantly decrease in the first five iterations. The convergence curves of $E_{rms}$ errors of all the joints turn to be stable after the ninth iteration, and finally almost converge to zero. The aforementioned evaluation indices of angular displacement errors are listed in

Table 4. The final converged angular displacement errors by the designed control law.

Joint No.	${\mathit{E}}_{\mathit{max}}$	${\mathit{E}}_{\mathit{ave}}$	${\mathit{E}}_{\mathit{rms}}$
1	$4.0\times {10}^{-5}$	$6.4\times {10}^{-6}$	$1.1\times {10}^{-5}$
2	$2.5\times {10}^{-5}$	$3.2\times {10}^{-6}$	$5.7\times {10}^{-5}$
3	$7.0\times {10}^{-5}$	$7.4\times {10}^{-6}$	$1.6\times {10}^{-5}$
4	$6.4\times {10}^{-5}$	$8.4\times {10}^{-6}$	$1.6\times {10}^{-5}$

, which are close to zero, which shows the effectiveness of error convergence by the designed controller.

To verify the robustness of the control system, periodic ${\tau }_{dis\_re}=ksin(\lambda t+\phi )$ and non-periodic disturbance ${\tau }_{dis}=2sin(q_d)-sin({\dot{q}}_d)$ are designed to simulate the external disturbances that can affect the tracking accuracy, such as the assembly errors, joint friction, unpredictable external environment during the production process, etc. The trajectory tracking errors of angular displacements with/without disturbances in the final iteration are depicted in Figure 11, from which the comparison shows that the two curves of the trajectory tracking errors are almost consistent. This means that even if there is an external disturbance, the designed controller can make the robot track the expected trajectory with ignorable errors, which implies that the designed control algorithm can well suppress various periodic and non-periodic disturbances with good robustness. Besides, the angular velocity errors of the actuated joints are shown in Figure 12, from which it can be seen that the errors are very small and smooth except at the start and end of the trajectory with the higher accelerations.

In order to show the advantage of the designed fuzzy adaptive ILC algorithm, a comparative study is carried out with the classical D-type and PD-type ILC algorithms. Figure 13 shows the comparison of the maximum initial and final converged angular errors of all the joints. It can be seen that the maximum initial angular errors generated by the D-type and PD-type ILC algorithms are equal to $0.87$ and $0.61$ degrees [34], respectively, which are much larger than that of fuzzy adaptive ILC, where the maximum initial angular error is equal to $0.028$ degrees. Moreover, after 15 iterations of learning control, the final angular errors by the three control laws converge to $1.9\times {10}^{-4}$, $1.5\times {10}^{-4}$ and $0.7\times {10}^{-4}$ degree maximally, respectively, which shows that the designed fuzzy adaptive ILC algorithm can speed up the convergence in fewer iterations and can make the trajectory tracking errors converge to smaller values. Compared to other ILC-based control laws, the fuzzy adaptive ILC designed in this work can ensure high-precision trajectory tracking for high-quality material handling tasks.

It is noteworthy that the previous implementation of simulation is carried out with 64-bit Windows 7 operation system, of which the processor is an Intel i5-9400f with 8 GB of RAM. The computational time of the designed control algorithm in each iteration is about 0.3–0.5 s, and thus, the optimal control parameters can be converged in seconds, which implies that the presented control law is suitable for stable repetitive pick-and-place tasks.

5. Conclusions

This paper presents the integrated control design of iterative learning algorithm, fuzzy rules and adaptive control, i.e., fuzzy adaptive ILC, for the parallel SCARA robot, aiming to improve the trajectory tracking accuracy for high-quality material handling tasks. A step-design approach is adopted to ensure the adaptability of the designed control law that is reflected in two aspects: ① the feedback gain of the controller is adjusted by the fuzzy rules; ② the adaptive unknown parameters are obtained by means of iterative learning estimation to suppress the uncertainties and external disturbances caused by the unknown parameters for high-precision trajectory tracking of the robot. The stability of the controller is analyzed and proved with the Lyapunov theory.

The effectiveness of the designed control algorithm is verified by observing the tracking errors in joint space, where the robot tracks along with a PnP testing trajectory. It turns out that the varying maximum, root-mean-squared and mean angular displacement errors of the actuation joints converge to almost zero values with the increasing iterations rapidly. Moreover, two kinds of external disturbances, i.e., periodic and non-periodic ones, are designed to simulate the external working environment of the robot, from which the results show that the designed control scheme can well suppress various disturbances with good robustness. Compared to different ILC-based control laws, the designed fuzzy adaptive ILC algorithm in this work can speed up the convergence of tracking errors to smaller values, which can ensure high-precision trajectory tracking. The presented results show the robustness, effectiveness and advantages of the designed control law, which can be generalized to the high-speed parallel PnP robots of this family.