Trajectory Tracking Control of Fast Parallel SCARA Robots with Fuzzy Adaptive Iterative Learning Control for Repetitive Pick-and-Place Operations
Abstract
:1. Introduction
2. Pick-and-Place Robot and Dynamic Model
3. Fuzzy Adaptive Iterative Learning Control Design
3.1. Design of the Iterative Learning Control Law
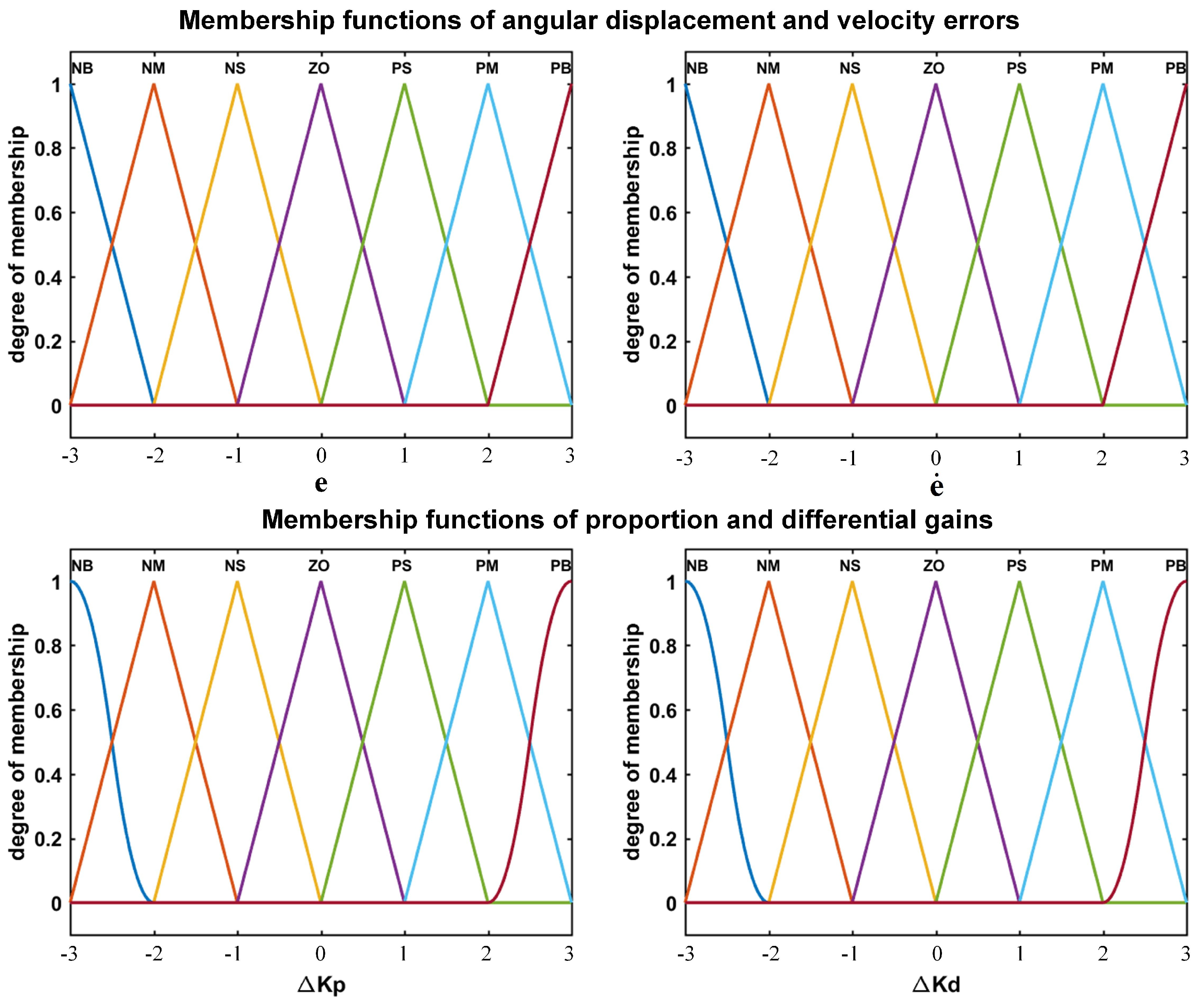
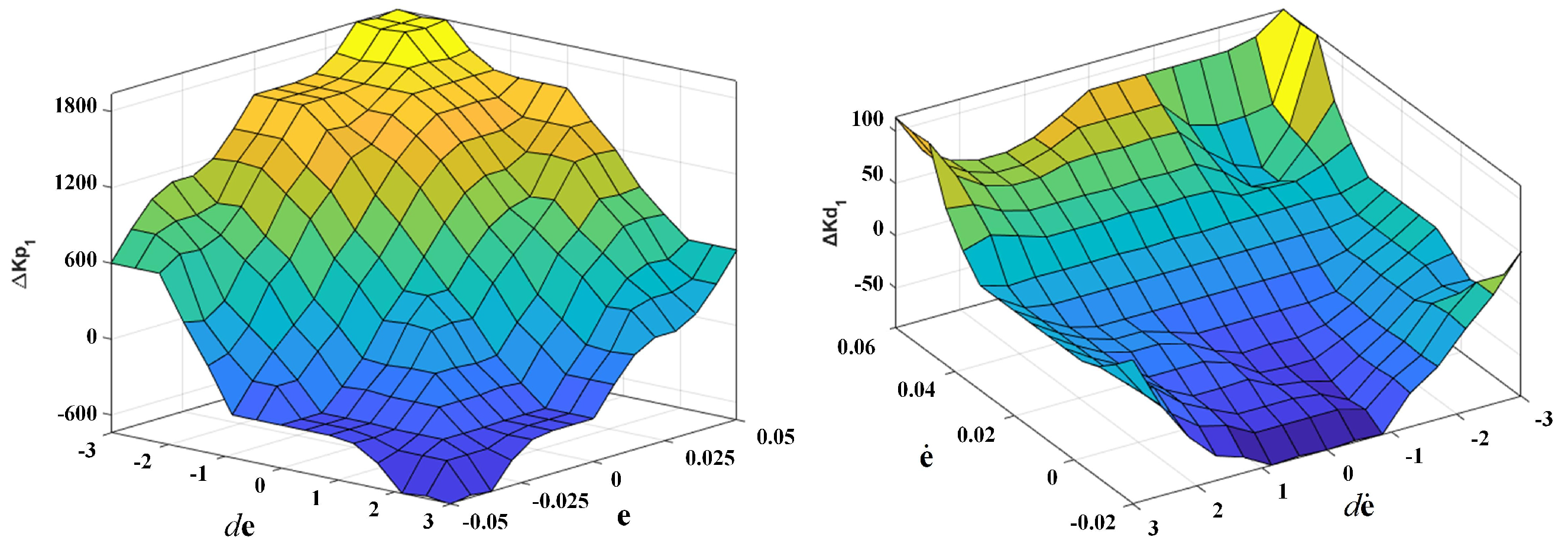
3.2. Fuzzy Controller Design
3.3. Adaptive Iterative Learning Law
3.4. Integration of Fuzzy Adaptive ILC
3.5. Controller Stability Analysis Using the Lyapunov Theory
- The inertia matrix is a positive-definite and bounded matrix, and thus, there exists with ,
- Matrix is a skew-symmetric matrix, which meets , . This existing skew asymmetry can be helpful in the control law design for robots.
- (1)
- Proof of the compound energy function being a non-incremental function
- (2)
- Proof of boundedness and convergence of motion errors
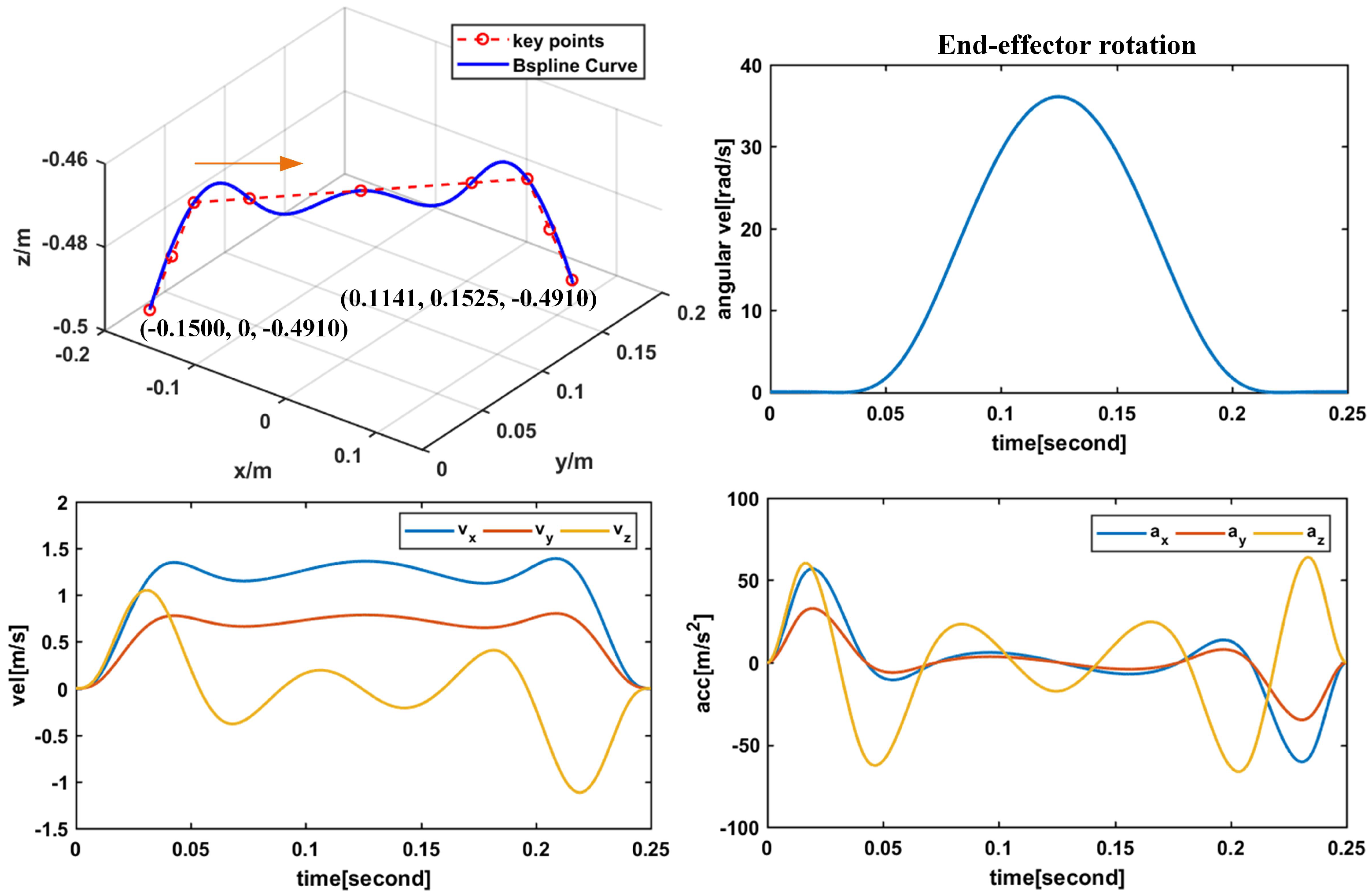
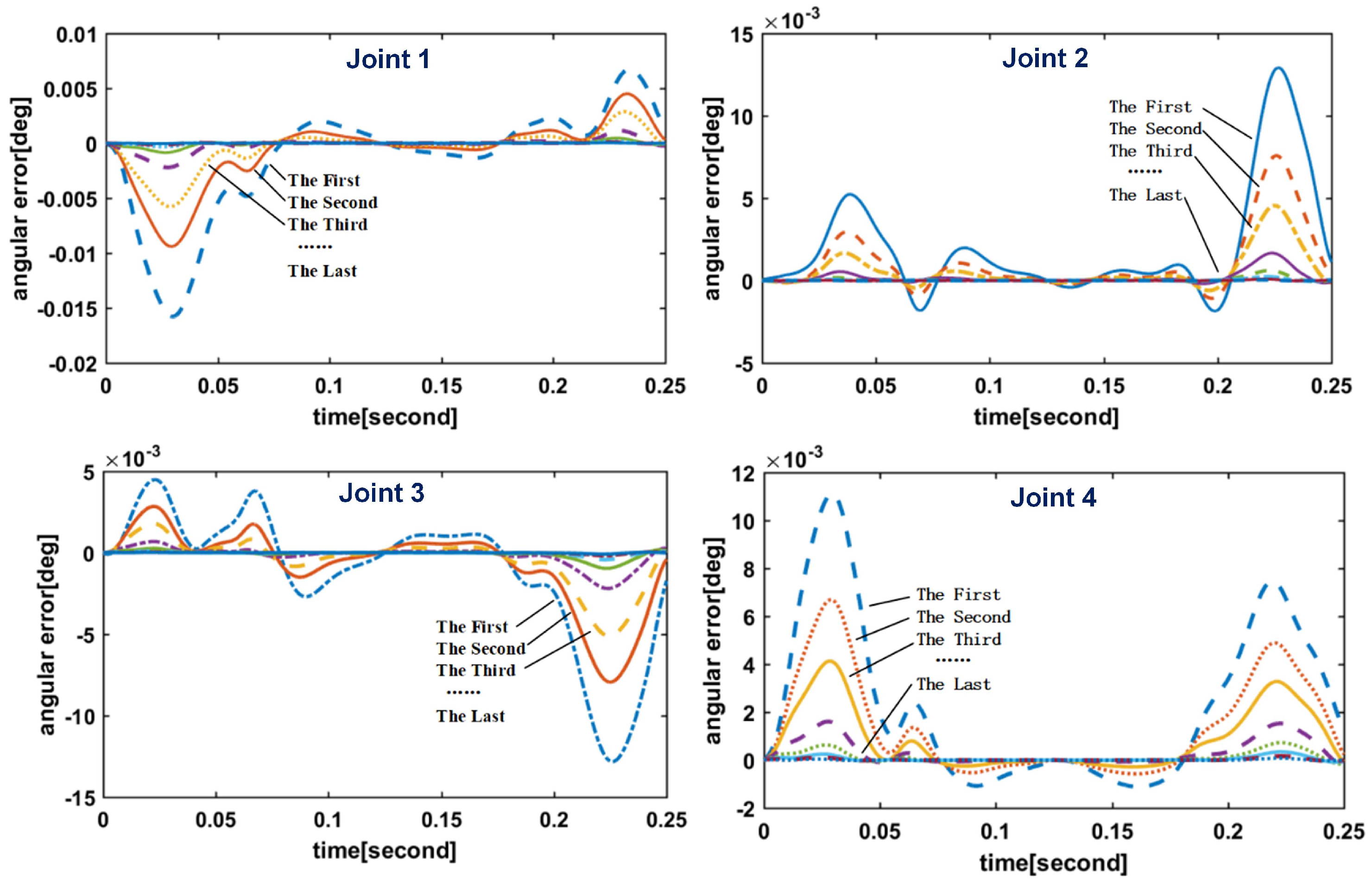
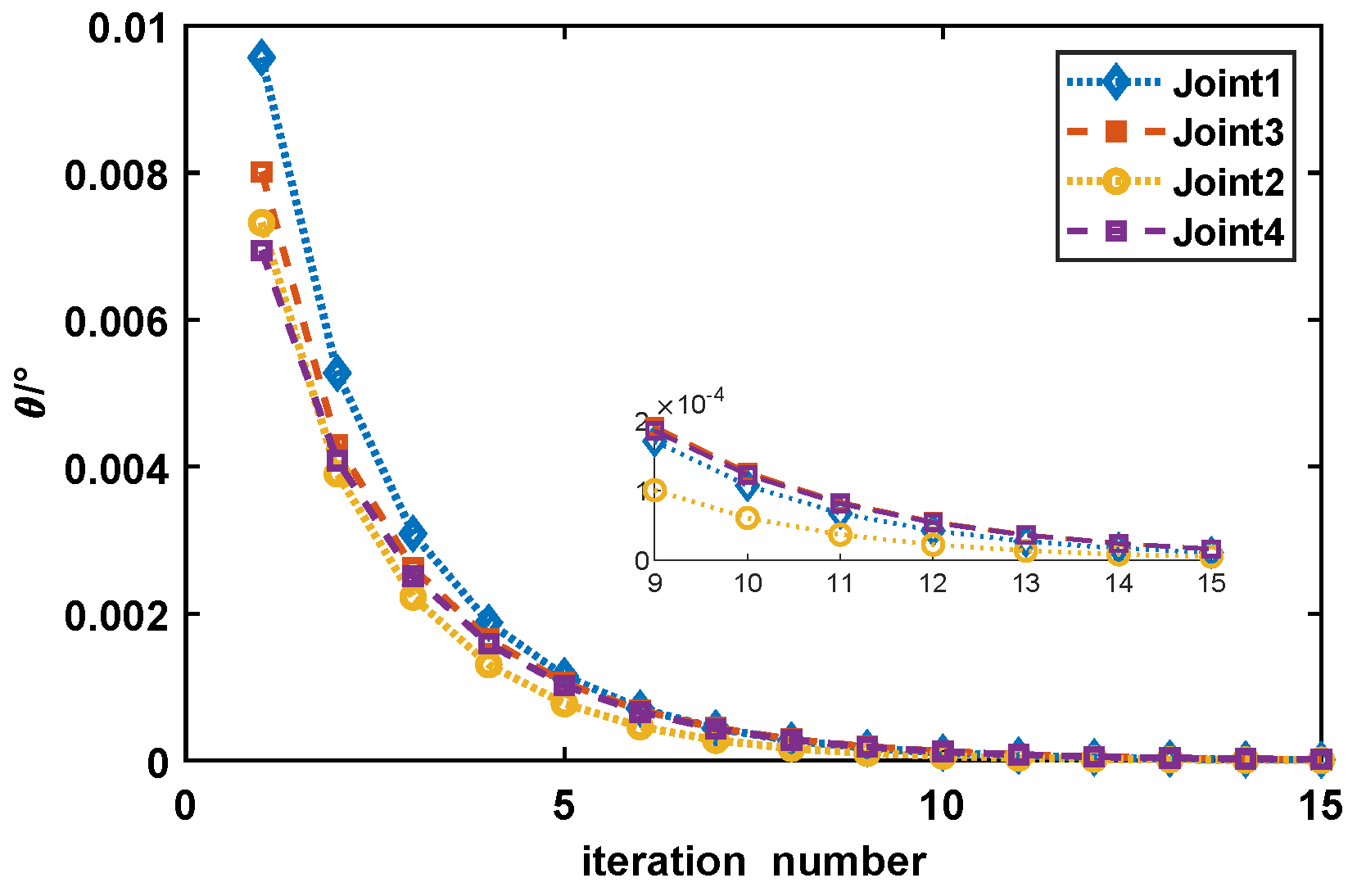
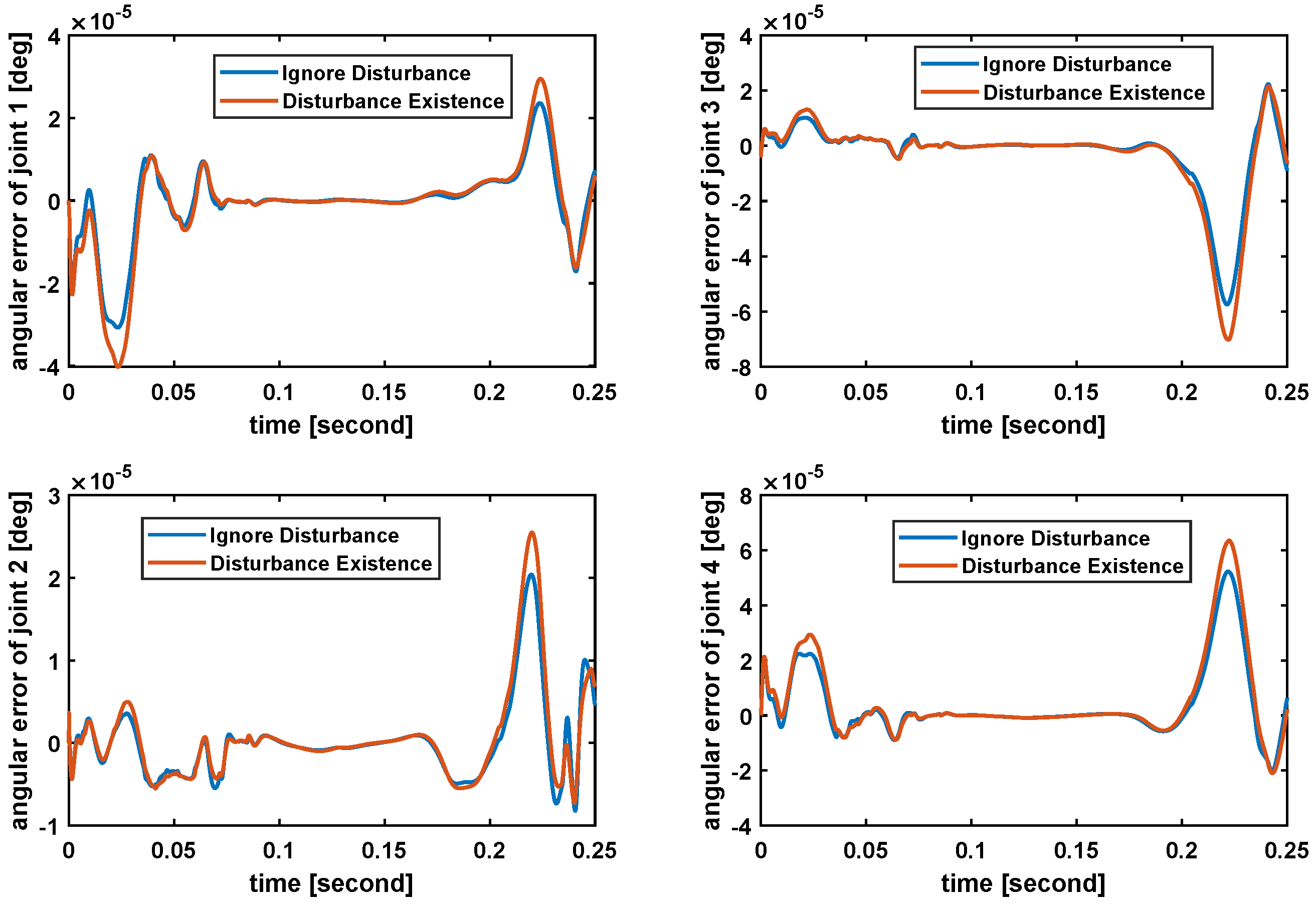
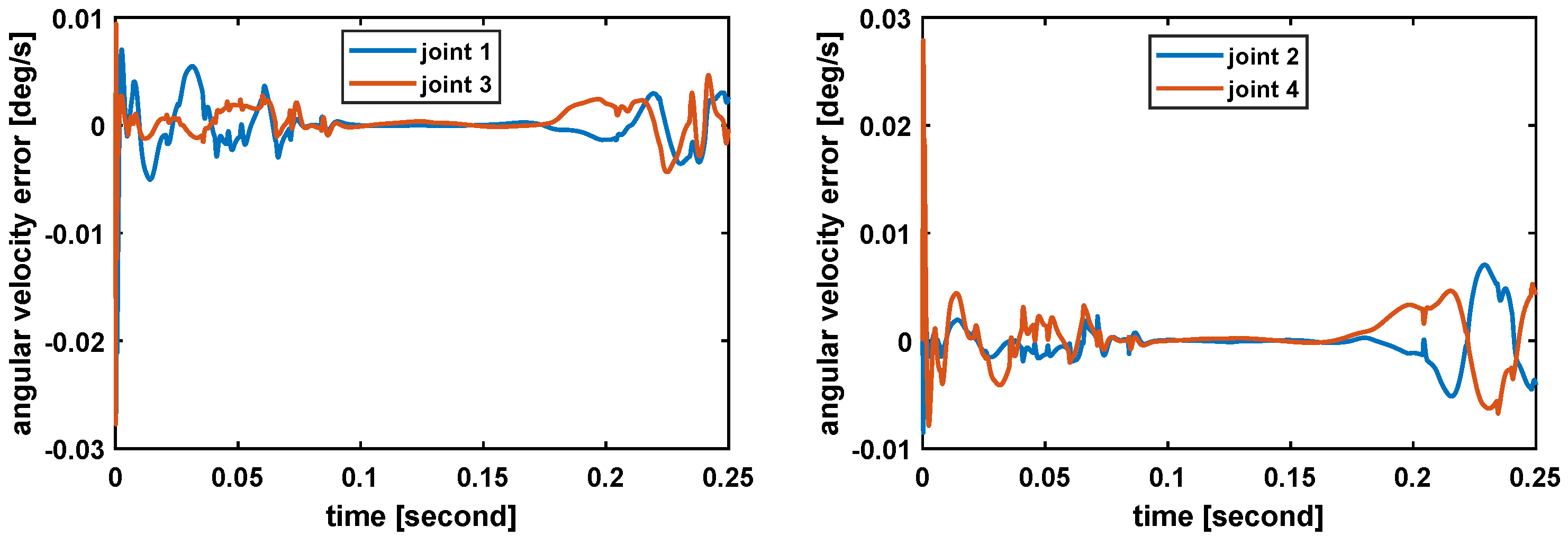
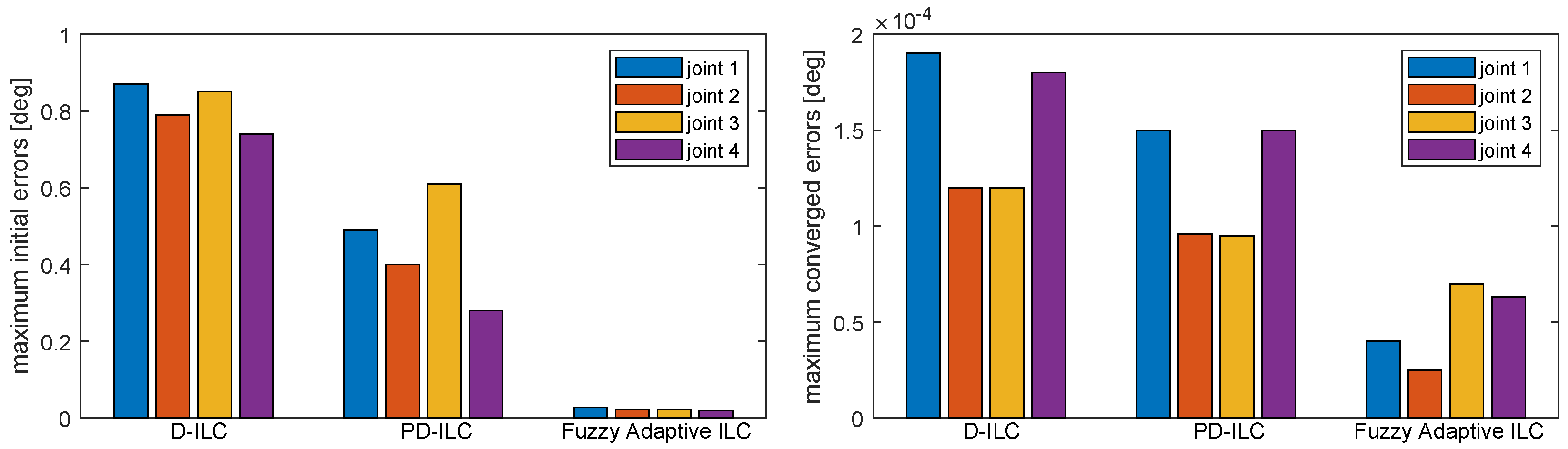
4. Results and Discussions of the Control Design
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, G.; Shen, H. Parallel PnP Robots; Springer: Singapore, 2021; pp. 1–15. [Google Scholar]
- Lin, Z.; Cui, C.; Wu, W. Dynamic modeling and torque feedforward based optimal fuzzy PD control of a high-speed parallel manipulator. J. Robot. Control 2021, 2, 527–538. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Trajectory Planning. In Robotics: Modelling, Planning and Control; Springer: London, UK, 2008; pp. 161–189. [Google Scholar]
- Zubizarreta, A.; Marcos, M.; Cabanes, I.; Pinto, C. A procedure to evaluate extended computed torque control configurations in the Stewart–Gough platform. Robot. Auton. Syst. 2011, 59, 770–781. [Google Scholar] [CrossRef]
- Codourey, A. Dynamic modeling of parallel robots for computed-torque control implementation. Int. J. Robot. Res. 1998, 17, 1325–1336. [Google Scholar] [CrossRef]
- Craig, J.J.; Hsu, P.; Sastry, S.S. Adaptive control of mechanical manipulators. Int. J. Robot. Res. 1987, 6, 16–28. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, G.; Lin, S.; Gao, J. Adaptive fuzzy computed-torque control for robot manipulator with uncertain dynamics. Int. J. Adv. Robot. Syst. 2012, 9, 237. [Google Scholar] [CrossRef]
- Hyon, S.; Suewaka, D.; Torii, Y.; Oku, N. Design and experimental evaluation of a fast torque-controlled hydraulic humanoid robot. IEEE/ASME Trans. Mechatron. 2017, 22, 623–634. [Google Scholar] [CrossRef]
- Koessler, A.; Bouton, N.; Briot, S.; Bouzgarrou, B.C.; Mezouar, Y. Linear adaptive computed torque control for singularity crossing of parallel robots. In ROMANSY 22–Robot Design, Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2019; pp. 222–229. [Google Scholar]
- Qi, Z.; McInroy, J.E.; Jafari, F. Trajectory tracking with parallel robots using low chattering, fuzzy sliding mode controller. J. Intell. Robot. Syst. 2007, 48, 333–356. [Google Scholar] [CrossRef]
- Choi, H.; Konno, A.; Uchiyama, M. Design, implementation, and performance evaluation of a 4-DOF parallel robot. Robotica 2010, 28, 107–118. [Google Scholar] [CrossRef]
- Azad, F.A.; Rahimi, S.; Hairi Yazdi, M.R.; Masouleh, M.T. Design and Evaluation of Adaptive and Sliding Mode Control for a 3-DOF Delta Parallel Robot. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; pp. 1–7. [Google Scholar]
- Bae, B.; Lee, D.-H. Design of a Four-Wheel Steering Mobile Robot Platform and Adaptive Steering Control for Manual Operation. Electronics 2023, 12, 3511. [Google Scholar] [CrossRef]
- Khosravi, M.A.; Taghirad, H.D. Robust PID control of fully-constrained cable driven parallel robots. Mechatronics 2014, 24, 87–97. [Google Scholar] [CrossRef]
- Tiep, D.K.; Lee, K.; Im, D.-Y.; Ryoo, Y.K. Design of Fuzzy-PID Controller for Path Tracking of Mobile Robot with Differential Drive. Int. J. Fuzzy Logic Intell. Syst. 2018, 18, 220–228. [Google Scholar] [CrossRef]
- Vivas, A.; Poignet, P. Predictive functional control of a parallel robot. Control Eng. Pract. 2005, 13, 863–874. [Google Scholar]
- Jia, H.; Shang, W.; Xie, F.; Zhang, B.; Cong, S. Second-order sliding-mode-based synchronization control of cable-driven parallel robots. IEEE/ASME Trans. Mechatron. 2020, 25, 383–394. [Google Scholar] [CrossRef]
- Sachan, S.; Swarnkar, P. Intelligent Fractional Order Sliding Mode Based Control for Surgical Robot Manipulator. Electronics 2023, 12, 729. [Google Scholar] [CrossRef]
- Rotea, M.A. The generalized H2 control problem. Automatica 1993, 29, 373–385. [Google Scholar] [CrossRef]
- Xu, S.Y.; Chen, T.W. Robust H-infinity control for uncertain stochastic systems with state delay. IEEE Trans. Autom. Control 2002, 47, 2089–2094. [Google Scholar]
- Hua, M.; Zhang, F.; Deng, F.; Fei, J.; Chen, H. Mixed H2/H∞ control for discrete-time periodic Markov jump systems with quantization effects and packet loss compensation. Nonlinear Anal. Hybrid Syst. 2023, 50, 101398. [Google Scholar] [CrossRef]
- Uchiyama, M. Formation of high-speed motion pattern of a mechanical arm by trial. Trans. Soc. Instrum. 1978, 14, 706–712. [Google Scholar]
- Boudjedir, C.E.; Boukhetala, D.; Bouri, M. Iterative Learning Control of a Parallel Delta Robot. In Advanced Control Engineering Methods in Electrical Engineering Systems; Springer International Publishing: New York, NY, USA, 2018; pp. 72–83. [Google Scholar]
- You, D.; Cui, L.; Bu, X.; Zhao, X.; Hou, R. Longitudinal Slippage Iterative Learning Trajectory Tracking Control of Wheeled Robots. Electron. Optics Contr. 2022, 29, 96–101. [Google Scholar]
- Xi, W.; Wang, Y.; Chen, B.; Wu, H. Iterative learning control of robot based on artificial bee colony algorithm. Proc. Ins. Mech. Eng. Part I J. Syst. Contr. Eng. 2018, 233, 1221–1238. [Google Scholar] [CrossRef]
- Liu, F.; Fan, Y. Higher-Order PID Sampled-Data Iterative Learning Control. Contr. Eng. China 2012, 19, 73–76. [Google Scholar]
- Wang, H.; Dong, J.; Wang, Y. Research on Open-Closed-Loop Iterative Learning Control with Variable Forgetting Factor of Mobile Robots. Discret. Dyn. Nat. Soc. 2016, 2016, 6452179. [Google Scholar] [CrossRef]
- Cao, W.; Dai, X.; Liu, Y. Discrete Iterative Learning Control with Variable Forgetting Factor for Mobile Robots. J. Beijing Uni. Technol. 2015, 41, 1516–1521. [Google Scholar]
- Norouzi, A.; Koch, C.R. Robotic Manipulator Control Using PD-type Fuzzy Iterative Learning Control. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–4. [Google Scholar]
- Patan, K.; Patan, M. Neural-network-based High-order Iterative Learning Control. In Proceedings of the 2019 American Control Conference, Philadelphia, PA, USA, 10–12 July 2019; pp. 2873–2878. [Google Scholar]
- Wu, G.; Zhang, X.; Zhu, L.; Lin, Z.; Liu, J. Fuzzy Sliding Mode Variable Structure Control of a High-speed Parallel PnP Robot. Mech. Mach. Theory 2021, 162, 104349. [Google Scholar] [CrossRef]
- Li, Q.; Wu, G.; Shen, H. Trajectory tracking control of SCARA parallel robot based on fuzzy adaptive iterative learning algorithm. In Proceedings of the Third International Conference on Mechanical Design and Simulation (MDS 2023), Xi’an, China, 3–5 March 2023; p. 126392N-(1–8). [Google Scholar]
- Valentine, F.A. A Lipschitz condition preserving extension for a vector function. Am. J. Math. 1945, 67, 83–93. [Google Scholar] [CrossRef]
- Li, Q.; Liu, E.; Cui, C.; Wu, G. An open-closed-loop iterative learning control for trajectory tracking of a high-speed 4-dof parallel robot. Intell. Robot. 2022, 2, 89–104. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy algorithms. Inf. Control 1968, 12, 94–102. [Google Scholar] [CrossRef]
- Åström, K.J.; Wittenmark, B. Adaptive Control; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Khalil, H.K. Lyapunov stability. Control. Syst. Robot. Autom. 2009, 12, 115. [Google Scholar]
- Ando, T. Matrix young inequalities. Oper. Theory Adv. Appl 1995, 75, 33. [Google Scholar]
- Wu, G.; Zhao, W.; Zhang, X. Optimum time-energy-jerk trajectory planning for serial robotic manipulators by reparameterized quintic NURBS curves. Proc. Ins. Mech. Eng. Part C-J. Mech. Eng. Sci. 2021, 235, 4382–4393. [Google Scholar] [CrossRef]
- Gauthier, J.F.; Angeles, J.; Nokleby, S. Optimization of a test trajectory for SCARA systems. In Advances in Robot Kinematics: Analysis and Design; Springer: Dordrecht, The Netherlands, 2008; pp. 225–234. [Google Scholar]

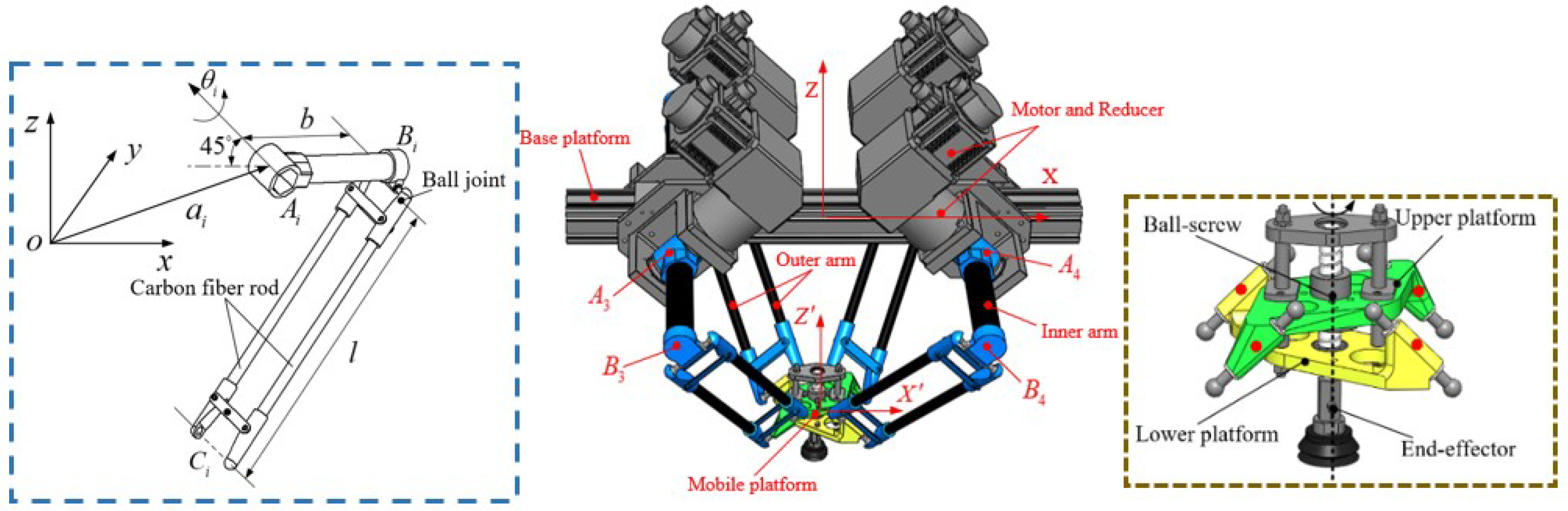



| Parameters | Meaning | Value | Unit |
|---|---|---|---|
| x-/y-coordinates of joint position | |||
| lengths of proximal/distal links | |||
| r | radius of moving platform | 100 | |
| h | pitch of lead screw | 10 | |
| masses of proximal/distal links | |||
| masses of upper/lower sub-platforms |
| Joint No. | |||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Niu, B.; Li, Q. Trajectory Tracking Control of Fast Parallel SCARA Robots with Fuzzy Adaptive Iterative Learning Control for Repetitive Pick-and-Place Operations. Electronics 2023, 12, 4995. https://doi.org/10.3390/electronics12244995
Wu G, Niu B, Li Q. Trajectory Tracking Control of Fast Parallel SCARA Robots with Fuzzy Adaptive Iterative Learning Control for Repetitive Pick-and-Place Operations. Electronics. 2023; 12(24):4995. https://doi.org/10.3390/electronics12244995
Chicago/Turabian StyleWu, Guanglei, Bin Niu, and Qiancheng Li. 2023. "Trajectory Tracking Control of Fast Parallel SCARA Robots with Fuzzy Adaptive Iterative Learning Control for Repetitive Pick-and-Place Operations" Electronics 12, no. 24: 4995. https://doi.org/10.3390/electronics12244995
APA StyleWu, G., Niu, B., & Li, Q. (2023). Trajectory Tracking Control of Fast Parallel SCARA Robots with Fuzzy Adaptive Iterative Learning Control for Repetitive Pick-and-Place Operations. Electronics, 12(24), 4995. https://doi.org/10.3390/electronics12244995







