Comparative Performance of UPQC Control System Based on PI-GWO, Fractional Order Controllers, and Reinforcement Learning Agent
Abstract
:1. Introduction
- Presentation of a UPQC system described by the authors and used in [25,26] as a benchmark for the comparative study of UPQC-APF performance, in which the controllers are of the following types: PI controller, PI controller optimized using GWO algorithm, FO-PI controller, TID controller, FO-Lead-Lag controller, and PI controller with RL-TD3 agent;
- Presentation, synthesis, and implementation of integer-order PI controllers optimized with the Ziegler–Nichols method and a computational intelligence GWO optimization method;
- Presentation, synthesis and implementation of FO-type controllers, as FO-PI controller, Tilt Integral Derivative (TID), and FO-Lead-Lag controller using FOMCON toolbox from MATLAB;
- Presentation, synthesis, and implementation of an RL-TD3 agent which will be used in tandem with a PI controller;
- Implementation in MATLAB/Simulink of the software applications for the calculation of steady-state error, ripple, and DF of the VDC voltage;
- Implementation in MATLAB/Simulink of the software applications for the calculation of the THD current and voltage on the load side in case of using linear load or nonlinear load (highly polluting in terms of harmonic content).
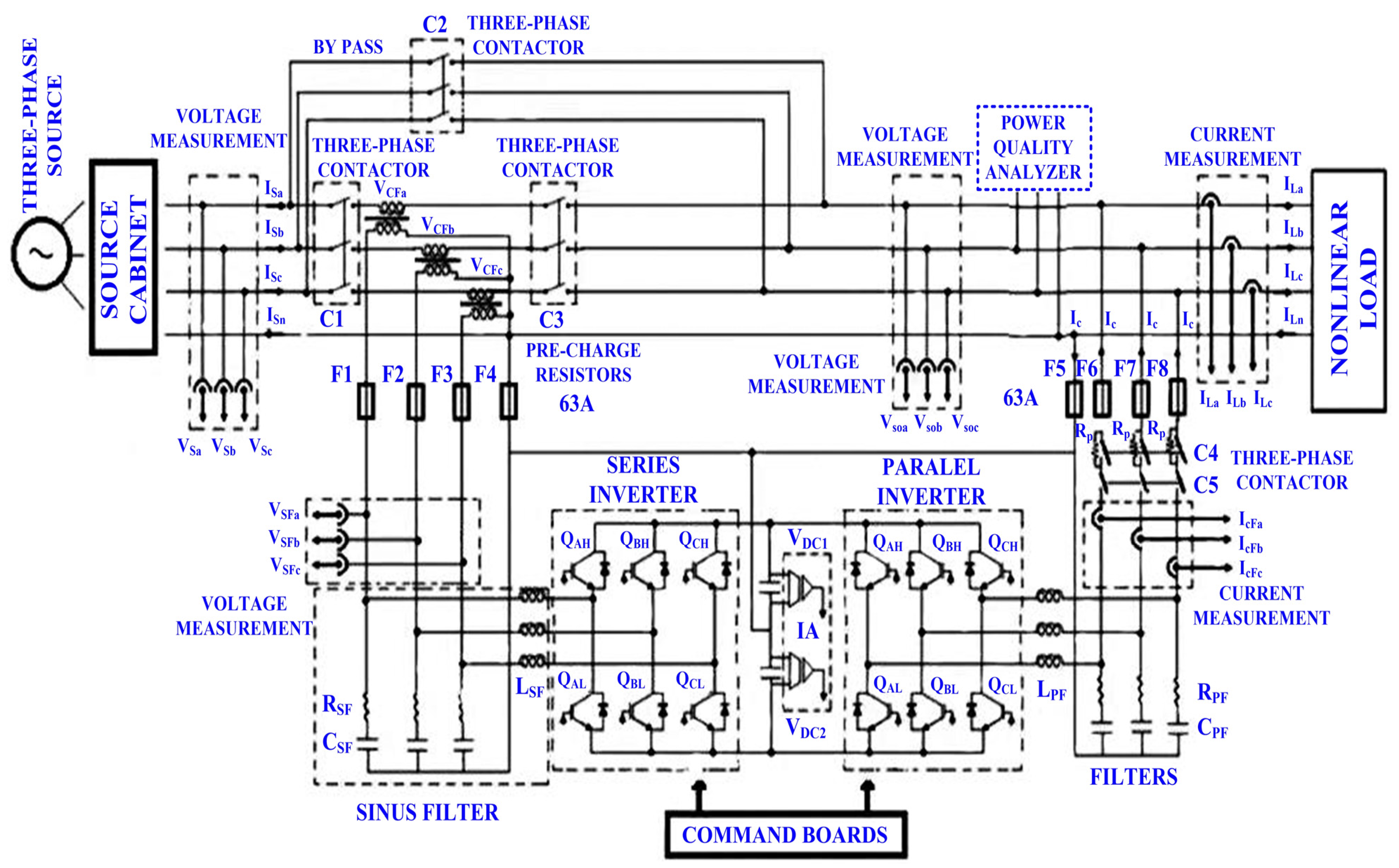
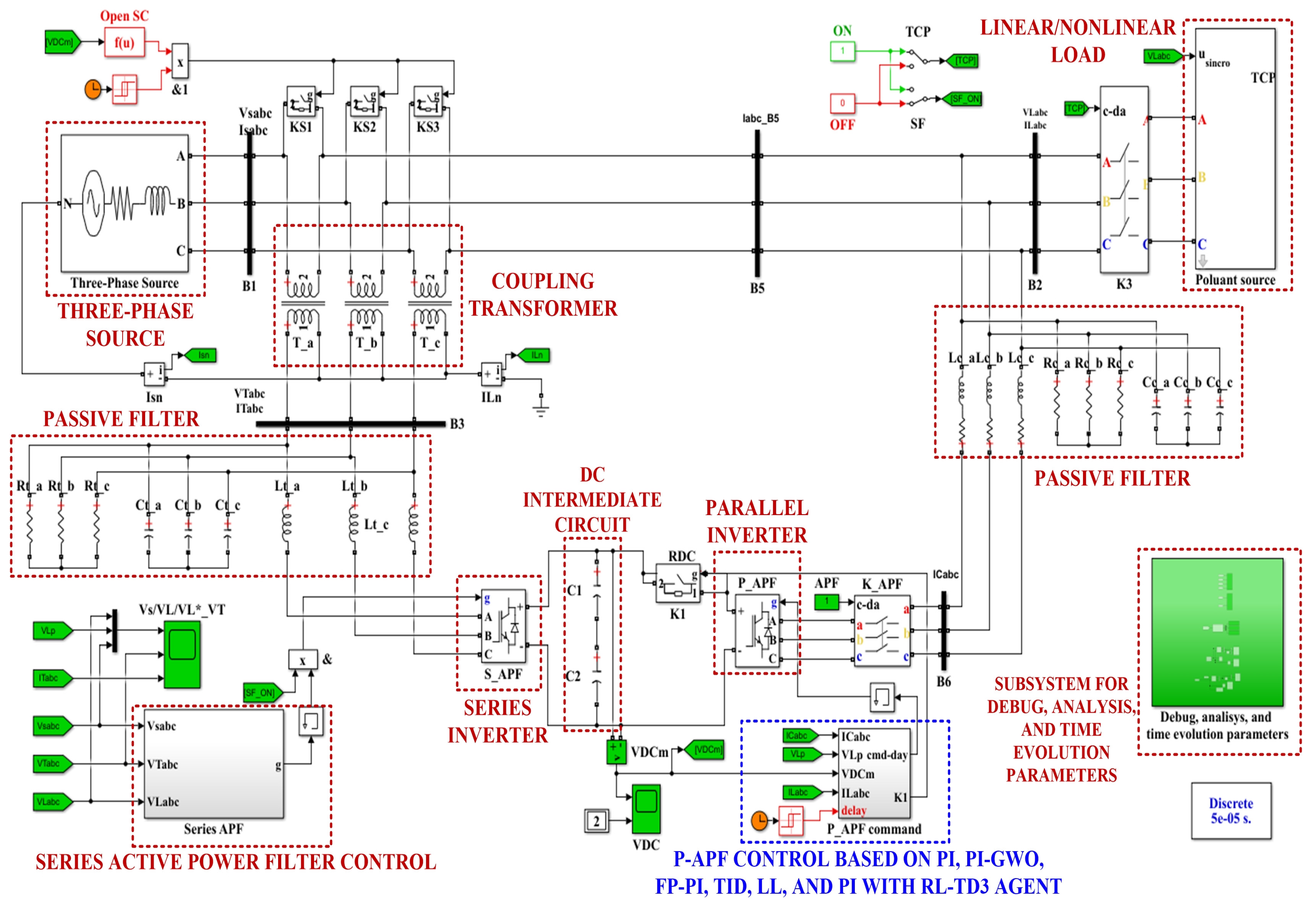
2. UPQC System Description
3. Controllers for Active Power Filter: Mathematical Description
3.1. PI Controller
3.2. Fractional Order PI Controller
3.3. Fractional Order TID Controller
3.4. Fractional Order Lead Lag Controller
3.5. Optimization of PI Controller Using GWO Algorithm
3.6. Improvement Performances of PI Controller Using RL-TD3 Agent
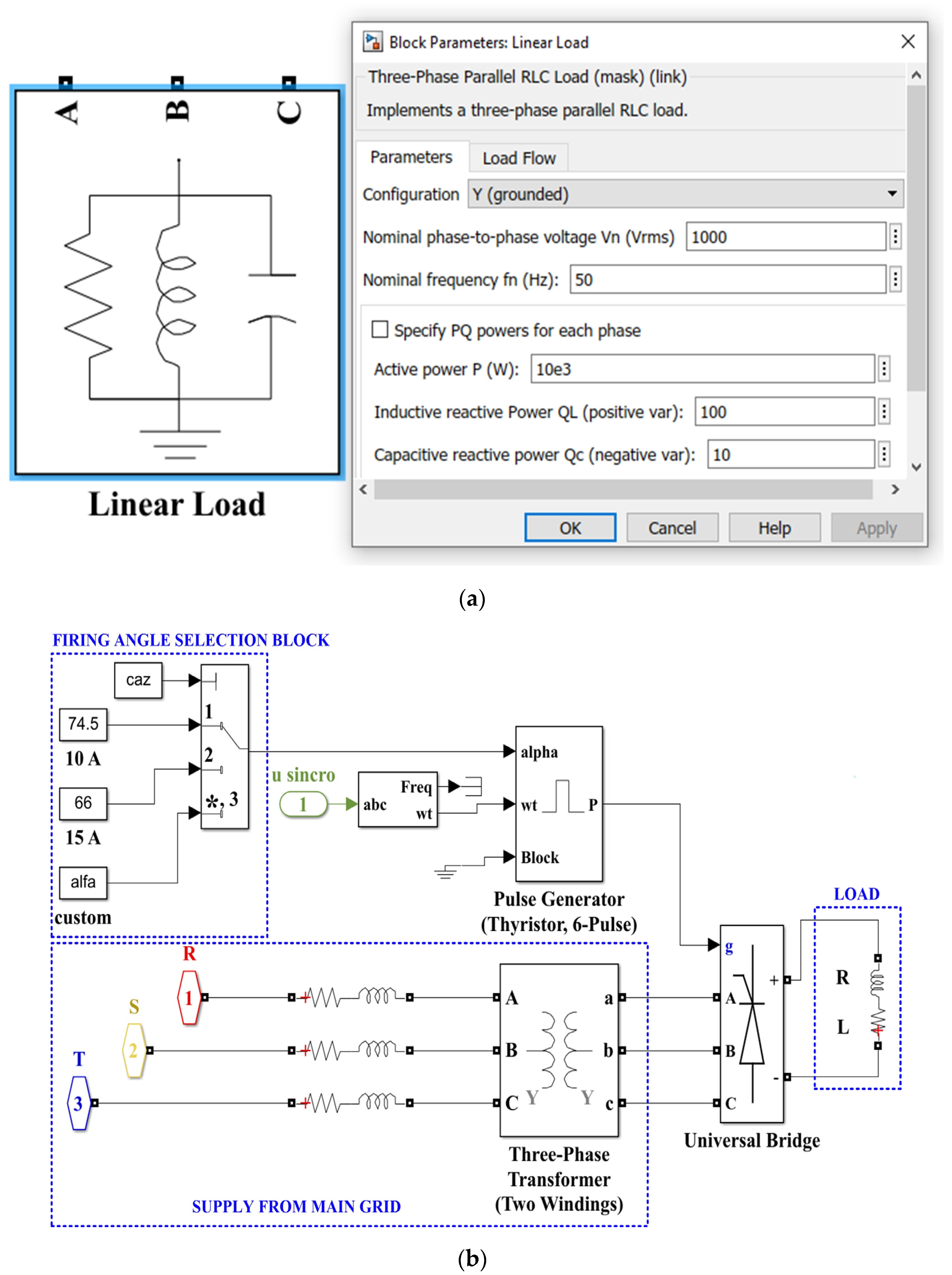
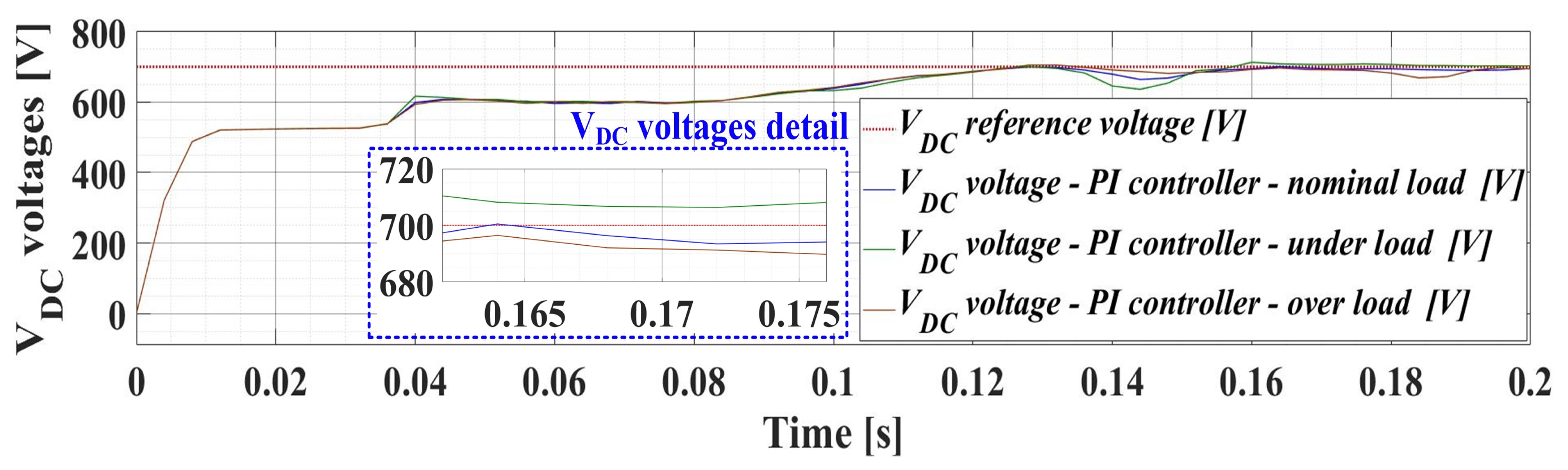
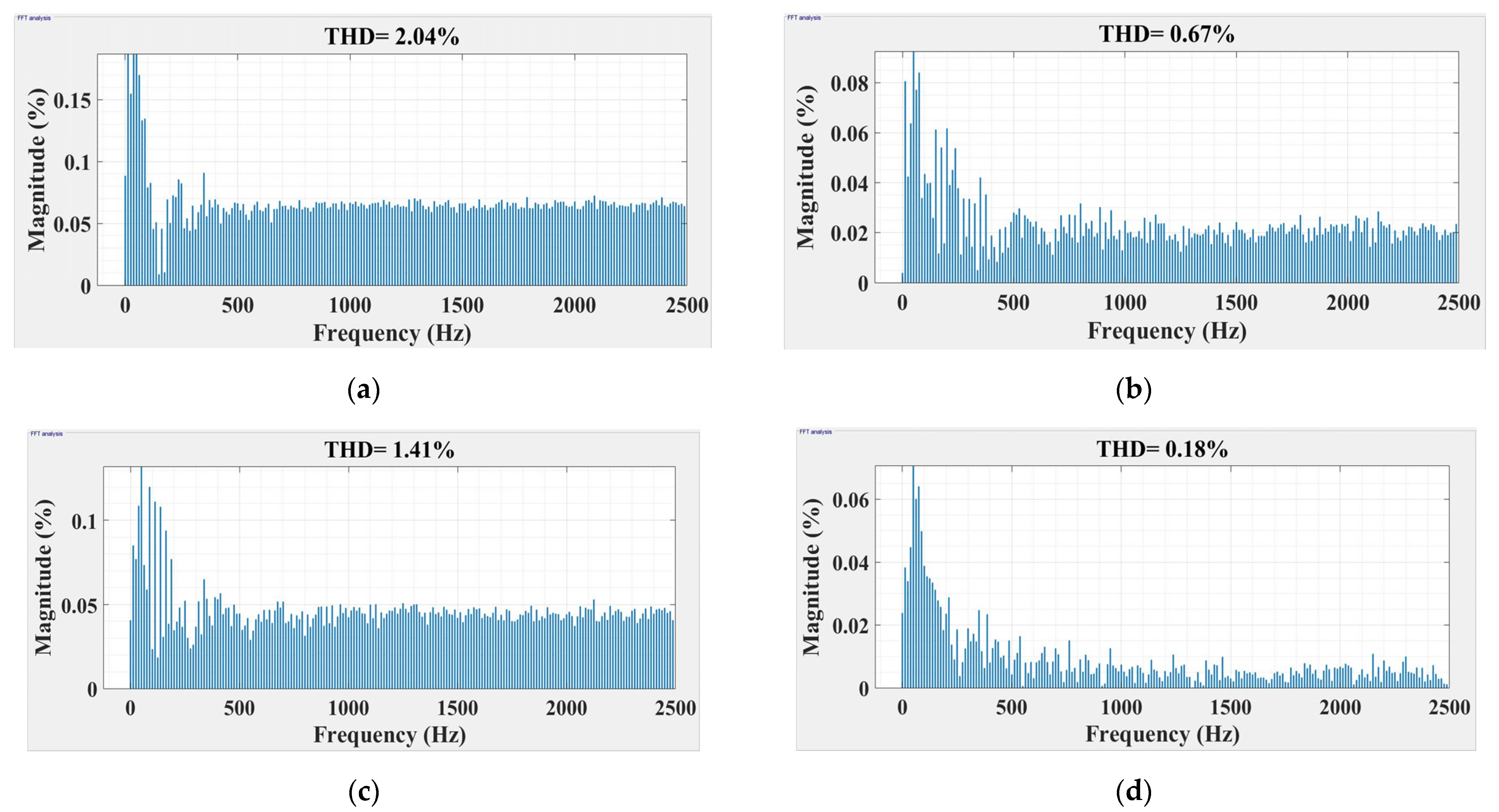
4. Numerical Simulations
- In the first stage, to limit the charging current, contactor K1 (short-circuiting the RDC resistor) is opened. When the voltage on the capacitors reaches 480 V, the second stage starts;
- In the second stage, the capacitors continue to charge directly, without driving the parallel filter elements. This stage continues until the voltage on the capacitors reaches 525 V. The two thresholds (480 V and 525 V, respectively) have been set through testing to ensure a reasonable dynamic charging rate. They can be set to different values;
- In the third stage, the parallel filter transistors start to be controlled.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


Appendix B


References
- Honarmand, M.E.; Hosseinnezhad, V.; Hayes, B.; Siano, P. Local Energy Trading in Future Distribution Systems. Energies 2021, 14, 3110. [Google Scholar] [CrossRef]
- Chartier, S.L.; Venkiteswaran, V.K.; Rangarajan, S.S.; Collins, E.R.; Senjyu, T. Microgrid Emergence, Integration, and Influence on the Future Energy Generation Equilibrium—A Review. Electronics 2022, 11, 791. [Google Scholar] [CrossRef]
- Ayalew, M.; Khan, B.; Giday, I.; Mahela, O.P.; Khosravy, M.; Gupta, N.; Senjyu, T. Integration of Renewable Based Distributed Generation for Distribution Network Expansion Planning. Energies 2022, 15, 1378. [Google Scholar] [CrossRef]
- Nafkha-Tayari, W.; Ben Elghali, S.; Heydarian-Forushani, E.; Benbouzid, M. Virtual Power Plants Optimization Issue: A Comprehensive Review on Methods, Solutions, and Prospects. Energies 2022, 15, 3607. [Google Scholar] [CrossRef]
- Maciążek, M. Active Power Filters and Power Quality. Energies 2022, 15, 8483. [Google Scholar] [CrossRef]
- Buła, D.; Grabowski, D.; Maciążek, M. A Review on Optimization of Active Power Filter Placement and Sizing Methods. Energies 2022, 15, 1175. [Google Scholar] [CrossRef]
- Yang, B.; Liu, K.; Zhang, S.; Zhao, J. Design and Implementation of Novel Multi-Converter-Based Unified Power Quality Conditioner for Low-Voltage High-Current Distribution System. Energies 2018, 11, 3150. [Google Scholar] [CrossRef] [Green Version]
- Sekhar, A.H.; Bharathi, S.L.K.; Asif, N.A.H.; Manikandan, P.V. Power Quality Enhancement Using Multi-Level Inverter with UPQC and Robust Back Propagation Neural Network Strategy. SPAST Abstr. 2021, 1. Available online: https://spast.org/techrep/article/view/2967 (accessed on 10 June 2022). [CrossRef]
- Gupta, A. Power quality evaluation of photovoltaic grid interfaced cascaded H-bridge nine-level multilevel inverter systems using D-STATCOM and UPQC. Energy 2022, 238, 121707. [Google Scholar] [CrossRef]
- Mahdi, D.I.; Gorel, G. Design and Control of Three-Phase Power System with Wind Power Using Unified Power Quality Conditioner. Energies 2022, 15, 7074. [Google Scholar] [CrossRef]
- Yang, D.; Ma, Z.; Gao, X.; Ma, Z.; Cui, E. Control Strategy of Intergrated Photovoltaic-UPQC System for DC-Bus Voltage Stability and Voltage Sags Compensation. Energies 2019, 12, 4009. [Google Scholar] [CrossRef] [Green Version]
- Garces-Gomez, Y.A.; Hoyos, F.E.; Candelo-Becerra, J.E. Classic Discrete Control Technique and 3D-SVPWM Applied to a Dual Unified Power Quality Conditioner. Appl. Sci. 2019, 9, 5087. [Google Scholar] [CrossRef] [Green Version]
- Afonso, J.L.; Tanta, M.; Pinto, J.G.O.; Monteiro, L.F.C.; Machado, L.; Sousa, T.J.C.; Monteiro, V. A Review on Power Electronics Technologies for Power Quality Improvement. Energies 2021, 14, 8585. [Google Scholar] [CrossRef]
- Das, S.R.; Ray, P.K.; Sahoo, A.K.; Ramasubbareddy, S.; Babu, T.S.; Kumar, N.M.; Elavarasan, R.M.; Mihet-Popa, L. A Comprehensive Survey on Different Control Strategies and Applications of Active Power Filters for Power Quality Improvement. Energies 2021, 14, 4589. [Google Scholar] [CrossRef]
- El Ghaly, A.; Tarnini, M.; Moubayed, N.; Chahine, K. A Filter-Less Time-Domain Method for Reference Signal Extraction in Shunt Active Power Filters. Energies 2022, 15, 5568. [Google Scholar] [CrossRef]
- Kołek, K.; Firlit, A. A New Optimal Current Controller for a Three-Phase Shunt Active Power Filter Based on Karush–Kuhn–Tucker Conditions. Energies 2021, 14, 6381. [Google Scholar] [CrossRef]
- Buła, D.; Grabowski, D.; Lewandowski, M.; Maciążek, M.; Piwowar, A. Software Solution for Modeling, Sizing, and Allocation of Active Power Filters in Distribution Networks. Energies 2021, 14, 133. [Google Scholar] [CrossRef]
- Kenjrawy, H.; Makdisie, C.; Houssamo, I.; Mohammed, N. New Modulation Technique in Smart Grid Interfaced Multilevel UPQC-PV Controlled via Fuzzy Logic Controller. Electronics 2022, 11, 919. [Google Scholar] [CrossRef]
- Mahar, H.; Munir, H.M.; Soomro, J.B.; Akhtar, F.; Hussain, R.; Elnaggar, M.F.; Kamel, S.; Guerrero, J.M. Implementation of ANN Controller Based UPQC Integrated with Microgrid. Mathematics 2022, 10, 1989. [Google Scholar] [CrossRef]
- Mota, D.d.S.; Tedeschi, E. On Adaptive Moving Average Algorithms for the Application of the Conservative Power Theory in Systems with Variable Frequency. Energies 2021, 14, 1201. [Google Scholar] [CrossRef]
- Karchi, N.; Kulkarni, D.; Pérez de Prado, R.; Divakarachari, P.B.; Patil, S.N.; Desai, V. Adaptive Least Mean Square Controller for Power Quality Enhancement in Solar Photovoltaic System. Energies 2022, 15, 8909. [Google Scholar] [CrossRef]
- Gaburro Bacheti, G.; Sartório Camargo, R.; Silva Amorim, T.; Yahyaoui, I.; Frizera Encarnação, L. Model-Based Predictive Control with Graph Theory Approach Applied to Multilevel Back-to-Back Cascaded H-Bridge Converters. Electronics 2022, 11, 1711. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.-I. Improved Performance in the Control of DC-DC Three-Phase Power Electronic Converter Using Fractional-Order SMC and Synergetic Controllers and RL-TD3 Agent. Fractal Fract. 2022, 6, 729. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.-I. Comparative Performance Analysis of the DC-AC Converter Control System Based on Linear Robust or Nonlinear PCH Controllers and Reinforcement Learning Agent. Sensors 2022, 22, 9535. [Google Scholar] [CrossRef] [PubMed]
- Nicola, M.; Sacerdoțianu, D.; Nicola, C.-I.; Ivanov, S.; Ciontu, M.; Nițu, M.-C. Improved Control Strategy of Unified Power Quality Conditioner Using Fractional Order Controller and Particle Swarm Optimization. In Proceedings of the International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 27–29 May 2021; pp. 1–6. [Google Scholar]
- Ivanov, S.; Ciontu, M.; Sacerdoțianu, D.; Radu, A. Simple control strategies of the active filters within a unified power quality conditioner (UPQC). In Proceedings of the International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 6–9 June 2017; pp. 1–4. [Google Scholar]
- Zychlewicz, M.; Stanislawski, R.; Kaminski, M. Grey Wolf Optimizer in Design Process of the Recurrent Wavelet Neural Controller Applied for Two-Mass System. Electronics 2022, 11, 177. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N.; Colak, I.; Thounthong, P.; Takorabet, N. Application of Fractional-Order PI Controllers and Neuro-Fuzzy PWM Technique to Multi-Rotor Wind Turbine Systems. Electronics 2022, 11, 1340. [Google Scholar] [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. Closed-loop identification of fractional-order models using FOMCON toolbox for MATLAB. In Proceedings of the 14th Biennial Baltic Electronic Conference (BEC), Tallinn, Estonia, 6–8 October 2014; pp. 213–216. [Google Scholar]
- Faria, R.d.R.; Capron, B.D.O.; Secchi, A.R.; de Souza, M.B., Jr. Where Reinforcement Learning Meets Process Control: Review and Guidelines. Processes 2022, 10, 2311. [Google Scholar] [CrossRef]
- Voncilă, I.; Selim, E.; Voncilă, M.-L. Use of fractal analysis for quality evaluation of control methods in induction motor drive systems. In Proceedings of the 6th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 19–21 October 2022; pp. 524–529. [Google Scholar]
- IEEE Std 1159-2019; IEEE Recommended Practice for Monitoring Electric Power Quality. Institute of Electrical and Electronics Engineers: New York, NY, USA, 2019.




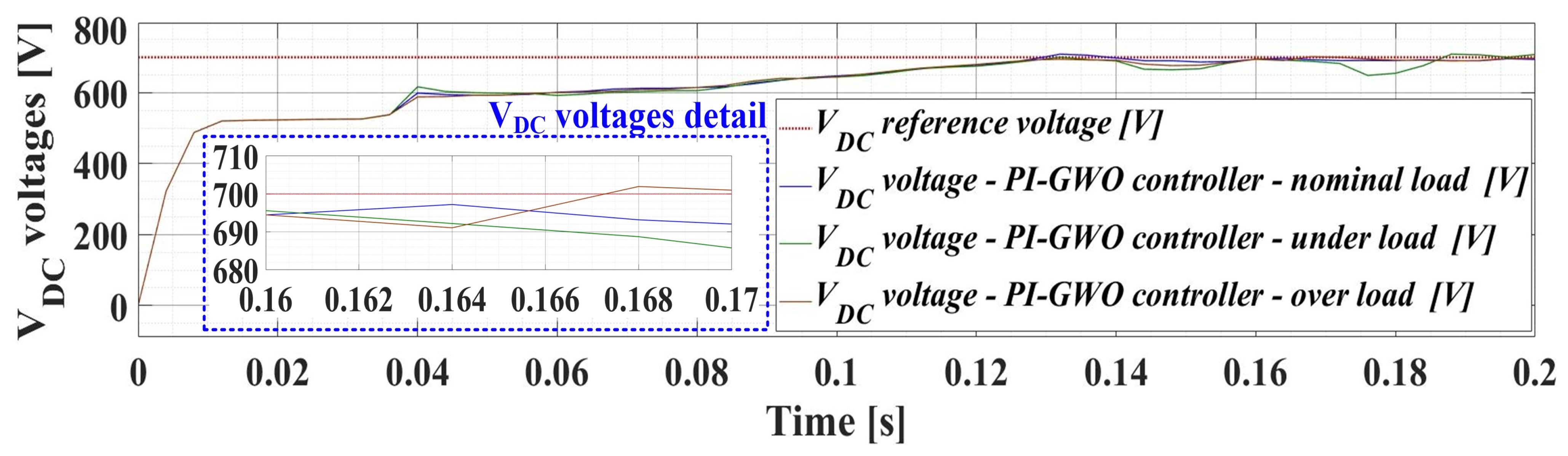

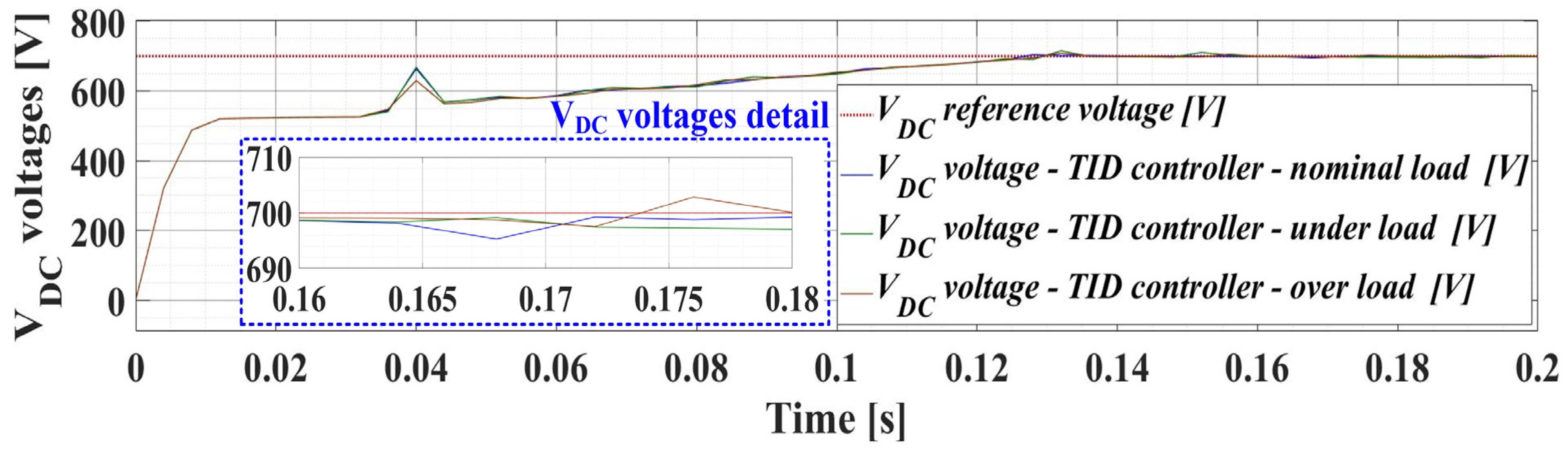




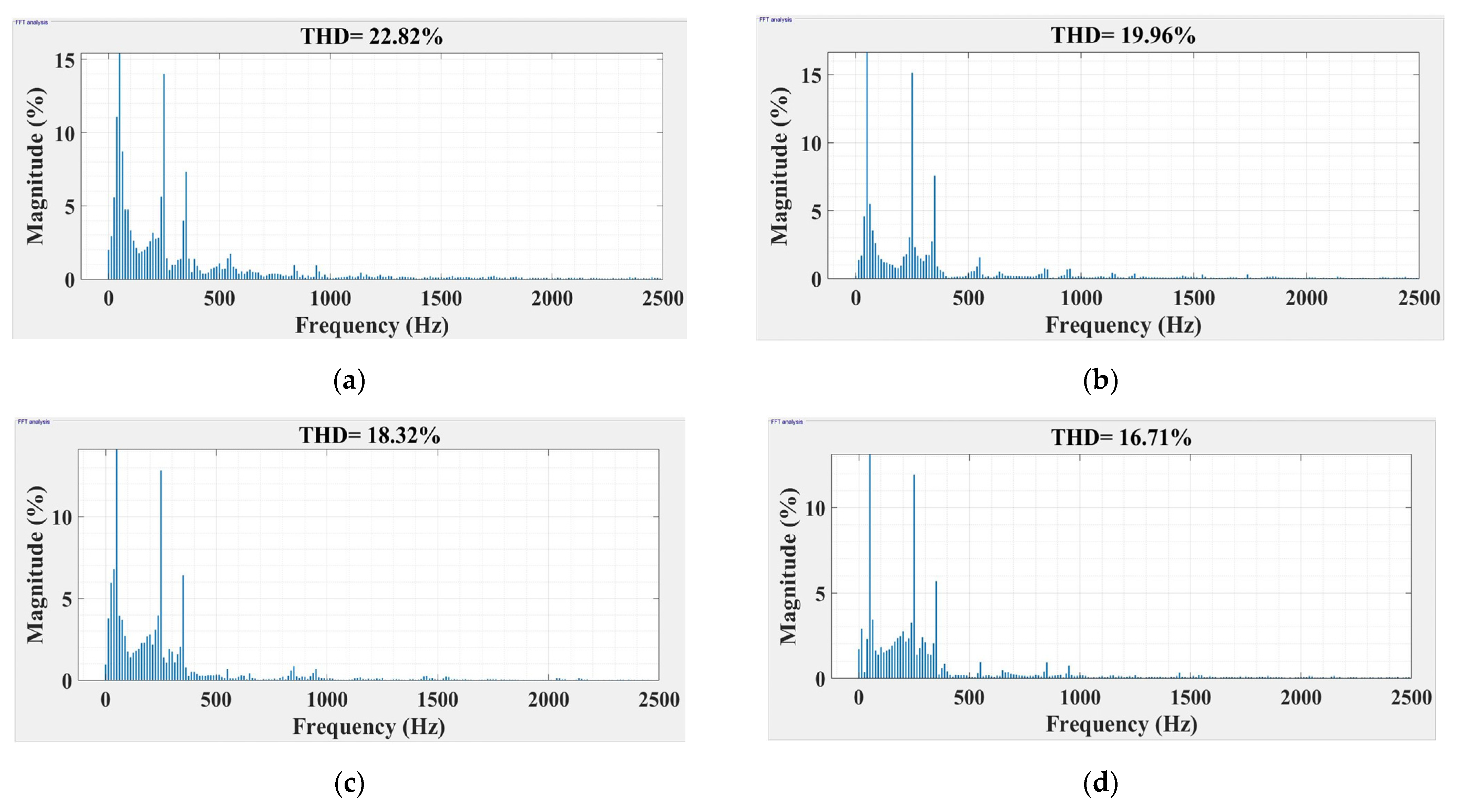
| Controller | Parameter Kp | Parameter Ki | Parameter λ |
|---|---|---|---|
| PI | 0.1 | 0.1 | – |
| PI-GWO | 0.18 | 39.51 | – |
| FO-PI | 2.38 | 0.85 | 0.73 |
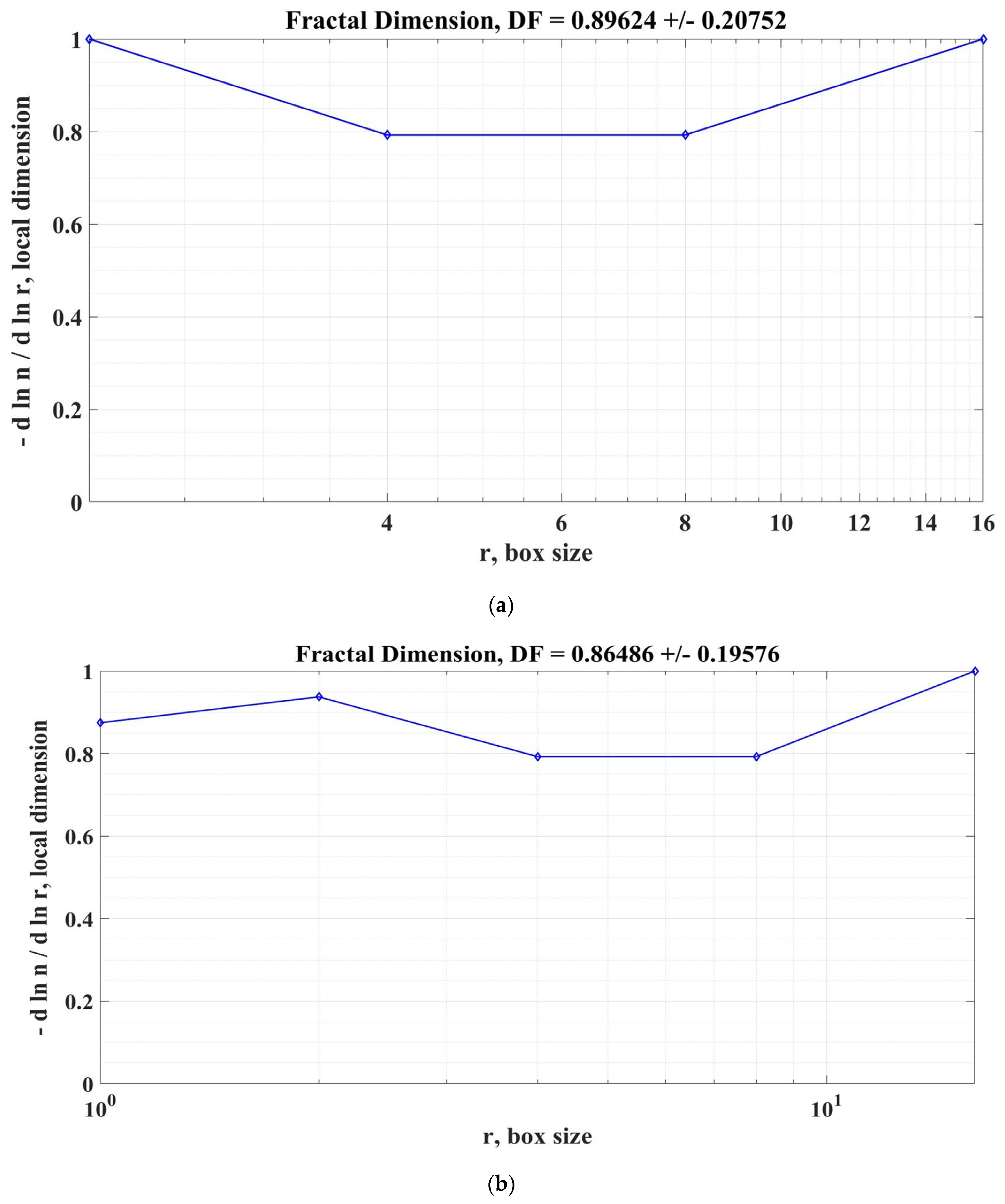
| Controller | Stationary Error [%] | Voltage Ripple [V] | DF |
|---|---|---|---|
| PI | 1 | 145.71 | 0.79248 +/− 0.17540 |
| PI-GWO | 0.50 | 143.76 | 0.83048 +/− 0.20534 |
| FO-PI | 0.41 | 142.92 | 0.83048 +/− 0.20534 |
| TID | 0.30 | 142.15 | 0.86486 +/− 0.19576 |
| FO-Lead-Lag | 0.25 | 141.82 | 0.86486 +/− 0.19576 |
| PI with RL-TD3 agent | 0.10 | 141.11 | 0.89624 +/− 0.20752 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicola, M.; Nicola, C.-I.; Sacerdoțianu, D.; Vintilă, A. Comparative Performance of UPQC Control System Based on PI-GWO, Fractional Order Controllers, and Reinforcement Learning Agent. Electronics 2023, 12, 494. https://doi.org/10.3390/electronics12030494
Nicola M, Nicola C-I, Sacerdoțianu D, Vintilă A. Comparative Performance of UPQC Control System Based on PI-GWO, Fractional Order Controllers, and Reinforcement Learning Agent. Electronics. 2023; 12(3):494. https://doi.org/10.3390/electronics12030494
Chicago/Turabian StyleNicola, Marcel, Claudiu-Ionel Nicola, Dumitru Sacerdoțianu, and Adrian Vintilă. 2023. "Comparative Performance of UPQC Control System Based on PI-GWO, Fractional Order Controllers, and Reinforcement Learning Agent" Electronics 12, no. 3: 494. https://doi.org/10.3390/electronics12030494
APA StyleNicola, M., Nicola, C.-I., Sacerdoțianu, D., & Vintilă, A. (2023). Comparative Performance of UPQC Control System Based on PI-GWO, Fractional Order Controllers, and Reinforcement Learning Agent. Electronics, 12(3), 494. https://doi.org/10.3390/electronics12030494









