Abstract
Existing photovoltaic (PV) power prediction methods suffer from insufficient data samples, poor model generalization ability, and the inability to share power data. In this paper, a hybrid prediction model based on federated learning (FL) is proposed. To improve communication efficiency and model generalization ability, FL is introduced to combine data from multiple locations without sharing to collaboratively train the prediction model. Furthermore, a hybrid LSTM-BPNN prediction model is designed to improve the accuracy of predictions. LSTM is used to extract important features from the time-series data, and BPNN maps the extracted high-dimensional features to the low-dimensional space and outputs the predicted values. Experiments show that the minimum MAPE of the hybrid prediction model constructed in this paper can reach 1.2%, and the prediction effect is improved by 30% compared with the traditional model. Under the FL mode, the trained prediction model not only improves the prediction accuracy by more than 20% but also has excellent generalization ability in multiple scenarios.
1. Introduction
Photovoltaic (PV) power generation is affected by many uncontrollable factors, such as solar radiance, temperature, humidity, wind speed, direction, etc. Therefore, the accurate prediction of PV power generation is very difficult [1]. The unpredictability of PV power generation not only affects economic efficiency but also adversely affects the stability, reliability, and dispatch of power system operation after a large-scale grid connection. A reliable PV power generation system is essential for the safe and stable operation of the grid [2]. Therefore, it is important to make accurate forecasts of PV power generation.
The PV power prediction methods [3] are now classified into physical prediction methods [4], statistical prediction methods [5], artificial intelligence prediction methods [6], and hybrid prediction methods [7]. The physical prediction method is mainly based on the interaction between physical laws in the atmosphere and solar radiation to establish a physical model for prediction. This method is complex to model, computationally intensive, and has unsatisfactory short-term prediction results. The statistical prediction method is mainly based on the correlation between the input and output of the prediction model, and predicts according to certain statistical laws. This method relies solely on historical solar data to build a model to capture the relationship between weather variables and PV power generation, and the forecasting process is relatively simple. Some scholars have also studied PV modules [8,9] to explore the relationship between PV cells and power generation load.
Artificial-intelligence-based PV power prediction models do not rely on the relationship between power and its influencing factors, but learn from a large amount of historical data to make predictions. This approach has tremendous advantages in dealing with non-stationary solar radiation intensity sequences with good robustness and accuracy [10]. In [11], a support vector regression-based PV power prediction model for different weather conditions was proposed. The weather conditions are divided into two categories, sunny and rainy, and the model is applicable to the prediction under arbitrary weather conditions; the experimental validation is carried out under different weather conditions separately, and the results show that the model has better prediction accuracy and less computational complexity. An extreme-learning-machine-based PV power prediction model is proposed to provide accurate day-ahead PV power generation [12]. Compared with other models, this model has improved prediction accuracy and little computational effort.
To overcome the shortcomings of a single model in processing data, hybrid forecasting methods [13,14,15] combine one of the above-advanced methods with physical or statistical methods to achieve high prediction accuracy. Different types of deep learning neural networks were used and compared in [16]. The compared deep learning neural networks are LSTM, bidirectional LSTM (BiLSTM), gated recurrent unit (GRU), bidirectional gated recurrent unit (BiGRU), one-dimensional convolutional neural network (CNN1D), and other hybrid configurations such as CNN1D-LSTM and CNN1D-GRU. The results show that all these models are well-suited for short-term prediction. In [17], an LSTM-RNN-based model for PV power prediction is proposed, which combines recurrent neural networks with long short-term memory networks. The model not only has a periodic structure and storage units, but also avoids the problem of a long-term dependence on traditional recurrent networks. In [7], a hybrid LSTM-convolutional network model for PV power output prediction is proposed, which first extracts the temporal features of the data using a long short-term memory network, and then extracts the spatial features of the data using a convolutional neural network model. The results show that the prediction results of the hybrid prediction model under different seasons are better than the single prediction model.
The application of machine learning methods in the field of PV power prediction has achieved certain results, but in practical applications, the existing methods still have the following problems. Firstly, they cannot cope with the problem of the insufficient number of samples and features of power generation data in real situations. Existing methods rely on training datasets with a sufficiently large number of samples and a sufficiently rich variety of features, but it is often difficult to meet this condition in actual load forecasting work [18,19]. Secondly, a model trained using only data from a single region can hardly meet the forecasting requirements of new regions. Finally, if we can realize the sharing of data between different regions to train models, we can effectively improve the model prediction ability [20]. However, at present, for data privacy protection, data such as historical power is strictly confidential, which limits data-sharing training.
Therefore, there is a lack of a method that enables the co-training of power prediction models while preserving data privacy. To address this need, this paper introduces the federated learning (FL) method. FL can achieve multiple data holders to collaboratively train machine learning models without sharing their data, reducing data communication costs and improving communication efficiency while preserving data privacy [21]. FL has been applied by researchers in several scenarios where data privacy and reduced communication overhead need to be considered [22]. In [23], deep reinforcement learning models are federalized to achieve a high-accuracy and low-latency device node selection. The authors in [24] applied FL to the edge computing process in the IoT framework. The researchers in [25] applied FL to fog computing. In [26], FL is applied to power metering systems for metering device fault diagnosis, wireless access security detection, and electricity bill risk identification scenarios. All of those achieved good results and proved the practicality and feasibility of applying FL methods in the field of power systems.
To address the above problems, this paper proposes a hybrid prediction model of PV power based on FL. The contributions of this article are as follows.
- (1)
- This paper proposes a hybrid prediction model. The model consists of LSTM and BPNN. The LSTM is used to extract important features from the time-series data, and the BPNN can compensate for the shortcomings of the LSTM network’s insufficient fitting ability to achieve a higher-accuracy energy consumption prediction.
- (2)
- This paper is the first to propose a FL-LSTM-BPNN model for PV power prediction. The hybrid prediction model is trained collaboratively under FL, and the data features of each company are federated. It can both improve the model generalization ability, reduce the communication cost, and protect the data privacy.
2. FL-Based Co-Training Method for Hybrid Prediction Models
2.1. Overall Program
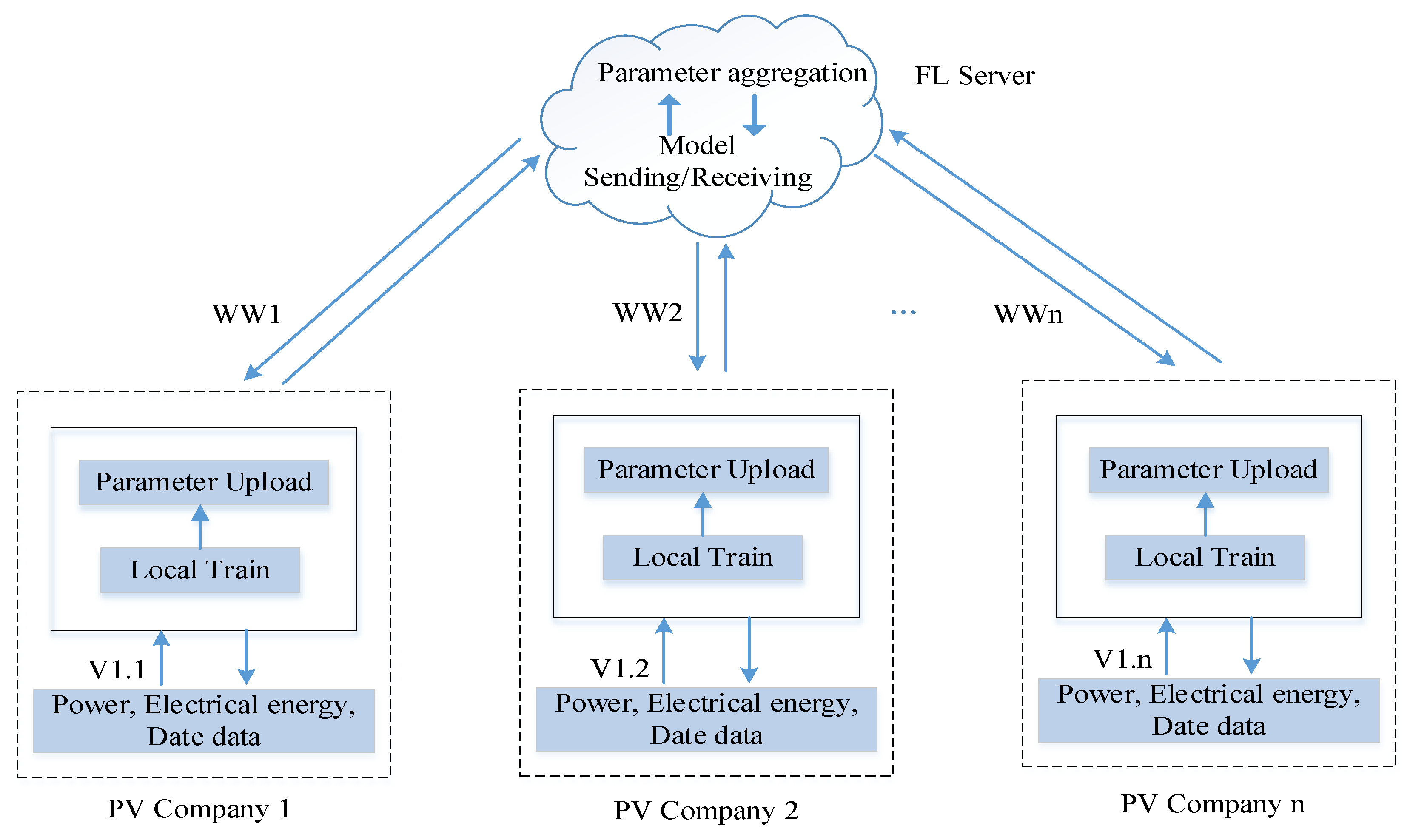
In this paper, the hybrid prediction method is used to improve the accuracy of predictions; the FL model co-training method is used to jointly train a joint prediction model in several places. This protects the privacy of data and also reduces the amount of data transmission and increases communication efficiency. The system flow of the proposed method is shown in Figure 1. The prediction models are deployed on each PV operator side Wn, and the PV operator can be a PV company in a region or a collection of certain PV power users.
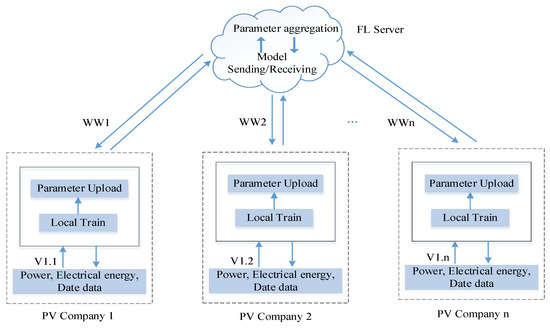
Figure 1.
Proposed System Flow.
The method in this paper is mainly deployed in the FL server and the local servers of the data holders. The aggregation algorithm is deployed in the FL server for model aggregation and model sending and receiving; the prediction model algorithm is deployed in the local server of each PV operator for model training and parameter uploading.
The whole training process is as follows: Firstly, the FL server sends down the initialization parameters of the prediction model to each local server, and then the global model parameters are sent down in subsequent rounds. The local servers use the initialization parameters for the first training, and each subsequent training is performed locally with the global parameters received by the FL server to obtain the local model parameters. In each round of communication, each operator uploads its respective local model parameters to the federation server for a new round of model aggregation and update until the model performance requirement or the specified number of communication rounds is reached.
Specific scheme: It is assumed that five power-generating companies participate in the model training and each of them has its different data. The hybrid prediction method of this paper is deployed in the local servers of the five participants. The model training process is performed in the respective local servers, while the aggregation of model parameters will be performed in the FL servers, and the prediction models with a high generalization capability will be derived through multiple rounds of FL aggregation. The approach in this paper keeps the data of each participant from leaving the local area, satisfying the need for respective data security while solving the problem of insufficient data.
2.2. Federated Learning Algorithm
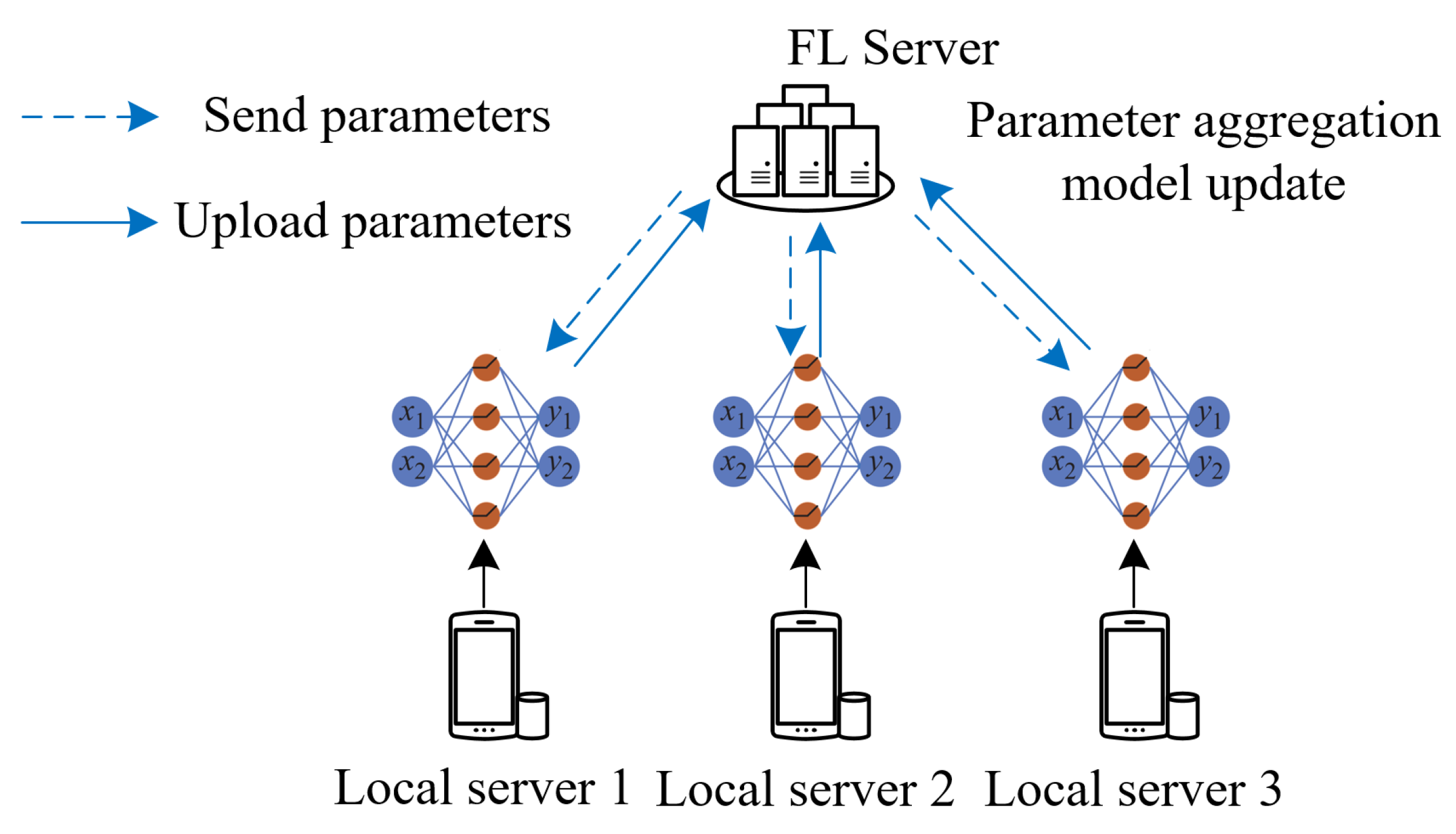
The FL framework is shown in Figure 2. In each round of iteration, independent participants train the local model separately and upload the trained model parameters to the central server, which completes the parameter aggregation and update, and sends the updated parameters to each participant to start a new round of iteration until the training converges.
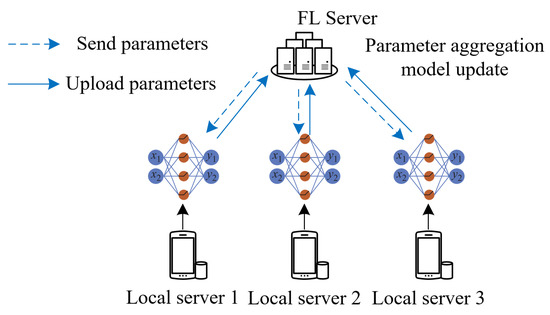
Figure 2.
FL Framework.
Among the algorithms in FL, the most commonly used aggregation algorithm is the federated average algorithm (FedAvg) [27]. The FedAvg algorithm uses the principle of weighted averaging, and this algorithm achieves the co-training of local models through multiple global iterations. For each global iteration, the number of participants is assumed to be N, the total amount of data owned is D, the amount of data for participant k is Dk, and the optimization function is ,
where is the loss prediction of the model parameter w for the jth data . For participant k, define as:
When the gradient of participant k is , the learning rate is R, and the parameters are updated after t global iterations as:
Then, the local model parameters of each participant are updated as follows:
2.3. Hybrid Prediction Model
The current single model has some shortcomings, such as local minimization, slow convergence, and overfitting. In this paper, a hybrid PV power prediction model is designed. In this paper, we propose a prediction method based on RNN and BPNN, which is divided into two stages: the feature extraction stage uses RNN to extract features, and the power prediction stage uses BPNN to output the predicted values, while the feature extraction process and the power prediction process are closely coupled, to minimize the prediction error to guide the feature extraction and power prediction, and finally achieve the extraction of effective features from the power data with time characteristics. The final result is to extract effective features from the power data with temporal characteristics, and then improve the prediction accuracy.
Werbos [28] and Rumelhart [29] proposed the error backpropagation algorithm (BP), respectively, to solve the training challenges of multilayer feedforward neural networks. BP neural networks (BPNN) usually consist of one input layer, multiple hidden layers, and one output layer. BPNNs have better nonlinear mapping characteristics and are capable of infinite approximations of relations that cannot be directly represented.
The recurrent neural network (RNN) is a class of neural networks specifically designed to process sequential data. Unlike BPNNs that only establish forward connections between neurons, RNNs also establish temporal connections between neurons, making the output of the current moment of the RNN dependent not only on the input of the current moment but also on the input of the previous moment.
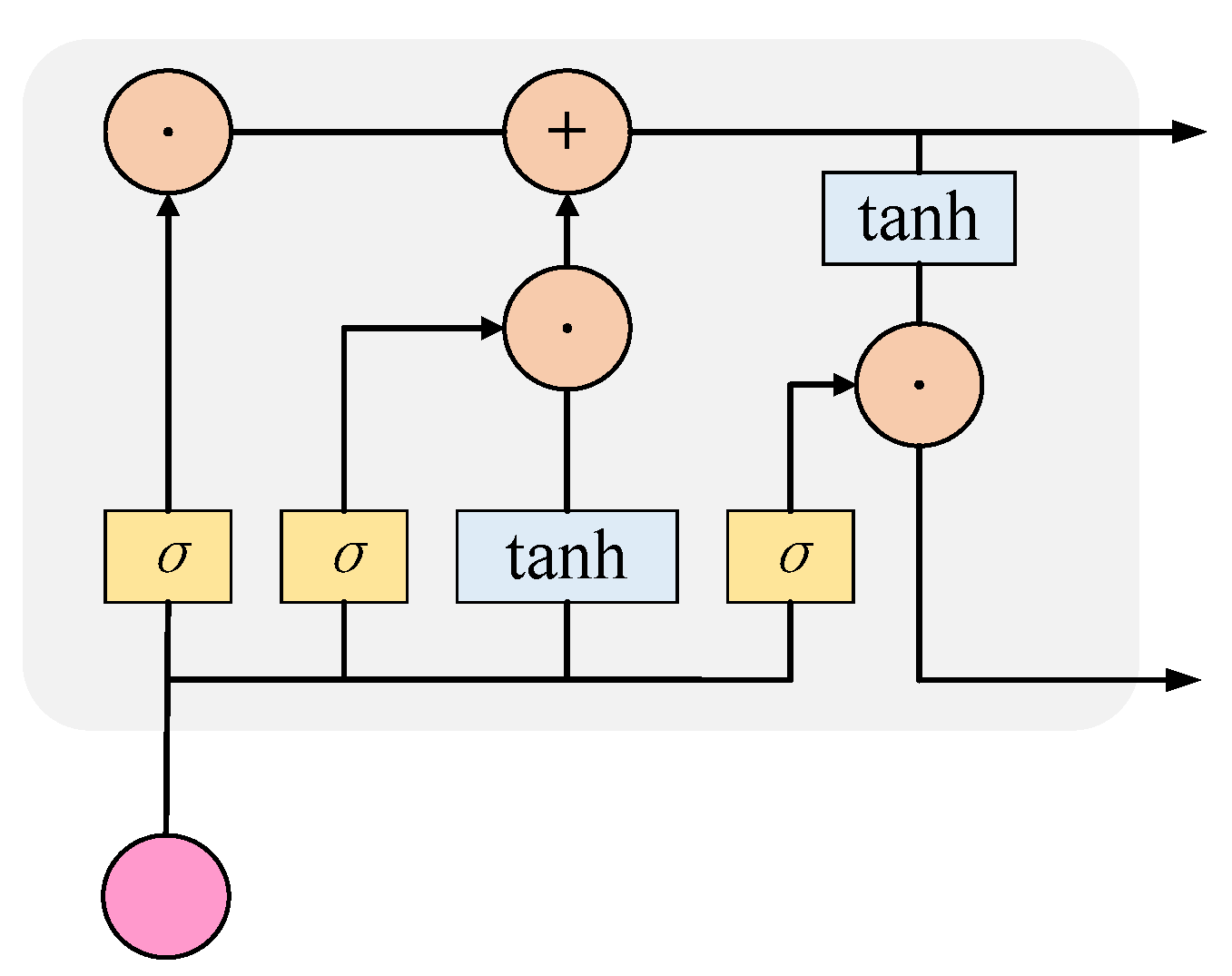
The long short-term memory (LSTM) [30] network is also developed from RNN. It alleviates the gradient disappearance problem during training by cleverly improving the network structure to achieve the prediction of time series with long intervals and long delays. The structure of the LSTM network is shown in Figure 3.
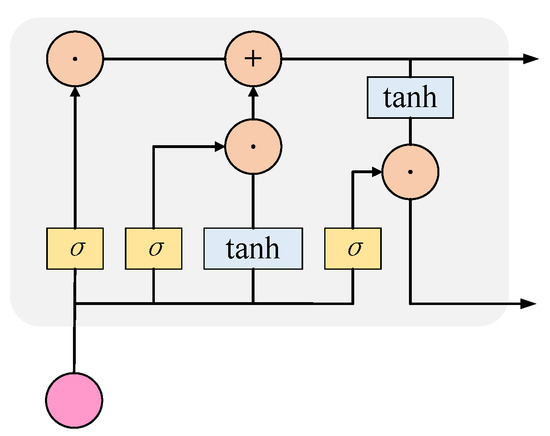
Figure 3.
Structure of LSTM network.
The LSTM adds cell states to preserve the previous information and has three control gates (forgetting gate, input gate, and output gate) within the cell to control the flow of information transmission. The forgetting gate receives the input xt of the current moment and the hidden state ht−1 of the previous moment, and calculates the proportion ft of the cell state ct−1 of the previous moment retained to the current moment, as shown in Equation (6). The input gate receives the input xt of the current moment and the hidden state ht−1 of the previous moment, and calculates the proportion it of the new information contained in xt and ht−1 that needs to be preserved to the cell state, as shown in Equation (7). The input xt of the current moment and the hidden state ht−1 of the previous moment are activated by the tanh function to generate the candidate cell state , as shown in Equation (8). The cell state ct of the current moment is determined by the cell state ct−1 of the previous moment, the candidate state , ft and it of the current moment together, as shown in Equation (9). The output gate receives the input xt of the current moment and the hidden state ht−1 of the previous moment and calculates the ratio ot of the cell state ct output to the output ht of the current moment, as shown in Equation (10). The final hidden state ht is determined jointly by the output gate ot and ct as shown in Equation (11). In short, the forgetting gate allows the LSTM to preserve long-term memory, the input gate prevents information that is not important for the current moment from entering the cell state, and the output gate ensures that the stored long-term memory has a positive effect on the current output.
where is the Sigmoid activation function , and tanh is the hyperbolic tangent activation function . xt is the input feature at moment t, and ht and ht−1 are the cellular hidden states at moment t and t−1, respectively. Wf, Wi, and Wo are the weight matrices of the forgetting gate, input gate, and output gate, respectively, and Wc is the weight matrix for computing the candidate states. ft, it, and ot are the forgetting gate, input gate, and output gate, respectively. bf, bi, and bo are the excitation threshold vectors of the forgetting, input, and output gates, respectively; bc is the excitation threshold vector for computing the candidate states; and ct and ct−1 are the cell states at moment t and moment t − 1, respectively.
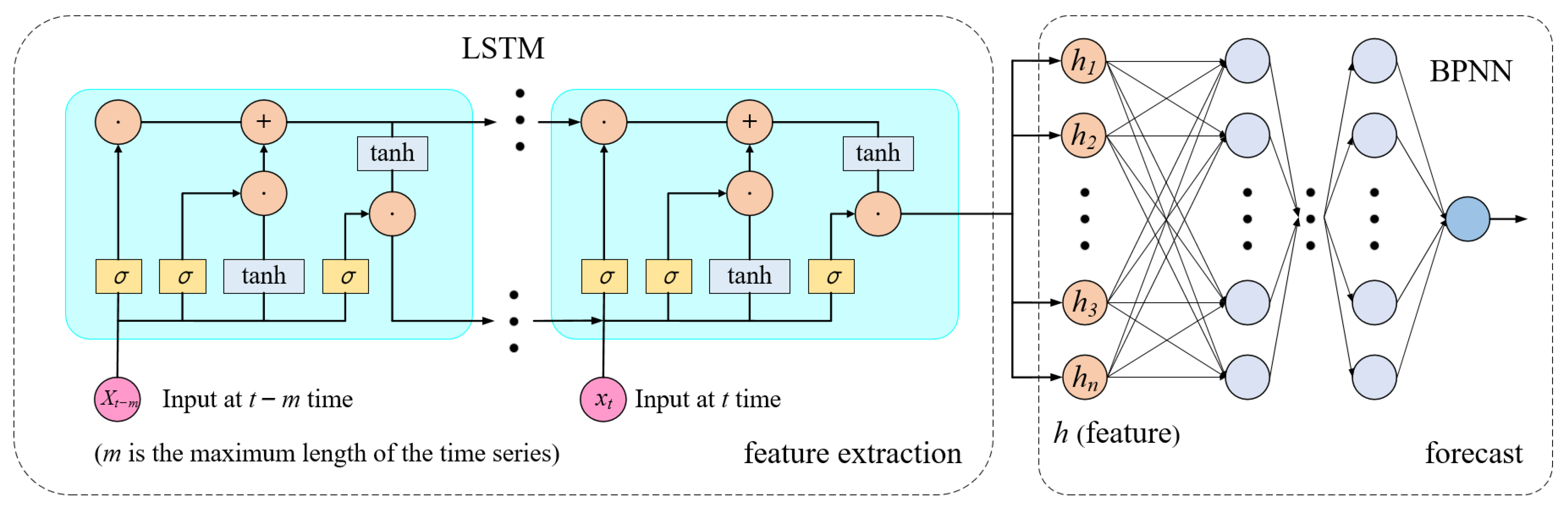
In this paper, a hybrid LSTM-BPNN prediction model is proposed, which consists of an LSTM and a BPNN connected back and forth, and the output of the LSTM is the input of the BPNN. The LSTM is used to extract important features from the time-series data, and the BPNN maps the extracted high-dimensional features to the low-dimensional space and outputs the predicted values. Using the powerful learning ability of BPNN for multivariate complex relationships, it can compensate for the shortcomings of the traditional recurrent neural network fitting ability to achieve a higher accuracy energy consumption prediction. The specific structure diagram of the LSTM-BPNN hybrid prediction model is shown in Figure 4.
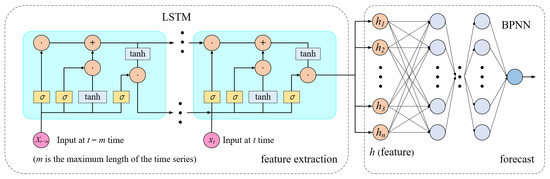
Figure 4.
LSTM-BPNN structure.
The number of time steps is an important hyperparameter of the hybrid model, which determines the length of the time series input to the predictive model when performing energy consumption prediction, with the physical meaning of the number of building history data contained in the input. In this paper, the discrete Fourier transform, which is commonly used in the field of digital signal processing, is used to determine the length of the time series [31]. The discrete Fourier transform can convert a finite sequence with the same sampling interval in the time domain to a sequence in the frequency domain, and the transformation equation is shown in Equation (12). The major period P of the time series is the reciprocal of the frequency f corresponding to the maximum value of the amplitude of the frequency domain sequence, P = 1/f:
where one of the variables is the nth number in a time-domain sequence of length N and X(k) is the kth number in a frequency-domain sequence of length N.
The essence of the hybrid model proposed in this paper is the combination of RNN and BPNN, so the backpropagation-through-time (BPTT) algorithm used to train RNN is still applicable to the hybrid model. The hyperparameter settings of the hybrid model affect the performance of the model, and the main hyperparameters include the cell hidden state dimension, the number of BPNN hidden layers, the BPNN activation function, the number of neurons in the BPNN hidden layers, etc. While training the hybrid model using the BPTT algorithm, a grid search algorithm is used to perform a hyperparameter search [32] until the optimal hybrid model is found.
3. Experiments
3.1. Data Acquisition and Experimentation Platform
In this paper, five mutually independent computers are used to simulate five PV operators (regions) involved in federation learning training, who do not share their respective data with each other, and one computer is used to simulate a federation server. The above devices can communicate with each other, peer to peer. The software and hardware environments of this paper are shown in Table 1, where the experiments are based on the deep learning open-source frameworks Tensorflow and Keras, and programmed in the Python language.

Table 1.
Experimental platform.
The data used in this paper are from one of the five PV power generation companies (five different regions) in China. The dataset contains PV forward active energy data, active power, voltage, current, and date information recorded every 15 min for 20 regions, which are organized into a dataset that can be used as the model input.
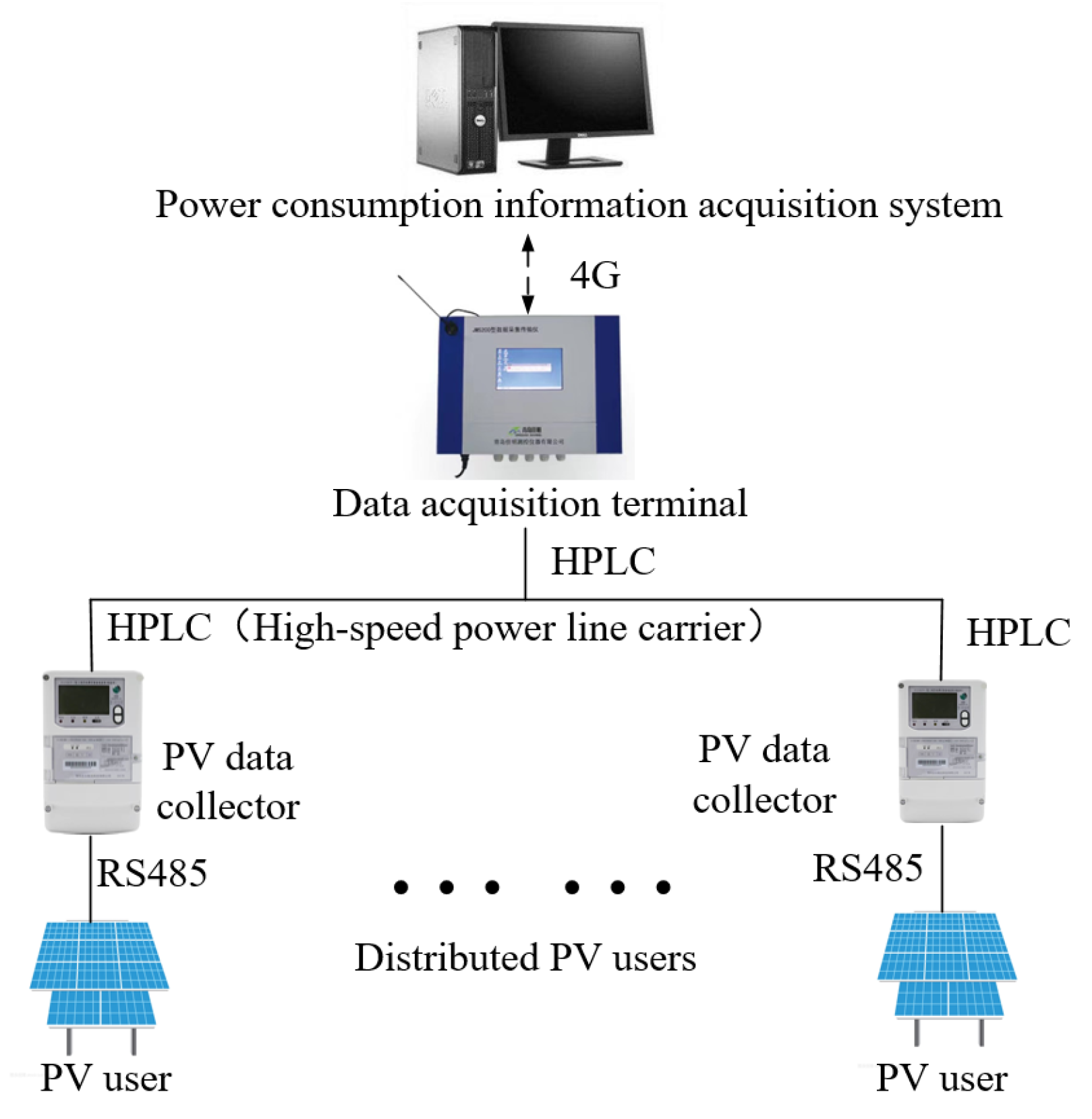
The data acquisition flow of our work is shown in the Figure 5. First, the photovoltaic data collector (smart meter) collects the current, voltage, and other effective data from each photovoltaic user. Then, the local communication HPLC (high-speed power line carrier) uploads the data collected by each smart meter to the local data acquisition terminal. Finally, the local data is transmitted to the main station through 4G network communication, that is, the electricity information collection system.
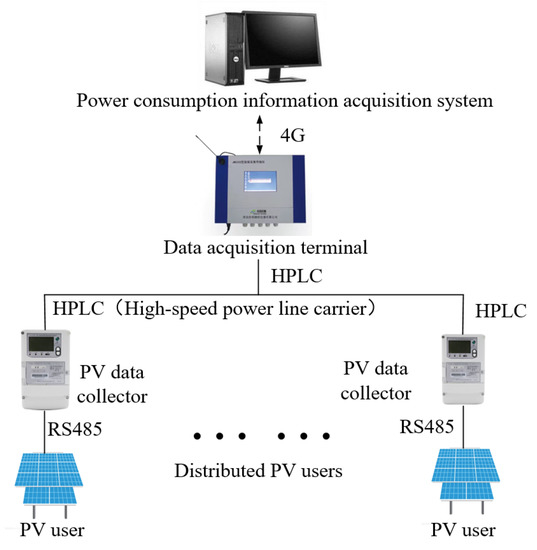
Figure 5.
Data Acquisition Flow.
3.2. Experimental Results and Analysis
In this paper, the common evaluation indicators in the field of forecasting are root-mean-square error (RMSE) and mean absolute percentage error (MAPE), respectively. The smaller the value of the indicator, the smaller the error between the predicted value and the true value, and the better the prediction of the model. The formula for calculating the indicator is shown in Equations (13) and (14)
where and denote the actual and predicted values of load, respectively; and n is the number of samples.
According to Heaton’s study, the number of neurons in the hidden layer of BPNN can be set as two-thirds of the sum of the number of neurons in the input layer and the number of neurons in the output layer. The hyperparameters to be optimized for the LSTM-BPNN model are the cell hidden state dimension, the number of BPNN hidden layers, and the BPNN activation function, respectively. The hyperparameters to be optimized for the LSTM model are the cell hidden state dimension. After the grid search is completed, the optimal hyperparameters of the LSTM-BPNN prediction model are shown in Table 2.

Table 2.
Optimal hyperparameters of the model.
The RMSE and MAPE results of the three prediction models (BPNN, LSTM, and LSTM-BPNN) with the same training set are shown in Table 3 below. Compared with BPNN and LSTM, the experimental results show that the proposed hybrid prediction model LSTM-BPNN has the smallest MAPE value of 2.63%. Therefore, the hybrid LSTM-BPNN model proposed in this paper possesses more accurate prediction results than the two original models.

Table 3.
Predictive evaluation indicators of the three models.
To verify the improvement of the prediction ability by the method in this paper, it is also important to exclude the influence of factors such as the date on the prediction accuracy. In this experiment, the time span owned by each region participating in the collaborative training is set to the same time, and the samples are also set to the same. The main period is 24 h, so the time step of the hybrid model is set to 24.
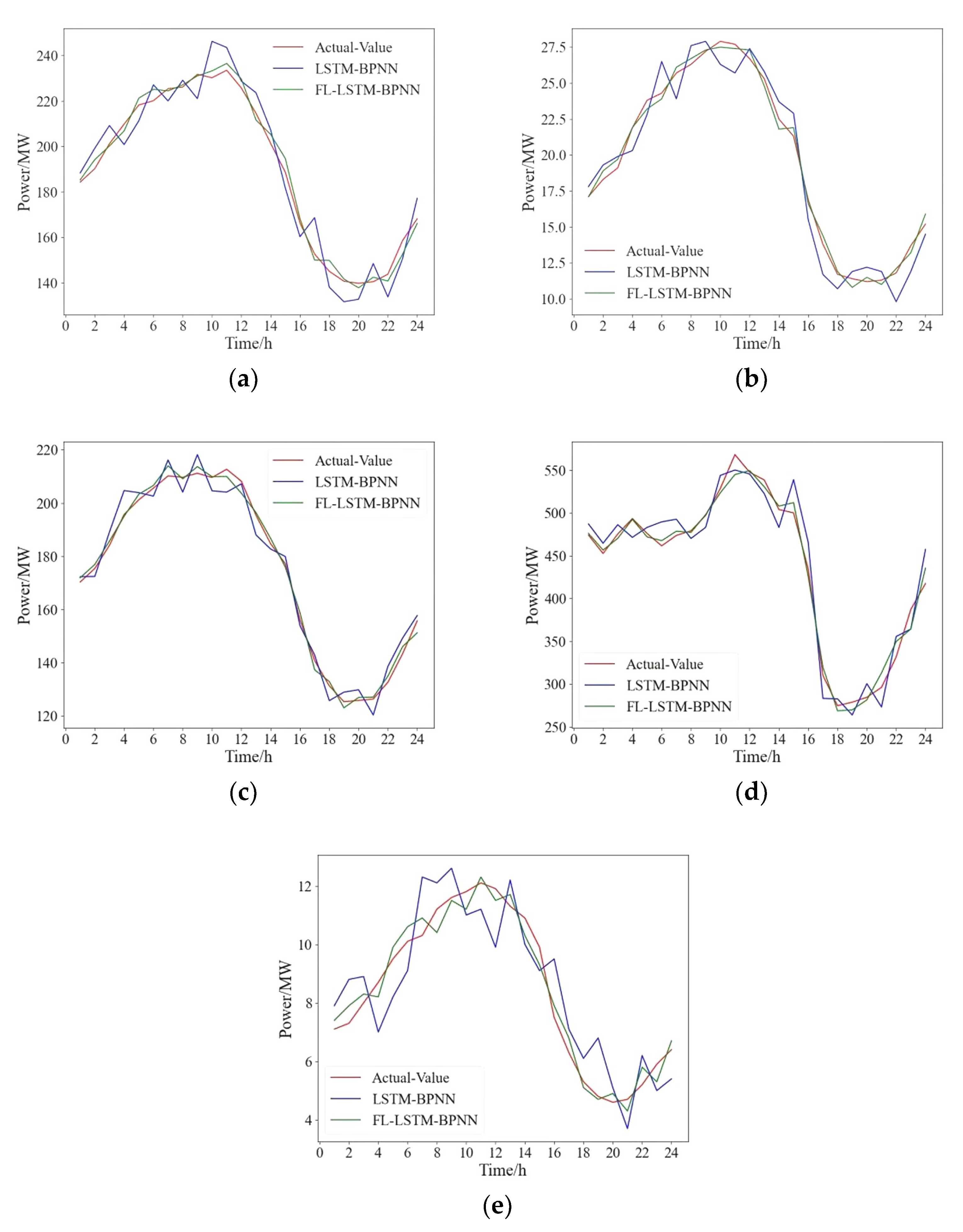
The specific experimental procedure is as follows: five regions are selected to participate in FL as mutually independent PV generators, noted as l1, l2, l3, l4, and l5, and the datasets selected from June to November 2022 measured data Vl1~Vl5 for these five regions, with one record every 1 h and more than 4000 data samples for each V. In order to verify the prediction ability of the method in this paper, the data samples from 1 June to 20 November are used as the model training sample set, and 24 data samples from 21 November are used as the test set. Firstly, each power generation company lk uses more than 4000 local data samples for the model training of the LSTM-BPNN prediction model proposed in this paper in a conventional model training manner, and the trained model is used as the local prediction model, and then the data from the test set is used for validation. Next, the FL training mechanism is used. The model parameters are distributed by the FL server, and each region lk is trained as a local model in turn. Following the FL process, the local model update, local model upload, server receiving model, and server model aggregation update processes are performed sequentially until the optimal prediction model is derived. We set the maximum number of cycles for local model training to 6000 and the maximum number of cycles for federated learning aggregation iterations to 1000. Finally, the federal model is then tested with the test set data. Finally, the local model prediction results (LSTM-BPNN) and federal model prediction results (FL-LSTM-BPNN) are compared and analyzed with the actual data in this paper, and the comparison graphs of the PV power prediction results for each region are shown in Figure 6a–e, and the comparison of the RMSE and MAPE results are shown in Table 4 and Table 5.
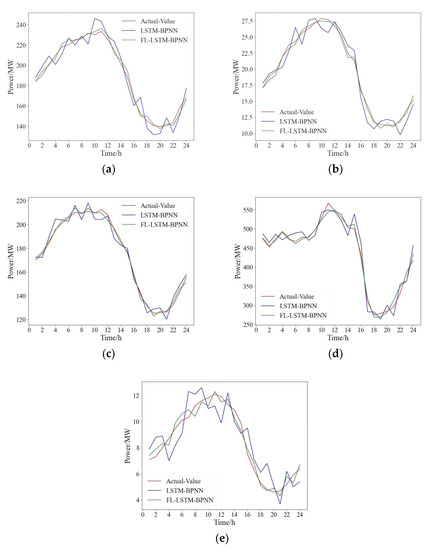
Figure 6.
Comparison of forecast curves for 5 regions: (a) area 1; (b) area 2; (c) area 3; (d) area 4; (e) area 5.

Table 4.
RMSE Comparison.

Table 5.
MAPE Comparison.
It is obvious from Figure 6 that there is a significant gap between the predicted curve and the actual power curve of the model trained using local data. However, the gap between the predicted curve and the actual curve of the model trained by the method in this paper is significantly reduced. As can be seen from Table 3 and Table 4, in the comparison of the results of the five experiments, the prediction results of the local models in each region have a large error relative to the actual load in that region, and the MAPE in region 5 even exceeds 10%, which is sufficient to show that the prediction model at the training using data from a single region alone does not have good results. Putting more emphasis on the necessity of co-training, this paper adopts the FL co-training method, and the error indicators of the trained models, RMSE and MAPE, have both decreased significantly. The most significant decrease in error is observed for region 2, where RMSE and MAPE are reduced by 65.80% and 65.98%, respectively, compared to the local model. This shows that the proposed method incorporates all the data features involved in the model training while protecting the data privacy of all parties, and compensates for the lack of comprehensive features in a single regional dataset. It is finally verified that the prediction models trained by the proposed method have a better prediction accuracy than the models trained on local datasets.
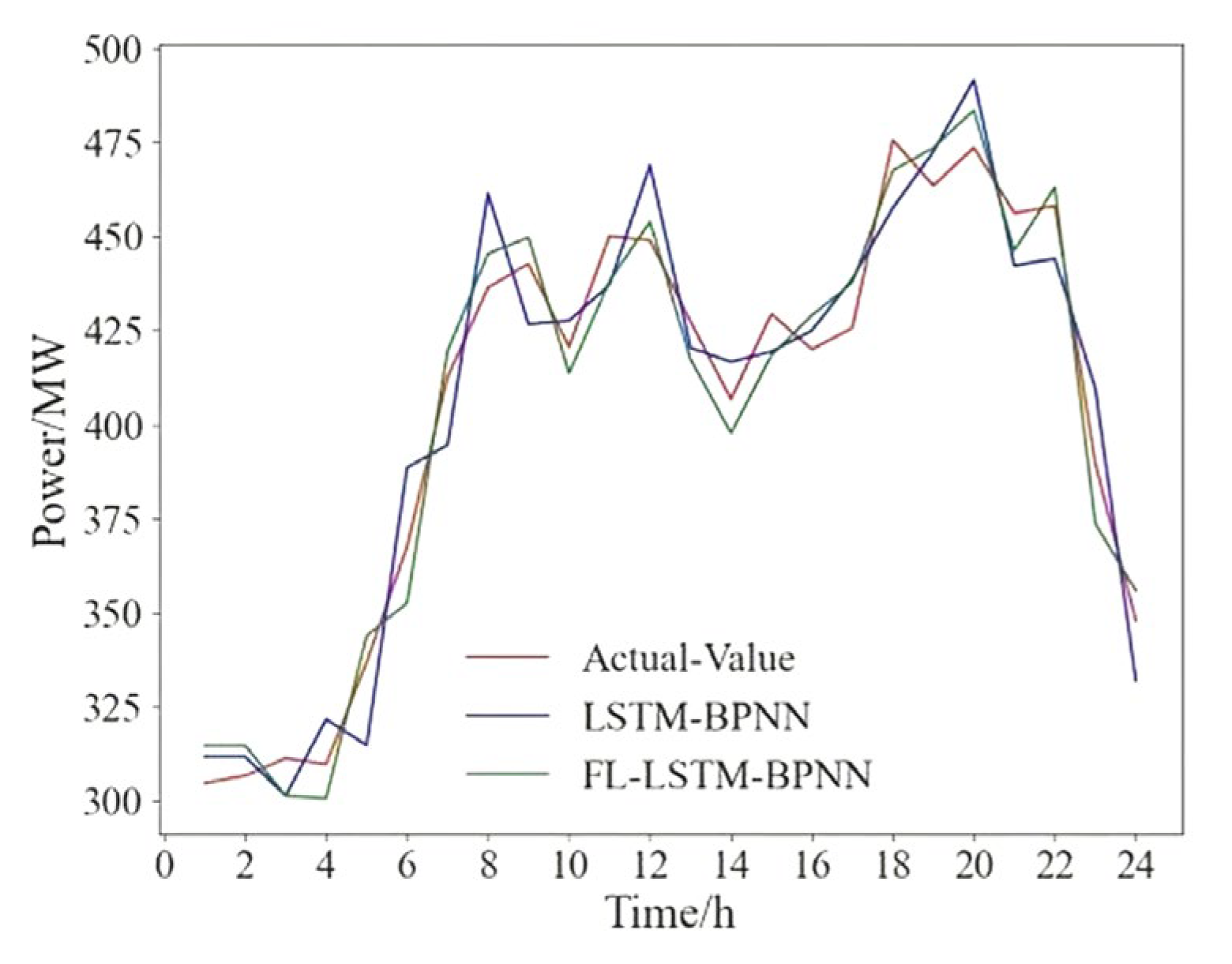
To verify that the FL-LSTM-BPNN PV power prediction model in this paper has a good generalization ability, the following experiments are conducted in this paper. The specific process is as follows: region 4 is taken as the new region to be predicted, regions l1–l4 are used to train the FL model, and the training results are tested with the data from region 4. In this paper, in order to see the advantages of the FL model more intuitively, the FL-LSTM-BPNN and LSTM-BPNN (the results of the model trained locally in region 4) are plotted against the actual power as shown in Figure 7, and the prediction error RMSE versus MAPE is shown in Table 6. To confirm the feasibility of the experiments, two other sets of experiments were conducted in this paper: region 1 and region 3 were used as new regions, respectively, and FL training was performed using data from the remaining four regions; the experimental results were compared and analyzed, and the comparison of prediction error is shown in Table 7 and Table 8.
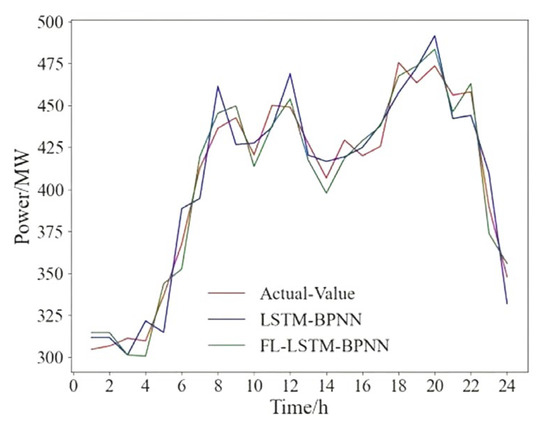
Figure 7.
Comparison of prediction curves for region 4.

Table 6.
Predicted results of RMSE and MAPE for region 4.

Table 7.
Predicted results of RMSE and MAPE for region 1.

Table 8.
Predicted results of RMSE and MAPE for region 1.
From Figure 7 and Table 5, it can be seen that the FL prediction model trained by the proposed method in this paper has a good prediction accuracy in the new region 5. Compared with the model trained with region 5 data only, the difference between the prediction curve and the true power curve of the method in this paper is the smallest, and the RMSE and MAPE are reduced by 34% and 31%, respectively. This is because the model of FL-LSTM-BPNN proposed in this paper learns the data features of multiple regions simultaneously, has a stronger adaptive ability, and has a good generalization ability. To further verify this feature, this paper uses region 1 and region 3 as new regions, respectively, and conducts experiments again. The RMSE and MAPE are reduced by 25% and 23% for region 1, and 24% and 21% for region 3, respectively, which also confirm the good adaptability and generalization ability of this paper.
4. Conclusions
To address the problems of insufficient data from a single data holder, poor generalization ability of the model, and the inability to share power-related data for training, in this paper, the FL-LSTM-BPNN mixed prediction model is first proposed. The collaborative training method of the short-term power prediction model using FL technology can realize the collaborative training of prediction models among PV operators with guaranteed data privacy. While the LSTM-BPNN hybrid prediction model is also used, the output of LSTM is the input of BPNN. RNN is used to extract important features from the time-series data, and BPNN maps the extracted high-dimensional features to the low-dimensional space and outputs the predicted values. This method is used to improve the accuracy of the PV power prediction. Finally, through quantitative experiments, the MAPE of the hybrid LSTM-BPNN prediction model proposed in this paper is 2.63%, which is a 20% improvement over the traditional LSTM model. In a large number of experiments under the collaborative model training mode of FL, the prediction performance indexes RMSE and MAPE of the model can be reduced by 60%, which verifies the improvement of the prediction accuracy of the model by the proposed method in this paper, and proves that the short-term load prediction model trained by the method in this paper has an excellent generalization ability in multiple scenarios.
In the future, our research should: (1) further study FL learning algorithms, optimize aggregation algorithms, and further improve model accuracy and convergence speed under FL; (2) study decentralized FL mechanisms to further improve model training efficiency and data privacy protection.
Author Contributions
Conceptualization, F.D.; Data curation, Y.W. and Z.S.; Formal analysis, H.W.; Funding acquisition, F.D.; Investigation, F.L. and Z.S.; Methodology, H.W., F.L. and F.D.; Resources, Y.W. and M.L.; Software, H.S. and M.L.; Validation, H..; Writing—original draft, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science and Technology Project of Natural State Grid Corporation of China (SGHEDK00DYJS2000044, 5400-202155405A-0-0-00), Natural Science Foundation of China (52167008), Science and Technology Project of Education Department of Jiangxi Province (GJJ210650).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lorenz, E.; Scheidsteger, T.; Hurka, J.; Heinemann, D.; Kurz, C. Regional PV power prediction for improved grid integration. Prog. Photovolt. Res. Appl. 2011, 19, 757–771. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Ogliari, E.; Leva, S.; Lughi, V. Advanced Methods for Photovoltaic Output Power Forecasting: A Review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Yang, D.; Dong, Z. Operational photovoltaics power forecasting using seasonal time series ensemble. Sol. Energy 2018, 166, 529–541. [Google Scholar] [CrossRef]
- Muhammad Ehsan, R.; Simon, S.P.; Venkateswaran, P.R. Day-ahead forecasting of solar photovoltaic output power using multilayer perceptron. Neural Comput. Appl. 2017, 28, 3981–3992. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. Photovoltaic power forecasting based LSTM-Convolutional Network. Energy 2019, 189, 116225. [Google Scholar] [CrossRef]
- Maleki, A.; Eskandar Filabi, Z.; Nazari, M.A. Techno-Economic Analysis and Optimization of an Off-Grid Hybrid Photovoltaic–Diesel–Battery System: Effect of Solar Tracker. Sustainability 2022, 14, 7296. [Google Scholar] [CrossRef]
- Sharifpur, M.; Ahmadi, M.H.; Rungamornrat, J.; Mohsen, F.M. Thermal Management of Solar Photovoltaic Cell by Using Single Walled Carbon Nanotube (SWCNT)/Water: Numerical Simulation and Sensitivity Analysis. Sustainability 2022, 14, 11523. [Google Scholar] [CrossRef]
- Alamin, Y.I.; Anaty, M.K.; Álvarez Hervás, J.D.; Bouziane, K.; Pérez García, M.; Yaagoubi, R.; del Mar Castilla, M.; Belkasmi, M.; Aggour, M. Very short-term power forecasting of high concentrator photovoltaic power facility by implementing artificial neural network. Energies 2020, 13, 3493. [Google Scholar] [CrossRef]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Idna Idris, M.Y.; Mekhilef, S.; Horan, B.; Stojcevski, A. SVR-based model to forecast PV power generation under different weather conditions. Energies 2017, 10, 876. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Ayadi, O.; Adeeb, J.; Alrbai, M.; Qawasmeh, B.R. Extreme learning machines for solar photovoltaic power predictions. Energies 2018, 11, 2725. [Google Scholar] [CrossRef]
- Si, Z.; Yang, M.; Yu, Y.; Ding, T.; Li, M. A Hybrid Photovoltaic Power Prediction Model Based on Multi-source Data Fusion and Deep Learning. In Proceedings of the 2020 IEEE 3rd Student Conference on Electrical Machines and Systems (SCEMS), Jinan, China, 4–6 December 2020; pp. 608–613. [Google Scholar]
- Tehrani, K.; Simde, D.; Fozing, J.; Jamshidi, M. A 3D Design of Small Hybrid Farm for Microgrids. In Proceedings of the 2022 World Automation Congress (WAC), San Antonio, TX, USA, 11–15 October 2022; pp. 1–6. [Google Scholar]
- Mubarak, H.; Hammoudeh, A.; Ahmad, S.; Abdellatif, A.; Mekhilef, S.; Mokhlis, H.; Dupont, S. A hybrid machine learning method with explicit time encoding for improved Malaysian photovoltaic power prediction. J. Clean. Prod. 2022, 382, 134979. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Lughi, V. Deep learning neural networks for short-term photovoltaic power forecasting. Renew. Energy 2021, 172, 276–288. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Sun, X.Y.; Li, J.Z.; Zeng, B.; Gong, D.W.; Lian, Z.Y. Small-sample day-ahead power load forecasting of integrated energy system based on feature trans-fer learning. Control. Theory Appl. 2021, 38, 63–72. (In Chinese) [Google Scholar]
- Zhang, Y.; Tao, Y.F.; Gong, D.W. Load forecasting of buildings using LSTM based on transfer learning with variable source do-main. Control. Decis. 2021, 36, 2328–2338. (In Chinese) [Google Scholar]
- Goncalves, C.; Bessa, R.J.; Pinson, P. Privacy-preserving distributed learning for renewable energy forecasting. IEEE Trans. Sustain. Energy 2021, 12, 1777–1787. [Google Scholar] [CrossRef]
- Konečný, J.; McMahan, H.B.; Yu, F.X.; Richtárik, P.; Suresh, A.T.; Bacon, D. Federated learning: Strategies for improving communication efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–19. [Google Scholar] [CrossRef]
- He, W.C.; Guo, S.Y.; Qiu, X.S.; Chen, L.; Zhang, S. Node selection method in federated learning based on deep reinforcement learning. J. Commun. 2021, 42, 62–71. (In Chinese) [Google Scholar]
- Mills, J.; Hu, J.; Min, G. Communication-efficient federated learning for wireless edge intelligence in IoT. IEEE Internet Things J. 2019, 7, 5986–5994. [Google Scholar] [CrossRef]
- Zhou, C.; Fu, A.; Yu, S.; Yang, W.; Wang, H.; Zhang, Y. Privacy-preserving federated learning in fog computing. IEEE Internet Things J. 2020, 7, 10782–10793. [Google Scholar] [CrossRef]
- Zheng, K.; Xiao, Y.; Wang, X. A Federated Learning Framework for Power Grid Metering System. Proc. CSEE 2020, 40, 122–133. [Google Scholar]
- Lee, J.; Sun, J.; Wang, F.; Wang, S.; Jun, C.H.; Jiang, X. Privacy-preserving patient similarity learning in a federated environment: Development and analysis. JMIR Med. Inform. 2018, 6, e20. [Google Scholar] [CrossRef]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhube, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Buck, J.R.; Schafer, R.W. Discrete-Time Signal Processing.; Prentice Hall: Upper Saddle River, NJ, USA, 2001; Volume 2. [Google Scholar]
- Heaton, J. Introduction to Neural Networks with Java; Heaton Research, Inc.: Chesterfield, MO, USA, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).