Meteorological Variables Forecasting System Using Machine Learning and Open-Source Software

Abstract

The techniques for forecasting meteorological variables are highly studied since prior knowledge of them allows for the efficient management of renewable energies, and also for other applications of science such as agriculture, health, engineering, energy, etc. In this research, the design, implementation, and comparison of forecasting models for meteorological variables have been performed using different Machine Learning techniques as part of Python open-source software. The techniques implemented include multiple linear regression, polynomial regression, random forest, decision tree, XGBoost, and multilayer perceptron neural network (MLP). To identify the best technique, the mean square error (RMSE), mean absolute percentage error (MAPE), mean absolute error (MAE), and coefficient of determination (${\mathrm{R}}^2$) are used as evaluation metrics. The most efficient techniques depend on the variable to be forecasting, however, it is noted that for most of them, random forest and XGBoost techniques present better performance. For temperature, the best performing technique was Random Forest with an ${\mathrm{R}}^2$ of 0.8631, MAE of 0.4728 °C, MAPE of 2.73%, and RMSE of 0.6621 °C; for relative humidity, was Random Forest with an ${\mathrm{R}}^2$ of 0.8583, MAE of 2.1380RH, MAPE of 2.50% and RMSE of 2.9003 RH; for solar radiation, was Random Forest with an ${\mathrm{R}}^2$ of 0.7333, MAE of 65.8105 $\mathrm{W}/{\mathrm{m}}^2$, and RMSE of 105.9141 $\mathrm{W}/{\mathrm{m}}^2$; and for wind speed, was Random Forest with an ${\mathrm{R}}^2$ of 0.3660, MAE of 0.1097 $\mathrm{m}/\mathrm{s}$, and RMSE of 0.2136 $\mathrm{m}/\mathrm{s}$.

1. Introduction

Since the 17th century, meteorological variables have been of great interest throughout history, with the creation of the first instruments for measuring meteorological variables aiming to accurately predict the weather. For this purpose, mathematical and statistical methods and computer programs are used, most of which are of a non-linear nature [1]. Nowadays, climatic conditions change under various influences. For example, atmospheric pollution is increasing, so climate change is occurring and threatening the planet [2], which is why the measurement of meteorological variables has grown in importance as the information provided by the meteorological stations is important for monitoring climate change [3].

Climate is defined by the grouping of meteorological phenomena that are related to each other; although each of them is studied separately, it must be taken into account that a change in one produces a variation in the others [4]. The actual weather is characterised by the wind, temperature, and humidity variables forced by radiative fluxes and surface latent and sensible heat fluxes. The local climate usually denotes the mean state of the atmosphere over a 20–30-year period for a given location and day (or season) of the year. For this reason, meteorological variables are usually modeled by means of computational, numerical, and statistical techniques, most of which are nonlinear [5]. Forecasting certain climatic variables is a great challenge due to the variable behavior of the climate, which makes it impossible to optimally manage renewable energies and obtain a greater benefit from them.

There are multiple scientific studies of modeling and prediction in order to forecast future conditions of phenomena in various fields; among the most prominent are ARIMA, Chaos Theory, and Neural Networks [6]. Forecasting models have evolved in recent decades, from smart systems with formal rules and logical theories, to the emergence of artificial intelligence techniques that allow us to propose alternatives in the treatment of information [7].

Currently, forecasting models have a high impact and are used for several applications, such as management of energy units for renewable resources microgrids [8,9], load estimation methods for isolated communities that do not receive energy or only receive it for a limited time each day [10,11], the operation of energy systems [12,13], in agriculture to predict the water consumption of plants and plan the irrigation sheet [14], in agriculture 4.0 for the prediction of variables that affect the quality of crops, for micronutrient analysis and prediction of soil chemical parameters [15], optimization of agricultural procedures and increasing productivity in the field, forecasting of SPI and Meteorological Drought Based on the Artificial Neural Network and M5P Model Tree [16], and in controllers based on forecasting models and predictive controllers. They are also used in the health field to predict the solar radiation index and to obtain a correct assessment in people with skin cancer [17], therefore, all the applications mentioned above need forecasting models that have the lowest error rate for their effective operation.

Having a forecasting model system is costly because computer packages are used in which licensing costs can be significant. On the other hand, free software is an option to reduce costs. This research proposes a system based on free software (Python), which is currently used at industrial level for its reliability, for example in applications such as the following: Advanced Time Series: Application of Neural Networks for Time Series Forecasting [18], Machine Learning in Python: main developments and technological trends in data science, Machine Learning and artificial intelligence [19], Development of an smart tool focused on artificial vision and neural networks for weed recognition in rice plantations, using Python programming language [20], etc.

In this research, different prediction techniques were evaluated and compared—among them, multiple linear regression, polynomial regression, random forest, decision tree, XGBoost, and multilayer perceptron neural network—in order to identify the best performing strategy, using evaluation metrics such as the root mean square error (RMSE) and the coefficient of determination (${\mathrm{R}}^2$). The variables to be predicted are temperature, relative humidity, solar radiation, and wind speed, from data taken from the weather station located in Ecuador, Tungurahua province, Baños. The predicted variables will be the inputs for a smart irrigation system and used for an energy management system of a microgrid based on predictive control, therefore, models with high approximation to online measurements are required.

The contributions of this work are as follows: (i) To design, validate, and compare different machine learning techniques, and with them select the best technique that adapts to climate variables for agriculture and energy applications, (ii) To develop a forecast system for climate variables of low cost based in free software (Python), (iii) To generate forecasting models that can be replicated for other types of variables applied to smart control systems based on forecasting models.

2. Design of Forecasting Models for Meteorological Variables

This section describes the prediction techniques used and their design. In this research, the following meteorological variables are studied and predicted: temperature, relative humidity, wind speed, and solar radiation.

The techniques designed, evaluated, and compared are the following: multiple linear regression, polynomial regression, random forest, decision tree, XGBoost, and neural network—multilayer perceptron. To obtain the forecast of meteorological variables, the design methodology shown in Figure 1 is implemented.

2.1. Obtaining the Database

For the implementation of the forecasting models, information was obtained from the page of the Tungurahua hydrometeorological network, where there are several meteorological stations, including the Baños family park, located in Ecuador, Tungurahua province, Baños, coordinates $X=\mathrm{9,845,439}, Y=\mathrm{791,471}$ that counts the parameters of precipitation $\left(\mathrm{mm}\right)$, temperature $\left(°\mathrm{C}\right)$, relative humidity $(\%)$, wind speed $\left(\mathrm{m}/\mathrm{s}\right)$, wind direction $(°)$, solar radiation $\left(\mathrm{W}/{\mathrm{m}}^2\right)$, and evapotranspiration $\left(\mathrm{mm}\right)$. For the design of the models, only the values of temperature, solar radiation, relative humidity, and wind speed were taken, since after a previous analysis of correlation between meteorological variables, the variables with lower correlation with the variable to be predicted are discarded. It is important to note that the values of temperature, solar radiation (net solar radiation at surface), and relative humidity were measured at a distance of 2 m, while the wind speed was measured at 10 m.

2.2. Data Preprocessing

From the database obtained, 1 year of information was available (from 23 July 2021 to 15 June 2022), which was preprocessed to take data every 5 min for each variable (temperature, relative humidity, wind speed, and solar radiation). To make a forecast, it is important to verify that there are no missing data in the measurements or to implement a data filling method; in this case, a Python algorithm was implemented, which calculates the average of the existing list of data and automatically fills in the missing data.

2.3. Dataset Division

To verify that the models work correctly, the available database is divided into three groups: training set, test set, and validation set. As its name indicates, the first one will be used to train the forecasting models, the second one will be used to evaluate the test set, and the third one to validate each of the implemented models [17,21].

After data preprocessing, a total of 93,780 data were obtained for each variable, where 80% of the database (75,024 data) is used to train the models, 20% (18,756 data) to test the models, and 2 days (576 data) were used for the validation of the models.

2.4. Design of the Forecasting Models

2.4.1. Multiple Linear Regression

It is a technique that allows modeling the relationship between a continuous variable and one or more independent variables by adjusting a linear equation. It is called simple linear regression when there is one independent variable, and if there is more than one, it is called multiple linear regression. In this context, the modeled variables are called dependent or response variables $\left(y\right)$; and the independent variables are called regressors, predictors, or features $\left(X\right)$ [22]. Multiple linear regression is defined by Equation (1)

$$y=a+b_1{X}_1+b_2{X}_2+\cdots +b_n{X}_n$$

(1)

where: $X_1,X_2,\dots X_n:$ are the predictor or independent variables, $b_1,b_2,\dots b_n:$ coefficients of the predictor variables, $a:$ constant of the relationship between the dependent and independent variable, and $y:$ predicted or dependent variable.

After performing different heuristic tests and using sensitivity analysis for this forecasting technique, it is deduced that the best parameters for tuning are those described in

Table 1. Tuning parameters for the multiple linear regression techniques.

Multiple Linear Regression
Predicted Variable	Inputs Variables
Temperature	Solar radiation, relative humidity, wind speed
Solar radiation	Temperature, relative humidity, wind speed
Wind speed	Temperature, solar radiation, relative humidity
Relative Humidity	Temperature, solar radiation, wind speed

.

2.4.2. Polynomial Regression

A linear regression with polynomial attributes that uses the relationship between the dependent $\left(y\right)$ and independent $\left(X\right)$ variables to find the best way to draw a line through the data points. This technique is used when the data are more complex than a simple straight line [23], and is defined by Equation (2).

$$y=a+b_1{X}_i+b_2{X}_i{}^2+b_3{X}_i{}^3+\dots +b_n{X}_i{}^n$$

(2)

where: $X_1,X_2,\dots X_n:$ are the predictor or independent variables, $b_1,b_2,\dots b_n:$ coefficients of the predictor variables, $a:$ constant of the relationship between the dependent and independent variable, and $y:$ predicted or dependent variable.

After performing different heuristic tests and using sensitivity analysis for this forecasting technique, it is deduced that the best parameters for tuning are those described in

Table 2. Tuning parameters for polynomial regression technique.

Polynomial Regression
Predicted Variable	Inputs Variables	Degree of the Polynomial
Temperature	Solar radiation, relative humidity, wind speed	4
Solar radiation	Temperature, relative humidity, wind speed	5
Wind speed	Temperature, solar radiation, relative humidity	6
Relative Humidity	Temperature, solar radiation, wind speed	4

.

2.4.3. Decision Tree

Values by learning decision rules derived from features and can be used for classification, regression, and multi-output tasks. Decision trees work by dividing the feature space into several simple rectangular regions, divided by parallel divisions of axes. To obtain a prediction, the mean or mode of the responses of the training observations, within the partition to which the new observation belongs, is used [23]. This is defined by Equation (3).

$$G_i=1-{\displaystyle \sum }_{k=1}^m{(P_{i,k})}^2$$

(3)

where: $P_{i,k}:$ is the radio of class $k$ instances among the training instances in the ith node, $m:$ number of class labels, and $G_i$ (Gini impurity): represents the measure for constructing decision trees.

After performing different heuristic tests and using sensitivity analysis for this forecast technique, it is deduced that the best parameters for tuning are those described in

Table 3. Tuning parameters for the decision tree technique.

Decision Tree
Predicted Variable	Inputs Variables	Max_Depth	Min_Samples_Leaf
Temperature	Solar radiation, relative humidity, wind speed	10	18
Solar radiation	Temperature, relative humidity, wind speed	10	7
Wind speed	Temperature, solar radiation, relative humidity	19	6
Relative Humidity	Temperature, solar radiation, wind speed	9	16

.

2.4.4. Random Forest

A supervised learning algorithm that uses an ensemble learning method for regression that combines predictions from several machine learning algorithms (decision trees) to make a more accurate prediction than a single model [23]. Figure 2 shows that the random forest algorithm is composed of a collection of decision trees, and each tree in the set is composed of a sample of data extracted from a training set (DATASET); for a regression task, the individual decision trees are averaged (Average) until the predicted value (Prediction) is obtained.

In general, deep decision trees tend to overfit, while random forests avoid this by generating random subsets of features and using those subsets to build smaller trees. The generalization error for random forests is based on the strength of the individual constructed trees and their correlation [24].

This technique has several parameters that can be configured, such as the following:

N° estimators: the number of trees in the forest. Max leaf nodes: the maximum number of leaf nodes, this hyperparameter sets a condition for splitting the tree nodes and thus restricts the growth of the tree. If after splitting there are more terminal nodes than the specified number, the splitting stops and the tree does not continue to grow, which helps to avoid overfitting. And Max features: the maximum number of features that are evaluated for splitting at each node, increasing max_features generally improves model performance, since each node now has a greater number of options to consider [23].

After performing different heuristic tests and using sensitivity analysis for this forecast technique, it is deduced that the best parameters for tuning are those described in

Table 4. Tuning parameters for the random forest technique.

Random Forest
Predicted Variable	Inputs Variables	N° Estimators	Max Leaf Nodes	Max Features
Temperature	Solar radiation, relative humidity, wind speed	100	3000	0.1
Solar radiation	Temperature, relative humidity, wind speed	100	3000	0.1
Wind speed	Temperature, solar radiation, relative humidity	100	2000	0.3
Relative Humidity	Temperature, solar radiation, wind speed	100	2000	0.2

.

2.4.5. Extreme Gradient Boosting (XGboost)

The XGBoost algorithm is a scalable tree-boosting system that can be used for both classification and regression tasks. It performs a second-order Taylor expansion on the loss function and can automatically use multiple threads of the central processing unit (CPU) for parallel computing. In addition, XGBoost uses a variety of methods to avoid overfitting [25].

Figure 3 shows the XGBoost algorithm; decision trees are created sequentially (Decision Tree-1, Decision Tree-2, Decision Tree-N) and weights play an important role in XGBoost. Weights are assigned to all independent variables, which are then entered into the decision tree that predicts the outcomes (Result-1, Result-2, Result-N). The weights of variables incorrectly predicted by the tree are increased and these variables are then fed into the second decision tree (Residual error). These individual predictors are then grouped (Average) to give a strong and more accurate model (Prediction).

After performing different heuristic tests and using sensitivity analysis for this forecast technique, it is deduced that the best parameters for its tuning are those described in

Table 5. Tuning parameters for the XGboost technique.

XGBoost
Predicted Variable	Inputs Variables	Max Depth	N° Estimators
Temperature	Solar radiation, relative humidity, wind speed	2	100
Solar radiation	Temperature, relative humidity, wind speed	2	20
Wind speed	Temperature, solar radiation, relative humidity	5	19
Relative Humidity	Temperature, solar radiation, wind speed	7	19

.

2.4.6. Neural Network—Multilayer Perceptron

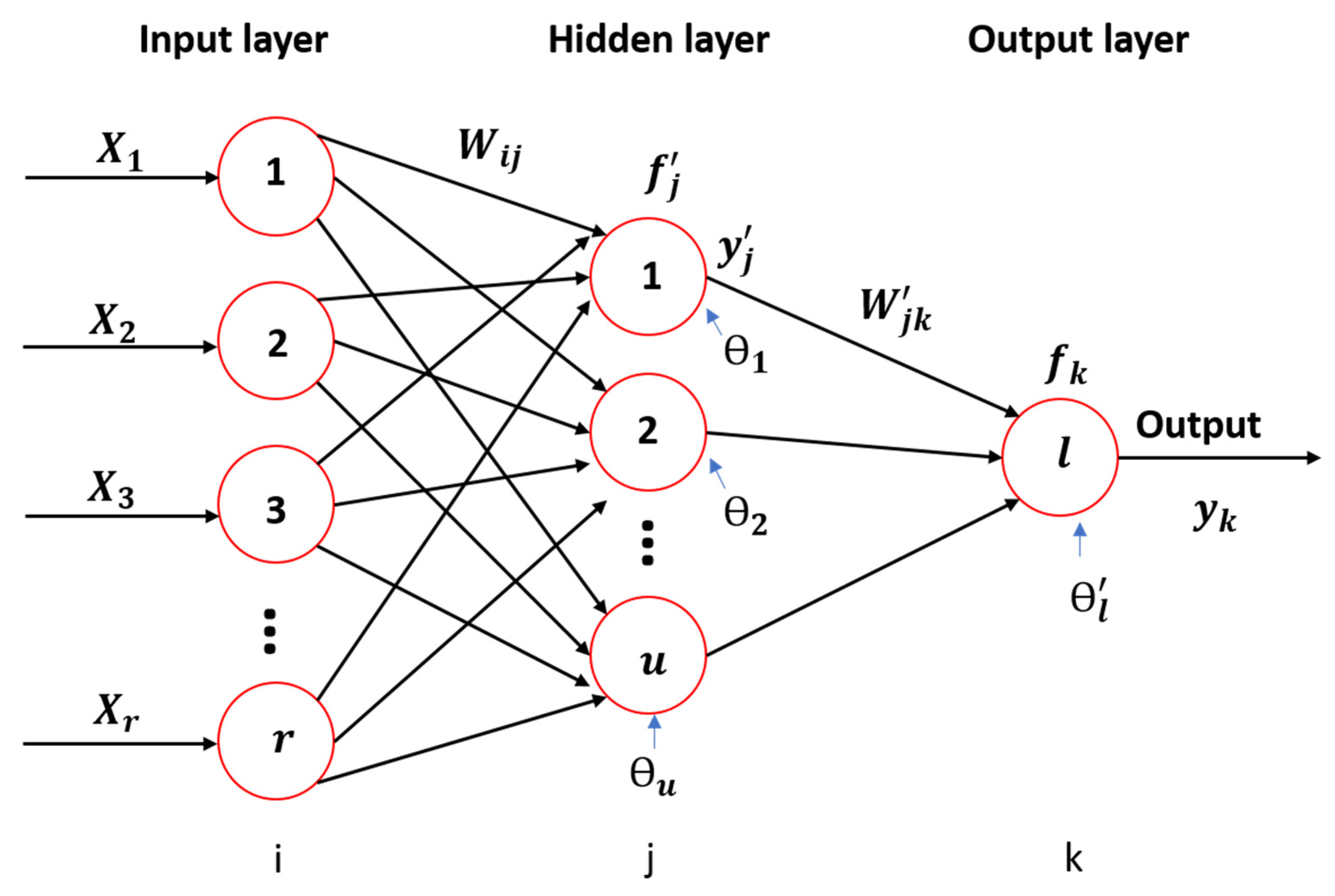
It is an effective and widely used model for modeling many real situations. The multilayer perceptron is a hierarchical structure consisting of several layers of fully interconnected neurons, which input neurons are outputs of the previous layer. Figure 4 shows the structure of a multilayer perceptron neural network; the input layer is made up of $r$ units (where $r$ is the number of external inputs) that merely distribute the input signals to the next layer; the hidden layer is made up of neurons that have no physical contact with the outside; the number of hidden layers is variable $\left(u\right)$; and the output layer is made up of $l$ neurons (where $l$ is the number of external outputs) whose outputs constitute the vector of external outputs of the multilayer perceptron [26].

The training of the neural network consists of calculating the linear combination from a set of input variables, with a bias term, applying an activation function, generally the threshold or sign function, giving rise to the network output. Thus, the weights of the network are adjusted by the method of supervised learning by error correction (backpropagation), in such a way that the expected output is compared with the value of the output variable to be obtained, the difference being the error or residual. Each neuron behaves independently of the others: each neuron receives a set of input values (an input vector), calculates the scalar product of this vector and the vector of weights, adds its own bias, applies an activation function to the result, and returns the final result obtained [26].

In general, all weights and biases will be different. The output of the multilayer perceptron neural network is defined by Equation (4). Where: $y_k$ is the output, $f_k$ activation function of output layer, ${\theta }_k^{\prime }$ bias of the output layer, $W_{ij}$ hidden layer weights, $y_j^{\prime }$ output of the hidden layer, $f_j^{\prime }$ activation function of the hidden layer, $X_i$ neuron inputs, $W_{jk}^{\prime }$ output layer weights, ${\theta }_j$ bias of hidden layer, $r$ is the number of inputs for the neuron $j$ from the hidden layer, and $u$ is the number of inputs for the neuron $k$ from the output layer [27].

$$\begin{array}{c}{y}_j^{\prime }=f_j^{\prime }\left({\displaystyle \sum }_{i=1}^r{X}_i{W}_{ij}-{\theta }_j\right)\\ y_k=f_k\left({\displaystyle \sum }_{j=1}^u{y}_j^{\prime }{W}_{jk}^{\prime }-{\theta }_k^{\prime }\right)\end{array}$$

(4)

For this research, backpropagation was used as a training technique. After performing different heuristic tests and using sensitivity analysis for this forecasting technique, it is deduced that the best parameters for its tuning are those described in

Table 6. Tuning parameters for the multilayer perceptron neural network technique.

Neural Network—Multilayer Perceptron
Predicted Variable	Inputs Variables	Input Layer Neurons	N° Epoch	Batch Size	Hidden Layer Neurons	Activation Function
Temperature	Solar radiation, relative humidity, wind speed	3	5000	128	32	Hidden: ReLU Out: Sigmoid
Solar radiation	Temperature, relative humidity, wind speed	3	5000	128	32	Hidden: ReLU Out: Sigmoid
Wind speed	Temperature, solar radiation, relative humidity	3	3000	128	32	Hidden: ReLU Out: Sigmoid
Relative Humidity	Temperature, solar radiation, wind speed	3	5000	128	32	Hidden: ReLU Out: Sigmoid

.

3. Results

3.1. Indicators for Assessing the Performance of Weather Forecasting Models

To measure the performance of the forecast techniques for each of the variables described above, two types of metrics were used: to evaluate the forecast accuracy, the mean square error RMSE is used, which allows comparing their results and defining the technique with the lowest error, and therefore, the best method for each variable to be predicted. In addition, to determine if the implemented models perform well in their training and to define their predictive ability, the coefficient of determination is ${\mathrm{R}}^2$.

3.1.1. Coefficient of Determination (${\mathrm{R}}^2$)

${\mathrm{R}}^2$ or coefficient of determination can be in the range of $\left[-\infty ,1\right]$ it is used to determine the ability of a model to predict future results. The best possible result is 1, and occurs when the prediction coincides with the values of the target variable, while the closer to zero, the less well-fitted the model is and, therefore, the less reliable it is. ${\mathrm{R}}^2$ can take negative values because the prediction can be arbitrarily bad [28]. It is defined as Equation (5), described by 1 minus the sum of total squares divided by the sum of squares of the residuals.

$${\mathrm{R}}^2=1-\frac{\sum {(y_c-{\widehat{y}}_c)}^2}{\sum {(y_c-\overline{y})}^2}$$

(5)

where: $y_c$: are the values taken by the target variable, ${\widehat{y}}_c$: are the values of the prediction, and $\overline{y}$: is the mean value of the values taken by the target variable.

3.1.2. Mean Square Error (RMSE)

The root mean square error, also known as root mean square deviation, measures the amount of error between two sets of data. That is, it compares the predicted value with the observed or known value [28]. It is given by Equation (6):

$$\mathrm{RMSE}=\sqrt{\frac{1}{o}{\displaystyle \sum }_{c=1}^o{(y_c-{\widehat{y}}_c)}^2}$$

(6)

where: $y_c$: are the values taken by the target variable, ${\widehat{y}}_c$: are the values of the prediction, and $o$: is the sample size.

3.1.3. Mean Absolute Percentage Error (MAPE)

Mean absolute percentage error is an evaluation metric for regression problems; the idea of this metric is to be sensitive to relative errors. MAPE is the mean of all absolute percentage errors between the predicted and actual values [29]. It is given by Equation (7):

$$\mathrm{MAPE}=\frac{1}{o}{\displaystyle \sum }_{c=1}^o\left|\frac{y_c-{\widehat{y}}_c}{y_c}\right|\ast 100\%$$

(7)

where $y_c$: are the values taken by the target variable, ${\widehat{y}}_c$: are the values of the prediction, and $o$: is the sample size.

Equation (7) helps to understand one of the important caveats when using MAPE, since to calculate this metric, you need to divide the difference by the actual value. This means that if you have actual values close to 0 or at 0, the MAPE score will receive a division error by 0 or will be extremely high. Therefore, it is recommended not to use MAPE when it has real values close to 0 [30].

3.1.4. Mean Absolute Error (MAE)

Mean absolute error is a common metric to use for measuring the error of regression predictions. The mean absolute error of a model is the mean of the absolute values of the individual prediction errors on over all instances in the test set. Each prediction error is the difference between the true value and the predicted value for the instance [16,31]. It is given by Equation (8):

$$\mathrm{MAE}=\frac{1}{o}{\displaystyle \sum }_{c=1}^o\left| y_c-{\widehat{y}}_c\right|$$

(8)

where: $y_c$: are the values taken by the target variable, ${\widehat{y}}_c$: are the values of the prediction, and $o$: is the sample size.

3.2. Case Study

For the implementation of the forecast techniques for meteorological variables (temperature, wind speed, solar radiation, and relative humidity), the Python programming language was used. Information was obtained from the Parque de la Familia Baños meteorological station, located in Ecuador, Tungurahua province, Baños, coordinates $X=\mathrm{9,845,439}$, $Y=\mathrm{791,471}$. From the database obtained, 1 year of information was available (from 23 July 2021 to 15 June 2022) with a sampling time of 5 min having a total of 93,780 data for each variable, where 80% of the database (75,024 data) is used to test the models, 20% (18,756 data) to test the models, and 2 days (576 data) were used for validation. To obtain the values of the evaluation metrics (RMSE, MAE, MAPE y ${\mathrm{R}}^2$) the validation data corresponding to the days 10 June 2022 and 11 June 2022 were used.

The forecast techniques implemented for all variables are the following: multiple linear regression, polynomial regression, decision tree, random forest, XGboost, and multilayer perceptron neural network.

To identify which of the models is more efficient, evaluation metrics such as root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE) are used over the entire validation range, while to evaluate whether the forecasting algorithms fit correctly, the ${\mathrm{R}}^2$ metric is used. It is important to note that these metrics evaluate different aspects; the RMSE, MAPE, and MAE evaluate the forecasting error, while R² allows to analyze how well a regression model fits the real data.

3.2.1. Temperature Forecasting

Table 7. Evaluation metrics for temperature forecasting.

Technique	Coefficient of Determination  $\left({\mathbf{R}}^2\right)$	Mean Absolute Error (MAE) $\left[°\mathbf{C}\right]$	Mean Absolute Percentage Error (MAPE) $[\mathbf{\%}]$	Mean Square Error (RMSE) $\left[°\mathbf{C}\right]$
Multiple linear regression	0.8244	0.6597	3.71	0.8453
Polynomial regression	0.8406	0.6097	3.51	0.8146
Decision tree	0.8593	0.5097	2.95	0.7333
Random forest	0.8631	0.4728	2.73	0.6621
XGboost	0.8599	0.5335	3.09	0.7565
Multilayer perceptron	0.8226	0.9124	5.51	1.2498

shows the results of the evaluation metrics: root mean square error (RMSE), mean absolute percentage error (MAPE), mean absolute error (MAE), and coefficient of determination (${\mathrm{R}}^2$) for each of the techniques used for temperature forecasting. The calculation of the root mean square error, mean absolute percentage error, and mean absolute error was obtained by averaging the errors of the validation data (576 data), while the calculation of the coefficient of determination (${\mathrm{R}}^2$) used the data from the training set and the test set (93,780 data).

Table 7 shows that ${\mathrm{R}}^2$ obtained from the implemented algorithms converge to appropriate values, i.e., there is a correct approximation between the real temperature and the predicted temperature, thus guaranteeing the good performance of the algorithm, which allows a comparison of the performance in terms of forecast error. Comparison of the root mean square errors (RMSE), mean absolute percentage errors (MAPE), and mean absolute errors (MAE), and analysis of the coefficient of determination ${\mathrm{R}}^2$ of the different techniques implemented show that the best performing technique for forecasting the temperature variable is Random Forest, with an ${\mathrm{R}}^2$ of 0.8631, MAE of 0.4728 °C, MAPE of 2.73%, and RMSE of 0.6621 °C. This is followed by XGBoost, with an ${\mathrm{R}}^2$ of 0.8599, MAE of 0.5335 °C, MAPE of 3.09%, and RMSE of 0.7565 °C.

Figure 5 shows the real (red) and prediction (blue) profiles using the different Machine Learning techniques to predict the temperature variable: (a) Multiple linear regression technique, (b) Polynomial regression technique, (c) Decision tree technique, (d) Random Forest technique, (e) XGboost technique, (f) Multilayer perceptron neural network technique. Figure 5c,d, validate that the best performance corresponds to the Decision tree and Random forest techniques.

3.2.2. Relative Humidity Forecasting

Table 8. Evaluation metrics for relative humidity forecasting.

Technique	Coefficient of Determination $\left({\mathbf{R}}^2\right)$	Mean Absolute Error (MAE) $\left[\mathbf{R}\mathbf{H}\right]$	Mean Absolute Percentage Error (MAPE) $[\mathbf{\%}]$	Mean Square Error (RMSE) $\left[\mathbf{R}\mathbf{H}\right]$
Multiple linear regression	0.7815	3.0900	3.56	3.7475
Polynomial regression	0.8420	2.2816	2.68	3.0163
Decision tree	0.8547	2.2685	2.65	3.2083
Random forest	0.8583	2.1380	2.50	2.9003
XGboost	0.8597	2.2907	2.67	3.1444
Multilayer perceptron	0.8013	4.6055	5.64	5.5759

shows the results of the evaluation metrics: root mean square error (RMSE), mean absolute percentage error (MAPE), mean absolute error (MAE), and coefficient of determination (${\mathrm{R}}^2$) for each of the techniques used for relative humidity forecasting. The calculation of the root mean square error, mean absolute percentage error, and mean absolute error was obtained by averaging the errors of the validation data (576 data), while the calculation of the coefficient of determination (${\mathrm{R}}^2$) used the data from the training set and the test set (93,780 data).

Table 8 shows that ${\mathrm{R}}^2$ obtained from the implemented algorithms converge to appropriate values, i.e., there is a correct approximation between the real relative humidity and the predicted relative humidity, thus guaranteeing the good performance of the algorithm, which allows a comparison of the performance in terms of forecast error. Comparison of the root mean square errors (RMSE), mean absolute percentage errors (MAPE), and mean absolute errors (MAE), and analysis of the coefficient of determination ${\mathrm{R}}^2$ of the different techniques implemented show that the best performing techniques for forecasting the relative humidity variable are Random Forest, with an ${\mathrm{R}}^2$ of 0.8583, MAE of 2.1380 RH, MAPE of 2.50%, and RMSE of 2.9003 RH; and XGBoost, with an ${\mathrm{R}}^2$ of 0.8597, MAE of 2.2907 RH, MAPE of 2.67%, and RMSE of 3.1444 RH.

Figure 6 shows the real (red) and prediction (blue) profiles using the different Machine Learning techniques to predict the relative humidity variable: (a) Multiple linear regression technique, (b) Polynomial regression technique, (c) Decision tree technique, (d) Random forest technique, (e) XGboost technique, (f) Multilayer perceptron neural network technique. Figure 6d and Figure 6c validate that the best performance corresponds to the Random forest and Decision tree techniques.

3.2.3. Solar Radiation Forecasting

Table 9. Evaluation metrics for solar radiation forecasting.

Technique	Coefficient of Determination $\left({\mathbf{R}}^2\right)$	Mean Absolute Error (MAE) $\left[\mathbf{W}/{\mathbf{m}}^2\right]$	Mean Square Error (RMSE) $\left[\mathbf{W}/{\mathbf{m}}^2\right]$
Multiple linear regression	0.6689	106.9741	164.7435
Polynomial regression	0.7394	76.6667	129.1836
Decision tree	0.7253	75.8177	127.3530
Random forest	0.7333	65.8105	105.9141
XGboost	0.7075	87.6137	145.0170
Multilayer perceptron	0.7423	88.5897	140.0681

shows the results of the evaluation metrics: root mean square error (RMSE), mean absolute error (MAE), and coefficient of determination (${\mathrm{R}}^2$) for each of the techniques used for solar radiation forecasting. The calculation of the root mean square error, and mean absolute error was obtained by averaging the errors of the validation data (576 data), while the calculation of the coefficient of determination (${\mathrm{R}}^2$) used the data from the training set and the test set (93,780 data).

Table 9 shows that ${\mathrm{R}}^2$ obtained from the implemented algorithms converge to appropriate values, i.e., there is a correct approximation between the real solar radiation and the predicted solar radiation, thus guaranteeing the good performance of the algorithm, which allows a comparison of the performance in terms of forecast error. Comparison of the root mean square errors (RMSE), and mean absolute errors (MAE), and analysis of the coefficient of determination ${\mathrm{R}}^2$ of the different techniques implemented show that the best performing techniques for forecasting the solar radiation variable are Random Forest with an ${\mathrm{R}}^2$ of 0.7333, MAE of 65.8105 $\mathrm{W}/{\mathrm{m}}^2$, and RMSE of 105.9141 $\mathrm{W}/{\mathrm{m}}^2$; and Decision Tree with an ${\mathrm{R}}^2$ of 0.7253, MAE of 75.8177 $\mathrm{W}/{\mathrm{m}}^2$, and RMSE of 127.3530 $\mathrm{W}/{\mathrm{m}}^2$.

Figure 7 shows the real (red) and prediction (blue) profiles using the different Machine Learning techniques to predict the variable solar radiation: (a) Multiple linear regression technique, (b) Polynomial regression technique, (c) Decision tree technique, (d) Random forest technique, (e) XGboost technique, (f) Multilayer perceptron neural network technique. Figure 7d validates that the best performance corresponds to the Random forest technique.

3.2.4. Wind Speed Forecasting

Table 10. Evaluation metrics for wind speed forecasting.

Technique	Coefficient of Determination $\left({\mathbf{R}}^2\right)$	Mean Absolute Error (MAE) $\left[\mathbf{m}/\mathbf{s}\right]$	Mean Square Error (RMSE) $\left[\mathbf{m}/\mathbf{s}\right]$
Multiple linear regression	0.3428	0.1614	0.3354
Polynomial regression	0.3770	0.1428	0.3159
Decision tree	0.2142	0.1256	0.2705
Random forest	0.3660	0.1097	0.2136
XGboost	0.3866	0.1439	0.3131
Multilayer perceptron	0.3270	0.1654	0.3616

shows the results of the evaluation metrics: root mean square error (RMSE), mean absolute error (MAE), and coefficient of determination (${\mathrm{R}}^2$) for each of the techniques used for wind speed forecasting. The calculation of the root mean square error and mean absolute error was obtained by averaging the errors of the validation data (576 data), while the calculation of the coefficient of determination (${\mathrm{R}}^2$) used the data from the training set and the test set (93,780 data).

Table 10 shows that ${\mathrm{R}}^2$ obtained from the implemented algorithms converge to appropriate values, i.e., there is an acceptable approximation between the real wind speed and the predicted wind speed, thus guaranteeing the good performance of the algorithm, which allows a comparison of the performance in terms of forecast error. Comparison of the root mean square errors (RMSE) and mean absolute errors (MAE) and analysis of the coefficient of determination ${\mathrm{R}}^2$ of the different techniques implemented show that the best performing techniques for forecasting the wind speed variable are Random Forest with an ${\mathrm{R}}^2$ of 0.3660, MAE of 0.1097 $\mathrm{m}/\mathrm{s}$, and RMSE of 0.2136 $\mathrm{m}/\mathrm{s}$; and XGBoost with an ${\mathrm{R}}^2$ of 0.3866, MAE of 0.1439 $\mathrm{m}/\mathrm{s}$, and RMSE of 0.3131 $\mathrm{m}/\mathrm{s}$. It should be taken into account that due to the high variability of wind speed, the implemented techniques have a lower coefficient of determination compared to the other variables; however, forecasts with acceptable errors were obtained. In this case, the value of the mean absolute percentage errors (MAPE) is not taken into account because it is used only when it is known that the quantity to be predicted remains well above 0.

Figure 8 shows the real (red) and prediction (blue) profiles using the different Machine Learning techniques to predict the wind speed variable: (a) Multiple linear regression technique, (b) Polynomial regression technique, (c) Decision tree technique, (d) Random forest technique, (e) XGboost technique, (f) Multilayer perceptron neural network technique. Figure 8d validates that the best performance corresponds to the Random forest technique.

4. Conclusions

For the forecasting of meteorological variables in this research, information obtained from the Parque de la Familia Baños meteorological station located in Ecuador was used and the following prediction techniques were tested: multiple linear regression, polynomial regression, decision tree, random forest, XGBoost, and multilayer perceptron neural network. For forecasting the temperature variable, a better result is obtained by using Random Forest with an ${\mathrm{R}}^2$ of 0.8631, MAE of 0.4728 °C, MAPE of 2.73%, and RMSE of 0.6621 °C. In addition, XGBoost also performed well with an ${\mathrm{R}}^2$ of 0.8599, MAE of 0.5335 °C, MAPE of 3.09%, and RMSE of 0.7565 °C. For forecasting the relative humidity variable, a better result is obtained by using Random Forest with an ${\mathrm{R}}^2$ of 0.8583, MAE of 2.1380 RH, MAPE of 2.50%, and RMSE of 2.9003 RH. In addition, XGBoost also performed well with an ${\mathrm{R}}^2$ of 0.8597, MAE of 2.2907 RH, MAPE of 2.67%, and RMSE of 3.1444 RH. For forecasting the solar radiation variable, a better result is obtained by using Random Forest with an ${\mathrm{R}}^2$ of 0.7333, MAE of 65.8105 $\mathrm{W}/{\mathrm{m}}^2$, and RMSE of 105.9141 $\mathrm{W}/{\mathrm{m}}^2$. In addition, Decision Tree also performed well with an ${\mathrm{R}}^2$ of 0.7253, MAE of 75.8177 $\mathrm{W}/{\mathrm{m}}^2$, and RMSE of 127.3530 $\mathrm{W}/{\mathrm{m}}^2$. For forecasting the wind speed variable, a better result is obtained by using Random Forest, with an ${\mathrm{R}}^2$ of 0.3660, MAE of 0.1097 $\mathrm{m}/\mathrm{s}$, and RMSE of 0.2136 $\mathrm{m}/\mathrm{s}$. In addition, XGBoost also performed well, with an ${\mathrm{R}}^2$ of 0.3866, MAE of 0.1439 $\mathrm{m}/\mathrm{s}$, and RMSE of 0.3131 $\mathrm{m}/\mathrm{s}$.

It can be observed that wind speed has the highest variability compared to the other predicted variables, therefore, the results of the techniques implemented show that the coefficient of determination ${\mathrm{R}}^2$ of this variable has a lower value. This is due to the type of signal we are trying to predict; however, acceptable predictions were obtained.

The prediction of meteorological variables (temperature, solar radiation, wind speed, and relative humidity) will allow future projects to be implemented in the study area, such as intelligent agriculture to support food problems in that area and the implementation of a microgrid based on renewable resources where prediction models will support the planning and operation of the microgrid in real time, allowing clean energy to this locality, contributing to the reduction in the use of fossil resources, which is the goal that different countries have set as part of their policies.