Flexible Frequency Response Strategy with Smooth Rotor Speed Recovery of a DFIG-Based Wind Turbine
Abstract
:1. Introduction
- Different stepwise inertial control schemes are analyzed.
- The incremental power of the proposed scheme is calculated based on the maximum dfsys/dt.
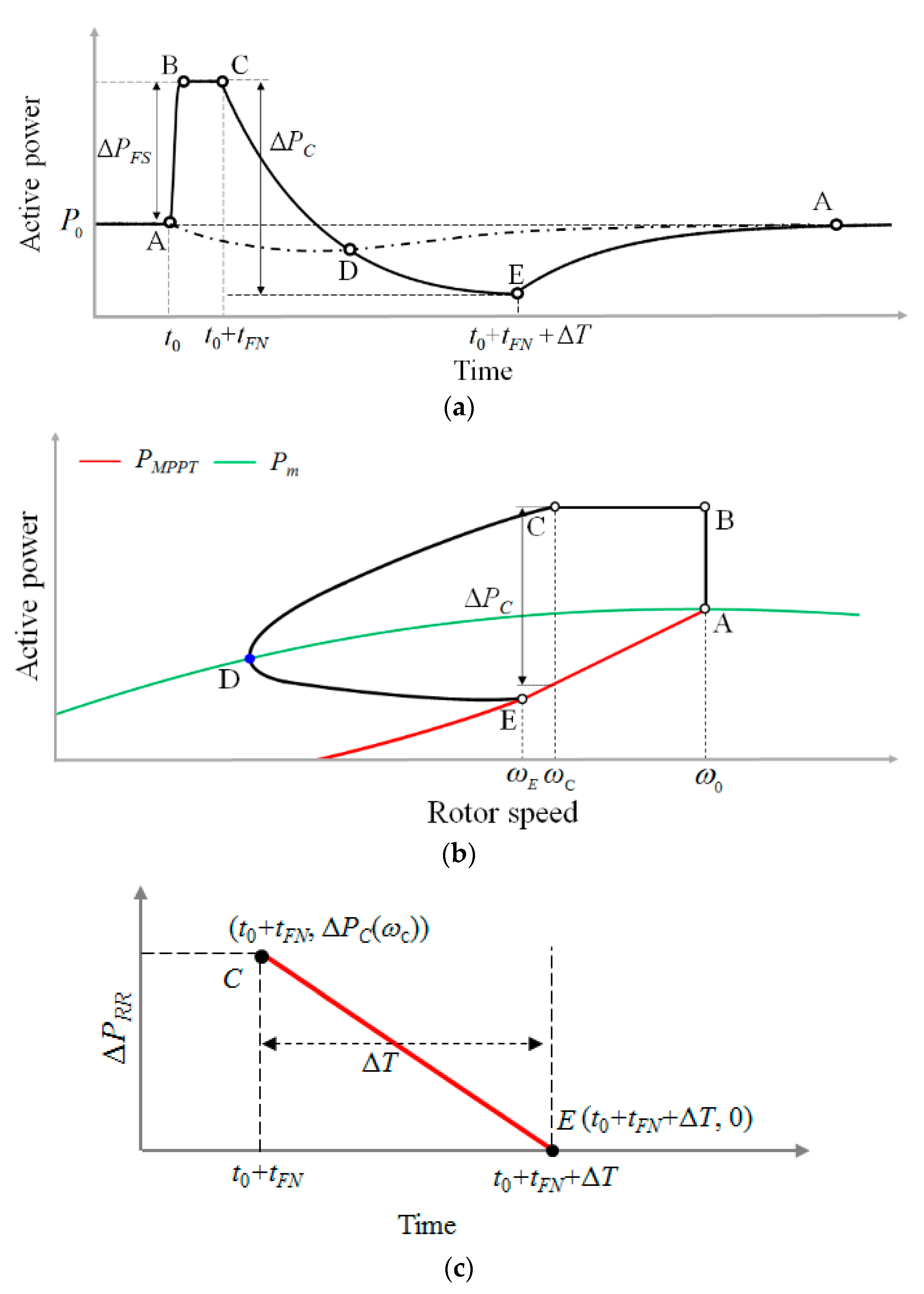
- The rotor speed recovery strategy is proposed to address the second frequency drop and speed recovery.
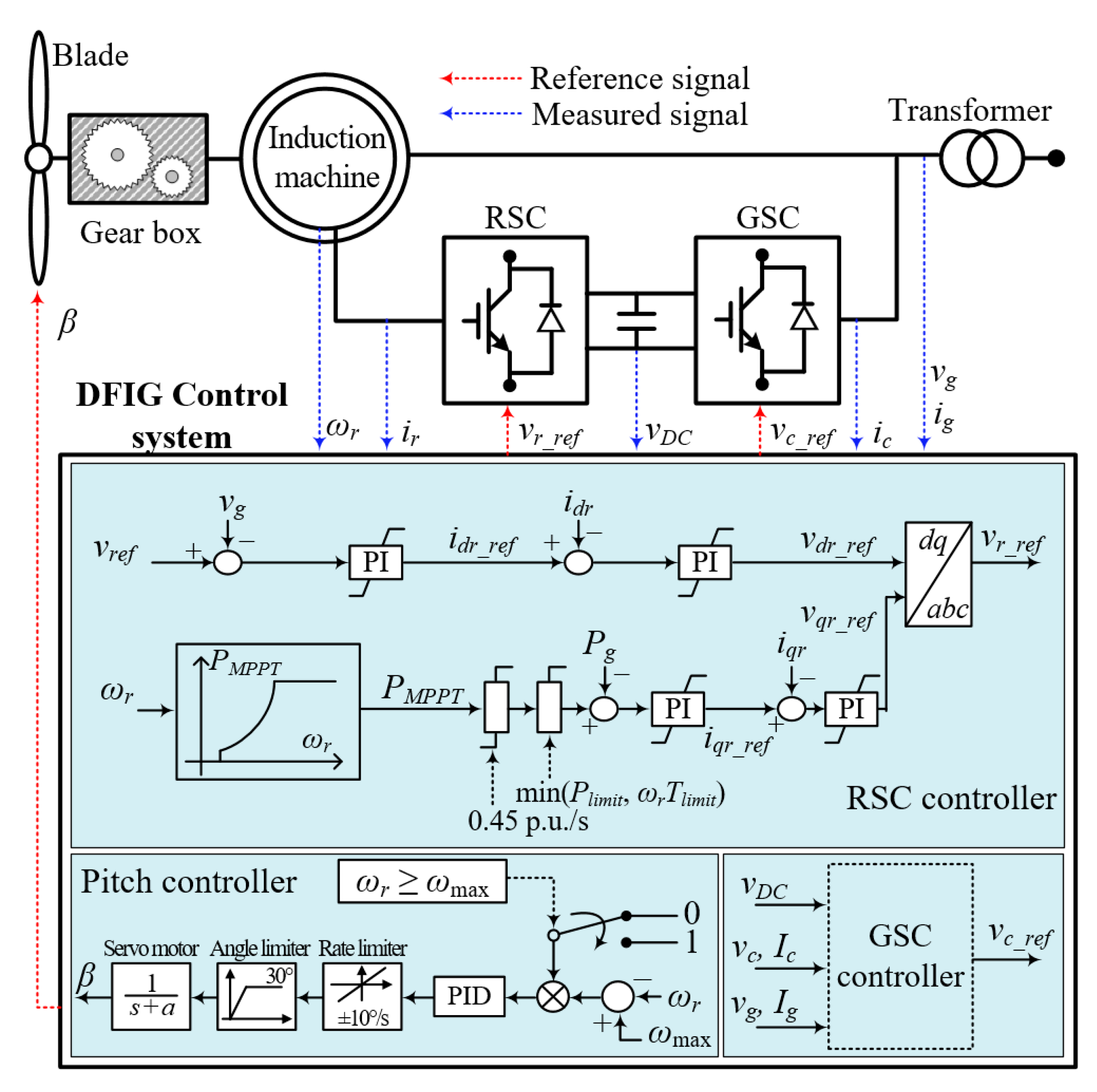
2. Modeling of a Doubly Fed Induction Generator
3. Stepwise Inertial Control of a DFIG for System Frequency Support
3.1. Conventional Inertial Control for System Frequency Support
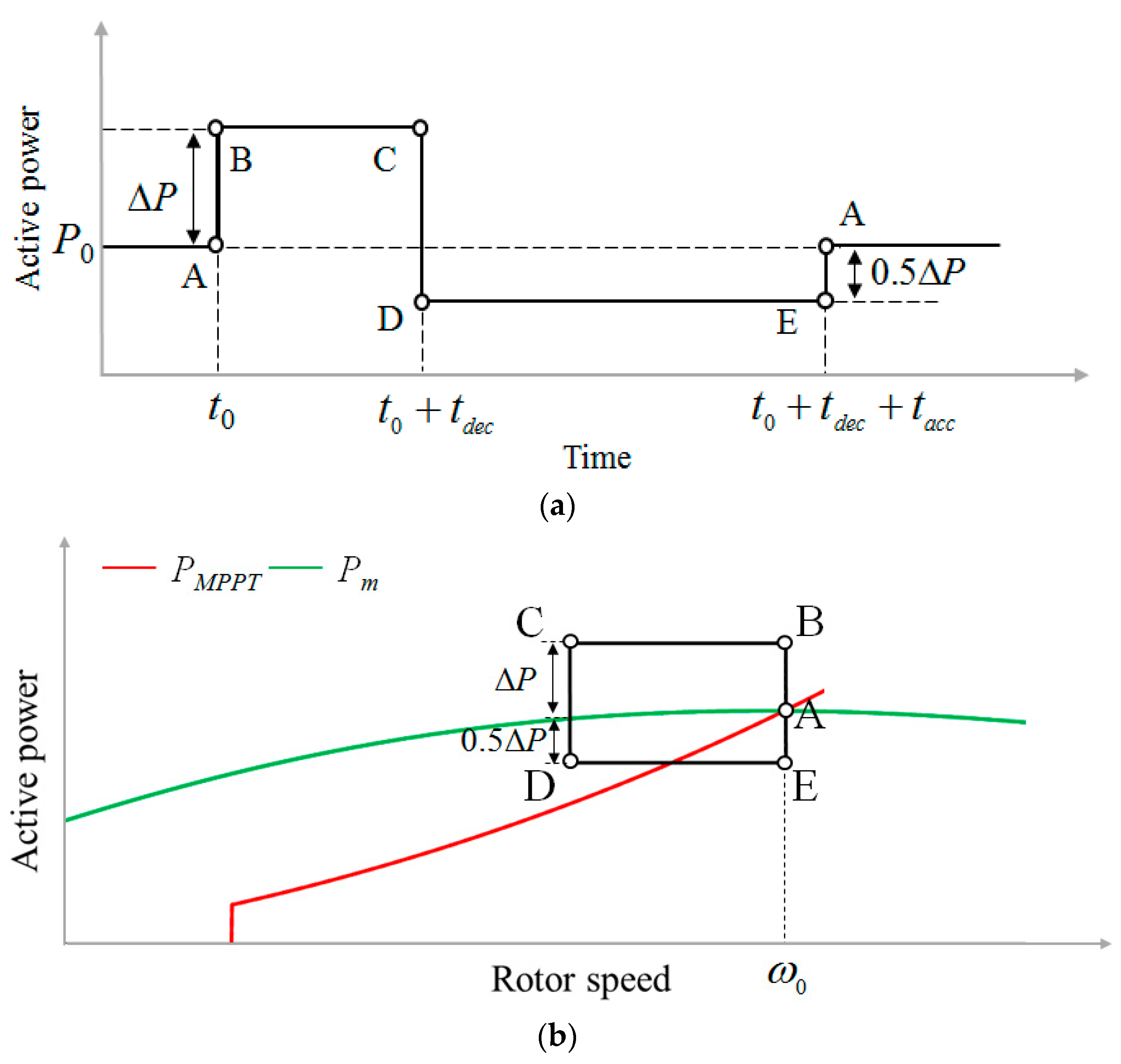
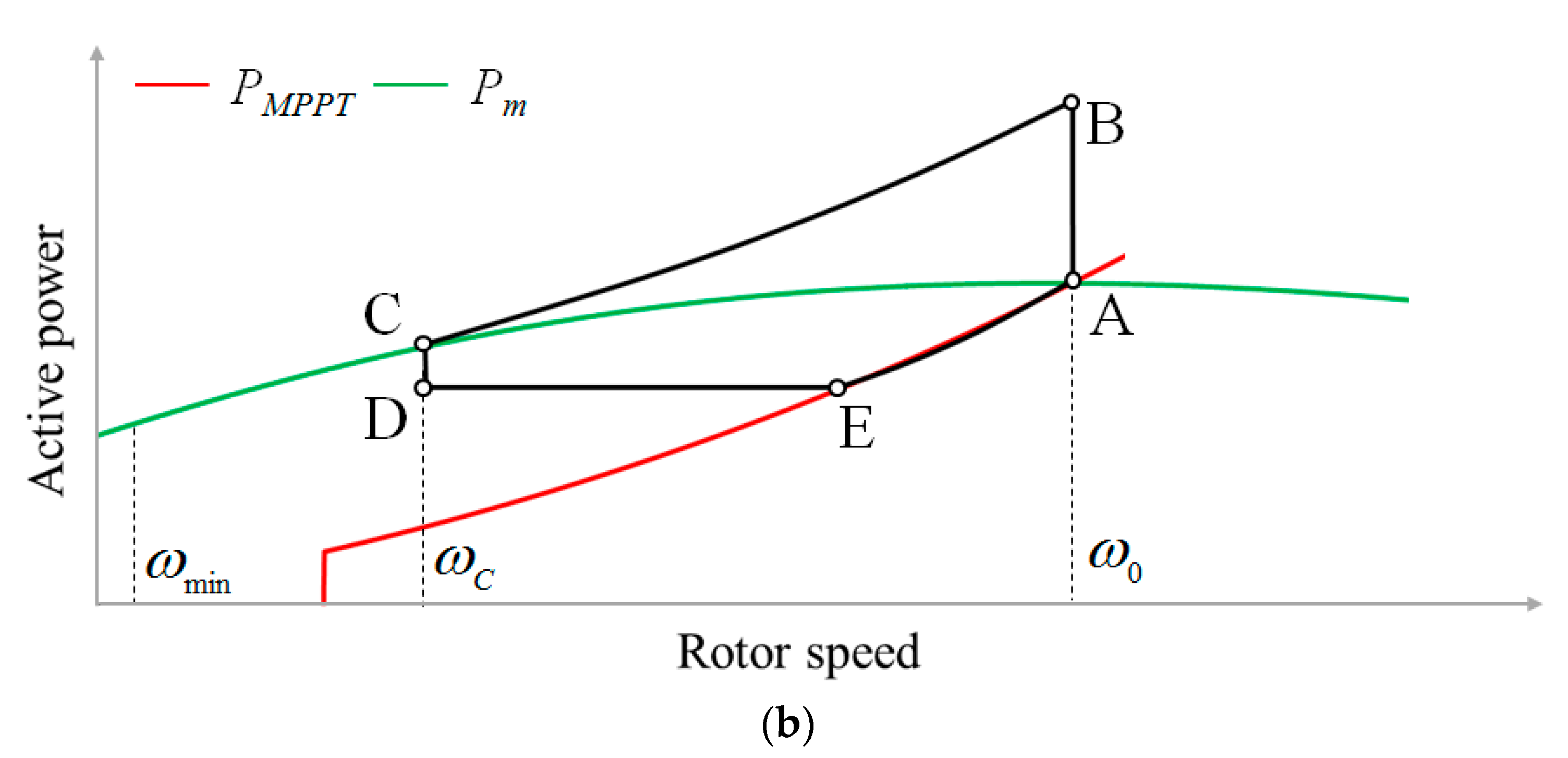
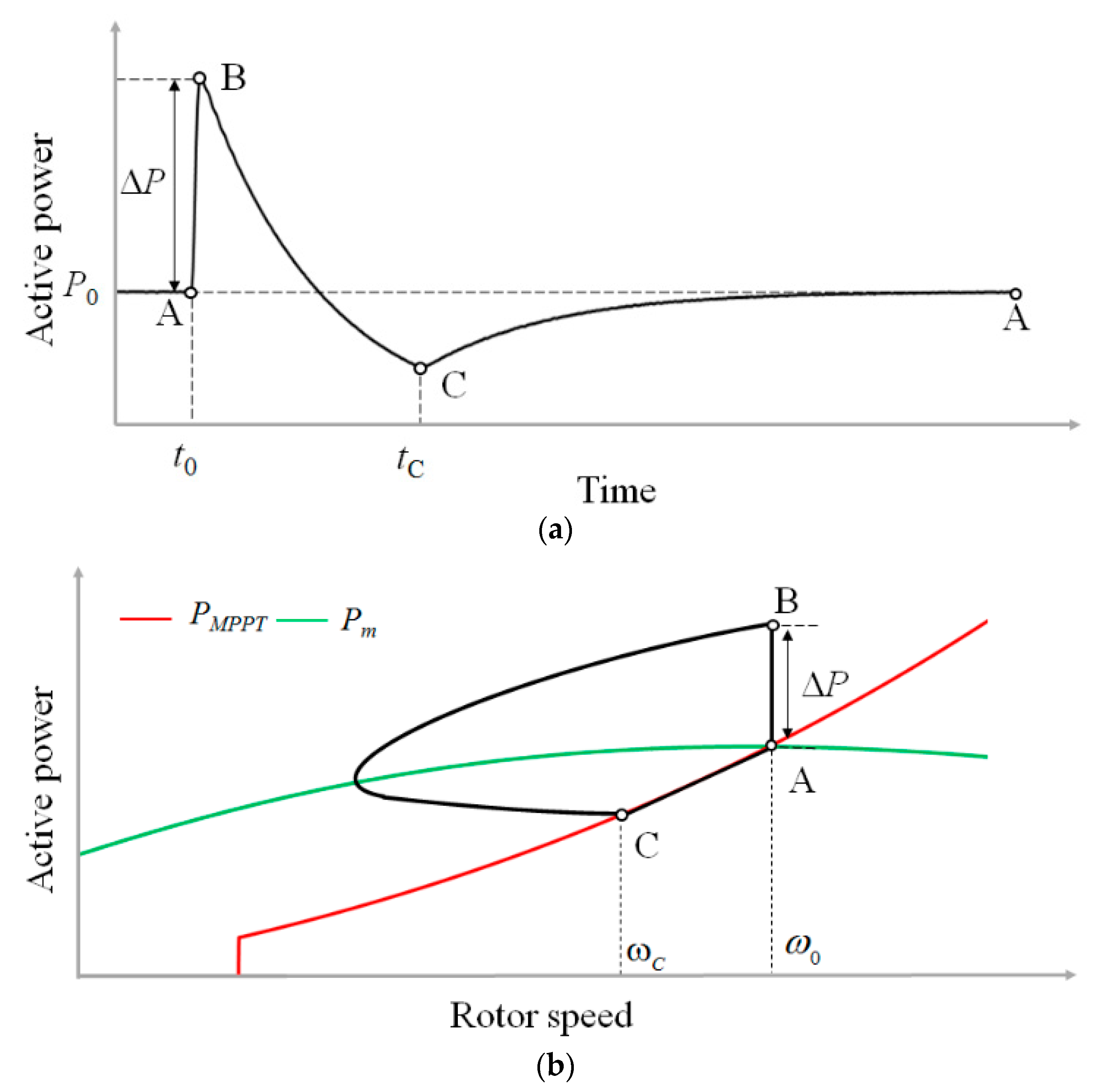
3.1.1. SIC #1
3.1.2. SIC #2
3.1.3. SIC #3
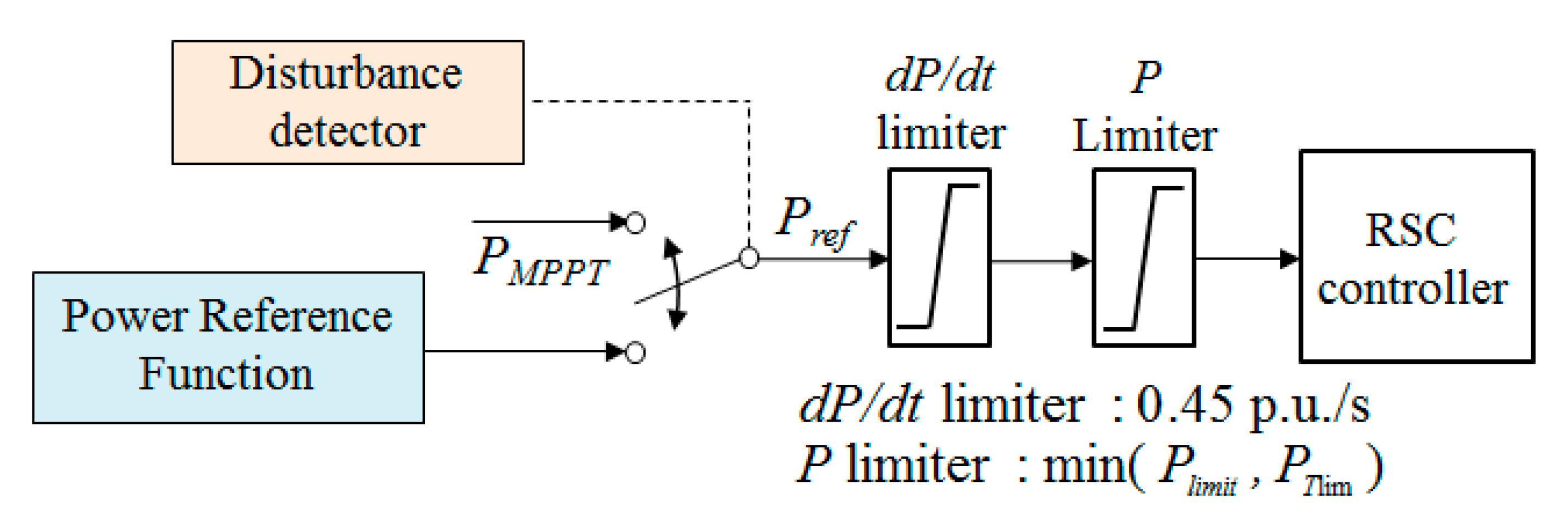
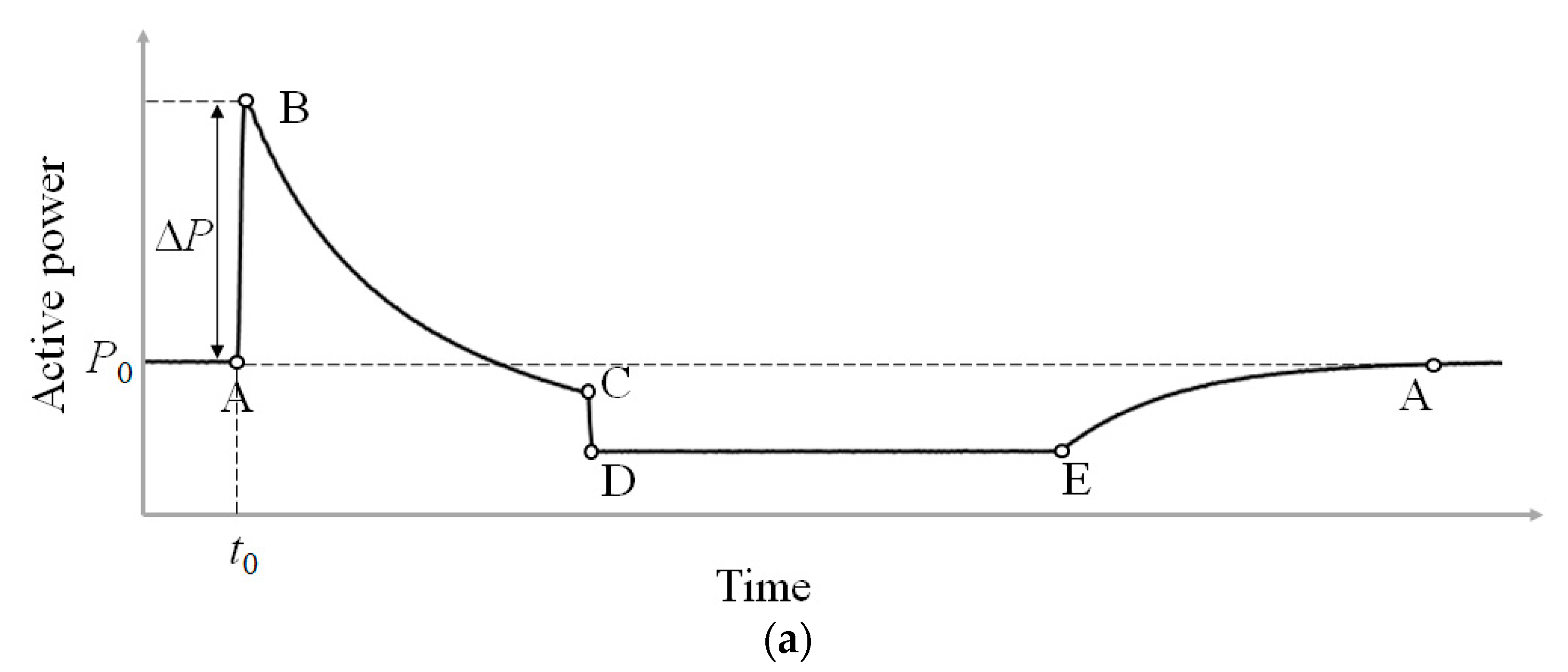
3.2. Proposed Inertial Control for System Frequency Support
4. Model System and Simulation Results
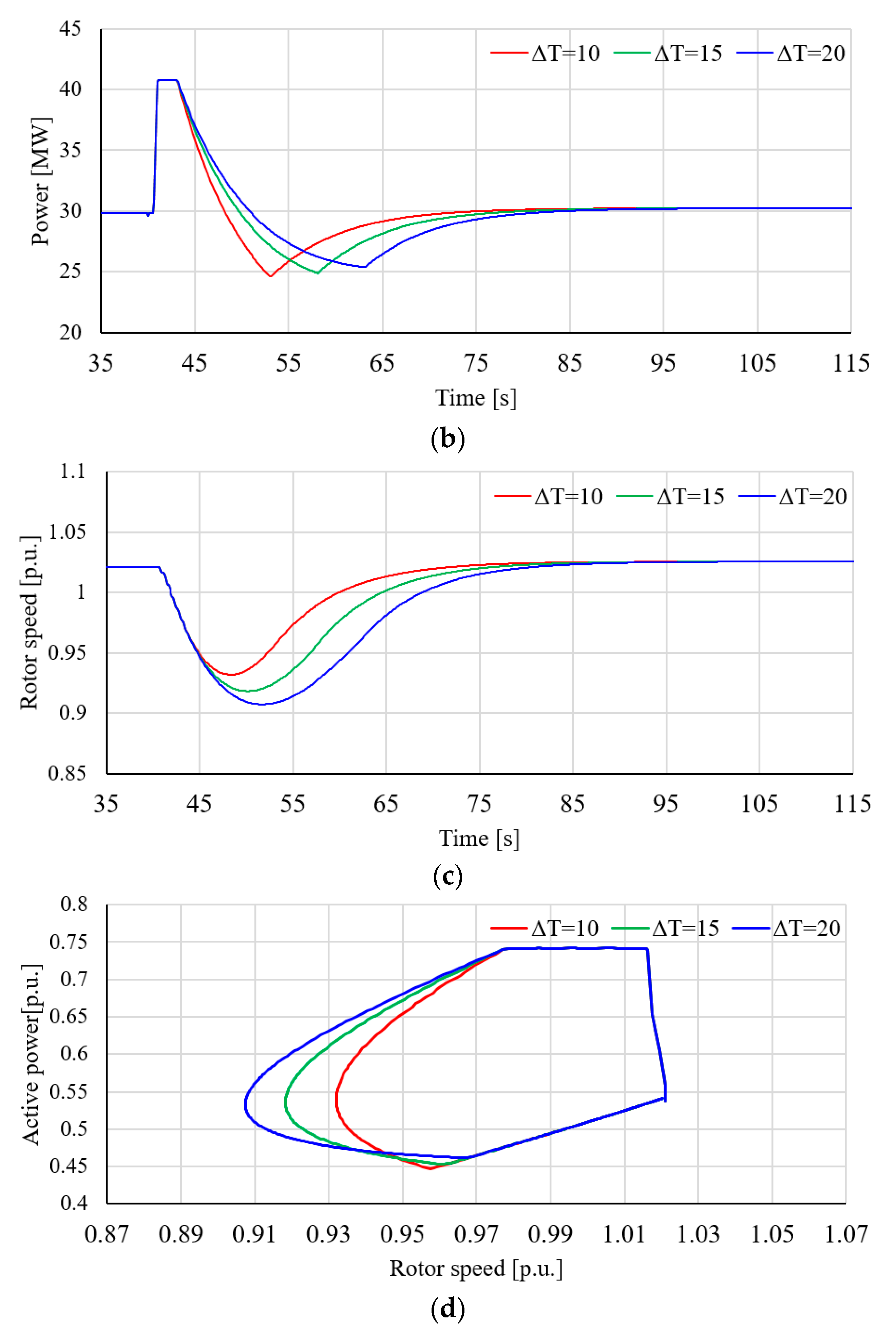
4.1. Case 1: Wind Speed = 9.0 m/s, Disturbance = 50 MW, and Wind Penetration = 10% with Proposed SIC with Various ΔT
4.2. Case 2: Wind Speed = 9.0 m/s, Wind Penetration = 10%, and Disturbance = 50 MW with Different SIC Methods
4.3. Case 3: Wind Speed = 9.0 m/s, Wind Penetration = 10%, and Disturbance = 90 MW with Different SIC Methods
4.4. Case 4: Wind Speed = 9.0 m/s, Wind Penetration = 20%, and Disturbance = 90 MW with Different SIC Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kheshti, M.; Lin, S.; Zhao, X.; Ding, L.; Yin, M.; Terzija, V. Gaussian Distribution-Based Inertial Control of Wind Turbine Generators for Fast Frequency Response in Low Inertia Systems. IEEE Trans. Sustain. Energy 2022, 13, 1641–1653. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, D.; Hu, J.; Zou, X.; Kang, Y.; Guerrero, J.M. Inertial PLL of Grid-Connected Converter for Fast Frequency Support. CSEE J. Power Energy Syst. 2022. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, L.; Liu, X.; Liu, Y. Frequency trajectory planning based strategy for improving frequency stability of droop-controlled inverter based standalone power systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 176–187. [Google Scholar] [CrossRef]
- Abuagreb, M.; Ajao, B.; Herbert, H.; Johnson, B.K. Evaluation of Virtual Synchronous Generator Compared to Synchronous Generator. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Duan, Q.; Zhao, C. Improved VSG Controlled SST in a Low-Voltage AC Distribution Network. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 25–27 November 2021; pp. 428–435. [Google Scholar]
- Hydro Québec TransÉnergie. Transmission Provider Technical Requirements for the Connection of Power Plants to the Hydro Québec Transmission System; Hydro Québec: Montréal, QC, Canada, 2009. [Google Scholar]
- National Grid UK. Grid Code Review Panel Paper, Future Frequency Response Services; National Grid: London, UK, 2010. [Google Scholar]
- Yang, D.; Yan, G.-G.; Zheng, T.; Zhang, X.; Hua, L. Fast Frequency Response of a DFIG Based on Variable Power Point Tracking Control. IEEE Trans. Ind. Appl. 2022, 58, 5127–5135. [Google Scholar] [CrossRef]
- Bao, W.; Ding, L.; Kang, Y.C.; Sun, L. Closed-loop synthetic inertia control for wind turbine generators in association with slightly over-speed deloading operation. IEEE Trans. Power Syst. 2023; early access. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, X.; Liu, H.; Liu, Y. Performance comparison of typical frequency response strategies for power systems with high penetration of renewable energy sources. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 41–47. [Google Scholar] [CrossRef]
- Lyu, X.; Zhao, Y.; Groß, D.; Liu, T. Receding horizon control based secondary frequency regulation for power systems with wind energy integration. Int. J. Electr. Power Energy Syst. 2022, 142, 108282. [Google Scholar] [CrossRef]
- Ye, Y.; Qiao, Y.; Lu, Z. Revolution of frequency regulation in the converter-dominated power system. Renew. Sustain. Energy Rev. 2019, 111, 145–156. [Google Scholar] [CrossRef]
- Ullah, N.R.; Thiringer, T.; Karlsson, D. Temporary primary frequency control support by variable speed wind turbines—Potential and applications. IEEE Trans. Power Syst. 2008, 23, 601–612. [Google Scholar] [CrossRef]
- Kheshti, M.; Ding, L.; Nayeripour, M.; Wang, X.; Terzija, V. Active power support of wind turbines for grid frequency events using a reliable power reference scheme. Renew. Energy 2019, 139, 1421–1454. [Google Scholar] [CrossRef]
- Yang, D.; Kim, J.; Kang, Y.C.; Muljadi, E.; Zhang, N.; Hong, J.; Song, S.-H.; Zheng, T. Temporary frequency support of a DFIG for high wind power penetration. IEEE Trans. Power Syst. 2018, 33, 3428–3437. [Google Scholar] [CrossRef]
- Lao, H.; Zhang, L.; Zhao, T.; Zou, L. Innovated inertia control of DFIG with dynamic rotor speed recovery. CSEE J. Power Energy Syst. 2022, 5, 1417–1427. [Google Scholar]
- Hafiz, F.; Abdennour, A. Optimal use of kinetic energy for the inertial support from variable speed wind turbines. Renew. Energy 2015, 80, 629–643. [Google Scholar] [CrossRef]
- Liu, K.; Qu, Y.; Kim, H.-M.; Song, H. Avoiding frequency second dip in power unreserved control during wind power rotational speed recovery. IEEE Trans. Power Syst. 2018, 33, 3097–3106. [Google Scholar] [CrossRef]
- Kang, M.; Muljadi, E.; Hur, K.; Kang, Y.C. Stable adaptive inertial control of a doubly-fed induction generator. IEEE Trans. Smart Grid 2016, 7, 2971–2979. [Google Scholar] [CrossRef]
- Yang, D.; Jin, Z.; Zheng, T.; Jin, E. An adaptive droop control strategy with smooth rotor speed recovery capability for type III wind turbine generators. Int. J. Electr. Power Energy Syst. 2022, 135, 107532. [Google Scholar] [CrossRef]
- Fernandez, L.M.; Garcia, C.A.; Jurado, F. Comparative study on the performance of control systems for doubly fed induction generator wind turbines operating with power regulation. Energy 2008, 33, 1438–1452. [Google Scholar] [CrossRef]
- Boukhezzar, B.; Siguerdidjane, H. Nonlinear control of a variable speed wind turbine using a two mass model. IEEE Trans. Energy Convers. 2010, 26, 149–161. [Google Scholar] [CrossRef]
- Ajjarapu, V.; McCalley, J.D.; Rover, D.; Wang, Z.; Wu, Z. Novel Sensorless Generator Control and Grid Fault Ride-Through Strategies for Variable-Speed Wind Turbines and Implementation on A New Real-Time Simulation Platform. Ph.D. Dissertation, Department of Electrical and Computer Engineering, Iowa State University, Ames, IA, USA, 2010. [Google Scholar]
- Abuagreb, M.; Allehyani, M.; Johnson, B.K. Design and Test of a Combined PV and Battery System under Multiple Load and Irradiation Conditions. In Proceedings of the 2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2019; pp. 1–5. [Google Scholar]
- Chauhan, U.; Singh, V.; Kumar, B.; Rani, A. An improved MVO assisted global MPPT algorithm for partially shaded PV system. J. Intell. Fuzzy Syst. 2020, 38, 6715–6726. [Google Scholar] [CrossRef]
- Abuagreb, M.; Ajao, B.; Johnson, B.K. Implementation of Emulated Inertia using PV Generation with Energy Storage to Improve Integrated Grid Response. In Proceedings of the 2020 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 6–7 February 2020; pp. 1–6. [Google Scholar]
- Allehyani, M.F.; Abuagreb, M.; Johnson, B.K. The Effect of Frequency Droop Damping on System Parameters and Battery Sizing during Load Change Condition. In Proceedings of the 2022 International Conference on Electrical, Computer and Energy Technologies (ICECET), Prague, Czech Republic, 20–22 July 2022; pp. 1–5. [Google Scholar]



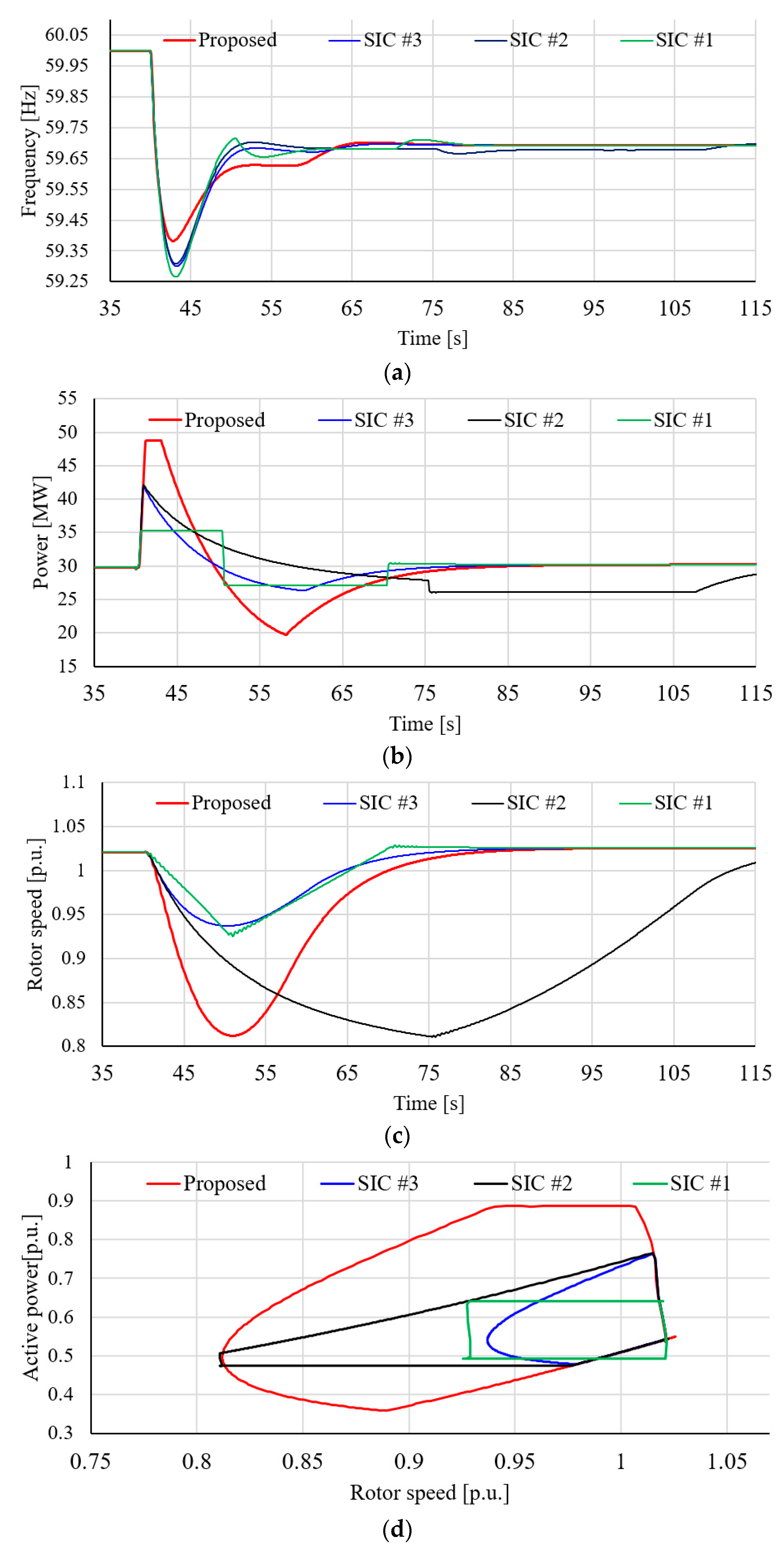
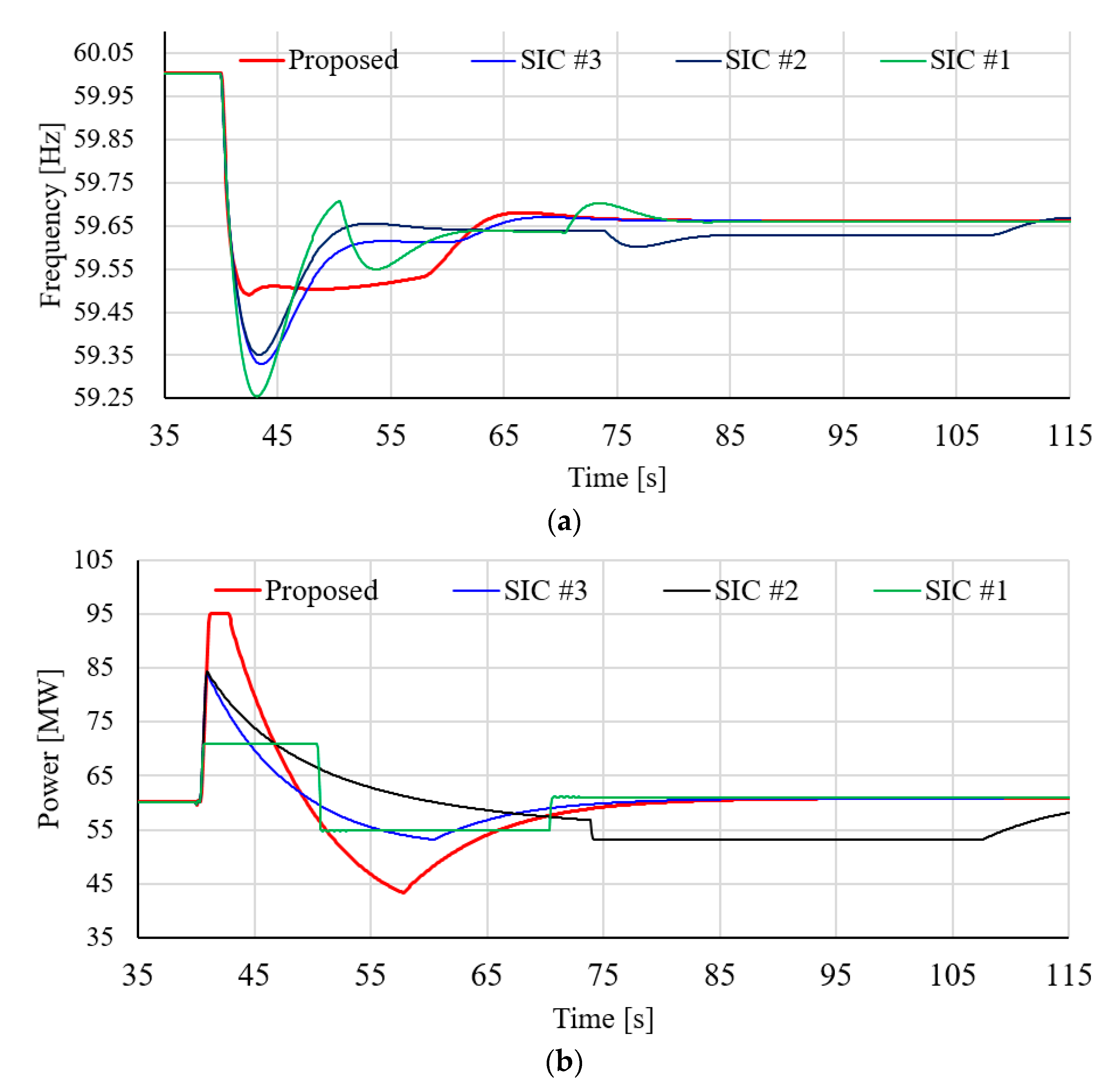
| Methods | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| Frequency nadir (Hz) | SIC #1 | 59.624 | 59.266 | 59.255 |
| SIC #2 | 59.669 | 59.308 | 59.35 | |
| SIC #3 | 59.661 | 59.303 | 59.338 | |
| Proposed SIC | 59.671 | 59.382 | 59.49 | |
| Second frequency nadir (Hz) | SIC #1 | 59.783 | 59.655 | 59.549 |
| SIC #2 | 59.803 | 59.666 | 59.577 | |
| SIC #3 | - | - | - | |
| Proposed SIC | - | - | - | |
| Nadir-based frequency response (MW/Hz) | SIC #1 | 133 | 122.6 | 120.8 |
| SIC #2 | 151.1 | 130.1 | 174.4 | |
| SIC #3 | 147.5 | 129.1 | 166.7 | |
| Proposed SIC | 152 | 145.6 | 177 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, X.; Sang, S.; Huang, J. Flexible Frequency Response Strategy with Smooth Rotor Speed Recovery of a DFIG-Based Wind Turbine. Electronics 2023, 12, 794. https://doi.org/10.3390/electronics12040794
Xue X, Sang S, Huang J. Flexible Frequency Response Strategy with Smooth Rotor Speed Recovery of a DFIG-Based Wind Turbine. Electronics. 2023; 12(4):794. https://doi.org/10.3390/electronics12040794
Chicago/Turabian StyleXue, Xiaocen, Shun Sang, and Jiejie Huang. 2023. "Flexible Frequency Response Strategy with Smooth Rotor Speed Recovery of a DFIG-Based Wind Turbine" Electronics 12, no. 4: 794. https://doi.org/10.3390/electronics12040794
APA StyleXue, X., Sang, S., & Huang, J. (2023). Flexible Frequency Response Strategy with Smooth Rotor Speed Recovery of a DFIG-Based Wind Turbine. Electronics, 12(4), 794. https://doi.org/10.3390/electronics12040794







