3D Imaging with Fringe Projection for Food and Agricultural Applications—A Tutorial
Abstract
:1. Introduction
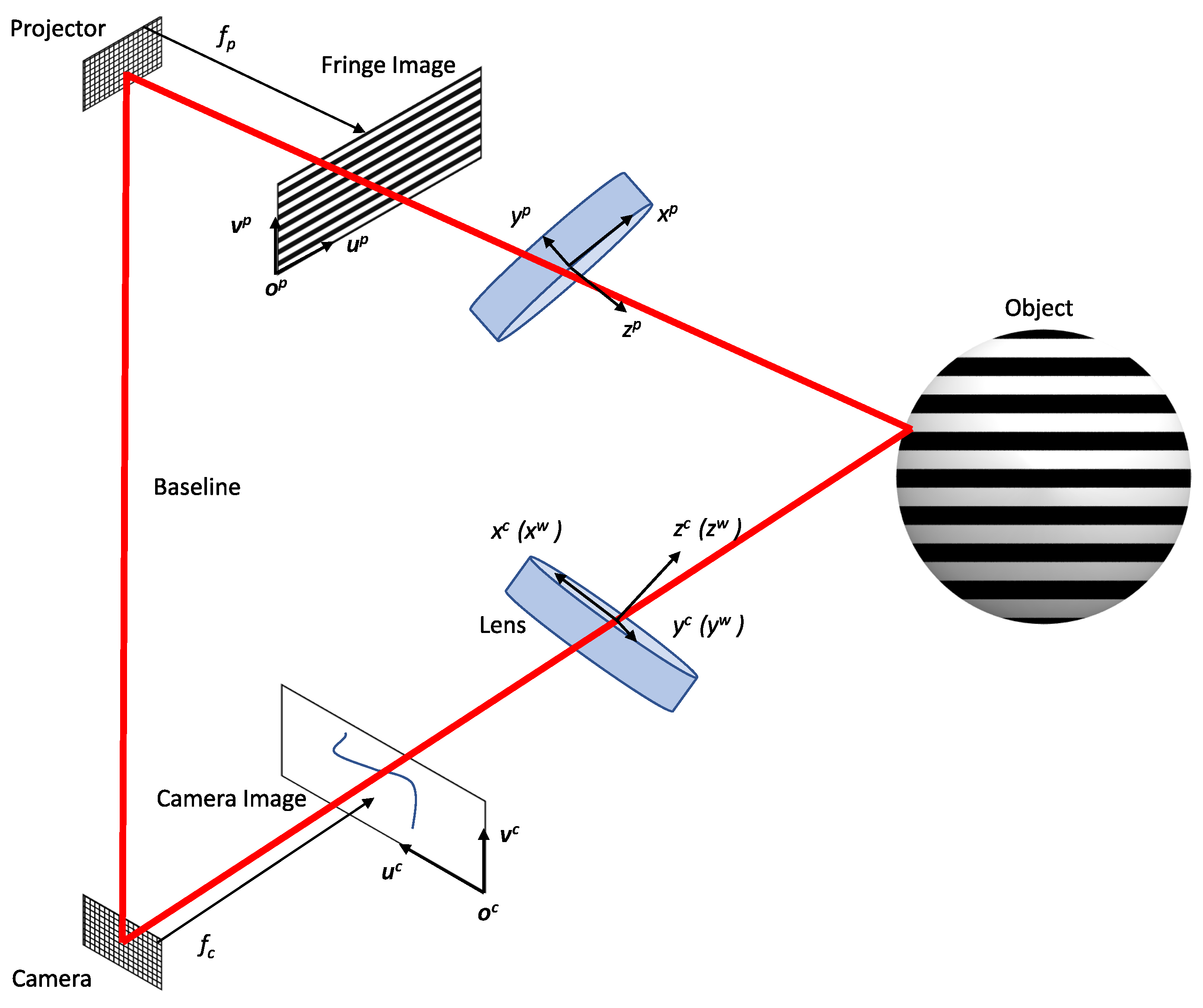
2. Principles of Fringe Projection Profilometry (FPP)
2.1. Fringe Pattern Generation
2.1.1. Digital Methods
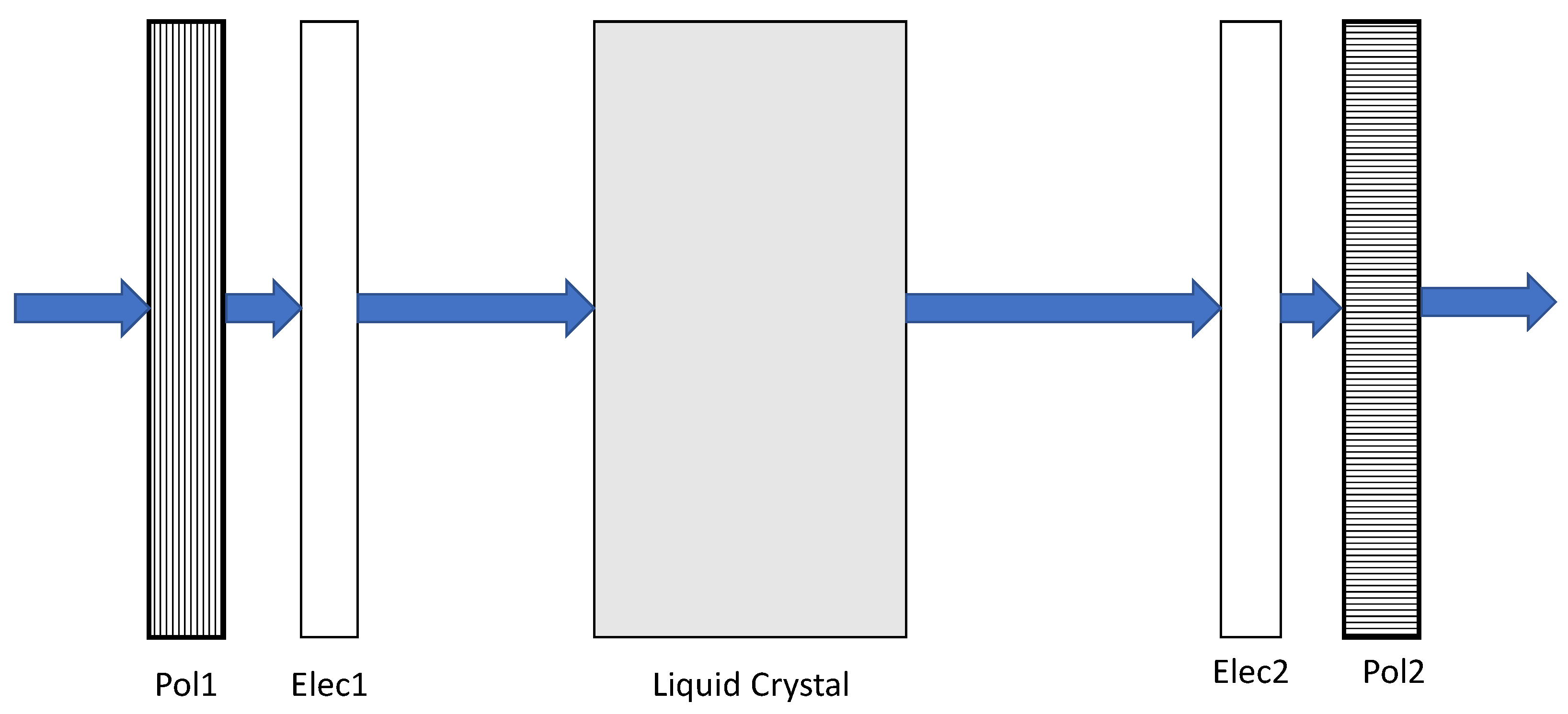
Liquid Crystal Display (LCD)
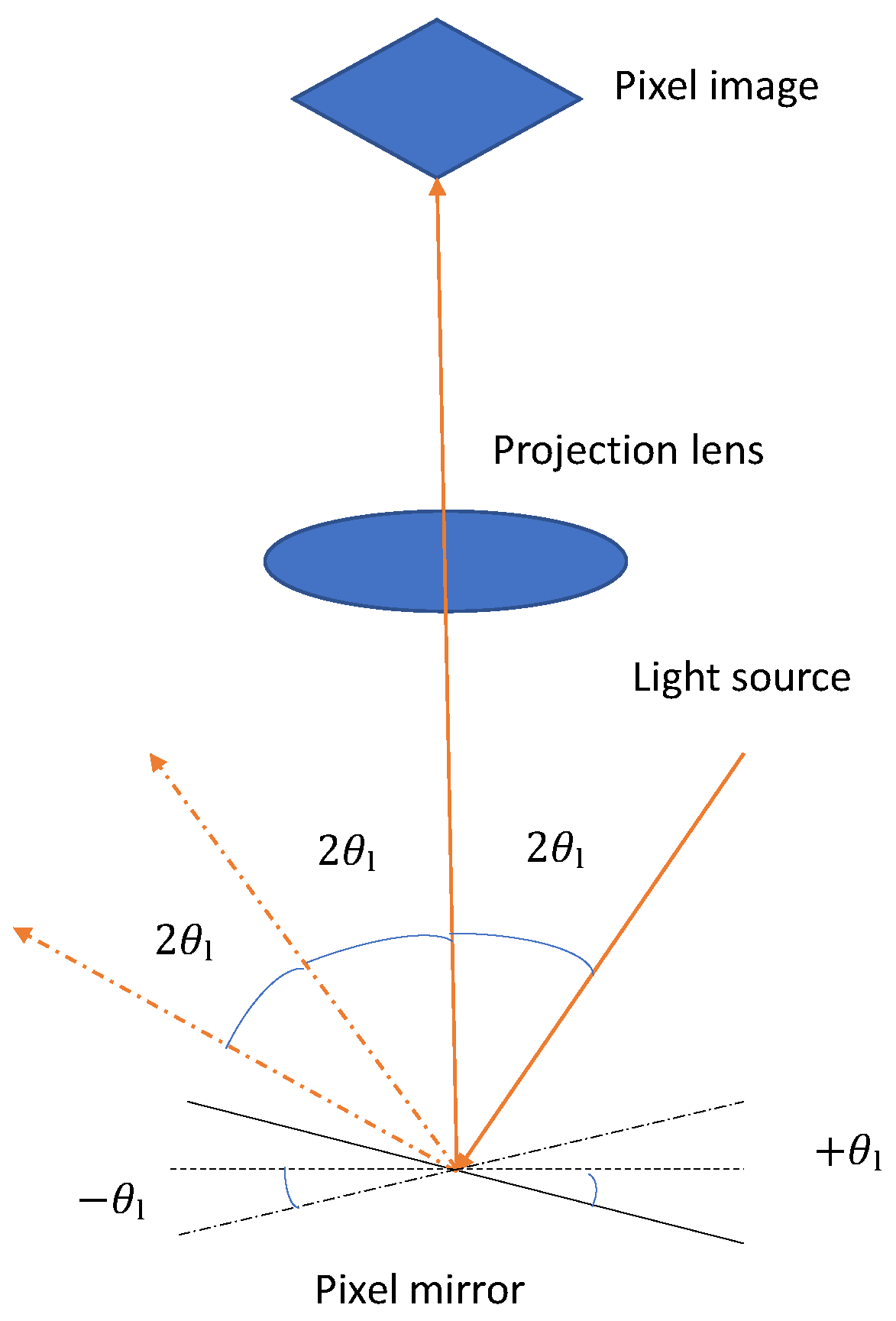
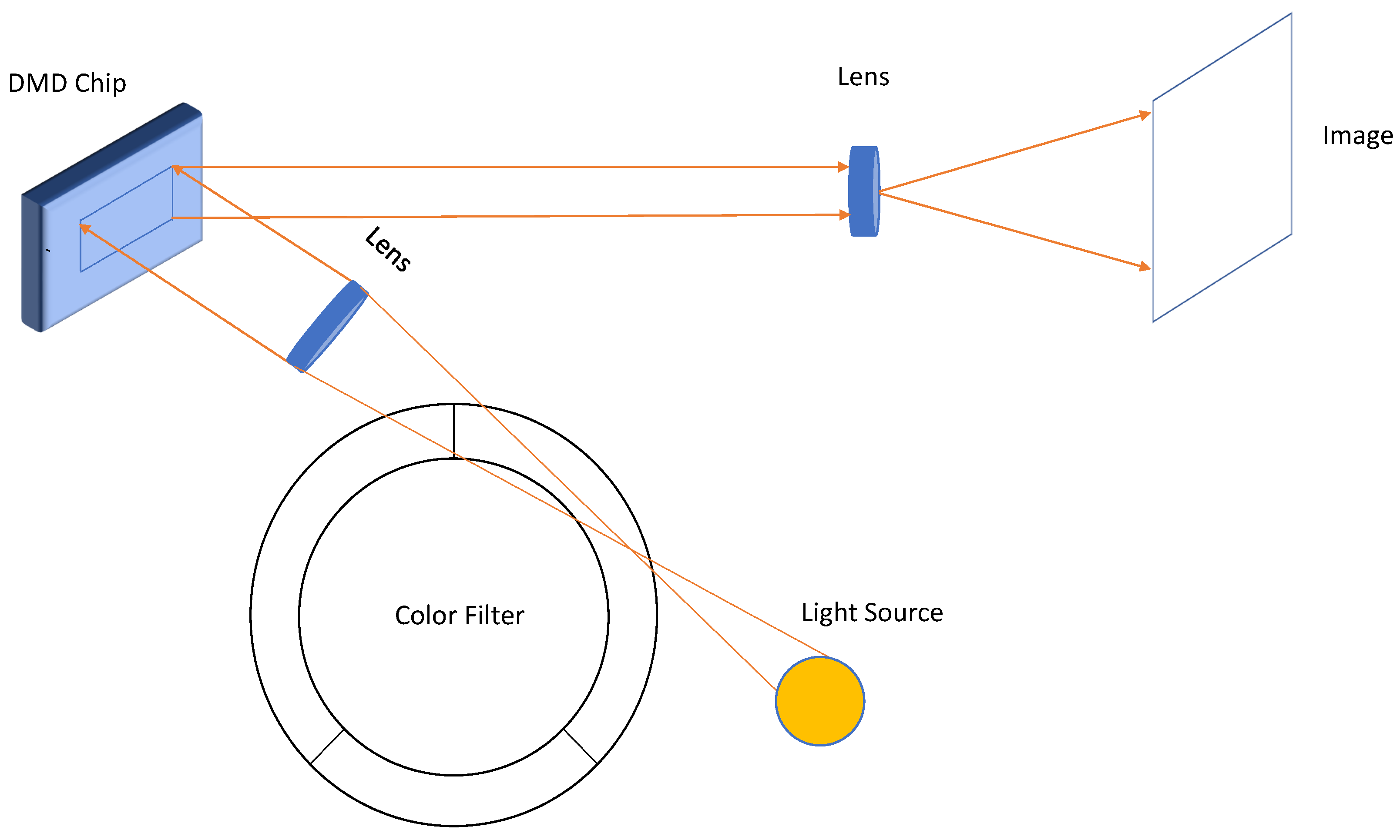
Digital Light Processing (DLP)
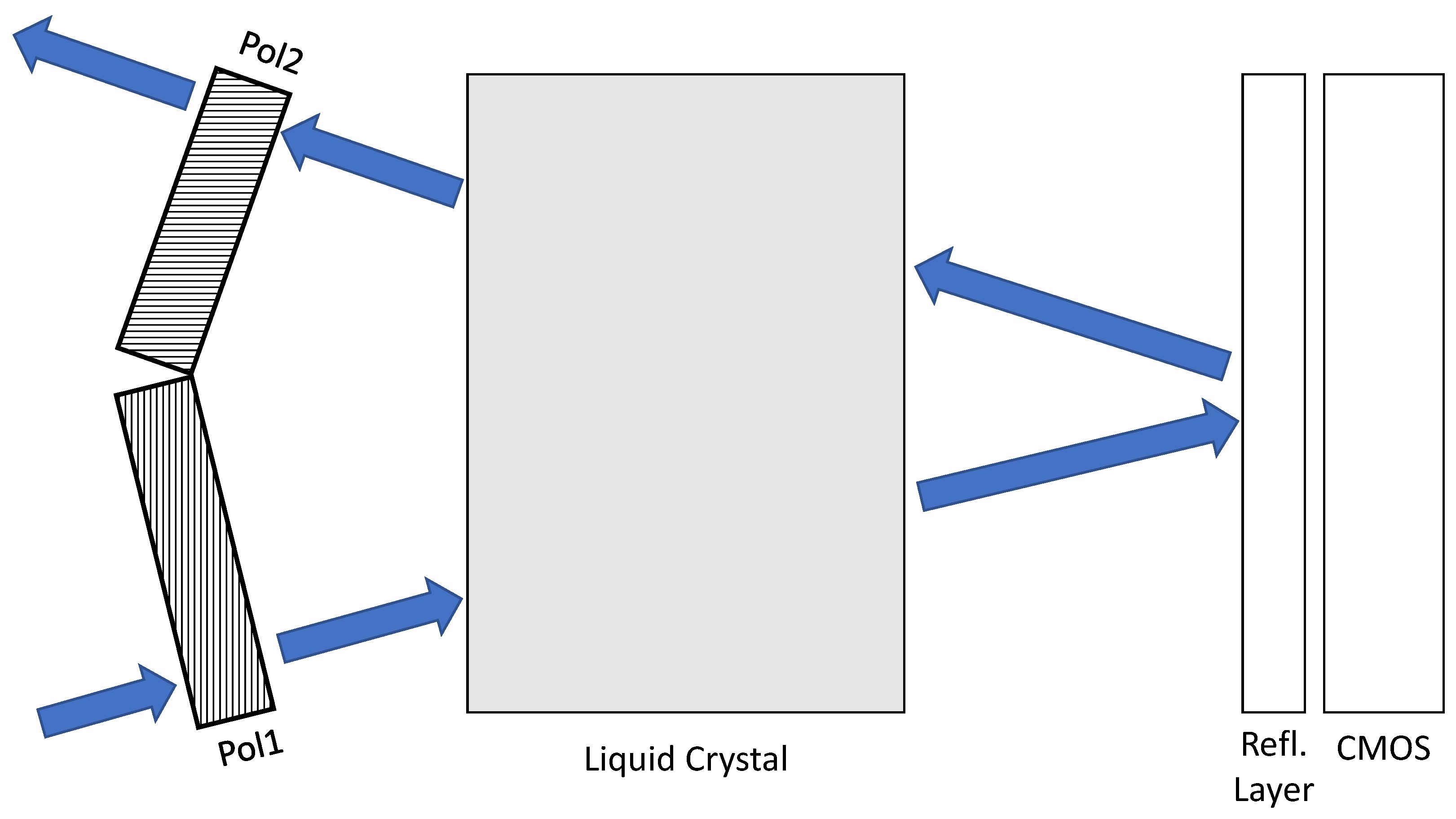
Liquid Crystal on Silicon (LCoS)
2.1.2. Performance Comparison of Digital Methods
Image Contrast
Grayscale Generation Speed
Color Generation Speed
Camera-Projector Synchronization
2.2. Fringe Image Analysis
2.2.1. Standard N-Step Phase Shifting Algorithm
2.3. Phase Unwrapping
2.3.1. Multi-Frequency Phase Unwrapping Algorithm
2.4. Calibration
2.5. 3D Reconstruction
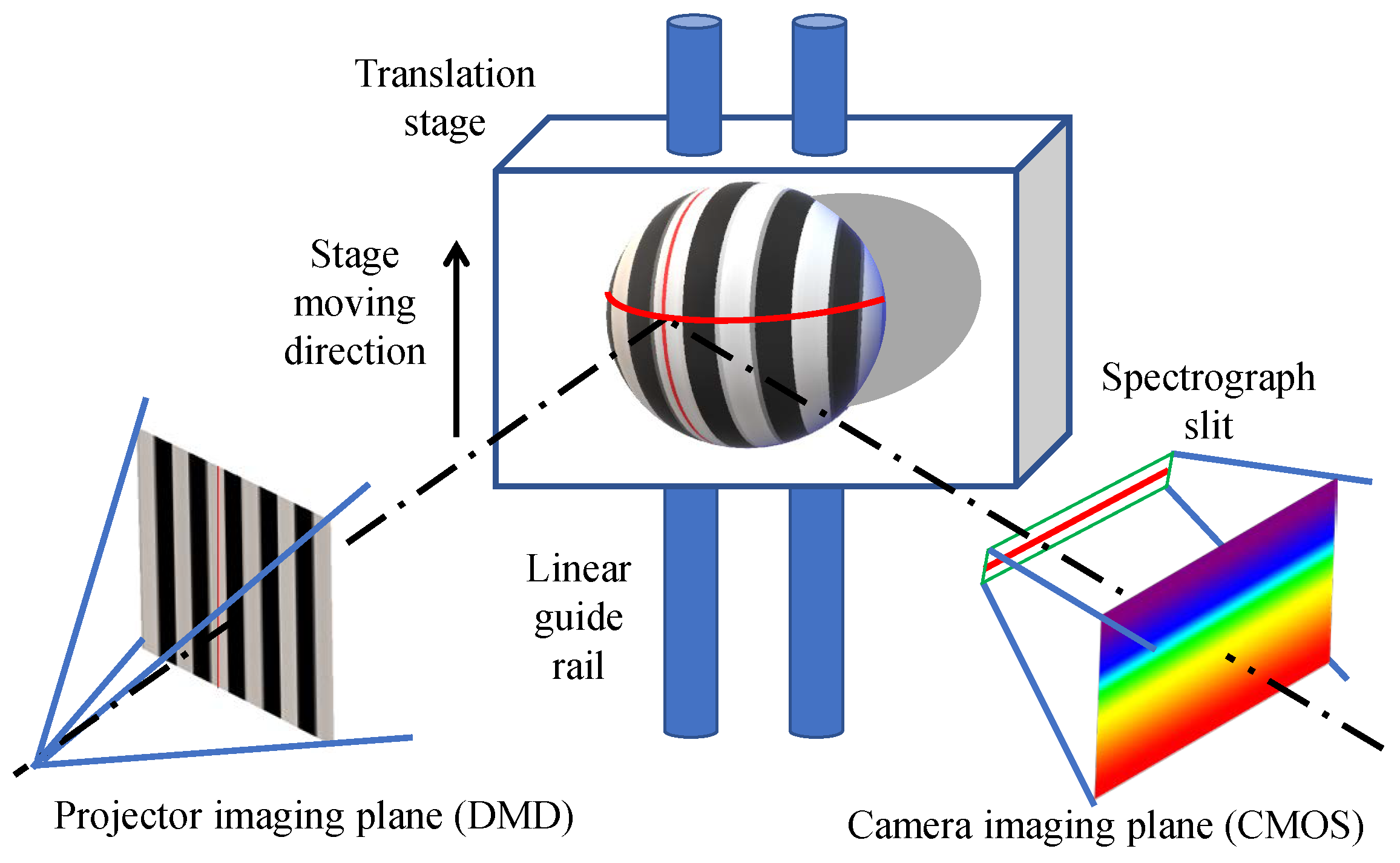
3. Hyperspectral 4D Imaging Based on FPP
4. Example Results
4.1. Example Application of 3D Imaging with FPP—Plant Phenotyping
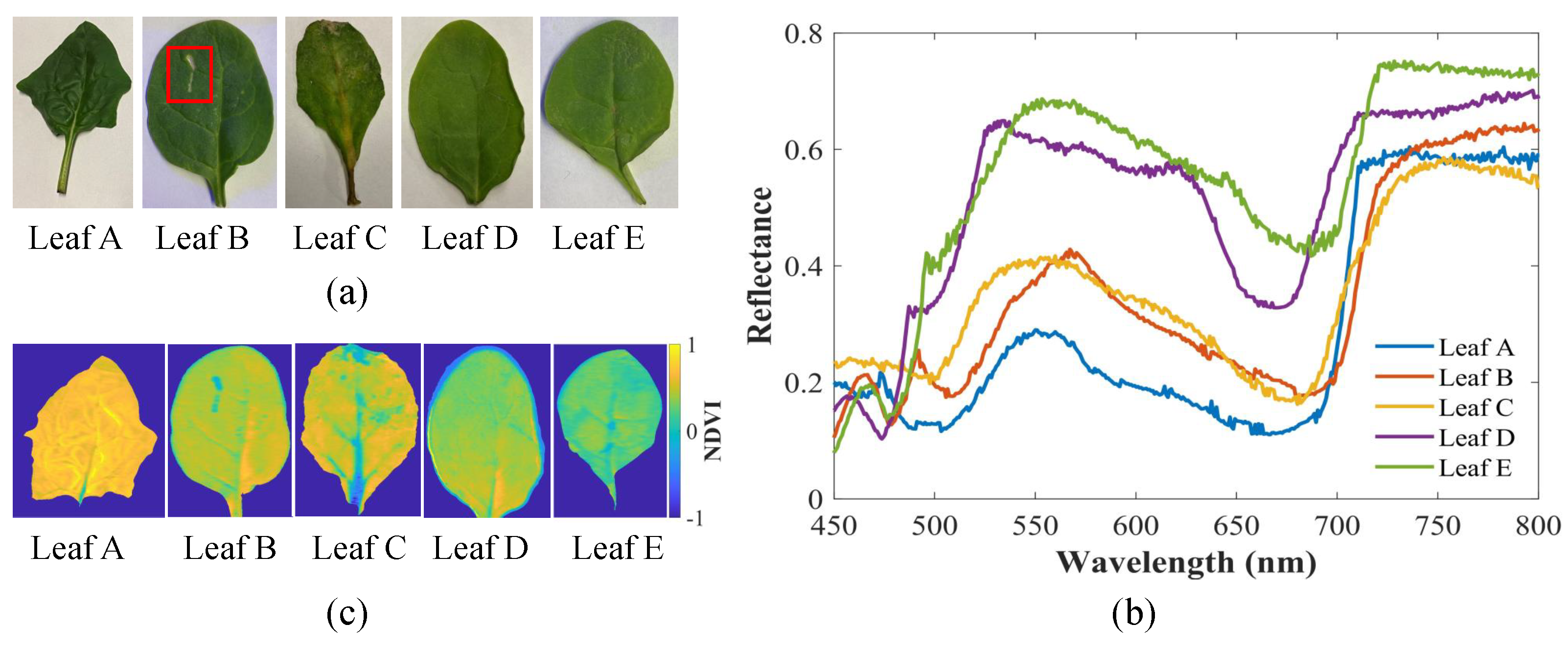
4.2. Example Application of 4D Imaging with FPP—Leafy Greens Nondestructive Evaluations
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giampieri, F.; Mazzoni, L.; Cianciosi, D.; Alvarez-Suarez, J.M.; Regolo, L.; Sánchez-González, C.; Capocasa, F.; Xiao, J.; Mezzetti, B.; Battino, M. Organic vs conventional plant-based foods: A review. Food Chem. 2022, 383, 132352. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Li, C. A modular agricultural robotic system (MARS) for precision farming: Concept and implementation. J. Field Robot. 2022, 39, 387–409. [Google Scholar] [CrossRef]
- Timsina, J. Can Organic Sources of Nutrients Increase Crop Yields to Meet Global Food Demand? Agronomy 2018, 8, 214. [Google Scholar] [CrossRef]
- Roberts, M.J.; Schlenker, W. Identifying Supply and Demand Elasticities of Agricultural Commodities: Implications for the US Ethanol Mandate. Am. Econ. Rev. 2013, 103, 2265–2295. [Google Scholar] [CrossRef]
- Ray, D.K.; Mueller, N.D.; West, P.C.; Foley, J.A. Yield Trends Are Insufficient to Double Global Crop Production by 2050. PLoS ONE 2013, 8, e66428. [Google Scholar] [CrossRef]
- Ye, S.; Song, C.; Shen, S.; Gao, P.; Cheng, C.; Cheng, F.; Wan, C.; Zhu, D. Spatial pattern of arable land-use intensity in China. Land Use Policy 2020, 99, 104845. [Google Scholar] [CrossRef]
- Egidi, G.; Salvati, L.; Falcone, A.; Quaranta, G.; Salvia, R.; Vcelakova, R.; Giménez-Morera, A. Re-Framing the Latent Nexus between Land-Use Change, Urbanization and Demographic Transitions in Advanced Economies. Sustainability 2021, 13, 533. [Google Scholar] [CrossRef]
- Ziem Bonye, S.; Yenglier Yiridomoh, G.; Derbile, E.K. Urban expansion and agricultural land use change in Ghana: Implications for peri-urban farmer household food security in Wa Municipality. Int. J. Urban Sustain. Dev. 2021, 13, 383–399. [Google Scholar] [CrossRef]
- Hawkesford, M.J.; Araus, J.L.; Park, R.; Calderini, D.; Miralles, D.; Shen, T.; Zhang, J.; Parry, M.A.J. Prospects of doubling global wheat yields. Food Energy Secur. 2013, 2, 34–48. [Google Scholar] [CrossRef]
- Ghobadpour, A.; Monsalve, G.; Cardenas, A.; Mousazadeh, H. Off-Road Electric Vehicles and Autonomous Robots in Agricultural Sector: Trends, Challenges, and Opportunities. Vehicles 2022, 4, 843–864. [Google Scholar] [CrossRef]
- Richards, T.J.; Rutledge, Z. Agricultural Labor and Bargaining Power. SSRN 2022. [Google Scholar] [CrossRef]
- Martin, T.; Gasselin, P.; Hostiou, N.; Feron, G.; Laurens, L.; Purseigle, F.; Ollivier, G. Robots and transformations of work in farm: A systematic review of the literature and a research agenda. Agron. Sustain. Dev. 2022, 42, 66. [Google Scholar] [CrossRef]
- Mavridou, E.; Vrochidou, E.; Papakostas, G.A.; Pachidis, T.; Kaburlasos, V.G. Machine Vision Systems in Precision Agriculture for Crop Farming. J. Imaging 2019, 5, 89. [Google Scholar] [CrossRef] [PubMed]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Illingworth, J.; Kittler, J. A survey of the Hough transform. Comput. Vis. Graph. Image Process. 1988, 44, 87–116. [Google Scholar] [CrossRef]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Behroozi-Khazaei, N.; Maleki, M.R. A robust algorithm based on color features for grape cluster segmentation. Comput. Electron. Agric. 2017, 142, 41–49. [Google Scholar] [CrossRef]
- Qureshi, W.S.; Payne, A.; Walsh, K.B.; Linker, R.; Cohen, O.; Dailey, M.N. Machine vision for counting fruit on mango tree canopies. Precis. Agric. 2017, 18, 224–244. [Google Scholar] [CrossRef]
- Giménez-Gallego, J.; González-Teruel, J.D.; Jiménez-Buendía, M.; Toledo-Moreo, A.B.; Soto-Valles, F.; Torres-Sánchez, R. Segmentation of Multiple Tree Leaves Pictures with Natural Backgrounds using Deep Learning for Image-Based Agriculture Applications. Appl. Sci. 2020, 10, 202. [Google Scholar] [CrossRef]
- Bargoti, S.; Underwood, J.P. Image Segmentation for Fruit Detection and Yield Estimation in Apple Orchards. J. Field Robot. 2017, 34, 1039–1060. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.; Tang, Y.; Zou, X.; Xiong, J.; Fang, Y. Color-, depth-, and shape-based 3D fruit detection. Precis. Agric. 2020, 21, 1–17. [Google Scholar] [CrossRef]
- Hu, X.; Yang, K.; Fei, L.; Wang, K. ACNET: Attention Based Network to Exploit Complementary Features for RGBD Semantic Segmentation. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1440–1444. [Google Scholar] [CrossRef]
- Xia, C.; Wang, L.; Chung, B.K.; Lee, J.M. In Situ 3D Segmentation of Individual Plant Leaves Using a RGB-D Camera for Agricultural Automation. Sensors 2015, 15, 20463–20479. [Google Scholar] [CrossRef] [PubMed]
- Rosell-Polo, J.R.; Gregorio, E.; Gené, J.; Llorens, J.; Torrent, X.; Arnó, J.; Escolà, A. Kinect v2 Sensor-Based Mobile Terrestrial Laser Scanner for Agricultural Outdoor Applications. IEEE/ASME Trans. Mechatronics 2017, 22, 2420–2427. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, C.; Paterson, A.H. High throughput phenotyping of cotton plant height using depth images under field conditions. Comput. Electron. Agric. 2016, 130, 57–68. [Google Scholar] [CrossRef]
- Cao, R. Describing Shrivel Development in ‘SunGold™’ Kiwifruit Using Fringe Projection and Three-Dimension Scanner: A Thesis Presented in Partial Fulfilment of the Requirements for the Degree of Master of Food Technology at Massey University, Manawatu, New Zealand. Master’s Thesis, Massey University, Manawatu, New Zealand, 2021. [Google Scholar]
- Lu, Y.; Lu, R. Structured-illumination reflectance imaging coupled with phase analysis techniques for surface profiling of apples. J. Food Eng. 2018, 232, 11–20. [Google Scholar] [CrossRef]
- Wang, W.; Li, C. Size estimation of sweet onions using consumer-grade RGB-depth sensor. J. Food Eng. 2014, 142, 153–162. [Google Scholar] [CrossRef]
- Hao, Z.; Yong, C.; Wei, W.; GuoLu, Z. Positioning method for tea picking using active computer vision. Nongye Jixie Xuebao 2014, 45, 61–78. [Google Scholar]
- Chen, J.; Chen, Y.; Jin, X.; Che, J.; Gao, F.; Li, N. Research on a Parallel Robot for Tea Flushes Plucking. In Proceedings of the 2015 International Conference on Education, Management, Information and Medicine, Shenyang, China, 24–26 April 2015; Atlantis Press: Dordrecht, The Netherlands, 2015; pp. 22–26. [Google Scholar] [CrossRef]
- Liu, H.; Bruning, B.; Garnett, T.; Berger, B. Hyperspectral imaging and 3D technologies for plant phenotyping: From satellite to close-range sensing. Comput. Electron. Agric. 2020, 175, 105621. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote. Sens. 2017, 9, 1110. [Google Scholar]
- Sahoo, R.N.; Ray, S.; Manjunath, K. Hyperspectral remote sensing of agriculture. Curr. Sci. 2015, 108, 848–859. [Google Scholar]
- Tolt, G.; Shimoni, M.; Ahlberg, J. A shadow detection method for remote sensing images using VHR hyperspectral and LIDAR data. In Proceedings of the 2011 IEEE international geoscience and remote sensing symposium, Vancouver, BC, Canada, 24–29 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 4423–4426. [Google Scholar]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar]
- Sima, A.A.; Buckley, S.J. Optimizing SIFT for matching of short wave infrared and visible wavelength images. Remote. Sens. 2013, 5, 2037–2056. [Google Scholar] [CrossRef] [Green Version]
- Monteiro, S.T.; Nieto, J.; Murphy, R.; Ramakrishnan, R.; Taylor, Z. Combining strong features for registration of hyperspectral and lidar data from field-based platforms. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1210–1213. [Google Scholar]
- Buckley, S.; Kurz, T.; Schneider, D.; Sensing, R. The benefits of terrestrial laser scanning and hyperspectral data fusion products. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2012, 39, 541–546. [Google Scholar]
- Behmann, J.; Mahlein, A.K.; Paulus, S.; Kuhlmann, H.; Oerke, E.C.; Plümer, L. Calibration of hyperspectral close-range pushbroom cameras for plant phenotyping. ISPRS J. Photogramm. Remote. Sens. 2015, 106, 172–182. [Google Scholar] [CrossRef]
- Yao, M.; Xiong, Z.; Wang, L.; Liu, D.; Chen, X. Computational Spectral-Depth Imaging with a Compact System. In Proceedings of the SIGGRAPH Asia 2019 Posters, Brisbane, Australia, 17–20 November 2019; pp. 1–2. [Google Scholar]
- Xu, J.; Zhang, S. Status, challenges, and future perspectives of fringe projection profilometry. Opt. Lasers Eng. 2020, 135, 106193. [Google Scholar] [CrossRef]
- Malacara, D. (Ed.) Optical Shop Testing, 2nd ed.; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Stoykova, E.; Minchev, G.; Sainov, V. Fringe projection with a sinusoidal phase grating. Appl. Opt. 2009, 48, 4774. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.A.; Porter, R.W. Ronchi’s Method of Optical Testing. Astrophys. J. 1929, 70, 175. [Google Scholar] [CrossRef]
- Wust, C.; Capson, D.W. Surface profile measurement using color fringe projection. Mach. Vis. Appl. 1991, 4, 193–203. [Google Scholar] [CrossRef]
- Deck, L.; De Groot, P. High-speed noncontact profiler based on scanning white-light interferometry. Appl. Opt. 1994, 33, 7334–7338. [Google Scholar] [CrossRef]
- Zhang, S. High-Speed 3D Imaging with Digital Fringe Projection Techniques; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Zhang, S.; Royer, D.; Yau, S.T. GPU-assisted high-resolution, real-time 3-D shape measurement. Opt. Express 2006, 14, 9120–9129. [Google Scholar] [CrossRef]
- Abdi, H. The method of least squares. Encycl. Meas. Stat. 2007, 1, 530–532. [Google Scholar]
- Zhang, S. Absolute phase retrieval methods for digital fringe projection profilometry: A review. Opt. Lasers Eng. 2018, 107, 28–37. [Google Scholar] [CrossRef]
- Suresh, V.; Liu, W.; Zheng, M.; Li, B. High-resolution structured light 3D vision for fine-scale characterization to assist robotic assembly. Dimens. Opt. Metrol. Insp. Pract. Appl. X 2021, 11732, 1173203. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Wyant, J.C. Two-wavelength phase shifting interferometry. Appl. Opt. 1984, 23, 4539–4543. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Wyant, J.C. Multiple-wavelength phase-shifting interferometry. Appl. Opt. 1985, 24, 804–807. [Google Scholar] [PubMed]
- Li, B.; Karpinsky, N.; Zhang, S. Novel calibration method for structured-light system with an out-of-focus projector. Appl. Opt. 2014, 53, 3415–3426. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zheng, Y.; Liu, L.; Li, B. 4D line-scan hyperspectral imaging. Opt. Express 2021, 29, 34835–34849. [Google Scholar]
- Cui, D.; Li, M.; Zhang, Q. Development of an optical sensor for crop leaf chlorophyll content detection. Comput. Electron. Agric. 2009, 69, 171–176. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar]
- Zheng, Y.; Wang, S.; Li, Q.; Li, B. Fringe projection profilometry by conducting deep learning from its digital twin. Opt. Express 2020, 28, 36568–36583. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Pang, Q. The elimination of errors caused by shadow in fringe projection profilometry based on deep learning. Opt. Lasers Eng. 2022, 159, 107203. [Google Scholar] [CrossRef]
- Ueda, K.; Ikeda, K.; Koyama, O.; Yamada, M. Absolute phase retrieval of shiny objects using fringe projection and deep learning with computer-graphics-based images. Appl. Opt. 2022, 61, 2750–2756. [Google Scholar] [CrossRef] [PubMed]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasubramaniam, B.; Li, J.; Liu, L.; Li, B. 3D Imaging with Fringe Projection for Food and Agricultural Applications—A Tutorial. Electronics 2023, 12, 859. https://doi.org/10.3390/electronics12040859
Balasubramaniam B, Li J, Liu L, Li B. 3D Imaging with Fringe Projection for Food and Agricultural Applications—A Tutorial. Electronics. 2023; 12(4):859. https://doi.org/10.3390/electronics12040859
Chicago/Turabian StyleBalasubramaniam, Badrinath, Jiaqiong Li, Lingling Liu, and Beiwen Li. 2023. "3D Imaging with Fringe Projection for Food and Agricultural Applications—A Tutorial" Electronics 12, no. 4: 859. https://doi.org/10.3390/electronics12040859
APA StyleBalasubramaniam, B., Li, J., Liu, L., & Li, B. (2023). 3D Imaging with Fringe Projection for Food and Agricultural Applications—A Tutorial. Electronics, 12(4), 859. https://doi.org/10.3390/electronics12040859







