A Polynomial Multiplication Accelerator for Faster Lattice Cipher Algorithm in Security Chip

Abstract

Polynomial multiplication is the most computationally expensive part of the lattice-based cryptography algorithm. However, the existing acceleration schemes have problems, such as low performance and high hardware resource overhead. Based on the polynomial multiplication of number theoretic transformation (NTT), this paper proposed a simple element of Montgomery module reduction with pipeline structure to realize fast module multiplication. In order to improve the throughput of the NTT module, the block storage technology is used in the NTT hardware module to enable the computing unit to read and write data alternately. Based on the NTT hardware module, a precalculated parameter storage and real-time calculation method suitable for the hardware architecture of this paper is also proposed. Finally, the hardware of polynomial multiplier based on NTT module is implemented, and its function simulation and performance evaluation are carried out. The results show that the proposed hardware accelerator can have excellent computing performance while using fewer hardware resources, thus meeting the requirements of lattice cipher algorithms in security chips. Compared with the existing studies, the computing performance of the polynomial multiplier designed in this paper is improved by approximately 1 to 3 times, and the slice resources and storage resources used are reduced by approximately 60% and 17%, respectively.

1. Introduction

In the era of widespread application of information technology, the importance of information security is also increasing day by day. As the cornerstone of information security, cryptographic algorithms play an important role in various industries. For example, public key cryptographic algorithms and symmetric cryptographic algorithms are deployed in power security chips for data encryption. However, the rapid development of quantum computing has brought huge security challenges to current cryptography [1]. Many cryptography problems seem to be no longer reliable in the face of quantum computing technology, such as Shor’s algorithm [2] and Grove’s algorithm [3]. Shor’s algorithm can solve large integer factorization problems and discrete logarithm problems, which are the foundations of the most widely used public key cryptography algorithms, RSA and ECC [4,5]. Grove’s algorithm solves the problem of unstructured database search, which can be used to attack traditional symmetric cryptographic algorithms (such as AES, TDES) [3].

Moreover, traditional cryptography technologies are also suffering from more and more side-channel attacks in real-world applications [6,7,8,9,10]. With the further development of quantum computers and quantum algorithms, the information security system based on the existing cryptography technology will be in jeopardy. Therefore, a new generation of cryptographic algorithms, called postquantum cryptography(PQC), is deployed to resist potential security risks [11].

The mainstream PQC algorithms can be divided into four categories according to the construct method [12]: multivariate cryptography [13], code-based cryptography [14], hash-based signatures [15], and lattice-based cryptography [16]. In order to promote the practical application of these algorithms, the efficient and reliable hardware implementation of PQC has become a concerned research direction. References [17,18], respectively, propose high performance and high-speed FPGA implementation of SIKE algorithm. Ferozpuri et al. implement a high-speed hardware of the rainbow signature scheme [19]. Reference [20] introduces a FPGA hardware framework of fault detection for inverted binary ring learning with errors (RLWE).

Among the PQC algorithms, lattice-based cryptography algorithms are popular due to their relatively simple structure and the fact that they can provide good security even in the worst cases [21]. Moreover, the majority lattice cryptography algorithm is based on the learning with errors (LWE) and RLWE problem [22], which are still unsolved by quantum computing, so the security is guaranteed. However, the RLWE-based lattice cryptographic algorithms have high computational complexity and low computational efficiency, which can’t meet the real-time and security computing requirements of the security chip. Therefore, the research on fast algorithms and hardware accelerators for polynomial multiplication is of great significance.

Polynomial multiplication is the main bottleneck in the RLWE problem. The number theoretic transform (NTT) is often used to calculate the polynomial multiplication because of its linear time complexity O (nlogn) [23]. Some researchers start with the core unit NTT to improve the efficiency [24,25,26]. Another part of the researchers is to optimize the polynomial multiplication operation in the lattice cipher algorithm [27,28,29]. However, the existing acceleration schemes have problems such as low computing performance and high hardware resource overhead. Further research is needed to optimize NTT to improve the performance of polynomial multipliers.

In order to effectively deploy the lattice cipher algorithm in the security chip and realize the real-time encryption of information, this paper proposes a polynomial multiplier hardware architecture suitable for the lattice cipher algorithm and the corresponding hardware architecture of the NTT module. The polynomial multiplier adopts polynomial multiplication based on NTT, and reduces the overhead of hardware resources by multiplexing the NTT hardware module. The main contributions of this paper are as follows.

(1) We propose two NTT module hardware architectures based on the performance and resource requirements of the NTT algorithm, which has the characteristics of high parallelism in operation, and improves the NTT module’s performance by increasing the number of parallel butterfly computing units.

(2) We propose an optimized modular multiplication operation unit based on the Montgomery modular multiplication algorithm. The module has a pipeline structure and can realize fast modular multiplication calculation.

(3) We propose a parameter storage and precalculation scheme based on the existing hardware resources, which effectively reduces the storage resources occupied by the scaling factor introduced by the negative packet convolution theory and the twiddle factor in the NTT operation.

(4) This paper implements a polynomial multiplication accelerator based on the NTT hardware module. In order to save hardware resources, this paper uses the similarities between NTT operation and INTT operation to reuse the core computing units and storage resources of NTT operation and INTT operation in the polynomial multiplier architecture and saves additional hardware overhead without affecting the overall computing performance.

The rest of this article is organized as follows. Section 2 introduces the related work. Section 3 introduces the hardware architecture of the core operator NTT module of polynomial multiplication. Section 4 introduces a polynomial multiplication accelerator for lattice cryptographic algorithms applied in security chips. Section 5 evaluates the performance and hardware resources designed in this paper through simulation experiments. Finally, Section 6 summarizes the full text.

2. Ralated Work

In order to improve the computational efficiency of lattice-based cryptographic algorithms, researchers focus on the core unit NTT and polynomial multiplication. In [30], Kim et al. optimized the implementation of NFT on GPU, and proposed to alleviate the main memory bandwidth bottleneck in NTT computation by dynamically generating twiddle factors. Mohsen et al. [31] analyzed the performance of NTT from various software implementation methods of the algorithm, evaluated the implementation of the NTT algorithm on a processor with SIMD function, and compared the software implementation performance of the radix-2 and radix-4 NTT algorithms in the literature. The results show that the performance of the NTT algorithm based on radix-2 is better. In terms of algorithm research, Xu et al. [32] proposed a general NTT algorithm, which uses the Cooley–Tukey butterfly to calculate the forward NTT operation and the Gentleman–Sande butterfly to calculate the reverse NTT operation. This scheme effectively eliminates the bit reversal operation. At the same time, the literature precomputes a short list of intermediate values related to parameters, so as to reduce the memory occupied by a large number of prestored parameters in exchange for short-term parameter calculation. In [30], Kim et al. analyzed the differences between NTT and DFT algorithms, optimized for the implementation of NTT on GPU, and proposed to alleviate the main memory bandwidth bottleneck in NTT computation by dynamically generating twiddle factors. For the butterfly computation of the core operator in the NTT algorithm, a configurable butterfly computation unit is proposed in [33]. The butterfly computation unit can be configured for both Cooley–Tukey and Gentleman–Sande algorithms. At the same time, three different NTT hardware architectures are proposed based on the butterfly unit to meet different performance requirements by increasing the number of parallel computing units. Reference [34] uses HLS to implement an NTT hardware architecture, in which the K-RED reduction method is used to optimize the modulo operation process, and a primitive memory write-back scheme is proposed to reduce the memory resources occupied by parameters. Reference [35] added a multichannel and reconfigurable design to the NTT architecture. The parallel four-channel butterfly calculation in the architecture greatly improves the computing speed, but it also generates a lot of hardware overhead.

In the study of polynomial multiplication, the literature [27] applied the FFT algorithm to the lattice cipher algorithm and firstly applied it to the reconfigurable lattice cipher hardware design, which made the calculation speed of polynomial multiplication significantly improved, but the performance was still difficult to meet the needs. Based on the FFT algorithm, [28] proposed a polynomial multiplier architecture that supports multiparameter configuration, making the design suitable for homomorphic encryption algorithms with different parameters. Reference [29] implements a polynomial multiplier with low resource overhead on FPGA for specific parameters, and reduces the use of DSP by multiplexing a single hardware computing unit.

3. NTT Hardware Architecture

3.1. NTT Algorithm

In the fast algorithm of polynomial multiplication, using the FFT algorithm to speed up polynomial multiplication is a common method. The NTT algorithm is an extension of the FFT algorithm in finite fields. Compared with the FFT algorithm, the NTT algorithm replaces the complex number operation in the FFT algorithm with the integer operation in the finite field, thereby avoiding the calculation precision error caused by the floating-point number operation. At the same time, the unit root on the finite field in the NTT algorithm replaces the unit root on the complex plane of the FFT algorithm. The definition of the NTT algorithm is as follows:

$$X\left(K\right)=\sum _{n=0}^{n-1}x\left(n\right)e^{-i\frac{2n\pi }{N}k},(k=0,1,2,\dots ,N-1).$$

(1)

Similarly, the calculation formula of the inverse transform INTT algorithm of the number theoretic transformation is as follows:

$$x\left(n\right)=\frac{1}{N}\sum _{k=0}^{N-1}X\left(k\right)W_N^{-nk}\left(modp\right),(n=0,1,2,\dots ,N-1),$$

(2)

where $W_N^{-nk}$ represents the root of unity $e^{-i\frac{2n\pi }{N}k}$.

Because the NTT algorithm is defined in a finite field, the operation results of NTT/INTT all need to take the modulo of p. 1/N in INTT is the inverse N-1 of order N in a finite field, and its relationship with N satisfies $N^{-1}·N\equiv 1\left(modp\right)$. The computational efficiency and time complexity of the NTT algorithm are similar to those of the FFT algorithm, but all its operations are integer operations, which are smaller than those involving trigonometric functions and floating-point numbers.

The NTT algorithm, like the FFT algorithm, is also divided into decimation in time (DIT) and decimation in frequency (DIF). These two extraction methods correspond to two kinds of butterfly calculations. The time extraction method NTT corresponds to the Cooley–Tukey butterfly calculation, and the frequency extraction method NTT corresponds to the Gentleman–Sande butterfly calculation. The complete Cooley–Tukey NTT algorithm is shown in Algorithm 1.

Algorithm 1: Cooley–Tukey NTT algorithm

In the algorithm, the $Rev\left(\right)$ function in the first line performs the bit-reversal operation. After the parity split and rearrangement in the time domain order, the order number of the polynomial coefficients is exactly the same as the original number, showing the phenomenon of bit reversal on the binary code, and after the NTT calculation, the serial number of the output result returns to the original serial number. Therefore, Cooley–Tukey NTT is input in reverse order, output in sequence, and data input requires bit-reversal operation.

The NTT and INTT operations are the core operators of polynomial multiplication, which determine the operational efficiency of polynomial multiplication. Therefore, the NTT module and the INTT module are the most important hardware units in the polynomial multiplier. The NTT and INTT operation formulas are very similar. When designing the NTT and INTT hardware modules, it is necessary to fully consider the characteristics and similarities and differences of the two operations. The core operators in NTT operation and INTT operation are butterfly calculations. In order to save hardware resource overhead, this paper considers the reuse of some hardware units based on the characteristics of NTT and INTT algorithms. The following will analyze the similarities and differences of the two algorithms. (1) This paper adopts the NTT and INTT algorithms based on time extraction, so the butterfly calculation structure in the two algorithms is the same. (2) The twiddle factors involved in the calculation in the NTT operation and the INTT operation are different. The twiddle factor is $W_N^{-i}$. (3) In the INTT operation formula, the coefficient of each result polynomial needs to be multiplied by the inverse N-1 of the order N. (4) Before performing the NTT operation, the polynomial coefficient needs to be multiplied by the scaling factor ${\phi }^i$ to complete the preprocessing; after performing the INTT operation, the polynomial coefficients need to be multiplied by ${\phi }^{-i}$ to complete the postprocessing.

Because DIT-NTT is used in this paper, according to the Cooley–Tukey butterfly calculation described in the previous algorithm, the coefficient data order of the polynomial needs to be bit-reversed before input. For the bit reverse operation function Rev mentioned in the algorithm, its implementation in hardware only requires the reverse combination of address lines, and does not require additional hardware design and resources, so it can be ignored. We carefully distinguish the data that needs to be selected.

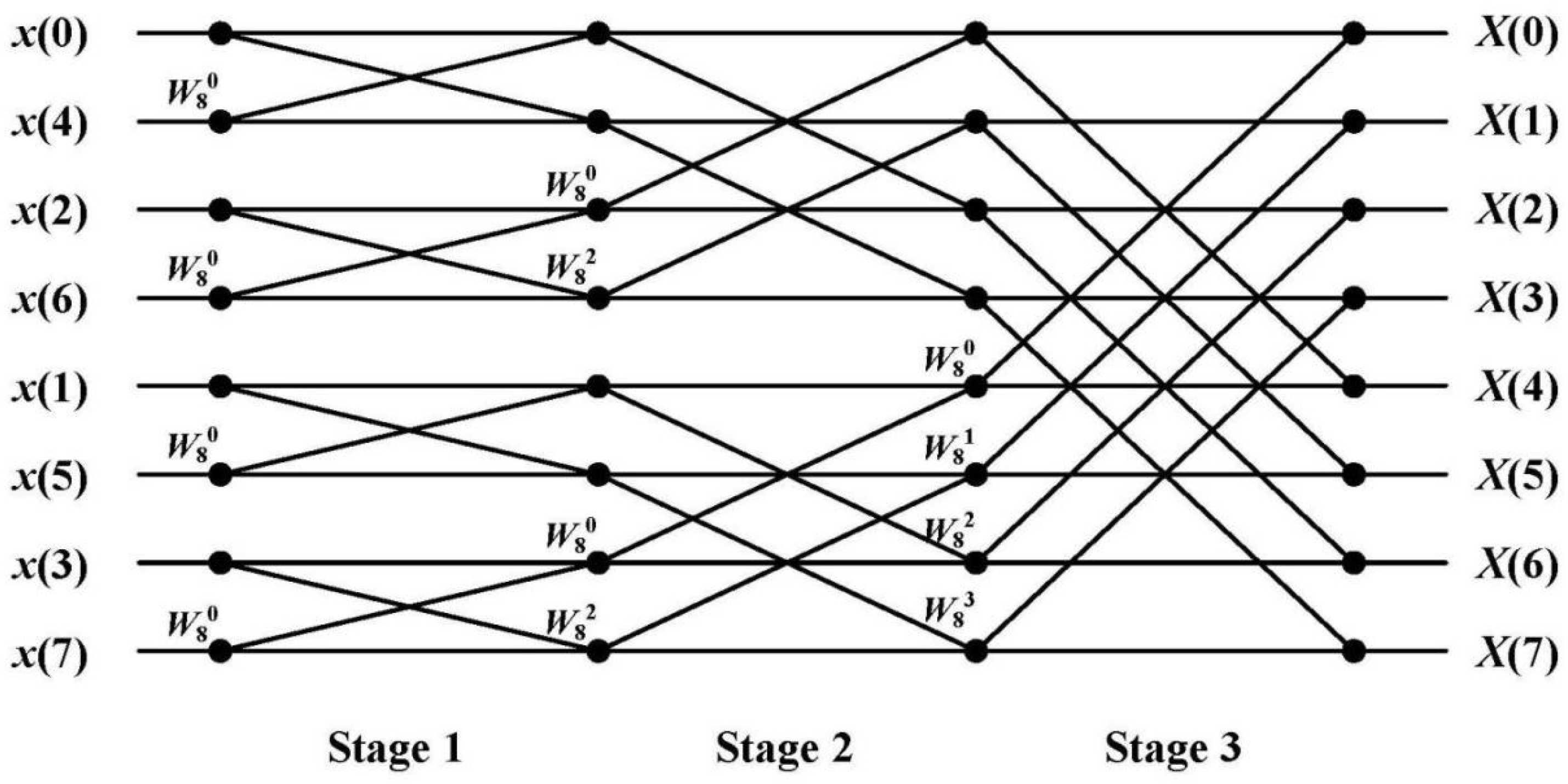
We take eight-point DIT-NTT as an example to analyze its operation characteristics. The Figure 1 below shows the eight-point DIT-NTT operation data flow. The eight-point DIT-NTT can be divided into three stages for radix-2 Cooley–Tukey butterfly calculation processing. Each intersection point in the middle in the figure represents a butterfly calculation process. It can be seen that each stage of the eight-point NTT operation requires four butterfly calculations, and the input and output data of different butterfly calculations in each stage are unrelated to each other, so different butterfly calculations can be design for parallel processing. Taking advantage of the high parallelism of NTT operation, in order to improve the computing speed of NTT module, butterfly computing units can be added to improve the parallelism of computing. At the same time, the operation structure can also be designed serially to form multilevel butterfly computing units to run sequentially, so as to realize the pipeline structure of butterfly computing units in the NTT module and improve the data throughput of the NTT module.

3.2. Hardware Architecture

According to the above analysis of NTT/INTT algorithm, this paper proposes two hardware architectures of NTT operation modules based on the characteristics of the algorithm, which are the low-cost L-NTT module and the high-performance H-NTT module.

3.2.1. L-NTT Hardware Architecture

The Figure 2 below shows the overall architecture of the L-NTT module. The hardware resources in the L-NTT module are shown in the figure. The operation part includes a butterfly calculation unit and a modular multiplication calculation unit. The storage part consists of three dual-port RAMs, including two RAM 0 and RAM 1 that store polynomial coefficients, a RAM_F that stores the twiddle factor WNi and the scaling factor ${\phi }_i$. In order to reduce the hardware resources used by the low-cost L-NTT module, this paper chooses to add a modular multiplication unit to the L-NTT module to calculate the twiddle factor $W_N^i$ in real time, so as to save the hardware resources required to store all the twiddle factors.

In the preparation stage of NTT operation, the coefficients of the input polynomial A are stored in RAM 0 and RAM 1 at the same time, which means that the data stored in RAM 0 and RAM 1 are the same before starting the NTT operation. When the NTT operation is performed, the pipeline operation starts in the butterfly computing unit after a certain computing cycle. At this time, the butterfly computing unit needs to read two polynomial coefficients and twiddle factors from the RAM as input in each cycle, and output two calculation results and store them in the RAM at the same time. In order to ensure that the access to RAM does not conflict during data reading and writing, and to ensure that the butterfly computing unit can continue to operate, the target RAM needs to be rotated during data reading and writing, and the data will be stored in RAM 0 and RAM 1 in turn. Because the L-NTT architecture only contains one butterfly computing unit, using the L-NTT module to perform a complete NTT operation needs to go through rounds of butterflies, calling a total of two butterfly computing units.

3.2.2. H-NTT Hardware Architecture

This paper also proposes a high-performance H-NTT hardware architecture. According to the characteristics of the NTT operation described above, each stage of the NTT operation can perform butterfly calculations in parallel. In this paper, a butterfly computing unit is added to the H-NTT module hardware architecture to take advantage of this parallelism. The hardware architecture diagram of the module is shown in the Figure 3. In the high-performance H-NTT module, the operation part includes two parallel butterfly computing units BU 0 and BU 1, and a modular multiplication unit; the storage part consists of five dual-port RAMs. In order to effectively reduce the storage resource overhead in hardware design, this paper adopts a data block storage scheme. In this scheme, data that does not have dependencies in computing is stored in blocks, so as to ensure that multiple computing units do not conflict when reading and writing data, and at the same time, the overall storage resource occupation is not increased. Among them, RAM 0 and RAM 1, respectively, store the first N/2 coefficients and the last N/2 coefficients of the polynomial, and RAM 2 and RAM 3 serve as temporary storage RAMs corresponding to RAM 0 and RAM 1.

In the preparation stage of the NTT operation, the coefficients of the polynomial A involved in the calculation need to be stored in RAM 0–3 after being processed in reverse order. The original even term of the polynomial A sequence is stored in RAM 0, and the original odd term of the sequence is stored in RAM 1. Taking the eight-point NTT as an example, after the coefficient terms of the eight-point NTT are processed in reverse order, the input of the butterfly calculation in the upper half is an even term, and the input of the butterfly calculation in the lower half is an odd term. Groups of coefficients are stored in RAM 0 and RAM 1. Meanwhile, the polynomial coefficient data is not stored in RAM 2 and RAM 3 at this time. Because each dual-port RAM supports reading two data at the same time, and two butterfly units need to read four data at the same time, conflicts will occur when the input data of the two butterfly units are read from the same RAM. In order to avoid the above situation, when performing butterfly calculation, let butterfly unit BU 0 calculate the butterfly calculation of the upper half, and butterfly unit BU 1 calculate the butterfly calculation of the lower half, so that the two butterfly units are calculating. At most, two pieces of data can be read from a piece of RAM at the same time. After the computation in the butterfly unit is completed, the resulting data will be restored in RAM. Because the butterfly computing unit is pipelined, it will read data from RAM 0 or RAM 1 in each cycle, and the butterfly computing result cannot be written back to the original RAM, so two temporary RAMs are needed to store the NTT operation.

In the first stage of NTT operation, the two butterfly calculation units BU 0 and BU 1, respectively, read four coefficient data from RAM 0 and RAM 1 and read the twiddle factor from RAM_F. The four resulting data are stored in the corresponding address positions in RAM 2 and RAM 3, respectively; when performing the second stage of NTT operation, BU 0 and BU 1 read four intermediate data from RAM 2, RAM 3, and RAM_F respectively and After calculating the rotation factor, the four resulting data are stored in the corresponding address positions in RAM 0 and RAM 1, respectively, and so on. RAM 0-1 and RAM 2-3 alternately read and write in different butterfly stages. It is ensured that there is no conflict between reading and writing the storage during the NTT operation.

In order to ensure the high-performance computing of H-NTT, all twiddle factors involved in butterfly calculation are prestored in dual-port RAM_F, and BU 0 and BU 1 can read two twiddle factors from RAM_F at the same time in each cycle. The modular multiplication unit in the H-NTT architecture is used to calculate the scaling factor in real time during the preprocessing and postprocessing stages of polynomial multiplication, which will be described later. If the H-NTT module is not used for preprocessing and postprocessing operations, the modular multiplication unit can be moved outside the H-NTT module and deployed.

3.2.3. Butterfly Unit

Butterfly calculation is a key step for NTT algorithm to accelerate polynomial multiplication, and it is also the core operator of NTT algorithm. The butterfly calculation of the NTT algorithm is divided into Cooley–Tukey butterfly calculation based on time extraction and Gentleman–Sande butterfly calculation based on frequency extraction. The internal operation order of the two butterfly calculations is different, but the amount of calculation is the same; that is, a butterfly calculation is completed. The shape calculation requires performing one modular multiplication and two modular additions and subtractions. In this paper, DIT-NTT based on Cooley–Tukey butterfly computing is used as the basic algorithm of hardware design. The hardware block diagram of the butterfly computing unit is as follows. Figure 4 represents the hardware architecture of the butterfly unit.

As shown above, the green area in the Figure 4 represents the modulo multiplication unit, which consists of a multiplier and a modulo module; the two yellow areas represent the modulo addition unit and the modulo subtraction unit, which are, respectively, composed of an adder/subtracter and a modulo module. Although the modulo multiplication unit in the green area and the modulo addition and subtraction unit in the yellow area both contain modulo modules, because the range of the result value after the multiplication operation may be much larger than the result value after the addition and subtraction operation, the corresponding modulo operation The complexity is also different. Therefore, this paper will carry out the targeted design of the modulo module in the modulo multiplication unit and the modulo addition and subtraction unit.

The butterfly unit has registers inserted on both the Input 1 and Input 2 branches. Before the data enters the modulo addition and subtraction unit, the data on the Input 2 branch will be subjected to a modular multiplication operation, but no operation occurs on the Input 1 branch. Therefore, some registers are inserted in the Input 1 branch to balance the delay, so that the two branches are connected. The data reaches the modulo addition and subtraction unit in the same clock cycle, and the number of registers inserted in the Input 1 branch is determined by the delay of the modulo multiplication unit. The function of the register after the modulo multiplication unit is to register the output.

According to the Cooley–Tukey butterfly calculation formula, in addition to inputting $X_0\left(k\right)$ and $X_1\left(k\right)$, the butterfly computing unit also needs to input a twiddle factor $W_N$ as a multiplication coefficient. The butterfly computing unit proposed in this paper adds a selector before the multiplier. The selector can select the input twiddle factor WN when performing the NTT operation according to the control signal, or select the input twiddle factor $W_N^{-1}$ when performing the INTT operation, so that the NTT and the INTT operation can realize the multiplexing of the butterfly computing unit to save hardware resources.

3.2.4. Modular Multiplication Unit

In the NTT operation, the input data of each butterfly calculation needs to be multiplied by the corresponding twiddle factor, so an efficient modular multiplication operation unit is required in the butterfly calculation unit. Generally speaking, the performance bottleneck of the modulo multiplication operation is the modulo operation. The modulo operation is defined as the remainder obtained by dividing a number by the modulo. In number theory, the modulo operation is often involved. For example, in a finite field, in order to ensure that the result of the field elements is still in the field after the operation, the modulo operation is performed with the feature p of the field as the modulo after the operation. NTT is an operation defined on a finite field, and the multiplication in its algorithm will also be replaced by modular multiplication.

There are two commonly used fast modular multiplication algorithms: Montgomery modular multiplication and Barrett modular multiplication. In order to realize efficient modular multiplication operation, this paper adopts Montgomery modular multiplication as the basic algorithm of hardware design. The Montgomery modular multiplication algorithm is a commonly used fast modular multiplication algorithm that consists of multiplication and Montgomery modular reduction.

The Montgomery modular reduction used in this paper is shown in Algorithm 2. Among them, for the multiplication result of z to be modulo taken, z is divided into high and low m bits, which are represented by $z_h$ and $z_l$, respectively. Here, m is the bit width of the modulus q and the parameter R. This paper adopts $m=16$, and $R=216$ at this time. Here, $q^{\prime }$ is the inverse of q in the case of modulo R. Generally, in the Montgomery modular reduction operation, the overhead of real-time calculation is relatively large, because this paper designs a modular multiplication unit with fixed parameters, which is calculated in advance and stored in storage. If there is a parameter change, it is necessary to reconfigure the modulus q and $q^{\prime }$.

It can be found from Algorithm 2 that in the process of Montgomery modular reduction, there is no operation of taking the modulo of q, and it has become the operation of taking the modulo of R and shifting. This is because the Montgomery modular reduction uses the properties of the aforementioned parameter R to convert the modulo operation in the algorithm from modulo q to modulo R or division R, and because R is a power of 2, both modulo R and division R can be achieved by shifting, the calculation is greatly simplified. Therefore, even if the Montgomery modular multiplication algorithm needs to preprocess the input data, the efficiency is still higher than the simple modulo operation.

This paper designs the Montgomery modular multiplication hardware unit according to Algorithm 2, which consists of a 16-bit multiplier and a Montgomery modular simple element serially connected. The hardware architecture of the Montgomery modular simple element is shown in the Figure 5. After the 32-bit product result z of the multiplier is registered and output, the output data is divided into high 16-bit and low 16-bit, and divided into two data paths. According to lines 2 to 3 of Algorithm 2, the lower 16-bit data $z_l$ is first multiplied by $q^{\prime }$ and then modulo R (the result is 16-bit lower), then multiplied by q and then shifted right by 16 bits (the result is higher 16-bit), and finally take the modulo q of the result of the subtraction from $z_h$ to get the final result. Because the data is already similar in size to q in the last modulo operation, the result can also be quickly obtained by taking modulo by subtraction.    

Algorithm 2: Montgomery modular reduction algorithm

Input:$z=z_h,z_l$; $IntR=2^m,R>q$ Modules q, $Int{q}^{\prime }=q^{-1}\left(modR\right)$ Output:$r=z{R}^{-1}modq$ 1  $z_l$ = $zmodR$; 2  T = $z_l$$\times q^{\prime }modR$; // $\phantom{(}$find the parameter T that makes $z+Tq$ an integer multiple of R$\phantom{(}$ 3  $T_h$ = $(T\times q)\gg m$; 4  r = $z_h$ − $T_h$; // $\phantom{(}$obtain the modulo result $(z+Tq)/R\left(modq\right)$$\phantom{(}$ 5  if $r>q$ then 6  $| r=r-q$ 7  end $\phantom{(}$ 8  return r

On the upper data path, $z_h$ does not participate in the operation. In order to balance the delay of the two data paths, so that the data can reach the subtractor at the same time, this paper inserts two-level registers on the $z_h$ path of the modular simple element. The two’s complement at the input of the adder in the figure means taking the two’s complement of q, adding r and the complement of q and selecting the final output through the carry signal. The entire Montgomery module reduction architecture implements a pipeline design.

4. Polynomial Multiplier Hardware Architecture

In the existing hardware research of polynomial multiplication accelerator, there is a lack of effective solutions to reduce storage resources. The storage of polynomial data and related parameters will generate more hardware resource overhead. It is obviously unwise to double the hardware overhead in order to improve the computing performance. Aiming at this problem, we propose a storage and precalculation method for twiddle factors, which can effectively reduce the hardware resource overhead. Based on this scheme, this paper completes the design and implementation of polynomial multiplier, and describes its overall hardware structure and modules.

4.1. Polynomial Multiplication Based on NTT Algorithm

The operation flow of the polynomial multiplication based on NTT used in this paper is shown in the Figure 6. In the figure, Coeff(a) and Coeff(b) are the coefficient representations of the polynomials A(x) and B(x), respectively, and Point(a) and Point(b) are the point value representations of the polynomials. After applying the negative packet convolution theorem, the coefficients Coeff(a) and Coeff(b) need to be precalculated with $\phi$ before the NTT operation. The coefficients of the resulting polynomial mean that the coefficient Coeff(c) needs to be calculated with $\phi$ after the INTT operation for postcalculation.

As shown in the Figure 6, in a polynomial multiplication operation, the two polynomial coefficients Coeff(a) and Coeff(b) involved in the calculation can perform NTT operations in parallel. In order to effectively utilize the characteristics of parallel computing in polynomial multiplication, this paper deploys two independent NTT modules in the polynomial multiplier, and processes Coeff(a) and Coeff(b) at the same time to double the efficiency of the polynomial evaluation stage.

In the point value multiplication stage of the polynomial, in the point values Point(a) and Point(b) of the polynomial, the point values in the corresponding order will be subjected to the modular multiplication operation. For two n-dimensional polynomials, the n times modular multiplication operation will be performed. Each butterfly computing unit includes a Montgomery modular multiplication unit. In order to reduce hardware resource overhead, this paper does not deploy additional modular multiplication units in the polynomial multiplier, but reuses the butterfly computing unit when multiplying point values. At this time, the input terminal Input 1 of the butterfly computing unit needs to be set to 0, Input 2 inputs the point value Point($a_i$), and the multiplexer MUX needs to select and input the corresponding point value Point($b_i$).

4.2. Parameter Storage and Precomputation Method

The twiddle factor is an important parameter in the butterfly calculation process. The polynomial multiplication is calculated by using the NTT algorithm, and the twiddle factor occurs when the polynomial coefficients are decomposed according to parity from a long sequence into a series of short sequences. In addition to the twiddle factor, there is an important parameter in the polynomial multiplication algorithm that applies the negative packet convolution theorem, the scaling factor ${\phi }^i$. The scaling factor is a primitive root of order 2N defined on the ring R whose relation to the twiddle factor satisfies ${\phi }^2=W_{N}modq$. The negative packet convolution theorem effectively avoids the increase in the amount of computation caused by the addition of 0 to the polynomial, but increases the preprocessing steps before the NTT operation and the postprocessing steps after the INTT operation. The so-called preprocessing and postprocessing operations are the polynomial coefficients. It is multiplied by the scaling factor or the corresponding, so it can be seen that the number of terms of the scaling factor and the number of terms of the polynomial coefficient are the same, and both are N.

The number of twiddle factors is not fixed. Because the twiddle factors are generated during the decomposition of the sequence of polynomial coefficients, the number of twiddle factors is related to the way the sequence is decomposed. The NTT algorithm used in this paper is the radix-2 DIT-NTT algorithm, which divides the sequence into two equal parts each time until it is decomposed into two coefficients per group. The twiddle factor in the base 2 DIT-NTT of N points has the following rules: the number of NTT points is $N=2^l$, the number of butterfly stages where the twiddle factor is located is s, and the maximum s is $l=lo{g}_{2}N$. Then, the twiddle factors involved in the butterfly calculation at this stage are $W_N^{k\times 2^{l-s}}$, where k is an integer satisfying $0\le k\le 2^{s-1}-1$. It can be found that there are $2^{s-1}$ twiddle factors for the existence of the butterfly in the sth stage. Therefore, the total number of twiddle factors in an N-point radix-2 DIT-NTT operation is $2^{l-1}$, which is N/2. The law of the twiddle factor in the inverse transform INTT operation is the same, and the number of twiddle factors is also N/2. Therefore, in a complete NTT-based polynomial multiplication, there are a total of N twiddle factors of $W_N^i$ and $W_N^{-i}$.

We propose a parameter storage and precomputation scheme of twiddle factors and scaling factors suitable for the polynomial multiplication hardware architecture proposed in this paper. First, analyze the use process of twiddle factor and scaling factor. In the preprocessing stage before the NTT operation, the polynomial coefficients $a_i$, $b_i$ are multiplied by the corresponding scaling factors, respectively. In this process, there is no dependency between the data of each multiplication operation, which is completely parallel. For butterfly calculations in NTT, the polynomial coefficients are also butterfly-calculated with the corresponding twiddle factors. Although the butterfly calculations in each operation stage can also be performed in parallel (that is, there is no dependency between the input and output data, but the input data of the butterfly calculation in the next operation stage is the output of the butterfly calculation in the previous operation stage), the butterfly computation within the NTT operation is not completely parallel.

Because the NTT hardware module proposed in this paper contains two butterfly computing units and a modular multiplication unit, if the twiddle factor is calculated in real time, the calculation delay of the two butterfly computing units will be different. Therefore, this paper chooses to prestore the rotation factor and calculate the scaling factor in real time. Because the $W_N^i$ and ${\phi }^i$ satisfy the following formula,

$$W_N^i={\phi }^{2i}modq,i=0,1,2,\dots ,\frac{N}{2}-1.$$

(3)

The prestored twiddle factor also contains all the even-numbered power terms of the scaling factor ${\phi }^{2i}$ and for the odd-numbered power terms ${\phi }^{2i+1}$, it needs to be generated by the precalculation performed ${\phi }^{2i+1}\times \phi$ by the modular multiplication unit before the operation. Based on the above method, the prestored parameters in the forward NTT operation process are only N/2 = 256 twiddle factors and a scaling factor, and the memory occupied is about 0.5 KB.

The prestored parameters in the INTT operation process are slightly different from NTT. According to the above description, the calculation parameters required for INTT operation and postprocessing operation are twiddle factors $W_N^{-i}$ and $n^{-1}{\phi }^{-1}$. If the same scheme as in the NTT operation is adopted, which is prestored $W_N^{-i}$ in memory and calculated $n^{-1}{\phi }^{-1}$ in real time, it will be found that when two multiply $n^{-1}{\phi }^{-1}$ calculations need to be performed in parallel during the postprocessing operation, the twiddle factor $W_N^{-i}$ needs to be calculated twice as follows:

$$\left\{\begin{array}{c}\hfill W_N^{-i}\times n^{-1}\to n^{-1}{\phi }^{-2i}\\ \hfill W_N^{-i}\times n^{-1}{\phi }^{-1}\to n^{-1}{\phi }^{-2i+1}\end{array}.\right.$$

(4)

It can be seen that the hardware architecture of the polynomial multiplier proposed in this paper contains two parallel NTT/INTT modules, and each NTT/INTT module contains an independent modular multiplication unit. Only one INTT operation needs to be performed in a polynomial multiplication operation. Therefore, when the INTT operation stage is reached, one NTT module is in an idle state. At this time, the idle modular multiplication unit can be called. The multiplication unit satisfies exactly two calculations in Equation 4. Before postprocessing, read the twiddle factor from RAM, input the two modulo multiplication units to multiply by, and then multiply the two calculation results with the corresponding terms of the result polynomial coefficients. Similarly, the prestored parameters required for the reverse INTT operation process and postprocessing process are N/2 = 256 twiddle factors, occupying approximately 0.5 KB of memory.

The parameter storage and precomputation of scaling factors proposed in this section fully combine the proposed NTT module architecture, which can reduce the memory occupied by the prestored parameters required by the entire polynomial multiplier to about 1 KB without adding additional hardware resources and reducing the overall computing performance. Compared with the 2.5 KB memory required by the combined parameters, it reduces by approximately 60%, significantly saving the hardware resource overhead.

4.3. Polynomial Multiplication Accelerator

4.3.1. Overall Architecture

The lattice cipher algorithm polynomial multiplier proposed in this paper adopts the parameters commonly used in lattice cipher algorithms based on RLWE: modulus q = 12,289, polynomial points N = 512, and the bit width of the hardware unit is 16 bits.

The hardware architecture of the polynomial multiplier based on NTT proposed in this paper is shown in the Figure 7. The polynomial multiplier architecture includes four parts, namely the operation unit part, the storage part, the storage control part and the polynomial multiplication flow control part.

The core part of the polynomial multiplier is the operation unit part, which is mainly composed of NTT/INTT modules. In order to satisfy the two input polynomials that can perform NTT operations at the same time, this paper deploys two parallel NTT modules in the polynomial multiplier hardware architecture, NTT 0 and NTT 1. At the same time, in order to meet the fast calculation requirements of polynomial multiplication, the NTT module deployed in the polynomial multiplier in this paper adopts the high-performance H-NTT module in 3.2. Each NTT module contains two parallel butterfly computing units and a modular multiplication unit. When performing NTT operation, each H-NTT needs to use four blocks of RAM to store polynomial coefficients, NTT 0 corresponds to RAM0-3, and NTT 1 corresponds to RAM 4-7.

The storage part is used to store the polynomial coefficients involved in the polynomial multiplication operation, the prestored twiddle factors and the intermediate data generated in the calculation. The storage part includes eight blocks of RAM0-7 for storing polynomial coefficients and point values, and two blocks of RAM_F0-1 for storing parameters, such as twiddle factors.

The storage control part is used to control the reading and writing of data. In the NTT operation process, each butterfly computing unit calculates different point groups in different NTT operation stages, and the output results are stored in different locations. Because there are two H-NTT modules in the polynomial multiplier, there are four butterfly computing units in total, corresponding to eight blocks of RAM. The storage module in the polynomial multiplier in this paper includes eight RAMs, 0–7, that store polynomial coefficients, and two RAM_F 0-1 that store twiddle factors. Each memory is a dual-port RAM with a size of bits. The total storage resources required by the entire polynomial multiplier are 40,960 bits, or 5 KB.

4.3.2. Preprocessing and Postprocessing

• Preprocessing operations for polynomial multiplier

The preprocessing process is to multiply the polynomial coefficients by the corresponding scaling factors ${\phi }^i$ in turn. In the polynomial multiplier proposed in this paper, two H-NTT modules NTT 0 and NTT 1 deployed in parallel precompute the input polynomials A and B, respectively. The following uses NTT 0 as an example to perform preprocessing on polynomial coefficients.

In the storage module of the polynomial multiplier, the scaling factor ${\phi }^i$ involved in the preprocessing is not prestored in the memory RAM_F 0-1, but needs to be calculated in real time. In the process of preprocessing, in order to reduce the overhead of hardware resources, this paper chooses to reuse the arithmetic units in the NTT module for calculation. In the H-NTT module, it contains two butterfly computing units and a modular multiplication unit. Each butterfly computing unit also contains a modular multiplication unit, can calculate ${\phi }^i\times {\alpha }_i$ by using the modular multiplication unit in the two butterfly computing units. When using the butterfly computing unit to calculate the modular multiplication, it is necessary to set the input of Input 1 to 0, and input the polynomial coefficient and scaling factor from Input 2 and the multiplexer, respectively. The twiddle factor $W_N^i$ prestored in RAM_F can be used as the even-numbered power term of the scaling factor ${\phi }^{2i}$, and the odd-numbered power term ${\phi }^{2i+1}$ is calculated ${\phi }^{2i}\times \phi$ by using the remaining modular multiplication units in the NTT module. Therefore, when calling the NTT module for preprocessing, the NTT module reads the scaling factor ${\phi }^{2i}$ and $\phi$ from RAM_F0, and then inputs ${\phi }^{2i}$ into butterfly computing unit BU 0 and modular multiplication unit, respectively, and inputs the polynomial coefficients of the corresponding sequence in the butterfly computing unit. Multiplication is obtained by multiplying the $\phi$ and ${\phi }^{2i}$ in the input modular multiplication unit, and then inputting another butterfly computing unit BU 1 to multiply the polynomial coefficients of the corresponding sequence. It can be seen that compared with the data path of calculation ${\phi }^{2i}\times {\alpha }_{2i}$ and ${\phi }^{2i+1}\times {\alpha }_{2i+1}$ , there is a delay of the modulo multiplication operation, which is about four cycles. However, it can be seen from the foregoing that the butterfly computing unit and the modular multiplication unit in the H-NTT module have a pipelined linear structure. Therefore, after beginning to call the NTT module for preprocessing, after a delay of a modular multiplication unit and a butterfly computing unit, the NTT module enters the pipeline operation. At this time, the NTT module has two polynomial coefficients input and two calculation results per cycle. Similarly, another NTT block NTT 1 in the polynomial multiplier preprocesses the polynomial coefficients B in the same way.

• Postprocessing operations for polynomial multiplier

The postprocessing process is to multiply the resulting polynomial coefficients $c_i$ by the corresponding scaling factors ${\phi }^{-i}$ in turn. Because this paper moves the multiply $n^{-1}$ in the INTT operation to the postprocessing process, the postprocessing process refers to multiplying the coefficients $c_i$ with the corresponding ones $n^{-1}{\phi }^{-i}$ in turn. The postprocessing in the polynomial multiplication only needs to be performed on the result polynomial, so the postprocessing operation stage only needs to call an NTT module NTT 0 for calculation. The following is an example of postprocessing performed by NTT 0 on the polynomial coefficients C.

Similar to the preprocessing stage, the scaling factor $n^{-1}{\phi }^{-i}$ involved in the postprocessing is not prestored in the memory RAM_F 0-1, and also needs to be calculated in real time by the twiddle factor. According to the calculation process of the preprocessing above, it can be known that the two butterfly computing units in the NTT module can be used for postprocessing at the same time, and two scaling factors $n^{-1}{\phi }^{-2i}$ and $n^{-1}{\phi }^{-2i-1}$ need to be input for two calculations. It can be seen that it is slightly different from the preprocessing stage. The two scaling factors in the postprocessing stage need to be calculated by modular multiplication, and can be calculated by using the modular multiplication unit MMU1 in the idle NTT 1. At the beginning of postprocessing, NTT 0 reads the resulting polynomial coefficients $c_{2i}$ and $c_{2i+1}$ from RAM where the polynomial coefficients are stored, and $n^{-1}$ and $n^{-1}{\phi }^{-i}$ from RAM_F0, and twiddle factors $W_N^{-i}$ from RAM_F1. Then input the twiddle factors $W_N^{-i}$ into the modular multiplication units MMU0 and MMU1 in NTT 0 and NTT 1 at the same time, and input $n^{-1}$ and $n^{-1}{\phi }^{-i}$ into the two modular multiplication units, respectively, to obtain the scaling factors $n^{-1}{\phi }^{-2i}$ and $n^{-1}{\phi }^{-2i-1}$ required for the postprocessing operation. Then separate the scaling factors into Input 2 butterfly computing units, and multiply with $c_{2i}$ and $c_{2i+1}$ to get the final postprocessing result. It can be seen that in the postprocessing stage, the two data paths for calculating $c_{2i}\times n^{-1}{\phi }^{-2i}$ and $c_{2i+1}\times n^{-1}{\phi }^{-2i-1}$ need to go through the delay of a modular multiplication unit and a butterfly calculation unit, and the input and output times are the same. After the above delay, the NTT module will also enter the pipeline operation.

Figure 8 shows the operation flow of the polynomial multiplier. It can be seen that NTT0 and NTT1 unit in multiplier can execute preprocessing, NTT and pointwise multiplication operation in parallel, and INTT operation and postprocessing are operated by NTT0 alone.

Figure 9 shows the pre/postprocessing operation flow of NTT module. BU0-1 means the first calculation performed by butterfly unit 0 in the H-NTT unit, and Mmult means the modular multiplication operation performed by Modmult unit in the H-NTT unit. It can be seen that in the NTT unit, BU0, and BU1 can be calculated in parallel, whereas BU1 needs to calculate the corresponding scaling factor ${\phi }^{2i+1}$ and ${\phi }^{-2i-1}$ through modular multiplication unit before calculation. In addition, it can also be seen that in a butterfly unit, the computing task is pipelined.

5. Experiments and Results

5.1. Experimental Setup

In this paper, the proposed H-NTT module-based polynomial multiplier is implemented on FPGA and the performance and hardware resource overhead of the design are evaluated on FPGA. After the polynomial multiplier is synthesized by the Synplify Premier tool and implemented by the Vivado tool, the hardware resource overhead report generated by the implementation of the polynomial multiplier and NTT module on the FPGA. To facilitate comparison, the FPGA platform used in this paper is the same as the existing design, which is the Xilinx Kintex 7 series development board.

In order to more clearly compare the comprehensive performance of the proposed polynomial multiplier and other designs in terms of hardware resource overhead and performance, it is necessary to integrate hardware resources and performance into the same parameter for further comparison. This paper will use the resource equivalent comparison method in the literature [36], which considers the replacement relationship of resources on the Xilinx K7 series FPGA board, and obtains the equivalent number of slices (ENS) shown in

Table 1. Equivalent slice number of FPGA hardware resources.

Resource	ENS
Slice	1
DSP	102
BRAM	56

.

For fair comparison, the computing performance in each design is normalized according to the settings, in which the computing time T and parameter N are normalized based on the experimental results. Because the modulo parameter q of the selected comparative literature is all 12,289, the parameter N can be used to represent the data size of the calculation.

The performance resource ratio(PRR) is a composite indicator of performance and hardware resources. The calculation formula of PRR is as follows:

$$PPR=ENS·T/N.$$

(5)

5.2. Experimental Results

The FPGA implementation hardware resource overhead of the two NTT modules proposed in this paper is shown in

Table 2. FPGA implementation resource comparison of NTT modules.

	N	LUT/FF	Slice	BRAM	DSP	Freq (MHz)	Cycle	Time ($\mathsf{\mu }$s)
H-NTT	512	696/403	241	2.5	9	246	1224	4.97
L-NTT	512	440/275	145	2	6	248	2412	9.72
[37]	512	1536/953	-	3	1	278	3443	12.3
[38]	256	875/486	-	-	4	248	3072	12.38
[34]	1024	898/1117	357	10	4	188	2032	10.81

. As can be seen from the table, the hardware resource overhead of the H-NTT module is larger than that of the L-NTT module. One H-NTT module consumes 241 slices, and one L-NTT module consumes 145 slices, which is because there are more computational units and memory blocks in the H-NTT module than in the L-NTT module. The internal RAM of H-NTT is three more blocks than that of L-NTT, but the overall usage of BRAM is not more than doubled. This is because the depth of each block of RAM in H-NTT is only half of that of RAM in L-NTT. This not only facilitates the collision between the two butterfly computing units in H-NTT when computing in parallel, but also greatly reduces the amount of BRAM used.

According to Table 2, the proposed two NTT architectures use less LUT, FF, and slice resources, but use more DSP resources. This is because the arithmetic units in the H-NTT and L-NTT architectures are mostly implemented by DSP. Moreover, the BRAM used by the two NTT modules is less than that of other designs, because the scaling factor in this paper is precalculated, which saves the RAM required for prestorage. The H-NTT module has a significantly shorter operation cycle when the frequency is similar to other designs. Therefore, compared with other NTT modules, the H-NTT module has the shortest operation time. In order to facilitate comparison, the computational performance of each design is normalized according to the settings in this paper. Due to the lack of slice resource and BRAM resource cost data in literature [38], normalized comparison cannot be carried out. The final calculated PPR results of the NTT module are shown in

Table 3. PRR comparison of NTT’s FPGA implementation.

	N	Slice	BRAM	DSP	Time ($\mathsf{\mu }$s)	PRR
H-NTT	512	241	2.5	9	4.97	1.00
L-NTT	512	145	2	6	9.72	1.31
[37]	512	549	3	1	12.30	1.56
[38]	256	-	-	4	12.38	-
[34]	1024	811	10	4	10.81	1.49

.

The proposed polynomial multiplier based on H-NTT module is implemented on FPGA and the performance and hardware resource cost of the design are evaluated. According to the Table 4, our implementation consumes a total of 485 slices, 18 DSPs, and five BRAMs, and the highest frequency achieved is 234.1 MHz. Compared with the Table 2, it can be seen that the main hardware resource overhead of the polynomial multiplier in this paper is about twice that of the H-NTT module. This is because the core operation unit of the polynomial multiplier consists of two parallel H-NTT modules. In addition to NTT operations, other operations in polynomial multiplication such as preprocessing, postprocessing, and INTT operations are multiplexed through H-NTT modules. The calculation unit and storage unit in the polynomial multiplier are completed, and no additional core operation unit is added to the polynomial multiplier, only the related control logic of the polynomial multiplier operation is added, and this part of the logic uses less hardware resources. Therefore, this paper effectively reduces the hardware resource overhead in the polynomial multiplier by multiplexing the computing units of the NTT module.

Furthermore, comparing with [28], in the case of the same parameter N, the slice occupancy and BRAM designed in this paper are much smaller, and the DSP occupancy is slightly more. From the perspective of computing performance, the frequency of our design is slightly lower, but the total number of calculation cycles is less; therefore, the calculation time to complete a 512-point NTT is less. The result indicates that in the case of slightly higher performance, the design of this paper reduces the resource occupation significantly. In addition, our design is compared with the other two designs with the same parameter N. The resource overhead of LUT, FF, slice, etc. in [27] is greater, but the DSP resources are much smaller than our design, because they use a single core. Although the work in [27] has less resource overhead, the number of computing cycles is more than three times, and the time to complete a polynomial multiplication operation is four times that of the design in our work, and the overall performance is low. The highest frequency in [39] is similar to our work, the number of calculation cycles and the overall calculation time are about 1/2, but its slice resource overhead is three times that of our design, the use of BRAM is also greater, and the overall hardware resources overhead is greater than in our work.

Table 4. FPGA implementation resource comparison of polynomial multipliers.

	N	LUT/FF	Slice	BRAM	DSP	Freq (MHz)	Cycle	Time ($\mathsf{\mu }$s)
This paper	512	1390/873	485	5	18	234.1	3120	13.32
[27]	512	1585/1205	615	4	1	196	10014	51.09
[28]	512	-/-	870	8.5	16	253.1	3630	14.32
[38]	256	1986/753	698	4	4	225.3	6900	25.74
[35]	512	4780/-	1744	24	16	232	5251	22.58
[40]	1024	1208/-	556	14	14	211.6	-	37.674
[39]	512	-/-	1246	6	16	249.3	1690	6.78

Table 4. FPGA implementation resource comparison of polynomial multipliers.

	N	LUT/FF	Slice	BRAM	DSP	Freq (MHz)	Cycle	Time ($\mathsf{\mu }$s)
This paper	512	1390/873	485	5	18	234.1	3120	13.32
[27]	512	1585/1205	615	4	1	196	10014	51.09
[28]	512	-/-	870	8.5	16	253.1	3630	14.32
[38]	256	1986/753	698	4	4	225.3	6900	25.74
[35]	512	4780/-	1744	24	16	232	5251	22.58
[40]	1024	1208/-	556	14	14	211.6	-	37.674
[39]	512	-/-	1246	6	16	249.3	1690	6.78

The performance resource ratio (PRR) of each design is shown in the

Table 5. PRR comparison of polynomial multiplier’s FPGA implementation.

	N	Slice	BRAM	DSP	Time ($\mathsf{\mu }$s)	PRR
This paper	512	485	5	18	13.32	1.00
[27]	512	615	4	1	51.09	1.39
[28]	512	870	8.5	16	14.32	1.22
[38]	256	698	4	4	25.74	1.98
[35]	512	1744	24	16	12.03	1.64
[40]	1024	556	14	14	37.674	1.50
[39]	512	1246	6	16	6.78	0.63

. According to the comparison results, the polynomial multiplier we proposed is better than most designs; only the PRR of the literature [39] is better than ours. However, compared with the literature [39], the slice and storage of our paper is less, thus being more appropriate for application situations that are sensitive to hardware resources. In addition, compared with other hardware designs with the same operation scale (parameter N is the same), the storage resource BRAM consumed by the design in this paper is significantly smaller. The BRAM resource overhead of the literature [27] is somewhat smaller than our design because its hardware is in the operation process. The parameters are all calculated in real time, which also causes the much longer calculation time. The comparison results prove that the storage and precomputing technology of the twiddle factor proposed in this paper can effectively reduce the storage resource overhead.

5.3. Discussion

In summary, the proposed hardware implementation has good overall performance. Compared with the modulo multiplication units in other designs, the Montgomery modulo multiplication unit we adopted not only optimizes the difficulty of modulo calculation in the process of modulo multiplication calculation, but also effectively uses the potential parallelism in the calculation process.

In addition, the parameter preprocessing schemepaper, which we proposed after in-depth analysis of the characteristics of parameters such as rotation factor, can significantly reduce the cost of storage resources. Compared with the work [28,35], although the calculation time is similar to the results of this paper, the RAM resources stored in parameters are more than twice of that in our paper. The hardware design scheme of polynomial multiplier proposed in this paper provides a novel design idea for ASIC implementation in security chip application scenarios. Compared to the FPGA, the implementation of ASIC pays more attention to the effective use of hardware resource in embedded application scenarios. In contrast with ARM RISC-V implementation, ASIC is able to obtain polynomial multiplication operation effect with higher performance at lower cost. In ASIC design, the comprehensive evaluation of performance and cost are the focus of attention. The PRR of the literature [39] is better than ours. However, the resource cost of our paper is less, which is still more appropriate for the ASIC implementation.

6. Conclusions

In order to solve the problem of low computational performance of current lattice cipher algorithms, the polynomial multiplier of its core operator is studied and designed in this paper. Two NTT module hardware architectures and an optimized modular multiplication unit are proposed. The hardware unit has a pipelined structure which can realize fast modular multiplication calculation and enable the computational units in the NTT module to read data alternately. Then we propose a parameter storage and precomputation scheme, which effectively reduces the memory. Finally, this paper implements a polynomial multiplier hardware based on NTT. The experimental results show that the polynomial multiplier proposed in this paper has good computing performance while using fewer hardware resources, which can effectively improve the computing efficiency of the lattice cipher algorithm and meet the application requirements in security chips.

As the future work, we are focusing on the real performance requirements in special application scenarios. By adjusting the number of butterfly computations deployed in parallel in the NTT module, the polynomial multiplier can address the requirements of speed and resource cost in different scenes. Moreover, the design in this paper is the underlying operator of lattice cipher algorithm, our future research will design a complete hardware accelerator, which is expected to further improve the computational performance of algorithm.