Side-Milling-Force Model Considering Tool Runout and Workpiece Deformation
Abstract
:1. Introduction
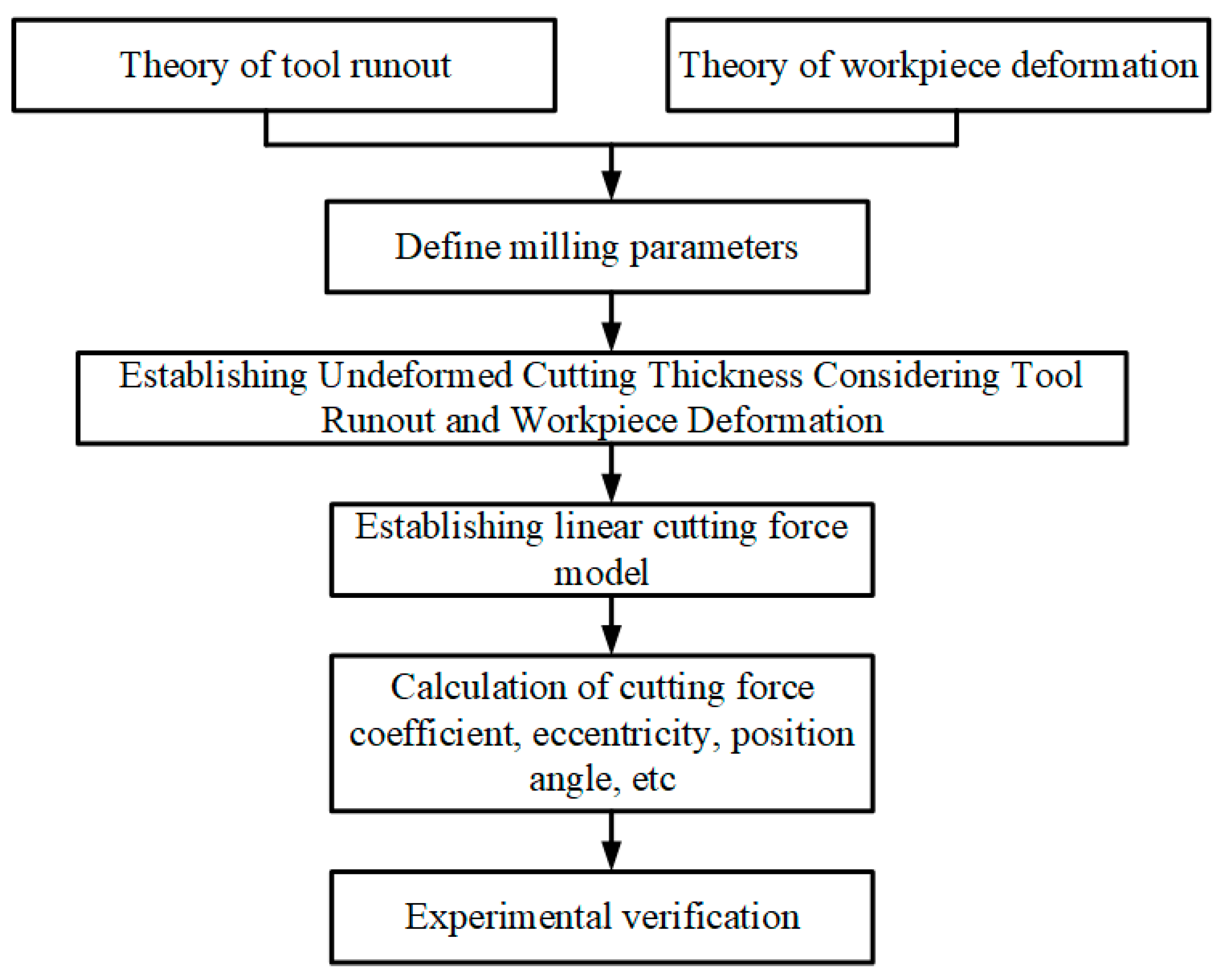
2. Theoretical Model
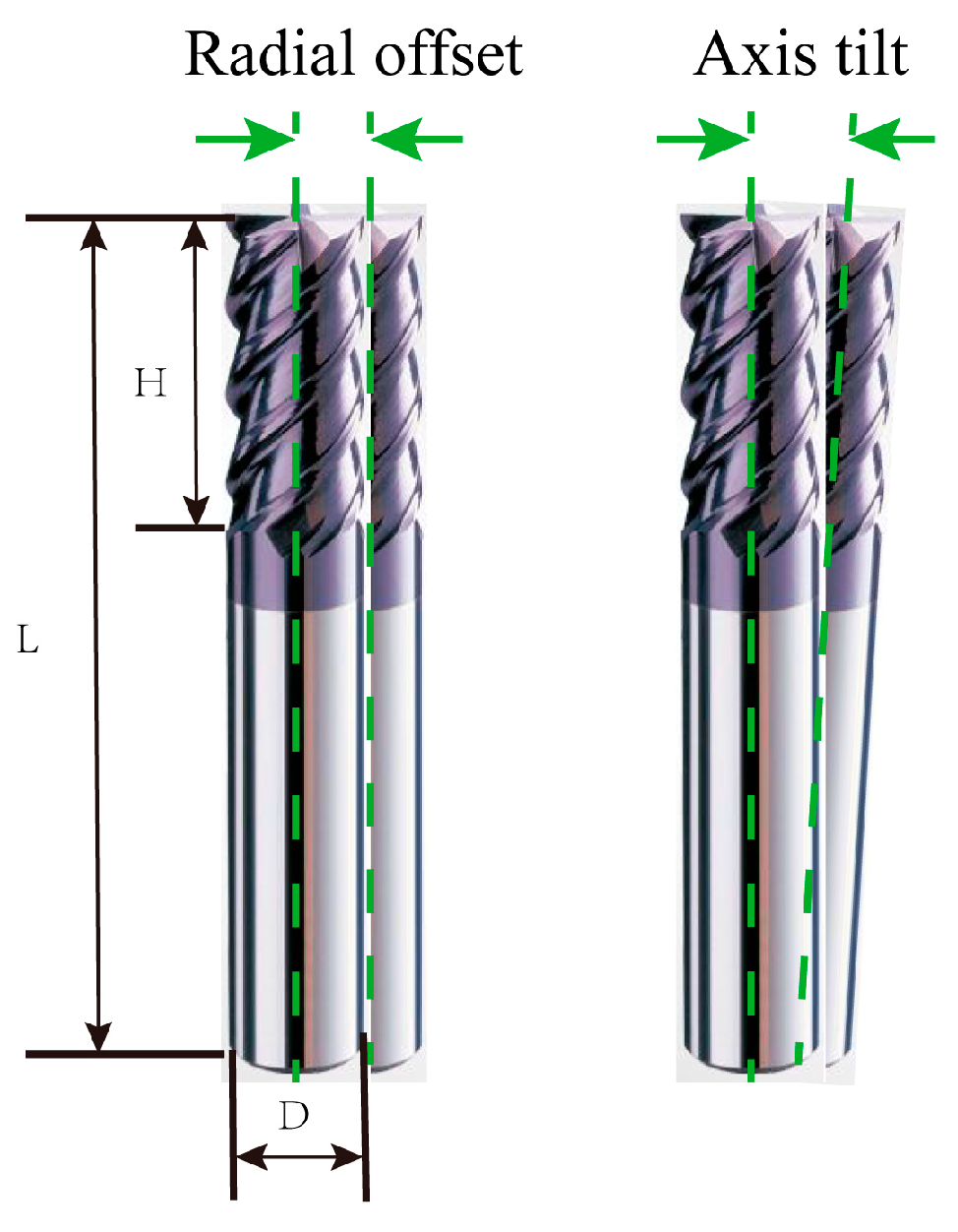
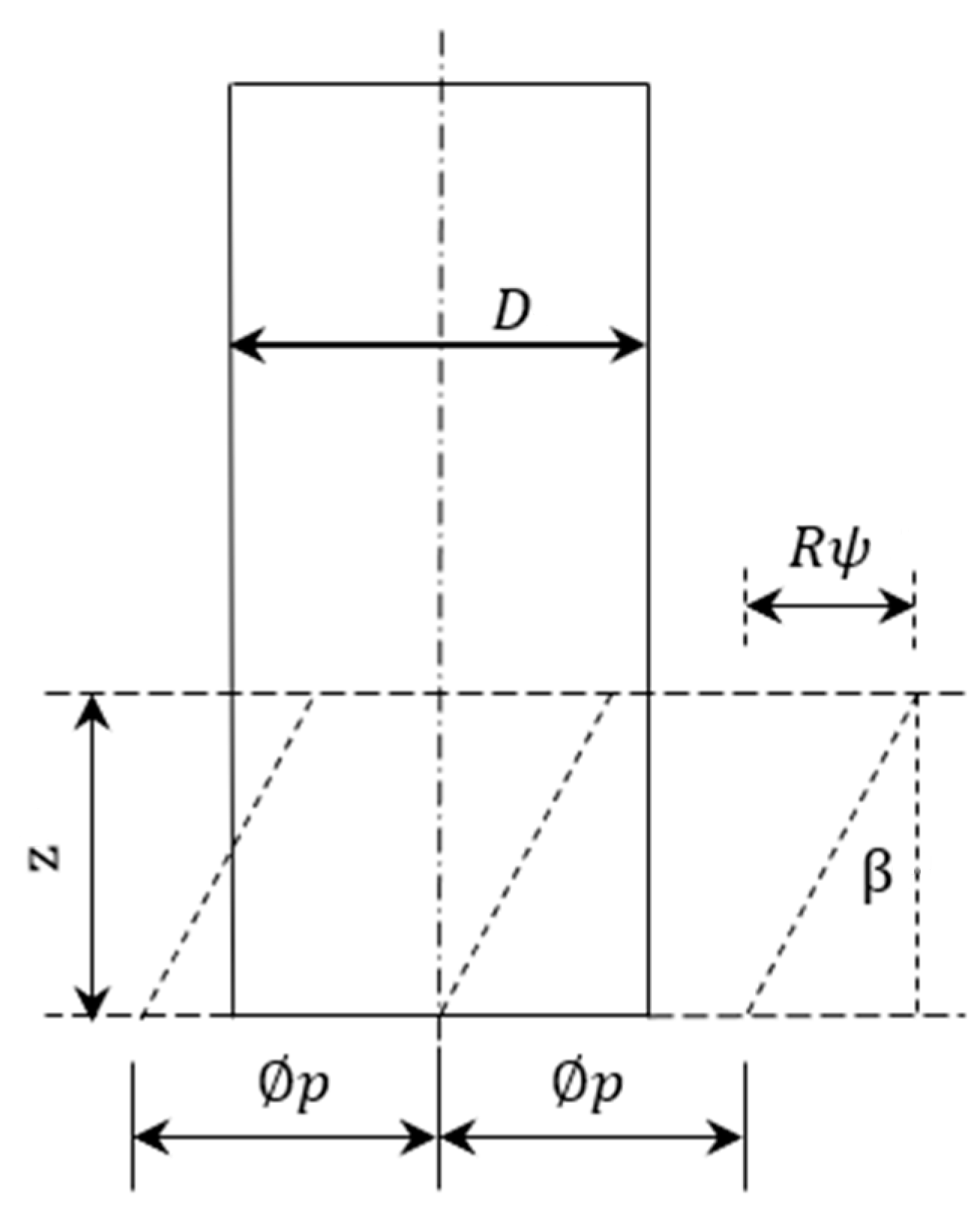
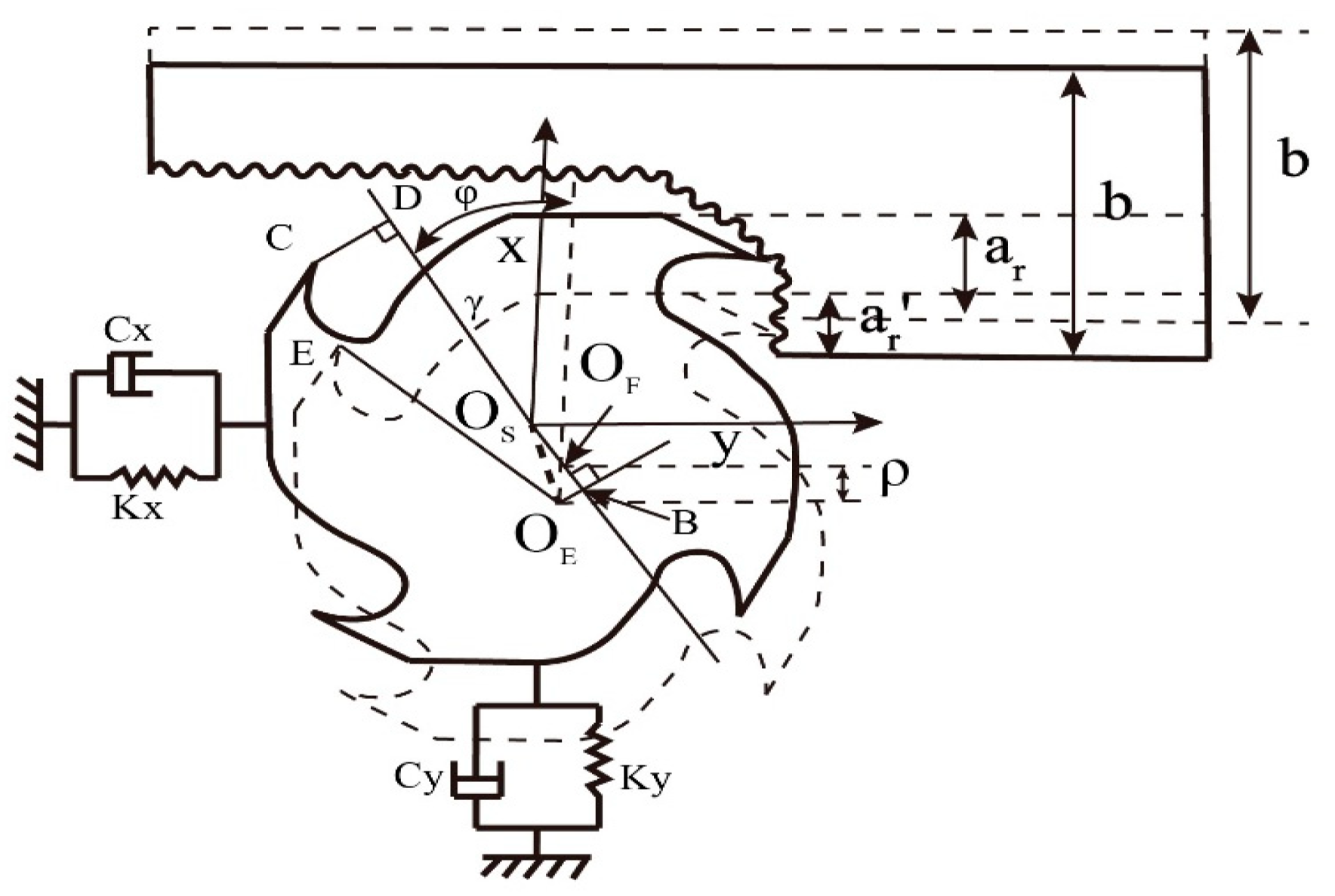
2.1. Meaning of Tool Runout and Definition of Parameters
2.2. Undeformed Cutting Thickness Model Considering Tool Runout and Workpiece Deformation
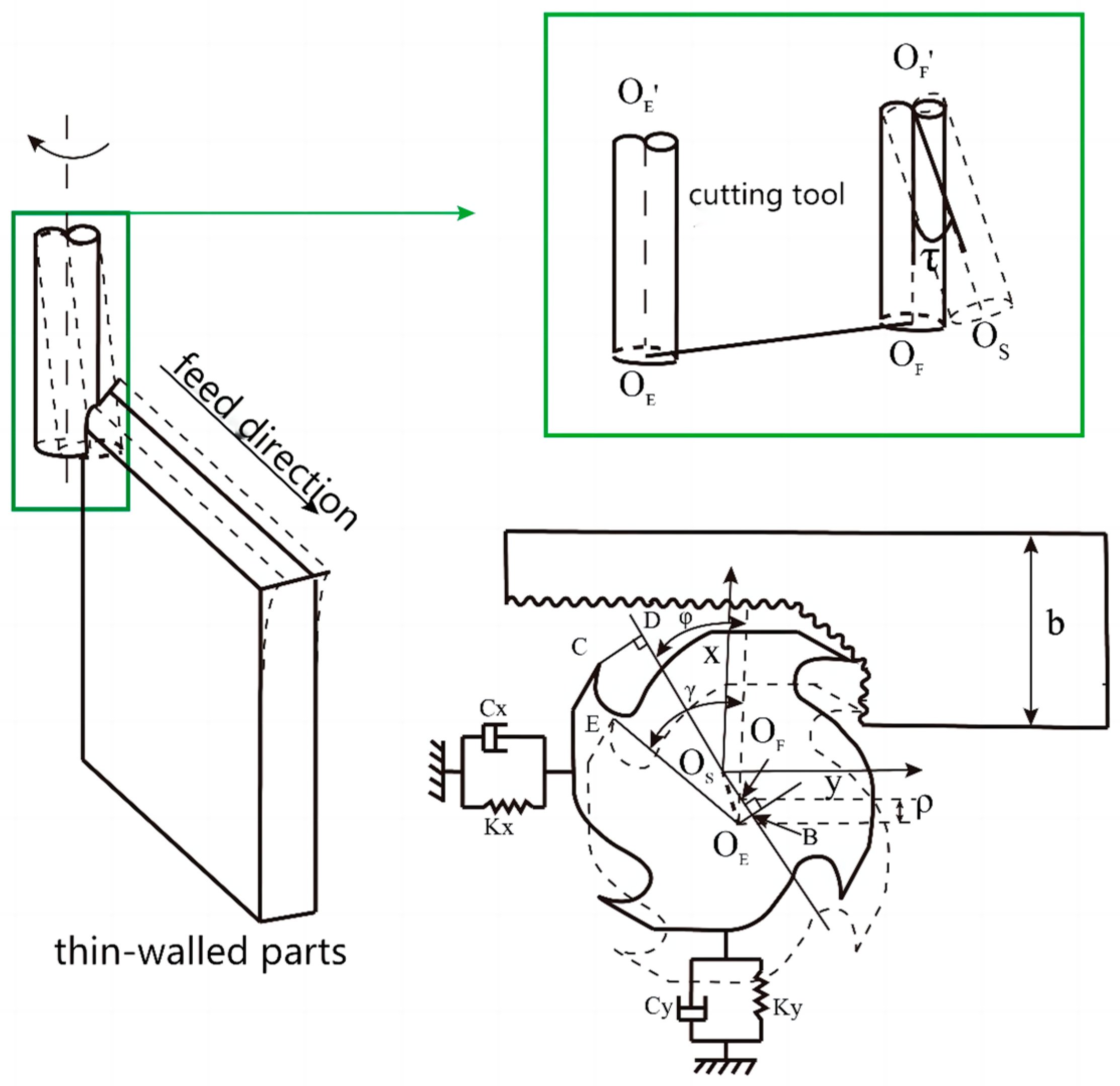
2.2.1. Geometric Parameter Definition of Milling Process
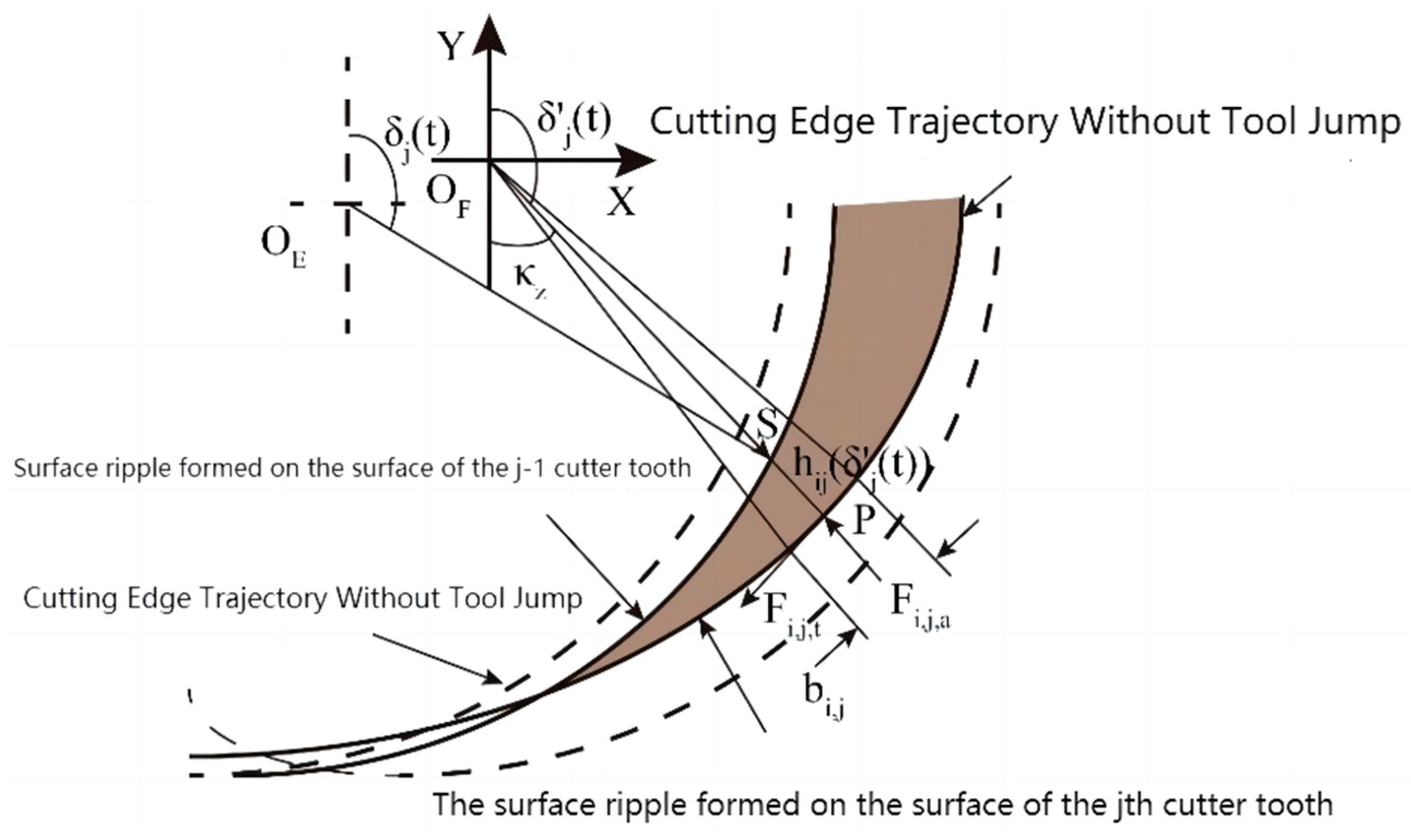
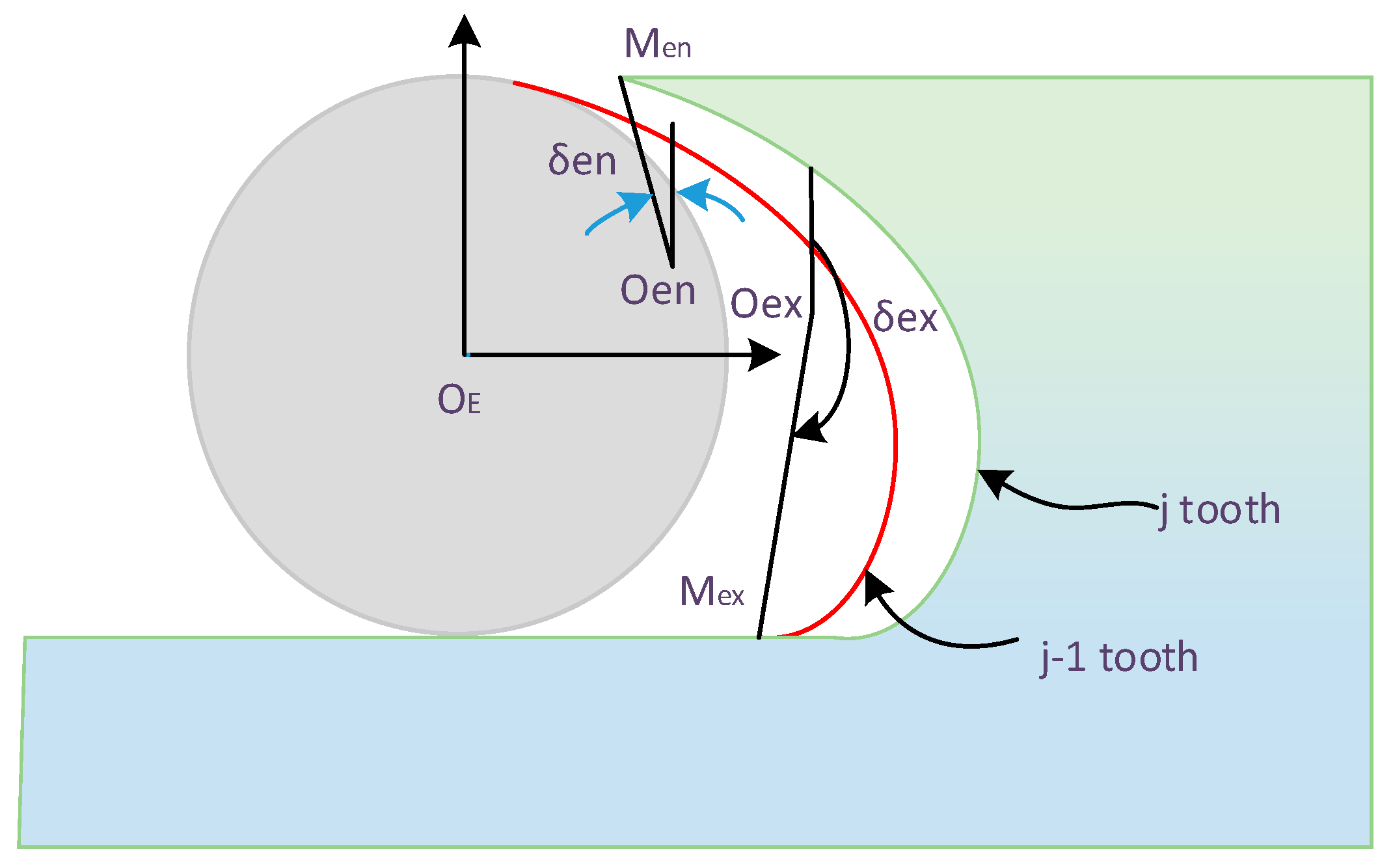
2.2.2. Undeformed Cutting Thickness Model Considering Tool Runout and Workpiece Deformation
3. Establishment of Milling Force Models for Titanium Alloy Thin-Walled Parts
4. Identification of Milling Force Coefficient
4.1. Experimental Theory of Milling Force Coefficient
4.2. Laboratory Equipment
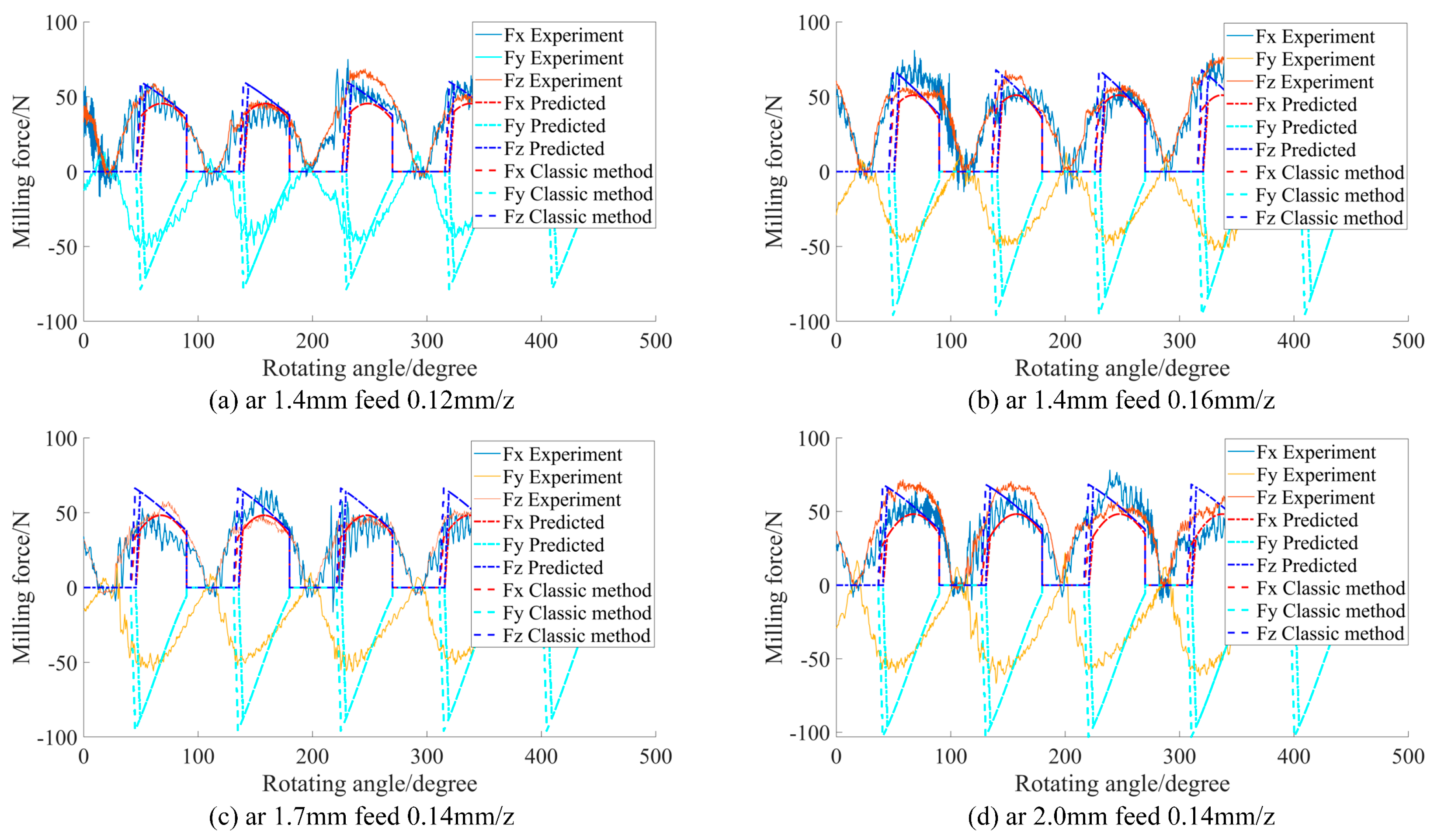
5. Experimental Verification and Result Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| uncut chip thickness | |
| the feed per tooth | |
| the tool contact angle | |
| eccentric distance | |
| position angle of the eccentric | |
| tangle | |
| position angle of the tilt angle | |
| the hanging length of the tool after installation | |
| D | the radial of the cutter. |
| H | the length of the cutting edge. |
| actual cutting radius | |
| lag angle | |
| helix angle | |
| rotation angle | |
| the angular velocity of the spindle | |
| the cutting time | |
| the number of milling cutter teeth | |
| the radial cutting depth | |
| offset of tool cycloid motion path in x direction | |
| offset of tool cycloid motion path in y direction | |
| the cutting-in angle | |
| cutting-out angle | |
| the point on the trochoid trajectory of the j − 1th tooth | |
| the center position of the j tooth corresponding to | |
| the time point of the J tooth corresponding to | |
| the subcycloid trajectory of the j − 1 tooth | |
| the time point of corresponding to the jth tooth | |
| , , | the edge force coefficients |
| , , | cutting-force coefficients |
| the axial height | |
| the undeformed cutting thickness | |
| the axial cutting depth of the tool |
References
- Andersson, C.; Andersson, M.; Ståhl, J.E. Experimental studies of cutting force variation in face milling. Int. J. Mach. Tools Manuf. 2011, 51, 67–76. [Google Scholar] [CrossRef]
- Matsumura, T.; Tamura, S. Cutting Force Model in Milling with Cutter Runout. Procedia CIRP 2017, 58, 566–571. [Google Scholar] [CrossRef]
- Dargusch, M.S.; Sun, S.; Ji, W.K.; Li, T.; Trimby, P.; Cairney, J. Effect of tool wear evolution on chip formation during dry machining of Ti-6Al-4V alloy. Int. J. Mach. Tools Manuf. 2017, 126, 86–98. [Google Scholar] [CrossRef]
- Liu, C.; Wu, J.Q.; Li, G.H.; Tan, G.Y. Frequency-spectrum cha-racteristics of force in end milling with tool wear and eccentricity. Int. J. Adv. Manuf. Technol. 2013, 67, 925–938. [Google Scholar] [CrossRef]
- Armarego, E.J.A.; Deshpande, N.P. Computerized End-Milling Force Predictions with Cutting Models Allowing for Eccentricity and Cutter Deflections. CIRP Ann.-Manuf. Technol. 1991, 40, 25–29. [Google Scholar] [CrossRef]
- Liang, S.Y.; Wang, J. Milling force convolution modeling for identification of cutter axis offset. Int. J. Mach. Tools Manuf. 1994, 34, 1177–1190. [Google Scholar] [CrossRef]
- Shi, H.R. An analytical expression for end milling forces and tool deflection using Fourier series. Int. J. Adv. Manuf. Technol. 2012, 59, 37–46. [Google Scholar]
- Cao, Q.; Xue, D.; Zhao, J.; Li, Y. A cutting force model considering influence of radius of curvature for sculptured surface machining. Int. J. Adv. Manuf. Technol. 2011, 54, 821–835. [Google Scholar] [CrossRef]
- Cao, Q.; Zhao, J.; Han, S.; Chen, X. Force coefficients identification considering inclination angle for ball-end finish milling. Precis. Eng. 2012, 36, 252–260. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.H.; Qin, G.H.; Tan, G. Efficient calibration of instantaneous cutting force coefficients and runout parameters for general end mills. Int. J. Mach. Tools Manuf. 2007, 47, 1767–1776. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.-H.; Dang, J.-W.; Yang, Y. New procedures for calibration of instantaneous cutting force coefficients and cutter runout parameters in peripheral milling. Int. J. Mach. Tools Manuf. 2009, 49, 1144–1151. [Google Scholar] [CrossRef]
- Desai, K.A.; Agarwal, P.K.; Rao, P.V.M. Process geometry modeling with cutter runout for milling of curved surfaces. Int. J. Mach. Tools Manuf. 2009, 49, 1015–1028. [Google Scholar] [CrossRef]
- Zhu, Z.; Yan, R.; Peng, F.; Duan, X.; Zhou, L.; Song, K.; Guo, C. Parametric chip thickness model based cutting forces estimation considering cutter runout of five-axis general end milling. Int. J. Mach. Tools Manuf. 2016, 101, 35–51. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.H. Calculations of chip thickness and cutting forces in flexible end milling. Int. J. Adv. Manuf. Technol. 2005, 29, 637–647. [Google Scholar] [CrossRef]
- Ratchev, S.; Govender, E.; Nikov, S.; Phuah, K.; Tsiklos, G. Force and deflection modelling in milling of low-rigidity complex parts. J. Mater. Process. Technol. 2003, 143–144, 796–801. [Google Scholar] [CrossRef]
- Ratchev, S.; Liu, S.; Huang, W.; Becker, A.A. An advanced FEA based force induced error compensation strategy in milling. Int. J. Mach. Tools Manuf. 2006, 46, 542–551. [Google Scholar] [CrossRef]
- Faassen, R.P.H.; Van De Wouw, N.; Nijmeijer, H.; Oosterling, J.A.J. An Improved Tool Path Model Including Periodic Delay for Chatter Prediction in Milling. J. Comput. Nonlinear Dyn. 2007, 2, 167. [Google Scholar] [CrossRef]
- Rodríguez, P.; Labarga, J.E. A new model for the prediction of cutting forces in micro-end-milling operations. J. Mater. Process. Tech. 2013, 213, 261–268. [Google Scholar] [CrossRef]
- Kaymakci, M.; Kilic, Z.M.; Altintas, Y. Unified cutting force model for turnin-g, boring, drilling and milling operations. Int. J. Mach. Tools Manuf. 2012, 55, 34–45. [Google Scholar] [CrossRef]
- Safari, H.; Sharif, S.; Izman, S.; Jafari, H.; Kurniawan, D. Cutting Force and Surface Roughness Characterization in Cryogenic High-Speed End Milling of Ti6Al-4V. Adv. Manuf. Process. 2014, 29, 350–356. [Google Scholar] [CrossRef]
- Azeem, A.; Feng, H.Y. Cutting force prediction for ball-end mills with non-horizontal and; rotational cutting motions. Int. J. Adv. Manuf. Technol. 2013, 67, 1833–1845. [Google Scholar] [CrossRef]
- Ji, C.; Li, Y.; Qin, X.; Zhao, Q.; Sun, D.; Jin, Y. 3D FEM simulation of helical milling hole process for titanium alloy Ti-6Al-4V. Int. J. Adv. Manuf. Technol. 2015, 81, 1733–1742. [Google Scholar] [CrossRef] [Green Version]
- Altintaş, Y.; Lee, P. A General Mechanics and Dynamics Model for Helical End Mills. Ann. Cirp 1996, 45, 59–64. [Google Scholar] [CrossRef]
- Izamshah, R.; Yuhazri, M.Y.; Hadzley, M.; Ali, M.A.; Subramonian, S. Effects of End Mill Helix Angle on Accuracy for Machining Thin-Rib Aerospace Component. Appl. Mech. Mater. 2013, 315, 773–777. [Google Scholar] [CrossRef]
- Mohd Hadzley, A.B.; Nurul Fatin, M.R.; Izamshah, R.; Siti Sarah, A.; Kasim, M.S.; Ali, M.A.; Sulaiman, M.A. Effects of Helix Angle on Cutting Performance for Machining Thin-Wall Aerospace Monolithic Component. Appl. Mech. Mater. 2014, 699, 3–8. [Google Scholar] [CrossRef]
- Arnaud, L.; Gonzalo, O.; Seguy, S.; Jauregi, H.; Peigné, G. Simulation of low rigidity part machining applied to thin-walled structures. Int. J. Adv. Manuf. Technol. 2011, 54, 479–488. [Google Scholar] [CrossRef]
- Altintas, Y. Discrete-Time Prediction of Chatter Stability, Cutting Forces, and Surface Location Errors in Flexible Milling Systems. J. Manuf. Sci. Eng. 2012, 134, 61–69. [Google Scholar]
- Kuntoğlu, M.; Aslan, A.; Pimenov, D.Y.; Usca, Ü.A.; Salur, E.; Gupta, M.K.; Mikolajczyk, T.; Giasin, K.; Kapłonek, W.; Sharma, S. A Review of Indirect Tool Condition Monitoring Systems and Decision-Making Methods in Turning: Critical Analysis and Trends. Sensors 2021, 21, 108. [Google Scholar] [CrossRef]
- Salur, E.; Aslan, A.; Kuntoglu, M.; Gunes, A.; Sahin, O.S. Experimental study and analysis of machinability characteristics of metal matrix composites during drilling. Compos. Part B Eng. 2019, 166, 401–413. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Matuszak, M.; Powałka, B.; Madajewski, M.; Maruda, R.W.; Królczyk, G.M. Prediction of cutting forces during micro end milling considering chip thickness accumulation. Int. J. Mach. Tools Manuf. 2019, 147, 103466. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Mrozek, K. Mechanical and technological aspects of micro ball end milling with various tool inclinations. Int. J. Mech. Sci. 2017, 134, 424–435. [Google Scholar] [CrossRef]
- Wojciechowski, S. The estimation of cutting forces and specific force coefficients during finishing ball end milling of inclined surfaces. Int. J. Mach. Tools Manuf. 2015, 89, 110–123. [Google Scholar] [CrossRef]
- Li, X.P.; Li, H.Z. Theoretical modelling of cutting forces in helical end milling with cutter runout. Int. J. Mech. Sci. 2004, 46, 1399–1414. [Google Scholar] [CrossRef]
- Li, H.Z.; Liu, K.; Li, X.P. A new method for determining the undeformed chip thickness in milling. J. Mater. Process. Technol. 2001, 113, 378–384. [Google Scholar] [CrossRef]



| Main Performance | Parameter |
|---|---|
| Maximum spindle speed | 6000 r/min |
| Stroke (x, y, z) | 850 mm, 500 mm, 630 mm |
| Maximum spindle torque | 70/909 (continuous/30 min) N.M |
| Max fastest feed rate | X, Y 24 m/min, Z 15 m/min |
| Maximum load of workbench | 500 kg |
| Power | 11/7.5 KW |
| Number | Spindle Speed (r/min) | Axial Cutting Depth (mm) | Radial Cutting Depth (mm) | Feed per Tooth (mm/z) | X-Axis Average Force (N) | Y-Axis Average Force (N) |
|---|---|---|---|---|---|---|
| 1 | 1000 | 0.4 | 10 | 0.02 | 18.8 | 23.0 |
| 2 | 1000 | 0.4 | 10 | 0.03 | 20.5 | 25.7 |
| 3 | 1000 | 0.4 | 10 | 0.04 | 23.5 | 33.0 |
| 4 | 1000 | 0.4 | 10 | 0.05 | 26.0 | 41.9 |
| Shear Force Coefficient | Numerical Value (MPa) | Tooth Force Coefficient | Numerical Value (N/m) |
|---|---|---|---|
| 1624.6 | 6.9 | ||
| 613.7 | 32.3 |
| Cutting Tool | Diameter (mm) | Number of Teeth | Helix Angle (°) | Eccentricity (mm) | Position Angle of Eccentricity (°) |
|---|---|---|---|---|---|
| Flat-head-milling-machine | 10 | 2 | 30 | 0.0027 | 5.33 |
| Spindle Speed (r/min) | Axial Cutting Depth (mm) | Radial Cutting Depth (mm) | Feed per Tooth (mm/z) |
|---|---|---|---|
| 1000 | 0.5 | 0.5 | 0.01 |
| Feed Rate (mm/min) | Fx (Proposed) | Fx (Classical) | Fy (Proposed) | Fy (Classical) | Fz (Proposed) | Fz (Classical) |
|---|---|---|---|---|---|---|
| 198 | 17.80% | 16.50% | 43.21% | 63.85% | 13.46% | 18.92% |
| 234 | 27.40% | 22.38% | 47.83% | 75.21% | 5.68% | 8.84% |
| 288 | 23.24% | 24.56% | 66.54% | 87.09% | 4.62% | 3.76% |
| Radial Depth (mm) | Fx (Proposed) | Fx (Classical) | Fy (Proposed) | Fy (Classical) | Fz (Proposed) | Fz (Classical) |
|---|---|---|---|---|---|---|
| 0.3 | 15.06% | 19.08% | 56.01% | 89.45% | 25.16% | 32.48% |
| 0.5 | 13.27% | 16.47% | 53.88% | 86.54% | 26.86% | 25.22% |
| 0.7 | 22.04% | 24.51% | 56.43% | 65.34% | 6.55% | 7.58% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, M.; Yu, X.; Bao, W.; Liu, C.; Xia, M. Side-Milling-Force Model Considering Tool Runout and Workpiece Deformation. Electronics 2023, 12, 968. https://doi.org/10.3390/electronics12040968
Xie M, Yu X, Bao W, Liu C, Xia M. Side-Milling-Force Model Considering Tool Runout and Workpiece Deformation. Electronics. 2023; 12(4):968. https://doi.org/10.3390/electronics12040968
Chicago/Turabian StyleXie, Miao, Xinli Yu, Wei Bao, Changfu Liu, and Min Xia. 2023. "Side-Milling-Force Model Considering Tool Runout and Workpiece Deformation" Electronics 12, no. 4: 968. https://doi.org/10.3390/electronics12040968
APA StyleXie, M., Yu, X., Bao, W., Liu, C., & Xia, M. (2023). Side-Milling-Force Model Considering Tool Runout and Workpiece Deformation. Electronics, 12(4), 968. https://doi.org/10.3390/electronics12040968








