Particle-In-Cell Simulations of High Efficiency 12-Vanes 2.45 GHz Continuous Wave Magnetron

Abstract

As an essential vacuum electronic device for producing the microwave, the magnetron has various applications. This study developed a novel high-efficiency 12-vanes CW magnetron and anode resonance system that improved mode separation, expanded the working space of π-mode and made other modes more challenging to trigger, ultimately eliminating the possibility of mode jumping. A magnetron was simultaneously supplied with a particular quantity of anode voltage, and the cathode was generated by the electron, and high-frequency field interaction of a homogeneous magnetic field. The work efficiency of the 12-vanes CW magnetron was significantly enhanced. Given an anode voltage of 8000 V and a magnetic flux density of 3980 Gs as a consequence of particle simulation, the variation trend of a magnetron’s output power oscillation curve correlated with the development of hexagonal spokes. After a period of stable operation, the magnetron’s fundamental parameters were determined to be as follows: the primary frequency oscillation frequency was 2.466 GHz, the anode collision current was 1.08 A, the amplitude of sinusoidal oscillation was 125, the output power was 7812.5 W, and the corresponding power conversion efficiency was 90.42%. Changing the magnitude of the anode voltage or magnetic flux density resulted in a reduction in power conversion efficiency within a particular range; however, between 85% and 90% stability was maintained.

1. Introduction

Today, the physical effects of the high-power microwave are extensively employed in the military, communications, medical, food heating, and drying fields, and have become an essential component of scientific research and production life [1,2,3,4,5,6,7,8,9,10]. The magnetron is a potential vacuum electronic device; compared to other vacuum electronic devices, the utility model offers benefits such as small volume, inexpensive manufacturing cost, high market share, high power, and high efficiency, among others [11,12,13,14]. Researchers have achieved advancements in boosting energy efficiency [15,16], stabilizing operating frequency ranges [17], and swiftly commencing oscillation conditions [17] due to the coaxial construction of CW magnetrons.

Exciting advancements have been achieved in the investigation of magnetrons for 2.45 GHz microwave oven. The 10-vanes magnetron at Sichuan University performed at an anode voltage of 4200 V and an anode collision current of 0.68 A, with an efficiency of 70.59% [18]. As the anode voltage and magnetic flux density were raised while the 2.45 GHz magnetron was operating, it was determined that the anode collision current gradually rose and virtually exhibited a positive proportional relationship [19]. Similarly, the anode voltage and magnetic flux density values obtained from the π-mode line had little effect on the resonant frequency of a 2.45 GHz magnetron operating in a stable manner [19]. There is a correlation between the anode voltage and the magnetron’s operational efficiency, according to research conducted at the University of New Mexico. As the anode voltage was raised from 4200 V to 8000 V, the efficiency of the 10-vanes magnetron improved from 72–75% to 83–85% [20]. The cathode branch’s current density can also be decreased. This gives a direction for an investigation into improving the efficiency of magnetrons operating at 2.45 GHz. Nevertheless, the study’s 10-vanes microwave ovens maintained an efficiency of 70–85%, making it incredibly challenging to achieve more than 85% energy efficiency for greater energy efficiency.

Recently, there has been a rise in attention to optimizing the process of energy transformation [21]. At the magnetron’s operational voltage, it is common knowledge that electrons in the resonant space are accelerated in the form of spokes toward the anode. In the oscillating condition, the electrons’ mobility energy is absorbed by the radial electric field, allowing the electron cloud to maintain phase with the high frequency field. A portion of the electron’s energy is dissipated as heat when it strikes the anode, but power loss reduces this efficiency. A loss will also be generated at the cathode because negative electrons are repelled. In addition, a resonant system’s oscillating surface will generate a high-frequency current; however, because of the skin effect, this current will be trapped at the surface of the resonant system and dissipate as heat. As a consequence, research into making magnetrons more effective has been a significant topic of discussion in recent years. However, the efficiency of electron conversion when using a magnetron is unsatisfactory. Even a minor modification will drastically alter the overall electronic efficiency of the structure or increase local performance [22,23,24]. This work presents a novel, highly efficient magnetron design on the foundational ideas of the 2.45 GHz magnetron. A total of 12 resonant cavity vanes were found to be optimal for maximizing output power while minimizing the magnetic flux density, which is necessary to prevent the anode from overheating.

The findings of a number of studies indicate that it is not possible to considerably enhance energy efficiency while keeping the same structure as a 2.45 GHz CW magnetron. This is due to the vast majority of 2.45 GHz CW magnetron constructions being made up of 10 vanes. As a consequence, the efficiency enhancement of 2.45 GHz CW magnetron has reached a roadblock. In today’s world, energy and environmental issues are increasingly prominent. By using continuous-wave magnetrons that have a better efficiency, there will be an improvement in the use of energy that reaches its greatest potential. As a consequence, in the research for this paper, we aimed to make improvements to the structure of the magnetron resonant cavity and change the original 10-vanes structure to a 12-vanes structure. As a result of this, we want to make some improvements on the structure of the magnetron resonant cavity. Consequently, it is good to increase the number of 12 vanes in order to produce greater power output, and the structure of the 12 vanes does not damage the electron clustering effect in the cavity. Under the influence of a particular voltage and magnetic flux density, a stable interaction can be achieved.

Simulation research was conducted using CST simulation software. To begin, the operational characteristics of the magnetron in π mode must be determined by using eigenmode and frequency-domain modelling in order to reduce the risk of mode hopping in the most effective way possible. In CW magnetron, the relationship between anode voltage and magnetic field is extremely important. One must then determine the magnetic field voltage (B-V) operation curve to make the magnetic field and voltage reach the optimal value, which can speed up the starting time and improve energy efficiency. After that, simulations of particles are performed. These simulations have the ability to calculate the change in physical phenomena from their beginning state to their end state within a certain amount of time. In addition, the simulations can calculate the interplay between electromagnetic fields and space charges. This leads to a major increase in the efficiency of the calculations and also makes the findings simple to notice. As a consequence, the results may be observed more easily. Not only is it possible to utilize particle modelling to compute the output power and efficiency of CW magnetrons, but their resonance frequency and average collision current can be also determined using this method.

There are a total of five sections in this article, including the introduction. The idea and design of the proposed improved coaxial magnetron are presented in Section 2. In Section 3, we conducted eigenmode and frequency simulations to evaluate the suggested designs. Section 4 focused on calculating the magnetron’s B-V function curve under standard operating circumstances. The suggested magnetron was simulated in three dimensions using a PIC in Section 5. This topic is concluded and discussed in Section 6.

2. Concept and Design of 12-Vanes Magnetron

The primary components of a coaxial magnetron are the cathode, the anode resonance system, the magnetic circuit portion, the input component, the output component, and the cooling system. Its many components profoundly affect the performance and efficiency of a magnetron, a kind of microwave oscillator with an orthogonal field.

The emission of electrons is accomplished mainly via the cathode module. Whenever the filament is subjected to enough current, it gradually releases electrons. In order to complete the energy exchange with the high-frequency field, the electron must be in the anode resonant system, which essentially controls the resonant frequency. It consists of an anode cylinder, an antenna, a vane connected to the inside of the anode cylinder, and a strap of varying lengths and widths. In this design, the resonant cavity is formed by a gap between a pair of vanes evenly spaced around the inner circumference of the anode cylinder. Connecting the vanes through a size–size strap helps to better separate the modes and prevents the modes from skipping over each other. By linking with a vane in the anode cylinder, the antenna is able to siphon power from the magnetron’s high-frequency field. For interactions between electron and high-frequency fields, the magnetic circuit component can generate a magnetic field with a constant intensity. Inductors and capacitors, which make up most of the input component, bring in the power. The energy a microwave oven emits is directly related to how the “output component” connects microwave power to the outside load. For the magnetron to function at a certain temperature, a cooling system must be employed to cool it to that temperature. Air-cooling systems are commonplace due to their ease of use and straightforward design. When the heat dissipation area is increased, the magnetron is cooled and returns to regular operation.

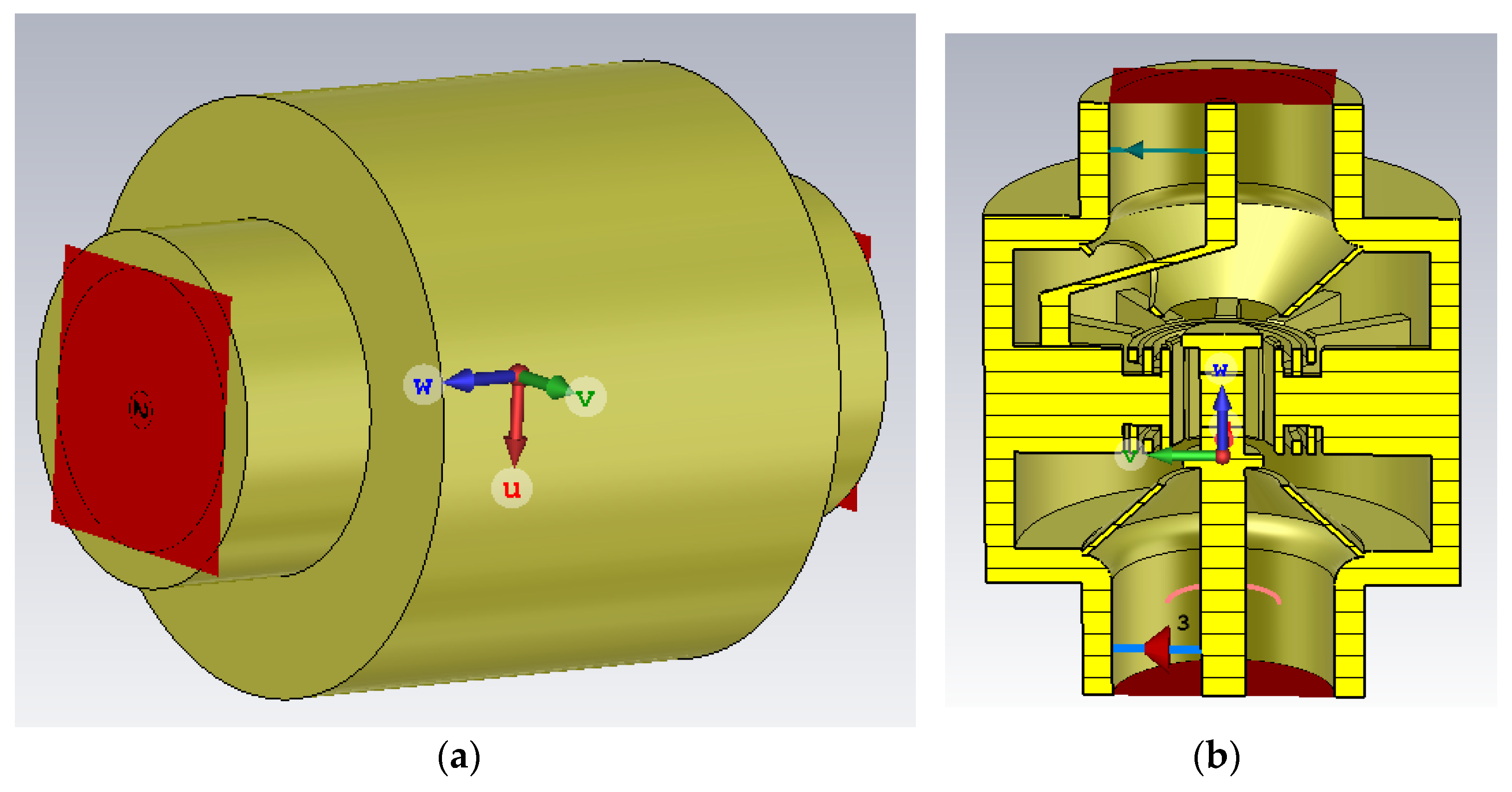
According to the magnetron structure research and analysis of the current 10-vanes magnetron model, the number of the vane and the resonator must be even. This is necessary to make the magnetron stable enough to function in π-mode. According to design experience, there is a tight link between the number of resonators and the electromagnetic wave’s wavelength; when the wavelength is 10 to 20 cm, the number of resonators is approximately 8 to 12. Choosing a larger number of resonators optimizes the power output efficiency. Increasing the number of cavities would be impossible, however, since doing so would destroy the electron clustering effect, reduce the effectiveness of the internal interaction, and make vibration essentially impossible. This resulted in the final decision of 12 vanes for the resonant cavity. The magnetron’s simulation model is shown in Figure 1, and the device’s exact dimensions are listed in

Table 1. Dimensions of the device.

Description	Value
Radius of the anode cylinder	17.78 mm
Height of the anode cylinder	27.94 mm
Diameter of the anode	8.89 mm
Radius of the cathode	1.91 mm
Length of the vanes	13.34 mm
Width of the vanes	9.53 mm
Thickness of the vanes	1.78 mm
Inner radius and outer radius and height of the large strap	7.21 × 7.98 × 1.27 mm
Inner radius and outer radius and height of the small strap	5.97 × 6.73 × 1.27 mm

.

3. Eigenmode and Frequency-Domain Simulation

The simulation results of the designs are presented in this section. CST Microwave Studio was used for simulations.

As can be observed in Figure 2, the electric field in the cavity direction was strictly positive and had negative spacing during the mode simulation phase. When in π-mode, the electric field was distributed so that the phase difference between any two adjacent resonators was 180°. According to our calculations, the resonant frequency of the π-mode was precisely 2.47 GHz. Determining the resonant frequency of the π−1 mode can assist in accurately portraying the mode separation qualities as they were intended. The following formula defines the pattern separation:

$$\gamma =\frac{\mathsf{\Delta }\omega }{{\omega }_{\pi }}=\frac{\left|{\omega }_{\pi }-{\omega }_{\left(\pi -1\right)}\right|}{{\omega }_{\pi }}$$

(1)

The resonant cavity theory states that the period of the electric field phase transition for the π−1 mode in a magnetron with 12 vanes is five, which means there are two neighboring resonators with the same electric field intensity direction and zero phase difference, leading to degeneracy. Calculations showed that 4.92 GHz was the resonant frequency of the π−1 mode. This design paradigm achieved a pattern separation of up to 99%, as defined by the standard. A greater pattern separation reduces the chance of jumping, making it more probable for π-patterns to vibrate.

4. Magnetic Field Voltage (B-V) Operation Curve

When the field and electron flow in a magnetron with a coaxial structure fulfill the required parameters, it is simple to generate an oscillating effect, which can cause a certain mode to vibrate. There are, however, two crucial circumstances. One reason is that if the applied voltage is too high, the electrons do not have time to draw the required arc before they immediately strike the anode, and there is not enough time and a high-frequency field for the electrons to complete the energy exchange. The second reason is that the anode voltage is too low, and the initial velocity of the electron is insufficient to cause it to strike the anode, preventing the production of a steady current. Both of these circumstances are averse to energy exchange. In other words, a magnetron can only operate within a specified voltage line (referred to as the cut-off voltage line) below the clamped region and another voltage line (referred to as the threshold voltage line) above the clamped area. Different modes have distinct threshold voltage lines and working voltage lines. The appropriate terms are provided below.

Cut-Off Voltage:

$$U_J=\frac{e{r}_a{}^2}{8m_e}{\left[1-{\left(\frac{r_c}{r_a}\right)}^2\right]}^2{B}^2$$

(2)

Threshold Voltage:

$$U_{tk}=\frac{{\omega }_k\left(r_a{}^2-r_c{}^2\right)}{2k}B-\frac{m_e{r}_a{}^2}{2e}{\left(\frac{{\omega }_k}{k}\right)}^2$$

(3)

Operating Voltage:

$$U_{ak}=\frac{{\omega }_k\left(r_a{}^2-r_c{}^2\right)}{2k}B-\frac{m_e{r}_a{}^2}{2e}{\left(\frac{{\omega }_k}{k}\right)}^2\left[1-{\left(\frac{r_c}{r_a}\right)}^2\right]$$

(4)

In the equation, e is the charge of the electron; m_e is the mass of the electron; r_a is the radius of the anode; r_c is the radius of the cathode; B is the flux density of the applied magnetic field; and U_tk represents the threshold voltage of the spatial harmonic in the order of k; ω_k represents the angular frequency of oscillating modes in the order of k.

The working voltage line, which lies between the cut-off and the threshold voltage line, has the same slope as the threshold voltage line. At the operating voltage, the outermost electrons of the electron cloud are synchronized with the high-frequency field to create the electron clustering effect, and the spoke-shaped anode can be created.

More precise function curves of working voltage and magnetic field are constructed following the resonant frequency of π-mode and π−1 mode and the particular size of the designed high-efficiency magnetron, as illustrated in Figure 3.

5. PIC Simulation

The efficient computing speed, high computing dependability, and robust data processing capabilities of the CST Particle Studio make it ideal for magnetron research and development.

To represent a point on the working voltage line in π-mode, an anode voltage of 8000 V, a magnetic flux density of 3980 Gs, a simulation duration of 1000 ns, and a DC emission model at the cathode were employed. The perfect outcome was achieved after several hours of simulation. The start-up operation of a high-efficiency magnetron is shown in Figure 4, which highlights several crucial steps.

The production mechanism of the electron spokes is intuitively depicted in Figure 4. As the simulation advanced to 100 and 300 ns, we observed that electrons began to emerge from the cathode and create a cloud of electrons on the cathode’s surface. When the duration was closer to 425 ns, the electrons assumed a configuration resembling a hexagonal star, commensurate with the number of spokes predicted by the π-model. As the electron commenced to exchange energy with the high-frequency field, its shape transformed into a distinct hexagonal star at approximately 450 ns.

The frequency spectrum of the output port was determined using the Fourier technique, resulting in a steady frequency spectrum. As shown in Figure 5, the principal frequency oscillation frequency was 2.466 GHz, and the eigenmode was almost identical to that of the π-mode in the spectrum simulation; consequently, we can conclude that the magnetron operated in the π-mode. Small oscillations at various frequencies competed with the π-pattern. However, the π-pattern eventually dominated the competition, and the device began to operate without issue.

Simultaneously, we discovered that the anode had essentially little anodic current in the first 400 ns, before the electrons impacted the anode vane, and that at approximately 425 ns, the anodic collision current rapidly rose, which is compatible with the formation process of the electron spokes. From 425 ns to the completion of the experiment, the average current was calculated to be 1.08 A.

Figure 6 depicts the high-efficiency magnetron’s output power oscillation curve, which also corresponds to the production of the electron spokes. The oscillation amplitude dramatically rose after 450 ns, then gradually stabilized. The readout oscillation had an amplitude of 125. We can determine the output power of 7812.5 W and the input power of 8640 W using normalization. The magnetron efficiency of 90.42% could be calculated using the input and output power of the particular values.

By comparing the simulation results of various anodic voltages obtained along the π-mode line, it can be demonstrated, as seen in Figure 7, that when the anodic voltage rose from 4200 V to 8000 V, the anode collision current gradually increased from 0.69 A to 1.08 A. The period of self-consistent interaction between electron and high frequency field was lengthened by increasing the anode voltage and magnetic flux density, and the time of stable high frequency oscillation was extended from 70 to 430 ns. As seen in Figure 7, as the anode voltage rose, the work efficiency of the magnetron exhibited a fluctuating upward trend; from 77.47% to 90.42%, the work efficiency improved substantially. It is important to note that when the anode voltage approached 7000 V, there was a decline in work efficiency, but the overall level remained steady at above 85%.

The magnetic flux density changed when an anode voltage of 8000 V was applied. When the magnetic flux density increased from 3950 Gs to 4000 Gs, there was a considerable association between the operating efficiency and magnetic flux density in magnetron π-mode. As seen in Figure 8, the total work efficiency of a magnetron operating in π-mode fluctuated before gradually declining. The highest value of work efficiency measured on the π-mode work line (3980 Gs) was 90.42%. At 3950 Gs, the work efficiency of the magnetron was 83.68%, and the work efficiency of the other points was steady at 85% or higher.

The magnetic flux density of a particular magnetron was 3980 Gs, which modified the magnitude of the anode voltage. As the anode voltage rose from 7940 V to 8080 V, there was a link between the operating efficiency of the magnetron π-mode and the anode voltage. As shown in Figure 9, the magnetron operated in π-mode, and the total work efficiency exhibited a fluctuating rising and gradually decreasing pattern. The highest value of work efficiency measured on the π-mode work line (8000 V) was 90.42%. At the remaining points within this range, productivity remained consistent at or above 85%.

6. Conclusions and Discussion

This research presented a novel 12-vanes 2.45 GHz continuous wave magnetron based on the existing magnetron construction. The anodic resonant system provides an appropriate resonant frequency with 12 resonators, and electrons can exchange energy efficiently in the resonant space. Electron emission from the cathode occurred, followed by a cluster effect, until the construction of a stable hexagonal star-shaped electron spokes, and the interaction were completed. Firstly, on the basis of the developed structure, the eigenmode simulation and mode separation calculation were shown, demonstrating that the structure fulfilled the fundamental criteria of the CW magnetron. According to the results of particle simulation, the output terminal frequency in π-mode (8000 V, 3980 Gs) was 2.46 GHz, the average collision current was 1.08 A, the output power was 7812.5 W, and the efficiency was 90.42%. In this design, the work efficiency of a 12-vanes magnetron was significantly enhanced, and high-efficiency energy production and high energy utilization were achieved.

The anode collision current increased gradually from 0.69 A to 1.08 A as the anode voltage increased from 4200 V to 8000 V, as shown in comparison with the simulation results of various anode voltages along the π-mode line. While the device’s oscillation time increased slightly, its productivity rose from 77.47% to 90.42%.

Calculating the values of the π-mode working line and the surrounding working points yielded some intriguing outcomes. In the π-mode, the highest possible value of work efficiency was 90.42%. When the magnetic flux density reached 3950 Gs, the magnetron’s efficiency decreased to 83.68%, i.e., if the magnetic flux density was adjusted near the π-mode line while the anode voltage was maintained at 8000 V. At the remaining facilities, productivity remained at or above 85%. Maintaining the magnetron’s operating efficiency between 86% and 90% for a given magnetic flux density of 3980 Gs was stable if the anode voltage was varied around the π-mode line. As can be seen, adjusting the magnetron’s magnetic flux density had a more noticeable impact on productivity than adjusting the anode voltage within a given range.

It is important to highlight that the aforementioned results were derived via simulation software in order to obtain the most accurate results possible. The application of the device in the real world might provide a few challenges. If the device is to maintain its high voltage operation, it is essential that the voltage characteristics of the magnetron material be taken into consideration. The increase in anode voltage will make it more difficult for the magnetron to vibrate, which in turn will need more time for effective interaction. On the other hand, the simulation offers the time required for the device to vibrate and work effectively. It is unknown whether the vibration speed is capable of satisfying the actual industrial needs as well as the living requirements of people. Because the existing magnetic circuit is not capable of satisfying the need for a high magnetic flux density, the magnetic circuit must be modified in order to satisfy the requirements that the magnetron has for the magnetic field. This is necessary in order to ensure that the magnetron produces the desired magnetic field. This is because simultaneously raising the magnetron’s flux density creates additional demands on the magnetic circuit. As a direct consequence, the conditions are satisfied. Additionally, the increased anode voltage will lead to an increase in the quantity of heat that is created, which will provide a significant problem for the system that is responsible for cooling the environment. In the case that this heat issue is not resolved, the magnetron could suffer irreparable damage as a result of the blow that is given to it as a consequence. Different cooling methods (air cooling and liquid cooling) will also affect the whole continuous wave magnetron, and researchers must consider various factors comprehensively. Furthermore, the cooling system will have a significant challenge due to the increased heat generated by the increased anode voltage. Researchers who create samples for future experimental testing should also give some thought to the aforementioned difficulties.