Fault-Tolerant Control Strategy for Sub-Modules Open-Circuit Fault of Modular Multilevel Converter
Abstract
:1. Introduction
2. The Principle of Hot-Reserved MMC
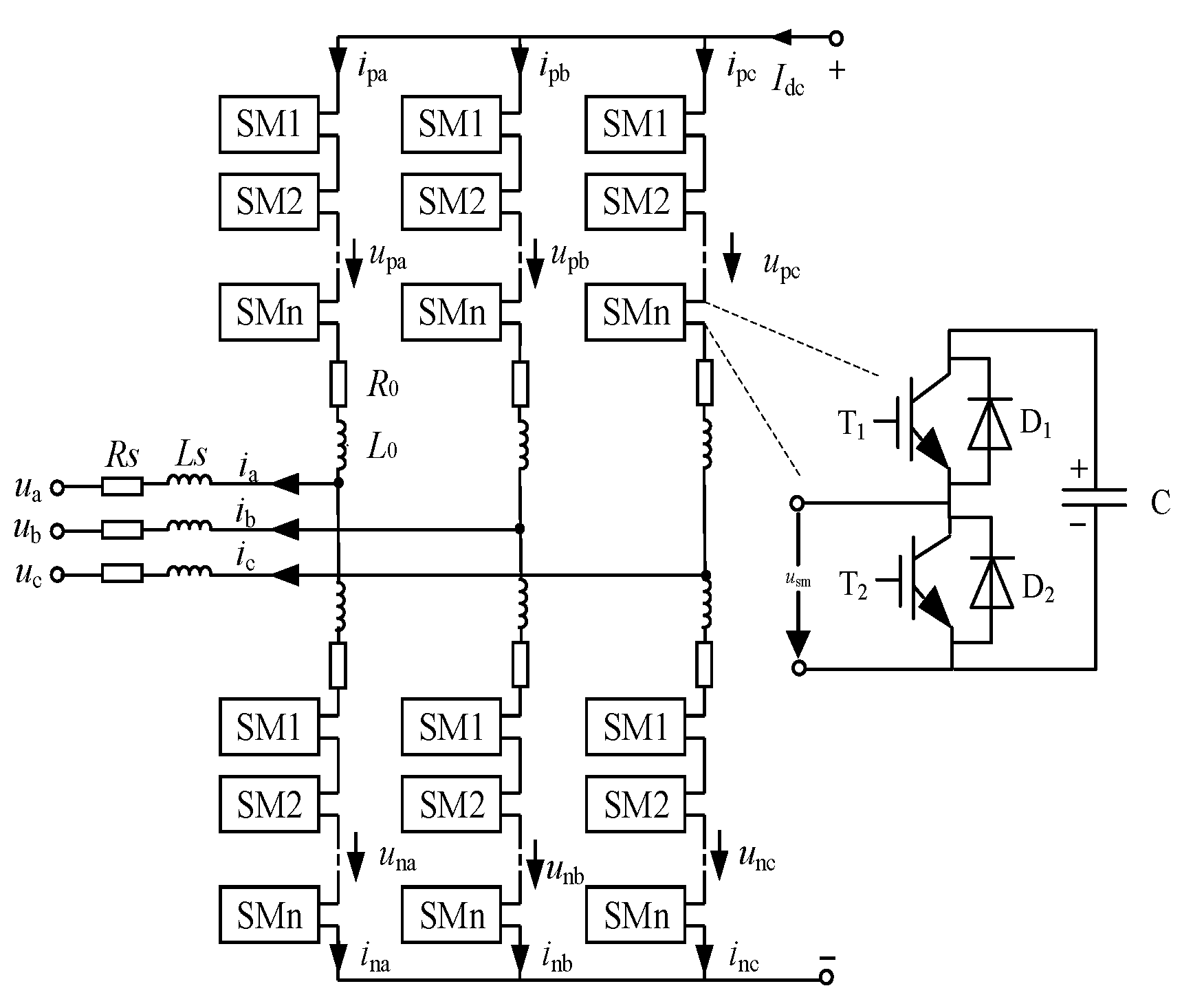
2.1. The Topology of MMC
2.2. Mathematical Model of Hot-Reserved MMC
3. Analysis of Sub-Module IGBT Open Circuit Fault
3.1. T1 Open-Circuit Fault
3.2. T2 Open-Circuit Fault
4. Sub-Module Fault Tolerance Control Strategy
4.1. Diagnosis of Single Sub-Module Open-Circuit Fault
4.2. Removal Strategy of Faulty Sub-Modules
4.3. Fundamental-Frequency Circulating Current Suppression Strategy
5. Simulation Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Perez, M.A.; Ceballos, S.; Konstantinou, G.; Pou, J.; Aguilera, R.P. Modular Multilevel Converters: Recent Achievements and Challenges. IEEE Open J. Ind. Electron. Soc. 2021, 2, 224–239. [Google Scholar] [CrossRef]
- Karami, E.; Gharehpetian, G.; Mohammadpour, H.; Khalilinia, A.; Bali, A. Generalised representation of multi-terminal VSC-HVDC systems for AC-DC power flow studies. IET Energy Syst. Integr. 2020, 2, 50–58. [Google Scholar] [CrossRef]
- Cupertino, A.; Pereira, H.; Seleme, S.; Teodorescu, R. On inherent redundancy of MMC-based STATCOMs in the over-modulation regio. IEEE Trans. Power Del. 2020, 35, 1169–1179. [Google Scholar] [CrossRef]
- Kish, G.J. On the Emerging Class of Non-Isolated Modular Multilevel DC–DC Converters for DC and Hybrid AC–DC Systems. IEEE Trans. Smart Grid 2019, 10, 1762–1771. [Google Scholar] [CrossRef]
- Farias, J.V.M.; Cupertino, A.F.; Pereira, H.A.; Seleme, S.I.; Teodorescu, R. On Converter Fault Tolerance in MMC-HVDC Systems: A Comprehensive Survey. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 7459–7470. [Google Scholar] [CrossRef]
- Faraz, G.; Li, Z.; Zhang, M.; Zhang, Z. Model based Switch Open Circuit Fault Diagnosis Techniques for Modular Multilevel Converters: A Survey. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 18–20 September 2021; pp. 981–986. [Google Scholar]
- Deng, F.; Chen, Y.; Dou, J.; Liu, C.; Chen, Z.; Blaabjerg, F. Isolation Forest Based Submodule Open-Circuit Fault Localization Method for Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2023, 70, 3090–3102. [Google Scholar] [CrossRef]
- Shao, S.; Watson, A.J.; Clare, J.C.; Wheeler, P.W. Robustness Analysis and Experimental Validation of a Fault Detection and Isolation Method for the Modular Multilevel Converter. IEEE Trans. Power Electron. 2016, 31, 3794–3805. [Google Scholar] [CrossRef]
- Yang, S.; Tang, Y.; Wang, P. Seamless Fault-Tolerant Operation of a Modular Multilevel Converter with Switch Open-Circuit Fault Diagnosis in a Distributed Control Architecture. IEEE Trans. Power Electron. 2018, 33, 7058–7070. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Xu, S.; Zhang, Y.; Chen, Z. Fault diagnosis and monitoring of modular multilevel converter with fast response of voltage sensors. IEEE Trans. Ind. Electron. 2020, 67, 5071–5080. [Google Scholar] [CrossRef]
- Zhou, D.; Yang, S.; Tang, Y. Submodule voltage similarity-based open-circuit fault diagnosis for modular multilevel converters. IEEE Trans. Power Electron 2019, 34, 8008–8016. [Google Scholar] [CrossRef]
- Liu, C.; Deng, F.; Heng, Q.; Zhu, R.; Liserre, M.; Wang, Z.; Chen, W. Fault Localization Strategy for Modular Multilevel Converters Under Submodule Lower Switch Open-Circuit Fault. IEEE Trans. Power Electron. 2020, 35, 5190–5204. [Google Scholar] [CrossRef]
- Khaleghi, M.; Iman-Eini, H.; Farhangi, S.; Farzamkia, S. Detection and Localization of Open-Circuit Fault in Modular Multilevel Converter. In Proceedings of the 2020 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 4–6 February 2020; pp. 1–6. [Google Scholar]
- Jin, Y.; Xiao, Q.; Jia, H.; Ji, Y.; Dragicevic, T.; Teodorescu, R.; Blaabjerg, F. A Novel Detection and Localization Approach of Open-Circuit Switch Fault for the Grid-Connected Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2023, 70, 112–124. [Google Scholar] [CrossRef]
- Venkatachari, S.; Mohammadhassani, A.; Mehrizi–Sani, A. Submodule Fault Detection in MMCs using Support Vector Classification. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Espoo, Finland, 18–21 October 2021; pp. 1–5. [Google Scholar]
- An, Y.; Sun, X.; Yuan, Q. IGBT Open Circuit Fault Diagnosis Method for a Modular Multilevel Converter Based on PNN-MD. In Proceedings of the 2020 4th International Conference on HVDC (HVDC), Xi’an, China, 6–9 November 2020; pp. 911–916. [Google Scholar]
- Kiranyaz, S.; Gastli, A.; Ben-Brahim, L.; Al-Emadi, N.; Gabbouj, M. Real-Time Fault Detection and Identification for MMC Using 1-D Convolutional Neural Networks. IEEE Trans. Ind. Electron. 2019, 66, 8760–8771. [Google Scholar] [CrossRef]
- Hao, L.; Zhang, J.; Gu, Y.; Chen, Z.; Xiong, F. Sub-Module Fault Tolerant Optimal Control Strategy of Modular Multilevel Converter Based on Estimation of Bridge Energy. Trans. China Electrotech. Soc. 2018, 33, 3697–3706. [Google Scholar]
- Wu, W.; Wu, X.; Jing, L.; Li, J.; Wang, S.; Wang, X. Energy rebalance control and safe operation region analysis of MMC with sub-module fault. Autom. Electr. Power Syst. 2016, 40, 20–26. [Google Scholar]
- Wang, J.; Tang, Y. A Fault-Tolerant Operation Method for Medium Voltage Modular Multilevel Converters with Phase-Shifted Carrier Modulation. IEEE Trans. Power Electron. 2019, 34, 9459–9470. [Google Scholar] [CrossRef]
- Xiao, Q.; Wang, J.; Jin, Y.; Chen, L.; Jia, H.; Dragicevic, T.; Teodorescu, R. A Novel Operation Scheme for Modular Multilevel Converter with Enhanced Ride-Through Capability of Submodule Faults. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1258–1268. [Google Scholar] [CrossRef]
- Farzamkia, S.; Iman-Eini, H.; Noushak, M.; Hadizadeh, A. Improved Fault-Tolerant Method for Modular Multilevel Converters by Combined DC and Neutral-Shift Strategy. IEEE Trans. Ind. Electron. 2019, 66, 2454–2462. [Google Scholar] [CrossRef]
- Wang, J.; Ma, H.; Bai, Z. A Submodule Fault Ride-Through Strategy for Modular Multilevel Converters with Nearest Level Modulation. IEEE Trans. Power Electron. 2018, 33, 1597–1608. [Google Scholar] [CrossRef]
- Geng, Z.; Han, M.; Khan, Z.W.; Zhang, X. Detection and Localization Strategy for Switch Open-Circuit Fault in Modular Multilevel Converters. IEEE Trans. Power Deliv. 2020, 35, 2630–2640. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, L. Overvoltage Suppression for Modular Multilevel Converter with Switch Open-Circuit Fault. IEEE Trans. Ind. Electron. 2022, 69, 11915–11925. [Google Scholar] [CrossRef]
- Liu, Z.; Xiao, L.; Wang, Q.; Li, J.; Wu, Q. Open-Circuit Fault Diagnosis for MMC Based on Event-Triggered and Capacitor Current State Observation. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 534–538. [Google Scholar] [CrossRef]








| Fault Types | iarm | Switching Signal | usm | Capacitor State (Fault) | Capacitor State (No Fault) | u∑ |
|---|---|---|---|---|---|---|
| T1 fault | >0 | 1 | uc | charge | charge | N × uc |
| 0 | 0 | bypass | bypass | N × uc | ||
| <0 | 1 | 0 | bypass | discharge | (N − 1) × uc | |
| 0 | 0 | bypass | bypass | N × uc | ||
| T2 fault | >0 | 1 | uc | charge | charge | N × uc |
| 0 | uc | charge | bypass | (N + 1) × uc | ||
| <0 | 1 | uc | discharge | discharge | N × uc | |
| 0 | 0 | bypass | bypass | N × uc |
| Item | Symbol | Value |
|---|---|---|
| System rated capacity/VA | S | 200 |
| AC voltage peak/kV | uj (j = a, b, c) | 200 |
| DC voltage/kV | Udc | ±200 |
| Arm inductance/mH | L0 | 10 |
| The number of sub-modules in an arm | N | 20 + 2 |
| Sub-module capacitance/mF | C | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Shu, H.; Liao, M. Fault-Tolerant Control Strategy for Sub-Modules Open-Circuit Fault of Modular Multilevel Converter. Electronics 2023, 12, 1080. https://doi.org/10.3390/electronics12051080
Jiang Y, Shu H, Liao M. Fault-Tolerant Control Strategy for Sub-Modules Open-Circuit Fault of Modular Multilevel Converter. Electronics. 2023; 12(5):1080. https://doi.org/10.3390/electronics12051080
Chicago/Turabian StyleJiang, Yaoxi, Hongchun Shu, and Mengli Liao. 2023. "Fault-Tolerant Control Strategy for Sub-Modules Open-Circuit Fault of Modular Multilevel Converter" Electronics 12, no. 5: 1080. https://doi.org/10.3390/electronics12051080
APA StyleJiang, Y., Shu, H., & Liao, M. (2023). Fault-Tolerant Control Strategy for Sub-Modules Open-Circuit Fault of Modular Multilevel Converter. Electronics, 12(5), 1080. https://doi.org/10.3390/electronics12051080






